Crystal structure, optical characterization, conduction and relaxation mechanisms of a new hybrid compound (C₆H₉N₂)₂[Sb₂Cl₈]

Abstract

Hybrid materials play a crucial role in the construction of flexible electronic devices due to the advantages of both organic and inorganic components. To this end, a new hybrid compound (C₆H₉N₂)₂[Sb₂Cl₈] was successfully fabricated using the slow evaporation solution growth approach at room temperature. In-depth research has been done on the structural, optical, and dielectric characteristics. This compound adopts the triclinic symmetry and crystallizes in the centrosymmetric space group P1̄. The inorganic and organic components respectively form anionic and cationic layers parallel to the ac-plane and alternate along the crystallographic b-axis. The [Sb₂Cl₈]²⁻ dimeric units are bound to the 2-amino-5-picolinium cations [(C₆H₉N₂)]⁺ through N–H⋯Cl hydrogen bonds. Optical absorption measurements showed a semiconductor behavior with a band gap of approximately 3.57 eV. In addition, DFT calculations were performed to investigate the absorption spectrum, wavelength, and HOMO–LUMO gap. The analysis of complex impedance spectra shows that the electrical conductivity of the sample is strongly frequency and temperature dependent, indicating a relaxation phenomenon and semiconductor-type behavior. Dielectric data obtained from complex impedance spectroscopy and ac conductivity with the use of the Maxwell–Wagner equivalent circuit model, and the universal power law have been investigated to explore the basic components of the electronic transport and relaxation process in our material.

---

1. Introduction

To fulfil the growing need for optoelectronic devices including light-emitting diodes, photovoltaics, flat-panel displays, and photodetectors, numerous crystalline and amorphous inorganic materials based on functional metal oxides are being researched for usage as insulators, semiconductors, and conductors.^1,2 Although these inorganic materials have been widely employed in optoelectronic applications, their existing stiffness cannot meet the industry's rising expectations.^3,4 To support the fourth industrial revolution, which, among other things, aims to automate manufacturing and industrial practices using modern smart technology, recent trends in research and development are focused on flexible and/or stretchable electronic materials and allied processes to meet the demand for shape-conformable and wearable devices.^5,6 Electronic skins, wearable smart devices, and flexible and/or rollable screens and batteries are becoming more prevalent⁷. As a result, next-generation electronics are shifting to shape-conformable, low-cost, large-area production using flexible or stretchable materials. Although crystalline metal oxides have better optoelectronic performance due to their large optical bandgaps and strong electrical conductivities, they are susceptible to mechanical stress, limiting their usage in upcoming flexible optoelectronic applications.⁸ Amorphous metal oxides have the potential to address the problem of mechanical deformation; yet, due to their low mechanical stability, these oxides have poor electrical characteristics.⁹ In contrast to inorganic materials inherent brittleness, organic materials have inherent flexibility due to their weak intermolecular connections.¹⁰ Inorganic materials have higher operational/environmental stability and electrical performance under demanding conditions, whereas flexible organic materials have lower stability and electrical performance. As a result, a hybrid structure composed of organic and inorganic components may be a promising material.^11,12 According to several research studies, the creation of inorganic-organic hybrid systems exhibits a variety of favourable features for optoelectronic applications as a result of the benefits of both organic and inorganic components.^13–15 In comparison to the organic or inorganic components alone, these hybrids have excellent structural, optical, and electrical characteristics.^16–19 Here, for the first time, we synthesized (C₆H₉N₂)₂[Sb₂Cl₈] single crystals via slow solvent evaporation. We performed a series of characterizations using single-crystal X-ray diffraction, Scanning electronic microscopy (SEM), ultraviolet-visible (UV-vis) spectroscopy, and complex impedance spectroscopy. The crystal structure, optical properties, and conduction mechanisms of (C₆H₉N₂)₂[Sb₂Cl₈] compound are also discussed.

2. Experimental

2.1. Synthesis of (C₆H₉N₂)₂[Sb₂Cl₈]

To synthesize crystals of (C₆H₉N₂)₂[Sb₂Cl₈], 1 mmol of 2-amino-5-picoline C₆H₈N₂ (0.108 g), 1 mmol of antimony(III) chloride SbCl₃ (0.228 g) and 1 mmol of hydrochloric acid HCl (0.036 g) were dissolved in a small amount of distilled water. The resulting solution was left at room temperature (about 28 °C), and as the solvent gradually evaporated, well-formed, colourless crystals of (C₆H₉N₂)₂[Sb₂Cl₈] were produced. The obtained product was filtered off and washed with a minimal quantity of distilled water. The chemical reaction can be written as the following equation: 2C₆H₈N₂ + 2SbCl₃ + 2HCl → (C₆H₉N₂)₂[Sb₂Cl₈].

The purity of the prepared crystals was verified through chemical analysis of the C, H, N and Cl elements. Anal. calc. for C₁₂H₁₈Cl₈Sb₂N₄ (M = 745.40 g mol⁻¹): N, 7.51; C, 19.31; H, 2.41; Cl, 38.10. Found: N, 7.48; C, 19.25; H, 2.37; Cl, 37.96. The yield of the synthesis reaction was 65%; the obtained mass of the sample was 0.24 g after the first recovery of the crystals.

2.2. Single crystal X-ray data collection

A high-quality crystal was chosen using a polarising optical microscope and placed on Micro Mount needles (MiTiGen) for single-crystal X-ray diffraction studies. X-ray intensity measurements were acquired at 296 K using an Iμs microfocus source (Mo-Ka radiation with λ = 0.71073 Å) using a Bruker APEX II Quazar diffractometer (4 circle Kappa goniometer, CCD detector). The crystal structure was solved in the triclinic symmetry with the centrosymmetric space group P1̄ using the ShelxT-2018 program²⁰ integrated into the WINGX interface.²¹ The positions of the H atoms are geometrically generated via the HFIX instruction included in SHELXL-2014 (ref. 22) and allowed to ride on their parent atoms with N–H = 0.86 Å and C–H = 0.93 or 0.96 Å. The nature of the atoms was distinguished from bond distance concerns. The experimental information for the structural determination is shown in Table 1. Selected bond distances and angles as well as hydrogen bonds are depicted in Tables S1 and S2 (ESI†) respectively. The drawing was created using DIAMOND 3.2 program.²³ Crystallographic data for the structures have been deposited at the Cambridge Crystallographic Data Center under the following number: CCDC 2225545 for (C₆H₉N₂)₂[Sb₂Cl₈].

Table 1 Crystallographic data and structure refinements of (C₆H₉N₂)₂[Sb₂Cl₈]

Formula	(C6H9N2)2[Sb2Cl8]
Temperature	296 K
Formula weight (g mol^−1)	745.40
Crystal system	Triclinic
Space group	P1̄
a	7.9767(7) Å
b	9.0843(8) Å
c	9.3456(8) Å
α	86.352(6)°
β	69.069(5)°
γ	74.829(5)°
Z	1
V	610.14(10) Å^3
μ (Mo Kα)	3.096 mm^−1
Index ranges	−10 < h < 10, −11 < k < 11, −12 < l < 12
Reflections collected	21 842
Independent reflections	2796
Reflections with I > 2σ(I)	2417
Rint	0.051
Absorption correction	Multi-scan
Refined parameters	119
R[F^2 > 2σ(F^2)]	0.0256
wR(F^2)	0.0451
Goodness of fit	1.038
Δρmin/Δρmax (Å^−3)	−0.38/0.37

---

2.3. Scanning electronic microscopy (SEM)

Investigation of the microstructure and chemical composition of the title compound was approved by scanning electron microscopy (SEM) and energy dispersive spectroscopy (EDS) (MIRA3 FEG microscope), coupled to an Oxford Instrument analyzer with several acceleration voltages.

2.4. Absorption measurements

UV-vis powder spectroscopy was performed at room temperature using a Shimadzu UV-3101PC scanning spectrophotometer within a wavelength range of 200 to 800 nm. The equipment can measure absorbance and reflection using spherical integration and xenon light.

2.5. Electrical impedance spectroscopy

A Solartron impedance analyzer to examine electrical transmission properties at frequencies ranging from 10² to 10⁷ Hz, temperatures ranging from 323 to 383 K, and a voltage of 0.5 V. The tests were performed on a pellet with a typical diameter of 8 mm and a thickness of 1.1 mm.

3. Results and discussion

3.1. SEM/EDS analysis

Before any crystal structure determination, micrographs were collected on several crystals to check the homogeneity and surface morphology of the crystal. The obtained micrographs are represented in Fig. 1(a–c), with different magnifications. These SEM images confirm the crystalline nature of the (C₆H₉N₂)₂[Sb₂Cl₈] compound, and the flat surfaces of the crystals indicate their good quality.^24,25 An energy-dispersive X-ray Spectrometer (EDS) coupled to the microscope, which was investigated in different spots as well as for different crystals, verified the presence of Sb, Cl, C, and N elements and their spatial distributions within the crystals Fig. S1 (ESI†).

Fig. 1 SEM images of (C₆H₉N₂)₂[Sb₂Cl₈] crystals grown by slow evaporation method at room temperature.

3.2. Crystal structure description

As per the results of the single crystal X-ray diffraction analysis of ambient temperature, (C₆H₉N₂)₂[Sb₂Cl₈] compound crystallizes in the triclinic system, centrosymmetric space group P1̄, with the unit cell parameters given in Table 1.

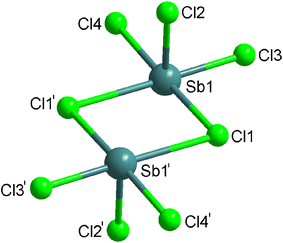
The asymmetric unit of (C₆H₉N₂)₂[Sb₂Cl₈], displayed in Fig. 2, contains only one Sb(III) antimony cation, surrounded by four Cl⁻ halides, and one protonated amine (C₆H₉N₂)⁺. It should be noted that all atoms of the asymmetric unit occupy a general position (Wyckoff site 2i). The coordination sphere around Sb(III) cation is completed by a fifth chloride ion, which corresponds to the symmetrical of Cl1 generated by the inversion center to form a square-based pyramid. In reality the coordination sphere around the Sb(III) ion could be described as octahedral, where one apex is occupied by the lone pair (E) carried by Sb(III) ion (5s²); the final geometry is therefore square-based pyramidal and the lone pair is stereo chemically active (Fig. S2 (ESI†)). The Sb(III) central ion is located some 0.1080(2) Å below the least-squares plane passing through Cl1/Cl3/Cl4/Cl1^I atoms, that form the pyramidal basal plane. The shortest Sb–Cl distance (Sb–Cl2) of 2.3677(8) Å, is trans to the lone pair, while the remaining four Sb–Cl bond lengths range from 2.4097(8) to 3.0196(9) Å, much shorter than the sum of van der Waals radii of Sb and Cl (4.0 Å according to Pauling).²⁶ The selected bond lengths and angles are indicated in Table S1.† These lengths are within the overall range of observation of the distances between halides and antimony according to the results of the literature.^27–31 Each square-based pyramid shares two corners (Cl1 and Cl1^I) with the adjacent square-based pyramid to form the [Sb₂O₈]²⁻ dimeric unit (Fig. 3). Each dimeric unit lies in special position on inversion center and the shortest Sb–Sb distance is equal to 4.2258(4) Å. The [Sb₂Cl₈]²⁻ dimeric unit are stacked in the structure in a manner that they form anionic inorganic stacks parallel to ac-plane at y = 0 and y = 1 (Fig. 4).

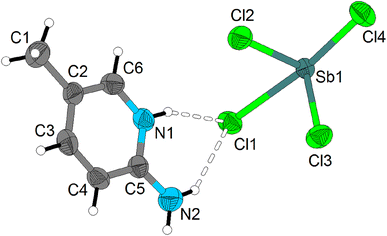Fig. 2 The asymmetric unit of (C₆H₉N₂)₂[Sb₂Cl₈]. Displacement ellipsoids are drawn at the 50% probability level. Hydrogen bonds are represented by dashed lines.

Fig. 3 The [Sb₂Cl₈]²⁻ dimeric unit in (C₆H₉N₂)₂[Sb₂Cl₈] (symmetry code: ^I 1 − x, −y, −z).

Fig. 4 Projection of the structure of (C₆H₉N₂)₂[Sb₂Cl₈] along the crystallographic c-axis.

The negative charges of the [Sb₂Cl₈]²⁻ dimeric units are compensated by the protonated amines (C₆H₉N₂)⁺. As the anionic part, these protonated amines are stacked one over the other along the crystallographic a-axis in such a way that they form an organic cationic pseudo-layer parallel to the ac-plane at y = 1/2 (Fig. S3 (ESI†)). Consequently, the crystal structure can be described as an alternation of organic and inorganic layers along the crystallographic b-axis (Fig. S4 (ESI†)). The main distances and angles of the protonated amines, given in Table S1,† are in good agreement with those found in other compounds containing the same organic cation.³² Contrary to the dimeric units which are isolated from each other, the protonated amines interact with each other by π–π interactions. These interactions are made following a parallel-displaced configuration of amine aromatic rings.^33,34 Indeed, the shorter distance between two parallel planes of two aromatic rings of adjacent amine is equal to 3.6473(2) Å (Fig. S4 (ESI†)).

The cohesion and the stability of the structure are ensured through N–H⋯Cl hydrogen bond established between the protonated amines and the [Sb₂Cl₈]²⁻ dimeric unit. Indeed, each protonated amine engages its hydrogen atoms of linked to nitrogen atoms in N–H⋯Cl hydrogen with two [Sb₂Cl₈]²⁻ dimeric unit (Fig. S4 (ESI†)). Within the N–H⋯Cl intermolecular interactions the N⋯Cl distance range from 3.246(2) to 3.487(3) Å while the N–H⋯Cl angles are comprised between 146.9 and 162.6° (Table S2†).

3.3. Optical absorption of (C₆H₉N₂)₂[Sb₂Cl₈]

UV-visible/NIR spectroscopy³⁵ is a simple and easy way to examine absorption behavior, extract various optical properties, and describe the strip structure of materials. Due to interactions between the radiation and the sample, some of the incident photons will be absorbed, reflected, or transmitted through the sample. The absorption of radiation in the UV-visible range induces electronic transitions and consequent disturbances in the electronic structure of atoms, ions, or molecules.

3.3.1. Electronic properties. To explain the experimental results and to get a deeper understanding of the electronic absorption spectrum of the (C₆H₉N₂)₂[Sb₂Cl₈] compound, TD-DFT calculations³⁶ have been performed using the Gaussian 09 package³⁷ within the IEFPCM solvation model in HCl solvent. The hybrid functional B3LYP³⁸ was employed in cooperation with D3 dispersion correction^39,40 and LanL2DZ as a basis set. Firstly, the geometrical structure of (C₆H₉N₂)₂[Sb₂Cl₈] was optimized with the DFT method at the same level of theory. Fig. S5 (ESI†) depicts the superposition of the simulated absorption spectrum and the experimental one. The electronic transitions are summarized in Table S3 (ESI†). Clearly, the predicted absorption spectrum is centred at 304 nm (f = 0.0227 a.u), which is in the same range as the experimental one. The molecular frontier orbitals HOMO and LUMO, are defined as the highest occupied molecular orbital and the lowest unoccupied molecular orbital, respectively. The HOMO orbital is viewed as an electron donor, while the LUMO is an electron acceptor. The frontier orbital gap, expressed as the difference between the HOMO and LUMO levels, evaluates the chemical reactivity and kinetic stability of a given molecule. Therefore, a molecule with a small frontier orbital gap is more polarizable, is generally associated with a high chemical reactivity, low kinetic stability, and is termed as soft molecule.^41–43 The HOMO and LUMO orbital surfaces are plotted in Fig. 5. Obviously, the HOMO orbitals are localized entirely on the organic part, while the LUMO ones are localized mainly on the inorganic part. The HOMO–LUMO energy gap is found to be 4.04 eV. As shown in Table S3 (ESI†), the HOMO → LUMO transition is found at 356 nm. The intense band may be assigned to HOMO−1 → LUMO+1 (87%) transition. This value explicates the eventual charge transfer interactions that take place within the molecules. By exploiting the HOMO and LUMO energy values, several global chemical reactivity descriptors have been calculated, such as, chemical potential (μ), electronegativity (χ), global hardness (η), global softness (ζ), and global electrophilicity index (ω) values to improve the understanding the reactivity of the investigated compound. These quantities are a good indication to highlight the connexion between chemical reactivity and strength of structure. These parameters are defined as the following:

η = 1/2(E_LUMO − E_HOMO), μ = 1/2(E_LUMO + E_HOMO), s = 1/2η, χ = −1/2(E_LUMO + E_HOMO), and ω = μ²/2η (1)

Fig. 5 The molecular frontier orbitals HOMO and LUMO computed with TD/B3LYP-D3/LanL2DZ method in HCl solvent.

As given in Table S4 (ESI†), the chemical hardness value (η) was found to be 2.02 eV, indicating that charge transfer occurs within the molecule. The electrophilic behavior of the molecule is established by the global electrophilic index (ω) which is equal to 11 eV. Additionally, chemical stability of the investigated molecule is determined by the chemical potential value (μ) which is −4.69 eV.

3.3.2. Optical band gap by Kubelka–Munk function. The optical band gap, which corresponds to electron excitation from the valence band to the conduction band, is important in several scientific disciplines, including photovoltaics, solar cells, lasers, photoluminescence, or diodes⁴⁴ According to R. E. Marotti⁴⁵ and R. Henriquez,⁴⁶ the wavelengths at which the optical gap occurs are where the shoulders in the R-reflecting spectrum appear. The shoulders may be highlighted by variation of the first derivative (1/R)(dR/dλ) according to the wavelength (Fig. S6 (ESI†)). The presence of a strong peak centred at 421 nm makes it possible to estimate the energy of the optical gap of (C₆H₉N₂)₂[Sb₂Cl₈] sample as a function of the relation between E_g and λ.⁴⁷

The resulting value of the optical band gap is E_g = 3.57 eV. This estimation allows us to determine the type of transition and then to deduce more precisely the value of the band gap by means of the Tauc formalism

[F_KM(R) × hν] = A₀(hν − E_g)ⁿ (3)

where F_KM (R) = (1 − R)²/2R is Kubelka–Munk function, A₀ is a material dependent constant, h is the Planck's constant and ν is the frequency of the light. The value of n varies in relation to the nature of the transition. It may be 1/2 when the transition is direct and 2 if the transition is indirect. In an authorized direct transition, the electron is transferred vertically from the top of the valence band to the bottom of the conduction band, with no change in momentum (wave vector). On the other hand, a transition from the valence to the conduction band should always be accompanied with a phonon in materials with an indirect band gap, from the bottom of the conduction band does not match the zero-crystal momentum in these materials. As the graph [F(R)hν]² is shows as a function of photonic energy hν (Fig. S7 (ESI†)), the band gap has been extracted from the extrapolation of the linear path to the x-axis at [F(R)hν]² = 0. The energy associated with the direct gap is 3.57 eV, which close to the result obtained with the Marotti method. This value is comparable to those found for other organic–inorganic semiconductors A₂Sb₂Cl₈; (Et₃BzN)₂Sb₂Cl₈,⁴⁸ (Et₄N)₂Sb₂Cl₈,⁴⁹ (Et₄N)₂Sb₂Cl₈.⁵⁰

So, the absorbance spectra of (C₆H₉N₂)₂[Sb₂Cl₈] and its semiconductor range of E_g indicate that it can be used in UV range applications such as ultraviolet detectors and for potential optoelectronics applications.⁵¹

3.4. Complex impedance analysis

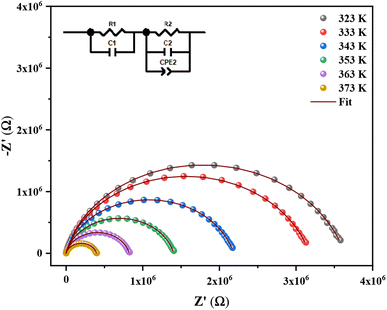
Fig. 6 displays the Nyquist plot of the (C₆H₉N₂)₂[Sb₂Cl₈] complex impedance spectrum as a function of temperature. Plots are characterized by the presence of a single depressed semicircle suggesting the intersection of two successive semicircles corresponding to the grain and grain boundary contributions. The electrode-sample interface does not contribute at all. Additionally, Fig. 6 shows that the semicircle width reduces as the temperature rises, indicating improvement of the dc conductivity. We employed the Maxwell–Wagner equivalent circuit model,⁵² which consists of a parallel arrangement of several resistors (R) and capacitors (C), to determine the contribution of the grain and the grain boundary different from the single depressed semicircle (inset Fig. 6). It consists of a parallel combination of a resistor and a capacitor (grain response) connected in series with another R–C–Q equivalent circuit (representing the usual grain boundary response), where the constant phase element (CPE) represents the effects of dipolar relaxation. With the equivalent circuitry, the impedance data for (C₆H₉N₂)₂[Sb₂Cl₈] were adjusted as shown in Fig. 6 (solid line). As it can be observed, the theoretical line calculated from the estimated values is well correlated with the experimental data. The extracted parameters for the circuit components are summarized in Table 2. It is clear that the grain and grain boundary resistances decrease with increasing temperature and that of the grain boundary higher than that of the grain. Generally, the disorder and instability of the atomic arrangement at the grain boundaries cause the grain to grow at high temperatures.⁵³ As temperature rises, the fraction of atoms at the grain border steadily increases while that in the grain interior gradually decreases. The degree of atomic disorder also increases as temperature rises, and at very high temperatures, the grain boundary may melt. As a result, as the temperature rises, the resistance of the grain and grain boundary decreases. The capacities of the grain and the grain boundary increase slightly with the temperature. The grain boundary capacity C_gb (C_gb = ε_gb × A/d where ε_gb is the intrinsically dielectric constant and A and d are the surface and width of the barrier layer, respectively) depends on the width of the barrier layer which decreases with the increase in temperature due to the increase of free ions at the frontiers. The layer width is inversely proportional to the ratio of trapped ion density to free ion density participating in the hopping process at grain boundaries. Trapped ion density decreases as temperature rises, indicating depopulation, while free ion density rises as temperature rises and the layer width decreases.⁵⁴

Fig. 6 Nyquist plot for C₆N₉N₂SbCl₄ compound at different temperatures.

Table 2 Equivalent circuit parameters obtained at some temperatures

T (K)	R1 (Ω)	C1 (×10^−10 F)	R2 (Ω)	C2 (×10^−11 F)	Q2 (×10^−10 F)	α2
323	10 951	4.66	3.63 × 10^6	2.78	3.39	0.774
333	7782	5.30	3.17 × 10^6	2.59	3.52	0.783
343	6016	6.14	2.18 × 10^6	2.39	3.38	0.796
353	5993	6.21	1.40 × 10^6	2.17	2.99	0.814
363	6296	5.68	816 700	1.95	2.65	0.831
373	4978	6.06	389 810	1.69	2.73	0.839

---

It is generally recognized that even with a very modest difference, the depiction of Z′ vs. Z′′/ω is a useful technique for differentiating the dielectric responses from contacts, grain boundaries, and bulk grains. Z′ vs. Z′′/ω for a temperature of 383 K is shown in Fig. 7. With the help of this illustration, two distinct linear dielectric responses are visible corresponding to the contribution of the bulk and grain boundaries, which are represented by the segments marked with the letters A and B and the borderline frequency f = 1258 Hz, respectively.^55,56

Fig. 7 The relative representation of Z′ vs. Z′′/ω at 383 K.

The theoretical formula created with an analogous circuit was used to derive the actual data for the real (Z′) and imaginary (Z′′) part of the whole impedance (eqn (3) and (4)). Fig. 8 and 9 illustrate the frequency dependency of the real and imaginary components of impedances in the selected temperature range (323–383 K). The actual (scatter) and theoretical (line) curves of the real and imaginary impedance exhibit excellent agreement at each temperature. These results demonstrate the adequacy of the proposed equivalent circuit for the chosen range temperature (323–383 K).

Fig. 8 Variation of the real part (Z′) of the impedance as a function of angular frequency at several temperatures.

Fig. 9 Variation of the imaginary part (Z′′) of the impedance as a function of angular frequency at several temperatures.

The real part of the impedance (Fig. 8) showed an inverse frequency dependency for all the temperatures until 100 Hz and then became extremely low and merged. This result could be connected to the release of space charge as a result of the material's decreased barrier characteristics with temperature rise, and it might also play a role in the material's increased conductivity at high frequencies. The presence of space charge polarisation can be used to explain the merging of the value of Z′ at all temperatures at higher frequencies.⁵⁷ Moreover, Z′ dropped as the temperature rose, indicating negative temperature coefficient of resistance (NTCR) behavior.⁵⁸

The Z′ behavior for our sample at lower and higher frequencies agrees well with the previous findings for other hybrid systems in the literature.^59,60

In Fig. 9, each curve's highest value, Z_max′′, is seen to decrease with rising temperature, showing the presence of a single relaxation peak with a distinctive frequency (ω_max). The relative representation of Z′ with regard to Z′′/ω (presented in Fig. 7) and a distinct arc at each temperature in the impedance planes (Fig. 6) were two factors that were used to validate the only dielectric relaxation. It is obvious that the relaxation peak shifts to the high-frequency region, which may result in an extension of the relaxation time and a reduction in the bulk material's resistance.⁶¹ Hence, this outcome supports the Arrhenius behavior in the investigated compound.⁶² In addition, when the frequency increases, we see a merging in the Z′′ plots, which is indicative of a build-up of space charges in the material because it does not need more time to relax due to the space charge polarization reducing with the frequency rising.⁶³

3.5. Alternating current (ac) conductivity

To better understand both the long-range (ω → 0) as well as the short-range electronic transport in (C₆H₉N₂)₂[Sb₂Cl₈], we have examined the alternating current conductivity spectra (σ_ac). When the frequency is low (ω → 0), the electron hops from one site to another throughout the whole lattice, producing long-range dynamics, whereas short-range dynamics are produced when the hopping motion of the electron is restricted to isolated sites at high frequencies.⁶⁴ Electron hopping may be thought of as the mobility of electron in an endless lattice of identical potential wells at low frequencies, whereas at high frequencies, the hopping of electron is constrained in a double well with infinite potential barriers via forward-backward hopping.⁶⁵

Fig. 10 displays the ac conductivity spectra of (C₆H₉N₂)₂[Sb₂Cl₈] compound for various temperatures. Due to the long-range mobility of electrons, the ac conductivity spectra for all temperatures show discrete plateaus that correlate to the dc conductivity (σ_dc), referring to σ_ac(ω → 0) = σ_dc. In Fig. 10, it can be shown that when the temperature rises, the frequency independent zone moves along the frequency spectrum towards higher frequencies. This is related to the reduction of relaxation times with increasing temperature. The frequency ω_H marks the transition in the conductivity isotherm from the frequency-independent dc region to the dispersive region. The Jonscher power law, eqn (6), has proved a good representation of the frequency dependence of the ac conductivity in our case.

Fig. 10 Frequency dependence of ac conductivity at several temperatures.

To analyze precisely the section of dispersion in conductivity, the value of the frequency factor α(ω) was calculated using eqn (8).

Fig. 11 shows the dependence of the frequency coefficient α(ω) for the hybrid (C₆H₉N₂)₂[Sb₂Cl₈]. The values of α(ω) are almost zero at all temperatures in the vicinity of the lowest measurement frequencies, which corresponds to a nearly constant value of conductivity (dc). With an increase in frequency, an increase in the value of α(ω) is observed until it reaches the maximum. In light of the reported quantum phenomenon of electron tunnelling, the similarity of conductivity and frequency factor, as indicated in ref. 66 and 67, suggests that the observed correlations are compatible with the hopping mechanism of charge transfer. The occurrence of a single maximum indicates the existence of a single relaxation time.⁶⁸ Fig. 12 depicts the Arrhenius curves for the hopping mechanism of charge transfer based on the following relation:

where E_a, σ₀ and k_B represent the activation energy, pre-exponential factor, and Boltzmann constant, respectively. The value of activation energy obtained from the linear fit is 0.63 eV, which is very close to for other organic–inorganic semiconductors, such as: [C₅H₆N₂Cl]₂[Sb₂Cl₈].⁶⁹

Fig. 11 Frequency dependence of frequency factor s(ω) for selected measurement temperatures.

Fig. 12 Reciprocal temperature dependence of σ_dc obtained from the complex impedance plot and the ac conductivity spectra.

Using the equation σ_dc = t/RA, we estimated the dc conductivity of our compound for different temperatures from the complex impedance plots, where R is the total resistance (R = R_g + R_gb), and t and A are the thickness and area of the sample, respectively. The dc conductivity obtained from the complex impedance plots at different temperatures is also displayed in Fig. 12. It should be noticed that the value of dc obtained from power law fits of ac conductivity corresponds exactly to that obtained from complex impedance plots.

4. Conclusion

In conclusion, the slow evaporation solution growth approach at room temperature was effective in producing the (C₆H₉N₂)₂[Sb₂Cl₈] compound. structural, optical, and comprehensive electric characteristics were examined. The TD/B3LYP-D3/lanl2dz level of theory has been used to record and simulate the absorption spectra. Theoretical absorption and actual spectra thus exhibit high agreement. Via UV-vis spectral analysis, the title compound's optical properties may be explored, and a band gap energy of 3.57 eV can be found. This value proves that the title compound is suitable for optoelectronics applications. It has been studied how temperature affects the electronic transport and relaxation processes in (C₆H₉N₂)₂[Sb₂Cl₈]. The Maxwell–Wagner equivalent circuit model and universal power law model were used to investigate the frequency dependence of the electric data within the frameworks of complex impedance spectroscopy and ac conductivity. Moreover, the elastic properties of (C₆H₉N₂)₂[Sb₂Cl₈] are worth exploring to complete this work.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

1. X. Yu, T. J. Marks and A. Facchetti, Metal oxides for optoelectronic applications, Nat. Mater., 2016, 15(4), 383–396,  DOI:10.1038/nmat4599.
2. J. Sheng, K. L. Han, T. Hong, W. H. Choi and J. S. Park, Review of recent progresses on flexible oxide semiconductor thin film transistors based on atomic layer deposition processes, J. Semicond., 2018, 39(1), 011008,  DOI:10.1088/1674-4926/39/1/011008.
3. H. B. Lee, W. Y. Jin, M. M. Ovhal, N. Kumar and J. W. Kang, Flexible transparent conducting electrodes based on metal meshes for organic optoelectronic device applications: a review, J. Mater. Chem. C, 2019, 7(5), 1087–1110,  10.1039/c8tc04423f.
4. X. Wang, D. Peng, B. Huang, C. Pan and Z. L. Wang, Piezophotonic effect based on mechanoluminescent materials for advanced flexible optoelectronic applications, Nano Energy, 2019, 55, 389–400,  DOI:10.1016/j.nanoen.2018.11.014.
5. Z. Ma, S. Li, H. Wang, W. Cheng, Y. Li and L. Pan, et al., Advanced electronic skin devices for healthcare applications, J. Mater. Chem. B, 2019, 7(2), 173–197,  10.1039/c8tb02862a.
6. S. Zhang, S. Li, Z. Xia and K. Cai, A review of electronic skin: soft electronics and sensors for human health, J. Mater. Chem. B, 2020, 8(5), 852–862,  10.1039/c9tb02531f.
7. Z. Ren, J. Yang, D. Qi, P. Sonar, L. Liu and Z. Lou, et al., Flexible Sensors Based on Organic–Inorganic Hybrid Materials, Adv. Mater. Technol., 2021, 6(4), 1–19,  DOI:10.1002/admt.202000889.
8. M. Annadhasan, A. R. Agrawal, S. Bhunia, V. V. Pradeep, S. S. Zade and C. M. Reddy, et al., Mechanophotonics: Flexible Single-Crystal Organic Waveguides and Circuits, Angew. Chem., Int. Ed., 2020, 59(33), 13852–13858,  DOI:10.1002/anie.202003820.
9. B. Yaglioglu, Y. J. Huang, H. Y. Yeom and D. C. Paine, A study of amorphous and crystalline phases in In2O3–10 wt.% ZnO thin films deposited by DC magnetron sputtering, Thin Solid Films, 2006, 496(1), 89–94,  DOI:10.1016/j.tsf.2005.08.255.
10. S. Saha, M. K. Mishra, C. M. Reddy and G. R. Desiraju, From Molecules to Interactions to Crystal Engineering: Mechanical Properties of Organic Solids, Acc. Chem. Res., 2018, 51(11), 2957–2967,  DOI:10.1021/acs.accounts.8b00425.
11. X. Zhang, C. Sun, Y. Zhang, H. Wu, C. Ji and Y. Chuai, et al., Bright Perovskite Nanocrystal Films for Efficient Light-Emitting Devices, J. Phys. Chem. Lett., 2016, 7(22), 4602–4610,  DOI:10.1021/acs.jpclett.6b02073.
12. Y. Q. Zhao, Q. R. Ma, B. Liu, Z. L. Yu, J. Yang and M. Q. Cai, Layer-dependent transport and optoelectronic property in two-dimensional perovskite: (PEA)₂PbI₄, Nanoscale, 2018, 10(18), 8677–8688,  10.1039/c8nr00997j.
13. D. O. Demchenko, N. Izyumskaya, M. Feneberg, V. Avrutin, Ü. Özgür, R. Goldhahn and H. Morkoç, Optical properties of the organic-inorganic hybrid perovskite CH₃NH₃PbI₃: Theory and experiment, Phys. Rev. B, 2016, 94, 075206,  DOI:10.1103/PhysRevB.94.075206.
14. Y. F. Ding, Q. Q. Zhao, Z. L. Yu, Y. Q. Zhao, B. Liu and P. B. He, et al., Strong thickness-dependent quantum confinement in all-inorganic perovskite Cs2PbI4with a Ruddlesden–Popper structure, J. Mater. Chem. C, 2019, 7(24), 7433–7441,  10.1039/c9tc02267h.
15. X. Z. Deng, Q. Q. Zhao, Y. Q. Zhao and M. Q. Cai, Theoretical study on photoelectric properties of lead-free mixed inorganic perovskite RbGe_1−xSn_xI₃, Curr. Appl. Phys., 2019, 19(3), 279–284,  DOI:10.1016/j.cap.2018.12.007.
16. S. Sidaoui, A. Ghoudi, A. Oueslati, M. Raduca, M. Badea and M. Andruh, et al., Crystal structure, thermal behavior and electric properties of a new semiconductor cobalt-based hybrid material, J. Mol. Struct., 2023, 1294, 136394,  DOI:10.1016/j.molstruc.2023.136394.
17. M. Abid Derbel, S. Nasr, H. Naïli and W. Rekik, Thermal behaviour and optical properties of a new dimeric 1D mixed halide hybrid material [CuBrCl(C₂H₈N₂)], Inorg. Chem. Commun., 2022, 142, 109654,  DOI:10.1016/j.inoche.2022.109654.
18. B. N. Ameni, O. Abderrazek, R. Thierry and R. Walid, A new supramolecular semiconductor cobalt organometallic complex: Structural study, optical and electrical properties, J. Mol. Struct., 2022, 1266, 133518,  DOI:10.1016/j.molstruc.2022.133518.
19. M. Gassara, R. Msalmi, X. Liu, F. Hassen, A. Moliterni and N. Ben Hamadi, et al., A promising 1D Cd-based hybrid perovskite-type for white-light emission with high-color-rendering index, RSC Adv., 2022, 12(52), 33516–33524,  10.1039/d2ra04676h.
20. G. M. Sheldrick, SHELXT – Integrated space-group and crystal-structure determination, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71(1), 3–8,  DOI:10.1107/s2053273314026370.
21. L. J. Farrugia, WinGXandORTEP for Windows: an update, J. Appl. Crystallogr., 2012, 45(4), 849–854,  DOI:10.1107/s0021889812029111.
22. G. M. Sheldrick, Crystal structure refinement withSHELXL, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71(1), 3–8,  DOI:10.1107/s2053229614024218.
23. M. Riedel, The Impact of Ozone on the Surface Conductivity of Single Crystal Diamond, Diamond Relat. Mater., 2004, 13, 746–750,  DOI:10.1016/s0925-9635(03)00525-9.
24. M. H. Mrad, I. Feddaoui, M. S. M. Abdelbaky, S. García-Granda and C. Ben Nasr, Elaboration, crystal structure, characterization and DFT calculation of a new Hg(II) inorganic-organic hybrid salt [C₆H₁₆N₂O]HgCl₄, J. Solid State Chem., 2020, 286, 121280,  DOI:10.1016/j.jssc.2020.121280.
25. P. Szklarz, M. Owczarek, G. Bator, T. Lis, K. Gatner and R. Jakubas, Crystal structure, properties and phase transitions of morpholinium tetrafluoroborate [C₄H₁₀NO][BF₄], J. Mol. Struct., 2009, 929(1–3), 48–57,  DOI:10.1016/j.molstruc.2009.04.014.
26. W. M. Malisoff, The Nature of the Chemical Bond. By Linus Pauling. Cornell University Press, Ithaca, N. Y. 450 pages, $4.50, Philos. Sci., 1941, 8(1), 133,  DOI:10.1086/286682.
27. M. Bujak and J. Zaleski, Structure of chloroantimonates(III) with an imidazolium cation: (C₃H₅N₂)[SbCl₄] and (C₃H₅N₂)₂[SbCl₅], J. Mol. Struct., 2003, 647(1–3), 121–128,  DOI:10.1016/s0022-2860(02)00509-4.
28. N. Weslati, I. Chaabane, A. Bulou and F. Hlel, Synthesis, crystal structure, thermal and dielectric properties of tetrapropylammonium tetrachloroantimonate(III), Phys. B, 2014, 441, 42–46,  DOI:10.1016/j.physb.2014.02.005.
29. A. V. Gerasimenko, A. V. Polishchuk, L. M. Volkova, E. T. Karaseva and V. E. Karasev, Synthesis and structure of nalidixium tetrachloroantimonate monohydrate, (C₁₂H₁₃N₂O₃)SbCl₄·H₂O, Russ. J. Coord. Chem., 2008, 34(1), 8–13,  DOI:10.1134/s1070328408010028.
30. Y. Guo, M. Zhang, L. Shen, Y. Y. Jin and Z. M. Jin, Synthesis and crystal structure of [(C₇H₁₀N)₂]²⁺ [Sb₂Cl₈]²⁻¹, Crystallogr. Rep., 2010, 55(7), 1194–1197,  DOI:10.1134/s1063774510070151.
31. I. Tlili, R. Essalhi, G. Mousdi, M. S. M. Abdelbaky and S. Chaabouni, Synthesis and characterization of a new organic-inorganic hybrid material based on antimony, J. Mol. Struct., 2022, 1251, 132012,  DOI:10.1016/j.molstruc.2021.132012.
32. R. Elwej, A. Bulou and F. Hlel, (C₆H₉N₂)₂HgCl₄ (I), (C₆H₉N₂)₂(Hg_0.75Cd_0.25)Cl₄ (II) and (C₆H₉N₂)₂(Hg_0.12Zn_0.88)Cl₄ (III) compounds: syntheses, crystal structure and spectroscopic properties, Synth. Met., 2016, 222, 372–382,  DOI:10.1016/j.synthmet.2016.11.008.
33. C. Janiak, A critical account on π–π stacking in metal complexes with aromatic nitrogen-containing ligands, J. Chem. Soc., Dalton Trans., 2000,(21), 3885–3896,  10.1039/b003010o.
34. N. J. Singh, S. K. Min, D. Y. Kim and K. S. Kim, Comprehensive Energy Analysis for Various Types of π-Interaction, J. Chem. Theory Comput., 2009, 5(3), 515–529,  DOI:10.1021/ct800471b.
35. W. Jabeur, R. Msalmi, M. Korb, M. Holub, E. Mosconi and E. Čižmár, et al., Optical and magnetic characterization of one-dimensional Cu(II)-based perovskite: a high UV-Vis-NIR absorber, J. Mater. Chem. C, 2021, 9(47), 17158–17166,  10.1039/d1tc04336f.
36. E. Runge and E. K. U. Gross, Density-Functional Theory for Time-Dependent Systems, Phys. Rev. Lett., 1984, 52(12), 997–1000,  DOI:10.1103/physrevlett.52.997.
37. M. Jar and C. Schlegel, Extended Jointly Gaussian Approach for Iterative Equalization, IEEE International Conference on Communications, 2010 DOI:10.1109/icc.2010.5502677.
38. K. Kim and K. D. Jordan, Comparison of Density Functional and MP2 Calculations on the Water Monomer and Dimer, J. Chem. Phys., 1994, 98(40), 10089–10094,  DOI:10.1021/j100091a024.
39. S. Grimme, Semiempirical hybrid density functional with perturbative second-order correlation, J. Chem. Phys., 2006, 124(3), 1–16,  DOI:10.1063/1.2148954.
40. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15) DOI:10.1063/1.3382344.
41. N. Mhadhbi, S. Saïd, S. Elleuch and H. Naïli, Crystal structure, spectroscopy, DFT studies and thermal characterization of cobalt(II) complex with 2-protonated aminopyridinium cation as ligand, J. Mol. Struct., 2016, 1108, 223–234,  DOI:10.1016/j.molstruc.2015.12.025.
42. S. Y. Ebrahimipour, M. Khosravan, J. White and S. Fekri, Preparation, crystal structure, spectroscopic studies, DFT calculations, antibacterial activities and molecular docking of a tridentate Schiff base ligand and its cis-MoO₂ complex, Appl. Organomet. Chem., 2018, 32(4), 1–11,  DOI:10.1002/aoc.4233.
43. Y. Dang, C. Zhong, G. Zhang, D. Ju, L. Wang and S. Xia, et al., Crystallographic Investigations into Properties of Acentric Hybrid Perovskite Single Crystals NH(CH₃)₃SnX₃ (X = Cl, Br), Chem. Mater., 2016, 28(19), 6968–6974,  DOI:10.1021/acs.chemmater.6b02653.
44. R. Kalthoum, M. Ben Bechir and A. Ben Rhaiem, CH₃NH₃CdCl₃: a promising new lead-free hybrid organic–inorganic perovskite for photovoltaic applications, Phys. E, 2020, 124, 114235,  DOI:10.1016/j.physe.2020.114235.
45. R. Marotti, Bandgap energy tuning of electrochemically grown ZnO thin films by thickness and electrodeposition potential, Sol. Energy Mater. Sol. Cells, 2004, 82(1–2), 85–103,  DOI:10.1016/j.solmat.2004.01.008.
46. R. Henríquez, P. Grez, E. Muñoz, H. Gómez, J. A. Badán and R. E. Marotti, et al., Optical properties of CdSe and CdO thin films electrochemically prepared, Thin Solid Films, 2010, 518(7), 1774–1778,  DOI:10.1016/j.tsf.2009.09.030.
47. K. Ben Brahim, M. Ben gzaiel, A. Oueslati, K. Khirouni, G. Mohamed and G. Corbel, et al., Organic–inorganic interactions revealed by Raman spectroscopy during reversible phase transitions in semiconducting [(C₂H₅)₄N]FeCl₄, RSC Adv., 2021, 11(30), 18651–18660,  10.1039/d1ra02475b.
48. B. Su, S. Geng, Z. Xiao and Z. Xia, Highly Distorted Antimony(III) Chloride [Sb₂Cl₈]₂⁻ Dimers for Near-Infrared Luminescence up to 1070 nm, Angew. Chem., Int. Ed., 2022, 61(33), 1–5,  DOI:10.1002/anie.202208881.
49. J. Zaleski, Crystal structure and X-ray investigation of phase transition of tetraethylammonium tetrachloroantimonate N(C₂H₅)₄SbCl₄, Ferroelectrics, 1997, 192(1), 71–79,  DOI:10.1080/00150199708216172.
50. U. Ensinger, W. Schwarz and A. Schmidt, Tetraalky lammonium - tetr achlor oantimonate (III). Struktur und Schwingungsspektren/Tetraalky lammonium Tetrachloroantimonates(III). Structure and Vibrational Spectra, Z. Naturforsch. B, 1982, 37(12), 1584–1589,  DOI:10.1515/znb-1982-1219.
51. A. Pathak, J. W. Shen, M. Usman, L. F. Wei, S. Mendiratta and Y. S. Chang, et al., Integration of a (–Cu–S–)n plane in a metal–organic framework affords high electrical conductivity, Nat. Commun., 2019, 10(1), 1–7,  DOI:10.1038/s41467-019-09682-0.
52. J. Liu, C. G. Duan, W. N. Mei, R. W. Smith and J. R. Hardy, Dielectric properties and Maxwell-Wagner relaxation of compounds ACu₃Ti₄O₁₂ (A = Ca, Bi_2/3,Y_2/3,La_2/3), J. Appl. Phys., 2005, 98(9), 1–6,  DOI:10.1063/1.2125117.
53. X. Lu, C. Dong, X. Guo, J. Ren, H. Xue and F. Tang, et al., Effects of grain size and temperature on mechanical properties of nano-polycrystalline Nickel-cobalt alloy, J. Mater. Res. Technol., 2020, 9(6), 13161–13173,  DOI:10.1016/j.jmrt.2020.09.060.
54. H. Rahmouni, M. Smari, B. Cherif, E. Dhahri and K. Khirouni, Conduction mechanism, impedance spectroscopic investigation and dielectric behavior of La_0.5Ca_0.5−xAg_xMnO₃ manganites with compositions below the concentration limit of silver solubility in perovskites (0 ≤ x ≤ 0.2), Dalton Trans., 2015, 44(22), 10457–10466,  10.1039/c5dt00444f.
55. D. Ah, A. Bougoffa, A. Zaouali, A. Benali, M. P. F. Graça and M. A. Valente, et al., Investigation of Cr substitution effect on the evolution of La_0.67Ca_0.2Ba_0.13Fe_1−xCr_xO₃ (x = 0 and 0.03) electrical properties under frequency and temperature variation, Eur. Phys. J. Plus, 2021, 136(8) DOI:10.1140/epjp/s13360-021-01780-7.
56. S. K. Jena, D. C. Joshi, S. Ghosh, K. Dasari and S. Thota, Dynamical response of localized electron hopping and dipole relaxation in Cu_1−xZn_xFe₂O₄ magnetoceramics, J. Phys. D: Appl. Phys., 2021, 54(42), 425303,  DOI:10.1088/1361-6463/ac16fc.
57. L. Singh, I. W. Kim, B. Cheol Sin, A. Ullah, S. Kook Woo and Y. Lee, Study of dielectric, AC-impedance, modulus properties of 0.5Bi_0.5Na_0.5TiO₃·0.5CaCu₃Ti₄O₁₂ nano-composite synthesized by a modified solid state method, Mater. Sci. Semicond. Process., 2015, 31, 386–396,  DOI:10.1016/j.mssp.2014.12.025.
58. M. Bourguiba, Z. Raddaoui, A. Dhahri, M. Chafra, J. Dhahri and M. A. Garcia, Investigation of the conduction mechanism, high dielectric constant, and non-Debye-type relaxor in La_0.67Ba_0.25Ca_0.08MnO₃ manganite, J. Mater. Sci.: Mater. Electron., 2020, 31(14), 11810–11818,  DOI:10.1007/s10854-020-03733-9.
59. P. Sengupta, P. Sadhukhan, A. Ray, R. Ray, S. Bhattacharyya and S. Das, Temperature and frequency dependent dielectric response of C₃H₇NH₃PbI₃: a new hybrid perovskite, J. Appl. Phys., 2020,(20), 127,  DOI:10.1063/1.5142810.
60. M. Ben Gzaiel, K. Khirouni and M. Gargouri, Optical and electrical studies on the semi-conductor compound for the photovoltaic applications, J. Organomet. Chem., 2021, 950, 121992,  DOI:10.1016/j.jorganchem.2021.121992.
61. C. Bharti and T. P. Sinha, Structural and ac electrical properties of a newly synthesized single phase rare earth double perovskite oxide: Ba₂CeNbO₆, Phys. B, 2011, 406(9), 1827–1832,  DOI:10.1016/j.physb.2011.02.038.
62. A. Dutta, C. Bharti and T. P. Sinha, AC conductivity and dielectric relaxation in, Mater. Res. Bull., 2008, 43(5), 1246–1254,  DOI:10.1016/j.materresbull.2007.05.023.
63. K. S. Cole and R. H. Cole, Dispersion and Absorption in Dielectrics II. Direct Current Characteristics, J. Chem. Phys., 1942, 10(2), 98–105,  DOI:10.1063/1.1723677.
64. X. Zheng, S. Wang, J. Wang, W. Hua, J. Zhang and L. Liu, Long-Range and Short-Range Transport Dynamics of Li Ions in LiMn₂O₄, J. Phys. Chem. C, 2020, 124(46), 25254–25261,  DOI:10.1021/acs.jpcc.0c08450.
65. A. Pogrebnjak, V. Ivashchenko, O. Maksakova, V. Buranich, P. Konarski and V. Bondariev, et al., Comparative measurements and analysis of the mechanical and electrical properties of Ti-Zr-C nanocomposite: Role of stoichiometry, Measurement, 2021, 176, 109223,  DOI:10.1016/j.measurement.2021.109223.
66. P. Żukowski, K. Kierczyński, T. N. Kołtunowicz, P. Rogalski and J. Subocz, Application of elements of quantum mechanics in analysing AC conductivity and determining the dimensions of water nanodrops in the composite of cellulose and mineral oil, Cellulose, 2019, 26(5), 2969–2985,  DOI:10.1007/s10570-019-02268-5.
67. P. Żukowski, P. Gałaszkiewicz, V. Bondariev, P. Okal, A. Pogrebnjak and A. Kupchishin, et al., Comparative Measurements and Analysis of the Electrical Properties of Nanocomposites Ti_xZr_1−xC + α-Cy (0.0 ≤ x ≤ 1.0), Materials, 2022, 15(22), 7908,  DOI:10.3390/ma15227908.
68. S. Karoui, H. Chouaib and S. Kamoun, Studies of electric, dielectric properties, and conduction mechanism of {(C₂H₁₀N₂)(MnCl(NCS)₂)₂}_n polymer, J. Phys. Org. Chem., 2020, 33(11), 1–15,  DOI:10.1002/poc.4101.
69. M. A. Fersi, R. Hajji, I. Chaabane and M. Gargouri, Synthesis, crystal structure and electrical properties of the new organic-inorganic hybrid compound bis(1-chlorido-4-aminopyridinium) octachlorodiantimoinate, Phys. E, 2017, 94, 167–173,  DOI:10.1016/j.physe.2017.08.010.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2225545. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3ra08885e

---