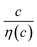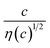Concentration dependence of resistance components in solutions containing dissolved Fe²⁺/Fe³⁺

Abstract

Electrolyte solutions containing Fe²⁺/Fe³⁺ are suitable for liquid thermoelectric conversion devices (LTEs), because they are inexpensive materials and exhibit a high electrochemical Seebeck coefficient α. Here, we investigated the concentration (c) dependence of resistance components, i.e., solvent (R_s), charge-transfer (R_ct), and diffusion (R_dif) resistances, of dissolved-Fe²⁺/Fe³⁺-containing aqueous, methanol (MeOH), acetone, and propylene carbonate (PC) solutions. We found that the c dependence of R_s and R_dif are well reproduced by empirical formulas, 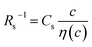and 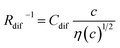, where η(c) is viscosity at c. We further found that the magnitudes of C_s and C_dif are nearly independent of solvent, suggesting that η is one of the significant solution parameters that determine R_s and R_dif.

---

1 Introduction

Energy-harvesting devices are attracting the current attention of researchers from the viewpoint of a basic power source for the internet of things (IoT) society as well as sustainable development goals (SDGs). Thermoelectric conversion devices (TEs) are promising because they cover the field from bioelectric and wearable electronics to industrial power generation. In particular, flexible TEs using cellulose gel¹ have excellent compatibility with various thermoelectric conversion materials. This is because cellulose can be used in the design of flexible and ion/electron conductive materials with robust mechanical properties. Flexible TEs are expected to be used not only for thermoelectric conversion but also for sensors and refrigeration units.

Among TEs, liquid thermoelectric conversion devices (LTEs) are promising because they are made of inexpensive materials. There is already a long history of LTE research.² Nevertheless, vigorous research has become more active in recent years and many research results have been reported.^3–19 The performance of LTEs is governed by the electrochemical Seebeck coefficient α, effective electric conductivity σ, and effective thermal conductivity κ of the electrolyte.²⁰ Unlike solid thermoelectric devices, σ is related to the charge transfer and diffusion processes of redox ions as well as the conventional ion migration. The magnitude of σ depends on the microscopic structure and material of the electrodes.^16,17 In addition, effective σ and κ are influenced by convection of the electrolyte induced by ΔT. The dimensionless figure of merit (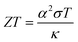, where T is temperature) is a measure of the LTE performance. With the increase of ZT, the thermal efficiency η increases toward the Carnot efficiency 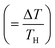, which is the maximum efficiency of a heat engine.²¹ To enhance ZT, it is effective to increase (decrease) α and σ (κ).

In recent years, research on LTEs using an organic electrolyte^18,19 has begun to attract attention, as has research on conventional LTEs using an aqueous electrolyte.^4–17 This is because the organic electrolytes exhibit both large α and small κ. In several organic solutions containing Fe²⁺/Fe³⁺, α is higher than the value (= 1.4 mV K⁻¹) of an aqueous solution. For example, α is 3.6 mV K⁻¹ in acetone solution and 1.8 mV K⁻¹ in propylene carbonate (PC) solution.²² In addition, κ of a typical organic solvent is ≈ 0.2 W K⁻¹ m⁻¹ and is approximately 33% of the value (= 0.6 W K⁻¹ m⁻¹) of water. Recently, Wake et al.^18,19 showed that LTEs composed of dissolved-Fe²⁺/Fe³⁺-containing methanol (MeOH) and acetone solutions exhibit a large power factor (PF = α²σ) comparable to that of the corresponding aqueous LTE. They also reported α and σ against solute concentration c. The disadvantage of organic electrolytes is a small σ value compared with that of an aqueous electrolyte. Except for aqueous electrolyte,⁷ there exists no detailed investigation on the resistance components. Therefore, the origin of the small σ in organic electrolytes is still unclear. Here, we will investigate the resistance components of several solutions containing dissolved Fe²⁺/Fe³⁺ against c to deeply understand σ and to obtain guidelines for increasing σ in organic electrolytes.

In general, the resistance R (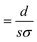, where d and s are the electrode distance and area, respectively) of an electrolyte solution consists of the solution resistance R_s due to ion migration, charge transfer resistance R_ct due to electron transfer, and diffusion resistance R_dif due to reactant/product diffusion.²³ Among them, R_s is derived from the balance between the electric force (=|z|eE_ef; |z|, e, and E_ef are the charge number, elementary charge, and electric field, respectively) and frictional force. According to Stokes’ law, the latter force is expressed as 6πηrv, where η, r, and v are the viscosity, effective radius, and velocity of the ion, respectively. Then, the mobility u 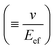of an ion is expressed as 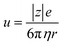and is inversely proportional to η. On the other hand, R_ct and R_dif are governed by the reaction kinetics in the vicinity of the electrode surface and are independent of d. The reaction rate k is expressed as 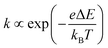, where ΔE (= E − E_eq; E and E_eq are the electrode and equilibrium potentials, respectively) and k_B are the overpotential and Boltzmann constant, respectively. In the region of 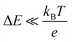, the charge-transfer current J_ct is expressed as 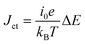,²³ where i₀ is the exchange current. Thus, R_ct is proportional to 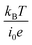and is independent of d. The physical meaning of R_dif is as follows. As the reaction progresses, the concentration of reactants/products at the electrode surface changes in a way that prevents further reaction. For the reaction to continue, the reactants/products must diffuse into/from the bulk region. Note that the diffusion current of reactants/products is driven by the concentration gradient created by the reaction at the electrode surface and is independent of d.

In this work, we investigated the c-dependence of R_s, R_ct, and R_dif of dissolved-Fe²⁺/Fe³⁺-containing aqueous, MeOH, acetone, and PC solutions. We found that the c-dependence of R_s and R_dif is well reproduced by empirical formulas, 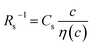and 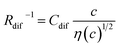. We further found that their coefficients, C_s and C_dif, are nearly independent of solvent, suggesting that η is one of the significant solution parameters that determine R_s and R_dif.

2 Experimental methods

2.1 Solution preparation

In this study, water, MeOH, acetone, and PC were selected as the solvents because they exhibit a high solubility of Fe(ClO₄)₂/Fe(ClO₄)₃. We prepared aqueous, MeOH, acetone, and PC solutions containing c M Fe(ClO₄)₂·6.0H₂O and c M Fe(ClO₄)₃·7.1H₂O. Distilled water, MeOH, acetone, PC, and solutes were purchased from FUJIFILM Wako Corp. and used as received. Table 1 shows the solubility s and critical concentration c* of Fe(ClO₄)₂/Fe(ClO₄)₃ in the four solvents. c* is defined as the concentration at which one Fe ion is dissolved per six solvent molecules. At c = c*, all solvent molecules are on average coordinated with Fe ions.

Table 1 Solubility s and critical concentration c* of Fe(ClO₄)₂·6.0H₂O/Fe(ClO₄)₃·7.1H₂O in several solvents at 298 K. c* is defined as the concentration at which one Fe ion is dissolved per six solvent molecules. MeOH and PC represent methanol and propylene carbonate, respectively

Solvent	s (M)	c* (M)
Water	2.5	4.62
MeOH	2.5	2.06
Acetone	1.2	1.12
PC	1.5	0.97

---

2.2 Total resistance

The total resistance R_tot of the electrolyte was measured in a two-pole cell at 298 K.²⁴ The electrodes were produced from a 220 μm graphite sheet (PREMA-FOIL, TOYO TANSO). The electrode distance d and area s are 1.0 cm and 0.42 cm², respectively. The voltage drop V was measured against the current I (I ≤ 0.4 mA) with a multimeter. I was changed in a stepwise manner at intervals of several minutes. V was stable and no change over time was observed. The slope of the I–V plot corresponds to R_tot.

2.3 Electrochemical impedance spectroscopy

R _ct and R_dif were evaluated in the same cell with the same electrodes. d and s are 1.0 cm and 0.42 cm², respectively. Electrochemical impedance spectroscopy (EIS) was performed at 298 K with use of a potentiostat (Vertex.one.EIS, Ivium Technologies). The frequency range was from 50 mHz to 100 kHz, and the amplitude was 10 mV. V was stable and no change over time was observed. It was confirmed that almost identical EIS data were obtained through multiple measurements.

The EIS data were analyzed with a Randles equivalent circuit,²³ which consists of R_s, R_ct, double layer capacitance C_d, and Warburg impedance Z_ω. Z_ω is expressed as Z_ω = A_W(ω^−1/2 − iω^−1/2), where A_W and ω are the Warburg coefficient and angular velocity, respectively. It was difficult to evaluate the magnitude of R_dif from A_W even though Z_ω describes the diffusion process of the reactants/products. In the present study, we tentatively evaluate the R_dif values by subtraction of R_s and R_ct from R_tot. We confirmed a positive correlation between A_W and R_dif (= R_tot − R_s − R_ct), which strongly supports the correctness of our evaluation method of R_dif (vide infra).

3 Results

3.1 Total resistance

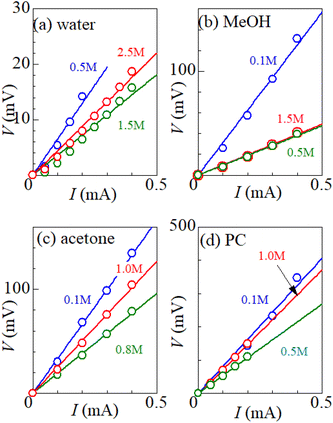
Fig. 1 shows examples of the I–V plot of several solutions containing dissolved Fe²⁺/Fe³⁺ at 298 K: (a) water, (b) MeOH, (c) acetone, and (d) PC. For all solutions, V increases in proportion to I. R_tot was evaluated from the slope of the plots, as indicated by the straight lines. The obtained R_tot values are listed in Table 2. In (a) the aqueous solution, R_tot decreases from 65.0 Ω at 0.5 M to 28.5 Ω at 1.5 M, and then increases to 37.9 Ω at 2.5 M. The decrease in R_tot in the low c region is due to the increase in the number (∝ c) of charge carriers, such as Fe²⁺ and Fe³⁺. This behavior is consistent with the literature.⁶ Similar local minima structures in the c–R_tot plot are also observed for the MeOH, acetone and PC solutions (Table 2).

Fig. 1 Voltage V against current I for several solutions containing dissolved Fe²⁺/Fe³⁺ at 298 K: (a) water, (b) MeOH, (c) acetone, and (d) PC. Data for three typical solute concentrations are shown for each solution: below the resistance minimum (blue), near the resistance minimum (green), and above the resistance minimum (red). The straight lines are the results of least-squares fits.

Table 2 Total resistance R_tot, solution resistance R_s, charge-transfer resistance R_ct, diffusion resistance R_dif, and Warburg coefficient A_W in solvents containing c M Fe(ClO₄)₂ and c M Fe(ClO₄)₃. R_dif was evaluated by subtraction of R_s and R_ct from R_tot

Solvent	c (M)	R tot (Ω)	R s (Ω)	R ct (Ω)	R dif (Ω)	A W (Ω s^−1/2)
Water	0.10	351.0	56.0	32.0	263.0	86.2
Water	0.20	236.0	35.4	16.1	184.5	42.8
Water	0.50	65.0	19.8	5.3	39.9	15.7
Water	0.80	42.6	18.1	3.8	20.7	10.8
Water	1.00	39.4	18.1	2.9	18.4	10.0
Water	1.50	28.5	16.3	2.1	10.1	9.1
Water	2.00	27.7	19.6	1.9	6.2	7.0
Water	2.50	37.9	20.0	1.9	16.0	10.4
MeOH	0.05	906.0	221.7	65.2	619.1	176.7
MeOH	0.10	314.0	126.0	22.6	165.4	63.0
MeOH	0.50	95.6	54.6	4.4	36.6	16.2
MeOH	1.00	95.2	60.9	1.8	32.5	9.1
MeOH	1.50	98.2	67.4	1.6	29.2	8.4
MeOH	2.00	110.0	75.5	2.4	32,1	6.8
MeOH	2.50	115.0	83.3	3.2	28.6	7.5
Acetone	0.05	692.0	439.2	35.6	227.2	134.6
Acetone	0.10	333.0	187.0	18.0	128.0	72.0
Acetone	0.20	225.0	130.4	8.6	86.0	29.0
Acetone	0.40	172.0	100.3	5.0	66.7	14.7
Acetone	0.80	192.0	126.8	2.8	62.4	9.0
Acetone	1.00	254.0	160.5	4.5	89.0	9.2
Acetone	1.20	251.0	180.0	4.5	66.5	8.8
PC	0.05	1265.0	726.8	75.6	425.6	255.8
PC	0.10	813.0	615.0	27.0	171.0	70.0
PC	0.20	528.0	387.6	11.5	128.9	31.2
PC	0.50	537.0	447.9	11.4	77.7	17.5
PC	1.00	741.0	663.3	12.9	64.8	15.0
PC	1.50	726.0	674.1	13.2	38.7	13.9

---

Let us estimate the maximum value of ZT in the aqueous electrolyte at 300 K with the use of R_tot shown in Table 2. The maximum value of σ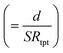 is 86.0 mS cm⁻¹ at c = 2.0 M. Kim et al.⁶ reported c-dependence of α and κ in an aqueous solution containing Fe(ClO₄)₂/Fe(ClO₄)₃. From the extrapolation of the reported data, we evaluated α = 1.76 mV K⁻¹ and κ = 0.4 W K⁻¹ m⁻¹ at 2.0 M. Then, we obtained ZT = 0.020 at 2.0 M. The ZT value is smaller than the value (= 0.036 (ref. 6) at 0.8 M) reported by Kim et al.,⁶ reflecting the smaller σ obtained in the present experiment. We note that effective σ of a LTE is influenced by the microscopic structure of the electrodes as well as the convection of the electrolyte.

3.2 Electrochemical impedance spectroscopy

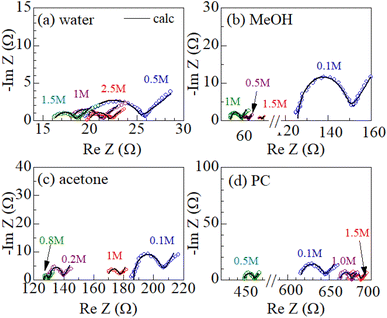
Fig. 2 shows examples of the Cole–Cole plots of complex impedance for several solutions containing dissolved Fe²⁺/Fe³⁺ at 298 K: (a) water, (b) MeOH, (c) acetone, and (d) PC. The Cole–Cole plot of 0.1 M MeOH solution (Fig. 2(b)) shows a prototypical shape. The plot shows a semicircle on the left side and a straight line with an inclination of 45° on the right side. The resistances on the left and right sides of the semicircle correspond to R_s and R_s + R_ct, respectively. The intersection of the straight line with the horizontal axis corresponds to R_s + R_ct − 2A_W²C_d. Similar behaviors are also observed in the other solutions. The solid curves in Fig. 1 are the results of least-squares fits with a Randles equivalent circuit composed of R_s, R_ct, C_d, and Z_ω. The Randles equivalent circuit well reproduces the observed complex impedance. Thus, we obtained R_s, R_ct, C_d, and A_W. We further evaluate R_dif (= R_tot − R_s − R_ct) with the use of R_tot. The obtained R_s, R_ct, R_dif, and A_W values are listed in Table 2.

Fig. 2 Cole–Cole plots of complex impedance for several solutions containing dissolved Fe²⁺/Fe³⁺ at 298 K: (a) water, (b) MeOH, (c) acetone, and (d) PC. The solid curves are the results of least-squares fits with a Randles equivalent circuit composed of R_s, R_ct, C_d, and Z_ω (see text).

A _W is expected to have a strong correlation with R_dif because Z_ω [= A_W(ω^−1/2 − iω^−1/2)] describes the diffusion process of the reactants/products. We calculated the correlation coefficient X between A_W and R_dif (= R_tot − R_s − R_ct) for each solution system; X = 0.976 for water, 0.995 for MeOH, 0.980 for acetone, and 0.988 for PC. The positive correlation (X ≥ 0.976) between A_W and R_dif strongly supports the correctness of our evaluation method of R_dif.

3.3 Concentration dependence of resistivity components

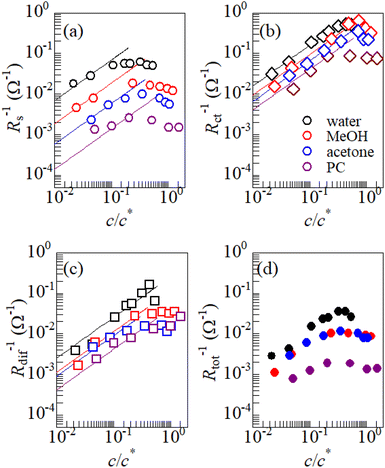
Fig. 3 shows the c-dependence of (a) R_s⁻¹, (b) R_ct⁻¹, (c) R_dif⁻¹, and (d) R_tot⁻¹ in several solutions containing dissolved Fe²⁺/Fe³⁺ at 298 K. For the convenience of explanation, the horizontal axis is normalized by the critical concentration c* of each solvent. At c = c*, all solvent molecules are on average coordinated with Fe ions.

Fig. 3 Solute concentration (c) dependence of (a) R_s⁻¹, (b) R_ct⁻¹, (c) R_dif⁻¹, and (d) R_tot⁻¹ in several solutions containing dissolved Fe²⁺/Fe³⁺ at 298 K. The horizontal axis is normalized by the critical concentration c* of each solvent. The straight lines in (a), (b), and (c) represent the linear relation with .

First, let us examine the solvent dependence of R_s⁻¹, R_ct⁻¹, and R_dif⁻¹. Significant solvent dependence is observed for (a) R_s⁻¹. R_s⁻¹ values at 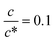are 69.5 × 10⁻³ Ω⁻¹ in water, 17.1 × 10⁻³ Ω⁻¹ in MeOH, 6.7 × 10⁻³ Ω⁻¹ in acetone, and 1.4 × 10⁻³ Ω⁻¹ in PC. The R_s⁻¹ values in organic solutions are much smaller than those in aqueous solutions. In contrast, R_ct⁻¹ and R_dif⁻¹ have relatively small solvent dependence. In this sense, reducing R_s is effective to reduce R_tot in organic solution. Shortening d is especially effective because κ (≈ 0.2 W K⁻¹ m⁻¹) of an organic solvent is much smaller than κ (= 0.6 W K⁻¹ m⁻¹) of water. Reflecting the small κ in organic solvent, a sufficient ΔT is expected between the electrodes, even in the cell with smaller d.

Next, let us investigate the 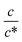dependence of R_s⁻¹, R_ct⁻¹, and R_dif⁻¹. In the small 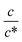region, R_s⁻¹ increases linearly with 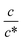as indicated by the straight lines in Fig. 3(a). The increase in R_s⁻¹ is due to the increase in the number (∝ c) of charge carriers, such as Fe²⁺ and Fe³⁺. Upon further increasing 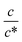beyond ∼0.3, R_s⁻¹ begins to decrease with 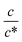. Similarly, in the small 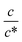region, R_ct⁻¹ and R_dif⁻¹ increase linearly with 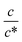as indicated by the straight lines in Fig. 3(b) and (c), respectively. The increase in R_ct⁻¹ and R_dif⁻¹ is due to the increase (∝ c) of reactant/product concentration, i.e., Fe²⁺/Fe³⁺. Upon further increasing 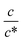beyond ∼0.5, R_ct⁻¹ and R_dif⁻¹ begin to saturate. The saturation of R_ct⁻¹ can be ascribed to the finite reaction number (N_reaction) per unit time at the electrode surface. The redox reaction cannot keep up with the supply of reactants when the number (N_reactant ∝ c) of reaching reactants per unit time exceeds N_reaction. In such a region, N_reaction becomes the rate-determining factor for the charge-transfer current J_ct, and hence, R_ct⁻¹. As a result, R_ct becomes constant at sufficiently large c.

4 Discussion

4.1 Concentration dependence of R_s

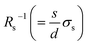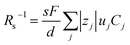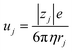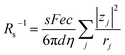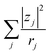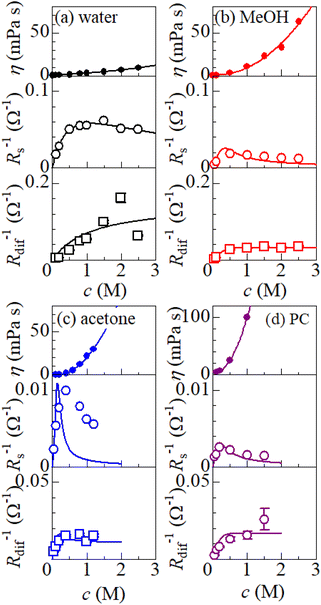
Now, let us discuss the solution parameters that determine R_s. is expressed as ,²³ where F, z_j, u_j, and C_j are the Faraday constant, charge number, mobility, and molar concentration of the j-th ion, respectively. By substituting , we obtain . Note that C_Fe²⁺ = C_Fe³⁺ = c in the present solutions. By assuming is independent of c in each solution, we obtain the simple relation 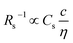, where C_s is a constant. The top panels of Fig. 4(a)–(d) show η of each solution against c. The η values were evaluated at 298 K using a sine-wave vibro viscometer (SV-10; A&D Company Limited). In all solutions, η increases nonlinearly with c. The solid curves are the results of least-squares fits with a quadratic function. With use of the quadratic function η(c), the empirical formula, 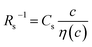, can be calculated.

Fig. 4 (a) Viscosity η (top), R_s⁻¹ (middle), R_dif⁻¹ (bottom) in aqueous solutions containing dissolved Fe²⁺/Fe³⁺ at 298 K against solute concentration c. (b) η, R_s⁻¹, and R_dif⁻¹ in MeOH solutions containing dissolved Fe²⁺/Fe³⁺ at 298 K against c. (c) η, R_s⁻¹, and R_dif⁻¹ in acetone solutions containing dissolved Fe²⁺/Fe³⁺ at 298 K against c. (d) η, R_s⁻¹, and R_dif⁻¹ in PC solutions containing dissolved Fe²⁺/Fe³⁺ at 298 K against c. The solid curves in the upper panels are the results of least-squares fits with a quadratic function. The solid curves in the middle panels are the results of least-squares fits with the function. The solid curves in the bottom panels are the results of least-squares fits with the function.

The middle panels of Fig. 4(a)–(d) show comparisons between observed R_s⁻¹ (open circles) and empirical formula (solid curves) against c. We note that there is only one fitting parameter (C_s) to adjust the magnitude but no parameter to adjust the shape. Nevertheless, the curve reproduces the observed R_s⁻¹ well, except for (c) acetone solution. In Table 3, we listed C_s. Except for the acetone solution, the solvent dependence of C_s is rather small, falling between 0.104 mPa s M⁻¹ Ω⁻¹ and 0.183 mPa s M⁻¹ Ω⁻¹. This is probably because the r value does not change greatly depending on the solvent.

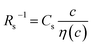Table 3 Coefficients (C_s and C_dif) of empirical formulas, and 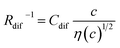, determined by least-squares fits with the observed data. MeOH and PC represent methanol and propylene carbonate, respectively

Solvent	C s (mPa s M^−1 Ω^−1)	C dif (mPa^1/2 s^1/2 M^−1 Ω^−1)
Water	0.183	0.125
MeOH	0.132	0.099
Acetone	0.019	0.053
PC	0.104	0.166

---

In (c) acetone solution, the shape of the c–R_s⁻¹ plot (open circles) is qualitatively different from the shape of the empirical formula (solid curve). In the region of c ≥ 0.5, the empirical formula results decrease steeply while the observed R_s⁻¹ decreases slowly. If C_s is set to ∼0.1, the agreement between the calculated and observed values is improved in the region of c ≥ 0.5 even though the calculated value is much larger in the region of c ∼ 0.3. This implies that an additional factor, e.g., the repulsive interaction between Fe ions, suppressed R_s in the region of c ∼ 0.3.

4.2 Concentration dependence of R_dif

Finally, let us consider the relationship between R_dif⁻¹ and η. R_dif⁻¹ is proportional to the diffusion current J_dif, which is expressed as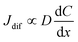 . Replacing the differential with the difference, we get 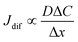,²³ where Δx and ΔC are the diffusion length and concentration difference between electrode surface and bulk solution, respectively. In one-dimensional diffusion, Δx is expressed as 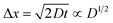, where t is the elapsed time. Then, J_dif is proportional to cD^1/2 because ΔC ∝ c. From the Stokes–Einstein equation, we obtain 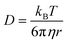. Finally, we obtain an empirical relation 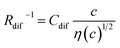, where C_dif is a constant. We can calculate the empirical formula with use of the quadratic function η(c).

The bottom panels of Fig. 4(a)–(d) show comparisons between the observed R_dif⁻¹ (open circles) and empirical formula (solid curves) against c. We note that there is only one fitting parameter (C_dif) to adjust the magnitude. Nevertheless, the curve reproduces the observed R_dif⁻¹ well. In Table 3, we list the C_dif values. The solvent dependence of C_dif is rather small, falling between 0.053 mPa^1/2 s^1/2 M⁻¹ Ω⁻¹ and 0.166 mPa^1/2 s^1/2 M⁻¹ Ω⁻¹. This is probably because the r value does not change greatly depending on the solvent.

5 Conclusions

In conclusion, we investigated the c-dependence of R_s, R_ct, and R_dif in dissolved-Fe²⁺/Fe³⁺-containing aqueous, MeOH, acetone, and PC solutions. We found that the c-dependence of R_s and R_dif is well reproduced by the empirical formulas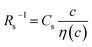 and 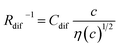. We further found that the magnitudes of C_s and C_dif are nearly independent of the solvent, suggesting that η is one of the significant solution parameters that determine R_s and R_dif. Our findings suggest that σ of the electrolyte solution can be increased through reducing η.

Author contributions

Dai Inoue: data curation, formal analysis, and investigation. Yutaka Moritomo: conceptualization, supervision, writing – original draft, and writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by JSPS KAKENHI (Grant No. 22KJ0413), Yazaki Memorial Foundation for Science and Technology, and joint research with Taisei Rotec Corporation.

Notes and references

1. Q. Long, G. Jiang, J. Zhou, D. Zhao, P. Jia and S. Nie, Nano Energy, 2024, 120, 109130.
2. T. Ikeshoji, Bull. Chem. Soc. Jpn., 1987, 60, 1505; I. Quickenden and Y. Mua, J. Electrochem. Soc., 1995, 142, 3985; Y. Mua and T. I. Quickenden, J. Electrochem. Soc., 1996, 143, 2558; J. Kawamura, M. Shimoji and H. Hoshino, J. Phys. Soc. Jpn., 1981, 50, 194; A. Schiraldi, E. Pezzati and P. Baldini, J. Phys. Chem., 1985, 89, 1528; R. Hu, B. A. Cola, N. Haram, J. N. Barisci, S. Lee, S. Stoughton, G. Wallace, C. Too, M. Thomas, A. Gestos, M. Ed Cruz, J. P. Ferraris, A. A. Zakhidov and R. H. Baughman, Nano Lett., 2010, 10, 838; D. R. MacFarlane, N. Tachikawa, M. Forsyth, J. M. Pringle, P. C. Howlett, G. D. Elliott, J. F. Davis Jr, M. Watanabe, P. Simon and C. A. Angell, Energy Environ. Sci., 2014, 7, 232; M. Bonetti, S. Nakamae, M. Roger and P. Guenoun, J. Chem. Phys., 2011, 134, 114513; T. J. Abraham, D. R. MacFarlane and J. M. Pringle, Chem. Commun., 2011, 47, 6260; M. Romano, S. Gambhir, J. Razal, A. Gestos, G. Wallace, J. Chen and J. Therm, J. Therm. Anal. Calorim., 2012, 109, 1229; M. S. Romano, N. Li, D. Antiohos, J. M. Razal, A. Nattestad, S. Beirne, S. Fang, Y. Chen, R. Jalili, G. G. Wallace, R. Baughman and J. Chen, Adv. Mater., 2013, 25, 6602; T. J. Abraham, D. R. MacFarlane and J. M. Pringle, Energy Environ. Sci., 2013, 6, 2639; A. Gunawan, C.-H. Lin, D. A. Buttry, V. Mujica, R. A. Taylor, R. S. Prasher and P. E. Phelan, Nanoscale Microscale Thermophys. Eng., 2013, 17, 304; N. Jiao, T. J. Abraham, D. R. MacFarlane and J. M. Pringle, J. Electrochem. Soc., 2014, 161, D3061; S. Uhl, E. Laux, T. Journot, L. Jeandupeux, J. Charmet and H. Keppner, J. Electron. Mater., 2014, 43, 3758; A. Gunawan, H. Li, C.-H. Lin, D. A. Buttry, V. Mujica, R. A. Taylor, R. S. Prasher and P. E. Phelan, Int. J. Heat Mass Transfer, 2014, 78, 423; M. A. Lazar, D. Al-Masri, D. R. MacFarlane and J. M. Pringle, Phys. Chem. Chem. Phys., 2016, 18, 1404.
3. Y. Liang, J. K.-H. Hui, M. Morikawa, H. Inoue, T. Yamada and N. Kimizuka, ACS Appl. Energy Mater., 2021, 4, 5326.
4. B. Yu, J. Duan, H. Cong, W. Xie, R. Liu, X. Ahuang, H. Wang, B. Qi, M. Xu and L. Wan, Science, 2020, 370, 342.
5. Y. Xaing, X. Guo, H. Zhu, Q. Zhang and S. Zhu, Chem. Eng. J., 2023, 461, 142018.
6. J. H. Kim, J. H. Lee, E. E. Palen, M.-S. Suh, H. H. Lee and R. J. Kang, Sci. Rep., 2019, 9, 8706.
7. M. A. Buckingham, F. Marken and L. Aldous, Sustainable Energy Fuels, 2018, 2, 2717.
8. J. Duan, G. Feng, B. Yu, J. Li, M. Chen, P. Yang, J. Feng, K. Liu and J. Zhou, Nat. Commun., 2018, 9, 5146.
9. T. Kim, J. S. Lee, G. Lee, H. Yoon, J. Yoon, T. J. Kangd and Y. H. Kim, Nano Energy, 2017, 31, 160.
10. M. Sindhuja, B. Lohith, V. Sudha, G. R. Manjunath and S. Harinipriya, Mater. Res. Express, 2017, 4, 075513.
11. H. Im, T. Kim, H. Song, J. Choi, J. S. Park, R. Ovalle-Robles, H. D. Yang, K. D. Kihm, R. H. Baughman, H. H. Lee, T. J. Kang and Y. H. Kim, Nat. Commun., 2016, 7, 10600.
12. H. Zhou, T. Yamada and N. Kimizuka, J. Am. Chem. Soc., 2016, 138, 10502.
13. A. H. Kazim and B. A. Cola, J. Electrochem. Soc., 2016, 163, F867.
14. S. W. Lee, Y. Yang, H.-W. Lee, H. Ghasemi, D. Kraemer, G. Chen and Y. Cui, Nat. Commun., 2014, 5, 3942.
15. Y. Tanaka, A. Wake, D. Inoue and Y. Moritomo, Jpn. J. Appl. Phys., 2024, 63, 014002.
16. S.-M. Jung, S.-Y. Kang, B.-J. Lee, J. Kwon, D. Lee and Y.-T. Kim, Adv. Funct. Mater., 2023, 33, 2304067.
17. B. Yu, H. Xiao, Y. Zeng, S. Liu, D. Wu, P. Liu, J. Guo, W. Xie, J. Duan and J. Zhou, Nano Energy, 2022, 93, 106795.
18. A. Wake, D. Inoue and Y. Moritomo, Appl. Phys. Express, 2022, 15, 054002.
19. A. Wake, D. Inoue and Y. Moritomo, Jpn. J. Appl. Phys., 2023, 62, 014002.
20. J. Duan, B. Yu, L. Huang, B. Hu, M. Xu, G. Feng and J. Zhou, Joule, 2021, 5, 768.
21. S. W. Angrist, Direct Energy Conversion, Allyn and Bacon, Inc., Boston, 1982.
22. D. Inoue, H. Niwa, H. Nitani and Y. Moritomo, J. Phys. Soc. Jpn., 2021, 90, 033602.
23. A. J. Bard, L. R. Faulkner, and H. S. White, Electrochemical Methods, Wiley, West Sussex, 2022.
24. Y. Fukuzumi, Y. Hinuma and Y. Moritomo, Jpn. J. Appl. Phys., 2019, 58, 065501.

---