 Open Access Article
Open Access ArticleBr doping-induced evolution of the electronic band structure in dimorphic and hexagonal SnSe2 thermoelectric materials†
Se-Jun Kim‡
a,
Minsu Heo‡a,
Sang-il Kim‡ a,
Hyunjin Parka,
Jeong-Yeon Kima,
Won-Seon Seob and
Hyun-Sik Kim
a,
Hyunjin Parka,
Jeong-Yeon Kima,
Won-Seon Seob and
Hyun-Sik Kim *a
*a
aDepartment of Materials Science and Engineering, University of Seoul, Seoul 02504, South Korea. E-mail: hyunsik.kim@uos.ac.kr
bDepartment of Materials Science and Engineering, Yonsei University, Seoul 03722, South Korea
First published on 27th February 2024
Abstract
SnSe2 with its layered structure is a promising thermoelectric material with intrinsically low lattice thermal conductivity. However, its poor electronic transport properties have motivated extensive doping studies. Br doping effectively improves the power factor and converts the dimorphic SnSe2 to a fully hexagonal structure. To understand the mechanisms underlying the power factor improvement of Br-doped SnSe2, the electronic band parameters of Br-doped dimorphic and hexagonal SnSe2 should be evaluated separately. Using the single parabolic band model, we estimate the intrinsic mobility and effective mass of the Br-doped dimorphic and hexagonal SnSe2. While Br doping significantly improves the mobility of dimorphic SnSe2 (with the dominant hexagonal phase), it results in a combination of band convergence and band flattening in fully hexagonal SnSe2. Br-doped dimorphic SnSe2 is predicted to exhibit higher thermoelectric performance (zT ∼0.23 at 300 K) than Br-doped fully hexagonal SnSe2 (zT ∼0.19 at 300 K). Characterisation of the other, currently unidentified, structural phases of dimorphic SnSe2 will enable us to tailor the thermoelectric properties of Br-doped SnSe2.
Global warming is disrupting ecosystems and reducing biodiversity, which is threatening food production and human well-being.1,2 The emission of greenhouse gases, such as carbon dioxide (CO2), is a major cause of global warming. Fossil fuels, such as coal, oil, and natural gas, are the main source of CO2 emissions. The burning of these fuels releases CO2 into the atmosphere, where it traps heat and contributes to climate change.3 Renewable and sustainable power generation technologies, such as solar, wind, and hydropower, offer a way to reduce CO2 emissions and combat global warming. These technologies do not produce greenhouse gases, and they can be used to generate electricity, heat homes and businesses, and power transportation.4 Among these renewable and sustainable power generation technologies, thermoelectric power generation technology is the only technology that can directly generate electricity from waste heat.5 The efficiency of thermoelectric devices is a key factor in their ability to convert waste heat into electrical energy. The higher the efficiency, the more electrical energy can be produced from the same amount of waste heat.6 To improve the efficiency of a thermoelectric power generation device, the performance of the thermoelectric materials used in the device should be increased. The thermoelectric performance of the material is defined with a dimensionless figure-of-merit, zT. The zT is expressed by the following eqn (1)
 | (1) |
Among the various thermoelectric materials, SnSe2 has received much attention because it has an intrinsically low κl due to its layered structure.19 The layered structure has a distinct difference between the bonding forces within layers and between layers. The bonds within the layer are covalent bonds, which are strong chemical bonds. The bonds between layers are van der Waals bonds, which are weaker secondary bonds. As a result, the κl along the axis of van der Waals bonding is low, which contributes to lowering κl.20–22 However, pristine SnSe2 has a low PF due to low σ.8 Wu et al. significantly increased Hall carrier concentration (nH) and Hall mobility (μH) compared to the pristine SnSe2 by Cl doping (12 mol%) at the Se sites. Consequently, the PF is significantly improved (0.0175 → 1.05 mW m−1 K−2) compared to pristine SnSe2 near room temperature.23 Wang et al. fabricated Cu-doped SnSe2, which resulted in a lower S compared to pristine SnSe2, but a higher PF (1.96 mW m−1 K−2) at 300 K due to an increase in nH.24 Li et al. achieved a high PF (0.35 mW m−1 K−2) by doping Ag at the Sn sites (1 mol%). The PF increase owing to the Ag doping could be attributed to the S improvement that outweighed the σ decrease. Although Ag doping improved the μH, it decreased the nH to an extent that the σ decreased with Ag doping.25 Zhou et al. improved the PF (1.2 mW m−1 K−2) of SnSe2 by co-doping Cu (between the layers of SnSe2) and Br (within the layers). The co-doping improved the σ by increasing the nH and μH at the same time.22 Recently, Liu et al. reported that Br doping at Se sites (SnSe2−xBrx for x = 0, 0.01, 0.03, 0.05, and 0.10) was effective in improving the PF.26 They confirmed that both the nH and μH increased (hence the σ increased) as the Br doping content increased up to x = 0.05. SnSe2 has a dimorphic structure, meaning that it can exist in two different crystal structures: hexagonal and unidentified structure.29–31 These two structures can coexist stably. Liu et al.26 found that the fraction of the hexagonal structure in SnSe2 increased for the Br doping content (x) smaller than 0.05 (although the hexagonal structure is already dominant). However, only the hexagonal structure was detected for x ≥ 0.05. In other words, the Br doping promoted the fraction of the hexagonal structure and increased the nH for x < 0.05, while it only increased the nH for x ≥ 0.05. However, how the fraction of hexagonal structure increase (induced by the Br doping) and the Br doping (when SnSe2 is fully hexagonal) affect the electronic band structure of SnSe2 is not studied.
In this study, changes in the electronic band structure of SnSe2 were investigated using the Single Parabolic Band (SPB) model both when Br doping increased the fraction of the hexagonal phase (SnSe2−xBrx for x < 0.05) and when it only increased the nH as the SnSe2−xBrx was fully hexagonal (x ≥ 0.05). The increase of the hexagonal phase improved the PF of the SnSe2−xBrx (x < 0.05) due to a significant increase in the non-degenerate mobility (μ0). The increase in the Br doping concentration (x) for x > 0.05 also improved the PF but this time by increasing the density-of-states effective mass  . The theoretical maximum PF of 1.27 mW m−1 K−2 was predicted when x = 0.03 (when the SnSe2−xBrx is not yet in full hexagonal phase) at room temperature. An additional 12% increase in 300 K zT (0.21 → 0.23) of SnSe1.7Br0.3 (x = 0.03) was expected once the nH was optimally tuned as the SPB model guided. Understanding the effects of Br doping on the electronic band structure of SnSe2, which changes with doping concentration, would enable the development of SnSe2 materials with tailored thermoelectric properties.
. The theoretical maximum PF of 1.27 mW m−1 K−2 was predicted when x = 0.03 (when the SnSe2−xBrx is not yet in full hexagonal phase) at room temperature. An additional 12% increase in 300 K zT (0.21 → 0.23) of SnSe1.7Br0.3 (x = 0.03) was expected once the nH was optimally tuned as the SPB model guided. Understanding the effects of Br doping on the electronic band structure of SnSe2, which changes with doping concentration, would enable the development of SnSe2 materials with tailored thermoelectric properties.
Single parabolic band model calculation
Electronic band parameters such as , μ0, weighted mobility (μW), and B-factor were calculated using the SPB model while assuming that only one parabolic band contributed to the electronic transport properties and that the acoustic phonon scattering mechanism was the dominant charge scattering mechanism. The purpose of employing the SPB model here is to guide the improvement of zT. Because most of the parameters in zT vary with nH, the optimization of the nH is essential for the zT increase. While the vast compositional space of promising thermoelectric materials offers immense potential, efficient optimization transcends solely experimental methods. While computationally intensive methods exist, for experimentalists, simplified Boltzmann transport equation-derived models often provide a pragmatic route to understand thermoelectric material properties. The SPB model, relying on a single parabolic band and effective mass, stands out for its simplicity and effectiveness. Notably, it enables complete characterization of the system using a minimal set of experimentally obtainable quantities (S, σ, κ, and nH), demonstrating its practical utility and simplicity.
, μ0, weighted mobility (μW), and B-factor were calculated using the SPB model while assuming that only one parabolic band contributed to the electronic transport properties and that the acoustic phonon scattering mechanism was the dominant charge scattering mechanism. The purpose of employing the SPB model here is to guide the improvement of zT. Because most of the parameters in zT vary with nH, the optimization of the nH is essential for the zT increase. While the vast compositional space of promising thermoelectric materials offers immense potential, efficient optimization transcends solely experimental methods. While computationally intensive methods exist, for experimentalists, simplified Boltzmann transport equation-derived models often provide a pragmatic route to understand thermoelectric material properties. The SPB model, relying on a single parabolic band and effective mass, stands out for its simplicity and effectiveness. Notably, it enables complete characterization of the system using a minimal set of experimentally obtainable quantities (S, σ, κ, and nH), demonstrating its practical utility and simplicity.
Estimation of density-of-states effective mass, 
Based on the experimental temperature-dependent S and 300 K nH from Liu et al.,26 nH-dependent S at 300 K was obtained. The  corresponding to the 300 K nH-dependent S measurement was then acquired by fitting the theoretical nH-dependent S constructed from the following eqn (2)–(4) to the nH-dependent S measurement.
corresponding to the 300 K nH-dependent S measurement was then acquired by fitting the theoretical nH-dependent S constructed from the following eqn (2)–(4) to the nH-dependent S measurement.
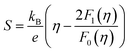 | (2) |
 | (3) |
 | (4) |
 . We changed η from −20 to 20 with a fitted
. We changed η from −20 to 20 with a fitted  to calculate a theoretical Seebeck pisarenko curve (S vs. nH) that agreed with the experimental nH-dependent S.26
to calculate a theoretical Seebeck pisarenko curve (S vs. nH) that agreed with the experimental nH-dependent S.26
Estimation of non-degenerate mobility, μ0
We computed theoretical nH-dependent Hall mobility (μH) using eqn (4) and (5).27
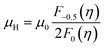 | (5) |
The μ0 included in μH (eqn (5)) was fitted so that the theoretical nH-dependent μH agreed with the experimental nH-dependent μH. When the nH was calculated to construct the theoretical nH-dependent μH, the same  fitted to construct the nH-dependent S of the same sample was adopted.
fitted to construct the nH-dependent S of the same sample was adopted.
Estimation of weighted mobility, μW, and B-factor, B
Once we have obtained the and μ0 of the SnSe2−xBrx samples, corresponding μW and B-factor were calculated using the following eqn (6) and (7), respectively.32–34 In eqn (6) and (7), the me is the electron rest mass.
and μ0 of the SnSe2−xBrx samples, corresponding μW and B-factor were calculated using the following eqn (6) and (7), respectively.32–34 In eqn (6) and (7), the me is the electron rest mass.
 | (6) |
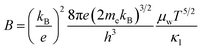 | (7) |
Results and discussion
Fig. 1(a) shows the experimental and calculated nH-dependent S of SnSe2−xBrx samples (x = 0, 0.01, 0.03, 0.05, 0.1) at 300 K. The symbols represent those measurements reported by Liu et al.26 (refer to Fig. S1(a) in ESI† for temperature-dependent S of SnSe2−xBrx at higher temperatures). The lines represent theoretical S as a function of nH for different x computed by using the SPB model. The experimental S (in symbols) decreases as x increases. The rate of S decrease is particularly high when x is low. For example, the experimental S of pristine SnSe2 (x = 0) decreases by more than 39% when x increases to 0.01 (475 → 289 μV K−1). In contrast, the experimental nH generally increases as x increases. For example, the nH of the x = 0.1 sample (4.6 × 1019 cm−3) is higher than that of the pristine sample (0.19 × 1019 cm−3) by more than a factor of 24. However, when x increases from 0.03 to 0.05, we observe a slight drop in nH from 2.0 × 1019 to 1.9 × 1019 cm−3. The x increase increases the fraction of the hexagonal phase within the sample only for x < 0.05. Because the SnSe2−xBrx samples with x ≥ 0.05 is fully hexagonal, the effect of Br doping would be different from that observed at x < 0.05. It is when the sample becomes fully hexagonal (x = 0.05) that we observe an exception in the general trend of increasing nH with an increasing x. The calculated nH-dependent S obtained by fitting (in lines) are all in agreement with the symbol data. This implies that the fitted
(in lines) are all in agreement with the symbol data. This implies that the fitted  accurately reflects the electronic band structure of the SnSe2−xBrx samples.
accurately reflects the electronic band structure of the SnSe2−xBrx samples.
 | ||
Fig. 1 (a) Experimental (symbols) and theoretical (lines) Hall carrier concentration (nH)-dependent Seebeck coefficient (S) of SnSe2−xBrx (x = 0–0.10) at 300 K.26 (b) Density-of-states effective mass  as a function of Br doping content (x) at 300 K. as a function of Br doping content (x) at 300 K. | ||
Fig. 1(b) shows the x-dependent 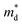 fitted using the SPB model at 300 K. Fig. 1(b) is divided into two regions: yellow and purple regions. The yellow region is when the SnSe2−xBrx samples exist as a dimorphic phase (hexagonal structure + unidentified structure). As the x increases from 0 to 0.05, the fraction of the hexagonal phase increases. At x = 0.05, the SnSe2−xBrx becomes fully hexagonal. The color of the background also changes from yellow to purple at x = 0.05, which means that the dimorphic structure transforms to the full hexagonal structure. For x ≥ 0.05, the samples are all hexagonal. So this region is colored in purple. The
fitted using the SPB model at 300 K. Fig. 1(b) is divided into two regions: yellow and purple regions. The yellow region is when the SnSe2−xBrx samples exist as a dimorphic phase (hexagonal structure + unidentified structure). As the x increases from 0 to 0.05, the fraction of the hexagonal phase increases. At x = 0.05, the SnSe2−xBrx becomes fully hexagonal. The color of the background also changes from yellow to purple at x = 0.05, which means that the dimorphic structure transforms to the full hexagonal structure. For x ≥ 0.05, the samples are all hexagonal. So this region is colored in purple. The  decreases from the pristine sample to x = 0.05 sample. For example, the
decreases from the pristine sample to x = 0.05 sample. For example, the 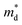 of pristine and x = 0.05 sample are 2.00 me and 1.26 me, respectively. This 37% decrease in
of pristine and x = 0.05 sample are 2.00 me and 1.26 me, respectively. This 37% decrease in 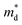 is closely related to the dimorphic structure changing to fully hexagonal phase. Once the Br doping finishes stabilizing the hexagonal phase, further Br doping starts to increase the
is closely related to the dimorphic structure changing to fully hexagonal phase. Once the Br doping finishes stabilizing the hexagonal phase, further Br doping starts to increase the  again. The
again. The  of the x = 0.1 sample increase to 1.83 me, which is approximately 45% heavier than that of x = 0.05 sample. The
of the x = 0.1 sample increase to 1.83 me, which is approximately 45% heavier than that of x = 0.05 sample. The  increase at x > 0.05 may be related to the band convergence. According to Kim et al.,34 there exists another conduction band near (in energy) the major conduction band in the calculated band structure of SnSe2. However, the change in μ0 with increasing x also needs to be evaluated to confirm a possible band convergence at x > 0.5. Our
increase at x > 0.05 may be related to the band convergence. According to Kim et al.,34 there exists another conduction band near (in energy) the major conduction band in the calculated band structure of SnSe2. However, the change in μ0 with increasing x also needs to be evaluated to confirm a possible band convergence at x > 0.5. Our  for SnSe2−xBrx determined by the SPB model spans a range of ∼1.0 to 2.0 me, aligning with values reported in previous studies also using the SPB model.35
for SnSe2−xBrx determined by the SPB model spans a range of ∼1.0 to 2.0 me, aligning with values reported in previous studies also using the SPB model.35
Fig. 2(a) shows the experimental and calculated nH-dependent μH at 300 K. The symbols represent the experimental nH-dependent μH of SnSe2−xBrx (x = 0, 0.01, 0.03, 0.05, 0.1) at 300 K reported by Liu et al.26 (refer to Fig. S1(b)† for temperature-dependent σ of SnSe2−xBrx at higher temperatures). The lines represent the nH-dependent μH calculated using the SPB model. The experimental μH initially increases as the x increases from 0 to 0.03. The amount of μH increase rapidly decreases as x approaches 0.03. When the x increases from 0.03 to 0.05, the change in μH is almost negligible. However, as x further increases to 0.1, the corresponding μH decreases significantly. The μH of the x = 0.05 sample (53.9 cm2 V−1 s−1) is approximately 8 times higher than that of the pristine sample (6.3 cm2 V−1 s−1). However, the μH of the x = 0.1 sample is 35% lower than that of the x = 0.05 sample. As the fraction of hexagonal structures occupying dimorphic structures increases up to x = 0.05, the corresponding μH increases. However, once the hexagonal structure is stabilized Br doping decreases the μH.
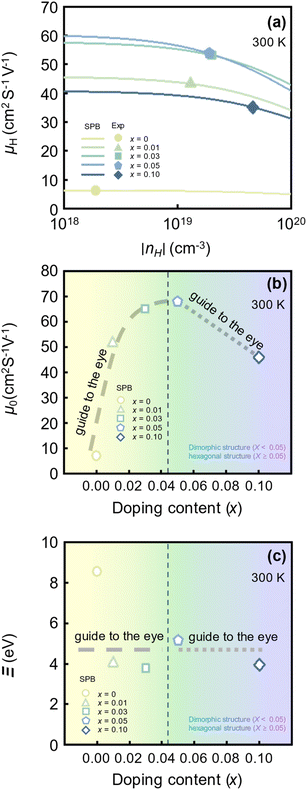 | ||
| Fig. 2 (a) Experimental (symbols) and theoretical (lines) Hall carrier concentration (nH)-dependent hall mobility (μH) of SnSe2−xBrx (x = 0–0.1) at 300 K.26 (b) Non-degenerate mobility (μ0) and (c) deformation potential (Ξ) as a function of Be doping content (x) at 300 K. | ||
Fig. 2(b) shows the x-dependent μ0 calculated using the SPB model. The μ0 as a function of x resembles an inverted U-shape. As the fraction of the hexagonal phase increases the μ0 saturates to 68.0 cm2 V−1 s−1 at x = 0.05. It is to be noted that the slight increase in hexagonal phase fraction significantly improves the μ0. For x ≥ 0.05, as the Br doping content increases in the fully hexagonal SnSe2−xBrx samples, the μ0 rapidly decreases back to 46.0 cm2 V−1 s−1 (x = 0.1). This is exactly the opposite of the trend observed in x-dependent  (Fig. 1(b)). If the change in μ0 with an increasing x for x ≥ 0.05 is negligible, we could have concluded that the
(Fig. 1(b)). If the change in μ0 with an increasing x for x ≥ 0.05 is negligible, we could have concluded that the 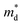 increase for x ≥ 0.05 is due to band convergence. On the contrary, the
increase for x ≥ 0.05 is due to band convergence. On the contrary, the 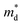 increase accompanied by a decrease in μ0 can be characterized by a simple band flattening which is not beneficial to the PF improvement. However, while the majority band is being flattened, the neighbouring band may also contribute to the electronic transport due to Br doping. This can be evaluated when the weighted mobility (μW) is calculated.
increase accompanied by a decrease in μ0 can be characterized by a simple band flattening which is not beneficial to the PF improvement. However, while the majority band is being flattened, the neighbouring band may also contribute to the electronic transport due to Br doping. This can be evaluated when the weighted mobility (μW) is calculated.
Fig. 2(c) shows the x-dependent deformation potential (Ξ) calculated by the SPB model. The Ξ is closely related to the μ0 as defined in eqn (8).
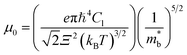 | (8) |
 are the elastic constant and the single band mass, respectively. The
are the elastic constant and the single band mass, respectively. The  is coupled to
is coupled to 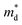 as shown below.
as shown below.
 | (9) |
The product between NV2/3 and 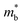 , where NV is the valley degeneracy, defines the
, where NV is the valley degeneracy, defines the  . When the
. When the 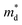 increase is driven by the NV increase (no change in
increase is driven by the NV increase (no change in 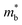 ), the band convergence occurs.13,28 However, when
), the band convergence occurs.13,28 However, when 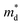 increase is driven by the
increase is driven by the  increase (no change in NV), a band flattening occurs. For this reason, the nature of
increase (no change in NV), a band flattening occurs. For this reason, the nature of  increase needs to be evaluated by the corresponding change in μ0. Unlike μ0, the Ξ is independent of
increase needs to be evaluated by the corresponding change in μ0. Unlike μ0, the Ξ is independent of  and captures the strength of the carrier–phonon interaction. According to Fig. 2(c), Br doping in SnSe2 decreases the Ξ, but varying Br doping content (x) does not have a strong impact on the Ξ. For example, the Ξ of SnTe decreased by more than 55% when it is doped with x = 0.01 Br (8.56 → 3.79 eV). However, it remained relatively constant for increasing x. In other words, neither changing the hexagonal phase (x < 0.05) nor increasing the Br doping content in a stabilized hexagonal phase (x ≥ 0.05) has a significant impact on how phonons scatter charged carriers.
and captures the strength of the carrier–phonon interaction. According to Fig. 2(c), Br doping in SnSe2 decreases the Ξ, but varying Br doping content (x) does not have a strong impact on the Ξ. For example, the Ξ of SnTe decreased by more than 55% when it is doped with x = 0.01 Br (8.56 → 3.79 eV). However, it remained relatively constant for increasing x. In other words, neither changing the hexagonal phase (x < 0.05) nor increasing the Br doping content in a stabilized hexagonal phase (x ≥ 0.05) has a significant impact on how phonons scatter charged carriers.
Fig. 3(a) shows the x-dependent μW of SnSe2−xBrx (x = 0.0–0.10) calculated by using the SPB model at 300 K. The μW, which is defined as the product of μ0 and  (as presented in eqn (6)), captures the potential of a material achieve a high PF, as it depends on both the μ0 and the
(as presented in eqn (6)), captures the potential of a material achieve a high PF, as it depends on both the μ0 and the  . Compared to the pristine SnSe2 sample (x = 0.0), the Br-doped SnSe2 samples (x > 0.0) have a significantly higher μW. When Br doping increases the fraction of the hexagonal phase (x < 0.05), the μW increases significantly (guide-to-the-eye in grey line). For example, the μW of the pristine sample (x = 0.0) and the x = 0.03 sample are 20.22 and 139.39 cm2 V−1 s−1, respectively, which is a 5.8-fold increase. Additional Br doping on stabilized hexagonal phase (x ≥ 0.05) also improves the μW (guide-to-the-eye in grey line). Although the μW increase is observed for both x < 0.05 and x ≥ 0.05 regions with increasing x, the reason behind the μW improvement differs. When x < 0.05, the μW increase with x is due to the μ0 increase (Fig. 2(b)), but when x ≥ 0.05, the μW increase can be attributed to the
. Compared to the pristine SnSe2 sample (x = 0.0), the Br-doped SnSe2 samples (x > 0.0) have a significantly higher μW. When Br doping increases the fraction of the hexagonal phase (x < 0.05), the μW increases significantly (guide-to-the-eye in grey line). For example, the μW of the pristine sample (x = 0.0) and the x = 0.03 sample are 20.22 and 139.39 cm2 V−1 s−1, respectively, which is a 5.8-fold increase. Additional Br doping on stabilized hexagonal phase (x ≥ 0.05) also improves the μW (guide-to-the-eye in grey line). Although the μW increase is observed for both x < 0.05 and x ≥ 0.05 regions with increasing x, the reason behind the μW improvement differs. When x < 0.05, the μW increase with x is due to the μ0 increase (Fig. 2(b)), but when x ≥ 0.05, the μW increase can be attributed to the  increase (Fig. 1(b)). The increase in
increase (Fig. 1(b)). The increase in  with increasing x at x ≥ 0.05 is due to both band flattening and band convergence. Specifically, the lowest conduction band that contributes majorly to electronic transports becomes heavier, while the second lowest conduction band approaches the lowest conduction band in energy as Br is doped into the fully hexagonal SnSe2. Evidence for band flattening and band convergence is provided by the decrease in μ0 (Fig. 2(b)) and the increase in μW (Fig. 3(a)) at x ≥ 0.05, respectively. The discontinuity in the μW when x increases from 0.03 to 0.05 is due to a sudden drop in the
with increasing x at x ≥ 0.05 is due to both band flattening and band convergence. Specifically, the lowest conduction band that contributes majorly to electronic transports becomes heavier, while the second lowest conduction band approaches the lowest conduction band in energy as Br is doped into the fully hexagonal SnSe2. Evidence for band flattening and band convergence is provided by the decrease in μ0 (Fig. 2(b)) and the increase in μW (Fig. 3(a)) at x ≥ 0.05, respectively. The discontinuity in the μW when x increases from 0.03 to 0.05 is due to a sudden drop in the 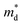 of the fully hexagonal phase x = 0.05 sample (Fig. 1(b)). Although the unidentified phase comprises a small fraction of the x = 0.03 sample, its conversion to hexagonal phase is responsible for the decrease in
of the fully hexagonal phase x = 0.05 sample (Fig. 1(b)). Although the unidentified phase comprises a small fraction of the x = 0.03 sample, its conversion to hexagonal phase is responsible for the decrease in 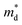 .
.
 | ||
| Fig. 3 (a) Calculated weighted mobility (μW) of SnSe2−xBrx (x = 0.0–0.10) estimated with varying Br doping content (x) at 300 K. (b) Calculated and experimental Hall carrier concentration (nH)-dependent power factor (PF) of SnSe2−xBrx (x = 0.0–0.10) at 300 K.26 | ||
Fig. 3(b) shows the PF as a function of the nH. The experimentally measured PF reported by Liu et al.26 is represented by the symbols, while the theoretically calculated PF is represented by the lines. Experimentally, Br doping improves the PF in both x < 0.05 and x ≥ 0.05 regions. When x < 0.05, the PF of the x = 0.03 sample (1.05 mW m−1 K−2) is approximately 25 times higher than that of the pristine SnS2 sample (0.04 mW m−1 K−2). For x ≥ 0.05, the PF of the x = 0.10 sample (1.00 mW m−1 K−2) is 27% higher than that of the x = 0.05 sample (0.79 mW m−1 K−2). From the x-dependent μW (Fig. 3(a)), we found that both band flattening and band convergence are present in the x = 0.10 sample. However, the theoretical maximum PF of the x = 0.10 sample (1.02 mW m−1 K−2) is not as high as that of the x = 0.03 sample (1.27 mW m−1 K−2). According to the SPB model, the PF of the x = 0.03 sample can be enhanced by more than 21% with an appropriate optimization of the nH (1.05 → 1.27 mW m−1 K−2). The theoretical maximum PF and its corresponding nH predicted by the SPB model exhibit reasonable agreement with those obtained from Density Functional Theory (DFT) calculations. For example, the SPB model predicts a peak PF of 0.17 mW m−1 K−2 for pristine SnSe2 (x = 0) at nH = 8 × 1019 cm−3 (Fig. 3(b)), while DFT calculations yield a peak PF of 0.13 mW m−1 K−2 at n = 5 × 1019 cm−3.36 It is important to note that the maximum PF is predicted to occur before the sample is fully hexagonal.
Fig. 4(a) shows the x-dependent B-factor of SnSe2−xBrx (x = 0.0–0.10) at 300 K calculated by the SPB model. The B-factor, which is proportional to the ratio of μ0 to κl, is related to the theoretically achievable zT (eqn (7)). The trend observed in the B-factor is similar to that observed in the μ0, as shown in Fig. 3(a). This is possible because the κl of the Br-doped SnSe2 decreases linearly with increasing x (Fig. 4(b)). When Br was first doped into SnSe2 with x = 0.01, its κl increased by 11% compared to the pristine SnSe2 (1.34 → 1.48 W m−1 K−1). However, when x was increased further, the κl decreased gradually. Both increasing the hexagonal phase fraction (0 < x < 0.05) and increasing the Br doping in the full hexagonal phase (x ≥ 0.05) reduced the κl (refer to Fig. S1(c)† for temperature-dependent total thermal conductivity (κtot) of SnSe2−xBrx at higher temperatures). The calculated Lorenz number (L) and κe used to estimate κl are provided in Fig. S2.† Initial increase in the κl of the x = 0.01 sample requires further study. While an initial increase in κl upon Br doping of SnSe2 has been reported previously,37 similar observations in Cl-doped SnSe2 suggest a broader phenomenon beyond specific dopant species.38 Elucidating the underlying mechanism governing this low-concentration dopant-induced thermal conductivity enhancement warrants further investigation. The effect of decreasing the unidentified phase on the B-factor is stronger than that of increasing the Br doping content in the fully hexagonal phase. Although the B-factor improved by a factor of 6 when pristine SnSe2 was doped with x = 0.03 (0.01 → 0.06), once SnSe2 was fully hexagonal, additional Br doping only improved the B-factor by 25% as x increased from 0.05 to 0.10 (0.04 → 0.05). However, if the x is increased beyond 0.10, the B-factor of the sample may become higher than that of the x = 0.03 sample due to the combined effects of band convergence and κl reduction becoming stronger.
 | ||
| Fig. 4 Calculated (a) B-factor and (b) lattice thermal conductivity (κl) of SnSe2−xBrx (x = 0.0–0.10) at 300 K. (c) Calculated and experimental27 zT of SnSe2−xBrx (x = 0.0–0.10) with varying Hall carrier concentration (nH). | ||
Fig. 4(c) shows experimental and calculated nH-dependent zT at 300 K (refer to Fig. S1(d)† for temperature-dependent zT of SnSe2−xBrx at higher temperatures). The symbols represent the measured values.26 The lines represent zT computed by the SPB model-based calculation. The calculated maximum zT of pristine SnSe2 is low, as illustrated in Fig. 4(c). Temperature-dependent zT calculations for pristine SnSe2 below 300 K are presented in Fig. S1 (ESI†), revealing a maximum at 300 K exceeding those at 50 and 100 K. This finding underscores the pronounced temperature-dependent zT of SnSe2.24 However, the maximum zT improves drastically as Br is doped into SnSe2. For example, the calculated maximum zT of pristine SnSe2 and x = 0.03 samples are 0.04 and 0.23, respectively, which is an increase of more than 5 times. Once the SnSe2 is a fully hexagonal phase (x ≥ 0.05), additional Br doping is also beneficial to the calculated maximum zT. The calculated maximum zT of the x = 0.05 and 0.10 samples are 0.16 and 0.19, respectively (19% improvement in zT). According to the SPB model calculations, adjusting the nH of the x = 0.03 sample to 3.6 × 1019 cm−3 can improve the zT to 0.23, an approximately 10% increase compared to the experimental zT. Furthermore, it is highly likely that further Br doping beyond x = 0.10 may result in even higher zT because of the interplay between the band convergence and intensified point-defect phonon scattering.
Conclusions
In summary, the effect of Br doping on the electronic band structure of dimorphic SnSe2 (SnSe2−xBrx for x = 0, 0.01, 0.03, 0.05, and 0.10) is investigated using the Single Parabolic Band (SPB) model. For Br doping concentrations (x) < 0.05, the fraction of the majority hexagonal phase increases with x, while the other phase remains unidentified. On the contrary, for x ≥ 0.05, the Br-doped SnSe2 is fully hexagonal. For all x, the Hall carrier concentration (nH) increases with x. The mechanisms underlying the power factor improvement of Br-doped SnSe2 with increasing nH differ depending on the x. For x < 0.05, the increasing hexagonal phase significantly improves the mobility, while for the x ≥ 0.05, the power factor is improved by a combination of band convergence and band flattening. The highest power factor is predicted when a small amount of unidentified phase exists in the SnSe2−xBrx (x = 0.03). Characterization of the unidentified phase in the dimorphic SnSe2 is to be carried out to tailor the thermoelectric properties of the SnSe2.Author contributions
Se-Jun Kim: conceptualization, investigation, writing – original draft. Minsu Heo: investigation, software, writing – original Draft. Sang-il Kim: validation, methodology, writing – original draft. Hyunjin Park: data curation. Jeong-Yeon Kim: visualization. Won-Seon Seo: validation. Hyun-Sik Kim: supervision, funding acquisition, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (RS-2023-00212959). This research was also supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2019R1A6A1A11055660).Notes and references
- T. Wu, L. Xia, M. Zhuang, J. Pan, J. Liu, W. Dai, Z. Zhao, M. Zhang, X. Shen, P. He, J. Zhang and Y. Qin, J. Mar. Sci. Eng., 2023, 11, 9 CrossRef.
- O. Adam, N. Liberty-Levi, M. Byrne and T. Birner, Geophys. Res. Lett., 2022, 50, e2022GL102546 CrossRef.
- A. A. Khasnis and M. D. Nettleman, Arch. Med. Res., 2005, 36, 689–696 CrossRef PubMed.
- J. Lee, K. A. Lin, S. Jung and E. E. Kwon, Chem. Eng. J., 2023, 452, 139218 CrossRef CAS.
- S. LeBlanc, Sustainable Mater. Technol., 2014, 1–2, 26–35 CrossRef.
- P. Fernández-Yáñez, V. Romero, O. Armas and G. Cerretti, Appl. Therm. Eng., 2021, 196, 117291 CrossRef.
- Y. Zheng, Q. Zhang, X. Su, H. Xie, S. Shu, T. Chen, G. Tan, Y. Yan, X. Tang, C. Uher and G. J. Snyder, Adv. Energy Mater., 2014, 5, 1401391 CrossRef.
- A. Pham, T. Vu, C. Cheng, T. Trinh, J.-E. Lee, H. Ryu, C. Hwang, S.-K. Mo, J. Kim, L. Zhao, A. Duong and S. Cho, ACS Appl. Energy Mater., 2020, 3, 10787–10792 CrossRef CAS.
- D. Enescu and E. O. Virjoghe, Renew. Sust. Energ. Rev., 2014, 38, 903–916 CrossRef.
- C. Zhou, Y. K. Lee, Y. Yu, S. Byun, Z.-Z. Luo, H. Lee, B. Ge, Y.-L. Lee, X. Chen, J. Y. Lee, O. Cojocaru-Mirédin, H. Chang, J. Im, S.-P. Cho, M. Wuttig, V. P. Dravid, M. G. Kanatzidis and I. Chung, Nat. Mater., 2021, 20, 1378–1384 CrossRef CAS PubMed.
- A. Sakai, T. Kanno, K. Takahashi, H. Tamaki, H. Kusada, Y. Yamada and H. Abe, Sci. Rep., 2014, 4, 6089 CrossRef CAS PubMed.
- Y. Pei, H. Wang and G. J. Snyder, Adv. Mater., 2012, 24, 6125–6135 CrossRef CAS PubMed.
- K. H. Lee, S.-i. Kim, H.-S. Kim and S. W. Kim, ACS Appl. Energy Mater., 2020, 3, 2214–2223 CrossRef CAS.
- S. Ning, S. Huang, Z. Zhang, N. Qi, M. Jiang, Z. Chen and X. Tang, J. Materiomics, 2022, 8, 1086–1094 CrossRef.
- M. Heo, S.-H. Kwon, S.-i. Kim, H. Park, K. H. Lee and H.-S. Kim, J. Alloys Compd., 2023, 954, 170144 CrossRef CAS.
- Y. Zheng, T. J. Slade, L. Hu, X. Y. Tan, Y. Luo, Z.-Z. Luo, J. Xu, Q. Yan and M. G. Kanatzidis, Chem. Soc. Rev., 2021, 50, 9022–9054 RSC.
- V. Karthikeyan, S. L. Oo, J. U. Surjadi, X. Li, V. C. S. Theja, V. Kannan, S. C. Lau, Y. Lu, K. Lam and V. A. L. Roy, ACS Appl. Mater. Interfaces, 2021, 13, 58701–58711 CrossRef CAS PubMed.
- Y. Zhang, Z. Li, S. Singh, A. Nozariasbmarz, W. Li, A. Genç, Y. Xia, L. Zheng, S. H. Lee, S. K. Karan, G. K. Goyal, N. Liu, S. M. Mohan, Z. Mao, A. Cabot, C. Wolverton, B. Poudel and S. Priya, Adv. Mater., 2022, 35, 2208994 CrossRef PubMed.
- Y. Wu, W. Li, A. Faghaninia, Z. Chen, J. Li, X. Zhang, B. Gao, S. Lin, B. Zhou, A. Jain and Y. Pei, Mater. Today Phys., 2017, 3, 127–136 CrossRef.
- G. Li, G. Ding and G. Gao, J. Condens. Matter Phys., 2016, 29, 015001 CrossRef PubMed.
- S. Bai, M. Wu, J. Zhang, D. Luo, D. Wan, X. Li and S. Tang, Chem. Eng. J., 2023, 455, 140832 CrossRef CAS.
- C. Zhou, Y. Yu, X. Zhang, Y. Cheng, J. Xu, Y. K. Lee, B. Yoo, O. Cojocaru-Mirédin, G. Liu, S.-P. Cho, M. Wuttig, T. Hyeon and I. Chung, Adv. Funct. Mater., 2019, 30, 1908405 CrossRef.
- S. Wu, C. Liu, Z. Wu, L. Miao, J. Gao, X. Hu, J. Chen, Y. Zheng, X. Wang, C. Shen, H. Yang and X. Zhou, Ceram. Int., 2019, 45, 82–89 CrossRef CAS.
- J. Wang, X. Jia, S. Lou, G. Li and S. Zhou, ACS Omega, 2020, 5, 12409 CrossRef CAS PubMed.
- F. Li, Z. Zheng, W. Wang, J.-F. Li, B. Li, A. Zhong, J. Luo and P. Fan, J. Mater. Sci., 2017, 52, 10506–10516 CrossRef CAS.
- M. Liu, J. Zhang, J. Xu, B. Hu, B. Liu, K. Sun, Y. Yang, J. Wang and B. Du, J. Solid State Chem., 2020, 289, 121468 CrossRef CAS.
- H. Park, S.-i. Kim, J.-Y. Kim, S.-M. Hwang and H.-S. Kim, Ceramics, 2023, 6, 504–513 CrossRef CAS.
- H.-S. Kim, N. A. Heinz, Z. M. Gibbs, Y. Tang, S. D. Kang and G. J. Snyder, Mater. Today, 2017, 20, 452–459 CrossRef CAS.
- V. P. Bhatt, K. Gireesan and G. R. Pandya, J. Cryst. Growth, 1989, 96, 649–651 CrossRef CAS.
- L. Amalraj, M. Jayachandran and C. Sanjeeviraja, Mater. Res. Bull., 2004, 39, 2193–2201 CrossRef CAS.
- M. Kumar, S. Rani, Y. Singh, K. S. Gour and V. N. Singh, RSC Adv., 2021, 11, 6477–6503 RSC.
- H. Naithani and T. Dasqupta, ACS Appl. Energy Mater., 2020, 3, 2200–2213 CrossRef CAS.
- M. Kim, S.-i. Kim, S. W. Kim, H.-S. Kim and K. H. Lee, Adv. Mater., 2021, 33, 2005931 CrossRef CAS PubMed.
- S.-i. Kim, J. Bang, J. An, S. Hong, G. Bang, W. H. Shin, T. Kim and K. Lee, J. Alloys Compd., 2021, 868, 159161 CrossRef CAS.
- Y. Wu, W. Li, A. Faghaninia, Z. Chen, J. Li, X. Zhang, B. Gao, S. Lin, B. Zhou, A. Jain and Y. Pei, Mater. Today, 2017, 3, 127–136 CrossRef.
- D. Sree Sourav, Md. Golam Rosul and M. Zebarjadi, J. Phys. Chem. C, 2017, 127, 6916–6924 Search PubMed.
- C. Zhou, Y. Yu, X. Zhang, Y. Cheng, J. Xu, Y. K. Lee, B. Yoo, O. Cojocaru-Mirédin, G. Liu, S.-P. Cho, M. Wuttig, T. Hyeon and I. Chung, Adv. Funct. Mater., 2020, 30, 1908405 CrossRef CAS.
- S. Wu, C. Liu, Z. Wu, L. Miao, J. Gao, X. Hu, J. Chen, Y. Zheng, X. Wang, C. Shen, H. Yang and X. Zhou, Ceram. Int., 2019, 45, 82 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra07751a |
| ‡ These authors contributed equally to this study. |
| This journal is © The Royal Society of Chemistry 2024 |
