Spiro-centre substitution effects in the intramolecular spin–spin interactions of spirobiacridine diradicals

Abstract

Spirobiacridine diradicals exhibit intramolecular ferromagnetic coupling owing to their unique cruciform structure (D_2d molecular symmetry). In this study, novel spirodiradicals 2,2′,7,7′-tetra(tert-butyl)-9,9′(10H,10′H)-spirobisilaacridine-10,10′-dioxyl (1-Si) and a Ge-centred derivative (1-Ge) were synthesized. These compounds exhibited a ground triplet spin state (S = 1), which was confirmed by spectroscopic and magnetic studies. Interestingly, the exchange coupling constant of 1-Ge (+19.3(2) K) was larger than that of 1-Si (+14.2(3) K), although the distance between intramolecular radical centres was increased owing to its larger bonding lengths. This result implies that σ*(Si–C_α)–π* hyperconjugation has a negative effect on spin–spin coupling.

---

Introduction

Organic radicals have many applications in spin trapping,¹ spin labelling,² dynamic nuclear polarization (DNP),³ organic catalysts,⁴ photochromic materials⁵ and molecular magnetic materials.⁶ In molecules containing more than two unpaired spins, spin–spin interaction is determined by two factors: (i) spin polarization and (ii) molecular symmetry. The former exploits the periodicity of the π-conjugation system⁷ and has been extensively studied in this field,⁸ whereas the latter utilizes the degeneracy of orbitals caused by symmetry.⁹ However, in this approach it is difficult to suppress Jahn–Teller distortions,¹⁰ resulting in slower progress compared to the spin-polarization approach.

The compound 9,9′(10H,10′H)spirobiacridine-10,10′-dioxyl (SBDO-C) has two orthogonal π systems, resulting in D_2d symmetry.¹¹ Each dihydroacridine moiety possesses one unpaired electron, and singly occupied molecular orbitals (SOMOs) are symmetric to the bisecting plane, resulting in the ground triplet state (S = 1). In fact, the spin state of this spirobiacridine diradical is dictated by its tetra(tert-butyl) derivative, 2,2′,7,7′-tetra(tert-butyl)-9,9′(10H,10′H)spirobiacridine-10,10′-dioxyl (1-C).¹² While the structural analysis of 1-C recognises the distortion in these acridine moieties, deviating from a strict D_2d symmetry, magnetic studies confirm the ground triplet state (2J/k_B = +23(1) K in ). Spirobiacridine diradicals, which can manifest the triplet state despite structural distortion, represent an ideal class of substances for exploring molecular designs based on molecular symmetry.¹³

A spiro centre plays a crucial role in the development of spiro compounds. Group 14 elements such as C, Si and Ge have been intensively studied.^14–16 In particular, silicon compounds exhibit a significant reduction in lowest unoccupied molecular orbital (LUMO) energy levels in π-conjugated systems, which is attributed to a robust σ*(Si–C) and π* hyperconjugation effect.¹⁷ The effect of spiro-centre elements on intramolecular spin–spin interaction through a spiro-skeleton has not been sufficiently investigated.¹⁸ In this study, we synthesized Si and Ge substitutes of 1-C, namely 2,2′,7,7′-tetra(tert-butyl)-9,9′(10H,10′H)spirobisilaacridine-10,10′-dioxyl (1-Si) and 2,2′,7,7′-tetra(tert-butyl)-9,9′(10H,10′H)spirobigermaacridine-10,10′-dioxyl (1-Ge). Based on the theoretical and experimental results, both compounds exhibited ground triplet states. Interestingly, the intramolecular exchange coupling constant of 1-Ge was larger than that of 1-Si, despite the longer distance between the radical centres.

Results and discussion

Synthesis and characterization

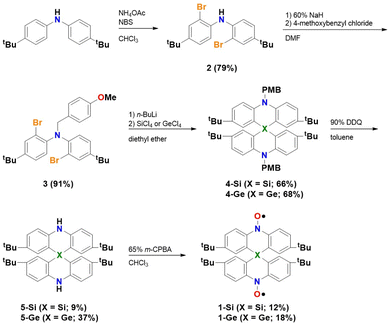
Compounds 1-Si and 1-Ge were synthesized according to the procedure shown in Scheme 1. The starting material, bis(4-tert-butylphenyl)amine, was dibrominated at the 2,2′-position using N-bromosuccinimide (NBS), resulting in 2. The amino site of 2 was protected by a p-methoxybenzyl (PMB) group. The subsequent lithiation of 3 with n-butyllithium was followed by the addition of tetrachlorosilane/germane, resulting in the formation of the spiro compounds 4-Si and 4-Ge. This spiro annulation reaction was based on the method reported by Ito and co-workers.¹⁹ After the deprotection reaction with 2,3-dichloro-5,6-dicyano-1,4-benzoquinone (DDQ), 1-Si and 1-Ge were synthesized via the oxidation of diamines 5-Si and 5-Ge, respectively, with m-chloroperbenzoic acid (m-CPBA). Dark red platelet polycrystals of 1-Si and 1-Ge were obtained through recrystallization from CH₂Cl₂ and n-hexane. Both compounds had a melting point above 200 °C, indicating their high thermal stability. The products were characterized using spectroscopic and X-ray crystallographic analyses.

Scheme 1 Synthetic routes for 1-Si and 1-Ge.

Electron spin resonance (ESR) spectroscopy

The ESR spectra of 1-Si and 1-Ge, measured in toluene at RT, showed a five-line pattern (Figs. S1 and S2†), which is attributed to the presence of two nitrogen atoms (I = 1) derived from intramolecular exchange coupling. These spectra reproduce those of 1-C.¹² The g values of 1-Si and 1-Ge were calculated to be 2.0064 and 2.0061, respectively. The hyperfine splitting constants a_N were characterized as 0.46 and 0.47 mT, respectively.

The frozen-solution ESR spectra of 1-Si and 1-Ge in degassed toluene at 100 K are shown in Figs. 1a and b, respectively. The experimental spectra exhibit the sum of zero-field splitting (ZFS) structures based on D_2d (D ≠ 0 and E = 0) and D₂ (D ≠ 0 and E ≠ 0) symmetries. The small central signal can be assigned to monoradicals as an impurity. These findings provide a good reproduction of the results for 1-C. In addition, a forbidden signal with |Δm_s| = 2 appeared at half field (Figs. S3 and S4†), indicating the presence of the triplet spin state (S = 1). ZFS parameters for 1-Si and 1-Ge were estimated using EasySpin software.²⁰ For 1-Si, the experimental spectrum was reproduced by simulating D₂/D_2d/monoradical components with an intensity ratio of 89.6%/6.6%/3.8%. The simulation gave g_xx = g_yy = 2.0048, g_zz = 2.0087, |D| = 7.37 × 10⁻³ mT and |E| = 7.67 × 10⁻⁴ mT for D₂ symmetry; g_xx = 2.0061, g_yy = 2.0036, g_zz = 2.0035 and |D| = 7.38 × 10⁻³ mT for D_2d symmetry; and g_xx = 2.0046, g_yy = 2.0039 and g_zz = 2.0147 for monoradical impurity. For 1-Ge, the experimental spectrum was reproduced by simulating three components with the intensity ratio of 91.2%, 5.6% and 3.2%. The ZFS parameters were g_xx = 2.0046, g_yy = 2.0048, g_zz = 2.0081, |D| = 6.64 × 10⁻³ mT and |E| = 7.83 × 10⁻⁴ mT for the D₂ symmetry; g_xx = g_yy = 2.0048, g_zz = 2.0019 and |D| = 6.67 × 10⁻³ mT for D_2d symmetry; and g_xx = 2.0047, g_yy = 2.0045 and g_zz = 2.0082 for monoradical impurity. The experimental |D| and g values of D₂ symmetry for 1-Si and 1-Ge led to dipole–dipole distances of 7.1 and 7.3 Å, respectively, from the point dipole approximation 2D = 3g²μ_B/r³. These values reproduced the crystallographically determined distances of 7.4 Å for 1-Si and 7.5 Å for 1-Ge (more details are given below). Compound 1-C had a dipole–dipole distance of 6.9 Å and an experimentally determined distance of 7.2 Å.¹²

Fig. 1 Frozen-solution ESR spectra for (a) 1-Si and (b) 1-Ge in degassed toluene solution at 100 K. Red and blue solid lines represent the experimental spectra. Black solid lines represent the simulated spectra. Red, blue and green markers correspond to D₂, D_2d and monoradical components.

Crystal structures

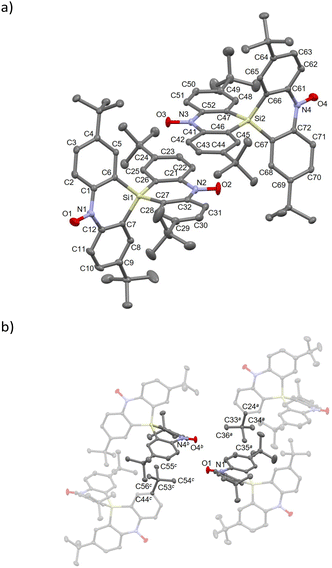
Compound 1-Si crystallized in the triclinic P1̄ space group (Table S1†). The crystal structure and molecular packing diagram are shown in Fig. 2. Two crystallographically independent molecules were present in a unit cell. The two independent molecules were denoted as 1-Si-a (the Si1 atom) and 1-Si-b (the Si2 atom). The N1–O1, N2–O2, N3–O3 and N4–O4 bond lengths are 1.288(1), 1.289(1), 1.288(1) and 1.288(1) Å, respectively, which are close to the typical values for nitroxides.²¹ The bond lengths between Si and neighbouring carbon (C_α) atoms are 1.850(1)–1.866(1) Å around the Si1 atom and 1.850(1)–1.868(1) Å around the Si2 atom. These values reproduce those of typical Si–C_sp² bonds.^{14c,16b,22,23} The Si atom connects two dihydroacridines, forming a cruciform structure with dihedral angles of 80.33° and 82.02° between the two dihydroacridine moieties. In addition, the dihedral angles between the terminal phenyl rings are 28.78° and 6.42° for the N1 and N2 sides, respectively, in 1-Si-a and 5.17° and 38.67° for the N3 and N4 sides, respectively, in 1-Si-b. High-planarity skeletons (small dihedral angles of 6.42 and 5.17°) result from the intermolecular π–π contact between the dihydroacridines, including the N2 and N3 atoms, as shown in Fig. 2a. In this contact, the N2–O2 and N3–O3 sites are positioned above the C41–C46 and C21–C26 sites, respectively. The N2⋯C41 and N3⋯C21 distances are 3.558(1) and 3.546(1) Å, respectively, slightly exceeding the sum of the van der Waals (vdW) radii (C/N: 3.3 Å),²⁴ indicating weak intermolecular contacts. Alternatively, low-planarity skeletons (large dihedral angles of 28.78 and 38.67°) appeared to be related to the intermolecular contacts around the tert-butyl groups (C33 and C53 atoms) and the dihydroacridine moieties (Fig. 2b). The intermolecular O1⋯O4 distance is 3.828(1) Å, exceeding the sum of the vdW radii (O/O: 3.04 Å).²⁴ Nevertheless, this can still contribute to strong intermolecular antiferromagnetic coupling owing to the direct contacts between the radical centres.

Fig. 2 Crystal structures of 1-Si. (a) Asymmetric units in the unit cell. (b) Intermolecular contacts around the O1 and O4 atoms. Symmetry codes: a = 1−x, 2−y, 1−z; b = x, 1+y, z; c = 1−x, 2−y, −z. Thermal ellipsoids for non-hydrogen atoms are drawn at the 50% probability level. The H atoms are omitted for clarity. The major configuration is shown with disordered tert-butyl groups.

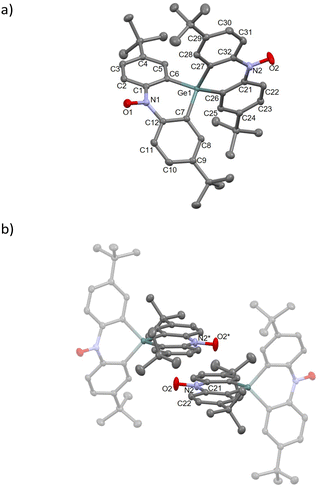
The compound 1-Ge crystallized in the monoclinic P2₁/n space group (Table S1†). The crystal structure and molecular packing diagram are shown in Fig. 3. The N1–O1 and N2–O2 bond lengths are 1.2868(15) and 1.2846(16) Å, respectively, which indicates the presence of a nitroxide group.²¹ Ge–C_α bond lengths are 1.9345(14)–1.9445(14) Å, which reproduce typical Ge–C_sp² bonds.^16b,23,25 The Ge atom connects two dihydroacridines, forming a cruciform structure with a dihedral angle of 84.99°. In addition, the dihedral angles between the terminal phenyl rings are 40.20° and 4.61° for the N1 and N2 sides, respectively. The former is attributed to the contact with the neighbouring tert-butyl groups and 1-Si. The O1 atom is located at 5.653(2) Å from the nearest neighbouring O atom (O1*), suggesting weak intermolecular interaction. Alternatively, a high-planarity skeleton results from the intermolecular π–π contact between the dihydroacridine moieties, as shown in Fig. 3b. The N2–O2 site is positioned above the C21–C22 site, and the O2⋯C21 and N2⋯C22 distances are 3.340(2) and 3.396(2) Å, respectively. These values are close to the sum of the vdW radii (C/O, 3.2 Å; C/N, 3.3 Å),²⁴ indicating strong interactions compared with 1-Si.

Fig. 3 Crystal structures of 1-Ge. (a) Asymmetric units in the unit cell. (b) Intermolecular contacts around the O2 atom. Symmetry code: * = 2−x, 1−y, 1−z. Thermal ellipsoids for non-hydrogen atoms are drawn at the 50% probability level. The H atoms are omitted for clarity.

Theoretical calculations

Density functional theory (DFT) calculations were performed for 1-Si (1-Si-a and 1-Si-b units) and 1-Ge during atomic coordination analysis based on the above crystallographic study. The calculated spin densities of the triplet (T) and broken-symmetry singlet (BS) states were mapped onto the molecular skeleton shown in Figs. S5–S7.† The triplet and singlet energy states are summarized in Tables S2–S4.† Exchange coupling constants 2J/k_B were +12.93, +11.25 and +13.81 K, respectively, as estimated by using Yamaguchi's equation.²⁶ Both 1-Si and 1-Ge, as well as 1-C (2J/k_B = +30.26 K),¹² exhibit the ground triplet state.

The exchange coupling constant 2J/k_B of +13.81 K for 1-Ge was larger than that of +12.93 and +11.25 K (a mean value of 12.09 K) for 1-Si. Despite the increase in the distance between the intramolecular radical centres (according to the ESR and structural studies), the observed enhancement in 2J/k_B is an intriguing result. However, the MOs for 1-Si-a, 1-Si-b and 1-Ge are complicated owing to the distortion of the spiro structure and the dihydroacridine moieties. Therefore, we confirmed the magnitude of the interaction by the optimized structure for model compounds, SBDO-C and the Si and Ge derivatives SBDO-Si and SBDO-Ge (for details, see ESI, Figs. S8–S10 and Tables S8–S13†). These calculations gave 2J/k_B values of +30.37, +18.42 and +21.06 K for SBDO-C, -Si and -Ge, respectively. The values for the Si and Ge derivatives were larger than the above-mentioned constants, implying the suppression of distortion for the dihydroacridine moieties.

To investigate the relationship between exchange couplings and intramolecular spin-centres distances, we calculated second model compounds (SBDO-C′ and -C′′), in which the spiro centres were replaced by a carbon atom in the optimised structural parameters of SBDO-Si and -Ge. The N–N distances for SBDO-C, -C′ and -C′′ were 5.93, 6.44 and 6.52 Å, respectively. The energy gaps between the bonding and antibonding orbitals resulting from spiro-conjugation (ΔE_spiro), as shown in Fig. 4a, showed a narrowing trend (Table 1). The exchange coupling constants (2J/k_B) for SBDO-C, -C′ and -C′′ were +30.37, +29.00 and +27.05 K, respectively. These values show a proportional change with respect to the distance between the radical centres. These findings imply that spirodiradicals not only rely on molecular symmetry, but also require space/bond interactions within each unit to enhance spin–spin interaction. In this case, the spiro-conjugation of the occupied MOs could play a role in the interaction of the two dihydroacridine radical units.

Fig. 4 Interaction of two π* orbitals that are (a) antisymmetric with respect to two σ_d planes and (b) symmetric and antisymmetric with respect to two σ_d planes. (c) Interaction of the π* orbitals and one of the σ* bondings between the spiro centre and the neighbouring atom.

Table 1 Energy gaps ΔE_spiro between the bonding and antibonding MOs from the spiro-conjugation in the unoccupied and occupied molecular orbitals (UMO and OMO, respectively) for the ground triplet state (S = 1)

	α spins		β spins
ΔEspiro	UMOs/eV	OMOs/eV	UMOs/eV	OMOs/eV
SBDO-C	1.001	1.169	1.088	1.130
SBDO-C′	0.438	0.429	0.461	0.423
SBDO-C′′	0.380	0.358	0.401	0.354
SBDO-Si	0.646	0.564	0.719	0.546
SBDO-Ge	0.491	0.430	0.524	0.420

---

The difference in the interactions of SBDO-Si and -C′ (+18.42 K vs. +29.00 K) showed a more pronounced change compared to that of SBDO-Ge and -C′′ (+21.06 K vs. +27.05 K). For SBDO-C, -Si and -Ge, ΔE_spiro values are summarized in Table 1. The tendency of the change in ΔE_spiro values with the SBDO-C, -Si and -Ge agrees with the SBDO-C, -C′ and -C′′ cases, and thus the pronounced difference cannot be only explained by it. Therefore, we should consider the contribution of hyperconjugation between the molecular orbitals of the dihydroacridine moieties and the σ*(Si–C_α) orbital. Fig. 5 presents the energy diagrams of the α and β spins in the triplet state for SBDO-C, -Si and -Ge (for more details, see Tables S11–S13†). For SBDO-C, the highest occupied MO (HOMO) and the lowest unoccupied MO (LUMO) were assigned to the bonding and antibonding orbitals based on the spiro-conjugation in the OMO and UMO, respectively. However, for SBDO-Si and -Ge, the HOMOs were the antibonding orbitals from the spiro-conjugation, whereas the LUMOs were the π* orbital of the dihydroacridine units. The energy levels of this orbital for SBDO-Si and -Ge were lower than that of SBDO-C. Here, the LUMOs for SBDO-Si and -Ge have the same phase with lobes at two neighbouring carbon atoms to the spiro centre (Fig. 4b). This symmetry allows the σ*(X–C_α) orbital to interact with the π* orbital, namely σ*(X–C_α)–π* hyperconjugation, as shown in Fig. 4c. This facilitates electron transfer from the spiro centre to the dihydroacridine moieties. In fact, the calculated spin densities of the Si spiro centre of −0.030 was lower than those of the spiro centres for SBDO-C and -Ge, as shown in Table S14.† On the other hand, the O atom for SBDO-Si was +0.474, which was the largest for the three compounds. These results indicate that for SBDO-Si, radical spin is localized at the NO site, resulting in small exchange coupling.

Fig. 5 Selected MO energy-level diagram for (left column) α and (right column) β spins in the triplet state for (left) SBDO-C, (centre) -Si and (right) -Ge. The MO images are superposed with an isovalue of 0.03. The red and blue MOs represent SOMOs and the lowest degenerate π*orbital, respectively.

For 1-Si, structural studies revealed two intermolecular contacts, namely indirect O2⋯O3 and direct O1⋯O4 interactions. Notably, to reduce computational costs, the dihydroacridine moiety, which is not involved in the contacts, and the tert-butyl groups were replaced by methyl groups. First, the indirect O2⋯O3 contact through C atoms was evaluated. The calculated spin densities of the T and BS states were mapped onto the molecular skeleton, as shown in Fig. S11.† The triplet and singlet energy states were E_T = −2080.30652569 au with 〈S²〉_T = 2.0024 and E_BS = −2080.30652658 au with 〈S²〉_BS = 0.2455. The intermolecular interaction 2J/k_B was estimated to be −0.32 K, indicating weak antiferromagnetic coupling. Next, the direct O1⋯O4 contact was evaluated. The calculated spin densities were mapped onto the molecular skeleton, as shown in Fig. S12.† The triplet and singlet energy states were E_T = −2080.31124125 au with 〈S²〉 _T = 2.0005 and E_BS = −2080.31133968 au with 〈S²〉 _BS = 0.2159. The intermolecular interaction 2J/k_B was estimated to be −34.81 K, indicating strong antiferromagnetic coupling.

For 1-Ge, an indirect O2⋯O2 contact was present, as shown in Fig. 3b. To reduce computational costs, the dihydroacridine moiety, which was not involved in the contacts, and the tert-butyl groups were replaced by methyl groups. The calculated spin densities of the T and BS states were mapped onto the molecular skeleton, as shown in Fig. S13.† The triplet and singlet energy states were E_T = −5655.17316304 au with 〈S²〉_T = 2.0006 and E_BS = −5655.17317585 au with 〈S²〉_BS = 0.2520. The intermolecular magnetic interaction 2J/k_B was estimated to be −4.62 K, indicating antiferromagnetic coupling.

Magnetic properties

Magnetic susceptibilities were measured for the polycrystalline samples 1-Si and 1-Ge at 2–300 K (Fig. 6). First, for 1-Si (Fig. 6a), the χ_mT value at 300 K was 0.718 cm³ K mol⁻¹, which was close to the value of 0.750 cm³ K mol⁻¹ expected for a species having two magnetically isolated radical centres (S = 1/2; g = 2.0). Upon cooling, the χ_mT value was plateaued up to 120 K and then displayed a decreasing behaviour. At 12 K, there was a difference in the slope of the change in the χ_mT value (Fig. S14†). The experimental data for 1-Si were analysed using PHI software.²⁷ The spin Hamiltonian is defined as the linear four S = 1/2 spin model: . This model assumes intramolecular coupling and the direct O1⋯O4 contact. The g value was fixed at 2.0064 from the ESR study. The best-fit curve was achieved with 2J/k_B = +14.2(3) K, 2J′/k_B = −41.2(2) K and TIP = −0.249(4) × 10⁻³ cm³ mol⁻¹. These exchange coupling constants almost reproduced the DFT calculation results. The field dependence of the magnetization curve at 2 K is shown in the inset of Fig. 6a. The M value was saturated and reached 0.90 μ_B at 7 T. This value was lower than the expected M value of 2.0 μ_B (S = 1 and g = 2.0) and close to the expected 1.0 μ_B (S = 1/2 and g = 2.0). This result indicates strong intermolecular antiferromagnetic coupling (J′). Namely, in the dimer, described in the 4-spin model based on the O1⋯O4 contact, the spin state reflects the cancellation of two spins. Note the monomer exhibited the ground triplet state, as confirmed by the experimental (2J/k_B = +14.2 K) and theoretical results.

Fig. 6 Temperature dependence of the product χ_mT measured at 5 kOe for (a) 1-Si and (b) 1-Ge. Solid lines represent the simulated curves. The inset shows the magnetization curve measured at 2.0 K.

For 1-Ge (Fig. 6b), the χ_mT value at 300 K was 0.714 cm³ K mol⁻¹, which was close to the expected value of 0.750 cm³ K mol⁻¹. Upon cooling, the χ_mT value increased abruptly at 252 K, which was a reversible process according to the results of the cooling and second heating measurements (Fig. S15†). This unique behaviour has been further investigated and will be reported in another paper. Upon further cooling, the χ_mT value increased and reached 0.950 cm³ K mol⁻¹ at 8.5 K, and then decreased to 0.699 cm³ K mol⁻¹ at 2.0 K. The experimental data of 1-Ge were analysed using PHI software.²⁷ The spin Hamiltonian is defined as the linear four S = 1/2 spin model: . This model assumes intramolecular coupling and the indirect O2⋯O2 contact. The best-fit curve was achieved with 2J/k_B = +19.3(2) K, 2J′/k_B = −3.69(1) K, g = 2.059(1) and TIP = −0.323(7) × 10⁻³ cm³ mol⁻¹. These exchange coupling constants almost reproduced the DFT calculation results. The field dependence of the magnetization curve at 2 K is shown in the inset of Fig. 6b. The M value was saturated and reached 2.00 μ_B at 7 T, which reproduces to be the expected M value (S = 1 and g = 2.0).

Conclusions

Novel spirobiacridine diradicals 1-Si and 1-Ge were prepared. These exhibited the ground triplet state (S = 1), as supported by spectroscopic and magnetic measurements and theoretical calculations. The compound 1-Ge exhibited large ferromagnetic coupling compared with 1-Si. According to the theoretical calculations for the optimized compounds, the Si-centred derivative could reduce exchange coupling owing to the presence of σ*(Si–C_α)–π* hyperconjugation. Therefore, molecular design based on molecular symmetry should consider not only the suppression of Jahn–Teller distortion but also the effective exchange path between the units; in the case of spirodiradicals, spiro-conjugation except for the SOMOs and the suppression of the hyperconjugation. The compound 1-Ge exhibited the reversible change in the magnetic behaviour. We plan to clarify this finding and report on it in a separate paper. The results of this study elucidate the effect of spiro-centre substitution on the interaction between two orthogonal π-conjugated systems. While σ*–π* conjugation had the negative effect in this study, exploring systems where hyperconjugation acts positively may lead to enhancements in spin–spin interaction. Such investigations are expected to advance structural organic chemistry as well as contribute to applications in organic magnets.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Part of this work was supported by “Advanced Research Infrastructure for Materials and Nanotechnology in Japan (ARIM)” of the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Grant Number A-22-UT-0080 and JXMXP1222UE5271.

References

1. (a) E. G. Janzen, Spin trapping, Acc. Chem. Res., 1971, 4, 31–40; (b) M. J. Davies, Detection and characterisation of radicals using electron paramagnetic resonance (EPR) spin trapping and related methods, Methods, 2016, 109, 21–30.
2. (a) J. F. W. Keana, Newer aspects of the synthesis and chemistry of nitroxide spin labels, Chem. Rev., 1978, 78, 37–64; (b) A. Bonucci, O. Ouari, B. Guigliarelli, V. Belle and E. Mileo, In-Cell EPR: Progress towards Structural Studies Inside Cells, ChemBioChem, 2020, 21, 451–460.
3. (a) O. Haze, B. Corzilius, A. A. Smith, R. G. Griffin and T. M. Swager, Water-Soluble Narrow-Line Radicals for Dynamic Nuclear Polarization, J. Am. Chem. Soc., 2012, 134, 14287–14290; (b) D. Wisser, G. Karthikeyan, A. Lund, G. Casano, H. Karoui, M. Yulikov, G. Menzildjian, A. C. Pinon, A. Purea, F. Engelke, S. R. Chaudhari, D. Kubicki, A. J. Rossini, I. B. Moroz, D. Gajan, C. Copéret, G. Jeschke, M. Lelli, L. Emsley, A. Lesage and O. Ouari, BDPA-Nitroxide Biradicals Tailored for Efficient Dynamic Nuclear Polarization Enhanced Solid-State NMR at Magnetic Fields up to 21.1 T, J. Am. Chem. Soc., 2018, 140, 13340–13349.
4. (a) L. Li, R. Matsuda, I. Tanaka, H. Sato, P. Kanoo, H. J. Jeon, M. L. Foo, A. Wakamiya, Y. Murata and S. Kitagawa, A Crystalline Porous Coordination Polymer Decorated with Nitroxyl Radicals Catalyzes Aerobic Oxidation of Alcohols, J. Am. Chem. Soc., 2014, 136, 7543–7546; (b) P. Qu, M. Kuepfert, S. Jockusch and M. Weck, Compartmentalized Nanoreactors for One-Pot Redox-Driven Transformations, ACS Catal., 2019, 9, 2701–2706.
5. (a) R. Dessauer, Photochemistry, History, and Commercial Applications of Hexaarylbiimidazoles, Elsevier, 2006; (b) A. Tokunaga, L. M. Uriarte, K. Mutoh, E. Fron, J. Hofkens, M. Sliwa and J. Abe, Photochromic Reaction by Red Light via Triplet Fusion Upconversion, J. Am. Chem. Soc., 2019, 141, 17744–17753.
6. (a) I. Ratera and J. Veciana, Playing with organic radicals as building blocks for functional molecular materials, Chem. Soc. Rev., 2012, 41, 303–349; (b) N. M. Gallagher, A. Olankitwanit and A. Rajca, High-Spin Organic Molecules, J. Org. Chem., 2015, 80, 1291–1298; (c) E. Jin, M. Asada, Q. Xu, S. Dalapati, M. A. Addicoat, M. A. Brady, H. Xu, T. Nakamura, T. Heine, Q. Chen and D. Jiang, Two-dimensional sp² carbon–conjugated covalent organic frameworks, Science, 2017, 357, 673–676.
7. H. M. McConnel, Ferromagnetism in Solid Free Radicals, J. Phys. Chem., 1963, 39, 1910.
8. (a) E. V. Tretyakov, P. V. Petunin, S. I. Zhivetyeva, D. E. Gorbunov, N. P. Gritsan, M. V. Fedin, D. V. Stass, R. I. Samoilova, I. Y. Bagryanskaya, I. K. Shundrina, A. S. Bogomyakov, M. S. Kazantsev, P. S. Postnikov, M. E. Trusova and V. I. Ovcharenko, Platform for High-Spin Molecules: A Verdazyl-Nitronyl Nitroxide Triradical with Quartet Ground State, J. Am. Chem. Soc., 2021, 143, 8164–8176; (b) H. Zhang, M. Pink, Y. Wang, S. Rajca and A. Rajca, High-Spin S = 3/2 Ground-State Aminyl Triradicals: Toward High-Spin Oligo-Aza Nanographenes, J. Am. Chem. Soc., 2022, 144, 19576–19591.
9. (a) M. Saunders, R. Berger, A. Jaffe, J. M. McBride, J. O'Neill, R. Breslow, J. M. Hoffmann, C. Perchonock, E. Wasserman, R. S. Hutton and V. J. Kuck, Unsubstituted cyclopentadienyl cation, a ground-state triplet, J. Am. Chem. Soc., 1973, 95, 3017–3018; (b) H. Thomann, M. Bernardo and G. P. Miller, Observation of triplet-state electron spin resonance in oxidized fullerene C60, J. Am. Chem. Soc., 1992, 114, 6593–6594; (c) W. T. Broden, R. Hoffmann, T. Stuyver and B. Chen, Dioxygen: What Makes This Triplet Diradical kinetically Persistent?, J. Am. Chem. Soc., 2017, 139, 9010–9018.
10. (a) T. Sugimoto, Y. Misaki, T. Kajita, T. Nagatomi, Z. Yoshida and J. Yamauchi, Tris(thioxanthen-9-ylidene)cyclopropane, and Its Radical Cation and Dication, Angew. Chem., Int. Ed. Engl., 1988, 27, 1078–1080; (b) T. Kodama, M. Aoba, Y. Hirao, S. M. Rivero, J. Casado and T. Kubo, Molecular and Spin Structures of a Through-Space Conjugated Triradical System, Angew. Chem., Int. Ed., 2022, 61, e20220688.
11. T. Ishida, M. Ooishi, N. Ishii, H. Mori and T. Nogami, Mono- and dinitroxide radicals from 9,9′(10H,10′H)-spirobiacridine: An approach to a D_2d triplet biradical, Polyhedron, 2007, 26, 1793–1799.
12. T. Kanetomo, K. Ichihashi, M. Enomoto and T. Ishida, Ground Triplet Spirobiradical: 2,2′,7,7′-Tetra(tert-butyl)-9,9′(10H,10′H)-spirobiacridine-10,10′-dioxyl, Org. Lett., 2019, 21, 3909–3912.
13. (a) N. L. Frank, R. Clérac, J.-P. Sutter, N. Daro, O. Kahn, C. Coulon, M. T. Green, S. Golhen and L. Ouahab, Synthesis, Crystal Structure, Magnetic, and Electron Paramagnetic Resonance Properties of a Spiroconjugated Biradical. Evidence for Spiroconjugation Exchange Pathway, J. Am. Chem. Soc., 2000, 122, 2053–2061; (b) A. Ito, M. Urabe and K. Tanaka, A Spiro-Fused Triarylaminium Radical Cation with a Triplet Ground State, Angew. Chem., Int. Ed., 2003, 42, 921–924; (c) Z. Yue, J. Liu, M. Baumgarten and D. Wang, Spirobifluorene Mediating the Spin–Spin Coupling of Nitronyl Nitroxide Diradicals, J. Phys. Chem. A, 2023, 127, 1565–1575.
14. (a) T. Iwamoto, M. Tamura, C. Kabuto and M. Kira, A Stable Bicyclic Compound with Two Si=Si Double Bonds, Science, 2000, 290, 504–506; (b) S. H. Lee, B.-B. Jang and Z. H. Kafari, Highly Fluorescent Solid-State Asymmetric Spirosilabifluorene Derivatives, J. Am. Chem. Soc., 2005, 127, 9071–9078; (c) X.-Y. Liu, X. Tang, Y. Zhao, D. Zhao, J. Fan and L.-S. Liao, Spirobi[dibenzo[b,e,][1,4]azasiline]: a novel platform for host materials in highly efficient organic light-emitting diodes, J. Mater. Chem. C, 2018, 6, 1023–1030.
15. (a) K. Ueda, M. Yamanoha, T. Sugimoto, H. Fujita, A. Ugawa, K. Yakushi and K. Kano, New Spiro Donor Molecules: Bis(tetrathiafulvalenyldithio)-methane and -germane, Chem. Lett., 1997, 26, 461–462; (b) Y. Guo, Z. Xia, J. Liu, J. Yu, S. Yao, W. Shi, K. Hu, S. Chen, Y. Wang, A. Li, M. Driess and W. Wang, A Tetra-amido-Protected Ge₅-Spiropentadiene, J. Am. Chem. Soc., 2019, 141, 19252–19256.
16. (a) B. H. Boo, J. Park, H. G. Yeo, S. Y. Lee, C. J. Park and J. H. Kim, Infrared and Raman Spectroscopy of 9,9′-Spirobifluorene, Bis(2,2′-biphenylene)silane, and Bis(2,2′-biphenylene)germane. Vibrational Assignment by Depolarization Measurement and HF and Density Functional Theory Studies, J. Phys. Chem. A, 1998, 102, 1139–1145; (b) A. G. Russell, N. S. Spencer, D. Philp, B. M. Kariuki and J. S. Snaith, The First Spirobifluorenes Containing Two Binaphthyl Moieties, Organometallics, 2003, 22, 5589–5592; (c) S. Furukawa, K. Hayashi, K. Yamagishi and M. Saito, Synthesis and properties of spiro-type heterasumanenes containing group 14 elements as bridging atoms, Mater. Chem. Front., 2018, 2, 929–934.
17. S. Yamaguchi, Y. Itami and K. Tamao, Group 14 Metalloles with Thienyl Groups on 2,5-Positions: Effects of Group 14 Elements on Their π-Electronic Structures, Organometallics, 1998, 17, 4910–4916.
18. (a) A. L. Shain, J. P. Ackerman and M. W. Teague, Intramolecular Triplet Exciton Transfer in Some Noncoplanar aromatic systems, Chem. Phys. Lett., 1969, 3, 550–551; (b) A. L. Shain, Dynamics of Intramolecular Triplet Exciton Transfer Using Electron Spin Resonance, J. Chem. Phys., 1972, 56, 6201–6212.
19. A. Ito, M. Urabe and K. Tanaka, Design of high-spin organic molecules: toward magnetic parts in molecular electronics, Curr. Appl. Phys., 2003, 3, 149–153.
20. S. Stoll and A. Schweiger, EasySpin, a comprehensive software package for spectral simulation and analysis in EPR, J. Magn. Reson., 2006, 178, 42–55.
21. T. Kanetomo, S. Ono, Y. Fukushima, Y. Takenouchi and M. Enomoto, Galvinoxyl-inspired dinitronyl nitroxide: structural, magnetic, and theoretical studies, Org. Chem. Front., 2023, 10, 3193–3200.
22. (a) A. Ito, K. Hata, K. Kawamoto, Y. Hirao, K. Tanaka, M. Shiro, K. Furukawa and T. Kato, para-Phenylene-Bridged Spirobi(triarylamine) Dimer with Four Perpendicularly Linked Redox-Active π Systems, Chem. – Eur. J., 2010, 16, 10866–10878; (b) N. Terada, K. Uematsu, R. Higuchi, Y. Tokimaru, Y. Sato, K. Nakano and K. Nozaki, Synthesis and Properties of Spiro-double Sila[7]helicene: The LUMO Spiro-conjugation, Chem. – Eur. J., 2021, 27, 9342–9349.
23. K. Clabron, B. Kahr and W. Kaminsky, Calculations of optical properties of the tetraphenyl-X family of isomorphous crystals (X = C, Si, Ge, Sn, Pb), CrystEngComm, 2002, 4, 252–256.
24. A. Bondi, van der Waals Volumes and Radii, J. Phys. Chem., 1964, 68, 441–451.
25. A. Karipides and D. A. Haller, The Crystal Structure of Tetraphenylgermanium, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 2889–2892.
26. K. Yamaguchi, T. Kawakami, Y. Takano, Y. Kitagawa, Y. Yamashita and H. Fujita, Analytical and ab initio studies of effective exchange interactions, polyradical character, unpaired electron density, and information entropy in radical clusters (R)_N: Allyl radical cluster (N=2–10) and hydrogen radical cluster (N=50), J. Quantum Chem., 2002, 90, 370–385.
27. N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes, J. Comput. Chem., 2013, 34, 1164–1175.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 23349212334922. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4qo00419a

---