Degradable bispiperidone derivative amine networks with monomer recovery

Abstract

Among various recycling strategies required for a circular economy of polymers, dynamic covalent chemistry (DCC) is gaining increasing interest. Established amine–aldehyde chemistry suffers from limited scope and toxicity. Ketones are alternatives but commonly less reactive and, as a consequence, have been investigated to the lower extent in the context of DCC. Here we report three bis(piperidin-4-one) derivatives as reactive, ketone-based building blocks for dynamic network formations with amines. By varying the bispiperidone linker unit, the electrophilicity of the carbonyl can be modulated. Contributions of aminal, hemiaminal, imine and enamine units are determined using model compounds, linear polymers and networks. NMR and AT-IR spectroscopic analyses suggest imine and enamine functionalities to be the main condensation products. The thermodynamics of the formation of the aminal, hemiaminal, imine and enamine functionalities are investigated using density functional theory (DFT) calculations, which confirm imine and enamine units to be the most stable reaction products. The DFT results further demonstrate how altering the experimental conditions can change product distribution different from those obtained in the experiments. Degradation of the networks in water depends on the pH of the medium and enables bispiperidone recovery.

---

Introduction

Light-weight, functional and durable polymers are of increasing interest in modern societies.¹ Since a large part of polymers is based on finite resources from petrochemical feedstocks,¹ sustainable approaches for their use are inevitable. Not only by exploiting renewable resources, but also especially by designing polymers for a circular economy including manufacturing, use and recycling a holistic rethinking is necessary.

If plastics are unavoidable, reusing them (primary recycling) is the aspired approach. Often material quality suffers from stress during use and as a result polymers undergo a loss of properties. Mechanical recycling (e.g. for PET^2,3 and PE^2,4) does not ideally change polymer structure (secondary recycling) and usually involves the central elements of collecting, sorting, washing, shredding and remoulding the waste polymer. However, due to remaining contaminants, side reactions and degradations of varying extent, mechanical recycling is only suitable for certain polymers with sufficiently good mechanical and thermal properties.⁵ Therefore, mechanical recycling involves a loss of polymer functionality also for those polymers that are considered stable resulting in downcycling and a limited number of reprocessing cycles.² One possibility addressing the limitations of mechanical recycling is tertiary recycling, which entails the degradation of the polymer structure to regain monomers and/or smaller building blocks, which can then be re-used for new polymerizations.^6,7 The degradation process can be carried out either by enzymatic recycling or chemical recycling. Enzymatic degradation of polymers is usually limited to very specific polymers, such as amorphous PET.^8–10 Chemical recycling requires defined responses of the polymer matrix to external stimuli to obtain the desired product.

Classical thermosets are network polymers that have high strength but cannot be remelted. Mechanical recycling as performed for thermoplastic materials is therefore not possible and chemical recycling is limited due to their cross-linked, rigid structure that often consists of stable bonds.^11–16 Therefore, at present, most of the discarded thermosets are subjected to landfilling or are energetically recycled (quaternary recycling), leading to an immense loss of resources and CO₂ emissions.^5,17

In industry the most widely used technique for chemical recycling is pyrolysis requiring harsh conditions and high energy to cleave covalent carbon bonds to gain pyrolysis oil.¹⁸ Moreover, due to the harsh processing conditions the recovery of high quality fibers from fiber-based composites is challenging.¹⁹ Through the use of dynamic covalent chemistry in polymers, stability originating from covalent bonds and cleavability of certain structural elements can be achieved.²⁰ Here, cleavability results from the responsiveness to chemical or physical environments. In terms of thermosets, dynamic covalent networks (DCNs) are gaining interest as they combine mechanical stability and recyclability of the material.^21–24 However, mechanical and thermal stability of DCNs may not be as high as those for permanent networks based on e.g. epoxy resins. Hence, the challenge is to balance the reversibility required for recycling/reprocessing and the stability of the DCN, which are often mutually exclusive. Various structures and chemistries can be used to make DCNs, for instance disulfide bonds,²⁵ Diels–Alder chemistry,²⁶ esters²⁷ and imines.²³ Among them, carbonyl-amine systems can offer a broad range of properties, such as self-healing, degradability and the ability for reshaping.^24,28–30 Uhlig et al. reported highly reactive piperidone derivates for the reversible and pH-dependent gelation of poly(vinylamine) water solutions.²⁸ Fengler et al. has further used a bispiperidone for the surface cross-linking of core–shell poly(vinylamine)-based particles.³¹ Here, we apply three of these rather rare reactive ketones, two of which are new, for network formation with aliphatic di- and triamines, and investigate their reactivity, network chemistry and degradation in water along with monomer recovery.

Experimental section

Materials

All substrates and materials were used as received from commercial suppliers, unless otherwise stated.

4-Piperidone hydrate hydrochloride was purchased from abcr GmbH. 1,3-Diaminopropane, 1,4-dioxa-8-azaspiro[4.5]decane and oxalyl dichloride were purchased from Acros Organics. 1,6-Diaminohexane was purchased from Carl Roth. N-Acetylpiperidin-4-one was purchased from J&K Scientific. Hexylamine was purchased from Merck. Adipyl dichloride, 1,3-dibromopropane and tris(2-aminoethylamine) were purchased from TCI.

Instrumentation

Nuclear magnetic resonance (NMR) analysis in CDCl₃ and D₂O was conducted on a Bruker Avance Neo 600 FT spectrometer (600 MHz) to record ¹H and ¹³C-{¹H} NMR spectra referenced via solvent signals and a TMS standard. Solid state NMR experiments were performed on a Bruker Digital Avance 400 spectrometer (400 MHz) equipped with double-tuned probes capable of MAS (magic angle spinning) in zirconium oxide rotors (3.2 mm) spinning at 15 kHz. ¹³C-{¹H}-CP-MAS NMR spectra were recorded using cross polarization (CP) with a contact time of 3 ms, a recycle delay of 6 s and ¹H decoupling using a TPPM (two pulse phase modulation) pulse sequence. The spectra are referenced to tetramethyl silane (TMS) using tetrakis(trimethylsilyl)silane (TTSS) as a secondary standard (3.55 ppm for ¹³C and 0.27 ppm for ¹H).

Infrared (IR) analysis was performed on an Alpha II FT-IR spectrometer from Bruker.

Thermogravimetric analysis (TGA) was performed on a Thermogravimetric Analyzer 7 from the PerkinElmer Company by heating samples from 30 to 650 °C at a heating rate of 10 K min⁻¹ under constant nitrogen flow before holding the temperature for 10 min at 650 °C under an air flow.

Elemental analysis of the elements C, H and N was quantitatively carried out using a varioMICRO CHNS device from Elementar Analysensysteme GmbH.

Synthetic procedures

1,2-Bis(4-oxopiperidin-1-yl)-ethane-1,2-dione (OBP). OBP was synthesized following the method of Uhlig et al.²⁸ and was purified via recrystallization in acetone.

Yield = 55%. mp 182 °C. Elemental analysis (found: C, 57.3; H, 6.4; N, 11.0. Calc. for C₁₂H₁₆N₂O₄: C, 57.1; H, 6.4; N, 11.1%).¹H NMR (CDCl₃, [ppm]): 2.57 (4H, t, ³J 6.4), 2.60 (4H, t, ³J 6.2), 3.73 (4H, t, ³J 6.2), 3.93(4H, t, ³J 6.4). ¹³C NMR (CDCl₃, [ppm]): 40.5, 40.6, 41.3, 45.1, 162.8, 205.4. HRMS (m/z): [M + H]+ calcd for C₁₂H₁₆N₂O₄ 253.1183; found 253.1183.

1,6-Bis(4-oxopiperidin-1-yl)-hexane-1,6-dione (ABP). ABP was synthesized following the method of Uhlig et al.²⁸ K₂CO₃ (9.60 g, 69.5 mmol) was dissolved in water (30 mL) and 4-piperidone hydrate hydrochloride (7.70 g, 50.1 mmol) was added. After stirring at room temperature for 30 min the obtained amine was extracted in dichloromethane by use of a perforator. After drying the organic phase over MgSO₄, the solution was transferred into a three-necked flask under an inert atmosphere and K₂CO₃ (12.4 g, 89.7 mmol) was added. While cooling at 0 °C, adipyl dichloride (3.05 g, 24.0 mmol) was added dropwise. The mixture was stirred at room temperature overnight. The solid was filtered off, the organic phase washed with aqueous NaHCO₃, dried over MgSO₄ and all solvent was removed under reduced pressure. The obtained solid was purified via recrystallization in ethyl acetate.

Yield = 57%. mp 111 °C. Elemental analysis (found: C, 62.1; H, 7.8; N, 9.1. Calc. for C₁₆H₂₄N₂O₄: C, 62.3; H, 7.8; N, 9.1%). ¹H NMR (CDCl₃, [ppm]): 1.75 (4H, p, ³J 3.4), 2.45–2.51 (12H, m), 3.76 (4H, t, ³J 6.3), 3.88 (4H, t, ³J 6.3). ¹³C NMR (CDCl₃, [ppm]): 24.86, 32.99, 40.81, 40.85, 41.25, 44.05, 171.35, 206.73. HRMS (m/z): [M + H]+ calcd for C₁₆H₂₄N₂O₄ 309.1809; found 309.1805.

1,3-Bis(1,4-dioxa-8-azaspiro[4.5]decane-8-yl)propane hydrobromide (EO₂-PBP). 1,4-Dioxa-8-azaspiro[4.5]decane (4.00 g, 28.0 mmol) was dissolved in acetonitrile (30 mL) and 1,3-dibromopropane (2.71 g, 13.4 mmol) was added dropwise while stirring. After heating at 60 °C for 5 h the white precipitate was filtered and washed with acetonitrile.

Yield = 99%. ¹H NMR (DMSO-d6, [ppm]): 1.90 (4H, d, ³J 12.1), 2.00 (4H, td, ³J 13.8, ³J 4.4), 2.13 (2H, p, ³J 8.0), 3.07 (4H, q, ³J 9.5), 3.20 (4H, q, ³J 8.0), 3.55 (4H, d, ³J 12.2), 3.94 (8H, s), 9.63 (2H, s). ¹³C NMR (DMSO-d6, [ppm]): 103.7, 64.2, 64.1, 52.0, 50.2, 31.5, 18.8.

1,3-Bis(4-oxopiperidin-1-yl)-pzropane-1,3-diyl (PBP). 1,3-Bis(1,4-dioxa-8-azaspiro[4.5]decane-8-yl)propane hydrobromide (5.00 g, 10.2 mmol) was dissolved in 1 M hydrochloric acid (50 mL) and heated to 80 °C for 20 h. The aqueous solution was quenched with NaHCO₃. The product was extracted in DCM, the organic phase dried over MgSO₄ and the solvent removed under reduced pressure. The obtained solid was purified via recrystallization in hexane/THF (10 : 1).

Yield = 78%. mp 50 °C. Elemental analysis (found: C, 65.45; H, 9.3; N, 11.8. Calc. for C₁₃H₂₂N₂O₂: C, 65.5; H, 9.3; N, 11.75%). ¹H NMR (CDCl₃, [ppm]): 1.75 (2H, p, ³J 7.4), 2.44 (8H, t, ³J 6.1), 2.51 (4H, t, ³J 7.4), 2.74 (8H, t, ³J 6.1). ¹³C NMR (CDCl₃, [ppm]): 25.6, 41.3, 53.3, 55.5, 209.1. HRMS (m/z): [M + H]+ calcd for C₁₃H₂₂N₂O₂ 239.1754; found 239.1754.

General procedure for the preparation of model compounds. N-Acetylpiperidin-4-one was dissolved in dichloromethane and the amine (1 eq.) was added. The mixture was heated at 60 °C for 20 h while the solvent was allowed to evaporate.

General procedure of polymerization. The bispiperidone and amine were each dissolved in methanol (ratio of functional groups NH₂ : C=O = 1 : 1). The solutions were combined and transferred into a mould within which they were heated to 60 °C for 20 h while the solvent was allowed to evaporate. The polymer was obtained as a clear, orange solid.

pH-Dependent degradation. The obtained polymer was immersed in an aqueous solution of defined pH value. The amount of polymer in the solution was kept at 10 mg mL⁻¹. Degradation was observed visually over time. To regain the bispiperidone, the aqueous solution was extracted with dichloromethane, and the solvent was removed under reduced pressure.

Computational details

The CREST software package^32–34 was used to find the initial structures of the molecules. First, a conformational search was carried out using the iterative meta-dynamics with a genetic structure crossing (iMTD-GC) algorithm. Afterwards, a structure optimization using the extended tight-binding approach GFN2-xTB was performed.^35–37 The methanol solvent was described in these calculations by the implicit solvent model, namely the analytical linearized Poisson–Boltzmann (ALPB) model.³⁸ Conformers up to 125.5 kJ mol⁻¹ above the lowest energy structure were searched. The 30 most energetically favorable conformers of each molecule were evaluated using density functional theory (DFT) calculations. These DFT calculations were performed using the Turbomole 7.5.1 software package,^39–41 in all cases using the resolution-of-identity (RI) approximation,^42,43 and the “multiple grid” m4.⁴⁴ The structures of the conformers were re-optimized at the PBE-D4/def2-SVP^44–51 (DCOSMO-RS⁵²) level of theory. The solvent model of DCOSMO-RS simulated methanol (relative permittivity ε_r = 32.6⁵³ and refractive index n_D = 1.3288 ⁵⁴). Based on the electronic energy, the most favorable conformer was selected for each molecule. These conformers were then re-optimized at the PBE0-D4/def2-TZVP^{45–51,55,56} (DCOSMO-RS) level of theory. The energetic minima of all optimized structures were verified by calculating vibrational frequencies. These were calculated semi-numerically including the fast contribution of the solvent.^57,58 These vibrational frequencies were also used to calculate thermal contributions. Finally, the electronic energy was calculated with a larger basis set to reduce the basis set superposition error. This was performed with single-point calculations of the re-optimized structure at the PBE0-D4/def2-QZVP⁵⁹ level of theory. The methanol solvent was again simulated with the DCOSMO-RS solvent model. This time the outlying charge correction (-out)⁶⁰ was additionally applied.

In addition, the conformers selected at the PBE-D4/def2-SVP (DCOSMO-RS) level of theory were re-optimized on the M06-2X/def2-TZVP level of theory with the SMD solvent model.^61,62 Again, the vibrational frequencies and thermal contributions were calculated at this level of theory. The electronic energy was calculated using M06-2X/def2-QZVP (SMD) single-point calculations. These calculations were performed with the Gaussian 16 C.01 software package.⁶³ For any option not mentioned, the values predefined in Turbomole 7.5.1 and Gaussian 16 C.01 were selected. For both methods [PBE0-D4/def2-QZVP//def2-TZVP (DCOSMO-RS-out) and M06-2X/def2-QZVP//def2-TZVP (SMD)] the thermal contributions were determined using the common rigid-rotator-harmonic-oscillator (RRHO) approximation, i.e. a particle-in-a-box-model is used for translational contributions, a rigid rotor approximation for the rotational contributions, and the harmonic oscillator approximation for the vibrational contributions.⁶⁴

The same concentration (either 0.35, 1, or 10 mol L⁻¹) was assumed for all molecules (educt and product). The concentration is included in the translational entropy. In order to obtain the desired concentration, the following correction term is applied

with the molar gas constant R, the temperature T and the new (V^new_m) and old (for Turbomole and 298.15 K, V^old_m = 0.02479 m³ mol⁻¹; Turbomole and 333.15 K, V^old_m = 0.02770 m³ mol⁻¹; Gaussian, V^old_m = 0.02734 m³ mol⁻¹) volumes.

Results and discussion

Design and synthesis of bispiperidone derivatives

The aim of this work was to design degradable polymer networks from reactive ketones, for which new monomers were designed. Based on the highly reactive oxalyl-bispiperidone (OBP) reported earlier,²⁸ we here attempt to modulate the electrophilicity and thus the reactivity of the bispiperidone (BP) monomer by tuning the linker group. We further anticipated that the electrophilicity of the monomer could additionally translate into different stabilities of the products, and hence pose a factor to control degradation. Next to the electrophilicity, the variation of the linker in between the two piperidone units impacts flexibility, with longer acyl or alkyl chains promising softer materials with lower glass transition temperatures.

Monomer synthesis is summarized in Scheme 1. NMR spectra are provided in the ESI (Fig. S3–S10†). While the synthesis of OBP has been reported by Uhlig et al.,²⁸ adipyl-bispiperidone (ABP) and propyl-bispiperidone (PBP) were synthesized for the first time. All three monomers were obtained as white powders in two steps after purification via recrystallization in 55% to 78% overall yield. The synthesis of PBP required a modulated reaction pathway including the protection of the ketone with ethylene glycol to allow for N-alkylation, otherwise self-condensation of piperidin-4-one was observed. The alkylated, protected species (EO₂-PBP) was obtained as the pure salt via precipitation, deprotected with hydrochloric acid and deprotonated by means of sodium bicarbonate. Crystallization of PBP turned out not to be straightforward, as the process seemed to be hindered.

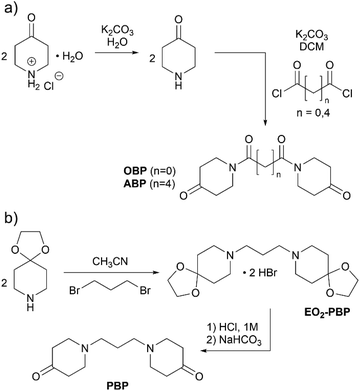Scheme 1 Synthesis of bispiperidone derivatives. (a) Syntheses of OBP and ABP and (b) synthesis of PBP.

In order to rank relative electrophilicities of OBP, ABP and PBP, we determined the ratio of their organic hydrates in D₂O (Fig. 1a). The bispiperidones were dissolved in an excess of deuterated water to allow equilibrium formation of both species. Diol formation of ketones is usually disfavoured as they are less electrophilic compared to aldehydes.^65,66 As a result, mostly aldehydes are employed while ketones are barely used. Due to the unusually high reactivity of piperidone,^28,67 equilibrium in water is shifted towards the geminal diol significantly. This allows comparison of electrophilicities in a simple way. All three bispiperidones show high electrophilicities with diol contents between 25 and 55%. The diol contents were determined by proton NMR analysis (Fig. 1b). Distinct signals of ketone and diol species were chosen for integration. More detailed information on the calculations and signal assignments can be found in the ESI (Scheme S1 and Fig. S11–S14†). Electrophilicity follows the row OBP (55% diol), ABP (33%) and PBP (25%). Taking cyclohexanedione for a common example of a diketone used for DCC as a reference, its diol content of 10% (Fig. S14†) corroborates the unusually high electrophilicity of the bispiperidones.

Fig. 1 (a) Equilibrium of ketone–diol of bispiperidones with D₂O. (b) ¹H NMR spectra of the bispiperidones in D₂O. The signals used for the calculation of the diol content and their corresponding integrals are assigned.

Spectroscopic elucidation of ketone-amine chemistry using model reactions

These highly reactive monomers allow polymerization at mild conditions without the use of a catalyst. However, the reaction of ketones with primary amines offers a broad range of structural units that can be potentially formed, depending on reaction conditions. Among these, imines, enamines, aminals and hemiaminals are possible and are in equilibrium with each other.⁶⁶ Except for hemiaminal formation, all reactions are condensation reactions that release water. To facilitate the spectroscopic investigation of polymers and polymer networks, we used model reactions. N-Acetylpiperidin-4-one (NAP) was reacted with aliphatic mono- and diamines (Fig. 4a–c). The products were analysed using ¹H and ¹³C NMR spectroscopy. Aminal 5- or 6-membered rings are observed quantitatively whenever using 1,3- or 1,2-substituted diamines as they are enthalpically favoured.²⁸ However, aminals were entirely absent when using monoamines or 1,x-diamines (x > 3). Instead, imines were found as well as tautomeric enamines. Due to the hindered rotation of the C=N bond of the imine as well as that of the N–C bond of the amide, which shows partial mesomeric double-bond character, carbon signals slightly differ in their chemical shift resulting in various signals (Fig. S15†). Differentiation between symmetric diimines or symmetric dienamines and the asymmetric imine–enamine species was not possible. The imine and enamine signals showed up in the spectra of the polymers (vide supra).

Theoretical investigation of the thermodynamics

In principle, it can be expected that imines, enamines, aminals and hemiaminals could be found as products, as they are all in equilibrium with each other.⁶⁶ However, in the experiment, only imines and enamines were detected when monoamines were used, and cyclo-aminals were detected when propane-1,3-diamine was used. To gain further insights into the selectivity of the reaction, we calculated the Gibbs energies of reactions at the DFT level of theory. Representative model reactions were analysed using NAP to represent ABP. To study OBP and PBP, the –CO–CH₃ group in NAP was replaced with –CO–COH and –CH₂–CH₃, respectively. The amines used were butan-1-amine and propane-1,3-diamine.

Scheme 2 presents the model reactions that were investigated. The calculated Gibbs energies of the reactions, ΔG_reac(c,T), are dependent on the concentration, c, and the temperature, T (see Fig. 2, Table S1 and Fig. S1, S2†). The structure-optimized products of Scheme 2 are also shown in Fig. 3. The standard Gibbs energy of the reaction/formation is the change in the Gibbs free energy resulting from the formation of 1 mol of product. At a temperature of 298.15 K and with a concentration of 1 M for all solutes (reactants and products), is calculated. It should be noted that the solvent is vaporised during the reaction, leading to an increase in the concentration of all solutes. Therefore, we calculated ΔG_reac(c,T) with three different concentrations: (i) the initial concentration of the reactants was c = 0.35 mol L⁻¹, (ii) c = 1 mol L⁻¹ was used to determine the standard Gibbs energy of reaction , and (iii) a concentration of c = 10 mol L⁻¹ was used to simulate the final part of the reaction when large amounts of the solvent methanol were evaporated. The reaction temperature was set to T = 333.15 K. Fig. 2 provides the free Gibbs energies of the reactions ΔG_reac(c,T). Table S1† includes additional values of ΔG_reac(c,T) with different concentrations c, and combinations of concentrations c and temperatures T. The solvent models DCOSMO-RS-out and SMD include similar interactions, but SMD lacks the important outlying charge correction. For PBE0-D4 we also used the modern D4 dispersion correction. Therefore, we consider the PBE0-D4/def2-QZVP//def2-TZVP (DCOSMO-RS-out) method to be superior to the M06-2X/def2-QZVP//def2-TZVP (SMD) method. Only the former is discussed in the manuscript. The results of M06-2X/def2-QZVP//def2-TZVP (SMD) are presented in the ESI† for completeness.

Fig. 2 Structures of the products of the reactions shown in Scheme 2 for R = –CO–CH₃. The structure optimization was performed at the PBE0-D4/def2-TZVP (DCOSMO-RS) level of theory. Potential intramolecular hydrogen bonds (blue) and van der Waals forces (orange) are shown. The length of the hydrogen bonds of 2.9 Å correlates to weak, electrostatic hydrogen bonds.⁶⁸

Fig. 3 The Gibbs energy of formation ΔG_reac(c,T) at various concentrations c and temperatures T is presented in kJ mol⁻¹. The reactions are shown in Scheme 2. The data were calculated at the PBE0-D4/def2-QZVP//def2-TZVP (DCOSMO-RS-out) level of theory. Table S1† in the ESI shows results obtained with different concentrations c, combinations of concentrations c and temperatures T, and using the M06-2X/def2-QZVP//def2-TZVP (SMD) level of theory.

Scheme 2 Reactions investigated by quantum chemical calculations for R = –CH₂–CH₃, –COCH₃, and –CO–COH.

The imines and enamines obtained in the experiment from the reaction with monoamines (Fig. 4b), and the cyclo-aminal product obtained from the reaction of the propane-1,3-diamine (Fig. 4a) represent the thermodynamically most favourable products in the calculations. The electron donating substituent R = –CH₂–CH₃ on the compounds leads to more positive Gibbs energies ΔG_reac(c,T) compared to the electron withdrawing substituents R = –CO–CH₃ and –CO–COH. The latter two increase electrophilicity and thus reactivity with nucleophiles, which is in agreement with the relative contents of diol formation (see Fig. 1). The free Gibbs energies ΔG_reac(c,T) are hardly different (<1 kJ mol⁻¹) between these two substituents. The enamine–imine bispiperidone formation (Scheme 2f) represents an exception [with –CO–COH −3.8 to −4.4 kJ mol⁻¹ more stable than –CO–CH₃ (Fig. 2 and Table S1†)]. This could be due to the intramolecular van der Waals interaction and hydrogen bonding that play a role in the enamine–imine bispiperidones (see Fig. 3).

Fig. 4 Schematic model reactions of (a) NAP and 1,3-diaminopropane, (b) NAP and hexylamine and (c) NAP and hexamethylenediamine. (d) Schematic polymerization of OBP and hexamethylenediamine. (e) ¹³C NMR spectra of the corresponding reaction products, with the ¹³C-{¹H}-CP-MAS-NMR spectrum shown for OBP-HMD.

In contrast to the formation of the imine and enamine (Scheme 2c and d), the formation of hemiaminal and aminal from monoamines is influenced by changes in concentration and by temperature. This is due to a reduction in the number of molecules during the reaction, making the formation of hemiaminals and aminals less entropically favourable. At higher temperatures, entropy has a greater impact. Thus, at higher temperatures, the formation of imine and enamine is more favourable than the formation of hemiaminal and aminal. However, at higher concentrations, the entropy is less affected by the loss in particle number. This means that the higher concentration mitigates the effect of the higher temperature. However, the formation of the hemiaminal is unfavourable under the given conditions. The formation of the aminals is favourable (exergonic) for R = –CO–CH₃ and –CO–COH at a temperature of T = 298.15 K and all concentrations, and at a temperature of T = 333.15 K and a concentration of c = 10 mol L⁻¹. However, in agreement with the experimental findings, the formation of the imine and enamine is thermodynamically preferred.

The formation of imines, enamines, cyclo-aminals, and enamine–imines is not affected by concentration, as the number of molecules remains constant in this reaction. However, concentration can still influence the reaction if the concentration of some of the reactants or products is changed. For example, increasing the concentration of the mono-piperidinone educt over diamine will move the equilibrium towards the formation of enamine–imine over cyclo-aminal. Higher temperatures reduce the probability of the formation of imine, enamine, cyclo-aminal and enamine–imine. This effect is minimal when forming imines and enamines from monoamines because the number of molecules remains constant during the reaction, and their size and flexibility only change slightly. Imines are the most favourable product when monoamines are used. Enamines are only 3–4 kJ mol⁻¹ less favourable. In a chemical equilibrium that would mean that around 25% of the imine will be in the enamine form. With the ethyl group, the enamine is even more stable. Higher concentrations begin to favour the aminal formation, but at the concentration of c = 10 mol L⁻¹ the imine is still more than 8 kJ mol⁻¹ more favourable. The calculations indicate that aminal formation can be further suppressed by increasing the reaction temperature (which would require changing the solvent).

The calculations demonstrate that the reaction with diamine results in the formation of cyclo-aminal, in agreement with the experiment. It does not lead to the formation of enamine–imine–bispiperidinone. The temperature has a greater impact on the formation of cyclo-aminal and enamine–imine–bispiperidinone than on the formation of imine and enamine from monoamine. One possible reason for this is that the size and flexibility of cyclo-aminal and enamine–imine changes more due to cyclisation, van der Waals interaction, and hydrogen bonding.

Polymers of bispiperidones and amines

Based on the results of the model compounds and theoretical calculations shown before, polymerisations were carried out. Here, the interpretation of NMR spectra became significantly more challenging (Fig. 4d). OBP-based polymers were insoluble leading to the need for solid-state NMR measurements (Fig. 5). Due to broad signals in solid-state carbon NMR spectra, overlapping of imine and amide carbonyl signals occurred. Direct comparison showed that both imine and enamine were present in the polymer as well (Fig. 4e). Additionally, IR spectroscopic analysis (Fig. S16†) confirmed imine and enamine formation.

Fig. 5 (a) Schematic formations of imine and enamine during polymerizations. (b) ¹³C-{¹H}-CP-MAS-NMR spectra of OBP (left), ABP (middle) and PBP (right) as polymers with TREN or HMD, and monomers. Ketone (orange), imine (green) and enamine (blue) signals are highlighted.

The assignments of model compounds and linear polycondensates from OBP and HMD were supported by the theoretical calculations shown before, which confirmed that aminals and hemiaminals are unfavored in comparison with imines and enamines, as long as ring formation is not possible.

Polycondensates from bispiperidones and 1,6-diaminohexane (HMD) and tris(aminoethyl)amine (TREN) were prepared as shown in Scheme 3. The ratio of primary amine to ketone was kept at 1 : 1 to achieve high conversion. In order to obtain homogeneous mixtures, both monomers were dissolved in methanol, the solutions mixed and heated to 60 °C in an open mould to allow evaporation of the solvent.

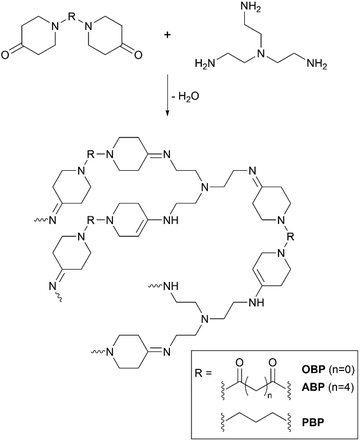Scheme 3 Schematic polymer structures of bispiperidone derivatives with TREN containing the imine and enamine groups.

The amide-containing linear polymers were insoluble in common solvents, such as chloroform, DCM, hexane, ethyl acetate, acetonitrile, DMF or DMAc, without showing the reaction. Either crosslinking due to small amounts of aminal formation, which cannot be seen in the spectroscopic analysis, or hydrogen bonding leading to network structures can cause this effect.^14–16,69

As found via the model reactions, the polymers were expected to contain imines and enamines as shown in the simplified reaction scheme in Fig. 5a. To obtain further proof, ¹³C solid-state NMR measurements of the reaction products of the reactions of TREN or HMD with the respective bispiperidone were conducted. The signals of OBP, ABP and PBP as educts were compared with those of both polymers in stacked spectra (Fig. 5b). High conversion of the reactive ketones is found, whose ¹³C signals appeared between 205 and 210 ppm, depending on the respective monomer. Additional signal broadening around 170 ppm indicated imine formation. IR spectroscopy confirmed these trends by a slight shift of the band at around 1630 cm⁻¹ of approximately 10 cm⁻¹, caused by overlapping of the C=N- and the amide C=O-stretch bands (Fig. S17†). In polymerizations of PBP the imine formation was observed most clearly, due to the absence of amide functionalities appearing at around 170 ppm (Fig. 5b, right). Enamine functionalities are proved by two broad signals at around 150 ppm, which occurred in the model compounds (Fig. 4e) as well.

pH-Dependent depolymerization and monomer recovery

In order to investigate pH-dependent polymer stability in aqueous media, defined amounts of polymer were added to aqueous solutions of defined pH values of 1, 8 and 12 and observed over time (Fig. S19†). After 3 h, all polymers were completely hydrolysed. All polymers show a lower stability in acidic media, which is expected as imine functionalities are acid labile and hydrolyse easily. The relative stabilities of the networks made from the three bispiperidones were determined by the visual disappearance of solid samples at defined pH values. PBP polymers were less stable than the amide-containing ones, i.e. they hydrolysed faster, which correlates with the trends in the equilibria with diols (Fig. 1). OBP networks appeared to be the slowest hydrolysing ones in aqueous solution.

After dissolution of the polymer networks in aqueous media, the bispiperidones could be recovered from dichloromethane (Fig. 6). Thus, the bispiperidones could be used as monomers for another cycle of polymerization. However, under basic conditions, decomposition of the educts seemed to occur as well (Fig. S20†).

Fig. 6 NMR spectra of the OBP monomer (top) to synthesize the polymer (center) with TREN from which the monomer OBP′ (bottom) could be regained. (a) ¹H NMR spectra of OBP and OBP′ measured in CDCl₃ and the hydrolyzed polymer measured in D₂O, and (b) ¹³C-{¹H}-CP-MAS-NMR spectra measured at 12 kHz, where * indicates spinning side bands.

Conclusions

We have reported new bispiperidones for use as highly reactive electrophiles in dynamic covalent reactions with bi- and trifunctional amines. By varying the linker of the bispiperidone, electrophilicity as well as properties of the resulting linear polymers and polymer networks can be modulated. Imines as major structural units in the polymers are found next to enamines, which is in contrast to previously reported dominating aminals and hemiaminals.²⁸ We explain this different behaviour by both the chemical structures of the amines used here, which do not allow five- and six-membered ring formation, as well as the absence of water in the reaction.

Furthermore, we investigated the thermodynamics of the formation of the aminal, hemiaminal, imine and enamine using density functional theory. The calculations are in good agreement with the experimental results. The results indicate that under the given reaction conditions, imine and enamine are thermodynamically more favourable than aminal and hemiaminal. Moreover, it has been found that aminals can be obtained by conducting the reactions at lower temperatures and higher concentrations. The calculated thermodynamics of the cyclo-aminal and enamine–imine formation also agrees with the experimental findings.

The polycondensates are susceptible to hydrolysis in aqueous media, with pH and the nature of the linker influencing the stability of the product. Bispiperidone recovery is possible, offering re-usability for another cycle of polymerization. Next to network degradation in aqueous media, mechanical properties and exchange reactions in bulk materials need to be probed to evaluate the full potential of bispiperidones as cross-linkers for the preparation of reversible networks.

Author contributions

Patricia Godermajer: writing – original draft, editing, investigation, methodology, visualization, formal analysis; Andreas Achazi: writing, theoretical investigation and validation; Doreen Mollenhauer: writing and editing the computational part, theoretical investigation and validation; Andreas Seifert: formal analysis, investigation and validation; Michael Sommer: writing – editing and review, conceptualization, funding acquisition, project administration, resources and supervision.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. Spange is acknowledged for fruitful discussions. M. Voigtländer is acknowledged for helping with bispiperidone synthesis. The DFG (project SO1213/20-1) is greatly acknowledged for funding. The authors acknowledge computational resources provided by the HPC Core Facility and the HRZ of the Justus-Liebig-University Giessen.

The coordinates of all optimized structures are available at: https://dx.doi.org/10.22029/jlupub-18387.

References

1. Plastics Europe AISBL, EPRO, “Plastics - the Facts 2022·Plastics Europe,” can be found under https://plasticseurope.org/knowledge-hub/plastics-the-facts-2022/, 2022.
2. Z. O. G. Schyns and M. P. Shaver, Macromol. Rapid Commun., 2021, 42, 2000415.
3. M. Frounchi, Macromol. Symp., 1999, 144, 465–469.
4. H. Jin, J. Gonzalez-Gutierrez, P. Oblak, B. Zupančič and I. Emri, Polym. Degrad. Stab., 2012, 97, 2262–2272.
5. J. M. Garcia and M. L. Robertson, Science, 2017, 358, 870–872.
6. I. A. Ignatyev, W. Thielemans and B. Vander Beke, ChemSusChem, 2014, 7, 1579–1593.
7. G. W. Coates and Y. D. Y. L. Getzler, Nat. Rev. Mater., 2020, 5, 501–516.
8. S. Sulaiman, S. Yamato, E. Kanaya, J.-J. Kim, Y. Koga, K. Takano and S. Kanaya, Appl. Environ. Microbiol., 2012, 78, 1556–1562.
9. V. Tournier, C. M. Topham, A. Gilles, B. David, C. Folgoas, E. Moya-Leclair, E. Kamionka, M.-L. Desrousseaux, H. Texier, S. Gavalda, M. Cot, E. Guémard, M. Dalibey, J. Nomme, G. Cioci, S. Barbe, M. Chateau, I. André, S. Duquesne and A. Marty, Nature, 2020, 580, 216–219.
10. C. Sonnendecker, J. Oeser, P. K. Richter, P. Hille, Z. Zhao, C. Fischer, H. Lippold, P. Blázquez-Sánchez, F. Engelberger, C. A. Ramírez-Sarmiento, T. Oeser, Y. Lihanova, R. Frank, H.-G. Jahnke, S. Billig, B. Abel, N. Sträter, J. Matysik and W. Zimmermann, ChemSusChem, 2022, 15, e202101062.
11. F. Bernardeau, D. Perrin, A.-S. Caro-Bretelle, J.-C. Benezet and P. Ienny, J. Mater. Cycles Waste Manage., 2018, 20, 1320–1336.
12. W. Post, A. Susa, R. Blaauw, K. Molenveld and R. J. I. Knoop, Polym. Rev., 2020, 60, 359–388.
13. E. Morici, S. C. Carroccio, E. Bruno, P. Scarfato, G. Filippone and N. T. Dintcheva, Polymers, 2022, 14, 2038.
14. E. Morici and N. T. Dintcheva, Polymers, 2022, 14, 4153.
15. M. R. Vengatesan, A. M. Varghese and V. Mittal, in Thermosets Second Ed, ed. Q. Guo, Elsevier, 2018, pp. 69–114.
16. J.-P. Pascault and R. J. J. Williams, in Handb. Polym. Synth. Charact. Process, John Wiley & Sons, Ltd, 2013, pp. 519–533.
17. G. Oliveux, L. O. Dandy and G. A. Leeke, Prog. Mater. Sci., 2015, 72, 61–99.
18. “Chemical recycling of plastic waste,” can be found under https://www.basf.com/global/en/who-we-are/sustainability/we-drive-sustainable-solutions/circular-economy/mass-balance-approach/chemcycling.html, 2023.
19. M.-S. Wu, B. C. Jin, X. Li and S. Nutt, Adv. Manuf.: Polym. Compos. Sci., 2019, 5, 114–127.
20. S. J. Rowan, S. J. Cantrill, G. R. L. Cousins, J. K. M. Sanders and J. F. Stoddart, Angew. Chem., Int. Ed., 2002, 41, 898–952.
21. N. Zheng, Y. Xu, Q. Zhao and T. Xie, Chem. Rev., 2021, 121, 1716–1745.
22. J. M. Winne, L. Leibler and F. E. Du Prez, Polym. Chem., 2019, 10, 6091–6108.
23. P. Taynton, H. Ni, C. Zhu, K. Yu, S. Loob, Y. Jin, H. J. Qi and W. Zhang, Adv. Mater., 2016, 28, 2904–2909.
24. Y. Spiesschaert, M. Guerre, I. De Baere, W. Van Paepegem, J. M. Winne and F. E. Du Prez, Macromolecules, 2020, 53, 2485–2495.
25. A. Takahashi, T. Ohishi, R. Goseki and H. Otsuka, Polymer, 2016, 82, 319–326.
26. S. Yu, R. Zhang, Q. Wu, T. Chen and P. Sun, Adv. Mater., 2013, 25, 4912–4917.
27. D. Montarnal, M. Capelot, F. Tournilhac and L. Leibler, Science, 2011, 334, 965–968.
28. T. Uhlig, C. Fengler, A. Seifert, F. Taubert, L. Kaßner, H.-J. Hähnle, C. Hamers, M. Wilhelm, S. Spange and M. Sommer, ACS Macro Lett., 2021, 10, 389–394.
29. W. Denissen, J. M. Winne and F. E. D. Prez, Chem. Sci., 2015, 7, 30–38.
30. C. J. Kloxin, T. F. Scott, B. J. Adzima and C. N. Bowman, Macromolecules, 2010, 43, 2643–2653.
31. C. Fengler, S. Spange, M. Sommer and M. Wilhelm, Macromolecules, 2022, 55, 349–358.
32. P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192.
33. P. Pracht and S. Grimme, Chem. Sci., 2021, 12, 6551–6568.
34. S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862.
35. P. Pracht, E. Caldeweyher, S. Ehlert and S. Grimme, ChemRxiv, 2019,  DOI:10.26434/chemrxiv.8326202.v1.
36. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
37. S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009.
38. S. Ehlert, M. Stahn, S. Spicher and S. Grimme, J. Chem. Theory Comput., 2021, 17, 4250–4261.
39. TURBOMOLE V7.5.1 a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from https://www.turbomole.org, 2021.
40. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
41. S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, J. Chem. Phys., 2020, 152, 184107.
42. K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290.
43. K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 242, 652–660.
44. K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124.
45. P. A. M. Dirac and R. H. Fowler, Proc. R. soc. Lond. Ser. A-Contain. Pap. Math. Phys. Character, 1929, 123, 714–733.
46. J. C. Slater, Phys. Rev., 1951, 81, 385–390.
47. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
48. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
49. E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112.
50. E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122.
51. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
52. S. Sinnecker, A. Rajendran, A. Klamt, M. Diedenhofen and F. Neese, J. Phys. Chem. A, 2006, 110, 2235–2245.
53. I. M. Smallwood, Handbook of Organic Solvent Properties, Hodder Headline Group, London UK, 1996.
54. CRC Handbook of Chemistry and Physics, W. M. Haynes, D. R. Lide and T. J. Bruno, CRC Press Boca Raton, FL, Boca Raton, FL, 2017.
55. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985.
56. F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152.
57. P. Deglmann, F. Furche and R. Ahlrichs, Chem. Phys. Lett., 2002, 362, 511–518.
58. P. Deglmann and F. Furche, J. Chem. Phys., 2002, 117, 9535–9538.
59. F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753–12762.
60. A. Klamt and V. Jonas, J. Chem. Phys., 1996, 105, 9972–9981.
61. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
62. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
63. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2019, 2019.
64. F. Jensen, Introduction to Computational Chemistry, John Wiley & Sons Ltd, Chichester, UK, 2006.
65. R. P. Bell and A. O. McDougall, Trans. Faraday Soc., 1960, 56, 1281–1285.
66. K. Schwetlick and Autorenkollektiv, in Organikum, Wiley-VCH, 2015, pp. 468–470.
67. J. J. Van Luppen, J. A. Lepoivre, R. A. Dommisse and F. C. Alderweireldt, Org. Magn. Reson., 1979, 12, 399–404.
68. G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, New York Oxford, 1997.
69. B. A. Miller-Chou and J. L. Koenig, Prog. Polym. Sci., 2003, 28, 1223–1270.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4py00025k

---