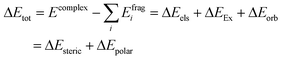Reinvigorating aza-Michael reactions under ionic liquid catalysis: a greener approach

Abstract

Cholinium α-amino carboxylates, which debuted in the ionic liquid arena over a decade ago, exhibit superior stability and suitable physical properties relative to other RTILs. Although synthetic pursuits in such media, leveraging their dual role as solvents and catalysts, have been scarce so far, we herein illustrate their catalytic advantage in aza-Michael reactions in terms of low loading, acceleration and improved yields with respect to conventional conditions and other imidazolium-based ILs. These highly structured salts most likely act through multiple and cooperative non-covalent interactions. These mechanistic features have also been investigated through high-level computational analyses as well.

---

Introduction

The use of neoteric solvents along with eco-friendly reaction conditions for improving organic transformations has become standard practice. Although the benefits of adopting such conditions can reasonably be justified, reassessment of some experimental variables often unveils both pros and cons that can further be tuned in terms of sustainability and efficiency. This is especially relevant for key reactions such as carbon–carbon and carbon–heteroatom bond-forming reactions, which are instrumental for molecular derivatisation and construction of complex skeleta. The aza-Michael reaction is, in context, a venerable synthetic transformation involving the addition of a primary or secondary amine (donor) to an activated double bond (acceptor), often an acrylate, producing amino ester derivatives.

Aza-Michael reactions can be conducted on a wide range of substrates under multiple solvent and temperature conditions.^1,2 Notably, solventless reactions at ambient temperature can successfully be achieved, and the addition proceeds with 100% atom economy, which in turn fulfils two or more principles for green chemistry. Significant advancements include intramolecular and organocatalytic variations, generally focusing on asymmetric reactions, thus expanding the scope and applicability towards chiral natural products and pharmaceuticals.^3–5 Aza-Michael reactions can also be tailored to polymer chemistry⁶ and biobased acceptors from renewable resources.⁷ Although essentially catalyst-free aza-Michael reactions are feasible, in line with Michael-type mechanisms, catalysis greatly enhances the reaction outcome and, in recent years, organocatalysts have shown significant improvements acting through both non-covalent interactions and covalent bond formation (e.g. via iminium ions).^3–5 The use of ionic liquids (ILs) in aza-Michael reactions has been reported for nearly two decades. Most cases involve conventional ionic liquids generated by tandem quaternisation/anion metathesis, leading to well-established imidazolium salts and others derived from bulky ammonium salts. In general, improvements are observed in acceleration, yields and recyclability relative to uncatalysed aza-Michael reactions.^8–20 It is widely accepted that such room-temperature ILs suffer from inherent drawbacks, namely tedious preparations, hygroscopicity, and worse, they are non-innocent ligands that may afford reactive intermediates and toxic species upon decomposition.

The alternative use of low-melting mixtures based on naturally occurring ligands has led to the broad class of deep eutectic solvents (DES), whose popularity has recently increased. This is well portrayed by choline-based ionic liquids^21,22 and those derived entirely from biomaterials.^23–25 In context, imidazolium-based ILs from naturally occurring amino acids were also described in early developments of the field,²⁶ and choline amino acid salts, [Cho][AA], entered into the repertoire of novel eutectic phases almost a decade ago, as non-toxic solvents for biomass pretreatment.²⁷ Synthetic applications, however, are still in the infancy. It is fair to mention that choline-proline, [Cho][Pro], the first prototype, was reported in 2007 as a catalyst in direct aldol reactions.²⁸ The catalyst can be regarded as a logical extension of proline as an organocatalyst for aldol condensations, although water was employed as an additive and reactivity (from 10 min to 24 h) was dependent on the carbonyl partners. Subsequent work described the preparation of other cholinium-amino carboxylates, namely [Cho][Ala], [Cho][Gly], [Cho][His], [Cho][Phe] and [Cho][Thr], which catalysed the Knoevenagel condensation, albeit surprisingly [Cho][Pro] was excluded from such a study.²⁹ In this case, the reactivity heavily depends on the acidity of the active methylene compound, whereas all the ILs have enough basic strength (pK_a ≥ 9) to promote H-abstraction and showed no appreciable conversion differences after three hours. Further studies and analyses of such cholinium salts, both experimental and theoretical, unveiled their distinctive structural features and capabilities.^30–32 Thus, the interaction and dynamics of liquids based on choline and amino acids, as portrayed by [Cho][Ala], suggest a strong H-bond, which, once formed, is persistent, and the proton resides exclusively on the choline hydroxyl. Moreover, no proton transfer occurs within the simulated temporal framework, and there is no evidence of medium-range spatial order.³³ The densities of [Cho][AA] are, however, quite similar without apparent correlation with molecular mass or ion sizes. The latter appears consistent with common dominant interactions between the cation and the anionic skeleton.^31,32 Further quantum calculations show the donor-to-acceptor H-bond as the primary interaction between the ionic pairs, with the charge delocalised over numerous atoms, thus reducing the strength of electrostatic interaction.^34–36 Because of the directional character of H-bonding, the interaction energies will be affected by the side chain of the amino acid moiety. As a result, the anions greatly dictate the mesoscopic structures of [Cho][AA], as non-polar fragments will segregate from the remaining charged network when interacting with external molecules.^31,32 Other properties of [Cho][AA], viscosity in particular, vary significantly, and, remarkably, some derivatives exhibit lubrication performance comparable to that found for olefin oils.³⁷

In an attempt to explore further the synthetic ability of [Cho][AA], we document our pursuits in the aza-Michael reaction, which has been described under a wide variety of conditions as already mentioned,^1,2 and provide insights into the catalytic performance of these neoteric liquids.

Results and discussion

We began a preliminary screening of aza-Michael reactions with a set of representative aliphatic amines and electron-withdrawing alkenes, such as dibutylamine and morpholine along with either methyl acrylate or acrylonitrile, with different [Cho][AA] as catalysts (Fig. 1). As the nucleophilicity of the amine increases and the Michael acceptor becomes more electrophilic and less sterically impeded at the β-carbon, uncatalysed reactions are easy to perform. However, they can take long, from hours to days to achieve completion.^1,2 As gathered in Table 1, condensations in the presence of [Cho][AA] generally proceeded quickly. They did go to completion within minutes (as monitored by TLC on checking the disappearance of the starting materials). Exceptions were the sluggish reaction observed for Bu₂NH/acrylonitrile pair with [Cho][Lys] or a reluctant reaction with [Cho][His], otherwise faster with other ILs.

Fig. 1 Representative aza-Michael reactions and amino acids used for generating [Cho][AA] ionic liquids. pK_a values for acid and basic groups are standard, and approximate data is rounded to the first decimal place for comparative purposes.

Table 1 Screening experiments for aza-Michael reaction models with [Cho][AA] ILs^a,b

Amine	Alkene	[Cho][AA]	Reaction time
a Reaction conditions: amine (1.2 mmol), alkene (1.0 mmol), [Cho][AA] (0.25 mmol). b All reactions were conducted at room temperature (ca. 25 °C) and monitored by TLC until the disappearance of the starting materials. c Incomplete reaction, even after heating at 60 °C.
Dibutylamine	Methyl acrylate	[Cho][Lys]	15 min
Dibutylamine	Acrylonitrile	[Cho][Lys]	2.5 h
Morpholine	Methyl acrylate	[Cho][Lys]	20 min
Morpholine	Acrylonitrile	[Cho][Lys]	15 min
Morpholine	Methyl acrylate	[Cho][Arg]	40 min
Morpholine	Methyl acrylate	[Cho][Glu]	50 min
Morpholine	Methyl acrylate	[Cho][His]	3 d^c
Morpholine	Methyl acrylate	[Cho][Pro]	5 min
Dibutylamine	Methyl acrylate	[Cho][Pro]	10 min
Morpholine	Acrylonitrile	[Cho][Pro]	10 min
Dibutylamine	Acrylonitrile	[Cho][Pro]	10 min

---

Clearly, [Cho][Pro] performs better than other combinations of choline cations and α-amino carboxylates. To ascertain the robustness of this system and verify actual catalytic assistance, we monitored the reaction completion at different molar ratios and included other amines (Table 2).

Table 2 Aza-Michael reactions monitored to completion under dual solvation/catalytic effects of [Cho][Pro]^a

Entry	Amine (mmol)	Alkene (mmol)	[Cho][Pro] (mmol)	Reaction time
a TLC monitoring until the disappearance of reagents. b Complete after the addition of morpholine. c Incomplete after 3 h. d Incomplete after 3 d.
1	Morpholine (1.2)	Methyl acrylate (1.0)	0.25	5 min
2	Morpholine (1.2)	Methyl acrylate (1.0)	0.1	10 min
3	Morpholine (1.2)	Methyl acrylate (1.0)	0.5	10 min
4	Morpholine (1.0)	Methyl acrylate (1.0)	0.5
5	Morpholine (2.0)	Methyl acrylate (1.0)	0.5	10 min
6	Morpholine (1.2)	Acrylonitrile (1.0)	0.25	10 min
7	Dibutylamine (1.2)	Methyl acrylate (1.0)	0.25	10 min
8	Dibutylamine (1.2)	Acrylonitrile (1.0)	0.25	10 min
9	Dibutylamine (1.2)	Methyl acrylate (1.0)	0.1	3 h^c
10	Dibutylamine (2.0)	Methyl acrylate (1.0)	0.5	3 h^c
11	Benzylamine (1.2)	Methyl acrylate (1.0)	0.25	10 min
12	Benzylamine (1.2)	Acrylonitrile (1.0)	0.25	5 min
13	Benzylamine (2.0)	Methyl acrylate (1.0)	0.5	10 min
14	Piperidine (1.2)	Methyl acrylate (1.0)	0.25	10 min
15	Piperidine (1.2)	Acrylonitrile (1.0)	0.25	5 min
16	Aniline (1.2)	Methyl acrylate (1.0)	0.25	10 min
17	Aniline (1.2)	Acrylonitrile (1.0)	0.25	5 min
18	Aniline (1.0)	Methyl acrylate (1.0)	0.25	30 min
19	Aniline (1.0)	Methyl acrylate (1.0)	0.1	3 d
20	Morpholine (1.2)	Methyl acrylate (1.0)	—	1.5 h
21	Dibutylamine (1.2)	Methyl acrylate (1.0)	—	3 d
22	Aniline (1.2)	Methyl acrylate (1.0)	—	3 d^d

---

Data collected in Table 2 show the beneficial effect of [Cho][Pro], using substoichiometric amounts of 10 mol%, 25 mol% and 50 mol%, aiding in dissolving the reaction mixture and affording rapid and complete transformations. A lower catalyst loading decreases reactivity slightly (entries 2, 9, and 19). A little excess of amine triggers the Michael addition (entry 4 or 18), although in general, archetypal primary and secondary amines exhibit good reactivity, including less basic aniline (entries 16–19) and the bulkier dibutylamine. Even if aliphatic primary amines tend to produce both mono- and bis-adducts,^1,2 the present reactions with acrylic acid derivatives gave rise to monoadducts and no evidence of alkene polymerisation could be observed. As expected, neat reactions work as well, albeit taking longer or remaining incomplete (entries 20–22), thus unravelling the catalytic intermediacy of the ionic liquid.

From a practical standpoint, product isolation can easily be accomplished and requires no more than extraction (see Experimental), drying and evaporation. In some cases, filtration through a short silica pad prior to evaporation removes insoluble impurities, leading to essentially pure adducts. Isolated yields, not optimised nevertheless, are good enough, and the reactions mentioned above are generally faster than those achieved with other conventional ILs as well as other green alternatives with other ILs (Table 3).

Table 3 [Cho][Pro]-mediated aza-Michael reactions and isolated yields

Entry	Amine	Alkene	Yield^a (%)	Reaction time (min)
				This study^b	Other studies
a Isolated yield, not optimised. b Amine 1.2 mmol, alkene 1.0 mmol, [Cho][Pro] 0.25 mmol, rt.
1	Morpholine	Methyl acrylate	100	5	10,^9 180,^38 90,^39 35^40
6	Morpholine	Acrylonitrile	83	10	90,^39 20,^40 30^41
7	Dibutylamine	Methyl acrylate	75	10	15,^9 300^39
8	Dibutylamine	Acrylonitrile	52	10	120^39
11	Benzylamine	Methyl acrylate	54	10	180,^38 150^39
12	Benzylamine	Acrylonitrile	89	5	30^41
14	Piperidine	Methyl acrylate	65	10	10,^9 120,^38 90,^39 30,^40 30^41
15	Piperidine	Acrylonitrile	91	5	10,^9 90,^38 15,^39 25^40
16	Aniline	Methyl acrylate	55	10	120,^41 180,^39 1440^40
17	Aniline	Acrylonitrile	51	5	150,^38 120^39

---

Furthermore, a scale-up test was carried out using the addition of morpholine to methyl acrylate at room temperature as a model reaction. In 2.5 mmol of ionic liquid, 12 mmol of the amine were reacted with 10 mmol of the alkene. The process, monitored by TLC, was completed within five minutes, and the adduct was successfully isolated in quantitative yield by flash chromatography, as described in the Experimental section.

The recyclability of [Cho][Pro] is worth mentioning without compromising its catalytic activity after several cycles. As displayed in Fig. 2, the reaction of morpholine with methyl acrylate was complete in 5 min when using the recovered IL up to five times.

Fig. 2 Reusability of [Cho][Pro] (0.25 mmol) as a catalyst for the standard aza-Michael coupling between morpholine (1.2 mmol) and methyl acrylate (1.0 mmol).

However, an elusive point with this family of ILs is their homogeneous character, a fact illustrated, as mentioned above, through disparate viscosity values and, surprisingly, some have been reported as solids at room temperature.³¹ The usual synthetic protocol involves a one-step neutralisation reaction of aqueous choline hydroxide, [Cho][OH], with the corresponding amino acids, which releases water as the only by-product, thus accounting for a green character indeed. In our hands, they were viscous yet handleable liquids. They do not need to be particularly dried, as water content can be tolerated and actually facilitates reaction work-up. The proton transfer reaction not only leads to a permanent formation of an alkylammonium salt but also avoids introducing foreign ions derived from alternative metathesis procedures. It is well known that the addition of water (even used as solvent) accelerates the aza-Michael reaction by activating both the donor and acceptor, which is associated with hydrogen bonding with surrounding water molecules.² This may explain the positive effect observed for [Cho][Pro]-mediated aldol reaction by deliberately adding one equivalent of water.²⁸

At first sight, there is no obvious reason to invoke differences in H-transfer to choline cation based on amino acid acidity (Fig. 1), at least in terms of the ΔpK_a rule, which is usually applied to rationalise the formation of solid salts and cocrystals.⁴² Dynamic simulations of some [Cho][AA] showcase heterogeneity features arising from segregation between the polar domain of electrostatic/H-bonding interactions and the non-polar one due to the anion side chains.^43,44 This sort of solvophobic effect manifests itself by adding an additive (e.g. alcohols), which alters the continuity of the [Cho][AA]-IL network by establishing competing IL-additive interactions.⁴⁵ Since one of the most relevant applications of [Cho][AA]-ILs is their capability for biomass solubilisation,³¹ this has been largely attributed to the anion side chain having excellent H-bond donors in the cases of [Arg] and [Lys] anions, which become stronger through polarisation by nearby cholinium cations.^31,32 However, an electrostatic effect alone cannot justify marked differences in reactivity, and steric and hydrophobic interactions should underpin the outperformance of [Cho][AA] as catalysts, the Pro-based IL in particular. Indeed, we reasoned that H-bonding represents the driving force to bring reaction partners together, a fact attributable to other less polarised choline-based ILs when interacting with covalent molecules.⁴⁶

On the other hand, the H-bond between choline and α-amino carboxylates, being strong enough as documented,³³ should most likely involve both electrostatic and covalent contributions.⁴⁷ The case of [Cho][Pro] should a priori be ascribed to the compelling evidence that proline acts as a bifunctional catalyst that lowers the activation barrier to C–N formation by charge stabilisation at the transition structure.^48,49 Having a less flexible secondary amine side chain than other amino acids, activation of the electrophile will produce a highly ordered intermediate towards nucleophilic attack, where the polarisation of the ionic catalyst will also enhance the orienting role of H-bond donor groups.

To elucidate the reaction mechanism behind the catalytic activity caused by the ionic liquid in the aza-Michael mentioned above reactions, we selected as starting materials those leading to the fastest reactions experimentally: proline as amino acid, morpholine as secondary amine, and methyl acrylate as 1,4-difunctionalised compound. The structures of ionic liquid pairs formed from choline and proline were obtained throughout MTD simulations (see computational details), which afforded 200 structures within a 6 kcal mol⁻¹ window. The most stable structure (Fig. 3) shows a hydrogen bond between the OH of choline and the carboxylate group of the amino acid. This result perfectly matches previous MD simulations and neutron diffraction analysis of choline-based ionic liquid.^31,32 However, one water molecule was included in the present case, in which an acid–base reaction between proline and choline hydroxide should have formed. Overall, this feature could also unveil the putative catalytic effect of water. Moreover, this water molecule forms non-covalent interactions with the same oxygen that interacts with both the OH of choline by hydrogen bonding and the ammonium ion of choline through dipole-induced dipole interactions.

Fig. 3 Optimised geometry of the ionic liquid (Liq) optimised at the ωB97X-D/def2-SVP level of theory in a cage (SMD method) having a dielectric constant similar to that of the ionic liquid.

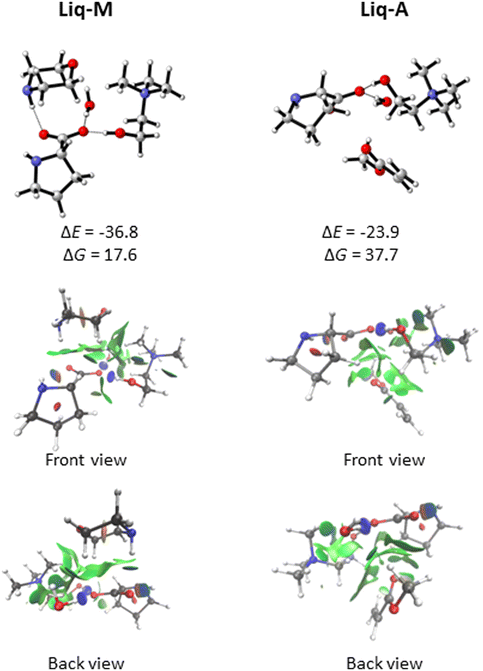
The ionic liquid (referred to as Liq, for simplicity) could then complex with either morpholine (M) or methyl acrylate (A). Our docking analysis (see Computational details) shows that the most favourable interactions of Liq with A (Liq-A in Fig. 4) are dispersion forces between A and the pocket generated by the aliphatic chains of proline and morpholine (for a visual description of such interactions, go to the NCI plots in Fig. 4). On the other hand, the strongest interaction energy between Liq and M (Liq-M in Fig. 4) is found when M acts as hydrogen donor with one oxygen of the carboxylate group of proline. In this case, the oxygen atom (ether bond) of morpholine is also forming dipole-induced dipole interactions with choline as well as the water molecule (NCI interactions, Fig. 4). From a quantitative standpoint, such non-covalent interactions between Liq and either M or A were estimated through an energy decomposition analysis (EDA). The energy change during the formation of a complex can be elucidated as:

where E_orb represents the orbital interaction term, which stabilises the complex, E_els refers to the electrostatic interaction and E_Ex is the exchange repulsion term, arising from the Pauli repulsion effect. These two last terms can be combined as the steric term (E_steric). The E_orb contribution stabilises the Liq-M complex (−8.6 kcal mol⁻¹) to a higher extent than Liq-A, being −5.4 kcal mol⁻¹. Otherwise, the steric term (E_els + E_Ex) favours the complexation of Liq with A with respect to Liq-M by 0.7 kcal mol⁻¹. Surely, the stabilising effect can also be ascribed to a closer proximity of M to Liq in Liq-M than that between A and Liq in Liq-A, since M forms stronger NCIs with Liq. All in all, the total interaction energy (E_tot) is more favourable for the Liq-M complex by −2.4 kcal mol⁻¹. Note that the total interaction energy obtained for the EDA analysis differs from the relative electronic energy of the complexes because of the distorted fragments employed, whereas ΔE is obtained from ground-state geometries.

Fig. 4 Optimised geometries of complexes Liq-M and Liq-A at the ωB97X-D/def2-TZVP//ωB97X-D/def2-SVP level of theory with bulk solvation (SMD method). Relative energies in kcal mol⁻¹ are given between Liq and M and A for Liq-M and Liq-A, respectively. NCI analyses of each structure are depicted below.

Fig. 5 shows the free energy profile at 298.15 K for the reaction involving the complex Liq-M with A. The first step yields the new C–N bond between the morpholine nitrogen atom and methyl acrylate's γ carbon (TS1). This process shows a free energy barrier of 18.7 kcal mol⁻¹ and leads to the zwitterionic intermediate Int1 through an endergonic process having a free energy change of 15.9 kcal mol⁻¹ along the reaction coordinate that links reactants to Int1, thus accounting for C–N bond formation. The enolate intermediate Int1 could evolve through two different reaction pathways. The less favoured pathway links Int2 with intermediate Int3 in which the Michael adduct (P) complexes with the ionic liquid. This process shows a 40.8 kcal mol⁻¹ free energy barrier corresponding to the transition structure TS2b. This transformation actually constitutes the second step of a typical 1,2-addition in an aza-Michael reaction. Instead, the first intermediate Int1 could lead to the unstable intermediate Int2 through another transition structure (TS2a) and proceed with a very low energy barrier (0.2 kcal mol⁻¹). This process involves a proton-transfer reaction from the NH of the morpholinium cation to the nitrogen atom of proline. The last step takes place by evolving Int2 into Int3 through the transition structure TS3. In this case, the positive charge held by the nitrogen atom at the proline moiety is alleviated by proton transfer to the β-carbon of the enolate. Notably, the latter's energy barrier is also low, being 0.5 kcal mol⁻¹ from Int2.

Fig. 5 Free energy profile in kcal mol⁻¹ for the aza-Michael reaction between methyl acrylate (A), morpholine (M) and the ionic liquid (Liq) computed at the ωB97X-D/def2-TZVP//ωB97X-D/def2-SVP level of theory with bulk solvation (SMD method) at 298.15 K.

When considering that the reaction outcome comes from the approach of morpholine to the β-carbon of acrylate in Liq-A complex, we characterised in addition the transition structure TS1′ (Fig. 6). This step, corresponding to the formation of the C–N bond, exhibits a free energy barrier of 20.3 kcal mol⁻¹. Taking into account that this initial step is 1.6 kcal mol⁻¹ less favourable than TS1 (Fig. 5) and that the Boltzmann population of the Liq-A complex with respect to Liq-M is 1.8×10⁻⁵ (see free energy differences in Fig. 4), we can assert with confidence that formation of the Michael adduct proceeds through the reaction of Liq-M and methyl acrylate.

Fig. 6 Optimised geometry of the transition structure TS1′ at the ωB97X-D/def2-TZVP//ωB97X-D/def2-SVP level of theory with bulk solvation (SMD method). Relative energy in kcal mol⁻¹ is given with respect to Liq-A and M.

The mechanistic study evidences that the participation of the ionic liquid (Liq), acting as a catalyst, in the reaction is critical to generating the Michael adduct. In the first step, the ionic liquid is not involved in any bond-forming and bond-breaking process; it merely interacts with the secondary amine through hydrogen bonding. After the formation of the C–N bond, there are two reaction pathways, which may or may not involve the Liq species. When Liq does not participate, the rate-determining step in the formation of the Michael adduct is the proton transfer from the ammonium ion, generated at the onset, to the anionic carbon of the enolate. As mentioned above, this stepwise process is a typical 1,2-addition, which shows a close energy profile to those of previous computational studies dealing with the addition of dimethylamine and ethyl acrylate.⁵⁰ This similarity in free energy profiles of the two isolated reactants justifies, in the present case, the negligible (or none) influence of Liq on the mechanistic outcome.

Conversely, when Liq is involved in the “reaction pocket”, there is a significant increase in the reaction rate, with the rate-determining step being the formation of the C–N bond. It has been shown that the participation of an additional amine during the reaction of secondary amines with acrylates also increases the proton transfer rate from the ammonium ion generated in the first step (Int1-like intermediates) to the anionic carbon of the enolate.⁵⁰ Although this amine-assisted mechanism increases the reaction rate, it is still the rate-determining step of the whole process. Moreover, for the ionic liquid-assisted reaction, the free energy profile changes substantially, and the rate-determining step involves the formation of the C–N bond. If we may say so, the actual catalyst of the reaction evaluated here is the nitrogen atom of the amino acid fragment, which transfers the proton from an ammonium ion (Int1) to the enolate carbon in two steps, thereby forming a new, highly unstable, zwitterionic intermediate (Int2), which evolves into the Michael adduct through a subsequent proton transfer.

Accordingly, this theoretical study provides further insight into both structural and reactivity aspects, particularly regarding the ionic liquid-amine type complexes. Five different amino acids and two amines have been used, and as already mentioned, the fastest reactions involve morpholine as amine and proline as amino acid. The increase in reaction rate could mainly be ascribed to both molecular rigidity and non-covalent interactions. Concerning the latter, morpholine affords the best complexes with choline-derived ILs for the reaction to occur because, along with H-bond interaction with the carboxylate group, the ether linkage also interacts strongly with the methyl groups of the ammonium ion of choline through extensive induced dipole–dipole interactions (Fig. 7). Such interactions contribute to packing tightly the amine to Liq. Concerning the latter and as inferred from computation, the proton transfer from the amino acid nitrogen atom represents the driving force supporting this mechanism. Clearly, this effect is constrained in the heterocyclic fragment of proline, whereas the other amino acids are prone to higher conformational freedom. An increase in the conformational landscape could give rise to more stable isomers than those needed for amine complexation, thus preventing both efficient approach and proton transfer.

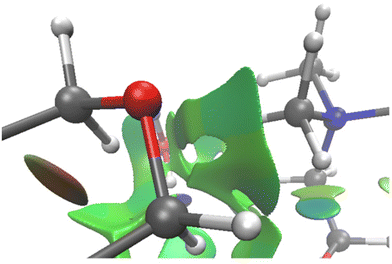Fig. 7 Zoomed NCI interactions of Liq-M near the surrounding environment of the morpholine oxygen atom.

Regarding the effect of the 1,4-difunctionalised compound, experiments show a faster reaction with methyl acrylate than with acrylonitrile. The main reason accounting for this fact should be due to the relative stability of the first intermediate (Int1). Since this specific process involves mesomeric effects where charge delocalisation from the β-carbon to the electron-withdrawing group occurs, enolate stability is enhanced relative to a cumulenic sp-like carbon formed with acrylonitrile. As a result, the first reaction step with acrylonitrile should be a more endergonic process than that of methyl acrylate, thus shifting the chemical equilibrium towards the reactants.

Experimental

Materials and methods

Solvents of HPLC grade were purchased from Scharlab S. L. and Labkem. Reagents were purchased from Acros Organics and Sigma-Aldrich. NMR spectra were recorded on a Bruker Avance 500 spectrometer at 500.15 MHz using CDCl₃ and D₂O as solvents and TMS as an internal standard. TLC was performed on silica gel plates coated with fluorescent indicator F254 from Merck KGaA. Flash chromatography was performed on Merck 60 silica gel (230–400 mesh).⁵¹

Amino acid-derived IL [Cho][Pro] was obtained following the protocol described previously.⁵² The synthesis of the ionic liquids [Cho][Arg], [Cho][Glu], [Cho][His], and [Cho][Lys] was conducted according to the methodology reported by Moriel et al.²⁹

General procedure for aza-Michael condensations

In a typical aza-Michael addition experiment, a mixture of the amine (1.2 mmol) and the alkene (1.0 mmol) were stirred in the ionic liquid (0.25 mmol) at room temperature until the completion of the reaction, as determined by TLC. Once the reaction is finished, to get rid of the IL and the excess amine, the mixture was dissolved in either DCM or Et₂O, and filtered off in an allihn-type filter tube (10 × 2 cm) through a bed of silica gel. The filtrate was evaporated at reduced pressure to yield the pure product. Alternatively, the reaction mixture can be diluted with water and extracted with either DCM or Et₂O. The organic phase was dried over anhydrous MgSO₄ and evaporated at reduced pressure to yield the pure product. In some cases, the product was further purified by flash chromatography. All the compounds have been identified by their NMR spectra, which match those of known samples.

12 mmol of morpholine, 10 mmol of methyl acrylate and 2.5 mmol of [Cho][Pro] were used in the scale-up experiment at room temperature. The reaction reached completion within 5 min, and the adduct was quantitatively isolated by flash chromatography.

Computational details

The first task in the computational study was to elucidate the structure of the catalyst, i.e., the ionic liquid. To this end, we optimised the geometry of water, deprotonated proline and choline with the tight-binding method GFN2-xTB⁵³ in benzaldehyde with the ALPB solvation model.⁵⁴ The dielectric constant of benzaldehyde was chosen for computational simulations as most ionic liquids have dielectric constants of approximately 15 on average;⁵⁵ and benzaldehyde (ε = 18.22) mimic well that polar character using both the SMD (see below) and ALPB solvent models. The three structures were placed randomly, and a non-covalent conformational sampling was carried out based on meta molecular dynamic simulations (MTD) within the NCI-iMTD workflow, implemented in the CREST software⁵⁶ at the level mentioned above of theory. The system was placed on an ellipsoid potential of 41.5, 28.0 and 27.3 Bohr to avoid complete dissociation of the resulting complexes. A total of six MTD simulations of 20 ps each were carried out to obtain a set of 200 conformers within a 6 kcal mol⁻¹ window at 298.15 K. The most stable conformer was optimised at the DFT level with the ωB97X-D method⁵⁷ in combination with the def2-SVP⁵⁸ basis set in benzaldehyde (SMD).⁵⁹ After obtaining the geometry of the ionic liquid, the most plausible interaction of the latter with both reagents, namely morpholine and methyl acrylate, was evaluated. To this end, we carried out an automated interaction site screening (aISS)⁶⁰ with the xTB program package^61,62 involving the pairs of ionic liquid-morpholine and ionic liquid-methyl acrylate, according to a similar methodology employed in previous work.⁶³ The final complexes denoted as Liq-M for morpholine and Liq-A for methyl acrylate were optimised at the above-mentioned DFT level of theory. Then, all electronic energies were refined with the same method and using the def2-TZVP basis set.⁵⁸ Relative energy comparison showed that the Liq-M complex is the most stable species and was used as a reagent for computing the mechanism of the aza-Michael reaction. All the stationary points were optimised without restrictions at the ωB97X-D/def2-SVP level of theory in benzaldehyde (SMD). Electronic energies were refined with the ωB97X-D method in combination with the def2-TZVP basis set in benzaldehyde (SMD). The level of theory employed is denoted by ωB97X-D/def2-TZVP//ωB97X-D/def2-SVP. All the minima and transition structures (TS) were characterised by hessian evaluation, obtaining zero and one imaginary frequency, respectively. Intrinsic reaction coordinate (IRC) analyses were conducted for all the characterised transition structures to ensure that all the saddle points belonged to the desired reaction path. The step size for the calculation of the reaction coordinate was set to 0.15 Bohr and an RMS Gradient Norm stopping criteria of 1.2×10⁻⁴ Hartree per Bohr. For the predictor step we used the local quadratic approximation, and the force constants were computed at every point. Non-covalent interactions (NCI) were obtained with NCIPLOT4.^64,65 A density cutoff of ρ = 0.5 au was applied, and isosurfaces of s(r) = 0.5 were coloured by sign(λ2)ρ in the [−0.03, 0.03] au range using VMD software.⁶⁶ All DFT calculations were carried out with the Gaussian 16 software package.⁶⁷ The EDA analysis was carried out with the Multiwfn software.⁶⁸

Product characterisation

[Choline][Proline]. ¹H NMR (500.15 MHz, CDCl₃): δ_H 3.94 (bs, 2H, CH̲₂–OH), 3.55 (m, 2H, CH̲₂–NMe₃), 3.37 (t, J_HH 4.5 Hz, 1H, CH–COO⁻), 3.01 (m, 1H, CH̲₂–NH), 2.69 (m, 1H, CH̲₂–NH), 1.98 (m, 1H, CH̲₂–CHCOO⁻), 1.66 (m, 2H, CH̲₂–(CH₂)₂), 1.59 (m, 1H, CH̲₂–CHCOO⁻).

[Choline][Arginine]. ¹H NMR (500.15 MHz, D₂O): δ_H 3.93 (m, 2H, CH̲₂–OH), 3.36 (t, J_HH 5 Hz, 2H, CH̲₂–NMe₃), 3.14 (m, 1H, CH̲–COO⁻), 3.08 (m, 11H, NMe₃, CH̲₂–NH), 1.48 (m, 4H, CH̲₂–CH̲₂–CH̲₂–NH₂).

[Choline][Histidine]. ¹H NMR (500.15 MHz, D₂O): δ_H 7.58 (s, 1H, NH–CH̲–N), 6.89 (s, 1H, NH–CH̲–C), 3.95 (m, 2H, CH̲₂–OH), 3.70 (dd, J_HH 5 Hz, J_HH 8 Hz, 1H, CH–COO⁻), 3.40 (t, J_HH 5 Hz, 2H, CH̲₂–NMe₃), 3.09 (bs, 9H, NMe₃), 3.03 (dd, J_HH 4.5 Hz, J_HH 15 Hz, 1H, CH̲₂–CHNH₂COO⁻), 2.91 (dd, J_HH 8 Hz, J_HH 15 Hz, 1H, CH̲₂–CHNH₂COO⁻).

[Choline][Lysine]. ¹H NMR (500.15 MHz, D₂O): δ_H 3.97 (m, 2H, CH̲₂–OH), 3.44 (t, J_HH 5 Hz, 2H, CH̲₂–NMe₃), 3.17 (t, J_HH 6.5 Hz, 1H, CH̲–COO⁻), 3.12 (s, 9H, NMe₃), 2.65 (t, J_HH 7 Hz, 2H, CH̲₂–NH₂), 1.52–1.44 (m, 4H, NH₂–CH̲₂–CH̲₂–CH̲₂–CH̲₂–CH), 1.26 (m, 2H, NH₂–CH̲₂–CH̲₂–CH̲₂–CH̲₂–CH).

[Choline][Glutamate]. ¹H NMR (500.15 MHz, D₂O): δ_H 3.98 (m, 2H, CH̲₂–OH), 3.68 (dd, J_HH 5 Hz, J_HH 7.5 Hz, 1H, CH–NH₂), 3.44 (t, J_HH 5 Hz, 2H, CH̲₂–NMe₃), 3.12 (s, 9H, NMe₃), 2.29 (dd, J_HH 3 Hz, J_HH 8 Hz, 2H, CH̲₂–CHNH₂), 2.07–1.95 (m, 2H, COO⁻–CH̲₂–CH̲₂).

3-(Benzylamino)propanenitrile. ¹H NMR (500.15 MHz, CDCl₃): δ_H 7.34–7.25 (m, 5H, arom), 3.83 (s, 2H, Ph–CH̲₂–NH), 2.92 (d, J_HH 7 Hz, 2H, NH–CH̲₂–CH₂), 2.50 (d, J_HH 6.5 Hz, 2H, NH–CH̲₂–CH̲₂), 1.69 (bs, 1H, NH).

Methyl 3-(benzylamino)propanoate. ¹H NMR (500.15 MHz, CDCl₃): δ_H 7.35–7.27 (m, 5H, arom), 3.83 (s, 2H, Ph–CH̲₂–NH), 3.71 (s, 3H, OCH₃), 2.93 (d, J_HH 6.5 Hz, 2H, NH–CH̲₂–CH₂), 2.57 (d, J_HH 6.5 Hz, 2H, NH–CH̲₂–CH̲₂), 1.82 (bs, 1H, NH).

3-Morpholinopropanenitrile. ¹H NMR (500.15 MHz, CDCl₃): δ_H 3.72 (t, J_HH 4.5 Hz, 4H, CH₂OCH₂), 2.68 (t, J_HH 7 Hz, 2H, N–CH̲₂CH₂CN), 2.54–2.50 (m, 6H, (CH̲₂)₂-N–CH₂CH̲₂CN).

Methyl 3-morpholinopropanoate. ¹H NMR (500.15 MHz, CDCl₃): δ_H 3.72–3.70 (m, 7H, CH₂OCH₂, OCH₃), 2.70 (t, J_HH 7 Hz, 2H, N–CH̲₂CH₂CO₂CH₃), 2.52 (t, J_HH 7.5 Hz, 2H, N–CH₂CH̲₂CO₂CH₃), 2.47 (bs, 4H, (CH̲₂)₂–N–CH₂CH₂COOCH₃).

¹³C NMR: (125 MHz, CDCl₃): δ_C 31.89 (1C, C̲H₂CO), 51.68 (1C, OCH₃), 53.40 (2C, CH₂NCH₂), 53.94 (1C, NC̲H₂CH₂), 66.92 (2C, CH₂OCH₂), 172.84 (1C, C=O).

3-(Dibutylamino)propanenitrile. ¹H NMR (500.15 MHz, CDCl₃): δ_H 2.78 (t, J_HH 7 Hz, 2H, N–CH̲₂CH₂CN), 2.44–2.40 (m, 6H, (CH̲₂)₂–N–CH₂CH̲₂CN), 1.44–1.28 (m, 8H, CH₃–(CH̲₂CH̲₂)₂), 0.91 (t, J_HH 7.5 Hz, 6H, 2CH₃).

Methyl 3-(dibutylamino)propanoate. ¹H NMR (500.15 MHz, CDCl₃): δ_H 3.68 (s, 3H, OCH₃), 2.79 (t, J_HH 7.5 Hz, 2H, N–CH̲₂CH₂CO₂CH₃), 2.46 (t, J_HH 7.5 Hz, 2H, CH̲₂CO₂CH₃), 2.41 (t, J_HH 7.5 Hz, 4H, (CH̲₂)₂–N–CH₂CH₂COOCH₃), 1.42 (q, J_HH 8 Hz, 4H, N(CH₂CH̲₂CH₂CH₃)₂), 1.31 (m, 4H, N(CH₂CH₂CH̲₂CH₃)₂), 0.92 (t, J_HH 7.5 Hz, 6H, 2CH₃).

3-(Phenylamino)propanenitrile. ¹H NMR (500.15 MHz, CDCl₃): δ_H 7.26–7.23 (m, 2H, arom), 6.81 (t, J_HH 7 Hz, 1H, arom), 6.66 (d, J_HH 8.5, 2H, arom), 3.73 (s, 1H, NH), 3.56 (t, J_HH 6.5 Hz, 2H, NHCH̲₂), 2.67 (t, J_HH 6.5 Hz, 2H, CH̲₂CO₂CH₃).

Methyl 3-(phenylamino)propanoate. ¹H NMR (500.15 MHz, CDCl₃): δ_H 7.23–7.17 (m, 2H, arom), 6.81–6.74 (m, 1H, arom), 6.72–6.65 (m, 2H, arom), 3.73 (s, 3H, OCH₃), 3.48 (t, J_HH 6.5 Hz, 2H, NHCH̲₂), 2.65 (t, J_HH 6.5 Hz, 2H, CH̲₂CO₂CH₃).

3-(Piperidin-1-yl)propanenitrile. ¹H NMR (500.15 MHz, CDCl₃): δ_H 2.69 (t, J_HH 7 Hz, 2H, NHCH̲₂), 2.51 (t, J_HH 7 Hz, 2H, CH₂CN), 2.45 (bs, 4H, CH₂NCH₂), 1.63–1.58 (m, 4H, 2CH₂), 1.48–1.43 (m, 2H, CH₂).

Methyl 3-(piperidin-1-yl)propanoate. ¹H NMR (500.15 MHz, CDCl₃): δ_H 3.68 (s, 3H, CH₃), 2.67 (t, J_HH 7 Hz, 2H, NHCH̲₂), 2.52 (t, J_HH 7.5 Hz, 2H, CH̲₂CO₂CH₃), 2.39 (bs, 4H, CH₂NCH₂), 1.57 (q, J_HH 5.5 Hz, 4H, 2CH₂), 1.45–1.42 (m, 2H, CH₂).

Conclusions

In conclusion, this study shows the positive effects, in terms of high-yielding fast reactions, operational simplicity, and greenness by using choline-amino acids ionic liquids in the venerable and otherwise synthetically useful aza-Michael addition through a set of benchmark reactions. The mechanism under such conditions has been evaluated by computation, showing the initial complexation of the ionic liquid with reactants, instrumental for the subsequent catalytic effect, together with intermediates and saddle point structures along the reaction pathway. Although some theoretical analyses have already highlighted the unique microstructure of [Cho][AA], our results reinforce that view and gain insight into the roles played by different electrostatic interactions in their catalytic effects, involving hydrogen bonding, hydration, and other cation–anion side chain interactions.

Author contributions

Conceptualisation: SI, IMLC. Funding acquisition: CJDV, IMLC. Investigation: SI, PC, CJDV, JGC, IMLC. Project administration: SI, IMLC. Supervision: PC, IMLC. Writing – original draft: PC. Writing – review & editing: SI, PC, CJDV, JGC, IMLC.

Conflicts of interest

The authors declare that part of this research has been patented previously (Spanish Patent no. ES 2904628 – B2. Date: 2022.10.25).

Data availability

ESI is available in a separate file.† Further data supporting this study are available from the corresponding author(s) upon request.

Acknowledgements

We thank the ‘Junta de Extremadura’ and ‘Fondo Europeo de Desarrollo Regional’ (European Regional Development Fund) for financial support (Grants GR21107, IB20026, and IB16167). Also, we thank the Research & Technological Innovation and Supercomputing Center of Extremadura (Cenits) and COMPUTAEX Foundation for allowing us to use the LUSITANIA computer resources.

References

1. A. Y. Rulev, Aza-Michael Reaction: A Decade Later – Is the Research Over?, Eur. J. Org. Chem., 2023, 26, e202300451.
2. A. Y. Rulev, Aza-Michael reaction: achievements and prospects, Russ. Chem. Rev., 2011, 80, 197–218.
3. M. Sánchez-Roselló, J. L. Aceña, A. Simón-Fuentes and C. del Pozo, A general overview of the organocatalytic intramolecular aza-Michael reaction, Chem. Soc. Rev., 2014, 43, 7430–7453.
4. P. Sharma, R. Gupta and R. K. Bansal, Recent advances in organocatalytic asymmetric aza-Michael reactions of amines and amides, Beilstein J. Org. Chem., 2021, 17, 2585–2610.
5. M. Sánchez-Roselló, M. Escolano, D. Gaviña and C. Pozo, Two Decades of Progress in the Asymmetric Intramolecular aza–Michael Reaction, Chem. Rec., 2022, 22, e202100161.
6. A. Genest, D. Portinha, E. Fleury and F. Ganachaud, The aza-Michael reaction as an alternative strategy to generate advanced silicon-based (macro)molecules and materials, Prog. Polym. Sci., 2017, 72, 61–110.
7. J. Peyrton and L. Avérous, Aza-Michael Reaction as a Greener, Safer, and More Sustainable Approach to Biobased Polyurethane Thermosets, ACS Sustainable Chem. Eng., 2021, 9, 4872–4884.
8. B. C. Ranu and S. Banerjee, Ionic Liquid as Catalyst and Reaction Medium. The Dramatic Influence of a Task-Specific Ionic Liquid, [bmIm]OH, in Michael Addition of Active Methylene Compounds to Conjugated Ketones, Carboxylic Esters, and Nitriles, Org. Lett., 2005, 7, 3049–3052.
9. M. L. Kantam, V. Neeraja, B. Kavita, B. Neelima, M. K. Chaudhuri and S. Hussain, Cu(acac)2 immobilized in ionic liquids: A recoverable and reusable catalytic system for aza-Michael reactions, Adv. Synth. Catal., 2005, 347, 763–766.
10. M. H. Ghasemi, E. Kowsari and A. Shafiee, Aza-Michael-type addition reaction catalysed by a supported ionic liquid phase incorporating an anionic heteropoly acid, Tetrahedron Lett., 2016, 57, 1150–1153.
11. E. Szánti-Pintér, L. Maksó, Á. Gömöry, J. Wouters, B. E. Herman, M. Szécsi, G. Mikle, L. Kollár and R. Skoda-Földes, Synthesis of 16α-amino-pregnenolone derivatives via ionic liquid-catalyzed aza-Michael addition and their evaluation as C17,20-lyase inhibitors, Steroids, 2017, 123, 61–66.
12. K. Boruah and R. Borah, Design of Water Stable 1,3-Dialkyl- 2-Methyl Imidazolium Basic Ionic Liquids as Reusable Homogeneous Catalysts for Aza-Michael Reaction in Neat Condition, ChemistrySelect, 2019, 4, 3479–3485.
13. L. Yang, L. W. Xu, W. Zhou, L. Li and C. G. Xia, Highly efficient aza-Michael reactions of aromatic amines and N-heterocycles catalyzed by a basic ionic liquid under solvent-free conditions, Tetrahedron Lett., 2006, 47, 7723–7726.
14. A. K. Verma, P. Attri, V. Chopra, R. K. Tiwari and R. Chandra, Triethylammonium acetate (TEAA): a recyclable inexpensive ionic liquid promotes the chemoselective aza- and thia-Michael reactions, Monatsh. Chem., 2008, 139, 1041–1047.
15. X.-B. Liu, M. Lu, T.-T. Lu and G.-L. Gu, Functionalized Ionic Liquid Promoted Aza-Michael Addition of Aromatic Amines, J. Chin. Chem. Soc., 2010, 57, 1221–1226.
16. X. Chen, X. Li, H. Song, Y. Qian and F. Wang, Solvent-free aza-Markovnikov and aza-Michael additions promoted by a catalytic amount of imidazolide basic ionic liquids, Tetrahedron Lett., 2011, 52, 3588–3591.
17. A. Ying, M. Zheng, H. Xu, F. Qiu and C. Ge, Guanidine-based task-specific ionic liquids as catalysts for aza-Michael addition under solvent-free conditions, Res. Chem. Intermed., 2011, 37, 883–890.
18. M. Chelghoum, M. Bahnous, A. Bouraiou, S. Bouacida and A. Belfaitah, An efficient and rapid intramolecular aza-Michael addition of 2′-aminochalcones using ionic liquids as recyclable reaction media, Tetrahedron Lett., 2012, 53, 4059–4061.
19. A. Ying, Z. Li, J. Yang, S. Liu, S. Xu, H. Yan and C. Wu, DABCO-based ionic liquids: Recyclable catalysts for aza-michael addition of α,β-unsaturated amides under solvent-free conditions, J. Org. Chem., 2014, 79, 6510–6516.
20. H. L. Hou, F. L. Qiu, A. G. Ying and S. L. Xu, DABCO-based ionic liquids: Green and efficient catalysts with a dual catalytic role for aza-Michael addition, Chin. Chem. Lett., 2015, 26, 377–381.
21. M. Avalos, R. Babiano, P. Cintas, J. L. Jiménez and J. C. Palacios, Greener Media in Chemical Synthesis and Processing, Angew. Chem., Int. Ed., 2006, 45, 3904–3908.
22. Y. Fukaya, Y. Iizuka, K. Sekikawa and H. Ohno, Bio ionic liquids: room temperature ionic liquids composed wholly of biomaterials, Green Chem., 2007, 9, 1155.
23. D. J. G. P. van Osch, C. H. J. T. Dietz, J. van Spronsen, M. C. Kroon, F. Gallucci, M. van Sint Annaland and R. Tuinier, A Search for Natural Hydrophobic Deep Eutectic Solvents Based on Natural Components, ACS Sustainable Chem. Eng., 2019, 7, 2933–2942.
24. B. B. Hansen, S. Spittle, B. Chen, D. Poe, Y. Zhang, J. M. Klein, A. Horton, L. Adhikari, T. Zelovich, B. W. Doherty, B. Gurkan, E. J. Maginn, A. Ragauskas, M. Dadmun, T. A. Zawodzinski, G. A. Baker, M. E. Tuckerman, R. F. Savinell and J. R. Sangoro, Deep Eutectic Solvents: A Review of Fundamentals and Applications, Chem. Rev., 2021, 121, 1232–1285.
25. C. Rizzo, S. Marullo, M. Benaglia and F. D'Anna, DBS–Based Eutectogels: Organized Vessels to Perform the Michael Addition Reaction, Eur. J. Org. Chem., 2023, 26, e202300263.
26. K. Fukumoto, M. Yoshizawa and H. Ohno, Room Temperature Ionic Liquids from 20 Natural Amino Acids, J. Am. Chem. Soc., 2005, 127, 2398–2399.
27. Q.-P. Liu, X.-D. Hou, N. Li and M.-H. Zong, Ionic liquids from renewable biomaterials: synthesis, characterization and application in the pretreatment of biomass, Green Chem., 2012, 14, 304–307.
28. S. Hu, T. Jiang, Z. Zhang, A. Zhu, B. Han, J. Song, Y. Xie and W. Li, Functional ionic liquid from biorenewable materials: synthesis and application as a catalyst in direct aldol reactions, Tetrahedron Lett., 2007, 48, 5613–5617.
29. P. Moriel, E. J. García-Suárez, M. Martínez, A. B. García, M. A. Montes-Morán, V. Calvino-Casilda and M. A. Bañares, Synthesis, characterization, and catalytic activity of ionic liquids based on biosources, Tetrahedron Lett., 2010, 51, 4877–4881.
30. L. Gontrani, Choline-amino acid ionic liquids: past and recent achievements about the structure and properties of these really “green” chemicals, Biophys. Rev., 2018, 10, 873–880.
31. S. Miao, R. Atkin and G. Warr, Design and applications of biocompatible choline amino acid ionic liquids, Green Chem., 2022, 24, 7281–7304.
32. H. S. Dhattarwal and H. K. Kashyap, Microstructures of Choline Amino Acid based Biocompatible Ionic Liquids, Chem. Rec., 2023, 23, e202200295.
33. M. Campetella, E. Bodo, R. Caminiti, A. Martino, F. D'Apuzzo, S. Lupi and L. Gontrani, Interaction and dynamics of ionic liquids based on choline and amino acid anions, J. Chem. Phys., 2015, 142, 234502.
34. M. Moosavi, N. Banazadeh and M. Torkzadeh, Structure and Dynamics in Amino Acid Choline-Based Ionic Liquids: A Combined QTAIM, NCI, DFT, and Molecular Dynamics Study, J. Phys. Chem. B, 2019, 123, 4070–4084.
35. A. Le Donne, H. Adenusi, F. Porcelli and E. Bodo, Structural Features of Cholinium Based Protic Ionic Liquids through Molecular Dynamics, J. Phys. Chem. B, 2019, 123, 5568–5576.
36. S. Miao, R. Atkin and G. G. Warr, Amphiphilic nanostructure in choline carboxylate and amino acid ionic liquids and solutions, Phys. Chem. Chem. Phys., 2020, 22, 3490–3498.
37. Y. Li, F. Yang, Y. Li, M. Cai, H. Li, X. Fan and M. Zhu, Choline amino acid ionic Liquids: A novel green potential lubricant, J. Mol. Liq., 2022, 360, 119539.
38. M. K. Chaudhuri, S. Hussain, M. L. Kantam and B. Neelima, Boric acid: A novel and safe catalyst for aza-Michael reactions in water, Tetrahedron Lett., 2005, 46, 8329–8331.
39. M. M. Hashemi, B. Eftekhari-Sis, A. Abdollahifar and B. Khalili, ZrOCl2·8H₂O on montmorillonite K10 accelerated conjugate addition of amines to α,β-unsaturated alkenes under solvent-free conditions, Tetrahedron, 2006, 62, 672–677.
40. B. C. Ranu and S. Banerjee, Significant rate acceleration of the aza-Michael reaction in water, Tetrahedron Lett., 2007, 48, 141–143.
41. V. R. Choudhary, D. K. Dumbre and S. K. Patil, FeCl 3 /Montmorillonite K10 as an efficient catalyst for solvent-free aza-Michael reaction between amine and α,β-unsaturated compounds, RSC Adv., 2012, 2, 7061–7065.
42. A. J. Cruz-Cabeza, Acid–base crystalline complexes and the pKa rule, CrystEngComm, 2012, 14, 6362.
43. M. Campetella, A. Le Donne, M. Daniele, L. Gontrani, S. Lupi, E. Bodo and F. Leonelli, Hydrogen Bonding Features in Cholinium-Based Protic Ionic Liquids from Molecular Dynamics Simulations, J. Phys. Chem. B, 2018, 122, 2635–2645.
44. H. S. Dhattarwal and H. K. Kashyap, Unique and generic structural features of cholinium amino acid-based biocompatible ionic liquids, Phys. Chem. Chem. Phys., 2021, 23, 10662–10669.
45. S. Miao, S. Imberti, R. Atkin and G. Warr, Nanostructure in amino acid ionic molecular hybrid solvents, J. Mol. Liq., 2022, 351, 118599.
46. Z.-T. Gao, Z.-M. Li, Y. Zhou, X.-J. Shu, Z.-H. Xu and D.-J. Tao, Choline chloride plus glycerol deep eutectic solvents as non-aqueous absorbents for the efficient absorption and recovery of HCl gas, New J. Chem., 2023, 47, 11498–11504.
47. P. Gilli, L. Pretto, V. Bertolasi and G. Gilli, Predicting Hydrogen-Bond Strengths from Acid−Base Molecular Properties. The p K a Slide Rule: Toward the Solution of a Long-Lasting Problem, Acc. Chem. Res., 2009, 42, 33–44.
48. A. G. Doyle and E. N. Jacobsen, Small-Molecule H-Bond Donors in Asymmetric Catalysis, Chem. Rev., 2007, 107, 5713–5743.
49. D. Enders, C. Wang and J. X. Liebich, Organocatalytic Asymmetric Aza-Michael Additions, Chem. – Eur. J., 2009, 15, 11058–11076.
50. G. B. Desmet, D. R. D′hooge, P. S. Omurtag, P. Espeel, G. B. Marin, F. E. Du Prez and M.-F. Reyniers, Quantitative First-Principles Kinetic Modeling of the Aza-Michael Addition to Acrylates in Polar Aprotic Solvents, J. Org. Chem., 2016, 81, 12291–12302.
51. W. C. Still, M. Kahn and A. Mitra, J. Org. Chem., 1978, 43, 2923–2925.
52. L. Mu, Y. Shi, X. Guo, T. Ji, L. Chen, R. Yuan, L. Brisbin, H. Wang and J. Zhu, Non-corrosive green lubricants: strengthened lignin–[choline][amino acid] ionic liquids interaction via reciprocal hydrogen bonding, RSC Adv., 2015, 5, 66067–66072.
53. C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions, J. Chem. Theory Comput., 2019, 15, 1652–1671.
54. S. Ehlert, M. Stahn, S. Spicher and S. Grimme, Robust and Efficient Implicit Solvation Model for Fast Semiempirical Methods, J. Chem. Theory Comput., 2021, 17, 4250–4261.
55. A. Rybinska-Fryca, A. Sosnowska and T. Puzyn, Prediction of dielectric constant of ionic liquids, J. Mol. Liq., 2018, 260, 57–64.
56. P. Pracht, F. Bohle and S. Grimme, Automated exploration of the low-energy chemical space with fast quantum chemical methods, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192.
57. J.-D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615.
58. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297.
59. A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113, 6378–6396.
60. C. Plett and S. Grimme, Automated and Efficient Generation of General Molecular Aggregate Structures, Angew. Chem., Int. Ed., 2023, 135, e202214477.
61. Semiempirical Extended Tight-binding Program Package, 2022, https://github.com/grimme-lab/xtb.
62. Documentation for xtb and Related Software, 2022, https://xtb-docs.readthedocs.io/.
63. J. García de la Concepción, M. Flores-Jiménez, L. A. Cuccia, M. E. Light, C. Viedma and P. Cintas, Revisiting Homochiral versus Heterochiral Interactions through a Long Detective Story of a Useful Azobis-Nitrile and Puzzling Racemate, Cryst. Growth Des., 2023, 23, 5719–5733.
64. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, Revealing Noncovalent Interactions, J. Am. Chem. Soc., 2010, 132, 6498–6506.
65. R. A. Boto, F. Peccati, R. Laplaza, C. Quan, A. Carbone, J.-P. Piquemal, Y. Maday and J. Contreras-García, NCIPLOT4: Fast, Robust, and Quantitative Analysis of Noncovalent Interactions, J. Chem. Theory Comput., 2020, 16, 4150–4158.
66. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38.
67. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
68. T. Lu and F. Chen, Multiwfn: A Multifunctional Wavefunction Analyzer, J. Comput. Chem., 2012, 33, 580–592.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ob02006a

---