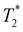Temperature dependence of the electron and hole Landé g-factors in CsPbI₃ nanocrystals embedded in a glass matrix

Abstract

The coherent spin dynamics of electrons and holes in CsPbI₃ perovskite nanocrystals in a glass matrix are studied by the time-resolved Faraday ellipticity technique in magnetic fields up to 430 mT across a temperature range from 6 K to 120 K. The Landé g-factors and spin dephasing times are evaluated from the observed Larmor precession of electron and hole spins. The nanocrystal size in the three studied samples varies from about 8 to 16 nm, resulting in exciton transition varying from 1.69 to 1.78 eV at a temperature of 6 K, allowing us to study the corresponding energy dependence of the g-factors. The electron g-factor decreases with increasing confinement energy in the NCs as a result of NC size reduction, and also with increasing temperature. The hole g-factor shows the opposite trend. Model analysis shows that the variation of g-factors with NC size arises from the transition energy dependence of the g-factors, which becomes strongly renormalized by temperature.

---

I Introduction

The successful synthesis of colloidal nanocrystals (NCs) from lead halide perovskites has greatly increased the possibilities for tailoring their material properties^1,2 and enhancing their attractiveness for applications in photovoltaics, optoelectronics, electronics, and beyond.^3–6 Lead halide perovskite NCs are commonly synthesized by colloidal chemistry in solutions and can be composed of hybrid organic–inorganic or fully inorganic materials. In comparison to the hybrid organic–inorganic perovskite NCs, fully inorganic NCs made of, e.g., CsPbI₃, CsPbBr₃, or CsPbCl₃, show considerably higher stability under ambient conditions. Further enhanced stability is achieved when the NCs are synthesized in a glass matrix from a melt,^7–12 which also facilitates their usage in optoelectronic applications.

Lead halide perovskite NCs also demonstrate interesting spin-dependent properties,¹³ which have been determined by several optical and magneto-optical techniques. Among them are optical orientation and optical alignment,¹⁴ polarized emission in the magnetic field,¹⁵ time-resolved Faraday/Kerr rotation,^16–20 time-resolved differential transmission,²¹ and optically detected nuclear magnetic resonance.²⁰ The reported spin dynamics cover wide temporal ranges from a few picoseconds for the fast exciton quantum beatings,^22–25 up to tens of nanoseconds for the carrier spin coherence²⁰ and spin dephasing¹⁷ times, and up to sub-milliseconds for the longitudinal spin relaxation times¹² at cryogenic temperatures. Among the above-mentioned techniques, time-resolved Faraday/Kerr rotation is particularly informative, as it provides comprehensive data on the electron and hole Landé g-factors, spin coherence, spin dephasing and longitudinal spin relaxation. It can reveal signals from long-living electrons and holes provided by photocharging of NCs.^17,19 In CsPbBr₃ NCs, the observation of coherent spin precession of carriers has been reported from cryogenic up to room temperatures.^16,19 Also all-optical manipulations of the spin coherence at room temperature have been demonstrated.¹⁸ The spin mode-locking effect reported recently for CsPb(Cl,Br)₃ NCs in a glass matrix demonstrates that advanced protocols of coherent spin synchronization can be implemented in perovskite NCs.²⁰

A key parameter in spin physics is the Landé g-factor, which determines the Zeeman splitting of charge carriers. In solid state systems, electrons and holes are quasi-particles and their g-factors might be drastically different from the g₀ ≈ 2 of a free electron. This difference is dictated by the band parameters of the system.²⁶ We recently showed experimentally and theoretically that in bulk lead halide perovskites the electron, hole, and exciton g-factors follow universal dependencies on the band gap energy.^27,28 In NCs, the additional mixing of the band states by confinement significantly contributes to the electron g-factor, causing deviations from the universal dependence for the bulk; however, mixing has only a weak effect on the hole g-factor,²⁹ as predicted theoretically and confirmed experimentally by low-temperature measurements at T = 5 K for CsPbI₃ NCs in glass. It is interesting to extend these experiments to higher temperatures, which could provide additional information about the band structure influence. At first glance, one would expect that the g-factor behaves according to the temperature shift of the band gap energy. However, it was shown for GaAs and CdTe semiconductors that the temperature dependence of the electron g-factor may also have other strong contributions,^30–33 the origin of which is not yet fully clarified even for conventional semiconductors.

In this paper, we study the coherent spin dynamics of electrons and holes in perovskite CsPbI₃ NCs in glass by the time-resolved Faraday ellipticity technique. The spin dynamics are measured in a temperature range of 6–120 K, from which the electron and hole g-factors as well as the spin relaxation times are evaluated. By analyzing NCs of different sizes in three samples at different temperatures, we measure the spin properties across a range of optical transition energies exceeding 100 meV. Our model analysis explains the observed qualitative trends for the carrier g-factor dispersion and its variation with temperature. Experiment and theory are also in good quantitative agreement for the hole g-factor, but show significant deviations for the electron g-factor, origins of which need to be understood further.

II Experimental results

We study experimentally a set of CsPbI₃ NCs embedded in a fluorophosphate glass matrix, namely, three samples with different NC sizes covering a range of 8–16 nm. We label them in this paper as samples #1, #2 and #3. The photoluminescence and absorption spectra of these samples at a temperature of T = 6 K are presented in the ESI Fig. S1.† The rather wide size dispersion in each sample together with the change between the samples allows us to cover the spectral range of exciton transitions of 1.69–1.78 eV at 6 K (Fig. 1d), see also ref. 29, where samples from the same synthesis procedure were investigated. By tuning the laser photon energy, we selectively address NCs with a specific exciton transition energy corresponding to a specific NC size. For that, spectrally narrow laser pulses with 1 meV width and 1.5 ps duration are used for excitation.

Fig. 1 Coherent spin dynamics in CsPbI₃ NCs at T = 6 K. (a) TRFE dynamics (black solid line) of sample #1, measured in B = 350 mT at the laser photon energy E_L = 1.703 eV. Red dashed line shows a fit to the signal, using eqn (2). The three lower traces show the decomposed contributions to the signal. (b) Magnetic field dependencies of the electron (red circles) and hole (blue triangles) Larmor precession frequencies. Fits to the experimental data with eqn (1) (solid lines) gives |g_e| = 2.33 and |g_h| = 0.14. (c) Magnetic field dependencies of the spin dephasing times for electrons (red circles) and holes (blue triangles). Solid lines show fits with eqn (3). (d) Spectral dependencies of the electron FE amplitude S_0,e for the studied samples #1 (green circles), #2 (red open circles), and #3 (black circles) in B = 430 mT. Lines are guides to the eye. (e) Spectral dependencies of the electron (circles) and hole (triangles) g-factors in the three studied samples. Solid lines give the calculations for CsPbI₃ NCs from ref. 29.

The time-resolved Faraday ellipticity (TRFE) technique is used to measure the coherent dynamics of electron and hole spins in a magnetic field to determine their parameters. This all-optical pump–probe technique exploits polarized laser pulses,^34,35 where spin-oriented carriers are photogenerated by the circularly-polarized pump pulses and the dynamics of their spin polarization are detected through the change of the ellipticity of the linearly polarized probe pulses.^36,37 The presented experiments are performed at cryogenic temperatures in the range of 6–120 K. Magnetic fields up to 430 mT are applied in the Voigt geometry, perpendicular to the light wave vector.

A. Electron and hole spin dynamics at T = 6 K

An example of the TRFE dynamics measured on sample #1 at T = 6 K for the laser photon energy E_L = 1.703 eV is shown in the top panel of Fig. 1a. The dynamics are measured with the magnetic field B = 350 mT applied perpendicular to the light wave vector (Voigt geometry). The TRFE signal contains two oscillating and one nonoscillating component. The oscillations are observed only in finite external magnetic field and we assign them to coherent spin precession of the charge carriers with the Larmor precession frequency ω_L, which is determined by the g-factor and scales with the magnetic field B according to:

ω_L = |g|μ_BB/ħ. (1)

Here, μ_B is the Bohr magneton and ħ is the reduced Planck constant. The decay of the oscillations is described by the spin dephasing time 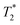, which in an inhomogeneous ensemble of NCs is commonly determined by the spread of Larmor precession frequencies. The dashed red line in Fig. 1a shows a fit to the spin dynamics using the following function:

Here, S_0,e and S_0,h are the initial light-induced spin polarizations of electrons and holes, respectively. S₁ is the initial spin polarization corresponding to the nonoscillating component. and are the electron and hole spin dephasing times, τ_no is the decay time of the nonoscillating component. The three contributions after decomposition are shown in Fig. 1a. One can see that the nonoscillating component with τ_no = 1.3 ns has a very small amplitude so we do not consider it any further in our analysis. We assign the fast and slow oscillating components to the electron (ω_L,e = 73.3 rad ns⁻¹, 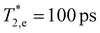) and hole (ω_L,h = 4.0 rad ns⁻¹, ) spin precession, respectively. We base this assignment on the known dependencies of the carrier g-factors on the band gap energy in lead halide perovskite bulk crystals²⁷ and on the confinement energy in nanocrystals.²⁹ The spin dynamics measured in different magnetic fields for samples #1 and #2 are shown in the ESI, Fig. S3 and S4.†

The magnetic field dependencies of the Larmor precession frequencies are shown in Fig. 1b. As expected, they show linear dependencies on the magnetic field strength without any offset for extrapolation to zero field which may arise from the exchange interaction effects between electrons and holes. According to eqn (1), the slopes of these dependencies correspond to the absolute values of the electron and hole g-factors |g_e| = 2.33 and |g_h| = 0.14. It was shown in ref. 29 that in CsPbI₃ NCs the electron g-factor is positive, while the hole g-factor crosses zero within the studied spectral range and can be either negative or positive. The TRFE technique does not provide direct information about the g-factor sign. It can, in principle, be identified through dynamic nuclear polarization detected via TRFE, as demonstrated for FA_0.9Cs_0.1PbI_2.8Br_0.2 crystals, but is very sensitive to temperature and was observed only at T = 1.6 K.³⁸ We show below that the analysis of the spectral dependence of the hole g-factor allows us to conclude that at an energy of 1.703 eV, g_h is negative, i.e. g_h = −0.14.

It is worth mentioning that the magnetic field dependencies of the Larmor precession frequencies shown in Fig. 1b have no offset at zero magnetic field. Therefore, we can safely assign the measured spin dynamics to independent resident electrons and holes confined in the NCs and not to carriers bound to excitons. More arguments along that line can be found in ref. 17 and 29. The resident carriers in the NCs can arise from long-living photocharging, where either the electron or the hole from a photogenerated electron–hole pair escapes from the NC. As a result, some NCs in the ensemble are charged with electrons, some NCs with holes, while the rest remain neutral.

The magnetic field dependencies of the spin dephasing times of electrons and holes are shown in Fig. 1c. With the magnetic field growing from 90 mT to 430 mT, dephasing times for both carriers decrease, namely, for the electrons from 260 ps to 90 ps and for the holes from 350 ps to 200 ps. This behavior is typical of inhomogeneous spin ensembles with a finite g-factor spread Δg and can be described by the following expression:³⁴

Here, is the spin dephasing time at zero magnetic field. Fitting the experimental data with eqn (3), yields Δg_e = 0.25 for the electrons and Δg_h = 0.07 for the holes. Thus, the relative spreads are Δg_e/g_e = 11% and Δg_h/g_h = 50%.

Fig. 1d shows the spectral dependence of the electron FE amplitude S_0,e for the three studied samples. These profiles can be considered as those of exciton absorption in the inhomogeneous NC ensembles. They have different widths with the narrowest distribution in sample #1 and the largest distribution in sample #3. The traces of three samples overlap spectrally with each other so that they continuously cover the spectral range of 1.69–1.78 eV at T = 6 K, in agreement with the variation of NC sizes from about 8 to 16 nm,²⁹ where the smallest NCs have the highest energy due to the strongest carrier quantum confinement.

The spectral dependencies of the electron and hole g-factors are shown in Fig. 1e. Both dependencies show monotonic changes with increasing energy. The electron g-factor decreases from +2.34 to +1.72 and the hole g-factor increases starting from a negative value of −0.19 and reaching a positive value of +0.36. The experimental results are in good agreement with the predictions of the tight-binding calculations from ref. 29 shown by solid lines, which account for the band mixing caused by electron and hole quantum confinement in CsPbI₃ NCs. Note, that in ref. 29 we measured the same CsPbI₃ NCs, but with a laser system having a high pulse repetition rate of 76 MHz, which has about three orders of magnitude smaller peak power. This limited the spectral range where the spin parameters could be reliably determined, e.g., for the hole g-factor it was only 1.68–1.72 eV compared to 1.68–1.78 eV in the present study, which limited systematic studies in the earlier work.

As mentioned above, from the Larmor precession frequency measured in TRFE experiments one can evaluate only the magnitude of the g-factor, but not its sign. The question about the sign is of particular importance for the hole g-factor, which is expected to cross zero in the considered spectral range. In ESI Fig. S5† we plot the dependence of |g_h| on the laser photon energy E_L, revealing a nonmonotonous behavior: |g_h| decreases in the spectral range from about 1.69 eV to 1.71 eV, but increases in the range from 1.71 eV to 1.78 eV. As the monotonic dependence was theoretically predicted,²⁹ we suggest that g_h < 0 for E_L < 1.71 eV, crosses zero at E_L ≈ 1.71 eV, and g_h > 0 for E_L > 1.71 eV. We use this reasoning for plotting the data in Fig. 1e.

B. Temperature dependence of spin dynamics

We next turn to the spin dynamics measured at various temperatures in order to extract the temperature dependencies of the spin related parameters in CsPbI₃ NCs. As the temperature changes, the band gap of the material also changes and one needs to tune the laser accordingly to ensure that NCs of the same size are addressed at different temperatures. This is difficult for strongly inhomogeneous samples, like for sample #3. Therefore, we start with the basic temperature trends for the most homogeneous sample #1. In the following, we measure the complete spectral dependencies at various temperatures for all samples.

Fig. 2a and b show the spin dynamics in sample #1 measured at various temperatures. The laser photon energy is adjusted to the maximum of the TRFE amplitude for each temperature, as shown in Fig. 2g. At T ≤ 15 K the FE dynamics consist of electrons, holes and nonoscillating components. The amplitude S₁ of the nonoscillating component decreases with temperature, and at T ≥ 55 K it is not detected, while the pronounced electron spin oscillations are seen up to T = 90 K. The hole spin oscillations almost disappear at around T = 25 K, when the laser photon energy is equal to 1.71 eV. Fig. 1e shows that the hole g-factor crosses zero around this energy. With further temperature increase, the hole spin oscillations become prominent again and are observed up to 65 K. Note that on another spot of this sample #1 we can measure spin oscillations up to 120 K, see the ESI, Fig. S6.†

Fig. 2 Temperature dependence of the spin dynamics in sample #1 for B = 430 mT. (a) TRFE traces at various temperatures from 15 to 90 K. (b) Zoom into dynamics from panel (a) at 15 K, 25 K, and 55 K to highlight the hole Larmor precession. (c) Temperature dependence of electron (red circles) and hole (blue triangles) FE amplitude. (d) Temperature dependence of electron and hole spin dephasing time . Temperature dependence of electron (e) and hole (f) g-factors and the corresponding laser photon energies (g).

The temperature dependencies of the FE amplitudes and spin dephasing times, evaluated by fitting the spin dynamics with eqn (2), are presented in Fig. 2c and d, respectively. The FE amplitudes of electrons and holes are close to each other in the whole temperature range and decrease with increasing temperature. The electron spin dephasing time shortens from 90 ps at T = 6 K to 50 ps at 90 K. The hole spin dephasing time decreases from 200 ps at T = 6 K to 80 ps at 55 K. We suggest that the shortening of the spin dephasing times is due to the acceleration of the carrier spin relaxation via their interaction with phonons at elevated temperatures.

C. Temperature dependence of g-factors

The temperature dependencies of the electron and hole g-factors are shown in Fig. 2e and f. They are measured at the maximum of the FE amplitude, which in sample #1 shifts from 1.703 eV at 6 K to 1.759 eV at 90 K, see Fig. 2g. The electron g-factor decreases with temperature from +2.34 to +1.82. The hole g-factor is equal to −0.14 at T = 6 K, crosses zero at about 30 K (E_L ≈ 1.710 eV), and reaches +0.34 at 65 K (E_L = 1.725 eV). This behavior is in line with the trend in the spectral dependencies of the g-factors shown in Fig. 1e. Namely, with increasing energy, regardless of whether achieved by laser energy tuning or a temperature shift, the electron g-factor decreases while the hole g-factor increases.

For closer insight into the mechanisms underlying the temperature dependence of the carrier g-factors, we measure the spectral dependencies of the g-factors at various temperatures. The results for sample #3 with the largest spectral broadening are shown in Fig. 3a for temperatures of 6, 50, 80, and 120 K. The corresponding spectral profiles of the FE amplitude are given in Fig. 3b. One can see that the total covered energy range increases up to 1.68–1.83 eV due to tuning with temperature. All experimental results on the carrier g-factors for the three studied samples at various temperatures from 6 to 120 K are collected and shown in Fig. 4. They are in agreement with the conclusions drawn for sample #1. Namely, the electron g-factor decreases with increasing energy, while the hole g-factor increases.

Fig. 3 Spectral and temperature dependencies of charge carrier g-factors in CsPbI₃ NCs of sample #3. (a) Spectral dependencies of the electron (circles) and hole (triangles) g-factors measured at temperatures of 6 K (black), 50 K (purple), 80 K (red), and 120 K (green). Solid lines are calculations for T = 6 K from ref. 29. (b) Electron TRFE amplitudes at the corresponding laser photon energies and temperatures.

Fig. 4 Spectral dependencies of the electron (a) and hole (b) g-factors in samples #1 (open triangles), #2 (closed triangles) and #3 (squares) at temperatures of 6 K (black symbols), 30 K (blue symbols), 50 K (purple symbols), 80 K (red symbols), and 120 K (green symbols). Solid lines are calculations for T = 6 K from ref. 29.

III Modeling and discussion

Let us analyze the factors that contribute to the temperature dependence of electron and hole g-factors in CsPbI₃ NCs. As the starting point we take the universal dependence of carrier g-factors on the band gap found experimentally and confirmed theoretically for lead halide perovskite bulk crystals at T = 5 K.²⁷ We recently extended these studies to address the role played by quantum confinement of charge carriers in NCs on the g-factors. The calculations predict that in NCs the hole g-factor follows the universal dependence, but the electron g-factor significantly deviates from the bulk trend.²⁹ We demonstrated this expectation experimentally for CsPbI₃ NCs at T = 5 K in ref. 29 and confirmed it in the present study for a much wider spectral range, see Fig. 1e. At cryogenic temperatures, good agreement between experiment and theory is found, which is remarkable, as the band parameters for lead halide perovskite crystals and NCs are not known with high precision.

To model the temperature modifications of the g-factors, information about the temperature dependence of the band parameters, the band gap energy, the band dispersion determining the carrier effective masses, the band mixing at finite wave vectors for confined carriers, etc. need to be known. Also carrier-phonon polaron formation may contribute. At present, the corresponding available information is limited. Also, the understanding of the band structure details of the lead halide perovskite crystal and NCs are far from being complete. Therefore, it is not possible to perform precise calculations for the temperature dependence of the g-factors. Instead, we perform estimations based on the available band structure information, details of which can be found in the ESI, section S5.† Our goal is to explore what factors are of importance and how close the model predictions can describe the experimental results.

We analyze the relatively small changes of the g-factors with energy, which arise from the temperature variations. Therefore, we consider them in the linear regime. For that, the results of ref. 29 may be compiled in the following manner:

Here E_g is the bulk band gap, E_e,h are the energies of quantum confinement of electrons and holes. Atomistic calculations predict that ζ^qc_e ≫ ζ^b_e, which is in good agreement with the experimental data. Moreover, this result is qualitatively reproduced in k·p calculations.²⁹

The temperature variation changes both the band gap and the quantum confinement energy. The bulk band gap change is linear with temperature.³⁹ The quantum confinement energy varies due to thermal expansion of the lattice and, therefore, the NC size, and also due to the temperature-induced variations of the carrier effective mass. The temperature expansion coefficient for CsPbI₃ is almost independent of the crystal phase. The temperature dependence of the effective masses is not well analyzed in the literature. In a simple two-band model, the effective mass of electrons and holes should increase with the increase of the bulk band gap.³⁹

The hole g-factor as a function of energy is expected to follow the bulk trend, as we showed in ref. 29. Quantum confinement does not change this result qualitatively. In accordance with the theoretical predictions, the temperature shifts the energies to larger values and the g-factors increase slightly, see Fig. 3a and 4b. This prediction is supported by the measured data.

For electrons, however, the situation is more complicated. We calculate the expected change in the electron g-factor with increasing temperature, following the procedure from ref. 29 with temperature-dependent values of the lattice constant and band gap. The variation in the band gap was accounted for by a change of the tight-binding parameter E_pc fitted to reproduce the experimental value from ref. 39, which closely match the temperature shifts that we measured in the studied NCs, see ESI Fig. S2.† We also consider the (almost negligible) change in the lattice constant .⁴⁰ In Fig. 5a, we show the calculated electron g-factors at different temperatures. From the atomistic calculations, it follows that the temperature variation results in a band gap change, which is reflected by a shift of the g-factor values following the universal dependence.²⁷

Fig. 5 (a) Electron g-factors calculated in the empirical tight-binding model following ref. 29 for CsPbI₃ NCs at different temperatures, see text for details. (b) Black and green open dots show the electron g-factors measured for sample #3 for the temperatures of 6 K and 120 K, respectively. Solid black and dashed green lines show the g-factors calculated in the empirical tight-binding model, see panel (a).

In Fig. 5b we compare the calculated variation of the g-factor with experimental data at temperatures of 6 K and 120 K. One can see that at T = 6 K the calculations and experimental values are much closer to each other than at 120 K. In theory, the main effect of a temperature increase is the change of the g-factor by the band gap energy, which roughly follows a universal dependence, with small changes in the slope of the electron g-factor as a function of transition energy. In contrast, the experimental data demonstrate strong renormalization of the electron g-factor with temperature (larger than expected from the theory) and a much smaller slope of the electron g-factor as a function of transition energy at elevated temperatures, see the ESI, Fig. S7.†

IV Conclusions

We have studied the spin dynamics of charge carriers in CsPbI₃ perovskite nanocrystals of different sizes by the time-resolved Faraday ellipticity technique in a temperature range from 6 K to 120 K. The spectral dependencies of the electron and hole g-factors correspond well to model predictions accounting for the mixing of the electronic bands with increasing confinement energy, which is accompanied by a decrease of the NC size. With increasing temperature, the NC optical transition shifts to higher energies due to the increase of the band gap energy. The g-factors are independent of temperature in the studied range when they are measured at the same energy. An increase in temperature shifts the spectral dependencies of the g-factors to higher energies, qualitatively following the model predictions. Namely, the electron g-factor decreases and the hole g-factor increases with increasing energy as a result of an increase in temperature. It is interesting and important to further investigate whether this trend also holds for higher temperatures, up to room temperature, as well as for other lead halide perovskite NCs. As indicated by the comparison, the experimentally observed g-factors show a stronger dependence on energy. The effect of quantum confinement on the g-factor value is strongly renormalized by temperature variation. Understanding of these details and underlying mechanisms would allow one to refine band parameters for lead halide perovskites and their NCs.

V Samples and methods

A. Samples

The studied CsPbI₃ nanocrystals embedded in fluorophosphate Ba(PO₃)₂–AlF₃ glass were synthesized by the rapid cooling of a glass melt enriched with the components needed for perovskite crystallization. Details of the method are given in ref. 11 and 20. The samples of fluorophosphate (FP) glass with the composition 35P₂O₅–35BaO–5AlF₃–10Ga₂O₃–10PbF₂–5Cs₂O (mol%) doped with BaI₂ was synthesized using the melt-quench technique. The glass synthesis was performed in a closed glassy carbon crucible at a temperature of T = 1050 °C. About 50 g of the batch was melted in the crucible for 30 minutes, then the glass melt was cast on a glassy carbon plate and pressed to form a plate with a thickness of about 2 mm. Samples with a diameter of 5 cm were annealed at the temperature of 50 °C below T_g = 400 °C to remove residual stresses. CsPbI₃ perovskite NCs were formed from the glass melt during quenching. The glass materials obtained in this way are doped with CsPbI₃ NCs. The dimensions of the NCs in the initial glass were regulated by the concentration of iodide and the rate of cooling of the melt without heat treatment above T_g. Three samples were investigated in this paper, which we label #1, #2 and #3. Their technology codes are EK31, EK7 and EK8, respectively. They differ in the NC sizes, which is reflected by the relative spectral shifts of their optical spectra. Note, that samples from the same synthesis (same codes) were investigated in ref. 29, even though their optical spectra slightly differ due to spatial inhomogeneity.

The change of the NC size was achieved by changing the concentration of iodine in the melt. Due to the high volatility of iodine compounds and the low viscosity of the glass-forming fluorophosphate melt at elevated temperatures, an increase in the synthesis time leads to a gradual decrease in the iodine concentration in the equilibrium melt. Thus, it is possible to completely preserve the original composition and change only the concentration of iodine due to a smooth change in the synthesis duration. Glass materials with NC sizes in a range of 8–16 nm were synthesized using different synthesis times. Glass materials with the photoluminescence lines centered at 1.801, 1.808 and 1.809 eV (room temperature measurements) were synthesized within 40, 35, and 30 min, respectively. NC sizes are evaluated from the spectral shift of the exciton line in the absorption spectra.

B. Time-resolved Faraday ellipticity

To study the coherent spin dynamics of carriers we use a time-resolved pump–probe technique with the detection of Faraday ellipticity (TRFE).^34,37 Spin oriented electrons and holes are generated by circularly polarized pump pulses. The used laser system (light conversion) generates pulses of 1.5 ps duration with a spectral width of about 1 meV at a repetition rate of 25 kHz (repetition period 40 μs). The laser photon energy is tuned in the spectral range of 1.65–1.85 eV in order to resonantly excite NCs of various sizes at various temperatures. The laser beam is split into the pump and probe beams with the same photon energies. The time delay between the pump and probe pulses is controlled by a mechanical delay line. The pump beam is modulated with an electro-optical modulator between σ⁺ and σ⁻ circular polarization at a frequency of 26 kHz. The probe beam is linearly polarized. The Faraday ellipticity of the probe beam, which is proportional to carrier spin polarization, is measured as a function of the delay between the pump and probe pulses using a balanced photodetector connected to a lock-in amplifier synchronized with the modulator. Both pump and probe beams have a power of 0.5 mW and spot sizes of about 100 μm. For the time-resolved measurements the samples are placed in a helium-flow optical cryostat and the temperature is varied in the range of 6–300 K. A magnetic field up to 430 mT is applied using an electromagnet perpendicularly to the laser beam (Voigt geometry, B⊥k).

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

Research performed at the P. N. Lebedev Physical Institute was financially supported by the Ministry of Science and Higher Education of the Russian Federation, contract no. 075-15-2021-598. E. V. K. and M. S. K. acknowledge the Saint-Petersburg State University (grant no. 122040800257-5).

References

1. M. V. Kovalenko, L. Protesescu and M. I. Bondarchuk, Properties and potential optoelectronic applications of lead halide perovskite nanocrystals, Science, 2017, 358, 745–750.
2. Al. L. Efros and L. E. Brus, Nanocrystal quantum dots: From discovery to modern development, ACS Nano, 2021, 15, 6192–6210.
3. J. Shamsi, A. S. Urban, M. Imran, L. De Trizio and L. Manna, Metal halide perovskite nanocrystals: synthesis, post-synthesis modifications, and their optical properties, Chem. Rev., 2019, 119, 3296–3348.
4. A. Dey, J. Ye, A. De, E. Debroye and S. K. Ha, et al., State of the art and prospects for halide perovskite nanocrystals, ACS Nano, 2021, 15, 10775–10981.
5. Y. Mu, Z. He, K. Wang, X. Pi and S. Zhou, Recent progress and future prospects on halide perovskite nanocrystals for optoelectronics and beyond, iScience, 2023, 25, 105371.
6. C.-Y. Huang, H. Li, Y. Wu, C.-H. Lin, X. Guan, L. Hu, J. Kim, X. Zhu, H. Zeng and T. Wu, Inorganic halide perovskite quantum dots: A versatile nanomaterial platform for electronic applications, Nano-Micro Lett., 2023, 15, 16.
7. P. Li, C. Hu, L. Zhou, J. Jiang, Y. Cheng, M. He, X. Liang and W. Xiang, Novel synthesis and optical characterization of CsPb₂Br₅ quantum dots in borosilicate glasses, Mater. Lett., 2017, 209, 483–485.
8. S. Liu, Y. Luo, M. He, X. Liang and W. Xiang, Novel CsPbI₃ QDs glass with chemical stability and optical properties, J. Eur. Ceram. Soc., 2018, 38, 1998–2004.
9. S. Liu, M. He, X. Di, P. Li, W. Xiang and X. Liang, Precipitation and tunable emission of cesium lead halide perovskites (CsPbX₃, X = Br, I) QDs in borosilicate glass, Ceram. Int., 2018, 44, 4496–4499.
10. Y. Ye, W. Zhang, Z. Zhao, J. Wang, C. Liu, Z. Deng, X. Zhao and J. Han, Highly luminescent cesium lead halide perovskite nanocrystals stabilized in glasses for light-emitting applications, Adv. Opt. Mater., 2019, 7, 1801663.
11. E. V. Kolobkova, M. S. Kuznetsova and N. V. Nikonorov, Perovskite CsPbX₃ (X = Cl, Br, I) nanocrystals in fluorophosphate glasses, J. Non-Cryst. Solids, 2021, 563, 120811.
12. V. V. Belykh, M. L. Skorikov, E. V. Kulebyakina, E. V. Kolobkova, M. S. Kuznetsova, M. M. Glazov and D. R. Yakovlev, Submillisecond spin relaxation in CsPb(Cl,Br)₃ perovskite nanocrystals in a glass matrix, Nano Lett., 2022, 22, 4583–4588.
13. Hybrid Organic Inorganic Perovskites: Physical Properties and Applications, ed. Z. V. Vardeny and M. C. Beard, World Scientific, 2022.
14. M. O. Nestoklon, S. V. Goupalov, R. I. Dzhioev, O. S. Ken, V. L. Korenev, Yu. G. Kusrayev, V. F. Sapega, C. de Weerd, L. Gomez, T. Gregorkiewicz, J. Lin, K. Suenaga, Y. Fujiwara, L. B. Matyushkin and I. N. Yassievich, Optical orientation and alignment of excitons in ensembles of inorganic perovskite nanocrystals, Phys. Rev. B, 2018, 97, 235304.
15. D. Canneson, E. V. Shornikova, D. R. Yakovlev, T. Rogge, A. A. Mitioglu, M. V. Ballottin, P. C. M. Christianen, E. Lhuillier, M. Bayer and L. Biadala, Negatively charged and dark excitons in CsPbBr₃ perovskite nanocrystals revealed by high magnetic fields, Nano Lett., 2017, 17, 6177–6183.
16. M. J. Crane, L. M. Jacoby, T. A. Cohen, Y. Huang, C. K. Luscombe and D. R. Gamelin, Coherent spin precession and lifetime-limited spin dephasing in CsPbBr₃ perovskite nanocrystals, Nano Lett., 2020, 20, 8626–8633.
17. P. S. Grigoryev, V. V. Belykh, D. R. Yakovlev, E. Lhuillier and M. Bayer, Coherent spin dynamics of electrons and holes in CsPbBr₃ colloidal nanocrystals, Nano Lett., 2021, 21, 8481–8487.
18. X. Lin, Y. Han, J. Zhu and K. Wu, Room-temperature coherent optical manipulation of hole spins in solution-grown perovskite quantum dots, Nat. Nanotechnol., 2022, 18, 124.
19. S. R. Meliakov, E. A. Zhukov, E. V. Kulebyakina, V. V. Belykh and D. R. Yakovlev, Coherent spin dynamics of electrons in CsPbBr₃ perovskite nanocrystals at room temperature, Nanomaterials, 2023, 13, 2454.
20. E. Kirstein, N. E. Kopteva, D. R. Yakovlev, E. A. Zhukov, E. V. Kolobkova, M. S. Kuznetsova, V. V. Belykh, I. A. Yugova, M. M. Glazov, M. Bayer and A. Greilich, Mode locking of hole spin coherences in CsPb(Cl,Br)₃ perovskite nanocrystals, Nat. Commun., 2023, 14, 699.
21. S. Strohmair, A. Dey, Y. Tong, L. Polavarapu, B. J. Bohn and J. Feldmann, Spin polarization dynamics of free charge carriers in CsPbI₃ nanocrystals, Nano Lett., 2020, 20, 4724–4730.
22. Y. Han, W. Liang, X. Lin, Y. Li, F. Sun, F. Zhang, P. C. Sercel and K. Wu, Lattice distortion inducing exciton splitting and coherent quantum beating in CsPbI₃ perovskite quantum dots, Nat. Mater., 2022, 21, 1282.
23. K. Gao, Y. Li, Y. Yang, Y. Liu, M. Liu, W. Liang, B. Zhang, L. Wang, J. Zhu and K. Wu, Manipulating Coherent Exciton Dynamics in CsPbI₃ Perovskite Quantum Dots Using Magnetic Field, Adv. Mater., 2024, 36, 2309420.
24. J. Zhu, Y. Li, X. Lin, Y. Han and K. Wu, Coherent phenomena and dynamics of lead halide perovskite nanocrystals for quantum information technologies, Nat. Mater., 2024, 23, 1027.
25. R. Cai, I. Wadgaonkar, J. W. M. Lim, S. Dal Forno, D. Giovanni, M. Feng, S. Ye, M. Battiato and T. C. Sum, Zero-field quantum beats and spin decoherence mechanisms in CsPbBr₃ perovskite nanocrystals, Nat. Commun., 2023, 14, 2472.
26. L. M. Roth, B. Lax and S. Zwerdling, Theory of optical magneto-absorption effects in semiconductors, Phys. Rev., 1959, 114, 90.
27. E. Kirstein, D. R. Yakovlev, M. M. Glazov, E. A. Zhukov, D. Kudlacik, I. V. Kalitukha, V. F. Sapega, G. S. Dimitriev, M. A. Semina, M. O. Nestoklon, E. L. Ivchenko, N. E. Kopteva, D. N. Dirin, O. Nazarenko, M. V. Kovalenko, A. Baumann, J. Höcker, V. Dyakonov and M. Bayer, The Landé factors of electrons and holes in lead halide perovskites: universal dependence on the band gap, Nat. Commun., 2022, 13, 3062.
28. N. E. Kopteva, D. R. Yakovlev, E. Kirstein, E. A. Zhukov, D. Kudlacik, I. V. Kalitukha, V. F. Sapega, D. N. Dirin, M. V. Kovalenko, A. Baumann, J. Höcker, V. Dyakonov, S. A. Crooker and M. Bayer, Weak dispersion of exciton Landé factor with band gap energy in lead halide perovskites: Approximate compensation of the electron and hole dependences, Small, 2023, 2300935.
29. M. O. Nestoklon, E. Kirstein, D. R. Yakovlev, E. A. Zhukov, M. M. Glazov, M. A. Semina, E. L. Ivchenko, E. V. Kolobkova, M. S. Kuznetsova and M. Bayer, Tailoring the electron and hole Landé factors in lead halide perovskite nanocrystals by quantum confinement and halide exchange, Nano Lett., 2023, 23, 8218–8224.
30. M. Oestreich and W. W. Rühle, Temperature dependence of the electron Landé g-factor in GaAs, Phys. Rev. Lett., 1995, 74, 2315.
31. M. Oestreich, S. Hallstein, A. P. Heberle, K. Eberl, E. Bauser and W. W. Rühle, Temperature and density dependence of the electron Landé g factor in semiconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 7911.
32. W. Zawadzki, P. Pfeffer, R. Bratschitsch, Z. Chen, S. T. Cundiff, B. N. Murdin and C. R. Pidgeon, Temperature and density dependence of the electron Landé g factor in semiconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 245203.
33. J. Hübner, S. Döhrmann, D. Hägele and M. Oestreich, Temperature-dependent electron Landé g factor and the interband matrix element of GaAs, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 193307.
34. D. R. Yakovlev and M. Bayer, Coherent spin dynamics of carriers, in Spin Physics in Semiconductors, ed. M. I. Dyakonov, Springer International Publishing AG, 2017, ch. 6, pp. 155–206.
35. V. V. Belykh, D. R. Yakovlev, M. M. Glazov, P. S. Grigoryev, M. Hussain, J. Rautert, D. N. Dirin, M. V. Kovalenko and M. Bayer, Coherent spin dynamics of electrons and holes in CsPbBr₃ perovskite crystals, Nat. Commun., 2019, 10, 673.
36. I. A. Yugova, M. M. Glazov, E. L. Ivchenko and Al. L. Efros, Pump-probe Faraday rotation and ellipticity in an ensemble of singly charged quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 104436.
37. M. M. Glazov, I. A. Yugova, S. Spatzek, A. Schwan, S. Varwig, D. R. Yakovlev, D. Reuter, A. D. Wieck and M. Bayer, Effect of pump-probe detuning on the Faraday rotation and ellipticity signals of mode-locked spins in (In,Ga)As/GaAs quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155325.
38. E. Kirstein, D. R. Yakovlev, M. M. Glazov, E. Evers, E. A. Zhukov, V. V. Belykh, N. E. Kopteva, D. Kudlacik, O. Nazarenko, D. N. Dirin, M. V. Kovalenko and M. Bayer, Lead-dominated hyperfine interaction impacting the carrier spin dynamics in halide perovskites, Adv. Mater., 2022, 34, 2105263.
39. Z. Yang, A. Surrente, K. Galkowski, A. Miyata, O. Portugall, R. J. Sutton, A. A. Haghighirad, H. J. Snaith, D. K. Maude, P. Plochocka and R. J. Nicholas, Impact of the halide cage on the electronic properties of fully inorganic cesium lead halide perovskites, ACS Energy Lett., 2017, 2, 1621.
40. D. M. Trots and S. V. Myagkota, High-temperature structural evolution of caesium and rubidium triiodoplumbates, J. Phys. Chem. Solids, 2008, 69, 2520.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr03132f

---