Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetic dimeric metal–porphyrin rings mechanically bonded around carbon nanotubes: the role of nanotube defects modulating magnetic properties†
Rocío
Sánchez-de-Armas
 *a,
Nicolás
Montenegro-Pohlhammer
*a,
Nicolás
Montenegro-Pohlhammer
 bc,
Emilio M.
Pérez
d,
Enrique
Burzurí
def and
Carmen J.
Calzado
bc,
Emilio M.
Pérez
d,
Enrique
Burzurí
def and
Carmen J.
Calzado
 a
a
aDpto. Química Física, Universidad de Sevilla, c/Profesor García González, s/n, 41012 Sevilla, Spain. E-mail: rociosa@us.es
bEscuela de Ingeniería Civil, Facultad de Ingeniería, Ciencia y Tecnología, Universidad Bernardo O'Higgins, Santiago, Chile
cUniversidad Bernardo OHiggins, Centro Integrativo de Biología y Química Aplicada (CIBQA), General Gana 1702, Santiago, Chile
dIMDEA Nanociencia C/Faraday 9, Ciudad Universitaria de Cantoblanco, 28049 Madrid, Spain
eDpto. Física de la Materia Condensada, Universidad Autónoma de Madrid, E-28049 Madrid, Spain
fCondensed Matter Physics Center (IFIMAC) and Instituto Universitario de Ciencia de Materiales “Nicolás Cabrera” (INC), Universidad Autónoma de Madrid, E-28049 Madrid, Spain
First published on 8th October 2024
Abstract
Carbon nanotubes constitute an excellent option to connect molecular nanomagnets (MNMs) to solid-state devices, allowing the electrical control of the molecule spin state. The main challenge in this area is to obtain stable nanohybrid structures that preserve the magnetic properties and functionality of the molecule. One of the strategies developed to build these structures combining MNMs and carbon nanotubes involves the encapsulation of the nanotube within magnetic organic macrocycle(s), leading to magnetic mechanically interlocked derivatives of carbon nanotubes (mMINTs). Recently, mMINTs with dimeric metal–porphyrin rings containing Cu2+ or Co2+ attached to carbon nanotubes have been synthesized. Different structural and spectroscopic techniques confirm that the metal centers in both mMINTs preserve the coordination sphere and structure of the free macrocycles, with only small deviations from the square planar geometry. However, different magnetic behaviors are observed depending on the metal. The Cu derivative has well-preserved spin geometry, with quantum coherence times on the microsecond scale, as in the free molecule (τ = 25 μs). In contrast, the continuous-wave electron paramagnetic resonance (EPR) spectrum measured on the Co derivative does not show any clear contribution from Co, although EXAFS unambiguously shows the presence of Co2+. In order to understand this different magnetic behavior, we studied mMINTs by means of periodic DFT calculations. The analysis of the optimized geometries, the spin density of the free macrocycles and the mMINTs, the adsorption energies, the extension of the charge transfer between the macrocycle and the nanotube and the density of states reveals a stronger macrocycle–nanotube interaction for the Co-mMINT. Our results point to carbon vacancies in the nanotubes as responsible for the different macrocycle–nanotube interaction and the observed loss of the Co2+ EPR signal in the Co-mMINT.
Introduction
Molecular nanomagnets (MNMs), such as porphyrins, organic radicals, and single-ion magnets like polyoxometalates or phthalocyanines, are hot candidates for spintronic and quantum technology applications.1–6 In particular, in recent years, metalloporphyrins and their derivatives have been extensively studied as potential qubits.7–11 The use of MNMs in solid-state devices requires their immobilization on a substrate, which can produce changes in their magnetic properties affecting quantum tunneling, magnetic hysteresis or quantum coherence times. These properties determine the quality of the systems to be used as a qubit.12–14The most commonly studied substrates for molecular nanomagnets are nanoparticles, metallic thin films, carbon-based nanostructures (graphene, fullerenes, and carbon nanotubes), metal–organic frameworks, and porous silicas.13 Among them, carbon nanotubes have emerged as an excellent option to connect magnetic molecules to real devices, allowing the electrical control of the spin state of the molecule, as some nanotubes are excellent electrical conductors.15,16 Several strategies have been explored to build nanohybrid structures combining magnetic molecules and carbon nanotubes, including both grafting the molecule on the external surface of the nanotube or encapsulating the molecule into the nanotube.17–20 The main challenge is to obtain stable structures that preserve the magnetic properties and functionality of the molecule.
Recently, a new clipping strategy to bind single-walled carbon nanotubes (SWNTs) to macrocycles to form rotaxane-like species has been developed.21 The product is a system with a SWNT encapsulated within organic macrocycle(s), called mechanically interlocked derivatives of carbon nanotubes (MINTs). The formation of MINTs has been shown to be a promising strategy to immobilize functional molecules to SWNT surfaces in a kinetically stable fashion, but without covalent modification of the SWNTs.22 The proposed method has been employed to several types of macrocycles which have led to species showing promising properties for various applications, such as for reinforcing polymers and designing new catalysts.22–25 Motivated by previous work, magnetic dimeric metal–porphyrin rings with copper or cobalt, both with S = 1/2, have been attached to SWNTs, to obtain magnetic MINTs (mMINTs).26 Different structural and spectroscopic techniques confirm that the metal center in both mMINTs preserve the coordination sphere and structure with respect to the free metal–porphyrins, with only small deviations from the square planar geometry. The Cu derivative has a well-preserved spin geometry and quantum coherence times (25 μs for the free molecule) remain in the microsecond scale in the mMINT derivative. In contrast, the continuous-wave electron paramagnetic resonance (EPR) spectrum measured on the Co derivative does not show any clear contribution from Co2+, although EXAFS unambiguously shows the presence of Co2+ in a slightly distorted square planar coordination sphere. It has been suggested that the proximity and interaction of the spin with the SWNT, and therefore its EPR spectrum, could be determined by the molecular orbital occupied by the unpaired electron on the metal, which is different for cobalt (dz2) and copper (dx2−y2) dimeric metal–porphyrin rings.
In this work, we have employed periodic DFT calculations to perform a detailed study of the electronic structure and magnetic properties of mMINTs containing dimeric metal–porphyrin rings with Co2+or Cu2+ and mixed mMINTs containing both metals. We have considered pristine nanotubes and analyzed the effect of the presence of carbon vacancies on the nanotubes. Carbon vacancies are intrinsic defects on carbon nanotubes, and their presence has been shown to determine the reaction tendency of these systems.18,27 For instance, they have been found to be responsible for the anomalously strong binding of NO2 molecules.28 For the studied systems, our results reveal that carbon vacancies play a key role in the macrocycle–nanotube interaction and, therefore, their inclusion is essential to get a realistic model of the system. We also found that in the presence of carbon vacancies the macrocycle–nanotube interaction is significantly stronger for the Co2+ derivative that for the Cu2+ one. This strong macrocycle–nanotube interaction modifies the electronic structure and magnetic properties of the Co2+ derivative and is responsible for the loss of the Co2+ EPR signal for Co atoms directly interacting with defects. Finally, our results allow us to predict a similar effect on the EPR spectra of mixed mMINTs, containing both Co2+ and Cu2+, where Co2+ would be EPR-silent and only the Cu2+ signal would be registered.
Computational details
The electronic structure and magnetic properties of mMINTs have been studied within periodic density functional theory (DFT) using the VASP (Vienna ab initio simulation package) code.29–32 We employed the generalized gradient approximation (GGA) with the revised Perdew–Burke–Ernzerhof functional (rPBE)33 and projector-augmented wave (PAW) potentials.34,35 Valence electrons are described using a plane-wave basis set with a cutoff of 500 eV and the Γ-point of the Brillouin zone is used.36 van der Waals interactions are taken into account through the DFT-D3 method of Grimme, with Becke–Johnson damping function.37,38 We have considered mMINTs containing two Co-porphyrins, two Cu-porphyrins as well as mixed mMINTs containing one Co-porphyrin and one Cu-porphyrin.We have used a 6,5-SWNT with optimized lattice parameters a = b = 7.50 Å and c = 40.96 Å, containing 364 carbon atoms. The nanotubes are placed along the z axis. 42.5 Å of vacuum are added in x and y directions to avoid the interaction between nanotubes (50.00 Å × 50.00 Å × 40.96 Å cell). To evaluate the effect of the presence of a defect on the nanotube, one C atom has been removed from the supercell, leading to a vacancy density of 0.1 nm−2.
To analyse the effect of the encapsulation of the SWNT on the electronic structure and magnetic properties of the macrocycles, we have also optimized isolated Co2+ and Cu2+ dimeric metal–porphyrin rings, in the same cell of the mMINTs (50.00 Å × 50.00 Å × 40.96 Å). Moreover, to assess the effect of dimer and mMINT formation on the porphyrin ring structure, the isolated Co and Cu porphyrin structures have also been optimized.
Electronic relaxation has been performed until the change in the total energy between two consecutive steps is smaller than 10−5 eV and the ionic relaxation has been performed until the Hellmann–Feynman forces were lower than 0.03 eV Å−1. For each structure we have optimized different spin-polarized magnetic solutions, considering ferromagnetic or antiferromagnetic interactions between the two metal atoms in the macrocycle. Several starting geometries have been used for geometry optimization runs.
Adsorption energies, Eads, are calculated as Eads = EmMINT − (Enanotube_opt + Edimer_opt). The energies of the nanotube (Enanotube_opt) and the dimeric porphyrin rings (Edimer_opt) are obtained from two independent geometry optimization calculations using the same supercell as the adsorbed molecule, in order to minimize numerical errors. Thus, negative adsorption energies represent bound states.
Finally, interaction energies, Eint, are calculated as Eint = EmMINT − (Enanotube_sp + Edimer_sp). The energies of the nanotube (Enanotube_sp) and the dimeric porphyrin rings (Edimer_sp) are obtained from a single point calculation of the carbon nanotube or the macrocycle with the optimized geometry of the whole mMINT system and using the same supercell as the whole system. Interaction energies are included in Table S2.†
Results and discussion
Free dimeric metal–porphyrin macrocycles
The structures of both Co2+ and Cu2+ dimeric metal–porphyrin rings have been optimized in two different magnetic states (Fig. 1). Co2+ and Cu2+ are both S = ½ centers and, therefore, the interaction between the two metals on each macrocycle can be ferromagnetic or antiferromagnetic, leading to one structure with total magnetization 0 (Cu-dimer-0 and Co-dimer-0 in Table 1) and another structure with total magnetization 2 (Cu-dimer-2 and Co-dimer-2 in Table 1). The energy difference between both magnetic solutions depends on the amplitude of the magnetic coupling between the metal centers.| Structure | ΔE | Magnetization | ||||
|---|---|---|---|---|---|---|
| Total | M1 | Ring1 | M2 | Ring2 | ||
| (Porph1) | (Porph2) | |||||
| Co-dimer-0 | 0.05 | 0.0 | −1.026 | 0.092 | 1.026 | −0.092 |
| (−0.934) | (0.934) | |||||
| Co-dimer-2 | 0.00 | 2.0 | 1.026 | −0.092 | 1.026 | −0.092 |
| (0.934) | (0.934) | |||||
| Cu-dimer-0 | 0.00 | 0.0 | 0.564 | 0.382 | −0.564 | −0.382 |
| (0.946) | (−0.946) | |||||
| Cu-dimer-2 | 0.15 | 2.0 | 0.564 | 0.382 | 0.564 | 0.382 |
| (0.946) | (0.946) | |||||
No structural differences have been found between both spin states. After the formation of the macrocycle, the porphyrin structure preserves the preexisting planar geometry (Table S1†). Inside the macrocycle, the two porphyrin rings are almost parallel. Distances between metallic centres are 12.49 Å and 12.51 Å for Co2+ and Cu2+ derivatives, respectively. Moreover, for both metals, we found no meaningful energy difference between both magnetic solutions (the energy difference being smaller than 0.2 kJ mol−1, Table 1). That is, the metal centers are not coupled, and the magnetic interaction between them is zero.
Fig. 1 shows the spin density for all the considered structures and spin states, calculated as the difference between the α and β electronic densities. Interestingly, there are appreciable differences in spin density depending on the metal. In the case of the Cu-dimer, the spin density is mainly localized on the porphyrin plane. The unpaired electron occupies the dx2−y2 orbital, with a non-negligible participation of the σ orbitals of the surrounding N porphyrin atoms (as shown in Table 1, the magnetization of the porphyrin rings is relevant for the Cu-dimer). In the case of the Co-dimer, the spin density is mainly out of the plane of the porphyrin ring. The unpaired electron occupies the dz2 orbital, with a minor participation of the porphyrin (Table 1). In both cases there is no spin density in the rest of the organic macrocycle.
Co2+ and Cu2+ mMINTs with pristine nanotubes
To study the encapsulation of the SWNT within the dimeric metal–porphyrin rings geometry optimizations have been run from several starting structures (Fig. 2). In the most stable structures metal–nanotube distances are 3.51–3.58 Å for the Co2+ dimer and 3.47–3.53 Å for the Cu2+ dimer (Table 2). There are no significant structural differences for the different metal derivatives and they also present almost identical adsorption energies (Table 2). In agreement with previous experimental work,26 we found that the metal centers in the mMINT porphyrins preserve the coordination sphere and structure when cycled, with only slight distortions of the square planar geometry. Moreover, optimized geometries, with the macrocycle embracing the nanotube, are consistent with the registered high-resolution microscopy (HR-TEM) images, as shown in Fig. 2 (bottom).26 | ||
| Fig. 2 Optimized structures of Co2+ (top) and Cu2+ (middle) mMINTs with pristine nanotubes with total magnetization 0 (Co-mMINT-0 and Cu-mMINT-0 in Table 2). There are no differences between structures with ferromagnetic and antiferromagnetic interactions of the unpaired electrons. Brown, light blue, red, white, dark blue and orange spheres represent C, N, O, H, Co and Cu, respectively. HR-TEM image showing a single Co-mMINT (bottom), where four Co2+ dimeric metal–porphyrin rings can be seen embracing the SWNT. Scale bar: 400 nm. Adapted with permission from J. Am. Chem. Soc., 2021, 143(50), 21286–21293. Copyright 2021 American Chemical Society. | ||
| Structure | E ads | Distances M–C | Magnetization | ||||||
|---|---|---|---|---|---|---|---|---|---|
| M1–C | M2–C | Total | M1 | Ring1 | M2 | Ring2 | NT | ||
| (Porph1) | (Porph2) | ||||||||
| Co-mMINT-0 | −241.2 | 3.51 | 3.58 | 0.0 | 1.023 | −0.089 | −1.024 | 0.090 | 0.000 |
| (0.934) | (−0.934) | ||||||||
| Co-mMINT-2 | −241.2 | 3.51 | 3.58 | 2.0 | 1.023 | −0.089 | 1.024 | −0.090 | 0.000 |
| (0.934) | (0.934) | ||||||||
| Cu-mMINT-0 | −244.1 | 3.47 | 3.53 | 0.0 | 0.563 | 0.382 | −0.562 | −0.381 | 0.000 |
| (0.945) | (−0.943) | ||||||||
| Cu-mMINT-2 | −244.1 | 3.47 | 3.53 | 2.0 | 0.563 | 0.382 | 0.562 | 0.381 | 0.000 |
| (0.945) | (0.943) | ||||||||
As in the case of free dimers, we found that structures with ferromagnetic (M-mMINT-2) and antiferromagnetic (M-mMINT-0) interactions between the unpaired electrons of the metal centers are degenerated for mMINTs. Interestingly, spin density remains unaltered after mMINT formation, with no spin density observed in the carbon nanotube, as shown in Fig. 3. Moreover, Fig. 4 (top) illustrates the charge density difference, Δρ, between the mMINT, the nanotube, and the dimer, denoted as Δρ = ρ(mMINT) − [ρ(nanotube) + ρ(dimer)]. Notably, there is no significant charge transfer between the dimers and the nanotube in any of the systems.
The magnetism of Co2+ and Cu2+ dimeric metal–porphyrin rings has been analyzed by electron paramagnetic resonance (EPR) spectroscopy. Interestingly, while in Cu-mMINT spectral features coming from the Cu porphyrin centers appear, no EPR signature of the Co-mMINT has been observed, although EXAFS unambiguously shows the presence of Co2+ in a slightly distorted square planar coordination sphere. Based on this observation, it has been suggested that the different molecular orbitals occupied by the unpaired electrons of Cu and Co, dx2−y2 and dz2, respectively, may determine the mean distance of the porphyrin to the nanotube and the strength of the interaction of the spin with the SWNT, and therefore its EPR spectrum. Interestingly, our results confirm that the choice of the metal determines the orbital occupied by the unpaired electron, the in-plane dx2−y2 orbital of Cu2+ derivatives and the out-of-plane dz2 orbital in the case of Co-mMINTs. However, the analysis of metal–NT distances, the adsorption energies, the spin density and the extension of the charge transfer between the macrocycle and the nanotube reveals a similar interaction between the macrocycle and the nanotube for both studied metals, which will not affect the magnetic properties of the porphyrin dimeric ring. Therefore, this first model is not able to explain the different behaviors for the Co-mMINT and Cu-mMINT observed in experiments.
Co2+ and Cu2+ mMINTs with defective nanotubes
Carbon vacancies are intrinsic defects on carbon nanotubes, and their presence has been shown to determine their reaction tendency.18,27,28 In fact, discrepancies between theoretical simulations and experimental results in studies concerning the adsorption of small molecules on carbon nanotube sidewalls have been ascribed to the use of non-realistic models, neglecting common topological and structural defects on nanotubes.28,39,40 In order to model our system in a more realistic way, we have analyzed the effect of introducing a carbon vacancy on the nanotube.Removing a C atom from the nanotube generates four unpaired electrons and produces a noticeable distortion of the structure near the vacancy, with the formation of a new carbon–carbon bond, leading to the creation of a pentagonal ring, and an out-of-plane shift of the dangling carbon atom opposite to the pentagon (labeled as Cvac) (Fig. S1†). The two remaining electrons can either couple ferromagnetically (resulting in a total magnetization of 2) or form a diamagnetic solution with a total magnetization of 0, with the diamagnetic solution being 21.1 kJ mol−1 more stable.28Fig. 5 shows the spin density for both solutions, calculated as the difference between the electronic density of α and β-electrons. In the ferromagnetic solution, two electrons occupy a different region of space: one electron is strongly localized on a carbon atom beside the vacancy (Cvac), having a σ-character, while the other electron strongly delocalizes on the π-states of the nanotube. In the diamagnetic solution there is only a residual spin density on the nanotube. Interestingly, the creation of a C vacancy on the nanotube has an important effect on the density of states (Fig. 6, top); it introduces states around the Fermi level, decreasing the band gap, and leading to more conductive species.
 | ||
| Fig. 5 Spin density for the defective nanotube with total magnetization 0 (top) and 2 (bottom). Plots are obtained with an isodensity value of 10−3 e bohr−3. | ||
Fig. 7 shows the optimized structure of Co2+ and Cu2+ mMINTs with defective nanotubes. For both metals we observe that, after the removal of one C atom of the nanotube, the macrocycle structure changes in such a way that one of the metal centers (M2) moves closer to the vacancy. This fact produces an increase of one of the metal–nanotube distances (dM1–C) from 3.5 Å to 4.1–4.2 Å and the decrease of the other metal–nanotube distance (dM2–C). However, this reduction of the distance between the metal that is close to the vacancy and the nanotube is different for both mMINTs: the dCu2–C distance is 2.8 Å and the dCo2–C distance is 2.0 Å (Table 3). These different distances constitute the first evidence of different interactions between the dimer and the defective nanotube depending on the metal. Adsorption energies also show a stronger interaction between the nanotube and the Co-mMINT. While for the Cu-mMINT the adsorption energy remains almost unaltered after C removal, for the Co-mMINT with defective nanotube the adsorption energy is around 33 kJ mol−1 larger than that for the Cu-mMINT (Table 3).
| Structure | E ads | Distance | Magnetization | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| M1–C | M2–Cvac | Total | M1 | Ring1 | M2 | Ring2 | Cvac | NT | ||
| (Porph1) | (Porph2) | |||||||||
| Co-mMINT-vac-0 | −259.6 | 4.162 | 1.995 | −0.853 | −1.026 | 0.092 | −0.135 | 0.008 | 0.093 | 0.157 |
| (−0.934) | (−0.127) | |||||||||
| Co-mMINT-vac-2 | −259.6 | 4.162 | 1.995 | 1.154 | 1.026 | −0.092 | −0.135 | 0.008 | 0.093 | 0.162 |
| (0.934) | (−0.127) | |||||||||
| Cu-mMINT-vac-0 | −226.8 | 4.111 | 2.785 | 0.044 | −0.552 | −0.377 | 0.568 | 0.375 | 0.123 | 0.038 |
| (−0.929) | (0.943) | |||||||||
| Cu-mMINT-vac-2 | −226.8 | 4.105 | 2.794 | −2.008 | −0.553 | −0.377 | −0.568 | −0.374 | −0.113 | −0.033 |
| (−0.930) | (−0.942) | |||||||||
Important differences between Co2+ and Cu2+ derivatives are found when analyzing total magnetization. Two different magnetic solutions, which are energetically degenerated, are obtained for each mMINT. For the Cu-mMINT total magnetization values are 0 (Cu-mMINT-vac-0) and 2 (Cu-mMINT-vac-2). Spin density plots for these two structures (Fig. 8) show that the spin density on the Cu-dimer remains unaltered after vacancy formation, with one unpaired electron on each dx2−y2 orbital and the participation of the porphyrin ring. The nanotube presents a residual spin density, exactly the same situation observed for the isolated nanotube. In contrast, total magnetization is strongly modified after vacancy creation for the Co derivative. We intended to get solutions with total magnetization of 0 and 2, resulting from antiferromagnetic or ferromagnetic interactions of Co2+ unpaired electrons, imposing initial magnetization 1 or −1 on each Co2+. However, after geometry optimization we obtained two equivalent magnetic solutions, with total magnetization around 1 (−0.853 for Co-mMINT-vac-0 and 1.154 for Co-mMINT-vac-2). In both structures spin density plots (Fig. 8) show one unpaired electron occupying the dz2 orbital of Co1 (the cobalt atom that is far away from the vacancy) while for Co2 (close to the vacancy) there has been a strong reduction of the magnetization (from −1.024 with the pristine nanotube to −0.135 with defects). These results are consistent with the charge density differences shown in Fig. 4(c), where we can appreciate a significant charge transfer from Co2 to the nanotube in the presence of a carbon vacancy.
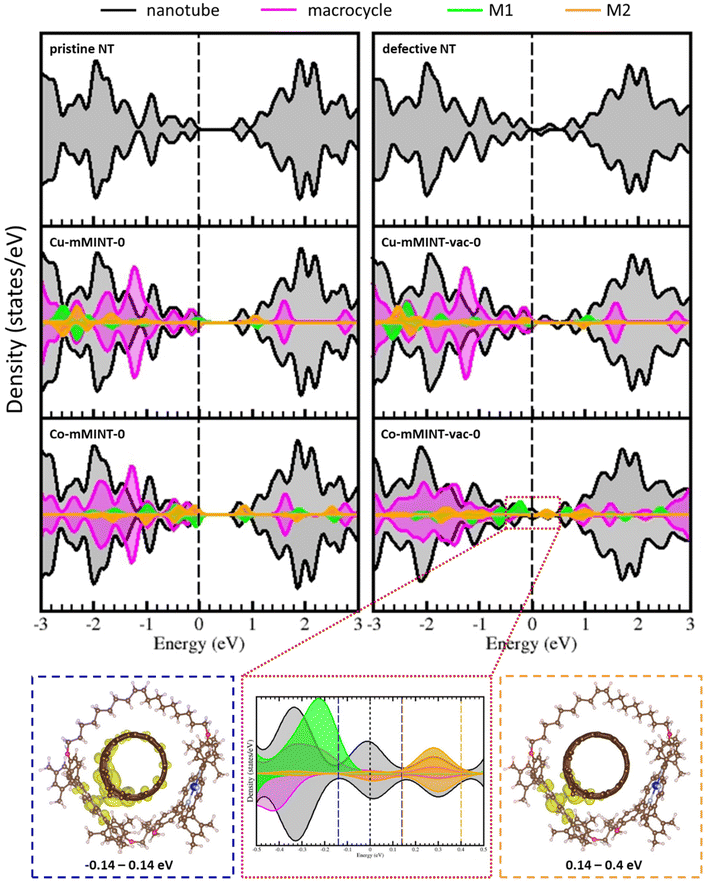
To gain a deeper insight into the electronic structure of mMINTs we compared the projected density of states (pDOS) for the mMINTs with and without carbon defects on the nanotube (Fig. 6). For both mMINTS with pristine nanotubes the highest occupied states are located on the metal atoms. The lowest unoccupied states correspond to nanotube states in the case of Cu-mMINT-0 while for Co-mMINT-0 they have contribution from both the nanotube and Co. In both cases pDOS show a band gap of about 0.7 eV, which disappears in the case of the defective nanotube, with the presence of some states in the (original) band gap region (range: 0.0–0.7 eV). The C vacancy does not affect the Cu states, as they appear exactly at the same energy as in the case of the pristine nanotube. The states related to the vacancy only have contribution from the nanotube for the system containing Cu. In contrast, we appreciate important changes in the states of the Co atom close to the vacancy, as the band gap states have contribution of both the nanotube and Co2 metal, indicating a strong interaction between the metal center and the nanotube. The states with macrocycle contribution are also influenced by the defect, becoming wider and stabilized (all states appear at lower energies) for the defective nanotube, because of the dimer–nanotube interaction. As Co1 remains far away from the vacancy, the states projected on this atom remain unaltered after the defect formation. Looking closer, the states around the Fermi level of Co-mMINT-vac-0 show a significant mixing of the Co2 dz2 orbital and those of the nanotube. Fig. 6 (bottom) shows the electronic density of the states immediately above and below the Fermi level, within the range −0.14 to 0.14 eV (blue box in Fig. 6) and the lowest unoccupied states in the range 0.14 to 0.4 eV (orange box in Fig. 6). The former are partially occupied, with a large contribution from nanotube states and a minor contribution of Co2 dz2 states. Interestingly, the lowest fully empty states show an important contribution from Co2 dz2 states. This indicates some extent of electron transfer from the Co2 atom to the nanotube and explains the total magnetization of about 1 obtained for both solutions. The unpaired electron of the Co2 center is transferred to the nanotube, and then the total magnetization of the mMINTs is 1, that is, the system contains a single unpaired electron located on the 3dz2 orbital of the Co1 atom, the one more distant to the carbon defect.
All the studied properties, geometries, adsorption energies, magnetization on different atoms, spin density representations, charge density differences and projected density of states, confirm stronger dimer–nanotube interactions for the Co-mMINT than for the Cu-mMINT when carbon vacancies are present on the nanotube. As a consequence of this strong interaction on Co-mMINT, magnetization on one Co atom is reduced, which could explain the loss of the Co2+ EPR signal for Co2.
Mixed mMINTs with defective nanotubes
Finally, we extended the study to mixed mMINTS containing both one Co2+ and one Cu2+ atom. As the importance of the inclusion of defects on the nanotube to model the macrocycle–nanotube interaction has been proven, one carbon vacancy has been introduced in the nanotube, and two different structures have been optimized, one with the Cu atom close to the defect (CoCu-mMINT-vac) and the other one with the Co atom close to the defect (CuCo-mMINT-vac). For each structure two almost degenerated magnetic solutions have been found. Selected distances, relative energies, adsorption energies, total magnetizations and magnetization on selected atoms for the four structures have been included in Table 4. Moreover, plots of the charge density differences are presented in Fig. 4 (bottom) and pDOS for the mixed mMINTs (with Cu2+ or Co2+ near the vacancy) are shown in Fig. S2.†| Structure | E rel | Magnetization | Distances | E ads | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Total | Co | RingCo | Cu | RingCu | Cvac | NT | Co–C | Cu–C | |||
| (Co-porf) | (Cu-porf) | ||||||||||
| Cu 2+ close to the defect | |||||||||||
| CoCu-mMINT-vac-0 | 23.18 | 0.001 | −1.037 | 0.087 | 0.567 | 0.376 | 0.075 | 0.015 | 4.064 | 2.883 | −237.4 |
| (−0.950) | (0.943) | ||||||||||
| CoCu-mMINT-vac-2 | 23.23 | 2.008 | 1.032 | −0.088 | 0.566 | 0.377 | −0.002 | −0.003 | 4.063 | 2.883 | −237.4 |
| (0.944) | (0.943) | ||||||||||
| Co 2+ close to the defect | |||||||||||
| CuCo-mMINT-vac-0 | 0.01 | 0.861 | 0.138 | −0.005 | 0.562 | 0.381 | −0.092 | −0.158 | 1.993 | 4.160 | −260.5 |
| (0.133) | (0.943) | ||||||||||
| CuCo-mMINT-vac-2 | 0.00 | 1.131 | −0.138 | 0.004 | 0.562 | 0.381 | 0.091 | 0.153 | 1.993 | 4.160 | −260.5 |
| (−0.134) | (0.943) | ||||||||||
In general, in the presence of a carbon vacancy, all the analyzed properties of the mixed mMINT with a Co atom close to the vacancy are very similar to those of the homonuclear Co derivative, while the properties of the mixed mMINT with Cu close to the vacancy are almost identical to those of the homonuclear Cu derivatives.
The heteronuclear dimeric ring is stabilized by about 23.2 kJ mol−1 when the vacancy is close to Co-porphyrin (CuCo-mMINT-vac). The adsorption energy for the most favorable mixed mMINT-vac structure is the same as that of the homonuclear Co-mMINT-vac. Hence, the CoCu-mMINT-vac adsorption energy is about 23 kJ mol−1 smaller, and similar to the adsorption energy of Cu-mMINT-vac.
Our results reveal that in mixed mMINTs Co2+ will approach carbon vacancies on the nanotube, and a significant charge transfer from Co2+ to the nanotube will occur. We can predict that in the EPR spectrum of mixed mMINTS containing both Cu2+ and Co2+, Co2+ will be silent if it is close to the vacancy. In other words, only the Cu signal would be registered, as strong Co–vacancy interactions produce an important modification of the macrocycle electronic structure and a decrease on cobalt magnetization, with consequent loss of the Co2+ EPR signal.
Conclusions
In this work we have performed a detailed theoretical study of mechanically bonded magnetic Co2+ and Cu2+ dimeric metal–porphyrin rings around carbon nanotubes (mMINTs) employing periodic DFT calculations. Our aim was to understand the differences found in the electron paramagnetic resonance (EPR) spectra of mMINTs containing different metals (Co2+ and Cu2+). While in the Cu-mMINT the spectral features coming from the Cu2+ porphyrin centers are observed once the macrocycle encapsulates the nanotube, no EPR signature of Co2+ was observed in the case of the Co-mMINT.In a first stage, we considered mMINTs formed with pristine nanotubes. For these systems, our results reveal that the interaction between the macrocycle and the nanotube will not affect the magnetic properties of the dimeric metal–porphyrin rings. Our model does not show any significant differences between the Co2+ and Cu2+ derivative properties that could explain the observed differences in registered spectra. We can conclude that the inclusion of defects on the nanotube is essential to get a realistic model and to simulate the dimer–nanotube interaction.
After the inclusion of a carbon vacancy in the systems, optimized geometries, spin density, magnetization on different atoms, adsorption energies, extension of the charge transfer between the macrocycle and the nanotube and density of states have been analyzed. Our results reveal that the macrocycle–nanotube interaction is stronger for the Co-mMINT than for the Cu-mMINT. As a consequence of this stronger interaction on Co-mMINT the electronic structure of the macrocycle is modified and magnetization on one Co2+ atom is reduced, which could explain the loss of the Co2+ EPR signal for Co atoms directly interacting with defects. As a consequence, the Co2+ EPR signal would decrease, and could be buried under the SWNT contribution in experimental measurements. Furthermore, a stronger interaction between the metal centers and the nanotubes could reduce coherence and broaden the signal, thereby contributing to a lower signal-to-noise ratio.
In all of the systems considered, the metal centers are not magnetically coupled, and the solutions with a ferromagnetic interaction and those with an antiferromagnetic interaction between them are degenerated.
Finally, we extended the work to include mixed mMINTs containing both one Co2+ and one Cu2+ atom. These mixed mMINTs have not yet been synthesized. We found that mixed mMINTs are more stable when the Co–porphyrin approaches a carbon vacancy on the nanotube. All the studied properties for such a structure are very similar to those of the system containing only Co2+ as the metal. The formation of mixed mMINTs involves a significant charge transfer from Co2+ to the nanotube as in the homonuclear Co derivative. We can predict that in the EPR spectrum of mixed mMINTs containing both Cu2+ and Co2+ only the Cu signal would be registered, as the strong Co–vacancy interaction causes an important modification of the macrocycle electronic structure and a decrease of cobalt magnetization, with a consequent loss of the Co2+ EPR signal.
Our work highlights the importance of incorporating defects into theoretical models to achieve more realistic representations of carbon nanotube derivatives. We have considered single carbon vacancies, as they are the most common defects in carbon nanotubes. Evaluating the impact of other types of defects, such as double vacancies, interstitials, bond rotations, or non-hexagonal rings, on the electronic structure and magnetic properties of carbon nanotube derivatives, although involving an extremely high computational cost, would also provide valuable insights and make a significant contribution to the field.
Author contributions
Conceptualization: R. Sánchez-de-Armas, C. J. Calzado, E. Burzurí, E. M. Pérez, and N. Montenegro-Pohlhammer; methodology: C. J. Calzado, R. Sánchez-de-Armas, and N. Montenegro-Pohlhammer; funding acquisition: C. J. Calzado, E. Burzurí, and E. M. Pérez; investigation: R. Sánchez-de-Armas, C. J. Calzado, and N. Montenegro-Pohlhammer; formal analysis: Sánchez-de-Armas, C. J. Calzado, N. Montenegro-Pohlhammer, and E. Burzurí; resources: E. M. Pérez, E. Burzurí, and C. J. Calzado; writing—original draft preparation: R. Sánchez-de-Armas and C. J. Calzado; writing—review and editing: R. Sánchez-de-Armas, C. J. Calzado, E. Burzurí, E. M. Pérez, and N. Montenegro-Pohlhammer.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the financial support through grant PID2021-127674NB-I00 funded by MCIN/AEI/10.13039/501100011033 and by “ERDF_A way of making Europe”. The technical support of the Supercomputing Team of the Centro Informático Científico de Andalucía (CICA) and the access to the computational facilities of the “Centro de Servicios de Informática y Redes de Comunicaciones” (CSIRC, Universidad de Granada, Spain) are also acknowledged. EB is thankful for funds from RYC2019-028429-I (EB) and PID2022-140923NB-C22 funded by MCIN/AEI/10.13039/501100011033. EP acknowledges financial support from the Ministry of Science of Spain (PID2020-116661RB-I00). IMDEA Nanociencia receives support from the “Severo Ochoa” Programme for Centres of Excellence in R&D (MICINN, Grant CEX2020-001039-S).References
- M. Cinchetti, V. A. Dediu and L. E. Hueso, Activating the molecular spinterface, Nat. Mater., 2017, 16, 507–515 CrossRef PubMed.
- E. Coronado, Molecular magnetism: from chemical design to spin control in molecules, materials and devices, Nat. Rev. Mater., 2020, 5, 87–104 CrossRef.
- M. N. Leuenberger and D. Loss, Quantum computing in molecular magnets, Nature, 2001, 410, 789–793 CrossRef PubMed.
- A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Molecular spins for quantum computation, Nat. Chem., 2019, 11, 301–309 CrossRef.
- S. Sanvito, Molecular spintronics, Chem. Soc. Rev., 2011, 40, 3336–3355 RSC.
- A. Chiesa, P. Santini, E. Garlatti, F. Luis and S. Carretta, Molecular nanomagnets: a viable path toward quantum information processing?, Rep. Prog. Phys., 2024, 87, 40 CrossRef.
- F. Santanni and A. Privitera, Metalloporphyrins as Building Blocks for Quantum Information Science, Adv. Opt. Mater., 2024, 12, 2303036 CrossRef.
- D. Ranieri, F. Santanni, A. Privitera, A. Albino, E. Salvadori, M. Chiesa, F. Totti, L. Sorace and R. Sessoli, An exchange coupled meso-meso linked vanadyl porphyrin dimer for quantum information processing, Chem. Sci., 2022, 14, 61–69 RSC.
- D. Ranieri, A. Privitera, F. Santanni, K. Urbanska, G. Strachan, B. Twamley, E. Salvadori, Y. Liao, M. Chiesa, M. Senge, F. Totti, L. Sorace and R. Sessoli, A Heterometallic Porphyrin Dimer as a Potential Quantum Gate: Magneto-Structural Correlations and Spin Coherence Properties, Angew. Chem., Int. Ed., 2023, 62, e202312936 CrossRef.
- F. Santanni, E. Little, S. Lockyer, G. Whitehead, E. Mcinnes, G. Timco, A. Bowen, R. Sessoli and R. Winpenny, Weak Exchange Interactions in Multispin Systems: EPR Studies of Metalloporphyrins Decorated with {Cr7Ni} Rings, Inorg. Chem., 2024, 63, 15460–15466 CrossRef PubMed.
- H. Xu, Y. Zhang and M. Wang, Tunable Quantum Coherence of Polymer-Attached Molecular Spins (PAMS): An Example of Metal-Porphyrin-Centred Four-Arm Star-Like Polymers, Macromolecules, 2024, 57, 2628–2638 CrossRef.
- G. Gabarró-Riera, G. Aromí and E. C. Sañudo, Magnetic molecules on surfaces: SMMs and beyond, Coord. Chem. Rev., 2023, 475, 26 CrossRef.
- M. Adamek, O. Pastukh, M. Laskowska, A. Karczmarska and L. Laskowski, Nanostructures as the Substrate for Single-Molecule Magnet Deposition, Int. J. Mol. Sci., 2024, 25, 38 Search PubMed.
- G. Gabarró-Riera and E. Sañudo, Challenges for exploiting nanomagnet properties on surfaces, Commun. Chem., 2024, 7, 99 CrossRef PubMed.
- A. Baydin, F. Tay, J. C. Fan, M. Manjappa, W. L. Gao and J. Kono, Carbon Nanotube Devices for Quantum Technology, Materials, 2022, 15, 26 CrossRef.
- J. Zhang, Y. Deng, X. Hu, X. N. Chi, J. Liu, W. G. Chu and L. F. Sun, Molecular Magnets Based on Graphenes and Carbon Nanotubes, Adv. Mater., 2019, 31, 6 Search PubMed.
- J. Villalva, A. Develioglu, N. Montenegro-Pohlhammer, R. Sanchez-de-Armas, A. Gamonal, E. Rial, M. Garcia-Hernandez, L. Ruiz-Gonzalez, J. S. Costa, C. J. Calzado, E. M. Perez and E. Burzuri, Spin-state-dependent electrical conductivity in single-walled carbon nanotubes encapsulating spin-crossover molecules, Nat. Commun., 2021, 12, 1578 CrossRef PubMed.
- R. Sanchez-de-Armas, N. Montenegro-Pohlhammer, A. Develioglu, E. Burzuri and C. J. Calzado, Spin-crossover complexes in nanoscale devices: main ingredients of the molecule-substrate interactions, Nanoscale, 2021, 13, 18702–18713 RSC.
- M. D. Giménez-López, F. Moro, A. La Torre, C. J. Gómez-García, P. D. Brown, J. van Slageren and A. N. Khlobystov, Encapsulation of single-molecule magnets in carbon nanotubes, Nat. Commun., 2011, 2, 6 Search PubMed.
- M. Urdampilleta, S. Klyatskaya, J. P. Cleuziou, M. Ruben and W. Wernsdorfer, Supramolecular spin valves, Nat. Mater., 2011, 10, 502–506 CrossRef PubMed.
- A. de Juan, Y. Pouillon, L. Ruiz-González, A. Torres-Pardo, S. Casado, N. Martín, A. Rubio and E. M. Pérez, Mechanically Interlocked Single-Wall Carbon Nanotubes, Angew. Chem., Int. Ed., 2014, 53, 5394–5400 CrossRef CAS PubMed.
- D. Wielend, M. Vera-Hidalgo, H. Seelajaroen, N. S. Sariciftci, E. M. Pérez and D. R. Whang, Mechanically Interlocked Carbon Nanotubes as a Stable Electrocatalytic Platform for Oxygen Reduction, ACS Appl. Mater. Interfaces, 2020, 12, 32615–32621 CrossRef PubMed.
- A. López-Moreno, B. Nieto-Ortega, M. Moffa, A. de Juan, M. M. Bernal, J. P. Fernández-Blázquez, J. J. Vilatela, D. Pisignano and E. M. Pérez, Threading through Macrocycles Enhances the Performance of Carbon Nanotubes as Polymer Fillers, ACS Nano, 2016, 10, 8012–8018 CrossRef PubMed.
- M. Blanco, B. Nieto-Ortega, A. de Juan, M. Vera-Hidalgo, A. López-Moreno, S. Casado, L. R. González, H. Sawada, J. M. González-Calbet and E. M. Pérez, Positive and negative regulation of carbon nanotube catalysts through encapsulation within macrocycles, Nat. Commun., 2018, 9, 7 CrossRef.
- W. Z. Zhang, M. Guillén-Soler, S. Moreno-Da Silva, A. López-Moreno, L. R. González, M. D. Giménez-López and E. M. Pérez, Mechanical interlocking of SWNTs with N-rich macrocycles for efficient ORR electrocatalysis, Chem. Sci., 2022, 13, 9706–9712 RSC.
- S. Moreno-Da Silva, J. I. Martínez, A. Develioglu, B. Nieto-Ortega, L. de Juan-Fernández, L. Ruiz-Gonzalez, A. Picón, S. Oberli, P. J. Alonso, D. Moonshiram, E. M. Pérez and E. Burzurí, Magnetic, Mechanically Interlocked Porphyrin-Carbon Nanotubes for Quantum Computation and Spintronics, J. Am. Chem. Soc., 2021, 143, 21286–21293 CrossRef.
- M. Kozlowska, J. Goclon and P. Rodziewicz, Impact of vacancy defects in single-walled carbon nanotube on the structural properties of covalently attached aromatic diisocyanates, Appl. Surf. Sci., 2016, 362, 1–10 CrossRef.
- F. Mercuri, A. Sgamellotti, L. Valentini, I. Armentano and J. M. Kenny, Vacancy-induced chemisorption of NO2 on carbon nanotubes: A combined theoretical and experimental study, J. Phys. Chem. B, 2005, 109, 13175–13179 CrossRef.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B, 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal-Amorphous Semiconductor Transition in Germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef PubMed.
- G. Kresse and J. Furthmuller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef.
- G. Kresse and J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef PubMed.
- B. Hammer, L. B. Hansen and J. K. Norskov, Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- P. E. Blochl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef.
- H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-zone Integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- F. Mercuri and A. Sgamellotti, Theoretical investigations on the functionalization of carbon nanotubes, Inorg. Chim. Acta, 2007, 360, 785–793 CrossRef CAS.
- J. M. H. Kroes, F. Pietrucci, A. C. T. van Duin and W. Andreoni, Atom Vacancies on a Carbon Nanotube: To What Extent Can We Simulate their Effects?, J. Chem. Theory Comput., 2015, 11, 3393–3400 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr02984d |
| This journal is © The Royal Society of Chemistry 2024 |