Quasi-1D Moiré superlattices in self-twisted two-allotropic antimonene heterostructures

Abstract

Two-dimensional heterostructures, characterized by a twist angle between individual sublayers, offer unique and tunable properties distinct from standalone layers. These structures typically introduce a realm of exotic quantum phenomena due to the appearance of new, long range periodicities associated with Moiré superlattices. Using molecular beam epitaxy, we demonstrate the growth of bi-allotropic 2D-Sb heterostructures on a W(110) substrate composed of twisted α (α-Sb) and β (β-Sb) phases of antimonene. Due to the relatively weak interaction between sublayers, the twist angle is intrinsically determined for each heterostructure, revealing its inherent self-twisted nature. The different atomic lattice symmetries of both allotropes lead to the formation of distinctive quasi-1D Moiré superlattices, while the random nature of the twist angle allows for a wide modulation of the Moiré potential landscape. The observed Moiré patterns on β-Sb/α-Sb heterostructures were compared with a simple model, revealing satisfactory agreement with the experiments and strongly validating the formation of self-twisted β-Sb/α-Sb heterostructures. The samples were characterized in situ using low energy electron microscopy and diffraction techniques providing a real-time tracking of the growth process and insight into the atomic structure of the synthesized nanostructures.

---

Introduction

The functionality of two-dimensional (2D) materials may be significantly enhanced when they are incorporated into a stack, known as a heterostructure, which exhibits new exotic properties distinct from those found in standalone 2D layers. Recently, 2D heterostructures also referred to as van der Waals-like (vdW) due to the relatively weak interaction between the individual 2D layers forming the stack, have rapidly gained prominence, resulting in numerous published studies.¹ While the door to the world of heterostructures remains wide open for scientists, a promising new subclass of heterostructures is emerging, distinguished by a twist angle between individual layers.^2,3 The introduction of a twist angle results in the formation of additional extra long-range lattice period modulation, observed as a Moiré superlattice. This in turn gives rise to a number of exotic quantum phenomena, including interlayer magnetism,⁴ flat bands,⁵ soliton superlattices,⁶ topological polaritons⁷ and interfacial charge polarization⁸ or interlayer excitons.⁹

One of the recently discovered 2D materials is antimonene (2D-Sb), which belongs to the xene mono-elemental class of 2D materials. Among phosphorene, arsenene and bismuthene, it represents a subclass of single-atom-thick films composed of elements of the 15^th group of the periodic table.^10,11 The existence of a stable 2D form of Sb exhibiting semiconducting electronic properties was first theoretically predicted in 2015 by Zhang et al.¹² and was later successfully synthesized by various preparation methods, including molecular beam epitaxy (MBE),^13–15 physical vapor deposition (PVD)¹⁶ and both mechanical^17,18 and liquid-phase exfoliation.¹⁹ Besides its semiconducting properties, which make it suitable for ultra-fast optoelectronics application,²⁰ antimonene exhibits additional valuable physical properties such as a tunable electronic band structure,²¹ strain-induced unpinned Dirac states,²² theoretically predicted magnetic order,²¹ high carrier mobility,²³ significant flexibility²⁴ and high stability under atmospheric conditions.¹⁴ In the case of antimonene-based van der Waals (vdW) heterostructures, two main groups can be distinguished: antimonene/metal and antimonene/semiconductor.²⁵ From the perspective of this publication, the latter group is of particular interest. In such heterostructures, the type of band gap alignment determines their potential application.²⁶ Currently, the InSe/Sb heterostructure, with its staggered type of band arrangement suitable for tunnelling field-effect transistors (TFETs), is the most extensively studied among antimony-based heterostructures.^27–31 Recently, the same type of band alignment has been theoretically predicted for 2D xene heterostructures based on group-15 elements, including P/As, P/Sb, As/Sb and Bi/Sb systems.^32–34 Generally, considering that all group-15 2D materials may have several stable allotropic forms, the following question arises: Is it possible to obtain a heterostructure consisting of two different allotropic forms of one 2D material? Regarding antimonene, among several theoretically predicted allotropic forms, only two have been identified as energetically stable.^35,36 These are the puckered alpha phase (α-Sb) and the low-buckled beta phase (β-Sb). α-Sb is characterized by a rectangular unit cell, while β-Sb has a buckled hexagonal structure. Theoretical predictions suggest that the energy stability of free-standing α-Sb and β-Sb thin layers is comparable.³⁵ This basically means that the allotropic form of the growing Sb layer can be determined by carefully selected preparation conditions. Various factors influence the grown layers including substrate symmetry, substrate temperature during deposition, deposition rate and post-deposition annealing treatment. So far, a temperature-induced transition from α-Sb to β-Sb phase antimonene deposited on the Bi₂Se₃ substrate has been already reported.³⁷

This report concerns the allotropic and structural properties of β-Sb/α-Sb heterostructures grown on the W(110) substrate. By carefully selecting the preparation conditions, specifically the temperature of the W(110) substrate during the Sb deposition process, we achieved combined growth of α-Sb and β-Sb phases, resulting in the formation of desired bi-allotropic heterostructures. Interestingly, the resulting layered stacks display a twist angle between individual sublayers. Due to the relatively weak interaction between these layers, the twist angle is intrinsically determined for each heterostructure, revealing its inherent self-twisted character. Moreover, the different atomic lattice symmetries of the allotropes lead to the formation of distinctive quasi-1D Moiré superlattices, while the random nature of the twist angle allows for a wide modulation of the Moiré potential landscape, likely exerting a significant impact on their electronic properties. Analogous quasi-1D Moiré patterns have been very recently reported for MoS₂/CrOCl heterostructures, which, in contrast to our system, involve stacking two different 2D materials.³⁸ In systems composed of hexagonal lattices, quasi-1D Moiré potential can be induced by uniaxial strain.^39,40

To enhance the informativeness of the terminology, the authors propose classifying a structure composed of at least two different allotropic forms of the same 2D material as a novel class of heterostructures: heteroallotropes.

Results and discussion

The formation of heteroallotropes was followed by low energy electron microscopy (LEEM) in the bright-field mode allowing direct observation of the sample surface in real space during the growth. Fig. 1a shows a set of LEEM images collected during deposition of Sb layers on a W(110) substrate at a temperature of 130 °C (see Movie_S1.avi in the ESI†). The growth of the Sb layer on W(110) is not straightforward and begins with the formation of a flat single-atom-thick Sb layer which covers the entire surface of the substrate. This peculiar structural phase, further called the Sb wetting layer (denoted on the first image as Sb WL), is essentially a new wire-like allotropic form of 2D-Sb on the W(110) substrate.⁴¹ Subsequent deposition of Sb molecules leads to the formation of the first α-Sb layer. Before the first layer is filled, the α-Sb phase forms islands (marked in the 1^st image) which are partially attached to the atomic steps of the W(110) substrate, resulting in smooth, slightly curved edges. The remaining part of the islands expands rapidly, exhibiting dendritic-like edges. A homogeneous contrast of the α-Sb phase islands observed from the initial stages of growth indicates a flat, single monolayer (ML) thickness of the first α-Sb layer. The second α-Sb layer (marked in the 2^nd image), visible on the subsequent images, appears as a darker area due to the quantum size effect (QSE) contrast mechanism.^42–45 The shape of the second α-Sb layer is fully dendritic (e.g. 3^rd image), regardless of the substrate steps, suggesting a weak interaction between the substrate and subsequent Sb layers, which is typical of 2D van der Waals-like materials. As the first α-Sb layer is almost completely filled, inclusions of the β-Sb phase begin to appear (marked in the 3^rd and 4^th images). In contrast to the dendritic-like structure of α-Sb, these inclusions exhibit a more compact shape (marked with #1–3 ROIs in the 4^th image). The final 5^th image in Fig. 1a shows the end stage of the tracked growth, where both the β-Sb and α-Sb are laterally enlarged. Additionally, longitudinal intersecting strips, indicative of the growth of bulk-like 3D Sb crystals, become apparent. In Fig. 1b, enlarged ROIs containing β-Sb inclusions are shown. Interestingly, the β-Sb phase does not grow directly on the Sb wetting layer. Instead, the nucleation process of the β-Sb phase is only observed after the completion of the bottom α-Sb layer, revealing the formation of a β-Sb/α-Sb heterostructure. In the ROIs #1, #2 and #3 the β-Sb phase appears after filling the 1^st, 2^nd and 3^rd α-Sb layer, respectively. The substrate temperature during the deposition process was selected to maximize the size of β-Sb phase inclusions. Lower temperatures promote a higher frequency of occurrence and a smaller size of β-Sb phase inclusions, while higher temperatures lead to the formation of isolated islands of α-Sb and β-Sb antimonene phases, which grow directly on the Sb wetting layer.

Fig. 1 (a) LEEM images collected during deposition of Sb on the W(110) substrate at 130 °C (FOV = 10 μm). (b) Enlarged ROIs #1 to #3 showing β-Sb phase inclusions on a filled α-Sb layer below. All LEEM images were collected with an electron energy of 6.75 eV.

Next, the structural properties of the grown nanostructures were investigated using diffraction techniques. Fig. 2a presents the LEED image of the clean W(110) substrate revealing a sharp 1 × 1 diffraction pattern indicative of high quality and purity of the substrate surface. The μLEED pattern collected for the region between β-Sb inclusions and Sb bulk-like crystals reveals the spot distribution corresponding to the α-Sb phase, while the diffraction patterns collected for the areas indicated as the β-Sb phase display three-fold symmetry corresponding to its honeycomb atomic structure, as shown in Fig. 2b and c, respectively. Additionally, the α-Sb phase diffraction pattern reveals two rotated in-plane structural domains (marked with dashed and solid lines) with the rotation angle of 94°. The common diagonal of both unit cells is parallel to the [1−10] direction of the W(110) substrate, while the other two diagonals are rotated by ±4° with respect to the orthogonal [001] direction of W(110). Each unit cell reveals a two-fold symmetry, corresponding to the slightly distorted rectangular unit cell of the puckered α-Sb phase in the real space, with additional spots associated with the underlaying Sb wetting layer.⁴⁶ The lattice parameters determined from the collected diffraction patterns are 4.39 ± 0.08 Å × 4.75 ± 0.08 Å for α-Sb and 4.26 ± 0.08 Å for the honeycomb structure of the β-Sb phase. While the α-Sb phase lattice parameters are in good agreement with the theoretical model of free-standing α-Sb, the β-Sb unit cell is tensile strained compared to the free-standing (4.12 Å) layer.³⁵ Nevertheless, the value obtained for the β-Sb phase is close to the bulk material value (4.31 Å), consistent with the natural occurrence of β-Sb in the layered Sb crystal.⁴⁷ Also, considering the high flexibility of the β-Sb phase, which theoretically can sustain strains up to 18%, our data are consistent with values available in the literature.²¹

Fig. 2 (a) LEED pattern acquired for a clean W(110) substrate with an electron energy of 46 eV. The μLEED patterns collected for selected areas of (b) α-Sb and (c) β-Sb phases with electron energies of 43 eV and 26 eV, respectively. The unit cells of the observed structures are marked with white lines. (d) Schematic representation illustrating the distribution of diffraction spots, with each hexagonal set denoted by a different colour, collected from several β-Sb inclusions.

A comparison of the diffraction pattern of the β-Sb phase (Fig. 2c) with the W(110) substrate (Fig. 2a) reveals that the low-index directions of both lattices do not coincide, suggesting the existence of more rotated in-plane structural domains of the β-Sb phase in β-Sb/α-Sb heterostructures. Consequently, the arrangement of several β-Sb inclusions located in different regions of the same sample was examined using μLEED. The obtained overall distribution of diffraction spots is shown schematically in Fig. 2d. The exemplary set of diffraction spots is represented by a hexagon and the [1−10] direction of the W(110) substrate is indicated by a horizontal line. The rotation angles determined relative to the [1−10] direction of the W(110) substrate appear to vary randomly, revealing the isotropic distribution of the orientation of the β-Sb phase in β-Sb/α-Sb heterostructures. It indicates that there is a very weak interaction between β-Sb and α-Sb phases. This means the independent growth and free-standing-like nature of the β-Sb phase. Consequently, a heterostructure composed of two twisted layers – a fixed α-Sb layer below and a rotatable β-Sb layer on top – should exhibit additional long-range periodicity leading to the formation of a Moiré superlattice. It should be visible through the appearance of additional spots in the diffraction patterns. Indeed, the diffraction pattern corresponding to the twisted β-Sb/α-Sb heterostructure reveals extra diffraction spots near the (00) spot, as well as those indicated by orange arrows on the overcontrasted LEED pattern in Fig. 3b. For clarity, the image without additional markings is presented in Fig. S2 of the ESI.†

Fig. 3 The μLEED patterns recorded for (a) the α-Sb phase and (b) the β-Sb/α-Sb heterostructure collected with electron energies of 43 eV and 26 eV, respectively. The orange arrows indicate the most distinctive spots beside the (1 × 1) spots. (c) The FFT image revealing the reciprocal lattice of the modeled β-Sb/α-Sb heterostructure. (d) and (e) The results of superposition of two α-Sb phase domains and the β-Sb layer, together with the corresponding FFT images. The arrows denoted as , and indicate the reciprocal lattice vectors of the α-Sb and β-Sb phases, respectively. φ₁ and φ₂ indicate the twist angles between α-Sb domains and the β-Sb sublayer. and presented on the enlarged area around the (00) spot define reciprocal lattice vectors corresponding to the primary period of the Moiré pattern, which is marked by the corresponding and real-space vectors on the ball models.

In general, the Moiré pattern can be described analytically and visualized using a ball model of superimposed atomic lattices.^48,49 Considering that the β-Sb/α-Sb heterostructure reported here consists of two twisted sublayers with different unit cells, symmetries and buckling parameters, the quantitative description of the predicted Moiré pattern is complex and beyond the scope of this article. Nevertheless, a simple model based on the fast Fourier transform (FFT) analysis allows for simulation of the expected Moiré pattern and qualitatively comparing it with the experimental data. An analogous analysis of the Moiré pattern was performed in the case of TMD/Bi₂Se₃ heterostructures.⁵⁰ Our analysis involves reproducing the ball model of atomic lattices of α-Sb and the twisted β-Sb layer on top. The model is based on the experimentally obtained lattice parameters and the twist angle determined from the diffraction patterns collected for α-Sb and β-Sb/α-Sb heterostructures, depicted in Fig. 3a and b, respectively. Subsequently FFT analysis is employed to obtain the reciprocal lattice of such a created heterostructure, which is then directly compared with the experimentally obtained diffraction pattern. The modeled layers of α-Sb and β-Sb phases along with the corresponding FFT images can be found in the ESI in section S3.† Considering the two structural-domain nature of the α-Sb phase, two twist angles should be accounted for in the following model. Hence, the rotation of the β-Sb sublayer with respect to the α-Sb phases was determined to be 49° ± 1° and 135° ± 1°, marked in Fig. 3b as φ₁ and φ₂, respectively. Fig. 3d and e show the result of the superposition of α-Sb and β-Sb sublayers reflecting the stack of the β-Sb/α-Sb heterostructure. Each domain of the α-Sb phase was considered separately, resulting in two presented models. Ball models were obtained using a logical AND operation between individual α-Sb and β-Sb atomic lattices. This operation provides a clear picture of the coincidence between individual α-Sb and β-Sb atomic lattices, where atoms (represented by dots) are visible only when atoms from both sublayers coincidence, while the absence of dots means that the coincidence does not occur. The size of the dots reflects the degree of coincidence. Next, considering the real system, where the small size of α-Sb domains does not allow the observation of a μLEED pattern of a single domain of the α-Sb phase, the final image presented in Fig. 3c is a sum of two FFT images corresponding to the modeled β-Sb/α-Sb heterostructures (Fig. 3d and e), each involving one domain of the α-Sb phase. Hence, the modeled reciprocal lattice has two components composed of two groups of spot rows marked with rounded rectangles. 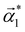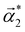The yellow and cyan rounded rectangles present the exemplary spot rows associated with both the α-Sb domains defined by the and reciprocal lattice vectors. Each group of rows corresponds to the quasi-1D stripe-like structures of the Moiré pattern and can be defined by a single reciprocal lattice vector denoted as 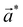and 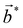, respectively. These vectors, marked in the vicinity of the (00) spot in Fig. 3d and e, correspond to the primary period of the Moiré pattern and after conversion to real-space are equal to 18.5 Å and 23.9 Å for and , respectively. The and vectors represent the distance between the subsequent rows of coincidence atoms in the real space and are marked on the modeled β-Sb/α-Sb heterostructures in Fig. 3d and e. It has to be emphasized that in the presented β-Sb/α-Sb heterostructure quasi-1D Moiré patterns are achieved just by stacking two allotropes with different atomic lattice symmetries, two- and three-fold for α-Sb and β-Sb phases, respectively. Moreover, in the studied antimonene heterostructure, the twisting angle can apparently change in a continuous way, resulting in a smooth variation of the observed long-range periodicity. A broader look at the realm of the Moiré patterns is available in the ESI (see Movie_S4.avi†), which shows the evolution of Moiré patterns as a function of twist angle in both real and reciprocal spaces.

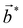Finally, the presented model (Fig. 3c) was compared with the experimentally obtained diffraction pattern collected for the β-Sb/α-Sb heterostructure (Fig. 3b). The similar distribution of spots in the vicinity of the (00) spot is observed in both cases, as seen in the insets. This set of spots can be defined with the same reciprocal lattice vectors and indicating exactly the same long-range periodicities in both cases. In contrast to the model, the absence of spot rows in the diffraction pattern was noticed, although the most distinctive spots indicated by the orange arrows in Fig. 3b align with the position of spots located at the cross of spot rows. Apparently, this superposition of spots enhances their intensity making them visible, while the intensity of the other spots remains too weak compared to the background. The comparison presented here reveals a similarity in spot distribution between the presented model and experimental data confirming that the additional diffraction spots observed in the LEED patterns collected for the β-Sb/α-Sb heterostructure are associated with the overlapping of the β-Sb and α-Sb sublayers resulting in the formation of a distinctive Moiré pattern. Consequently, the presence of the observed Moiré pattern, a phenomenon commonly associated with 2D heterostructures, robustly supports the existence of the β-Sb/α-Sb heterostructures in the investigated system. Beside the discussed diffraction spots, whose distribution aligns with the model, additional spots in Fig. 3b (Fig. S2 in the ESI†) are observed (unmarked). These are likely attributed to the complexity of the real heterostructure compared to the model. Factors such as buckling and puckering of the sublayers likely contribute to the complexity of the real Moiré pattern. Nonetheless, the proposed simple model effectively reproduces the most pronounced features observed in the experiment.

Conclusions

In conclusion, the LEEM technique, employing both diffraction methods and real-space imaging, was utilized to investigate the allotropic and structural properties of 2D-Sb nanostructures on the W(110) substrate. We successfully demonstrate the synthesis of bi-allotropic β-Sb/α-Sb heterostructures. Interestingly, the twist angle between stacked layers is intrinsically determined for each heterostructure, showing its inherent self-twisted character. Additionally, the different atomic lattice symmetries of both allotropes lead to the formation of distinctive quasi-1D Moiré superlattices. The self-accommodating nature of the twist angle allows for modulation of the quasi-1D Moiré potential landscape and, likely, its electronic properties. The proposed model of twisted layers exhibits satisfactory agreement with the experimentally observed quasi-1D Moiré patterns, strongly validating the formation of self-twisted β-Sb/α-Sb heterostructures.

Experimental

The experiment has been performed in situ using a low energy electron microscope (LEEM) produced by Elmitec, Clausthal-Zellerfeld, Germany. The microscope operates under ultra-high vacuum (UHV) conditions with a base pressure of 5.0 × 10⁻¹¹ mbar. To investigate the structural properties of the sample, diffraction techniques including low energy electron diffraction (LEED) and area selected (μLEED) were used, which are an integral part of the LEEM method. The μLEED allows acquiring diffraction patterns from the selected nanostructure with a lateral size of at least 400 nm. The Sb layers were deposited by the molecular beam epitaxy (MBE) method on an atomically smooth and clean W(110) substrate. Before the deposition process, the W(110) substrate was cleaned by alternating cycles of heating under an oxygen partial pressure of 4.0 × 10⁻⁷ mbar and short electron bombardment flashes at 2000 °C until a sharp (1 × 1) diffraction pattern of the W(110) surface appears. Next, to obtain the presented β-Sb/α-Sb heterostructures, Sb molecules were deposited on a clean W(110) substrate at a temperature of 130 °C. The Sb growth rate was calibrated in bright field LEEM operating mode and was estimated to be 5 min per ML, where 1 ML corresponds to the continuous single layer of the α-Sb phase deposited at a temperature of 115 °C on the W(110) substrate. At such a temperature the Sb layer covers continuously the entire substrate.⁴⁶ All presented LEED patterns were filtered using an FFT band-pass filter to remove the background from inelastically scattered electrons. The lattice parameters of the grown nanostructures were determined from the diffraction patterns by comparing the spot distribution with those collected for the W(110) substrate, which has known lattice parameters.

Author contributions

P. D. conducted data analysis, wrote the manuscript and drafted the schematic figures; M. G. conducted the experiments and the data analysis; R. Z. conceived and supervised the project; all authors discussed the results and approved the manuscript.

Data availability

The data used in this work are publicly available on the Zenodo open repository platform.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been supported by the National Science Centre, Poland under grant no. 2020/37/B/ST5/03540.

References

1. P. V. Pham, S. C. Bodepudi, K. Shehzad, Y. Liu, Y. Xu, B. Yu and X. Duan, Chem. Rev., 2022, 122, 6514–6613.
2. S. K. Behura, A. Miranda, S. Nayak, K. Johnson, P. Das and N. R. Pradhan, Emergent Mater., 2021, 4, 813–826.
3. M. Szendrő, P. Süle, G. Dobrik and L. Tapasztó, npj Comput. Mater., 2020, 6, 91.
4. W. Chen, Z. Sun, Z. Wang, L. Gu, X. Xu, S. Wu and C. Gao, Science, 2019, 366, 983–987.
5. Y. Cao, V. Fatemi, A. Demir, S. Fang, S. L. Tomarken, J. Y. Luo, J. D. Sanchez-Yamagishi, K. Watanabe, T. Taniguchi, E. Kaxiras, R. C. Ashoori and P. Jarillo-Herrero, Nature, 2018, 556, 80–84.
6. G. X. Ni, H. Wang, B. Y. Jiang, L. X. Chen, Y. Du, Z. Y. Sun, M. D. Goldflam, A. J. Frenzel, X. M. Xie, M. M. Fogler and D. N. Basov, Nat. Commun., 2019, 10, 4360.
7. G. Hu, Q. Ou, G. Si, Y. Wu, J. Wu, Z. Dai, A. Krasnok, Y. Mazor, Q. Zhang, Q. Bao, C. W. Qiu and A. Alù, Nature, 2020, 582, 209–213.
8. C. R. Woods, P. Ares, H. Nevison-Andrews, M. J. Holwill, R. Fabregas, F. Guinea, A. K. Geim, K. S. Novoselov, N. R. Walet and L. Fumagalli, Nat. Commun., 2021, 12, 347.
9. A. Ciarrocchi, F. Tagarelli, A. Avsar and A. Kis, Nat. Rev. Mater., 2022, 7, 449–464.
10. Z. Wu and J. Hao, npj 2D Mater. Appl., 2020, 4, 1–13.
11. S. Zhang, S. Guo, Z. Chen, Y. Wang, H. Gao, J. Gómez-Herrero, P. Ares, F. Zamora, Z. Zhu and H. Zeng, Chem. Soc. Rev., 2018, 47, 982–1021.
12. S. Zhang, Z. Yan, Y. Li, Z. Chen and H. Zeng, Angew. Chem., 2015, 127, 3155–3158.
13. J. Ji, X. Song, J. Liu, Z. Yan, C. Huo, S. Zhang, M. Su, L. Liao, W. Wang, Z. Ni, Y. Hao and H. Zeng, Nat. Commun., 2016, 7, 13352.
14. X. Wu, Y. Shao, H. Liu, Z. Feng, Y. L. Wang, J. T. Sun, C. Liu, J. O. Wang, Z. L. Liu, S. Y. Zhu, Y. Q. Wang, S. X. Du, Y. G. Shi, K. Ibrahim and H. J. Gao, Adv. Mater., 2017, 29, 1605407.
15. Y. Shao, Z. L. Liu, C. Cheng, X. Wu, H. Liu, C. Liu, J. O. Wang, S. Y. Zhu, Y. Q. Wang, D. X. Shi, K. Ibrahim, J. T. Sun, Y. L. Wang and H. J. Gao, Nano Lett., 2018, 18, 2133–2139.
16. S. Kuriakose, S. K. Jain, S. A. Tawfik, M. J. S. Spencer, B. J. Murdoch, M. Singh, F. Rahman, E. L. H. Mayes, M. Y. Taha, R. T. Ako, V. Bansal, T. Ahmed, S. Sriram, M. Bhaskaran, S. Balendhran and S. Walia, Adv. Mater. Interfaces, 2020, 7, 2001678.
17. P. Ares, F. Aguilar-Galindo, D. Rodríguez-San-Miguel, D. A. Aldave, S. Díaz-Tendero, M. Alcamí, F. Martín, J. Gómez-Herrero and F. Zamora, Adv. Mater., 2016, 28, 6332–6336.
18. R. Gusmão, Z. Sofer, D. Bouša and M. Pumera, Angew. Chem.,– Int. Ed., 2017, 56, 14417–14422.
19. C. Gibaja, D. Rodriguez-San-Miguel, P. Ares, J. Gómez-Herrero, M. Varela, R. Gillen, J. Maultzsch, F. Hauke, A. Hirsch, G. Abellán and F. Zamora, Angew. Chem.,– Int. Ed., 2016, 55, 14345–14349.
20. H. Zhang, S. Sun, X. Shang, B. Guo, X. Li, X. Chen, S. Jiang, H. Zhang, H. Ågren, W. Zhang, G. Wang, C. Lu and S. Fu, Nanophotonics, 2022, 11, 1261–1284.
21. X. Fan, Y. Li, L. Su, K. Ma, J. Li and H. Zhang, Appl. Surf. Sci., 2019, 488, 98–106.
22. Q. Lu, J. Cook, X. Zhang, K. Y. Chen, M. Snyder, D. T. Nguyen, P. V. S. Reddy, B. Qin, S. Zhan, L. D. Zhao, P. J. Kowalczyk, S. A. Brown, T. C. Chiang, S. A. Yang, T. R. Chang and G. Bian, Nat. Commun., 2022, 13, 4603.
23. Y. Wu, K. Xu, C. Ma, Y. Chen, Z. Lu, H. Zhang, Z. Fang and R. Zhang, Nano Energy, 2019, 63, 103870.
24. M. Zhao, X. Zhang and L. Li, Sci. Rep., 2015, 5, 16108.
25. J. Li, W. Zhou, L. Xu, Y. Huang, S. Zhang and H. Zeng, Appl. Phys. Lett., 2022, 121, 100501.
26. V. O. Özçelik, J. G. Azadani, C. Yang, S. J. Koester and T. Low, Phys. Rev. B, 2016, 94, 035125.
27. A. Sengupta, A. Dominguez and T. Frauenheim, Appl. Surf. Sci., 2019, 475, 774–780.
28. Z. Zhang, Y. Zhang, Z. Xie, X. Wei, T. Guo, J. Fan, L. Ni, Y. Tian, J. Liu and L. Duan, Phys. Chem. Chem. Phys., 2019, 21, 5627–5633.
29. N. F. Shen, X. D. Yang, X. X. Wang, G. H. Wang and J. G. Wan, Chem. Phys. Lett., 2019, 727, 50–54.
30. Z. Zhang, Y. Zhang, Z. Xie, X. Wei, T. Guo, J. Fan, L. Ni, Y. Tian, J. Liu and L. Duan, Phys. Chem. Chem. Phys., 2019, 21, 5627–5633.
31. K. Zheng, H. Cui, J. Yu and X. Chen, IEEE Trans. Electron Devices, 2022, 69, 1155–1161.
32. L. Lin, S. Li, W. Yu, L. Zhu, J. Huang, Z. Zhang, H. Tao and W. B. Zhang, Vacuum, 2020, 176, 109296.
33. W. Li, X. Fang, D. Wang, F. Tian, H. Wang, D. Fang, J. Li, X. Chu, H. Zhao, D. Wang and X. Ma, Phys. E, 2021, 134, 114933.
34. S. M. Mozvashi, S. I. Vishkayi and M. B. Tagani, Phys. E, 2020, 118, 113914.
35. G. Wang, R. Pandey and S. P. Karna, ACS Appl. Mater. Interfaces, 2015, 7, 11490–11496.
36. S. Zhang, M. Xie, F. Li, Z. Yan, Y. Li, E. Kan, W. Liu, Z. Chen and H. Zeng, Angew. Chem., 2016, 128, 1698–1701.
37. C. Hogan, K. Holtgrewe, F. Ronci, S. Colonna, S. Sanna, P. Moras, P. M. Sheverdyaeva, S. Mahatha, M. Papagno, Z. S. Aliev, M. Babanly, E. V. Chulkov, C. Carbone and R. Flammini, ACS Nano, 2019, 13, 10481–10489.
38. X. Guo, J. Liao, D. Yang, M. M. Al-Makeen, H. Xie, X. Zheng and H. Huang, Appl. Phys. Lett., 2024, 124, 241602.
39. A. Sinner, P. A. Pantaleón and F. Guinea, Phys. Rev. Lett., 2023, 131, 166402.
40. Y. Bai, L. Zhou, J. Wang, W. Wu, L. J. McGilly, D. Halbertal, C. F. B. Lo, F. Liu, J. Ardelean, P. Rivera, N. R. Finney, X. C. Yang, D. N. Basov, W. Yao, X. Xu, J. Hone, A. N. Pasupathy and X. Y. Zhu, Nat. Mater., 2020, 19, 1068–1073.
41. A. Stępniak-Dybala, T. Jaroch, M. Krawiec, P. Dróżdż, M. Gołębiowski and R. Zdyb, Nano Lett., 2023, 23, 9894–9899.
42. M. S. Altman, W. F. Chung, Z. Q. He, H. C. Poon and S. Y. Tong, Appl. Surf. Sci., 2001, 169–170, 82–87.
43. E. Bauer, J. Electron Spectrosc. Relat. Phenom., 2020, 241, 146806.
44. R. Zdyb and E. Bauer, Surf. Rev. Lett., 2002, 9, 1485–1491.
45. R. Zdyb and E. Bauer, Phys. Rev. Lett., 2002, 88, 166403.
46. T. Jaroch, L. Żurawek, A. Stępniak-Dybala, M. Krawiec, M. Kopciuszyński, P. Dróżdż, M. Gołębiowski and R. Zdyb, submitted to nano letters.
47. O. Ü. Aktürk, V. O. Özçelik and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 235446.
48. M. Yakes and M. C. Tringides, J. Phys. Chem. A, 2011, 115, 7096–7104.
49. T. Jaroch, M. Krawiec and R. Zdyb, 2D Mater., 2021, 8, 035038.
50. Z. Hennighausen, C. Lane, I. G. Buda, V. K. Mathur, A. Bansil and S. Kar, Nanoscale, 2019, 11, 15929–15938.

---

Footnote

† Electronic supplementary information (ESI) available: A movie captured during deposition of Sb on the W(110) substrate, an over-contrasted μLEED pattern recorded for the β-Sb/α-Sb heterostructure, atomic ball models of the α-Sb and β-Sb phases, and a movie illustrating the evolution of Moiré patterns as a function of twist angle. See DOI: https://doi.org/10.1039/d4nr02970d

---