The impact of sequence periodicity on DNA mechanics: investigating the origin of A-tract's curvature

Abstract

Periodic sequences in phase with DNA helical shape are prevalent in genomes due to their capacity to modulate DNA elasticity on a global scale. However, how this occurs is not well understood. We use all-atom molecular dynamics simulations on 40 bp DNA fragments to assess the effect of periodicity on bending, twisting, and stretch elasticity. We observe that DNA static curvature is the mechanical parameter most influenced by periodicity, with A-tract sequences having the greatest effect. A-tracts generate global curvature by bending in distinct directions (minor groove and backbones) that complement the bending of the rest of DNA, which predominantly is towards the major groove. Even if A-tracts are rigid at the local scale, these small bends integrate with the greater bends from the sequences between, producing an amplifying effect. As a result, our findings support a ‘delocalized bend’ model in which the A-tract operates as an ‘adaptable mechanical part’. By understanding how global curvature emerges from local fluctuations, we reconcile previous contradictory theories and open an avenue for manipulating DNA mechanics through sequence design.

---

Introduction

The mechanical properties of DNA are fundamental to many biological processes, for which decoding the complex rules of flexibility is vital for understanding. The bendability of DNA molecules is responsible for DNA packing within cells,¹ gene regulation,^2–4 and protein interactions.^5,6 DNA looping is involved in regulatory regions by bringing together far away sites along the chain,^7–9 and some processes such as DNA repair and methylation require change of flexibility at the individual nucleotide level.^10–13

A variety of methods have been employed to probe the sequence features responsible for mechanical variation in DNA. Structural imaging methods such as X-ray crystallography give atomistic information but lack dynamics.^14,15 There has been success with experiments involving techniques such as atomic force microscopy (AFM),^16,17 cyclization,^4,18–20 and optical/magnetic tweezers^17,21,22 which reveal dynamic behaviour but only at the global scale. This leaves a need for techniques able to study the local dynamics at the atomistic level, which is filled by computational simulations.²³

Based on the findings of all-atom simulations and X-ray database analysis, it has been determined that YR (pyrimidine–purine) base-pair (bp) steps are the most flexible, often exhibiting hinge-like behaviour.^14,24–26 In contrast, RR (purine–purine) steps function as intermediaries, while RY (purine–pyrimidine) steps are the most rigid. However, this principle is an oversimplified description due to the influence of the particular attributes of individual bases. Through the analysis of all possible tetramers from the ABC simulation database,²⁷ we found A/T rich sequences tend to exhibit more extreme mechanical properties, including the most rigid (AAAA, AATT) and the most flexible (TATA, CACA), compared to sequences abundant in G/C, which are more average.²⁶

An important factor for controlling DNA bendability at the longer scale is the repetitive placement of particular sequences in phase with the helical pitch. A-tracts sequences have been studied extensively due to their periodic distribution in genomes as well as their key role in nucleosome positioning and DNA looping.^28,29 It is widely recognised that multiple short phased A-tracts introduce a directional bend in the DNA helical axis, although this is counter-intuitive given that these sequences possess a straight structure and rigid mechanical properties.^17,29,30 This has been explained by the fact that DNA in solution tends to bend toward the major groove at the base-pair level, which makes the local molecular contour be writhed or crooked^31–33 (see Fig. 1). Then, the action of phased A-tracts would be to provide proper helical phasing and not counteract the net curvature produced by the sequences in between, according to the non-A-tract model.^29,34,35 However, the mechanism that determines the strong curvature caused by A-tracts is still not clear. Bending at the edges of A-tracts, as proposed in the junction model,^29,36 or at the A-tracts themselves towards the minor groove, as suggested in the wedge model,^29,37 might also be the cause.

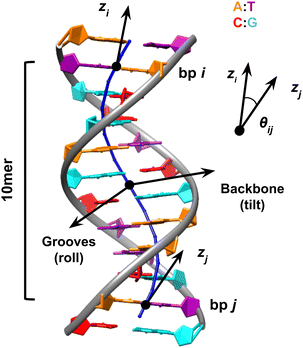Fig. 1 Sequence-averaged DNA presents a crooked shape due to its propensity to bend towards the major groove at the bp step level. This structure is built using average helical parameters²⁷ with A represented in orange, T in purple, C in red, and G in cyan. The local molecular contour (in blue) is defined by the midpoint between bp steps.³² This scheme also illustrates the expansion of 3DNA's algorithm by the SerraNA program to consider pairs of bp that are not adjacent, using a 10mer as an example. The bending angle (θ_i,j) between two bp i and j is determined by the directional vectors (ẑ_i and ẑ_j) originating from them. The direction in which bending occurs is decided at the midpoint, according to the orientation of grooves or backbones. The bending angle is partitioned into two angles, which are equivalent to roll and tilt, as defined at the level of two 2 bp.

Further periodic signals have been detected by the utilisation of high-throughput cyclization assays, which are capable of ascertaining the inherent bendability of thousands of DNA sequences.²⁰ Sequences that have the greatest tendency for cyclization are distinguished by the repeating of in-phase A/T dinucleotides on one hand and in-phase G/C dinucleotides on the other. These two motifs are interconnected by virtue of being separated by half of the helical repeat (5, 15, 25 bp).²⁰ However, the exact influence of these correlations on the curvature and dynamics of DNA is still unknown.

The field of DNA nanotechnology has just started to exploit the growing understanding of DNA elasticity. To construct complex shapes, for instance, twisting and curvature have been altered by removing and adding bp.³⁸ Still, the application of sequence-dependent flexibility in the manipulation of DNA nanostructures is infrequent. Recently, a Brownian ratchet employing sequence-dependent flexibility gradients has been suggested as a novel approach to facilitate the transportation of positively charged nanoparticles.³⁹ However, A-tracts have been the sole motif specifically used in the construction of sequence-specific designs so far, including DNA minicircles⁴⁰ and lipid bilayers encircled by DNA.⁴¹

Although the origins of flexibility at the bp level are well-established,^14,42 there have been limited efforts to understand how these bends combine to produce global bending. These studies have primarily relied on simple mesoscopic models using the nearest-neighbour approximation (only interactions between two bp),^30,43,44 despite the well-established impact of the sequence context.^36,45 A new bp-level model incorporating long-range effects through the implementation of machine learning techniques has been recently developed, although it has not yet been employed to calculate global elastic properties.⁴⁶ All these limitations hinder our capacity to precisely predict the mechanical characteristics of genomic sequences or design sequences for DNA nanotechnology.

We previously developed the Length-Dependent Elastic Model (LDEM) to characterize the evolution of DNA mechanical properties as length scale progressively increases from a single bp, through the analysis of all-atom molecular dynamics simulations.³¹ Using this model, we observed that the transition from local to global elasticity typically occurs within the length of one DNA turn, resulting in long-range values that are consistent with DNAs at the kbp scale.^26,31 The elastic constants undergo significant changes at small lengths, until they reach approximately 10 bp or a full helix turn.^26,31 As the length continues to increase, the elastic constants hit a plateau, indicating that they remain moderately constant without any major alterations (see Fig. S1†). This implies that the global elastic properties of a sequence motif can be determined through all-atom simulations of relatively short DNA fragments (30–50 bp). The implementation of the LDEM in the SerraNA program allows for the execution of all these calculations in a highly efficient manner (https://github.com/agnesnoy/SerraNA)²⁶ and has been employed in the present study.

Here, we conduct a systematic analysis of how sequence periodicity affects DNA mechanical characteristics in terms of bending, twisting and stretching, using all-atom molecular dynamics. The goal is to understand why the repetition of certain sequences results in DNA fragments with exceptional mechanical properties. For these reasons, we designed and modelled a series of 40 bp-long sequences with different periodic patterns, taking into account the general YR/RR/RY principle of DNA mechanics while integrating the most malleable (TATA, CACA) and rigid (AAAA) tetramer motifs²⁶ (see Fig. 2). The 40 bp length was selected as a compromise between capturing the plateau behaviour while optimizing computational resources, as they are among the longest linear DNA molecules simulated with an atomic description of the entire system, including the solvation box.^26,47

Fig. 2 Total (A), dynamic (A_d) and static (A_s) persistence lengths of modelled DNA fragments. Sequences are grouped according to the constituent bases (A/T, G/C and mixture) and coloured according to their pattern. The out-of-phase sequences were positioned following their equivalent in-phase sequence pattern to facilitate comparison. Error bars represent the confidence intervals of the directional decay fitting at 70% as calculated by SerraNA. Y refers to pyrimidines and R to purines.

Materials and methods

Design of DNA sequences

A total of 24 linear DNA fragments containing 40 bp were built using the NAB module from Amber20.⁴⁸ Sequences were designed under the assumption that helical pitch was effectively 10 bp at this limited scale. They were classified primarily into three categories: (i) uniform, including (R)₄₀, (YR)₂₀; (ii) periodic, including (R₅YRYRY)₄, (R₅Y₅)₄, (R₉Y)₄; and (iii) non-periodic, including variants of the motifs listed above. Sequences were also grouped by base composition being A/T, C/G or mixture (see Fig. 2).

Simulations

A CG segment was placed at each end of the 40 bp sequences to prevent end melting during the simulation. The resulting 44 bp sequences were built using the nucleic acid builder utility in Amber20 with bsc1 force-field.^48,49 The structures were solvated in TIP3P octahedral boxes⁵⁰ and Na⁺/Cl⁻ pairs, using Smith-Dang parameters,⁵¹ to achieve a physiological salt concentration of 200 mM. Simulations were carried out with the pmemd.cuda code from Amber20⁴⁸ using periodic boundary conditions and Particle Mesh Ewald.⁵² Movements of hydrogen atoms were annihilated using SHAKE,⁵³ which allowed us the use of a 2 fs integration step. The systems were subjected to a minimisation/equilibration process according our standard protocols^25,26 and followed by 500 ns of productive simulations, which provides an adequate sampling for elastic constant calculations.²⁶ Simulations were performed at constant temperature (300 K) and pressure (1 atm) using the Berendsen thermostat and barostat.⁵⁴

Structural parameters and elastic constants

The elastic constants for bending, twisting, and stretching were estimated for each DNA molecule using SerraNA, as detailed before.^26,31 This application employs the helical coordinate system, as defined by the 3DNA program,⁵⁵ to analyse all the frames from simulations at the bp level. SerraNA expands the 3DNA's algorithm to characterize the geometry of not only two consecutive bp, but also those separated by an increasing number of nucleotides (see Fig. 1).

The program utilises the worm-like chain model (WLC) to compute persistence lengths (A) by fitting the directional decay between the tangent vectors (ẑ_i and ẑ_j) of two bp (i and j) that are separated by a growing number of bp steps N with a distance rise b of 0.34 nm. By assuming a sufficiently weakly bending molecule, SerraNA simplifies WLC's formula (〈cos θ_i,j〉 = e^−Nb/A), considering only the quadratic approximation:

where 〈θ_i,j²〉 are obtained from the simulated ensemble using all sub-fragments with length N for a particular DNA molecule, and A can be read off using the above definition.

The net linear increase in 〈θ_i,j²〉 with length comes from the distribution of static bends along a molecule (〈θ_s²〉) and the dynamic bends induced by thermal fluctuations (〈θ_d²〉).^56,57 SerraNA obtains the former from the average bp step parameters, which determine the local static bends, and the latter though 〈θ²〉 = 〈θ_s²〉 + 〈θ_d²〉.^26,31 Then, the static and dynamic contributions of the persistence lengths (A_s, A_d) are determined using the fitting of the linear directional decays, following the same approximations as before:^26,31

which provides the heuristic expression 1/A = 1/A_s + 1/A_d ^56,57 when combined.

The direction of bending is established by partitioning it into two components: roll (towards the grooves) and tilt (towards the backbone). The decomposition of bending is defined according to the orientation of DNA's grooves and backbones at the mid-point between the two bp considered, as defined in the 3DNA algorithm (see Fig. 1).

The bulk torsional modulus for each sequence (C) is determined by taking the overall average of C_i,j values obtained for all sub-fragments longer than 10 bp (after the transition from short- to long-range behaviour).³¹ Each individual C_i,j is obtained from the elastic matrix F_i,j = k_BTbNV_i,j⁻¹, where V_i,j⁻¹ represents the inverse covariance matrix extracted from simulations using the bending, twisting and stretching parameters for that particular sub-fragment comprised between bp i and j.^26,31 Covariance matrices (V_i,j) are assumed to have a multi-Gaussian distribution, and while this is not always the case for short sub-fragments due to their bimodality,^27,45,58 this behaviour rapidly dissipates as the DNA reaches the length of a complete helical turn.²⁶

Similarly, stretch moduli for each sub-fragment (B_i,j) are calculated using the diagonal term of F associated with the end-to-end distance. Because the stretching response of relatively short DNA molecules is affected by long end-effects, the bulk stretch modulus (B) is determined through the linear fitting of its length dependency, using only the central 18mer and sub-fragments exceeding 10 bp^26,31 (see Fig. S1†). This limited fitting has been demonstrated to be enough for capturing long-range behaviour, resulting in values that are comparable to those obtained through single-molecule techniques.

Results and discussion

In order to discern the consequences of sequence periodicity on DNA deformability, we investigated a series of linear DNA fragments of 40 bp, combining different sequence motifs: (i) uniform sequences as (R)₄₀ and (YR)₂₀, expected to be rigid and flexible, respectively; (ii) periodic in-phase sequences of alternating rigid and flexible pentamers ((R₅YRYRY)₄); (iii) periodic in-phase sequences with the flexible part reduced to minimum ((R₉Y)₄); (iv) periodic sequences of alternating rigid pentamers (R₅), placing hinge (YR) and anti-hinge (RY) steps half-turn from each other and a full turn from themselves (R₅Y₅)₄; (v) out-of-phase variations of (R₅YRYRY)₄, such as (R₄YRYR)₅ and (R₃YRY)₆ R₃Y; and (vi) out-of-phase variations of (R₅Y₅)₄, such as (R₄Y₄)₅ and (R₆Y₆)₃R₄.

Persistence length correlates with the amount of flexible bp steps

Persistence length values A obtained from our simulations are larger than the general experimental measurements of 45–55 nm^16,21,22 but in agreement with other simulation data^26,30,47,59 (see Fig. 2 and Table S1†). This is common for MD simulations, possibly due to an overestimation of stacking interactions⁶⁰ or the simulations being conducted in much more controlled salt conditions of monovalent (Na⁺, Cl⁻) ions only, compared to experimental conditions where there are other species such as Mg²⁺, Hepes and Tris^16,21,22 which significantly affect DNA flexibility.^21,61 Nevertheless, our simulations can reproduce the degree of change observed in single-molecule experiments¹⁷ when comparing sequences with phased A-tracts (yielding an average ± standard deviation of 63 ± 6 and 44 ± 3 nm, respectively) and those without (67 ± 8 and 47 ± 4 nm), resulting in an identical decrease of 6%.

The variability of persistence lengths observed in Fig. 2 underscores the sequence-dependent nature of DNA flexibility at this global length scale, as documented in prior research.^{19,20,26,30,62} One can easily see that the nature of bp steps plays a significant role when comparing sequences made up of identical bases. At the A/T block, (A)₄₀ presents a larger A than (TA)₂₀ due to the accumulation of flexible TA steps. However, for the G/C group, this order is reversed and (G)₄₀ is more flexible than the (GC)₂₀. A similar observation was previously made at the tetramer level (GGGG vs. GCGC).²⁶ This can be explained by the fact that the GG step has a considerably lower stacking energy than CG and GC,^63,64 which leads to weaker interactions between adjacent bps, thereby permitting bending and deformation. Overall, the remaining sequences, including those in the mixed group, fall within the range of values derived from their respective polydinucleotide sequences, regardless of whether they exhibit periodicity in phase or not (see Fig. 2). Nevertheless, some R_NY_M sequences are exceptionally stiff as a result of the accumulation of poly(R) and RY steps, both being similarly rigid and not compensated by the flexible YR steps.

All these results suggest that the total number of flexible bp steps determines the persistence lengths of individual DNA fragments. We verified this idea by finding a measurable correlation between the global value of A for each individual DNA fragment and the mean value obtained from all the constituent tetramers in that specific sequence (with a correlation coefficient of 0.52, see Fig. S2†). When we only consider the bendability caused by thermal fluctuations (i.e. A_d), the correlation coefficient increases to 0.57, but it decreases to 0.51 when we only consider the static curvature (i.e. A_s) (see Fig. S2†). This suggests that the flexible or rigid character of the constituent bp steps dictate A_d. On the contrary, our results indicate that a large number of short curved motifs is not sufficient to predict a strong global curvature; rather, they must be arranged in a particular manner (see below).

In-phase periodicity increases overall DNA curvature

The A_s data is significantly more varied than the A and A_d data, which agrees with Mitchell et al.³⁰ and Velasco-Berrelleza et al.,²⁶ who found sequence-dependent variation in A to be primarily due to changes in intrinsic shape (i.e. A_s), rather than to thermal fluctuations (A_d). Additionally, we noted that the A/T group has the greatest degree of variance, while the G/C group presents the least, consistent with our findings at shorter length scales.²⁶

By employing the non-curved features of A-tracts, we observe that curvature rises with the in-phase alternation of curved and non-curved blocks (Fig. 2). Our simulations show that (R₅YRYRY)₄ in the T/A and C/A groups have lower A_s (i.e., stronger curvature) than the corresponding (RY)₂₀. This impact is decreased when the flexible YRYRY section is reduced to a single RY and YR step in (R₉Y)₄ sequences. However, curvature rises in (R₅Y₅)₄ sequences, indicating that the separation of alternating RY and YR steps by 5 bps is a very efficient way for causing curvature. Finally, we notice that deviations from in-phase periodicity reduce or maintain DNA curvature, but never increase it (Fig. 2).

In summary, our simulations suggest that alternating curved and non-curved sections on DNA, aligned with its helical structure, are essential for creating a significant overall curvature. This is especially true when A-tracts are present, regardless of the length or composition of sequences between (T/A, C/A, or G/C motifs), as seen in previous experiments.^17,29 Our findings are consistent with high-throughput cyclization data, which identified A/T and G/C dinucleotides separated by half a DNA turn.²⁰ Although the same study found a weak spatial association between AA and CA, gel electrophoresis experiments have demonstrated that the presence of CA steps helps to generate a particularly large curvature with A-tracts,⁶⁵ which is in agreement with our simulations. Lastly, our measurement of the degree of bending per decamer containing an A-tract is 17.7 ± 0.5 degrees, which agrees really well with the value of 18 degrees found by gel electrophoresis⁶⁶ and NMR structures⁶⁷ (see Fig. 3).

Fig. 3 Bending profiles along DNA fragments for increasing sub-fragment lengths (2, 5, 10 and 30 bps), where values are assigned based on the mid-position of each sub-fragment. Sequence patterns ((R)₄₀, (YR)₂₀, (R₉Y)₄, (R₅Y₅)₄ and (R₅YRYRY)₄) are organised by columns and base groups (A/T, A/C and G/C) are organised by rows with the exception of (A₅CGCGC)₄ and the out-of-phase periodic sequence (A₄T₄)₅. YR and RY bp steps are shaded in grey and yellow, respectively. Standard deviations range from ∼3–15 degrees, therefore these have been excluded to aid visualisation of the key trends. Peaks in bending profiles imply global curvature given DNA's helical structure and chirality (tendency to bend towards the major groove). The peaks are larger in the presence of A-tracts, especially for the C/A group of sequences, followed by the T/A and hence lowest for the G/C ones, which aligns with global A_s values.

A-tract curvature is induced via the delocalized-bend model

We then investigated the connection between local and global bending to determine which are the structural factors that contribute to create a significant curvature when A-tracts are present. A clear pattern at the dinucleotide level confirms the basic notion that YR steps exhibit the most pronounced local bends (similar to hinges), RY steps display the least bending (anti-hinges), and RR steps exhibit an intermediate behaviour (Fig. 3). Because the strongest local bends always point towards the major groove (giving positive values for roll; see Fig. S3†), they cancel each other out in uniform or out-of-phase sequences, due to their all-around orientation (Fig. S4†). Then, the bending profiles for these sequences become flatter as we extend the length of the sub-fragments, indicating that there is no prevailing curvature direction and that bending magnitude increases due to thermal fluctuations (Fig. 3). In contrast, in most in-phase periodic sequences, local bends couple to build up a large curvature, due to the consistent placement of their major grooves on the same side of the DNA. This is reflected by the presence of peaks in the bending profiles, showing regardless of the length of the sub-fragments (Fig. 3).

Therefore, our findings would initially suggest that the source of bending is outside the A-tracts and that their primary function is simply to be stiff and not counteract the net curvature caused by the sequences between, as per the non-A-tract model. Nevertheless, upon closer inspection of the global bending profiles, we observe that the largest curvature is not centred around YR steps, but rather is displaced in most cases (Fig. 3).

To establish the orientation of the global DNA curvature presented for each fragment, we decomposed the bending angles into the roll and tilt components according to the midpoint of the selected sub-fragments (see Methods and Fig. 1). We chose to examine the 10 possible 30 bp sub-fragments from the 40 bp sequences because their midpoints cover the whole central DNA turn, thus accounting for every conceivable orientation of the global curvature (see Fig. 4). We observe that the largest curvature arises from a combination of bending towards the grooves and backbones, with the latter being equally important as the former (Fig. 4A and S4†). A-tract sequences bend towards the minor groove and backbone, while sequences in between bend towards the major groove, as shown in representative structures matching the two-component bending profiles (Fig. 4B). In contrast the equivalent non-curved sequences, like (G₅CGCGC)₄ and (G₅C₅)₄, have a flatter profile without bending towards the minor groove and backbones, demonstrating the significance of bending in A-tracts (Fig. 4C, S3 and S4†).

Fig. 4 Direction of bending for selected sequences. The two-component bending profiles, toward grooves (blue) and backbones (green), (A), as well as representative structures aligning with them (B) for the most curved sequences. (A) By using the ten 30 bp sub-fragments from the 40 bp sequences, we identify the best curvature direction, as their medium positions cover the whole central DNA turn (black left bracket in (B)). Positive numbers in the blue line indicate a major groove (M) bend, while negative values indicate a minor groove (m) bend, both contained in red left brackets in (B). Vertical blue and green lines depict the profiles’ peaks, showing which bp faces the major groove or backbone in the preferred bending orientation. YR are shaded in grey and RY in yellow. (B) Structures in orange (A), purple (T), red (C), and cyan (G) correspond to the plot above. (C) Plots identical to those in (A), except for sequences lacking distinct curvature, as shown by the comparatively flat profiles. In each panel, dashed lines indicate molecular midpoints.

This preferred curved orientation is commonly observed in our simulations for various sequences (such as (A₅CACAC)₄, (A₅CGCGC)₄, (A₅C₅)₄ and (A₉C)₄) and is consistent with previous high-resolution structures^67,68 and simulations.^10,59 Specifically, A-tracts shift from a positive tilt at the 5′ junction to negative at the 3′ junction, displaying a bending toward the minor groove (negative roll) in the middle closer to the 3′ junction.

Because curvature emerges from bends inside and outside A-tracts, our results support the delocalized-bend model proposed by Crothers and co-workers.^68,69 This model amalgamates aspects from the alternative theories: curvature arises from phased combinations of bending towards the major groove (as in the non-A-tract model) and towards the minor groove and backbone (A-tract model). The equivalence in bending between (A₅CACAC)₄ and (A₅C₅)₄ sequences suggests that the bend at the 5′ junction is critical, hence providing support for the junction model. Nevertheless, our simulations show that YR steps at the 5′ junction are not particularly flexible, contrary to what was initially proposed by this hypothesis.^29,36 Rather, their significance is derived from the positioning of A-tracts to bend towards the minor groove and backbone, as well as non-A-tracts to bend towards the major groove. Collectively, the combination of these local effects produces a global curvature that is directed into the minor groove at the A-tracts, slightly shifted towards the 3′-end. This correlates well with the overall bending orientation deduced from gel electrophoresis and hydroxyl-radical cutting.^36,66,70

A-tracts are versatile segments that enhance the curvature of adjacent sequences

Based on our calculations, the mechanical property that makes A-tracts essential for inducing large curvature in DNA is the ability to bend in any direction, albeit only marginally, owing to their rigid nature.^71,72 This differentiates them from the remaining DNA sequences, which are restricted to bending in the direction of the major groove. As a result, A-tracts contribute to the global curvature through their distinctive bends toward the minor groove and backbones, which complement the common DNA bends toward the major groove. This explains why the nature of the sequences between them has such a negligible effect on this curvature.²⁹ The (A₉C)₄ sequence demonstrates the adaptability of A-tracts, as they bend towards the minor groove and two backbones, allowing the isolated YR steps to bend in the direction of the major groove (Fig. 4).

Stretch and torsion moduli

The average stretch (B) and torsion moduli (C) for all our modelled DNA fragments are 1882 ± 455 and 104 ± 18 (±standard deviation), respectively (see Table S1†). These values are in reasonably good agreement with the results obtained from single-molecule experiments, which are typically around 1500 pN and 100 nm.^73–76 Recent experiments have shown that DNA fragments containing A-tracts have higher stretching rigidity (2400 ± 220 pN),¹⁷ which could explain the comparatively high value of B in our proposed sequences. By analyzing all simulations without A-tracts, we obtain a lower average (1608 ± 582), which is more consistent with the experiments conducted on random DNA.⁷⁶ The remaining sequences (with A-tracts) provide a higher average (2018 ± 336), which, although not identical to the experimental result, replicates the observed trend.

Our simulations reveal that periodicity has no major effect on the stretch modulus of a certain sequence (Fig. 5A). Instead, the mechanical parameter appears to be influenced by the flexible character of the constituent steps, as evidenced by the correlation between global and local values with a coefficient of 0.48, in a similar manner to the dynamic persistence length (A_d) (Fig. S2†). Contrary to the persistence length, G/C sequences exhibit the largest variability, whereas the A/T group presents the lowest (Fig. 5A). This agrees with the fact that the stretch modulus is determined by the crookedness of the molecule, i.e. the oscillations of bp centres around the molecular axis.³³ Then, the change in DNA contour length is mostly due to aligning the base pair centers with the helical axis, rather than separating successive base pairs, which is prevented by the strong stacking interactions.^31,33,77 Consequently, GG is the most crooked polydinucleotide sequence³³ and presents the lowest stretch modulus, whereas GC is among the least crooked sequences³³ with a high modulus. Sequences abundant in A/T are comparatively rigid despite their weak stacking interactions,⁶⁴ due to their comparatively low crookedness.³³

Fig. 5 (A) Stretch (B) and (B) twist modulus (C) for all modelled DNA fragments. Sequences are grouped according to the constituent bases (A/T, G/C and mixture) and coloured according to their pattern. Error bars for stretching are the 70% confidence intervals of the linear fitting, while for twisting are the standard deviation obtained from considering all sub-fragments longer than 10 bp, as it is calculated by SerraNA and described in the Method section. Y refers to pyrimidines and R to purines. (C) Length dependence of C for all simulated sequences, colored based on the value at the dinucleotide level. C remains constant when variance simply adds up as we increase the length of the fragment; C increases when fluctuations between neighbouring sections are negatively correlated, and decreases when these are positively correlated.

The global torsional modulus of individual DNA segments is not influenced by periodicity and shows a weak correlation with the constituent oligomers (with a coefficient of 0.09), suggesting a complex transition between the short and long-range behaviour (Fig. 5B and S2†). Typically, the torsional modulus shows a crossover from relative soft values of around 30–60 nm at the dinucleotide level to a large-scale asymptotic value between 90–120 nm. However, our results indicate that this transition does not occur in a uniform fashion. Instead, the different sequences exhibit varying capacities to connect local oscillations within neighboring sequences in order to produce global fluctuations. When examining sequences with similar torsion modulus at the dinucleotide level, we notice that they exhibit a distinct rate of change as the DNA length increases (see Fig. 5C). In some sequences, the local fluctuations exhibit a high anti-correlation as length increases, generating a rigid torsional modulus, whereas, in others, the local fluctuations are more independent resulting in a softer global elastic constant (Fig. 5C).

The varying capacity to connect local and global variations for the different sequences could be caused by the distinct levels of crookedness, as suggested by the remarkable correlation between twist and stretch elastic constants (with a coefficient of 0.73, see Fig. S5†). It is worth noting that a crooked DNA fragment can alternatively be described as locally supercoiled or writhed. Therefore, alterations in this structural parameter can be counterbalanced by fluctuations in twist, as per the DNA topology relation. In this, the total number of times one strand revolves around the other (i.e. the linking number) is equal to the sum of twist and writhe. We anticipate that the potential correlation between twist elasticity and crookedness will be the focus of subsequent research.

Conclusions

In this study, we performed all-atom molecular dynamics simulations for numerous 40 bp DNA sequences with varying levels of periodicity and analysed their elasticity and static curvature using our software SerraNA. We found that the dynamic persistence length is primarily influenced by the quantity of flexible bp steps, whereas curvature is influenced by sequence periodicity aligning with the helical shape of DNA. This is due to the fact that, when position periodically, the structural features of a specific sequence (major groove, minor groove, backbones) always face the same side of the DNA, multiplying the effect of its inherent curvature.

Our simulations indicate that A-tract is the sequence motif that generates the largest curvature when positioned at in-phase regular intervals, in agreement with previous experiments.²⁹ By examining how global curvature emerges from local bends, we provide a comprehensive understanding of the origin of this curvature, tying together previous theories (A-tract, non-A-tract, and junction), which focused on the separate structural factors. We show that curvature can be attributed to the coordination of bends, both inside and outside A-tracts, supporting the delocalized-bend model proposed by Crothers and co-workers.⁶⁸ On one hand, DNA bending occurs predominantly at the flexible YR steps and, on average, is directed toward the major groove. On the other hand, A-tracts possess the distinct capacity of flexing in the other directions (minor groove and backbones), even if it is only marginally due to their rigid nature. Major curvature therefore emerges from the phased combination of strong bending toward the major groove in non-A-tract sequences and weak bending toward the minor groove and backbone in A-tracts. The combination of these local effects produces a global curvature that is directed into the major groove at the 5′ junction of A-tracts and into the minor groove at the 3′ junction, explaining the junction model derived from biochemical studies.

A-tracts's fundamental property for inducing large curvature is their mechanical adaptability, which enables them to bend in various directions and couple with the directions of the surrounding sequences, thereby producing an amplifying effect. Thus, A-tracts operate as mechanically versatile elements. The composition of the sequences between A-tracts hardly affects this curvature because the vast majority of DNA sequences predominantly bend in the direction of the major groove.

Finally, our simulations reveal that the stretch and twist elastic constants are independent of DNA periodicity. While the number of flexible bp steps influences stretch modulus in the same way as dynamic persistence length does, torsional modulus has a more complex link between local and global elasticity that needs additional investigation. Overall, the findings presented in this work not only bring new insights into the flexible features of periodic sequences in genomes, but also facilitate the development of sequences with ad hoc mechanical characteristics that can be utilized in DNA nanotechnology.

Author contributions

A. N. conceived the study. T. G. performed the simulations. T. G. and A. N. analysed them. A. N. and T. G. wrote the manuscript.

Data availability

Simulations are available at the MDposit database (https://mdposit-dev.mddbr.eu/#/browse), and data are available in the ESI† and the University of York Data Repository (https://doi.org/10.15124/e33eb7cf-b8d8-49bd-9833-ee47d5b56eb3).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Elliot W. Chan and Victor Velasco-Berrelleza for technical guidance. This work was supported by the Engineering and Physical Sciences Research Council (EPSRC) EP/N027639/1 to AN; EP/T022205/1, EP/T022167/1 and EP/X035603/1 for computational resources]; and the Physics of Life Network UK [EP/T022000/1 to T. G.]

References

1. A. Marin-Gonzalez, J. G. Vilhena, R. Perez and F. Moreno-Herrero, Q. Rev. Biophys., 2021, 54, e8.
2. J. R. Goñi, A. Pérez, D. Torrents and M. Orozco, Genome Biol., 2007, 8, R263.
3. S. H. Kim, M. Ganji, E. Kim, J. van der Torre, E. Abbondanzieri and C. Dekker, eLife, 2018, 7, e36557.
4. A. Basu, D. G. Bobrovnikov, Z. Qureshi, T. Kayikcioglu, T. T. M. Ngo, A. Ranjan, S. Eustermann, B. Cieza, M. T. Morgan, M. Hejna, H. T. Rube, K.-P. Hopfner, C. Wolberger, J. S. Song and T. Ha, Nature, 2021, 589, 462–467.
5. J. Li, J. M. Sagendorf, T.-P. Chiu, M. Pasi, A. Pérez and R. Rohs, Nucleic Acids Res., 2017, 45, 12877–12887.
6. F. Battistini, A. Hospital, D. Buitrago, D. Gallego, P. D. Dans, J. L. Gelpí and M. Orozco, J. Mol. Biol., 2019, 431, 3845–3859.
7. V. Lioy, A. Cournac, M. Marbouty, S. Duigou, J. Mozziconacci, O. Espéli, F. Boccard and R. Koszul, Cell, 2018, 172, 771–783.
8. T. Hsieh, C. Cattoglio, E. Slobodyanyuk, A. Hansen, O. Rando, R. Tjian and X. Darzacq, Mol. Cell, 2020, 78, 539–553.
9. N. Krietenstein, S. Abraham, S. Venev, N. Abdennur, J. Gibcus, T. Hsieh, K. Parsi, L. Yang, R. Maehr, L. Mirny, J. Dekker and O. Rando, Mol. Cell, 2020, 78, 554–565.
10. J. Curuksu, K. Zakrzewska and M. Zacharias, Nucleic Acids Res., 2008, 36, 2268–2283.
11. G. Rossetti, P. D. Dans, I. Gomez-Pinto, I. Ivani, C. Gonzalez and M. Orozco, Nucleic Acids Res., 2015, 43, 4309–4321.
12. A. Afek, H. Shi, A. Rangadurai, H. Sahay, A. Senitzki, S. Xhani, M. Fang, R. Salinas, Z. Mielko, M. Pufall, G. Poon, T. Haran, M. Schumacher, H. Al-Hashimi and R. Gordan, Nature, 2020, 587, 291–296.
13. A. Pérez, C. Castellazzi, F. Battistini, K. Collinet, O. Flores, O. Deniz, M. Ruiz, D. Torrents, R. Eritja, M. Soler-López and M. Orozco, Biophys. J., 2012, 102, 2140–2148.
14. W. K. Olson, A. A. Gorin, X.-J. Lu, L. M. Hock and V. B. Zhurkin, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 11163–11168.
15. A. A. Kornyshev, D. J. Lee, A. Wynveen and S. Leikin, Nucleic Acids Res., 2011, 39, 7289–7299.
16. A. K. Mazur and M. Maaloum, Nucleic Acids Res., 2014, 42, 14006–14012.
17. A. Marin-Gonzalez, C. L. Pastrana, R. Bocanegra, A. Martín-González, J. G. Vilhena, R. Pérez, B. Ibarra, C. Aicart-Ramos and F. Moreno-Herrero, Nucleic Acids Res., 2020, 48, 5024–5026.
18. Y. Zhang and D. M. Crothers, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 3161–3166.
19. S. Geggier and A. Vologodskii, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 15421–15426.
20. A. Basu, D. Bobrovnikov, B. Cieza, J. Arcon, Z. Qureshi, M. Orozco and T. Ha, Nat. Struct. Mol. Biol., 2022, 29, 1178–1187.
21. C. G. Baumann, S. B. Smith, V. A. Bloomfield and C. Bustamante, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 6185–6190.
22. J. Lipfert, G. M. Skinner, J. M. Keegstra, T. Hensgens, T. Jager, D. Dulin, M. Köber, Z. Yu, S. P. Donkers, F.-C. Chou, R. Das and N. H. Dekker, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15408–15413.
23. G. da Rosa, L. Grille, V. Calzada, K. Ahmad, J. P. Arcon, F. Battistini, G. Bayarri, T. Bishop, P. Carloni, T. Cheatham III, R. Collepardo-Guevara, J. Czub, J. R. Espinosa, R. Galindo-Murillo, S. A. Harris, A. Hospital, C. Laughton, J. H. Maddocks, A. Noy, M. Orozco, M. Pasi, A. Pérez, D. PetkevičiūGerlach, R. Sharma, R. Sun and P. D. Dans, Biophys. Rev., 2021, 13, 995–1005.
24. F. Lankaš, J. Šponer, J. Langowski and T. E. Cheatham, Biophys. J., 2003, 85, 2872–2883.
25. A. Noy and R. Golestanian, J. Phys. Chem. B, 2010, 114, 8022–8031.
26. V. Velasco-Berrelleza, M. Burman, J. W. Shepherd, M. C. Leake, R. Golestanian and A. Noy, Phys. Chem. Chem. Phys., 2020, 22, 19254–19266.
27. M. Pasi, J. H. Maddocks, D. Beveridge, T. C. Bishop, D. A. Case, T. Cheatham, P. D. Dans, B. Jayaram, F. Lankaš, C. Laughton, J. Mitchell, R. Osman, M. Orozco, A. Pérez, D. Petkevičiūtė, N. Spackova, J. Šponer, K. Zakrzewska and R. Lavery, Nucleic Acids Res., 2014, 42, 12272–12283.
28. E. Segal and J. Widom, Curr. Opin. Struct. Biol., 2009, 19, 65–71.
29. T. E. Haran and U. Mohanty, Q. Rev. Biophys., 2009, 42, 41–81.
30. J. S. Mitchell, J. Glowacki, A. E. Grandchamp, R. S. Manning and J. H. Maddocks, J. Chem. Theory Comput., 2017, 13, 1539–1555.
31. A. Noy and R. Golestanian, Phys. Rev. Lett., 2012, 109, 228101.
32. T. Sutthibutpong, S. A. Harris and A. Noy, J. Chem. Theory Comput., 2015, 11, 2768–2775.
33. A. Marin-Gonzalez, J. G. Vilhena, F. Moreno-Herrero and R. Perez, Phys. Rev. Lett., 2019, 122, 048102.
34. D. S. Goodsell and R. E. Dickerson, Nucleic Acids Res., 1994, 22, 5497–5503.
35. S. B. Dixit, F. Pitici and D. L. Beveridge, Biopolymers, 2004, 75, 468–479.
36. H.-S. Koo, H.-M. Wu and D. M. Crothers, Nature, 1986, 320, 501–506.
37. A. Bolshoy, P. McNamara, R. E. Harrington and E. N. Trifonov, Proc. Natl. Acad. Sci. U. S. A., 1991, 88, 2312–2316.
38. H. Dietz, S. M. Douglas and W. M. Shih, Science, 2009, 325, 725–730.
39. S. Park, J. Song and J. S. Kim, Sci. Adv., 2019, 5, eaav4943.
40. T. L. Schmidt and A. Heckel, Nano Lett., 2011, 11, 1739–1742.
41. K. Iric, M. Subramanian, J. Oertel, N. P. Agarwal, M. Matthies, X. Periole, T. P. Sakmar, T. Huber, K. Fahmy and T. L. Schmidt, Nanoscale, 2018, 10, 18463–18467.
42. A. Pérez, F. Lankaš, F. J. Luque and M. Orozco, Nucleic Acids Res., 2008, 36, 2379–2374.
43. W. K. Olson, N. L. Marky, R. L. Jernigan and V. B. Zhurkin, J. Mol. Biol., 1993, 232, 530–554.
44. V. B. Zhurkin, M. Y. Tolstorukov, F. Xu, A. V. Colasanti and W. K. Olson, in Sequence-Dependent Variability of B-DNA, Springer US, 2005, pp. 18–34.
45. A. Balaceanu, D. Buitrago, J. Walther, A. Hospital, P. D. Dans and M. Orozco, Nucleic Acids Res., 2019, 47, 4418–4430.
46. D. Farré-Gil, J. P. Arcon, C. A. Laughton and M. Orozco, Nucleic Acids Res., 2024, gkae444.
47. H. Dohnalová and F. Lankaš, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 12, e1575.
48. D. Case, K. Belfon, I. Ben-Shalom, S. Brozell, D. Cerutti, T. Cheatham III, V. Cruzeiro, T. Darden, R. Duke, G. Giambasu, M. Gilson, H. Gohlke, A. Goetz, R. Harris, S. Izadi, S. Izmailov, K. Kasavajhala, A. Kovalenko, R. Krasny, T. Kurtzman, T. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, V. Man, K. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, A. Onufriev, F. Pan, S. Pantano, R. Qi, D. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. Simmerling, N. Skrynnikov, J. Smith, J. Swails, R. Walker, J. Wang, L. Wilson, R. Wolf, X. Wu, Y. Xiong, Y. Xue, D. York and K. P. A. Kollman, University of California, San Fransisco, 2020.
49. I. Ivani, P. D. Dans, A. Noy, A. Pérez, I. Faustino, A. Hospital, J. Walther, P. Andrio, R. Goñi, A. Balaceanu, G. Portella, F. Battistini, J. L. Gelpí, C. González, M. Vendruscolo, C. A. Laughton, S. A. Harris, D. A. Case and M. Orozco, Nat. Methods, 2015, 13, 55–58.
50. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
51. D. E. Smith and L. X. Dang, J. Chem. Phys., 1994, 100, 3757–3766.
52. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
53. J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
54. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
55. X.-J. Lu and W. Olson, Nucleic Acids Res., 2003, 31, 5108–5121.
56. E. N. Trifonov, R. K. Tan and S. C. T. Harvey, DNA Bending & Curvature, 1988.
57. J. A. Schellman and S. C. Harvey, Biophys. Chem., 1995, 55, 95–114.
58. P. D. Dans, A. Balaceanu, M. Pasi, A. S. Patelli, D. Petkevičiūtė, J. Walther, A. Hospital, G. Bayarri, R. Lavery, J. H. Maddocks and M. Orozco, Nucleic Acids Res., 2019, 47, 11090–11102.
59. T. Dršata, N. Špačková, P. Jurečka, M. Zgarbová, J. Šponer and F. Lankaš, Nucleic Acids Res., 2014, 42, 7383–7394.
60. K. Liebl and M. Zacharias, J. Chem. Theory Comput., 2023, 19, 1529–1536.
61. S. Guilbaud, L. Salomé, N. Destainville, M. Manghi and C. Tardin, Phys. Rev. Lett., 2019, 122, 028102.
62. H.-M. Chuang, J. G. Reifenberger, H. Cao and K. D. Dorfman, Phys. Rev. Lett., 2017, 119, 227802.
63. D. Svozil, P. Hobza and J. Sponer, J. Phys. Chem. B, 2010, 114, 1191–1203.
64. F. Kilchherr, C. Wachauf, B. Pelz, M. Rief, M. Zacharias and H. Dietz, Science, 2016, 353, aaf5508.
65. B. A. Beutel and L. Gold, J. Mol. Biol., 1992, 228, 803–812.
66. H. S. Koo and D. M. Crothers, Proc. Natl. Acad. Sci. U. S. A., 1988, 85, 1763–1767.
67. D. MacDonald, K. Herbert, X. Zhang, T. Polgruto and P. Lu, J. Mol. Biol., 2001, 306, 1081–1098.
68. A. Barbič, D. P. Zimmer and D. M. Crothers, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 2369–2373.
69. D. Strahs and T. Schlick, J. Mol. Biol., 2000, 301, 643–663.
70. A. M. Burkhoff and T. D. Tullius, Nature, 1988, 331, 455–457.
71. A. D. DiGabriele, M. R. Sanderson and T. A. Steitz, Proc. Natl. Acad. Sci. U. S. A., 1989, 86, 1816–1820.
72. A. D. DiGabriele and T. A. Steitz, J. Mol. Biol., 1993, 231, 1024–1039.
73. Z. Bryant, M. D. Stone, J. Gore, S. B. Smith, N. R. Cozzarelli and C. Bustamante, Nature, 2003, 424, 338–341.
74. F. Mosconi, J. F. M. C. Allemand, D. Bensimon and V. Croquette, Phys. Rev. Lett., 2009, 102, 078301.
75. J. Lipfert, J. W. Kerssemakers, T. Jager and N. H. Dekker, Nat. Methods, 2010, 7, 977–980.
76. P. Gross, N. Laurens, L. B. Oddershede, U. Bockelmann, E. J. G. Peterman and G. J. L. Wuite, Nat. Phys., 2011, 7, 731–736.
77. J. Luengo-Márquez, J. Zalvide-Pombo, R. Pérez and S. Assenza, Nanoscale, 2023, 15, 6738–6744.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr02571g

---