Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The influence of drying routes on the properties of anisotropic all-cellulose composite foams from post-consumer cotton clothing†
Carina
Schiele
 a,
Maria-Ximena
Ruiz-Caldas
a,
Maria-Ximena
Ruiz-Caldas
 a,
Tingting
Wu
bc,
Elisabetta
Nocerino
ad,
Agnes
Åhl
a,
Tingting
Wu
bc,
Elisabetta
Nocerino
ad,
Agnes
Åhl
 a,
Aji P.
Mathew
a,
Aji P.
Mathew
 a,
Gustav
Nyström
a,
Gustav
Nyström
 *b,
Lennart
Bergström
*b,
Lennart
Bergström
 *ae and
Varvara
Apostolopoulou-Kalkavoura
*ae and
Varvara
Apostolopoulou-Kalkavoura
 *ab
*ab
aDepartment of Materials and Environmental Chemistry, Stockholm University, SE-10691 Stockholm, Sweden. E-mail: lennart.bergstrom@mmk.su.se; varvara.apostolopoulou@mmk.su.se
bCellulose & Wood Materials Laboratory, Empa, Überlandstrasse 129, CH-8600, Dübendorf, Switzerland. E-mail: gustav.nystroem@empa.ch
cInstitute of Sustainability for Chemicals, Energy and Environment (ISCE2), Agency for Science, Technology and Research (A*STAR), 1 Pesek Road, Jurong Island 627833, Singapore
dLaboratory for Neutron Scattering and Imaging, Paul Scherrer Institute (PSI), Villigen, CH-5232, Switzerland
eWallenberg Initiative Materials Science for Sustainability, Department of Materials and Environmental Chemistry, Stockholm University, 114 18 Stockholm, Sweden
First published on 27th June 2024
Abstract
Biopolymer-based functional materials are essential for reducing the carbon footprint and providing high-quality lightweight materials suitable for packaging and thermal insulation. Here, cellulose nanocrystals (CNCs) were efficiently upcycled from post-consumer cotton clothing by TEMPO-mediated oxidation and HCl hydrolysis with a yield of 62% and combined with wood cellulose nanofibrils (CNFs) to produce anisotropic foams by unidirectional freeze-casting followed by freeze drying (FD) or supercritical-drying (SCD). Unidirectional freeze-casting resulted in foams with aligned macropores irrespective of the drying method, but the particle packing in the foam wall was significantly affected by how the ice was removed. The FD foams showed tightly packed and aligned CNC and CNF particles while the SCD foams displayed a more network-like structure in the foam walls. The SCD compared to FD foams had more pores smaller than 300 nm and higher specific surface area but they were more susceptible to moisture-induced shrinkage, especially at relative humidities (RH) > 50%. The FD and SCD foams displayed low radial thermal conductivity, and the FD foams displayed a higher mechanical strength and stiffness in compression in the direction of the aligned particles. Better understanding how drying influences the structural, thermal, mechanical and moisture-related properties of foams based on repurposed cotton is important for the development of sustainable nanostructured materials for various applications.
Introduction
The design of safe and functional materials from renewable feedstocks for high-performance is a key challenge. As a non-toxic, biodegradable and highly abundant material, cellulose is a strong candidate for such endeavors. Cellulose nanomaterials (CNMs) extracted from wood have been assembled into functional and bio-based materials such as films, coatings, beads, capsules, continuous fibers, hydrogels, cushioning materials, foams and aerogels.1,2 There is a growing interest to replace or reduce the use of virgin resources (i.e. wood) and instead extract CNMs from post-consumer clothing, e.g. in the form of cellulose nanocrystals (CNCs).3 Using post-consumer clothing as a CNM source can increase the sustainability of CNM extraction,4 and also partly mitigate the growing problem of textile waste.5Assembling upcycled textile fibers into functional and lightweight materials such as packaging and insulation materials that can replace fossil-based materials can also reduce the carbon footprint. However, it is essential that the biobased and upcycled foams display mechanical robustness, high moisture resilience and a low thermal conductivity. In porous materials like foams and aerogels, the thermal conductivity is mostly determined by the heat transfer via gas and solid conduction.6 Both modes can be influenced by the composition, density and structure of the material with the pore size playing a major role on the gas conduction and the type of bonds and interfaces in the solid part determining the solid conduction.7–10
The ability to attract and hold water plays an important part in the moisture resilience of a material and is especially important for materials based on cellulose which is a well-known hygroscopic material. The composition and functional groups of a material as well as its particular structure have a big influence on its interaction with moisture.11,12
The mechanical robustness and load-bearing ability of a material is determined by the strength of the chemical bonds present in it as well as the occurrence of defects and dislocations in the alignment of the material.13
Foams prepared by unidirectional freeze-casting, under a temperature gradient result in highly anisotropic structures, typically featuring aligned columnar macropores.14,15 Ambient drying is the most sustainable drying technique16 but susceptible to drying-induced shrinkage and deformations. Freeze drying (FD) and supercritical drying (SCD) are known to avoid capillary forces and therefore prevent shrinkage and keep structural integrity.17,18 While studies on isotropic polysaccharide-based porous materials prepared via supercritical drying revealed smaller pore sizes and a larger surface area than porous materials with the same composition prepared via freeze drying,19–21 studies on anisotropic materials are sparse.15 Previous studies confirmed that anisotropic CNF-based foams can be prepared following both drying strategies by applying unidirectional ice-templating prior to drying which result in foams with aligned macropores due to the large ice-crystals.15,22,23 Anisotropic cotton CNC-based foams have also been prepared by freeze-casting and freeze drying.18
In this study, we prepared anisotropic composite foams from upcycled post-consumer cotton CNCs and wood-derived CNFs with different densities by unidirectional freeze-casting and subsequent drying. The effect of freeze drying and supercritical drying on the structural features such as pore size, alignment and surface area of the foams were connected to the thermal conductivity, mechanical properties and moisture resilience.
The FD foams displayed higher macropore alignment, bigger pore sizes, lower surface area and a higher moisture resilience than the SCD foams. The nanoparticles inside the foam wall were aligned for the FD foams but not for the SCD foams that correlated well with the higher Young's Modulus and toughness, and lower radial thermal conductivity of the FD foams.
Experimental section
Materials
Sorted and clean post-consumer cotton clothing was provided by Wargön Innovation, primarily consisting of dyed T-shirts and other tops based on visual assessment. Never-dried sulfite softwood cellulose pulp (Domsjö dissolving Plus) was provided by Domsjö Fabriker AB (Aditya Birla Domsjö, Sweden). Sodium hypochlorite (NaClO, 6–14% Fisher Scientific), 2,2,6,6-tetramethyl-1-piperidinyloxy free radical (TEMPO, ≥98%, Alfa Aesar), standardized sodium hydroxide (NaOH, 0.1 M Fisher Chemical™), sodium hydroxide pellets (NaOH, >98% Honeywell Fluka™), sodium bromide (NaBr, BioUltra, P99.5%, Sigma Aldrich), hydrochloric acid (HCl, 37 wt% AnalaR® Normapur®) were used as received. Deionized (DI) water was used for all solutions and dispersions.Extraction of CNCs and CNFs
The post-consumer cotton clothing was cut into ∼1 cm2 pieces using a paper guillotine. No pretreatment was performed prior to the TEMPO-oxidation. The cotton derived TEMPO-oxidized cellulose nanocrystals (CNCs) were prepared by TEMPO-mediated oxidation followed by HCl hydrolysis as described in our previous work.18 In brief, square pieces of cotton were oxidized with NaClO using TEMPO/NaBr as a catalyst/co-catalyst system. NaClO was added dropwise, maintaining the pH above 10 with 1 M NaOH. After four hours, the mixture was vacuum-filtered through a 5 μm nylon mesh and rinsed with deionized water. The oxidized cotton was then hydrolyzed with 4 M HCl at 80 °C for four hours, followed by cooling in an ice bath. The suspension was cleaned by centrifugation (Sorvall LYNX 6000, Thermo Scientific, USA) for 10 min and 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000g (11
000g (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880 rpm). Further, the sediment was dialyzed for about 8–10 days until the conductivity of the dialysis water was below 2 μS cm−1 for two consecutive days. The clean dispersion was immersed in an ice bath and sonicated at 60% of amplitude with an on/off pulse of 2 s for 10 min using an ultrasonic homogenizer (500 W, 20 kHz, Q500, Qsonica). The CNCs were neutralized with NaOH until reaching a pH of 7.8. The starting CNC dispersion was concentrated to 9 wt% using a rotary evaporator at 60 °C under vacuum. The CNC yield was calculated from the dry mass recovered after the TEMPO-mediated oxidation and the HCl hydrolysis. The yield was calculated according to the following equation with the reported value being the average of three batches:
880 rpm). Further, the sediment was dialyzed for about 8–10 days until the conductivity of the dialysis water was below 2 μS cm−1 for two consecutive days. The clean dispersion was immersed in an ice bath and sonicated at 60% of amplitude with an on/off pulse of 2 s for 10 min using an ultrasonic homogenizer (500 W, 20 kHz, Q500, Qsonica). The CNCs were neutralized with NaOH until reaching a pH of 7.8. The starting CNC dispersion was concentrated to 9 wt% using a rotary evaporator at 60 °C under vacuum. The CNC yield was calculated from the dry mass recovered after the TEMPO-mediated oxidation and the HCl hydrolysis. The yield was calculated according to the following equation with the reported value being the average of three batches: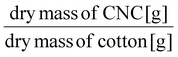 | (1) |
The wood derived TEMPO-oxidized cellulose nanocrystals (CNCs) were prepared by TEMPO-mediated oxidation followed by mechanical defibrillation as described previously.22
Preparation of anisotropic foams
Composite CNC and CNF anisotropic foams with varying densities were prepared by ice-templating. The composite CNC and CNF foams were prepared from 1, 3 and 5 wt% dispersions in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5
1, 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 9
1 and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 CNC
1 CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF mass ratios respectively. The dispersions of CNMs were ice-templated in molds with copper bottoms and Teflon walls placed on a copper block immersed in liquid nitrogen ensuring unidirectional freezing from the bottom to the top. Two different mold sizes (1.5 × 2.0 cm and 4.0 × 2.5 cm) were used, adding 5 and 30 g of dispersions, respectively.
CNF mass ratios respectively. The dispersions of CNMs were ice-templated in molds with copper bottoms and Teflon walls placed on a copper block immersed in liquid nitrogen ensuring unidirectional freezing from the bottom to the top. Two different mold sizes (1.5 × 2.0 cm and 4.0 × 2.5 cm) were used, adding 5 and 30 g of dispersions, respectively.
The frozen dispersions were dried by two different routes: FD and SCD. The anisotropic FD foams were obtained through ice sublimation at −60 °C and 0.024 mbar over four days, using a freeze dryer (Christ Alpha 1-2LDplus, Germany). Prior to the SCD, the unidirectionally frozen dispersions were placed in 99.9% ethanol solution to allow the solvent exchange from water to ethanol due to its miscibility with carbon dioxide used for the supercritical drying. In order to achieve an ethanol content of >99.5% in the alcogels, the solvent exchange using fresh ethanol had to be repeated 4 times. The exchanged alcogels were then supercritically dried using the Separex Supercritical Fluid Technology (France). The first step of SCD process was the pressurization to reach 120 bar and 45–47 °C which lasted 45 min. The main step was the drying, performed at 120 bar and 45–47 °C and lasted 5–10 h depending on the number of samples loaded. The last step included 1 h depressurization. There was shrinkage observed after the supercritical drying which is estimated to be about 39%, 46%, 66% for CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF_9
CNF_9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1_SCD, CNC
1_SCD, CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF_5
CNF_5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1_SCD and CNC
1_SCD and CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF_1
CNF_1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1_SCD, respectively and 19%, 26%, 32% for the freeze dried foams CNC
1_SCD, respectively and 19%, 26%, 32% for the freeze dried foams CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF_9
CNF_9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1_FD, CNC
1_FD, CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF_5
CNF_5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1_FD and CNC
1_FD and CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF_1
CNF_1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1_FD, respectively.
1_FD, respectively.
Characterization
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. The samples were prepared by peeling off a layer of a dried foam wall layer with a sticky carbon tape on the sample holder and coating with Au particles using a gold sputter JFC 1200 fine coater (Japan), operating at 10 mA for 60 seconds, yielding particles in the size range 5 to 15 nm.
000. The samples were prepared by peeling off a layer of a dried foam wall layer with a sticky carbon tape on the sample holder and coating with Au particles using a gold sputter JFC 1200 fine coater (Japan), operating at 10 mA for 60 seconds, yielding particles in the size range 5 to 15 nm.
The degree of orientation of the columnar macropores was assessed using the “OrientationJ” plugin of Fiji. It compared the orientation angle of a pixel with respect to its neighboring pixel. The resulting histograms of the frequency plotted against the orientation angle, were then fitted to a Gaussian curve and the full width half maximum (fwhm) of the curve was derived. The fwhm was then used to determine the orientation degree following eqn (2).
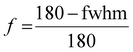 | (2) |
The SCD samples were also tested for CO2 adsorption at 0 °C and 1 atm following the same protocol for the degassing. The CO2 adsorption was repeated 5 consecutive times for each sample.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF-1
CNF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1:FD) 10 mW and 20s (CNC
1:FD) 10 mW and 20s (CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF-1
CNF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1:SCD), 10 mW and 40s (CNC
1:SCD), 10 mW and 40s (CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF-5
CNF-5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1:FD, CNC
1:FD, CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF-5
CNF-5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1:SCD, CNC
1:SCD, CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF-9
CNF-9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1:SCD), 15 mW and 40s (CNC
1:SCD), 15 mW and 40s (CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF-5
CNF-5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1:FD,) respectively. The measurements were conducted at 295 K and 7, 20, 35, 50, 65 and 80% RH in a customized cell as described before.24 The radial thermal diffusivity and conductivity were determined using the volumetric specific heat capacity of the foams at the specific RH as input information. The latter was derived from the specific heat capacity (Cp) of the wet solid material (Cpwet) derived from eqn (3) multiplied with the density of the wet foam derived from eqn (4).
1:FD,) respectively. The measurements were conducted at 295 K and 7, 20, 35, 50, 65 and 80% RH in a customized cell as described before.24 The radial thermal diffusivity and conductivity were determined using the volumetric specific heat capacity of the foams at the specific RH as input information. The latter was derived from the specific heat capacity (Cp) of the wet solid material (Cpwet) derived from eqn (3) multiplied with the density of the wet foam derived from eqn (4).| Cpwet = (1 − H2Ow) × Cpdry + CpH2O × H2Ow | (3) |
 | (4) |
Here H2Ow is the wt% of water at a certain RH derived from the moisture uptake experiments, CpH2O is the Cp of water (4181 J kg−1 K−1) and Cpdry is the Cp of the dry solid. Isotropic reference samples were prepared via crash freezing in liquid nitrogen and measured with the isotropic mode of the Hot Disk to determine the volumetric Cp of the isotropic reference sample which was divided by its density to derive Cpdry. Furthermore is mdry the mass of the dry foam, mH2O the mass of water adsorbed on the foam, Vdry the volume of the dry foam and shrink% the percentage of volume shrinkage. The axial thermal diffusivity and conductivity were obtained using the software provided by Hot Disk. The error bars of the thermal conductivity measurements represent the sample standard deviation of n = 15. The super-insulating reference material (polyurethane aerogel) was purchased from the Center of Applied Energy Research e.V.25,26
To derive the scale factor C, proportional to the specific surface area, the high q region of SAXS 1D patterns (0.07 Å−1 < q < 0.14 Å−1 for FD foams, 0.10 Å−1 < q < 0.14 Å−1 for SCD foams) was fitted with the Porod model.27–29
 | (5) |
For the orientation degree f, the 2D scattering pattern was azimuthally integrated and fitted to a Gaussian curve. The fwhm of the intensity was used to calculate f.
Results and discussion
CNCs from post-consumer cotton clothing (Fig. 1a) and CNFs from wood (Fig. 1b) were used as building blocks for the preparation of anisotropic foams by unidirectional ice-templating (Fig. 2a). Due to the very high cellulose content of cotton clothing (>90%),30 the processing into CNCs did not require any time- and energy-demanding pretreatment of the clothing. The wood CNFs were extracted from sulfite softwood pulp by TEMPO-mediated oxidation followed by grinding as described in previous work.22,23 Both cotton CNCs and wood CNFs were extracted using the same chemicals-to-cellulose ratio and had COO− functional groups on the C6 of cellulose and Na+ as counter-ion. However, as the crystallite size of cotton and wood differ,31 the degree of substitution of the C6 is not the same resulting in different surface charges for the two CNMs. Cotton CNCs and wood CNFs had a surface charge of 1142 ± 90 and 1646 ± 28 mmol COO− per kilogram of cellulose, respectively (Fig. S1a and b†). The surface charge of the oxidized cotton CNCs corresponds well to the highest value reported for functionalization of the C6 of cellulose in cotton.31 Cotton clothing-derived CNCs exhibited a larger diameter (5.8 ± 2.6 nm) than wood-derived CNFs (2.7 ± 0.9 nm). This difference is attributed to the larger crystallite size of cotton compared to wood pulp32 (Fig. 1 and Fig. S2†). Conversely, the aspect ratio was smaller for cotton clothing CNCs (29 ± 13) than for wood CNFs (120 ± 91), due to the different preparation methods of acidic hydrolysis and mechanical fibrillation, respectively. Since sodium hypochlorite, a cost-effective bleaching agent,33 was used as oxidizing agent in the TEMPO-mediated oxidation the dye molecules of the cotton clothing were degraded resulting in CNCs with a light-yellow haze.Aqueous dispersions of CNCs and CNFs with different solid contents (1 wt%, 3 wt% and 5 wt%) and different CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF mass ratios (1
CNF mass ratios (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5
1, 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 9
1 and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) were unidirectional freeze cast (Fig. 2a) and either freeze dried (Fig. 2b) or subjected to ethanol exchange to allow subsequent supercritical drying with CO2 (Fig. 2c). The CNFs, even at small quantities (0.5 wt% in dispersion), ensured the integrity of the alcogels during the ice-to-ethanol exchange step due to the fibrils’ large aspect ratios and entanglements. On the other hand, ice-templated specimens made entirely from CNCs did not result in self-standing alcogels, which can be attributed to the weak network formation at low and intermediate concentrations of the rigid rod-like CNCs. We have investigated the properties and structural features of composite foams of three different compositions (and densities) that were prepared by either FD (Fig. 2d) or SCD (Fig. 2e) resulting in six different foams (Table S1†). The FD foams (Fig. 2g and Fig. S3†) exhibited a more ordered structure compared to the SCD ones (Fig. 2f and Fig. S3†) resulting in clearly defined honeycomb macropores. The honeycomb structures of the FD foams show a higher resemblance with those of unidirectionally freeze-cast and freeze dried foams prepared from CNFs than those prepared by CNCs, which give honeycomb structures with a higher aspect ratio.34–36 This suggests that in our CNC–CNF composite foams, the macropore formation is dominated by the entangled CNF network, which restrains the ice crystal growth to a honeycomb morphology even though the CNC loading is high. The CNCs, which do not entangle are expected to decorate and reinforce the CNF network but not contribute to the morphology.37
1) were unidirectional freeze cast (Fig. 2a) and either freeze dried (Fig. 2b) or subjected to ethanol exchange to allow subsequent supercritical drying with CO2 (Fig. 2c). The CNFs, even at small quantities (0.5 wt% in dispersion), ensured the integrity of the alcogels during the ice-to-ethanol exchange step due to the fibrils’ large aspect ratios and entanglements. On the other hand, ice-templated specimens made entirely from CNCs did not result in self-standing alcogels, which can be attributed to the weak network formation at low and intermediate concentrations of the rigid rod-like CNCs. We have investigated the properties and structural features of composite foams of three different compositions (and densities) that were prepared by either FD (Fig. 2d) or SCD (Fig. 2e) resulting in six different foams (Table S1†). The FD foams (Fig. 2g and Fig. S3†) exhibited a more ordered structure compared to the SCD ones (Fig. 2f and Fig. S3†) resulting in clearly defined honeycomb macropores. The honeycomb structures of the FD foams show a higher resemblance with those of unidirectionally freeze-cast and freeze dried foams prepared from CNFs than those prepared by CNCs, which give honeycomb structures with a higher aspect ratio.34–36 This suggests that in our CNC–CNF composite foams, the macropore formation is dominated by the entangled CNF network, which restrains the ice crystal growth to a honeycomb morphology even though the CNC loading is high. The CNCs, which do not entangle are expected to decorate and reinforce the CNF network but not contribute to the morphology.37
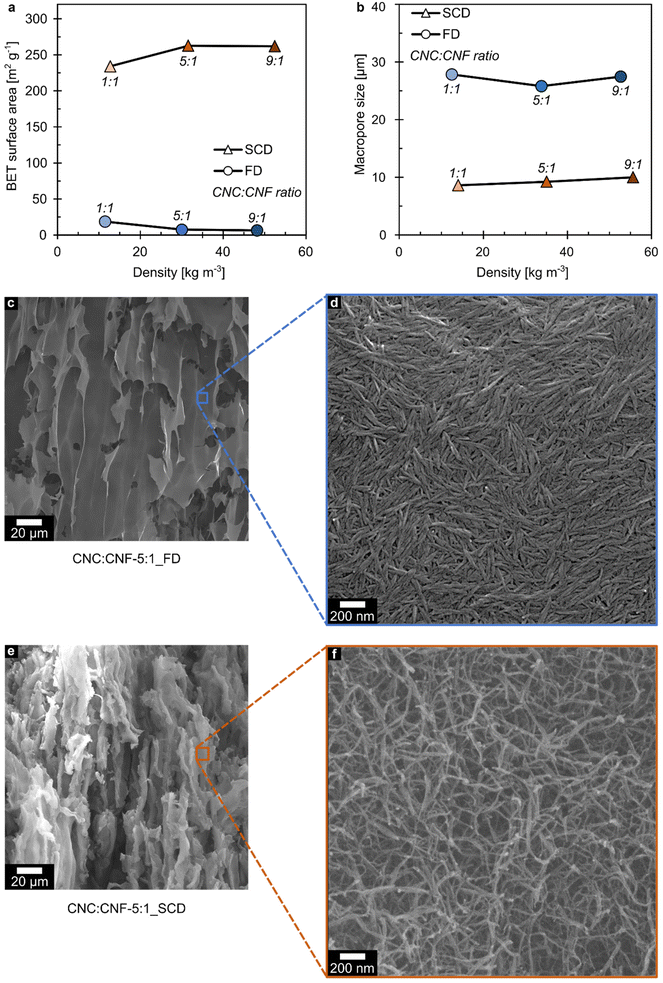
Both the FD and SCD foams possess a hierarchical pore structure consisting of macropores and nanosized pores. The macropores are templated by the unidirectional grown ice crystals during ice-templating while nanosized pore structures are created in the foam walls.15,22,38 The SCD foams displayed a much larger fraction of nanosized pores (Fig. S4†) and higher BET specific surface area than the FD foams (Fig. 3a and Table S2†). The BET specific surface area ranged between 234–263 m2 g−1 for the SCD foams and was about 20-fold lower for the FD foams with 6–19 m2 g−1. A similar trend concerning the specific surface area with respect to the CNC loading and foam density was found by small-angle X-ray scattering (SAXS) experiments. 1D SAXS patterns were fitted with a Porod function to derive a scale factor C which is proportional to the specific surface area (Table S3†). Since the SCD foams displayed a high surface area, their CO2-uptake via physisorption at standard pressure and 273 K was investigated for CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF-5
CNF-5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1_SCD and CNC
1_SCD and CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF-9
CNF-9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1_SCD and ranged between 0.379–0.385 mmol g−1 (Table S2†). These values lie in the same span as the CO2 uptake of hydrothermally carbonized chitosan.39 Although the CO2-uptake decreased slightly in the following cycles, it stayed around 0.38 mmol g−1 for up to four cycles (Fig. S5†). At the same time, all the SCD foams had smaller macropore sizes (8–10 μm) and narrower macropore distribution compared to the FD foams (26–38 μm) (Fig. 3b and Table S2†). High-resolution SEM images of the foam walls confirm the BET surface area and display denser packaging of the nanoparticles in CNC
1_SCD and ranged between 0.379–0.385 mmol g−1 (Table S2†). These values lie in the same span as the CO2 uptake of hydrothermally carbonized chitosan.39 Although the CO2-uptake decreased slightly in the following cycles, it stayed around 0.38 mmol g−1 for up to four cycles (Fig. S5†). At the same time, all the SCD foams had smaller macropore sizes (8–10 μm) and narrower macropore distribution compared to the FD foams (26–38 μm) (Fig. 3b and Table S2†). High-resolution SEM images of the foam walls confirm the BET surface area and display denser packaging of the nanoparticles in CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF-5
CNF-5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1_FD (Fig. 3c and d) while CNC
1_FD (Fig. 3c and d) while CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF-5
CNF-5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1_SCD (Fig. 3e and f) showed a much more network-like structures incorporating small pores. The very low BET specific surface area of the FD foams decreased as a function of density. The densely packed foam walls become even more tightly packed with increasing foam density resulting in lower specific surface area.34 The more network like structure of the SCD foams however behaves differently allowing for more accessible sites with an increase in nanoparticles and therefore a higher surface area with increasing density within the tested density range. It can be speculated that the difference in the foam wall density between the two drying techniques is either caused by local shrinkage and densification during the freeze drying process or by particle-rearrangement in the SCD foams which could appear during the solvent exchange (water–ethanol and/or ethanol–liquid CO2).
1_SCD (Fig. 3e and f) showed a much more network-like structures incorporating small pores. The very low BET specific surface area of the FD foams decreased as a function of density. The densely packed foam walls become even more tightly packed with increasing foam density resulting in lower specific surface area.34 The more network like structure of the SCD foams however behaves differently allowing for more accessible sites with an increase in nanoparticles and therefore a higher surface area with increasing density within the tested density range. It can be speculated that the difference in the foam wall density between the two drying techniques is either caused by local shrinkage and densification during the freeze drying process or by particle-rearrangement in the SCD foams which could appear during the solvent exchange (water–ethanol and/or ethanol–liquid CO2).
The foams with identical composition that had been prepared by FD and SCD showed differences regarding their structural integrity upon moisture exposure. The FD foams adsorbed slightly more water as a function of RH compared to the SCD foams of the same CNC–CNF ratio (Fig. 4a). The larger macropores allow for easier uptake of water. The effect of the macropore size is in accordance with our previous work on the moisture uptake of freeze dried CNM foams40 with reduced moisture-uptake for foams with smaller macropores. As a function of foam density and CNC loading, both the FD and the SCD foams show reduced moisture uptake. The cotton CNCs have a much higher crystallinity index than wood CNF, (Fig. S6 and Table S4†) inhibiting the moisture uptake to a certain extent. Our previous work confirmed that the crystalline cellulose is less susceptible to moisture resulting in lower moisture uptake.40
The moisture induced shrinkage of the FD and SCD foams was also tested as a function of RH. The SCD foams were significantly more susceptible to shrinking at 80% RH compared to their counterpart FD foams (Fig. 4b). This unexpected behavior indicated that the shrinkage is related to both the composition and the structure. Apparently, the highly ordered honeycomb structure of FD foams is more robust to resist the shrinkage induced by high RH. Additionally, it can be stated that the foams with higher density and higher CNC loading were more resistant to shrinkage, with CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF-5
CNF-5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1_FD and CNC
1_FD and CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF-9
CNF-9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1_FD foams showing no significant volume loss up to 80% RH.
1_FD foams showing no significant volume loss up to 80% RH.
Tomographic imaging of CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF-5
CNF-5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 foam at low (35% RH, Fig. 5a) and high RH (90% RH, Fig. 5b) revealed a swelling and collapse of the SCD foam wall structure at high RH while the more ordered and rigid foam wall structure of the FD foam (Fig. 5c and d) displayed no changes upon moisture exposure. The scale factor C indicated an increase in specific surface area with increasing RH for the SCD foams which might be related to the swelling of the foam walls (Table S3†). 2D patterns of both SAXS and wide-angle X-ray scattering (WAXS) analysis displayed an isotropic particle orientation in the case of the SCD foams (Fig. 5e and f), with the nanoparticles having different rotations angles. In contrast, anisotropic particle orientation was found for the FD foams, which displayed a preferred orientation along the ice-growth direction (Fig. 5g and h). The orientation degree of the FD foams derived from the SAXS 2D patterns ranged between 0.89–0.92 (Fig. 5j), which describes bundles of particles. Furthermore, the orientation degree derived from the WAXS 2D patterns was 0.62–0.71 (Fig. 5k), which describes smaller entities like individual particles. The columnar alignment of the macropores was estimated from SEM images of the foams cut along the axial direction applying the OrientationJ plugin of Fiji. They displayed anisotropic behavior for all types of foams although the anisotropy was lower in the SCD foams compared to the FD foams (Fig. 5i). The general decrease in the orientation degree f with increasing density can possibly be related to the solid-content related change in viscosity of the dispersion which become more gel-like impeding the freeze-casting process. This suggests a hierarchical orientation in the foams with an orientation in the particle level and the columnar macropore level. The lack of orientation in the particle level for the SCD foams matches the network-like structure observed in high-resolution SEM while the alignment of the nanoparticles in the foam wall of the FD sample is reflected in their dense packing.
1 foam at low (35% RH, Fig. 5a) and high RH (90% RH, Fig. 5b) revealed a swelling and collapse of the SCD foam wall structure at high RH while the more ordered and rigid foam wall structure of the FD foam (Fig. 5c and d) displayed no changes upon moisture exposure. The scale factor C indicated an increase in specific surface area with increasing RH for the SCD foams which might be related to the swelling of the foam walls (Table S3†). 2D patterns of both SAXS and wide-angle X-ray scattering (WAXS) analysis displayed an isotropic particle orientation in the case of the SCD foams (Fig. 5e and f), with the nanoparticles having different rotations angles. In contrast, anisotropic particle orientation was found for the FD foams, which displayed a preferred orientation along the ice-growth direction (Fig. 5g and h). The orientation degree of the FD foams derived from the SAXS 2D patterns ranged between 0.89–0.92 (Fig. 5j), which describes bundles of particles. Furthermore, the orientation degree derived from the WAXS 2D patterns was 0.62–0.71 (Fig. 5k), which describes smaller entities like individual particles. The columnar alignment of the macropores was estimated from SEM images of the foams cut along the axial direction applying the OrientationJ plugin of Fiji. They displayed anisotropic behavior for all types of foams although the anisotropy was lower in the SCD foams compared to the FD foams (Fig. 5i). The general decrease in the orientation degree f with increasing density can possibly be related to the solid-content related change in viscosity of the dispersion which become more gel-like impeding the freeze-casting process. This suggests a hierarchical orientation in the foams with an orientation in the particle level and the columnar macropore level. The lack of orientation in the particle level for the SCD foams matches the network-like structure observed in high-resolution SEM while the alignment of the nanoparticles in the foam wall of the FD sample is reflected in their dense packing.
The thermal conductivity along the radial and axial (Fig. 6a and b) directions were determined using the transient hot disk method. The hot disk technique was validated in regards to the guarded hot disk technique applied on a super-insulating reference material (Fig. S7†).25,26
The FD foams displayed a significantly higher thermal anisotropy in comparison to the SCD foams as estimated from the ratio of the average axial and radial thermal conductivity (Fig. 6c). The high degree of thermal anisotropy of FD foams can be related to the highly aligned CNMs in the columnar foam walls and the macropore orientation. The thermal conductivity of the foams in the radial direction remained around 25–30 mW m−1 K−1 for densities up to 40 kg m−3 and then increased with increasing densities, which is in line with previous studies on anisotropic CNC-based foams.34 Previous work has related the increase of the radial thermal conductivity with increasing density of the foams with a reduction in interparticle distance that reduces phonon scattering.9 It is interesting to note that the SCD foams displayed a thermal anisotropy that is around 2 although the nanoparticles in the foams wall are not preferentially aligned in the freezing direction (Fig. 5j and Fig. S8†). The relatively low radial thermal conductivity of the SCD foams may be related to the oriented macropores and to the small pores in the foam walls (Fig. 3f and Fig. S4, Table S2†). The CNC–CNF foams in this study displayed a similar thermal conductivity as freeze dried anisotropic cotton-CNC foams of similar density18 and a higher radial thermal conductivity compared to freeze dried anisotropic wood-CNF foams22,41,42 with a lower foam density. It should be noted that the anisotropic all-cellulose composite foams from post-consumer cotton clothing and wood displayed a radial thermal conductivity similar to commercial fossil-based insulation materials such as polyurethane and polystyrene (20–45 mW m−1 K−1).43–45
The FD foams showed a higher Young's modulus (Fig. 6d) and a higher toughness (Fig. 6e) than the SCD foams along the axial direction. The better load-bearing properties of the FD foams compared to the SCD foam can be related to the preferential orientation of the nanoparticles in the FD foams that contrasts to the more isotropic organization of the nanoparticles in the SCD foams. The difference was more pronounced for the foams with higher density and a higher share of cotton CNCs. While the specific Young's modulus (Table S6†) of the FD composite foams increased with increasing density from 35 kN m kg−1 for CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF-1
CNF-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1_FD to 81 kN m kg−1 for CNC
1_FD to 81 kN m kg−1 for CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF-9
CNF-9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1:FD, the SCD composite foams displayed a low specific Young's modulus of 13–14 kN m kg−1 for all compositions. The specific Young's modulus of CNC
1:FD, the SCD composite foams displayed a low specific Young's modulus of 13–14 kN m kg−1 for all compositions. The specific Young's modulus of CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF-9
CNF-9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1:FD is in fact significantly larger than previously reported anisotropic wood-CNC based foams,36 cotton-CNC based foams18 and wood-CNF based foams.46
1:FD is in fact significantly larger than previously reported anisotropic wood-CNC based foams,36 cotton-CNC based foams18 and wood-CNF based foams.46
Conclusion
We have investigated how the properties of foams prepared from post-consumer cotton CNCs and wood-derived CNFs by unidirectional ice-templating depends on the drying method: freeze drying or supercritical-drying. Nitrogen sorption combined with SEM imaging and X-ray scattering showed that the FD foam walls are composed of tightly packed and aligned nanoparticles while the SCD foams displayed a more open and random network structure with no preferential orientation of the CNMs. The SCD foams had a bigger share (1–3% for SCD vs. ≤0.1% for FD) of pores below 300 nm in the foam walls, resulting in at least 12–43 times higher specific surface area than the FD foams. The differences in porosity and particle packing reflected in the moisture resilience, providing the FD foams with lower shrinkage over a wider humidity range in comparison to the SCD foams.The thermal conductivity in the radial direction was lower than in the axial direction for all foams, irrespective of the density, composition and drying method. The thermal anisotropy was relatively large for the FD foams which was related to the highly aligned CNMs in the foams walls but the SCD foams also displayed a thermal anisotropy around 2 despite the lack of preferential orientation of the nanoparticles. The significantly higher specific Young's modulus and specific toughness in the axial direction of the FD foams compared to the SCD foams could also be related to the preferential axial orientation of the CNMs. Overall, the FD foam with a CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNF ratio of 5
CNF ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and a dry density of 34 kg m−3 (at 50% RH) combined high Young's modulus (2600 kPa), low radial thermal conductivity, and strong moisture resilience. Its SCD counterpart with a density of 44 kg m−3 (50% RH) revealed a high surface area (263 m2 g−1) and possibilities towards adsorption application and CO2 uptake (0.38 mmol g−1 after 4 cycles).
1 and a dry density of 34 kg m−3 (at 50% RH) combined high Young's modulus (2600 kPa), low radial thermal conductivity, and strong moisture resilience. Its SCD counterpart with a density of 44 kg m−3 (50% RH) revealed a high surface area (263 m2 g−1) and possibilities towards adsorption application and CO2 uptake (0.38 mmol g−1 after 4 cycles).
The identification of the fundamental differences between the FD and SCD foams, despite their identical chemical composition, paves the way to tailor materials suitable for future applications in adsorption, cushioning, packaging, and thermal management. Additionally, it could be shown that cotton clothing derived CNCs can be successfully prepared into lightweight foams, offering a path to repurpose textile waste.
Author contributions
C. S.: conceptualization, investigation, methodology, data curation, visualisation, validation, formal analysis and writing the original and final draft. M.-X. R.-C.: investigation, methodology and review/editing the final draft. T. W.: methodology and review/editing the final draft. E. N. and A. Å.: investigation, methodology, data curation, validation and review/editing the original and final draft. A. P. M.: resources, funding acquisition, review/editing the final draft. G. N.: conceptualization, resources and review/editing the final draft. L. B: conceptualization, resources, funding acquisition and review/editing the original and final draft. V. A.-K: conceptualization, investigation, methodology, data curation, validation, project administration, funding acquisition and writing the original and final draft. All co-authors: writing/review/editing the final draft.Data availability
The data supporting this article have been included in the main manuscript or as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the financial support from the Stiftelsen Konung Carl XVI Gustafs 50-årsfond för vetenskap, teknik och miljö, 2022, the SSF funded graduate school SwedNess (grant number: SNP21-0004 and GSn15-008) and the Swedish Research Council (grant number: 2023-05572). We also acknowledge support from the Wallenberg Initiative Materials Science for Sustainability (WISE) funded by the Knut and Alice Wallenberg Foundation (KAW). We acknowledge DESY (Hamburg, Germany), a member of the Helmholtz Association HGF, for the provision of experimental facilities. Parts of this research were carried out at PETRA III, and we would like to sincerely thank André Luiz Coelho Conceição for assistance in using P62. Beamtime was allocated for proposal I-20230270 EC.We acknowledge MAX IV Laboratory for time on Beamline ForMAX under Proposal 20230555, and we would like to sincerely thank, Kim Nygård, Mira Viljanen, Samuel McDonald and Jackson Silva for their support during the measurements.
Research conducted at MAX IV, a Swedish national user facility, is supported by the Swedish Research council under contract 2018-07152, the Swedish Governmental Agency for Innovation Systems under contract 2018-04969, and Formas under contract 2019-02496.
The authors would also like to thank Malwine Lühder for her support during the SAXS and tomography measurements, Emma Berling for the support in foam preparation, Thomas Bergmann for support with supercritical drying as well as Enrico Boschi and Luiz Guilherme Garcia Greca for the guidance and support in the EMPA labs. The Swedish Science Council is gratefully acknowledged for the research infrastructure grant (project number: 2021-00318) for the electron microscopy facilities at Stockholm University and Kjell Jansson is thanked for the help when collecting the high-resolution SEM images.
References
- E. Niinivaara and E. D. Cranston, Carbohydr. Polym., 2020, 247, 116664 CrossRef CAS PubMed.
- E. Di Maio, S. Iannace and G. Mensitieri, Supercritical Fluid Science and Technology, Elsevier, 2021, vol. 9, pp. 21–32 Search PubMed.
- M.-X. Ruiz-Caldas, V. Apostolopoulou-Kalkavoura and A. P. Mathew, Cell Rep. Phys. Sci., 2024, 5, 101795 CrossRef CAS.
- M. X. Ruiz-Caldas, V. Apostolopoulou-Kalkavoura, A. K. Hellström, J. Hildenbrand, M. Larsson, A. Jaworski, J. S. M. Samec, P. Lahtinen, T. Tammelin and A. P. Mathew, J. Mater. Chem. A, 2023, 11, 6854–6868 RSC.
- United States Environmental Protection Agency (EPA), Textiles: Material-Specific Data, https://www.epa.gov/facts-and-figures-about-materials-waste-and-recycling/textiles-material-specific-data.
- V. Apostolopoulou-Kalkavoura, P. Munier and L. Bergström, Adv. Mater., 2020, 2001839, 1–17 Search PubMed.
- M. Pfundstein, R. Gellert, M. Spitzner and A. Rudolphi, Insulating Materials, Institut für internationale Architektur-Dokumentation GmbH & Co. KG, 2008 Search PubMed.
- K. Raed, U. Gross, K. Raed and U. Gross, Int. J. Thermophys., 2009, 30, 1343–1356 CrossRef CAS.
- J. A. Diaz, Z. Ye, X. Wu, A. L. Moore, R. J. Moon, A. Martini, D. J. Boday and J. P. Youngblood, Biomacromolecules, 2014, 15, 4096–4101 CrossRef CAS PubMed.
- G. Chen, Int. J. Therm. Sci., 2000, 39, 471–480 CrossRef CAS.
- S. Han, J. Hong, Q. Luo, H. Xu, H. Tan, Q. Wang, J. Tao, Y. Zhou, L. Peng, Y. He, J. Shi, N. Ma, Y. Cheng and H. Su, Atmospheric Chemistry and Physics Discussions, 2021, pp. 1–25 Search PubMed.
- A. Célino, S. Fréour, F. Jacquemin and P. Casari, Front. Chem., 2014, 1, 1–12 RSC.
- M. Piggott, Load Bearing Fibre Composites, Springer, New York, 2007, vol. 2, pp. 40–65 Search PubMed.
- P. Munier, K. Gordeyeva, L. Bergström and A. B. Fall, Biomacromolecules, 2016, 17, 1875–1881 CrossRef CAS PubMed.
- T. Wu, Z. Zeng, G. Siqueira, K. De France, D. Sivaraman, C. Schreiner, R. Figi, Q. Zhang and G. Nyström, Nanoscale, 2020, 12, 7383–7394 RSC.
- C. Antonini, T. Wu, T. Zimmermann, A. Kherbeche, M.-J. Thoraval, G. Nyström and T. Geiger, Nanomaterials, 2019, 9, 1142 CrossRef CAS PubMed.
- T. Budtova, in Cellulose Science and Technology: Chemistry, Analysis, and Applications, 1st edn, 2019, pp. 371–392 Search PubMed.
- M.-X. Ruiz-Caldas, C. Schiele, E. Hadi, M. Andersson, P. Mohammadpour, L. Bergström, A. P. Mathew and V. Apostolopoulou-Kalkavoura, Carbohydr. Polym., 2024, 338, 122212 CrossRef CAS PubMed.
- S. Groult and T. Budtova, Carbohydr. Polym., 2018, 196, 73–81 CrossRef CAS PubMed.
- K. Sakai, Y. Kobayashi, T. Saito and A. Isogai, Sci. Rep., 2016, 6, 20434 CrossRef PubMed.
- O. Korhonen and T. Budtova, Composites, Part A, 2020, 137, 106027 CrossRef CAS.
- V. Apostolopoulou-Kalkavoura, S. Hu, N. Lavoine, M. Garg, M. Linares, P. Munier, I. Zozoulenko, J. Shiomi and L. Bergström, Matter, 2021, 4, 276–289 CrossRef CAS.
- K. Kriechbaum, P. Munier, V. Apostolopoulou-Kalkavoura and N. Lavoine, ACS Sustainable Chem. Eng., 2018, 6, 11959–11967 CrossRef CAS.
- V. Apostolopoulou-Kalkavoura, K. Gordeyeva, N. Lavoine and L. Bergström, Cellulose, 2018, 25, 1117–1126 CrossRef CAS.
- Center of Applied Energy Research , Reference Materials, https://en.cae-zerocarbon.de/Thermal-Reference-Material.html, (accessed 16 April 2024).
- H.-P. Ebert, S. Braxmeier, G. Reichenauer, F. Hemberger, F. Lied, D. Weinrich and M. Fricke, Int. J. Thermophys., 2021, 42, 21 CrossRef CAS.
- L. A. Feigin and D. I. Svergun, Structure Analysis by Small-Angle X-Ray and Neutron Scattering, Plenum Press, New York, 1987 Search PubMed.
- G. Porod, Kolloid-Z., 1951, 124, 83–114 CrossRef CAS.
- SasView , Porod function, https://www.sasview.org/docs/old_docs/4.1.2/user/models/porod.html, (accessed 16 April 2024).
- Z. Wang, Z. Yao, J. Zhou and Y. Zhang, Carbohydr. Polym., 2017, 157, 945–952 CrossRef CAS PubMed.
- Y. Okita, T. Saito and A. Isogai, Biomacromolecules, 2010, 11, 1696–1700 CrossRef CAS PubMed.
- K. Daicho, K. Kobayashi, S. Fujisawa and T. Saito, Biomacromolecules, 2020, 21, 939–945 CrossRef CAS PubMed.
- T. V. Bommaraju, Water Qual. Res. J., 1995, 30, 339–361 CrossRef CAS.
- V. Apostolopoulou-Kalkavoura, P. Munier, L. Dlugozima, V.-L. Heuthe and L. Bergström, Sci. Rep., 2021, 11, 18685 CrossRef CAS PubMed.
- P. Munier, K. Gordeyeva, L. Bergström and A. B. Fall, Biomacromolecules, 2016, 17, 1875–1881 CrossRef CAS PubMed.
- C. Schiele, A. Di, S. E. Hadi, P. K. B. Rangaiah, R. Augustine and L. Bergström, Adv. Mater. Interfaces, 2024, 11, 2300996 CrossRef CAS.
- S. Gupta, F. Martoïa, L. Orgéas and P. J. J. Dumont, Appl. Sci., 2018, 8, 2463 CrossRef CAS.
- B. Wicklein, A. Kocjan, G. Salazar-Alvarez, F. Carosio, G. Camino, M. Antonietti and L. Bergström, Nat. Nanotechnol., 2015, 10, 277–283 CrossRef CAS PubMed.
- J. A. O. Chagas, G. O. Crispim, B. P. Pinto, R. A. S. San Gil and C. J. A. Mota, ACS Omega, 2020, 5, 29520–29529 CrossRef CAS PubMed.
- M. Garg, V. Apostolopoulou-Kalkavoura, M. Linares, T. Kaldéus, E. Malmström, L. Bergström and I. Zozoulenko, Cellulose, 2021, 28, 9007–9021 CrossRef CAS.
- A. Di, C. Schiele, S. E. Hadi and L. Bergström, Adv. Mater., 2023, 35, 2305195 CrossRef CAS PubMed.
- K. Kriechbaum, V. Apostolopoulou-Kalkavoura, P. Munier and L. Bergström, ACS Sustainable Chem. Eng., 2020, 8, 17408–17416 CrossRef CAS PubMed.
- B. Petter Jelle, Energy Build., 2011, 43, 2549–2563 CrossRef.
- M. Jerman and R. Černý, Energy Build., 2012, 53, 39–46 CrossRef.
- U. Jarfelt, O. Ramnäs, U. Jarfelt and O. Ramnäs, 0th International Symposium on District Heating and Cooling Sektion 6 a Heat distribution-pipe properties Thermal conductivity of polyurethane foam Best performance.
- P. Munier, V. Apostolopoulou-Kalkavoura, M. Persson and L. Bergström, Cellulose, 2020, 27, 10825–10836 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr01720j |
| This journal is © The Royal Society of Chemistry 2024 |