Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The role of fluocerite in the genesis of bastnäsite: mechanistic insights and transformation pathways†
Luca
Terribili
 *a,
Remi
Rateau
*a,
Remi
Rateau
 a,
Melanie
Maddin
a and
Juan Diego
Rodriguez-Blanco
ab
a,
Melanie
Maddin
a and
Juan Diego
Rodriguez-Blanco
ab
aDepartment of Geology, School of Natural Sciences, Trinity College Dublin, College Green, Dublin D02PN40, Ireland. E-mail: terribil@tcd.ie
biCRAG, Department of Geology, School of Natural Sciences, Trinity College Dublin, College green, Dublin D02PN40, Ireland
First published on 12th June 2024
Abstract
Fluocerite is a rare earth element (REE) fluoride found as an accessory mineral in magmatic-hydrothermal REE ore deposits, including alkaline complexes and carbonatites, where it is often associated with REE-fluorocarbonates. This study investigates the crystallisation kinetics, mechanisms and energetics of fluocerite (REEF3) and its role as a precursor phase of bastnäsite, one of the key minerals used for the extraction of REE. Fluocerite was synthesized by reacting pure fluorite (CaF2) with La-, Ce- and Nd-bearing solutions at temperatures ranging from ambient to low hydrothermal (30–90 °C). The synthetic fluocerites were then placed in contact with Na2CO3 solutions at temperatures up to 200 °C. A combined approach using powder X-ray diffraction and scanning electron microscopy with energy dispersive spectroscopy was used to determine the nature and quantify the crystallising solids. Our findings reveal a temperature-dependent fluorite–fluocerite transformation, with completion observed within 1 hour at 90 °C and extending to around 30 days at 30 °C. The rate of crystallisation decreases proportionally with the atomic number of the rare earth elements. On the other hand, the carbonation reaction of fluocerite exhibits a significantly slower rate, by ∼3 orders of magnitude, in comparison to the fluorite–fluocerite transformation, regardless of temperature conditions. The synthetic La, Ce and Nd fluocerites transformed into bastnäsite at all temperatures, also forming cerianite (CeO2) in the Ce-bearing experiments and metastable kozoite, NdCO3OH(orth), in the Nd-bearing experiments. Activation energies of fluocerite nucleation increase proportionally with the ionic radii of the REE (81 ± 6 (La); 84 ± 5 (Ce), 96 ± 10 (Nd) kJ mol−1), while the activation energies associated with fluocerite crystallisation are slightly higher for La (90 ± 12 kJ mol−1) and similar for Ce and Nd (76 ± 12 and 72 ± 8 kJ mol−1, respectively).
Introduction
The peculiar electromagnetic properties of the rare earth elements1–5 make them indispensable in high-tech industries and clean energy applications (i.e., from wind turbines to rechargeable electric car batteries).6–8 However, REE are considered as critical resources because of the concerns over potential supply disruptions and looming shortages in the near future.9There are a wide range of ore deposits where REE can be found. Among them there are magmatic-hydrothermal ones, including alkaline complexes and carbonatites4,10,11 of which an example is the Bayan Obo REE deposit in China, the largest known in the world.3,4,10–12 These kinds of deposits can also constitute ideal sources for REE-enriched hydrothermal fluids, leading to deposits containing both primary igneous and hydrothermal REE mineralization.13 Hydrothermal aqueous fluids are of primary importance in the post-magmatic phase formation of carbonatite and alkaline associated REE deposits11,12,14,15 mobilising the REE and concentrate them, in some cases even to economic level.10–12,16 Nevertheless, REE could require an atypical hydrothermal activity such as, for example, the presence of hydrothermal fluids containing significant amounts of F and Cl.10,11,13 The enrichment in F in the hydrothermal fluids in carbonatite and alkaline REE deposits is thought to be produced by fluorite and fluorocarbonates (i.e. bastnäsite, synchysite and parisite)12 which are common and important constituents of these deposits.11,12,14,17–22
One accessory mineral found in magmatic-hydrothermal REE ore deposits is fluocerite, a fluoride mineral with chemical formula REEF3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 that can be associated with monazite, xenotime, REE-bearing fluorite, bastnäsite, cerianite, synchysite, samarskite, zircon, thorite, allanite, cerite or gadolinite.23,24 Fluocerite is LREE enriched12,25,26 and usually displays the following order of preference for the REE: Ce > La > Nd.25 Even if fluocerite is not as common as fluorocarbonates in nature it has been documented in several locations worldwide but always as a minor phase (e.g.,12,16,17,19,23,24,26–31). It has also been suggested that the formation of fluorocarbonates and cerianite (CeO2) may have involved the carbonation and oxidation of a fluocerite precursor.12,16,24,29 This hypothesis could shed light on the difference between natural observations and the results anticipated by experimental studies. Fluocerite is typically found in limited quantities in rare earth element REE-bearing deposits, whereas experimental studies predict its abundant precipitation in F- and REE-enriched hydrothermal fluids.12,32,33
16 that can be associated with monazite, xenotime, REE-bearing fluorite, bastnäsite, cerianite, synchysite, samarskite, zircon, thorite, allanite, cerite or gadolinite.23,24 Fluocerite is LREE enriched12,25,26 and usually displays the following order of preference for the REE: Ce > La > Nd.25 Even if fluocerite is not as common as fluorocarbonates in nature it has been documented in several locations worldwide but always as a minor phase (e.g.,12,16,17,19,23,24,26–31). It has also been suggested that the formation of fluorocarbonates and cerianite (CeO2) may have involved the carbonation and oxidation of a fluocerite precursor.12,16,24,29 This hypothesis could shed light on the difference between natural observations and the results anticipated by experimental studies. Fluocerite is typically found in limited quantities in rare earth element REE-bearing deposits, whereas experimental studies predict its abundant precipitation in F- and REE-enriched hydrothermal fluids.12,32,33
The literature on fluocerite primarily focuses on natural samples, mentioning its presence in specific ore deposits and occasionally delving into its chemistry, crystal orientation, and formation conditions in detail.12,23–26,31,34 Only a few experimental studies have dealt with its synthesis16,35 or its occurrence as a secondary phase.11 To date, and to the best of our knowledge there is no experimental work addressing the kinetics and mechanisms of fluocerite formation nor investigating its potential role as precursor of REE-fluorocarbonates. The present work will try to fill this knowledge gap and contribute to shed light on the crystallisation mechanisms of REE-fluorocarbonates, which are still unclear.16 Enhancing our understanding of this topic will contribute to further advancements in comprehending the complex mineralisation processes taking place in REE-bearing deposits such as carbonatites.36,37
We present a comprehensive multi-stage experimental investigation into the kinetics and mechanisms of La-, Ce-, and Nd-bearing fluocerite crystallisation, encompassing reactions involving fluorite and their carbonation processes across a spectrum of temperatures, from ambient to low hydrothermal conditions. Our study does not only elucidate the intricate processes involved in fluocerite formation processes but also underscores the significance of the fluorine ion in the crystallization of bastnäsite.
Materials and methods
In order to study the kinetics and mechanisms which rule the transformation reaction fluorite–fluocerite–bastnäsite two set of experiments were carried out. The first set involved the fluorite–fluocerite transformation while the second focused on the fluocerite–bastnäsite one. The fluorite–fluocerite experiments were carried out at 30, 50, 70, and 90 °C by adding 0.5 g of pure fluorite powder (CaF2) in a glass bottle reactor to 80 mL of 50 mM La-, Ce- or Nd-bearing aqueous solutions, preheated to specific temperatures. The reactors were then sealed and placed in a preheated oven. All the solutions were prepared using reagent grade REE nitrate hexahydrates (La(NO3)3·6H2O, Ce(NO3)3·6H2O, Nd(NO3)3·6H2O; Sigma-Aldrich 99.99% trace metals basis) and pure deionized (Milli-Q) water.The fluocerite–bastnäsite experiments were carried out at 50, 90 and 200 °C by adding the synthetic fluocerite powder obtained from the fluorite–fluocerite experiments to a 50 mM Na2CO3 solution, prepared using reagent grade chemicals and pure deionized (Milli-Q) water. For the experiments carried out at 50 and 90 °C, 0.25 g of fluocerite were added to a glass bottle reactor with 80 mL of Na2CO3-bearing solution and placed in a preheated oven. For the 200 °C experiments, 0.25 g of fluocerite powder was added to 20 mL of CO3-bearing solution solutions in 20 ml Teflon-lined stainless-steel autoclaves at saturated water vapor pressures and placed in a preheated oven. To monitor the ongoing fluocerite–bastnäsite transformation reaction, 5 mL suspensions were regularly extracted from the reactor using a pipette at specific intervals, in all experiments except the one conducted at 200 °C. For the experiments at 200 °C, multiple repetitions were performed to gather samples at various time intervals. The collected samples were immediately filtered using a vacuum filtration system with 0.2 μm polycarbonate filters and rinsed with isopropanol to prevent potential recrystallisation or formation of other solids from any residual interstitial water and then quickly dried in air.38–40 For the 200 °C fluocerite–bastnäsite reaction, the resultant solution was cooled to room temperature and subsequently filtered entirely using the aforementioned method.
The nature of the new crystallised solid was determined with powder X-ray diffraction (XRD). The samples were analysed with a Bruker D5000 powder X-ray diffractometer (Cu Kα radiation, 0.02 per step from 5° to 70° in 2θ at 0.2° min−1) located at TRinity Technology and Enterprise Centre (Dublin). Identification of crystalline phases present in the samples was carried out with a Bruker DIFFRAC.EVA software in combination with the ICDD Powder Data File (PDF-4, The International Centre for Diffraction Data). Pattern-matching refinement, quantification of crystalline phases was carried out with the Rietveld refinement software TOPAS,41 using the structural files from the American Mineralogist Crystal Structure Database (Fluorite: AMCSD 0011683; Fluocerite-(Ce): AMCSD 0009548; Bastnasite-(Ce): AMCSD 0001553; Cerianite-(Ce): AMCSD 0011686; Kozoite-(Nd): AMCSD 0002475).
Images of the samples were obtained with scanning electron microscopy equipped with energy dispersive spectroscopy (SEM-EDS) to study potential changes in the morphology and size of the crystalline phases. In order to prepare the samples for SEM characterisation, these were placed on mounts and Au–Pd or C coated respectively for imaging or the EDS analyses. SEM-EDS analyses were conducted using a Tescan TIGER MIRA3 FEG-SEM operating under high vacuum conditions and equipped with two Oxford Instruments X-Max 150 mm2 energy dispersive spectroscopy (EDS) detectors running Oxford Instruments AZtec analysis software. The analyses were carried out using a beam current of 300 pA and an accelerating voltage of either 5 or 10 kV, for detailed imaging, or 20 kV, for EDS analysis at the iCRAG Lab at TRinity College Dublin.
Multiple Point EDS analyses and compositional maps were carried out on the samples to determine the atomic % of La, Ce, Nd, Ca and O present in the crystalline phases. The standard used for the SEM-EDS analysis was a Co wire with a degree of purity of 99.995%. The particle size distribution in the samples was measured with ImageJ Software.42–44
Quantification of the reaction extents was used to provide information on the rate of crystallisation by using the empirical Avrami equation:45
| α = 1 − exp(−kt)n | (1) |
−ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1 − α) = n ln(1 − α) = n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k + n k + n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t t | (2) |
The reaction with kinetics that conform to this equation give a straight line when −ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1 − y) is plotted against ln
ln(1 − y) is plotted against ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t.40,46–48 The empirical parameter n value is given by the value of the slope, which can be used to compare reaction mechanism. Parallel lines indicate a constant value of n, suggesting that the reaction mechanism is the same. The intercept on the y axis gives the value of n
t.40,46–48 The empirical parameter n value is given by the value of the slope, which can be used to compare reaction mechanism. Parallel lines indicate a constant value of n, suggesting that the reaction mechanism is the same. The intercept on the y axis gives the value of n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k, by which the k value can be determined.40,48
k, by which the k value can be determined.40,48
The apparent activation energy of crystallisation (Ea(cryst.)) (eqn (3)) and the apparent activation energy for nucleation (Ea(nucl.)) (eqn (4)) were calculated using the derived induction times (t0) and rate constants (k) as a function of temperature using an Arrhenius approach.49–51Ea(cryst) is an “apparent” activation energy because it represents contributions from all of the many processes occurring in the reaction (e.g., dissolution, aggregation) and not just the potential barrier for a single reaction.49,50,52 The t0 values were determined through the interpolation of the curve obtained from the % transformation values from fluorite to fluocerite vs. time.
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = ln k = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A(cryst.) − (Ea(cryst.)/RT) A(cryst.) − (Ea(cryst.)/RT) | (3) |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t0 = ln t0 = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A(nucl.) − (Ea(nucl.)/RT) A(nucl.) − (Ea(nucl.)/RT) | (4) |
In the equations A is a pre-exponential factor (s−1), Ea(cryst.) is the activation energy for crystallization (kJ mol−1), Ea(nucl.) is the activation energy for crystallization (kJ mol−1), R is the gas constant (8.314 J mol−1 K−1), and T is temperature (K).
Results
Experimental results revealed that the kinetics of fluorite–fluocerite transformation were dependent on temperature and influenced by the mass of REE. Also, the fluocerite carbonation experiments revealed the formation of newly-formed CO3-bearing phases. The combined use of powder X-ray powder diffraction (XRD) and scanning electron microscopy with energy dispersive spectroscopy (SEM-EDS) allowed the identification and quantification of the newly formed phases, which were used to derive the kinetics and mechanistic processes. Selected examples of the Rietveld refinement (Fig. SI-1†) and unit cells parameters from the refinements are presented in the ESI (Tables SI-1, SI-2, SI-3†).Fluorite–fluocerite transformation
The interaction between the fluorite powder and the preheated 50 mM La, Ce, and Nd-bearing solutions resulted in the crystallisation of fluocerite (PDF 00-002-0529) as the sole product phase, irrespective of the REE used or the temperature. The XRD analyses carried out of the solids, taken at increasing time intervals, revealed a progressive replacement of the original fluorite by fluocerite (Fig. 1). | ||
| Fig. 1 Powder X-ray diffraction patterns of the Ce 70 °C experiment showing the progressive replacement from fluorite to fluocerite. | ||
The analysis of the quantitative data obtained via Rietveld refinement highlighted the temperature and the atomic number of REE as crucial factors influencing the kinetics of the fluorite–fluocerite transformation. Experimental observations showed that the transformation rates were notably faster with lower atomic number REE. For instance, experiments conducted with La exhibited the most rapid transformation rates (>175, 25, 2.5, and <1 hours at 30, 50, 70, and 90 °C, respectively). Similar trends were evident in experiments involving Ce and Nd, albeit with longer transformation times compared to La (Fig. 2).
 | ||
| Fig. 2 Crystallisation reaction curves of fluocerite for La (a), Ce (b), Nd (c) experiments carried out at temperatures from 30 to 90 °C. | ||
Specifically, transformation reactions at 30 °C required >100, >175, and >720 hours in the La, Ce, and Nd systems, respectively (Fig. 3). Detailed values regarding the extent of transformation reactions and the weight percentage of fluorite versus fluocerite are provided in Tables SI-4, SI-5, and SI-6.†
SEM imaging revealed that the crystalline morphology of fluocerite was found to be influenced by the presence of different REE in the starting solution and by variations in reaction temperatures, consistently resulting in flat hexagonal crystals in all experiments (Fig. SI-2†). The presence of different REE affected the crystalline dimensions, including diameter and thickness (Fig. 4a–c). It was then possible to recognise a general trend in which fluocerite dimensions increased with the increasing REE ionic radius (see Table 1).
| T (°C) | La | Ce | Nd | |||
|---|---|---|---|---|---|---|
| Diameter (μm) | Thickness (μm) | Diameter (μm) | Thickness (μm) | Diameter (μm) | Thickness (μm) | |
| 30 | 0.75 ± 0.13 | 0.14 ± 0.04 | 1.22 ± 0.33 | 0.23 ± 0.05 | 2.44 ± 0.40 | 0.84 ± 0.22 |
| 50 | 1.49 ± 0.35 | 0.25 ± 0.07 | 0.80 ± 0.14 | 0.13 ± 0.04 | 2.12 ± 0.54 | 0.63 ± 0.18 |
| 70 | 0.70 ± 0.13 | 0.08 ± 0.02 | 1.26 ± 0.27 | 0.17 ± 0.06 | 2.56 ± 0.88 | 0.83 ± 0.37 |
| 90 | 1.64 ± 0.75 | 0.46 ± 0.18 | 2.70 ± 0.94 | 1.45 ± 0.68 | 4.45 ± 0.53 | 1.30 ± 0.30 |
Fluocerite-La consisted of very thin (<500 nm) crystals with average sizes of 1.5 μm (Fig. 4a). Conversely, the largest fluocerite-Nd crystals crystallised as hexagonal prisms with sizes reaching 6 μm and thicknesses of 2–3 μm (Fig. 4c). Also, at the earliest stages of the crystallisation reactions and at the lower temperatures, fluocerite crystals showed a rounded and sub hexagonal morphology which became more euhedral with time and/or temperature (Fig. SI-3†). At 30 °C, crystals in all REE systems showed a rounded shape throughout the reaction. At 50 °C, this shape persisted for up to 1 day for La, 2 days for Ce, and 4 days for Nd. At 70 °C, the duration shortened to 4 hours for La, 5 hours for Ce, and 10 hours for Nd. At the highest temperature (90 °C) all fluocerites crystals appeared to be flat euhedral hexagons. Sometimes minor imperfections were visible on the (001) face of the crystals, consisting of growth steps of sub-hexagonal morphology. These defects were more common in the Nd system (Fig. 4d and e). Along the lateral faces, at temperature <90 °C it was also possible to see the internal layered arrangement of the growing hexagonal crystals, consisting of nanodomains (<100 nm) stacked on top of each other (Fig. 4f).
Results from energy dispersive spectroscopy (EDS) microanalysis on selected fluocerite crystals revealed the presence of REE (La, Ce, Nd) and F (Table SI-7†), supporting the XRD data. In addition, they revealed the presence of trace amount of Ca quantifiable in <6 atomic% or below the detection limit.
Fluocerite–bastnäsite transformation
Experimental results revealed that the transformation reactions involving synthetic La-, Ce- and Nd-fluocerite powders with a preheated 50 mM Na2CO3 resulted into the crystallisation of bastnäsite (PDF 00-002-1433) (Table SI-8†) as primary phase at all the temperatures tested (50, 90 and 200 °C) and regardless the REE in the system. Cerianite (CeO2; PDF 00-043-1002) was also found in the Ce system whereas kozoite (PDF 00-027-1296) in the Nd system, along with bastnäsite.The analysis of the quantitative data obtained by Rietveld refinement showed that the mineralogy of the final products of the fluocerite carbonation experiments were strongly REE dependent. In the La system the primary and only phase present was bastnäsite whereas in Ce and Nd system bastnäsite was always coexisting with cerianite and kozoite, respectively (Fig. 5a, b and c). The only experiments that showed a different trend were the Ce and Nd ones, in which the primary phases were cerianite and kozoite with bastnäsite only occurring as a minor phase (see Tables SI-10 and SI-11†). Irrespective of the particular REE employed and the temperature conditions, none of the reactions led to a complete transformation of fluocerite into the newly formed phases (Fig. 5a, b and c). Following the initial stages of the reactions, data indicated a deceleration in the transformation process from fluocerite to the CO3-bearing phases and cerianite, with the weight percentage of the involved phases exhibiting stability and minor fluctuations over extended periods. There were two exceptions to this general trend: first, the experiment at 50 °C in the La system, in which fluocerite was progressively replaced by bastnäsite during all the duration of the experiment (see Table SI-9†). Second, the Ce system, which showed a different general trend, with a progressive increase in the weight % of cerianite at all tested temperatures.
 | ||
| Fig. 5 Powder X-ray diffraction patterns showing the transformation of the La- (a), Ce- (b) and Nd-fluocerite (c) to REE-fluorocarbonates, at 90 °C (La), 70 °C (Ce), and 200 °C (Nd). | ||
The SEM images taken at different times after the beginning of the interaction between synthetic fluocerites and CO3-bearing solution revealed that nm-sized rare earth carbonates (bastnäsite and kozoite) started to grow on the surfaces of fluocerites and quickly covered the host crystals forming a crust. The same phenomenon was observed during the formation of cerianite in the Ce system.
SEM imaging revealed that the REE-bearing carbonates showed very similar morphology. Bastnäsite and kozoite appeared like individual nm-sized (∼50 nm) crystals fully covering the surfaces of the fluocerite host (Fig. 6a–f).
In particular, bastnäsite crystallised as nanodomains with a columnar prismatic arrangement. At higher temperatures and after longer reaction times, these bastnäsite nanocrystals increased in size and became more euhedral, with a pseudo columnar morphology (Fig. 7 and 8).
 | ||
| Fig. 7 (a and b) SEM micrographs showing a general view of La-fluocerite crystals replaced by bastnäsite at 90 °C. (c and d) Closer views of nano-bastnäsite overgrowths. | ||
 | ||
| Fig. 8 SEM micrographs of bastnäsite replacing Nd-fluocerite at 90 °C (a, b and c) and 200 °C (d, e and f). | ||
Overall, the bastnäsite nanostructures consisted of numerous small prisms that exhibited a reduction in thickness as they crystallised closer to the (001) faces of the fluocerite substrate (Fig. 8b–e), sometimes showing spindle-shaped morphologies while other ones (Fig. 8f) consisted of numerous units of similar size and shape (sometimes reaching 500 nm), with the same orientation.
Cerianite, on the contrary, crystallised as nanoaggregates of crystals covering the surface of fluocerite during the early stages of the reactions, growing in size (up to ∼100 nm) and developing a cubic or bipyramidal morphologies at higher temperatures and after long reaction times (Fig. 9).
A noteworthy observation is the non-random orientation of REE-fluorocarbonates, indicative of epitaxial overgrowth. Specifically, the fluocerite–bastnäsite epitaxial relationship was defined by the parallel alignment of the crystallographic axes of the bastnäsite to those of the underlying fluocerite substrate (Fig. 10).
 | ||
| Fig. 10 Schematic diagram showing the epitaxial relationships between fluocerite, bastnäsite and cerianite crystals. | ||
Additionally, in the Ce experiments, a substantial number of cerianite crystals were identified, oriented precisely along the (001) plane of the fluocerite substrate (Fig. 9) with a perfect matching of the (111) crystallographic plane of cerianite to the (001) plane of fluocerite. At the highest tested temperatures and longest reaction times (i.e., 200 °C after 60 days; see Fig. 11), intriguing dissolution features were observed in the original fluocerite crystals within both the La and Ce systems. These features manifested as dissolution progressing from the central area of crystal towards its edges (see Fig. 11b and d). In certain instances, this dissolution process advanced to the extent that skeletal hexagonal rings of the original fluocerite crystal were left behind.
 | ||
| Fig. 11 SEM micrographs of skeletal Ce- (a and b) and La-fluocerite (c and d) crystals occurring at 200 °C after reaction times >48 h. | ||
Discussion
Our findings illustrate that REE ionic radii and temperature have a significant impact on the kinetics of the fluorite to fluocerite transformation reaction, as well as the crystalline morphology of the resulting solids. Additionally, the reaction of synthetic La-, Ce-, and Nd-bearing fluocerites with a CO3-rich solution results in the formation of REE-fluorocarbonates and cerianite. The use of individual REE ions proves to be a key factor, profoundly influencing the crystallization pathways, polymorph selection, and the thermodynamically stable end product upon completion of the reactions.Fluorite to fluocerite transformation
Fluocerite resulted to be the only product of the fluorite–fluocerite transformation reaction irrespectively of the REE ion present in the aqueous solution and of temperatures. The XRD and SEM data support a solvent-mediated surface precipitation and subsequent mineral replacement reaction that is dependent on temperature and the type of REE. The rate of transformation is directly proportional to the temperature and the atomic mass of the REE. In order to calculate the reaction rates (k) (Table 2), data obtained from fluorite to La, Ce and Nd fluocerite reaction curves (Fig. 1) were fitted to a JMAK (Johnson–Mehl–Avrami–Kolmogorov) particle nucleation model, which is based on the Avrami equation.| T (°C) | La | Ce | Nd | ||||||
|---|---|---|---|---|---|---|---|---|---|
| n | k (×10−3 s−1) | t 0 (s) | n | k (×10−3 s−1) | t 0 (s) | n | k (−10−3 s−1) | t 0 (s) | |
| 30 | 1.31 | 0.006 | 2100 | 1.08 | 0.003 | 7200 | 2.91 | 0.001 | 216![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 50 | 0.88 | 0.078 | 192 | 1.36 | 0.014 | 900 | 1.62 | 0.005 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
| 70 | 0.76 | 0.864 | 36 | 0.95 | 0.193 | 108 | 1.30 | 0.027 | 1230 |
| 90 | 0.95 | 1.617 | 10.8 | 0.78 | 0.277 | 33 | 1.52 | 0.054 | 510 |
| E a(cryst.) kJ mol−1 | 90(12) | 76(12) | 72(8) | ||||||
| E a(nucl.) kJ mol−1 | 81(6) | 83(5) | 96(10) | ||||||
While the JMAK model is primarily associated with solid-state transformations and phase transitions in materials such as metals and alloys, it has also been adapted and applied to describe mineral-water interaction reactions, particularly in the context of mineral dissolution, precipitation, and transformation in aqueous environments (e.g.,53–56). Each reaction curve obtained in this study fit to this model with a good R2 (>90%). The data plots of −ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1 − α) against ln
ln(1 − α) against ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t shows that reaction rates display close to parallel lines with similar n values (Fig. SI-4†). This indicates that the main crystallisation mechanism remains the same regardless of the different REE used or the temperature.46,47 The activation energies of nucleation and crystallisation for La, Ce and Nd fluocerites (Table 2), were calculated by plotting, respectively, the ln of the induction times (t0) and reactions rate (k) against the inverse of the temperature, as showed in Fig. 12.
t shows that reaction rates display close to parallel lines with similar n values (Fig. SI-4†). This indicates that the main crystallisation mechanism remains the same regardless of the different REE used or the temperature.46,47 The activation energies of nucleation and crystallisation for La, Ce and Nd fluocerites (Table 2), were calculated by plotting, respectively, the ln of the induction times (t0) and reactions rate (k) against the inverse of the temperature, as showed in Fig. 12.
The determined n values from the fluorite–fluocerite transformation reactions, using the JMAK model, are presented in Table 2. The n constant in the Avrami equation, denoted as n = d + 1, has been found to be related to the crystal growth dimensionality.55,57 For instance, a mineral undergoing spherulitic growth, occurring in three dimensions, would typically exhibit n = 4. In our experiments, a direct proportionality can be observed between the n values and the dimensionality of fluocerite growth for each REE, with lighter REE elements favouring linear growth (e.g., La-fluocerite with n values between 0.95 and 1.31; average of 0.98) and heavier elements displaying two-dimensional growth tendencies (e.g., Nd-fluocerite with n values between 1.52 and 2.91, average values of 1.84). It needs to be highlighted that in the hexagonal system, the two directions [100] and [010] within the basal plane (perpendicular to [001]) are equivalent in terms of crystallographic symmetry. Therefore, the growth of this basal plane should be considered unidimensional.
Data analyses reveal that La had the fastest reaction kinetics, followed very closely from Ce, while Nd showed the longest ones. These difference in kinetics can be explained by the progressive increasing of the ionic potential along the lanthanide series. REE3+ ionic radii decrease with increasing atomic number (a phenomenon known as the lanthanide contraction58). This decrease in REE3+ ionic radii is translated into an increase in the ionic potentials, which are calculated by dividing the ion's valence by its ionic radius. In solution, all ions are solvated, but they must remove their solvation shells to integrate into a crystalline structure. The ionic potential of the REE3+ cation determines its ability to retain water molecules in its solvation shell.59–61 Ions with higher ionic potentials require more energy to dehydrate before incorporating into mineral structures. Consequently, higher ionic potentials are translated into higher temperatures or longer times required for the initiation (nucleation) and completion of the crystallization reactions.59,62 The ionic potentials calculated for La3+, Ce3+, and Nd3+ are 2.60, 2.70, and 2.77 Å−1 respectively.63 La3+ would require the least energy for dehydration, followed closely by Ce3+, while Nd3+ would require the highest energy. This aligns with the longer kinetics observed in fluorite–fluocerite transformation reactions for heavier REE compared to lighter ones. The activation energies for nucleation exhibit a rising trend, correlating to the REE atomic numbers, ranging from 81 to 96 kJ mol−1. Conversely, the activation energies for crystallisation are similar between Ce and Nd (76 and 72 kJ mol−1 respectively) and slightly higher for La (90 kJ mol−1) (Table 2). These small discrepancies can be attributed to minor factors influencing the fluorite to fluocerite replacement reactions, such as slight variations in the initial fluorite powder's particle size distribution or the presence of Ca impurities in the structure of fluocerite affecting its solubility.
Fluocerite – REE-fluorocarbonates transformation
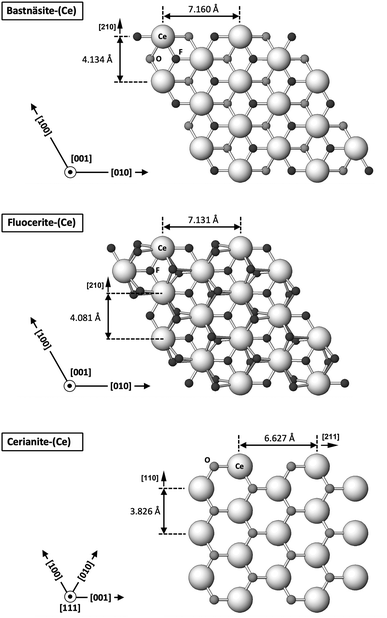
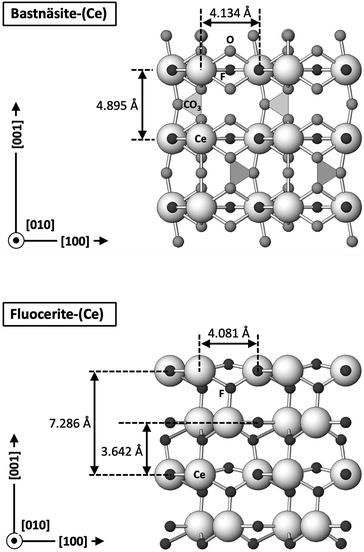
The carbonation of synthetic La-, Ce-, and Nd-fluocerite led to the formation of various phases, influenced by the specific REE present in each experiment. Bastnäsite was predominant in La and Nd systems, while cerianite was the main phase forming in the Ce system (with minor amounts of bastnäsite). The newly formed REE-fluorocarbonates nucleated on the surfaces of the host grains and continued to grow in size eventually forming a crust on the fluocerite crystals. The final result consisted of a solution-mediated pseudomorphic replacement reaction in which the original morphology and dimensions of the fluocerite grains remained constant, but most the host mineral was replaced by the newly formed phases.A significant feature observed in the carbonation experiments is the presence of oriented overgrowths of the newly formed phases (bastnäsite and cerianite) on the surface of fluocerite. The epitaxial overgrowth observed between bastnäsite and fluocerite is not unexpected, given their shared crystal system (hexagonal) and similarities in space group. Fluocerite-Ce crystallises in the trigonal system with space group P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c1, with lattice parameters of a = b = 7.131 Å and c = 7.286 Å.64 Bastnäsite belongs to the hexagonal crystal system with space group P
c1, with lattice parameters of a = b = 7.131 Å and c = 7.286 Å.64 Bastnäsite belongs to the hexagonal crystal system with space group P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) c2, characterized by lattice parameters a = 7.118(1) Å and c = 9.762(1) Å.65 These structural similarities suggest a favourable fit for epitaxial growth (Fig. 13 and 14).
c2, characterized by lattice parameters a = 7.118(1) Å and c = 9.762(1) Å.65 These structural similarities suggest a favourable fit for epitaxial growth (Fig. 13 and 14).
 | ||
| Fig. 14 Projection of the crystal structures of the (010) slices of Ce-bastnäsite and Ce-fluocerite showing the main directions of epitaxy and the repeating periods. | ||
The misfit values (Table 3) have been calculated using the expression:
| Minerals | Directions of alignment | Misfit (%) |
|---|---|---|
| Fluocerite–Bastnasite | (001)fc[010]fc||(001)bast[010]bast | −0.42% |
| (001)fc[210]fc||(001)bast[210]bast | −1.28% | |
| (010)fc[100]fc||(010)bast[100]bast | −1.28% | |
| (010)fc[001]fc||(010)bast[001]bast | −25.60% | |
| Fluocerite–Cerianite | (001)fc[210]fc||(111)cer[110]cer | +6.66% |
| (001)fc[010]fc||(111)cer[211]cer | +7.61% |
The other epitaxial overgrowth was only observed in the Ce experiments: when Ce-bastnäsite undergoes complete breakdown as a consequence of the Ce3+ to Ce4+ oxidation process,68 cerianite can grow epitaxially on the non-replaced remnants of fluocerite crystals, specifically on their (001) surfaces. Although cerianite is a cubic mineral (space group Fm3m; a = 5.42(1) Å), the epitaxial overgrowth is feasible by the similar repeating periods of the (111) plane of cerianite and the (001) plane of fluocerite (Table 3 and Fig. 13) with calculated misfit values <+8%, positive values that indicate that the unit cell of cerianite is slightly expanded along the different directions of epitaxy of fluocerite. With time, the Ce3+ to Ce4+ oxidation would be translated into the full transformation of Ce-fluocerite into cerianite. The smaller molar volume of cerianite (32.21 cm3 mol−1 (ref. 69)) compared to fluocerite (23.86 cm3 mol−1 (ref. 69)) generates porosity on the (001) face of the latter during the replacement, often resulting in skeletal crystals (Fig. 11).
All these epitaxial overgrowths between bastnäsite, cerianite and fluocerite have in common the close similarity in arrangement of the Ce–O and Ce–F groups of these three minerals (Fig. 13) and their similar bond distances (Ce–O distance of 2.34 Å in cerianite, Ce–F distances of 2.39 Å and 2.42 Å in bastnäsite and fluocerite, respectively)64,65,70 further supporting these structural matches. However, it is important to consider that the minerals obtained in our study were synthesized with targeted chemistries, using single REE. Although oriented overgrowth has been described in natural samples,67 these three minerals often consist of complex solid solutions comprising multiple REE alongside other cations such as Ca and Sr.26,71,72 These chemical variability has the potential to influence the matching of unit cells and subsequently impact the kinetics of mineral replacement processes, as well as the resulting solid morphology.
No experiment resulted in the complete carbonation of the original fluocerite phase at any temperature, irrespective of the REE used. To better understand this partial carbonation reaction, it is important to evaluate the structural relationship between the host mineral and the newly formed REE-fluorocarbonates, taking two main factors into account: (i) The higher molar volumes of the REE-fluorocarbonates (e.g., 42.52 cm3 mol−1 for La-Bastnäsite; 45.59 cm3 mol−1 for Nd-kozoite69) compared to fluocerite (e.g., 32.99 cm3 mol−1 for Fluocerite-La69) promote partial equilibrium situations (e.g.,68,73,74). They occur when reactive host grains of fluocerite are covered by a crust of the precipitating REE-fluorocarbonate phases, which isolate the reactive solid from the aqueous solution, slowing down the carbonation reaction. (ii) Also, the bastnäsite overgrowth is aligned with the orientation of the fluocerite due to the lattice matching between the two minerals, with very low misfit values (Table 365). This epitaxial overgrowth of the REE-fluorocarbonates crystals relative to the host fluocerite surfaces results in a highly uniform coating, further enhancing the partial equilibrium situation. As a comparison, it is worth noting that while the molar volume of fluocerite (e.g., La-fluocerite 32.99 cm3 mol−1 (ref. 69)) is larger than that of fluorite (24.55 cm3 mol−1 (ref. 69)), the fluorite–fluocerite transformation experiments did not result in a clearly defined state of partial equilibrium. This can be attributed to the lack of oriented overgrowth of fluocerite on the host fluorite crystals, hindering the complete coating of the host fluorite and allowing a full replacement reaction. However, it cannot be ruled out that in some experiments some partial equilibrium could have occurred at the very late stages of the reaction. Supporting this hypothesis is the observation of very minor quantities of fluorite persisting for an extended period at the end of some of the experiments (Tables SI-4, SI-5 and SI-6†).
Carbonation experiments in the La and Nd systems showed very similar trends with small variations. For example, only the La experiment at 50 °C showed a full replacement of the host fluocerite, which could be explained by the small particle size of the host. Also, in the Nd experiments the formation of bastnäsite took place via kozoite (NdCO3OH), an orthorhombic precursor of bastnäsite that belongs to the ancylite mineral group.75 Its occurrence solely in the Nd system can be attributed to the longer lifetime of Nd-kozoite compared to La-kozoite in crystallisation from solution experiments and in mineral replacement reactions (e.g.,48,59,76).
The Ce system deserves a separate discussion. Unlike the La and Nd systems, the Ce experiments did not achieve a state of partial equilibrium. To account for this behaviour, we propose a multi-step crystallization process: fluocerite → bastnäsite → cerianite. This way, the process in the Ce system would involve three main steps: (i) dissolution of host crystals in the CO3-bearing solution with the release of Ce3+ and F−, leading to the crystallisation of bastnäsite-Ce; (ii) redox oxidation from Ce3+ to Ce4+, which happens since Ce4+ has a stable electronic configuration of a nearest noble gas and is more stable than Ce0 and Ce3+,77,78 and (iii) subsequent decarbonation of bastnäsite-Ce and decrease of pH, followed by cerianite crystallization. The works of Szucs et al. (2023)68 and Janos et al. (2017),79 who synthesized cerianite via homogeneous precipitation, validate this hypothesis since they both reported Ce carbonates as intermediate phases. In our experiments, Ce fluorocarbonates are metastable and the decarbonation process during the transformation from bastnäsite-Ce to cerianite is translated into an increase of the porosity since the smaller molar volume of the latter (32.21 cm3 mol−1 (ref. 69)) compared to the former (23.86 cm3 mol−1 (ref. 69)). Cerianite is the most thermodynamically stable phase in this system, as its solubility (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kcer = −59.3 ± 0.3 in 0.01 M NaClO4
Kcer = −59.3 ± 0.3 in 0.01 M NaClO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80) is lower compared to bastnäsite81 or fluocerite.82
80) is lower compared to bastnäsite81 or fluocerite.82
In La and Ce carbonation experiments conducted at 200 °C for 60 days, SEM analyses also unveiled intriguing morphologies characterized by skeletal crystals (Fig. 11). Remarkably, the (001) faces of fluocerite exhibited complete dissolution in the central region, leaving behind only the hexagonal rings of the original crystal. We suggest that dissolution may begin at the center of the fluocerite hexagonal crystals, spreading outward. Three main factors could drive this process: (i) enhanced isolation of the host fluocerite crystal rims from the fluid by a thicker bastnäsite crust during carbonation, (ii) preferential dissolution of the central area of thin fluocerite crystals, and (iii) porosity development during the coupled dissolution of Ce-bastnäsite and crystallisation of cerianite. Further in-depth experimental investigation into the dissolution of fluocerite would be needed to fully comprehend the specific mechanisms of formation of these skeletal crystals.
Implications
Our experiments demonstrate that fluocerite can act as a transient precursor to bastnäsite and cerianite. The primary mechanism for the formation of these minerals involves a dissolution-recrystallization process mediated by the hydrothermal solution, resulting in a pseudomorphic mineral replacement. The ionic potential of the three tested REE plays a crucial role in this process, influencing the kinetics and stability of the mineral phases. Additionally, while the aqueous solution facilitates these mineralogical transformations, the structural similarity between bastnäsite and fluocerite promotes partial equilibrium situations. This highlights the intricate interplay between ionic potential, solution chemistry, and structural factors in driving the observed mineral replacement reactions.Our understanding of the crystallisation mechanisms of fluocerite and its role as a precursor phase to bastnäsite and cerianite allows comprehending the geological origin of critical minerals that crucial for rare earth element extraction. Our experimental results align with research on natural fluocerite, which has been found in REE ore deposits and associated with REE bearing minerals (e.g.,23,24,26,29) and has been suggested to be a precursor phase in the formation of fluorocarbonates and cerianite.12,16,23,24,26,29 This work also provides new insights into the formation of REE-fluorocarbonates and cerianite in REE hydrothermal systems, such as those found in carbonatite deposits, of which an example is Bayan Obo REE deposit in China, the largest known in the world.3,4,10–12
Although the association between F− and REE is well established, there are gaps in the understanding of its significance for the genesis REE deposits.83 REE deposits generally display an association between REE and Fe mineralizations and F-bearing minerals, suggesting the presence of F-rich mineralizing fluids.83,84 Hydrogeochemical modelling of high-temperature experimental data has revealed that Cl−, SO42− and HCO3−/CO32− ions play a main role as ligands for the transport of the REE at hydrothermal conditions33,59,85 as well as OH− in near-neutral and alkaline conditions.59 Also, F− has long been considered one of the primary ligands facilitating the solubility and hydrothermal transport of REE.32,33,85 However, recent studies suggest that F− functions as a depositional ligand, promoting the effective formation of monazite, xenotime, and bastnäsite in REE-bearing solutions containing phosphate and/or carbonate.32,33,85
In our carbonation experiments we were able to synthesise bastnäsite at low hydrothermal conditions (50–90 °C). This result was unexpected because the non-fluorobastnäsite (hydroxylbastnäsite, REECO3OH) is known to form at hydrothermal conditions, usually above 150–200 °C.48,59,68,76,86 According to Hsu (1992)87 and Wakita and Kinoshita (1979)88 the lower limit of the La- and Ce-hydroxylbastnäsite is at temperatures comprised between 100 and 115 °C at 1 atm whereas La- and Ce-fluorobastnäsite resulted to be stable at higher temperature compared to their corresponding hydroxylbastnäsites.87 We hypothesize that the incorporation of F− into the hydration shell of REE3+ could lower the energy required for desolvation of the REE3+ ion, allowing the nucleation of fluorobastnäsite under low hydrothermal conditions. This REE-F association would play a similar role than the Mg2+-SO42− ion in calcite: It is known that the structural incorporation of Mg2+ into growing calcite crystals requires high temperatures.89–91 However, experimental work has found that SO42− facilitates the desolvation of the Mg2+ ion during the growth of calcite in Mg-rich fluids.92–94 These studies, also supported by molecular modelling showing that substitution of the MgSO4 ion into the calcite surface is energetically more favoured than pure Mg2+, demonstrated that the Mg2+-SO42− ion pairing effect enhances the incorporation of Mg2+ into calcite, especially at ambient conditions. Our findings indicate that the low-temperature formation of fluorobastnäsite could be facilitated by the formation of REE3+-F− ion pairs, akin to a similar effect observed with Li+ ions, where the energy barrier for Li+ desolvation is decreased in the presence of F−.95
Although our experiments involve single REE ions, the results provide valuable insights into the mechanisms of bastnäsite formation in natural fluids. Bastnäsite is naturally enriched in light REE, as heavy REE are too small to form this mineral and typically enter as impurities along with light REE.65 This suggests that bastnäsite would be the final thermodynamically stable phase in nature. While the formation of metastable kozoite (a known precursor of bastnäsite59,76) cannot be entirely ruled out, it would be very scarce compared to bastnäsite. The presence of kozoite-(Nd) in experiments not involving fluocerite is quite common across a wide range of temperatures, from ambient to over 200 °C, both in crystallisation from solution experiments76 and in mineral replacement reactions.48,59,96 Also, natural fluocerite and bastnäsite containing some Ce are susceptible to oxidation, leading to the crystallization of cerianite that would replace the host solid at the nanoscale, accumulating as a discrete phase.96
Our findings suggest that the formation of bastnäsite from fluocerite at low hydrothermal conditions could offer valuable insights for laboratory and industrial synthesis of these and other REE crystalline compounds. These minerals are valued for their optical properties97–100 and other industrial applications, including in oxygen sensors, scintillators, lasers, telecommunications, and photonic and biophotonic devices.35,99 The methodology employed in our study is simple, environmentally friendly, highly reproducible, and cost-effective for producing fluocerite and bastnasite and could serve as a foundation for refining and innovating targeted synthesis methods for REE-bearing compounds.
Conclusions
This study presents groundbreaking insights into the crystallisation pathways, mechanisms and kinetics of fluocerite formation from fluorite and its subsequent transformation into bastnäsite and cerianite. It highlights the significant influence of REE mass, temperature, and structural compatibility between all these crystalline phases, as well as the interplay between the molar volume differences of the reacting minerals and the epitaxial overgrowth of bastnäsite on fluocerite, which can be translated into partial equilibrium situations during carbonation processes. Additionally, this work offers insights into the geological origins of these REE-bearing minerals, emphasizing the role of F− ions in facilitating the low-temperature synthesis of REE-fluorocarbonates, which may also impact laboratory and industrial production of REE fluorides used in technological applications.Author contributions
Luca Terribili: experimental work, data analysis and interpretation, manuscript writing – original draft, review and editing; Remi Rateau: data analysis; Melanie Maddin: data analysis; Juan Diego Rodriguez-Blanco: conceptualization, data analysis, writing (review and editing), supervision, validation, funding acquisition.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This publication has emanated from research conducted with the financial support of Science Foundation Ireland, Geological Survey of Ireland and the Environmental Protection Agency under the SFI Frontiers for the Future Programme 19/FFP/6771 “SEparating Critical metals ThrOugh mineRal crystallization (SEleCTOR)” (rodrigjd-SFI-17/RC-PhD/3481). We are extremely grateful for the help of Colin Reid, Paul Guyett and Leona O'Connor from the iCRAG Lab at TCD, and Dr Robbie Goodhue in Unit 7, Trinity Technology and Enterprise Centre (TTEC).References
- K. Smith Stegen, Energy Policy, 2015, 79, 1–8 CrossRef.
- J. M. Klinger, Extr. Ind. Soc., 2015, 2, 572–580 Search PubMed.
- V. Balaram, Geosci. Front., 2019, 10, 1285–1303 CrossRef CAS.
- N. Dushyantha, N. Batapola, I. M. S. K. Ilankoon, S. Rohitha, R. Premasiri, B. Abeysinghe, N. Ratnayake and K. Dissanayake, Ore Geol. Rev., 2020, 122, 103521 CrossRef.
- D. Gielen and M. Lyons, Critical materials for the energy transition: Rare earth elements, International Renewable Energy Agency, Abu Dhabi, 2022 Search PubMed.
- K. M. Goodenough, F. Wall and D. Merriman, Nat. Resour. Res., 2017, 27, 201–216 CrossRef.
- B. Zhou, Z. Li and C. Chen, Minerals, 2017, 7(11), 203 CrossRef.
- S. Carrara, S. Bobba, D. Blagoeva, P. Alves Dias, A. Cavalli, K. Georgitzikis, M. Grohol, A. Itul, T. Kuzov, C. Latunussa, L. Lyons, G. Malano, T. Maury, A. Prior Arce, J. Somers, T. Telsnig, C. Veeh, D. Wittmer, C. Black, D. Pennington and M. Christou, Publications Office of the European Union, Luxembourg, 2023 Search PubMed.
- J. Lucas, P. Lucas, T. Le Mercier, A. Rollat and W. Davenport, Rare Earths – Science, Technology, Production and Use, Elsevier, Amsterdam, 2015 Search PubMed.
- Z. Weng, S. M. Jowitt, G. M. Mudd and N. Haque, Applied Earth Science, Trans. Inst. Min. Metall., Sect. B, 2013, 122(2), 83–96 CAS.
- M. R. Payne, A. P. Gysi and N. C. Hurtig, Chem. Geol., 2023, 617, 121256 CrossRef CAS.
- W. Zhang, W. T. Chen and A. E. Williams-Jones, Contrib. Mineral. Petrol., 2023, 178, 34 CrossRef CAS.
- Z. Weng, S. M. Jowitt, G. M. Mudd and N. Haque, Econ. Geol., 2015, 110, 1925–1952 CrossRef.
- W. Zhang, W. T. Chen, T. P. Mernagh and L. Zhou, Miner. Deposita, 2021, 57(6), 1–19 Search PubMed.
- M. Smith, J. Kynicky, C. Xu, W. Song, J. Spratt, T. Jeffries, M. Brtnicky, A. Kopriva and D. Cangelosi, Lithos, 2018, 308–309, 65–82 CrossRef CAS.
- A. C. Strzelecki, A. Migdisov, H. Boukhalfa, K. Sauer, K. G. McIntosh, R. P. Currier, A. E. Williams-Jones and X. Guo, Nat. Geosci., 2022, 15, 327–333 CrossRef CAS.
- A. E. Williams-Jones, I. M. Samson and G. R. Olivo, Econ. Geol., 2000, 95(2), 327–341 CrossRef CAS.
- A. P. Gysi and A. E. Williams-Jones, Geochim. Cosmochim. Acta, 2013, 122, 324–352 CrossRef CAS.
- A. P. Gysi, A. E. Williams-Jones and P. Collins, Econ. Geol., 2016, 111(5), 1241–1276 CrossRef.
- C. D. Beard, K. M. Goodenough, A. M. Borst, F. Wall, P. R. Siegfried, E. A. Deady, C. Pohl, W. Hutchison, A. A. Finch, B. F. Walter, H. A. Elliott and K. Brauch, Econ. Geol., 2022, 118(1), 32 Search PubMed.
- A. K. Patel, B. Mishra, D. Upadhyay and K. L. Pruseth, Econ. Geol., 2022, 117, 683–702 CrossRef.
- P. L. Verplanck, G. L. Farmer, R. M. Kettler, H. A. Lowers, C. A. Johnson, A. E. Koenig and M. J. Blessington, Ore Geol. Rev., 2022, 146, 104953 CrossRef.
- S. I. Lahti and V. I. Suominen, Bull. Geol. Soc. Finl., 1988, 60, 45–53 CAS.
- D. Holtstam and U. B. Andersson, Can. Mineral., 2007, 45, 1073–1114 CrossRef CAS.
- A. E. Williams-Jones and S. A. Wood, Geochim. Cosmochim. Acta, 1992, 56(2), 725–738 CrossRef CAS.
- M. T. Styles and B. R. Young, Mineral. Mag., 1983, 47, 41–46 CrossRef CAS.
- E. W. M. Heinrich and E. B. Gross, Am. Mineral., 1960, 45, 455–459 CAS.
- R. M. Perhac and E. W. Heinrich, Econ. Geol., 1964, 59(2), 226–239 CrossRef CAS.
- G. J. Beukes, H. D. Bruiyn and W. A. Westhuizen, S. Afr. J. Geol., 1991, 94, 313–320 CAS.
- A. E. Williams-Jones, A. A. Migdisov and I. M. Samson, Elements, 2012, 8, 355–360 CrossRef CAS.
- M. M. Muller, H. J. Kleebe, S. Lauterbach and G. Zito, Z. Kristallogr., 2011, 226, 467–475 CrossRef.
- A. A. Migdisov and A. E. Williams-Jones, Miner. Deposita, 2014, 49(8), 987–997 CrossRef CAS.
- A. A. Migdisov, A. E. Williams-Jones, J. Brugger and F. A. Caporuscio, Chem. Geol., 2016, 439, 13–42 CrossRef CAS.
- B. Maximov and H. Schulz, Acta Crystallogr., 1985, 41(2), 88–91 Search PubMed.
- W. A. Crichton, P. Bouvier, B. Winklerd and A. Grzechnik, Dalton Trans., 2010, 39, 4302–4311 RSC.
- J. Berndt and S. Klemme, Nat. Commun., 2022, 13, 2892 CrossRef CAS PubMed.
- G. M. Yaxley, M. Anenburg, S. Tappe, S. Decree and T. Guzmics, Annu. Rev. Earth Planet. Sci., 2022, 50, 261–293 CrossRef CAS.
- J. D. Rodriguez-Blanco, S. Shaw and L. G. Benning, Mineral. Mag., 2008, 72, 283–286 CrossRef CAS.
- D. J. Tobler, J. D. Rodriguez-Blanco, H. O. Sørensen, S. L. S. Stipp and K. Dideriksen, Cryst. Growth Des., 2016, 16(8), 4500–4508 CrossRef CAS.
- L. Terribili, R. Rateau, A. M. Szucs, M. Maddin and J. D. Rodriguez-Blanco, Cryst. Growth Des., 2024, 24(2), 632–645 CrossRef CAS PubMed.
- A. A. Coelho, Topas Academic v4.1, Coelho Software, Brisbane, Australia, 2007 Search PubMed.
- W. S. Rasband, ImageJ, U. S. National Institutes of Health, Bethesda, Maryland, USA, 1997–2018 Search PubMed.
- M. D. Abramoff, P. J. Magalhaes and S. J. Ram, Biophotonics Int., 2004, 11(7), 36–42 Search PubMed.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed.
- M. Avrami, J. Chem. Phys., 1939, 7, 1103 CrossRef CAS.
- A. Putnis, Introduction to Mineral Sciences, Cambridge University Press, Cambridge, 1992 Search PubMed.
- F. Xia, J. Brugger, G. Chen, Y. Ngothai, B. O'Neill, A. Putnis and A. Pring, Geochim. Cosmochim. Acta, 2009, 73(7), 1945–1969 CrossRef CAS.
- A. M. Szucs, M. Maddin, D. Brien, P. C. Guyett and J. D. Rodriguez-Blanco, Global Challenges, 2022, 2200085 Search PubMed.
- S. Shaw, S. E. Pepper, N. D. Bryan and F. R. Livens, Am. Mineral., 2005, 90(11–12), 1852–1860 CrossRef CAS.
- L. E. Davidson, S. Shaw and L. G. Benning, Am. Mineral., 2008, 93(8–9), 1326–1337 CrossRef CAS.
- J. D. Rodriguez-Blanco, S. Shaw and L. G. Benning, Nanoscale, 2011, 3, 265–271 RSC.
- A. C. Lasaga, Kinetic Theory in the Earth Sciences, Princeton University Press, Princeton, New Jersey, 1998 Search PubMed.
- N. Yee, S. Shaw, L. G. Benning and T. H. Nguyen, Am. Mineral., 2006, 91(1), 92–96 CrossRef CAS.
- K. M. Peterson, P. J. Heaney and J. E. Post, Chem. Geol., 2016, 444, 27–36 CrossRef CAS.
- G. Montanari, J. D. Rodriguez-Blanco, N. Bovet, S. L. S. Stipp and D. J. Tobler, Cryst. Growth Des., 2017, 17, 5269–5275 CrossRef CAS.
- M. Ossorio, T. M. Stawski, J. D. Rodriguez-Blanco, M. Sleutel, J. M. García-Ruiz, L. G. Benning and A. E. S. Van Driessche, Minerals, 2017, 7, 140 CrossRef.
- L. Granasy, T. Pusztai, G. Tegze, J. A. Warren and J. F. Douglas, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011605 CrossRef PubMed.
- A. Jordens, Y. P. Cheng and K. E. Waters, Miner. Eng., 2013, 41, 97–114 CrossRef CAS.
- A. M. Szucs, A. Stavropoulou, C. O'Donnell, S. Davis and J. D. Rodriguez-Blanco, Cryst. Growth Des., 2021, 21(1), 512–527 CrossRef CAS.
- L. B. Railsback, Geology, 2003, 31(9), 737–740 CrossRef CAS.
- G. H. Cartledge, J. Am. Chem. Soc., 1928, 50(11), 2855–2863 CrossRef CAS.
- G. H. Cartledge, J. Am. Chem. Soc., 1928, 50(11), 2863–2872 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- A. K. Cheetham, B. E. F. Fender, H. Fuess and A. F. Wright, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 94–97 CrossRef.
- Y. Ni, J. M. Hughes and A. N. Mariano, Am. Mineral., 1993, 78(3–4), 415–418 CAS.
- J. H. Van Der Merwe, Crit. Rev. Solid State Mater. Sci., 1978, 7, 209–231 CrossRef CAS.
- A. G. Walton, in Nucleation, ed. A. C. Zettlemoyer, Dekker, New York, 1969, pp. 225–307 Search PubMed.
- A. M. Szucs, M. Maddin, D. Brien, R. Rateau and J. D. Rodriguez-Blanco, RSC Adv., 2023, 13, 6919–6935 RSC.
- A. V. Chichagov, D. A. Varlamov, R. A. Dilanyan, T. N. Dokina, N. A. Drozhzhina, O. L. Samokhvalova and T. V. Ushakovskaya, Crystallogr. Rep., 2001, 46, 876–879 CrossRef.
- S. Vyas, R. W. Grimes, D. H. Gay, A. L. Rohl and J. Chem, Soc., Faraday Trans., 1998, 94, 427–434 RSC.
- A. N. Zaitsev, A. R. Chakhmouradian, O. I. Siidra, J. Spratt, C. T. Williams, C. J. Stanley, S. V. Petrov, S. N. Britvin and E. A. Polyakova, Mineral. Mag., 2011, 75(6), 2813–2822 CrossRef CAS.
- Y. Singh, G. Nagendra Babu, R. Viswanathan, M. Sai Baba, A. K. Rai and P. S. Parihar, Central Eur. J. Geosci., 2014, 6(4), 492–505 Search PubMed.
- H. C. Helgeson, Geochim. Cosmochim. Acta, 1968, 32(8), 853–877 CrossRef CAS.
- J. D. Rodríguez, A. Jiménez, M. Prieto, L. Torre and S. García-Granda, Am. Mineral., 2008, 93, 928–939 CrossRef.
- R. Miyawaki, S. Matsubara, K. Yokoyama, K. Takeuchi, Y. Terada and I. Nakai, Am. Mineral., 2000, 85(7–8), 1076–1081 CrossRef CAS.
- B. Vallina, J. D. Rodriguez-Blanco, A. P. Brown, J. A. Blanco and L. G. Benning, Nanoscale, 2015, 7, 12166–12179 RSC.
- D. G. Brookins, Yttrium and the Rare Earth Elements (REE), in Eh-pH diagrams for geochemistry, ed. D. G. Brookins, Springer Berlin Heidelberg, Berlin, Heidelberg, 1988 Search PubMed.
- B. Bilal, E. Müller and E. Z. Naturforsch, A: Phys. Sci., 1992, 47(9), 974–984 CAS.
- P. Janos, J. Henych, J. Pfeifer, N. Zemanova, V. Pilarova, D. Milde, T. Opletal, J. Tolasz, M. Maly and V. Stengl, Environ. Sci.: Nano, 2017, 4, 1283–1293 RSC.
- T. V. Plakhova, A. Y. Romanchuk, S. N. Yakunin, T. Dumas, S. Demir, S. Wang, S. G. Minasian, D. K. Shuh, T. Tyliszczak, A. A. Shiryaev, A. V. Egorov, V. K. Ivanov and S. N. Kalmykov, J. Phys. Chem., 2016, 120(39), 22615–22626 CAS.
- M. Voigt, J. D. Rodriguez-Blanco, B. Vallina, L. G. Benning and E. H. Oelkers, Chem. Geol., 2016, 430, 7077 CrossRef.
- T. Mioduski, C. Guminski, D. Zeng and J. Phys, Chem. Ref. Data, 2015, 44(1), 013102–013101 CrossRef.
- Y. Xing, B. Etschmann, W. Liu, Y. Mei, Y. Shvarov, D. Testemale, A. Tomkins and J. Brugger, Chem. Geol., 2018, 504, 158–176 CrossRef.
- S. Salvi and A. E. Williams-Jones, Geochim. Cosmochim. Acta, 1996, 60, 1917–1932 CrossRef CAS.
- E. P. Perry and A. P. Gysi, Geofluids, 2018, 5382480, 1–19 CrossRef.
- B. Vallina, J. D. Rodriguez-Blanco, J. A. Blanco and L. G. Benning, Mineral. Mag., 2014, 78, 1391–1397 CrossRef.
- L. C. Hsu, Mineral. Petrol., 1992, 47, 87–101 CrossRef CAS.
- H. Wakita and S. Kinoshita, Bull. Chem. Soc. Jpn., 1979, 52, 428–432 CrossRef CAS.
- W. Mejri, A. Korchef, M. Tlili and M. Ben Amor, Desalin. Water Treat., 2014, 52(25–27), 4863–4870 CrossRef CAS.
- G. D. Saldi, G. Jordan, J. Schott and E. H. Oelkers, Geochim. Cosmochim. Acta, 2009, 73(19), 5646–5657 CrossRef CAS.
- D. Di Tommaso and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2010, 12(4), 894–901 RSC.
- M. R. Nielsen, K. K. Sand, J. D. Rodriguez-Blanco, N. Bovet, J. Generosi, K. N. Dalby and S. L. S. Stipp, Cryst. Growth Des., 2016, 16, 6199–6207 CrossRef CAS.
- H. Sakuma, M. P. Andersson, K. Bechgaard, S. L. S. Stipp and J. Phys, Chem. C, 2014, 118(6), 3078–3087 CAS.
- D. Kralj, J. Kontrec, L. Brecevic, G. Falini and V. Nothing-Laslo, Chem. – Eur. J., 2004, 10, 1647–1656 CrossRef CAS PubMed.
- J. Zheng, Y. Wang, J. Wang, H. Yuan, Y. Liu, T. Liu, J. Luo, J. Nai and X. Tao, Appl. Mater. Interfaces, 2022, 14(43), 48762–48769 CrossRef CAS PubMed.
- M. Maddin, R. Rateau, A. M. Szucs, L. Terribili, B. Hoare, P. C. Guyett and J. D. Rodriguez-Blanco, Global Challenges, 2024, 2400074 CrossRef.
- G. Hass, J. B. Ramsey and R. Thun, J. Opt. Soc. Am., 1959, 49(2), 116–120 CrossRef CAS.
- M. M. Lezhnina, T. Jüstel, H. Kätker, D. U. Wiechert and U. H. Kynast, Adv. Funct. Mater., 2006, 16(7), 935–942 CrossRef CAS.
- V. Bartunek, V. Jakes, V. Kral and J. Rak, J. Fluorine Chem., 2012, 135, 358–361 CrossRef CAS.
- R. K. Sharma, A. V. Mudring and P. Ghosh, J. Lumin., 2017, 189, 44–63 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr01614a |
| This journal is © The Royal Society of Chemistry 2024 |