Giant Rashba-splitting of one-dimensional metallic states in Bi dimer lines on InAs(100)

Abstract

Bismuth produces different types of ordered superstructures on the InAs(100) surface, depending on the growth procedure and coverage. The (2 × 1) phase forms at completion of one Bi monolayer and consists of a uniformly oriented array of parallel lines of Bi dimers. Scanning tunneling and core level spectroscopies demonstrate its metallic character, in contrast with the semiconducting properties expected on the basis of the electron counting principle. The weak electronic coupling among neighboring lines gives rise to quasi one-dimensional Bi-derived bands with open contours at the Fermi level. Spin- and angle-resolved photoelectron spectroscopy reveals a giant Rashba splitting of these bands, in good agreement with ab initio electronic structure calculations. The very high density of the dimer lines, the metallic and quasi one-dimensional band dispersion and the Rashba-like spin texture make the Bi/InAs(100)-(2 × 1) phase an intriguing system, where novel transport regimes can be studied.

---

Introduction

The Rashba–Bychkov (RB) effect lifts the spin degeneracy of the electronic bands in crystalline solids with broken structural inversion symmetry,¹ typically caused by the presence of a surface or an interface. This effect has attracted great attention as a fundamental mechanism for spin generation/control in spintronic devices,^2,3 owing to the spin-momentum locking, which constraints the spin and momentum directions of an electron to be mutually perpendicular. The RB effect has been detected by angle-resolved photoelectron spectroscopy (ARPES) in many two-dimensional (2D) systems and classified according to the Rashba parameter α_R, which quantifies the energy–momentum separation of the bands with opposite spins.^4–7α_R depends on the atomic spin–orbit coupling (SOC) and the gradient of the electron potential across the structural discontinuity (surface/interface plane).^8–11 The giant RB effect (α_R > 3 eV Å) has been suggested to play a key role in spin-to-charge conversion phenomena occurring in 2D heterostructures.^12–15 The discovery of a large Rashba splitting in the metallic states of Pb on Ge(111) has opened the way to spin accumulation, filtering and injection in semiconductor materials.¹⁶

The RB effect can significantly influence the electronic structure and spin texture of one-dimensional (1D) systems, such as quantum wires, and favor the emergence of a specific spintronic functionality.¹⁷ In a 1D system subject to the RB interaction the spin degeneracy of the spin-split bands at the time-reversal symmetry point can be removed by an external magnetic field opening a gap. If this gap opens at the Fermi level (E_F), a pure and non-dissipative spin current can be established by applying a voltage. The exploitation of this mechanism is not trivial due to the scarcity of systems with genuine 1D RB-like spin texture. As an example, the 1D bands of Bi chains on Ag(110) display giant RB splitting, but the density of states of the system at E_F is dominated by bulk Ag states.¹⁸ Semiconductor substrates, on the other hand, can support the formation of 1D structures with RB-split metallic states, as experimentally demonstrated for Au chains on Si(557),¹⁹ and theoretically predicted for Bi-adsorbed In atomic chains on Si(111).²⁰

Bi is known to form different types of superstructures on III–V semiconducting surfaces.^21–34 Some of these are based on Bi stripes displaying quasi 1D bands with giant RB splittings.^{28,30–32,34} Bi-terminated III–V semiconductors are expected to be non-metallic, according to the electron counting model, in order to decrease the surface energy.³⁵ A notable exception to this model is the metallic behavior of Bi dimer lines grown on GaAs(100) (the so-called (2 × 1) phase), which emerges from scanning tunneling spectroscopy (STS) measurements and finds confirmation in density functional theory (DFT) calculations (without SOC).^23,24 This full-monolayer phase made of symmetric dimers is stabilized by stress relief and pseudogap formation²³ and was predicted to maintain long range compositional uniformity even at high temperature.³⁶ An in-depth analysis aimed at establishing the dimensionality of the Bi-derived states and the magnitude of the RB effect in this and similar systems (Bi/GaAs_xN_1−x(100)-(2 × 1)²² and Bi/InAs(100)-(2 × 1)²⁶) is still missing.

The present study reports on the electronic structure of the Bi/InAs(100)-(2 × 1) phase, which is examined by STS, photoelectron spectroscopy with spin analysis and DFT calculations. The (2 × 1) phase occurs at the completion of one Bi monolayer and consists of an array of uniformly oriented Bi dimer lines. The electronic coupling between neighboring lines turns out to be much weaker than along the dimer lines, thus giving rise to Bi-derived bands with highly anisotropic in-plane dispersion. The Fermi surface presents open quasi 1D contours with RB-like spin texture and giant splitting with α_R values up to 4.6 eV Å, owing to the large SOC of Bi and the low structural symmetry. These findings suggest that the Bi/InAs(100)-(2 × 1) phase could support the generation of non-dissipative and spin-polarized currents and find application in spin-to-charge conversion processes.

Methods

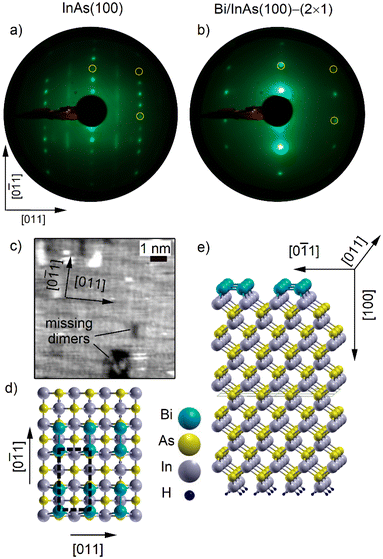
Undoped n-type wafer substrates of InAs(100) were treated with Ar ion sputtering (800 eV) and annealing (720 K) cycles. This procedure results in the formation of the (4 × 2)/c(8 × 2) surface reconstruction visible in the low-energy electron diffraction (LEED) pattern of Fig. 1(a).^26,37,38 Bi was deposited from a resistively heated source in excess to one monolayer (1 ML corresponds to one Bi atom per (1 × 1) surface unit cell of InAs(100)) on the substrate kept at 300 K. The Bi/InAs(100) interface displays the following sequence of ordered superstructures for decreasing Bi coverage: (2 × 6) for more than 1.33 ML Bi,^21,29,33 (2 × 10) at about 1.2 ML Bi,²⁶ (2 × 1) at 1 ML Bi,²⁶ (2 × 8) coexisting with (2 × 4) below 1 ML Bi,²⁴ (2 × 4) at 0.38 ML Bi.²¹ 60-Minute-long annealing at 550 K was necessary to release Bi exceeding 1 ML from the surface and stabilize the (2 × 1) phase (LEED pattern in Fig. 1(b)). This phase consists of a uniform array of Bi dimer lines running along the [011] direction, as shown in the scanning tunneling microscopy (STM) image of Fig. 1(c).²⁶ STM and STS data were acquired with a home-made instrument at 300 K for the clean InAs(100) surface and at 70 K for the Bi/InAs(100)-(2 × 1) phase by using a gold tip. The bias voltage and current were set to of V_bias = −0.5 V and I = 3 × 10⁻¹¹ A to acquire constant current topographic maps. The differential conductance (dI/dV) curves were measured by the lock-in technique with a 20 mV modulation of V_bias. Photoelectron spectroscopy measurements were carried out at the VUV-Photoemission, BaDElPh³⁹ and NanoESCA⁴⁰ beamlines of the Elettra Synchrotron (Trieste, Italy) at liquid nitrogen temperature. Core level and ARPES spectra were collected with hemispherical electron spectrometers at the VUV-Photoemission and BaDElPh beamlines. Spin- and momentum-resolved constant energy maps of the photoelectron signal were acquired at the NanoESCA beamline using a momentum microscope, which is equipped with a W(100)-based spin detector.⁴¹ The analysis of the spin-resolved maps was performed following the procedure described in ref. 42.

Fig. 1 (a) LEED pattern of clean InAs(100) with (4 × 2)/c(8 × 2) reconstruction at 48 eV primary electron energy. Yellow circles mark the position of the (1 × 1) spots. (b) LEED pattern of the Bi/InAs(100)-(2 × 1) phase at 46 eV primary electron energy. Yellow circles mark the position of the (1 × 1) spots. (c) Constant current STM image of the Bi/InAs(100)-(2 × 1) phase. Light gray rectangles represent the Bi dimers. Missing dimers appear as dark regions. (d) Top view and (e) three-dimensional rendition of the structural model used to calculate the electronic structure of the Bi/InAs(100)(2 × 1) phase. The dashed rectangle in (d) represents the (2 × 1) surface unit cell.

DFT calculations were performed in the local density approximation⁴³ using the full potential linearized augmented plane-wave method, as implemented in the Fleur code.⁴⁴ The Bi/InAs(100)-(2 × 1) system was simulated with a slab of 21 atomic layers based on the symmetric dimer model proposed for the Bi/GaAs(100)-(2 × 1) system:²⁴ one-atom-thick Bi dimer lines running along the [011] direction on the top surface; 19 atomic layers of InAs(100), with outermost In planes, as the substrate; hydrogen-terminated bottom surface. Fig. 1(d and e) display the top view and the three-dimensional representation of this structural model. The in-plane lattice constant (4.27 Å) and interlayer distance between In (or As) planes (3.02 Å) were set to those of bulk InAs. Structural relaxation on the Bi-terminated side of the slab led to 2.96 Å Bi–In interlayer distance, 3.07 Å Bi–Bi distance in the dimers and 0.5% expansion of the interlayer distance between the topmost In planes. Compared to the 1 × 1 Bi monolayer, about 0.31 eV/Bi are gained by Bi dimerization. Hydrogen atoms were placed on the bottom surface to saturate the dangling bonds. An attractive potential term of 2.67 eV was applied to the p-states of In and As to get a better description of the band gap and SOC was included in a self-consistent manner. The In terminations on both sides of the InAs substrate led to an artificial hole doping of the system and to a difference of 0.22 eV between the E_F position in the calculations and experiments.

Results and discussion

Fig. 1(c) shows a typical STM image acquired on a sample displaying the (2 × 1) LEED pattern (Fig. 1(b)). The observation of light gray rectangles with 2 : 1 ratio between the long side (aligned with the [01̄1] substrate axis) and the short side (aligned with the [011] substrate axis) is a signature of the dimerization of Bi atoms, which are not resolved individually in the present image,²⁶ in analogy to similar systems.^22,23 The dimers form an array of parallel lines running along the [011] axis. The continuity of the Bi dimer lines is occasionally interrupted by missing dimers (dark gray areas), as reported for the Bi/GaAs(100)-(2 × 1) phase.²³ The structural features observed in the STM image are reproduced by the model of the Bi/InAs(100)-(2 × 1) phase. Bi atoms forming dimers present a reduced Bi–Bi distance along [01̄1] with respect to the surface lattice constant of the substrate (Fig. 1(d)). These Bi dimers give rise to the parallel lines seen in Fig. 1(e).

Fig. 2 compares STS and photoelectron spectra of the clean InAs(100) surface and Bi/InAs(100)-(2 × 1) phase. The dI/dV signal of clean InAs(100) (top spectrum of Fig. 2(a)) is close to zero over an interval of 0.30 eV including E_F that can be identified with the bulk bandgap of the substrate.⁴⁵ The dI/dV signal of the Bi/InAs(100)-(2 × 1) phase (collected away from missing dimer regions, bottom spectrum of Fig. 2(a)) is more than a factor 10 higher than the noise level at E_F, thus attesting the metallic character of the (2 × 1) phase. The peaks observed at −0.2, −0.08 and 0.08 eV (black arrows) will be discussed later in connection with the ARPES and DFT analyses.

Fig. 2 (a) dI/dV spectra for clean InAs(100) at 300 K (top spectrum) and Bi/InAs(100)-(2 × 1) at 70 K (bottom spectrum). Negative V_bias values indicate occupied states. (b) Survey photoelectron spectra at hν = 70 eV of clean InAs(100) (top spectrum) and Bi/InAs(100)-(2 × 1) (bottom spectrum) and (c) corresponding spectra near E_F. (d–f) Core level spectra hν = 70 eV and related fittings of the (e) As 3d (f) Bi 5d and (g) In 4d lines for the clean InAs/(100) surface (top) and Bi/InAs(100)-(2 × 1) phase (bottom).

Survey spectra of the photoelectron signal at hν = 70 eV for the two systems (Fig. 2(b)) are useful to compare the intensities of the core level lines. In both cases, the much higher signal of In with respect to As has combined structural and electronic origin, as the sputtering/annealing procedure results in an excess of In at the surface and In 4d states have 5.6 times larger photoionization cross section than As 3d states.⁴⁶ The zoom of the photoelectron signal near E_F for InAs(100) (top spectrum) and Bi/InAs(100)-(2 × 1) (bottom spectrum) in Fig. 2(c) highlights the semiconducting vs. metallic properties of the two systems.

Fig. 2(d–f) show the analysis of the As 3d, Bi 5d and In 4d levels of InAs(100) (top spectra) and Bi/InAs(100)-(2 × 1) (bottom spectra), respectively. The As 3d spectrum of clean InAs(100) can be fitted with two doublets related to sub-surface As atoms (red line, As 3d_5/2 at 40.50 eV) and bulk-like As atoms (green line, As 3d_5/2 at 40.69 eV). The sub-surface component is suppressed due to a restructuring of the (4 × 2)/c(8 × 2) termination, occurring in correspondence with the formation of the (2 × 1) phase. The Bi 5d spectrum can be fitted with one doublet (blue line, Bi 5d_5/2 at 23.55 eV) very similar to that of metallic Bi,⁴⁷ at variance with the two doublets used in the literature.²⁶ The slight asymmetry of the peaks (tail on the high binding energy side) is interpreted as a signature of the metallic character of the Bi/InAs(100)-(2 × 1) phase,⁴⁸ rather than ascribed to the presence of another phase.²⁶ This interpretation is in agreement with the data of Fig. 2(a and c) and will be strengthened by the ARPES and DFT analyses reported in Fig. 3 and 4. Two doublets corresponding to surface (red line, In 4d_5/2 at 17.48 eV) and bulk (green line, In 4d_5/2 at 17.23 eV) components are sufficient to fit the In 4d spectrum of clean InAs(100). After the formation of the (2 × 1) phase, the surface doublet is quenched and another doublet appears on the low binding energy side of the bulk component. This new doublet has an asymmetric shape (blue line, In 4d_5/2 at 16.93 eV) that is compatible with metallic In⁴⁹ in contact with surface metallic Bi.

Fig. 3 (a–c) Constant energy cuts of the photoelectron signal for the Bi/InAs(100)-(2 × 1) phase taken at 0.15 eV binding energy with hν = 65 eV and p-polarized light. Black dashed lines indicate the edges of the SBZs. (a) Original data. (b) High-symmetry points of the central SBZ (thick black line), and constant energy contours of the S₁–S₄ bands (red/blue continuous lines) are plotted on the original data. (c) Second derivative of the original data along the k_x axis. (d) Spin-polarized constant energy cut at 0.15 eV. SQA and SBZs (dashed lines) are shown. (e–i) ARPES spectra collected along the green dashed lines shown in panel (b). All data are displayed in the second derivative form. (e–g) Spectra along three equivalent directions. (h) Spectra along the S̄–Ȳ–S̄ direction. (i) Spectra along the direction.

Fig. 4 (a) Spin-resolved DFT calculations. The size of the symbols is proportional to the in-plane component of the spin polarization along the k_y axis. The location of E_F in the calculation (left axis) and in the experiment (right axis) differ by 0.22 eV. (b) Comparison between the band dispersion calculated by DFT and measured by ARPES along the S̄–Ȳ–S̄ direction using the experimental energy scale.

Fig. 3(a–c) show a constant energy cut of the photoelectron signal of the Bi/InAs(100)-(2 × 1) phase acquired at 0.15 eV below E_F with the momentum microscope. This instrument allows to scan simultaneously an area of the (k_x,k_y) space including several surface Brillouin zones (SBZs) of the system. For clarity, the edges of the (2 × 1) SBZs (black dashed lines) are overlaid to the data. The central SBZ (rectangle with thick black edges, and ) and its high symmetry points are reported in Fig. 3(b). The photoelectron signal is characterized by four bands S₁–S₄, which are elongated in the k_y direction and cross the edges of neighboring SBZs. Fig. 3(c) displays the second derivative of the original data taken along the k_x axis, to better visualize low intensity sections of S₁–S₄. All the features observed in Fig. 3(a–c) are absent in the clean substrate (Fig. S1 of the ESI†),⁵⁰ reflect the periodicity of the (2 × 1) superstructure, and, therefore, can be identified as Bi-derived electronic states. The wavy S₁/S₂ and straight S₃/S₄ constant energy contours are schematically represented by red and blue continuous lines for positive k_x values in Fig. 3(b), where the color is assigned on the basis of the spin analysis.

In the spin-resolved constant energy map of Fig. 3(d) the spin quantization axis (SQA), determined by the experimental geometry,⁴⁰ is parallel to the k_y axis. The intensity of red and blue colors for spin-up and spin-down states, respectively, is proportional to their spin projection along the SQA. The most evident feature of Fig. 3(d) is the full reversal of the spin texture with respect to the k_y axis. Portions of the S₁–S₃ contours are highlighted by red/blue dashed lines for positive k_x values to guide the eye. S₁ and S₂ display high and opposite spin polarizations, thus suggesting they form a RB pair. The spin analysis of S₃ and S₄ is hindered by their low intensity close to k_x = 0 axis, while their high spin-polarization clearly emerges at larger |k_x| values. The high spin-polarization of the S₁–S₄ states in Fig. 3(d) means that the spins of the Bi-derived bands are almost parallel or anti-parallel to the SQA.

The ARPES spectra of Fig. 3(e–i) show the energy–momentum dispersion of the S₁–S₄ bands along the segments marked by the green dashed lines in Fig. 3(b). Also in this case the data are presented in the second derivative form to enhance the sensitivity to weak features. The three ARPES maps taken along equivalent directions (Fig. 3(e–g)) demonstrate the strong state-dependent modulation of the photoelectron signal in the (k_x,k_y) plane, due to matrix element effects. S₁ and S₂ clearly cross E_F, thus making the Bi/InAs(100)-(2 × 1) phase metallic, in agreement with the analysis displayed in Fig. 2. This metallic character is a distinctive feature of the (2 × 1) phases that 1 ML Bi forms on GaAs(100)^23,24 and GaAs_xN_1.x(100).²² All S₁–S₄ states can be observed simultaneously along the S̄–Ȳ–S̄ direction of Fig. 3(h). The dispersion of S₃ and S₄ (Fig. 3(g and h) and Fig. S2 of the ESI†) closely reminds the RB-split states observed in the (2 × 1) phases of Bi on the (110) surfaces of III–V semiconductors.^28,30–32 This suggests that also S₃/S₄ form a RB pair of bands, in analogy to S₁/S₂. Fig. 3(i) shows the ARPES spectra along the direction. The flat feature represents the S₃/S₄ crossing point. The minimum at 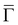(0.2 eV) and the flat dispersion about Ȳ (0.08–0.1 eV) can be directly correlated to the peaks observed at the same energies in the occupied part of the STS spectrum in Fig. 2(a). The STS peak at 0.08 eV above E_F can be linked to the maxima of the S₃ and S₄ bands (see Fig. 4), which cross E_F and, therefore, contribute to the metallicity of the system.

The data of Fig. 3 clearly demonstrate that all S₁–S₄ bands have an anisotropic in-plane dispersion, which can be associated to the structural properties of the (2 × 1) phase. Due to the formation of the Bi dimers, the separation between Bi atoms in neighboring dimer lines is larger than along the lines. Correspondingly, the electronic coupling of Bi-related states along the dimer lines is stronger that perpendicular to them, thus resulting in steeply dispersing and flat bands, respectively, and open elongated contours. Overall, the ARPES and spin polarization analyses allow to describe S₁/S₂ and S₃/S₄ as RB-split pairs of bands with quasi 1D and metallic character.

In order to interpret the experimental findings described above, the electronic structure of the Bi/InAs(100)-(2 × 1) system was computed by DFT using the model reported in Fig. 1(d and e), which is based on the symmetric dimer model proposed for the Bi/GaAs(100)-(2 × 1) system.²⁴Fig. 4(a) shows the spin-resolved DFT band structure calculations along the high-symmetry directions of Bi/InAs(100)(2 × 1). The size of the symbols is proportional to the spin polarization of the states, with the SQA oriented along the k_y axis. Red/blue colors correspond to up/down spin channels, in analogy to the experiment. The horizontal dashed line indicates the experimental position of E_F, which lies 0.22 eV above E_F in the calculations. This difference has been evaluated by aligning the experimental and calculated S₃/S₄ bands (Fig. 4(b)). It derives from the artificial hole doping due to the excess of In atoms in the model (10 In planes vs. 9 As planes). To ease the comparison between experiment and theory, the energy scale of the calculations will be referred to the experimental position of E_F (right axis of Fig. 4(a)) from here onwards. The electronic structure in the proximity of E_F is characterized by four spin-polarized and Bi-derived bands, which are labeled with S₁–S₄ in analogy to the experiment. The additional bands crossing E_F along 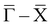and 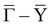and showing no spin-polarization originate from the H-terminated surface and are not relevant to the present discussion.

All S₁–S₄ bands display quasi 1D character, which emerges by comparing their steep dispersion along and Ȳ–S̄ (parallel to the Bi dimer lines) with their flat dispersion along and X̄–S̄ (perpendicular to the Bi dimer lines). The spin analysis reveals that S₁/S₂ and S₃/S₄ form two RB pairs. The strength of the RB effect can be evaluated in the proximity of 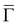and Ȳ through α_R = 2·ΔE/Δk, as shown in Fig. 4(b). The S₁/S₂ pair presents giant α_R values of 4.6 eV Å along S̄–Ȳ–S̄ and 3.5 eV Å along 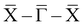. For the S₃/S₄ pair α_R is 2.3 eV Å along S̄–Ȳ–S̄ and 2.7 eV Å along 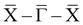. In Fig. 4(b) the calculated bands are overlaid to the ARPES data of Fig. 3(h) to demonstrate the correspondence between theory and experiment. The slight offset of the experimental S₁/S₂ pair with respect to the calculations can indicate that the spin-splitting and, consequently, the α_R value are larger than predicted. A similar effect is seen Fig. S2 of the ESI† for the S₃/S₄ pair. The overall good agreement allows to describe the Bi/InAs(100)-(2 × 1) phase as an array of Bi dimer lines with metallic character determined by two pairs of bands displaying quasi 1D dispersion and RB-like spin texture.

The RB states of the present system display a unique combination of metallic character, giant Rashba parameter and strong 1D anisotropy. The measured Rashba parameter of 4.6 eV A is larger than the giant values reported for the metallic states of BiTeI (3.85 eV A (ref. 51)), Bi/Ag(111) (3.05 eV A (ref. 6)), free-standing atomic Te chains (2.17 eV A (ref. 52)) and metallic nanowires on semiconducting substrates (0.8–3.5 eV A (ref. 20, 53 and 54)). It approaches the largest α_R value so far observed in semiconducting Bi lines (5.5 eV A (ref. 28)). We emphasize that this giant value originates primarily from the large SOC of Bi and the 1D anisotropy of the dimer lines, and is rather insensitive to the choice of the potential and therefore of the substrate's gap (Fig. S3†). The unique properties of the Bi/InAs(100)-(2 × 1) phase can find application in spin-to-charge conversion via the inverse Edelstein effect.⁵⁵ The Rashba-split surface states could carry a charge current in response to the nonzero spin density associated to spin injection from an adjacent ferromagnetic layer.¹² Such an interface can be used to detect spin currents with an efficiency that is expressed by λ = α_Rτ_s/ħ, where τ_s is the spin-relaxation time.⁵⁶ Assuming the average spin-relaxation time of 5 fs,^28,56 one may expect an efficiency of about 3.5 nm, which is significantly larger than in 2D RB systems (0.3 nm (ref. 12)) and topological insulators (2.1 nm (ref. 57)). The decoupling of the S₁/S₂ surface bands from the bulk states of the semiconductor substrate near E_F ¹⁵ and the reduced back-scattering associated to the quasi 1D dispersion^58–60 could favor even larger τ_s values. From the fundamental point of view, the S₁/S₂ bands could be also used for studying exotic electronic phenomena, such as Majorana bound states⁶¹ and spin-dependent density waves.⁶² At variance with the S₁/S₂ bands, the maxima of the S₃/S₄ pair lie just above E_F close to . Most likely these maxima produce the peak located at 0.08 eV in the unoccupied part of the STS spectrum (Fig. 2(a)). In fact, S₁ and S₂ are expected to give rise to a featureless dI/dV signal, due to their steep dispersion and distance from 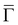near E_F. The vicinity of the S₃/S₄ crossing point to E_F at , which is a time-reversal symmetry point of the system, can realize the scenario depicted in ref. 17: an external magnetic field could open a gap between S₃ and S₄; if the gap includes E_F, the application of a voltage would allow the flow of a non-dissipative, pure spin current through the Bi dimer lines. Notably, the exact location of the S₃/S₄ bands with respect to E_F can be tuned by external doping or gating, thanks to the semiconducting nature of the substrate, to meet the requirements of ref. 17.

Conclusion

The present work reports on the electronic structure of the Bi/InAs(100)-(2 × 1) phase. This system can be described as a compact array of Bi dimer lines, whose metallic character is determined by two pairs of quasi 1D bands displaying RB-type spin texture. The robust metallicity and giant Rashba parameter of S₁/S₂ pair can be of interest for spin-to-charge conversion devices, with potentially high efficiency enhanced by the 1D anisotropic dispersion and semiconducting substrate. The location of the low-lying S₃/S₄ pair, with a crossing point at very close to E_F, appears to be suitable to host pure spin-polarized and non-dissipative currents, upon the application of an external magnetic field. The experimental verification of these novel transport properties would open new perspectives for the exploitation of the RB effect in spintronic devices.

Author contributions

P. M. Sheverdyaeva: investigation, data curation, validation, formal analysis, writing – original draft, project administration. G. Bihlmayer: resources, software, conceptualization, validation, writing – review and editing. S. Modesti: investigation, data curation, validation, formal analysis, writing – review and editing. V. Feyer, M. Jugovac, G. Zamborlini, C. Tusche, Ying-Jiun Chen, X. L. Tan, K. Hagiwara, L. Petaccia, S. Thakur, A. K. Kundu: investigation, data curation, validation, writing – review & editing. Carlo Carbone: validation, writing – review & editing. Paolo Moras: conceptualization, supervision, validation, writing – review & editing. All authors participated in the analysis and discussion of the results.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge EUROFEL-ROADMAP ESFRI of the Italian Ministry of University and Research. G. B. gratefully acknowledges the computing time granted through JARA-HPC on the supercomputer JURECA at Forschungszentrum Jülich. A. K. K. acknowledges receipt of a fellowship from the ICTP-TRIL Programme, Trieste, Italy and funding from the US Department of Energy, Office of Basic Energy Sciences, contract no. DE-SC0012704. C. T. and Y.-J. C. acknowledge support by the German Federal Ministry of Education and Research (BMBF) under grant no. 05K19PGA. We acknowledge Elettra Sincrotrone Trieste for providing access to its synchrotron radiation facilities (beamtime no. 20170258, 20175193, 20185310).

References

1. Y. A. Bychkov and E. I. Rashba, Oscillatory effects and the magnetic susceptibility of carriers in inversion layers, J. Phys. C: Solid State Phys., 1984, 17, 6039.
2. A. Manchon, H. Koo, J. Nitta, S. M. Frolov and R. A. Duine, New perspectives for Rashba spin–orbit coupling, Nat. Mater., 2015, 14, 871.
3. I. Žutić, J. Fabian and S. Das Sarma, Spintronics: Fundamentals and applications, Rev. Mod. Phys., 2004, 76, 323.
4. S. LaShell, B. A. McDougall and E. Jensen, Spin Splitting of an Au(111) Surface State Band Observed with Angle Resolved Photoelectron Spectroscopy, Phys. Rev. Lett., 1996, 77, 3419.
5. Y. M. Koroteev, G. Bihlmayer, J. E. Gayone, E. V. Chulkov, S. Blügel, P. M. Echenique and P. Hofmann, Strong Spin-Orbit Splitting on Bi Surfaces, Phys. Rev. Lett., 2004, 93, 046403.
6. C. R. Ast, J. Henk, A. Ernst, L. Moreschini, M. C. Falub, D. Pacilé, P. Bruno, K. Kern and M. Grioni, Giant Spin Splitting through Surface Alloying, Phys. Rev. Lett., 2007, 98, 186807.
7. A. Tamai, W. Meevasana, P. D. C. King, C. W. Nicholson, A. de la Torre, E. Rozbicki and F. Baumberger, Spin-orbit splitting of the Shockley surface state on Cu(111), Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 075113.
8. G. Bihlmayer, S. Blügel and E. V. Chulkov, Enhanced Rashba spin-orbit splitting in Bi/Ag(111) and Pb/Ag(111) surface alloys from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 195414.
9. J. Premper, M. Trautmann, J. Henk and P. Bruno, Spin-orbit splitting in an anisotropic two-dimensional electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 073310.
10. S. Mathias, A. Ruffing, F. Deicke, M. Wiesenmayer, I. Sakar, G. Bihlmayer, E. V. Chulkov, Yu. M. Koroteev, P. M. Echenique, M. Bauer and M. Aeschlimann, Quantum-Well-Induced Giant Spin-Orbit Splitting, Phys. Rev. Lett., 2010, 104, 066802.
11. H. Bentmann, T. Kuzumaki, G. Bihlmayer, S. Blügel, E. V. Chulkov, F. Reinert and K. Sakamoto, Spin orientation and sign of the Rashba splitting in Bi/Cu(111), Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 115426.
12. J. C. Rojas Sánchez, L. Vila, G. Desfonds, S. Gambarelli, J. P. Attané, J. M. De Teresa, C. Magén and A. Fert, Spin-to-charge conversion using Rashba coupling at the interface between non-magnetic materials, Nat. Commun., 2013, 4, 2944.
13. R. Sun, S. Yang, X. Yang, E. Vetter, D. Sun, N. Li, L. Su, Y. Li, Y. Li, Z. Z. Gong, Z. K. Xie, K. Y. Hou, Q. Gul, W. He, X. Q. Zhang and Z. H. Cheng, Large Tunable Spin-to-Charge Conversion Induced by Hybrid Rashba and Dirac Surface States in Topological Insulator Heterostructures, Nano Lett., 2019, 19, 4420.
14. J. Li, P. Xu, J. Shen, Y. Cai and X. Jin, Spin-charge conversion in Bi(√3×√3)R30°/Ag(111) structure, J. Magn. Magn. Mater., 2021, 540, 168471.
15. J. Shen, Z. Feng, P. Xu, D. Hou, Y. Gao and X. Jin, Spin-to-Charge Conversion in Ag/Bi Bilayer Revisited, Phys. Rev. Lett., 2021, 126, 197201.
16. K. Yaji, Y. Ohtsubo, S. Hatta, H. Okuyama, K. Miyamoto, T. Okuda, A. Kimura, H. Namatame, M. Taniguchi and T. Aruga, Large Rashba spin splitting of a metallic surface-state band on a semiconductor surface, Nat. Commun., 2010, 1, 17.
17. C. H. L. Quay, T. L. Hughes, J. A. Sulpizio, L. N. Pfeiffer, K. W. Baldwin, K. W. West, D. Goldhaber-Gordon and R. de Picciotto, Observation of a one-dimensional spin–orbit gap in a quantum wire, Nat. Phys., 2010, 6, 336.
18. P. M. Sheverdyaeva, D. Pacilè, D. Topwal, U. Manju, M. Papagno, V. Feyer, M. Jugovac, G. Zamborlini, I. Cojocariu, C. Tusche, X. L. Tan, K. Hagiwara, Y.-J. Chen, J. Fujii, P. Moras, L. Ferrari, E. Vescovo, G. Bihlmayer and C. Carbone, One-dimensional Rashba states with unconventional spin texture in Bi chains, Phys. Rev. B, 2022, 106, 045108.
19. T. Okuda, K. Miyamoto, Y. Takeichi, H. Miyahara, M. Ogawa, A. Harasawa, A. Kimura, I. Matsuda, A. Kakizaki, T. Shishidou and T. Oguchi, Large out-of-plane spin polarization in a spin-splitting one-dimensional metallic surface state on Si(557)-Au, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 161410.
20. T. Tanaka and Y. Gohda, First-principles prediction of one-dimensional giant Rashba splittings in Bi-adsorbed In atomic chains, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98, 241409(R).
21. P. Laukkanen, M. Ahola, M. Kuzmin, R. E. Perälä, I. J. Väyrynen and J. Sadowski, Bi-induced (2 × 6), (2 × 8), and (2 × 4) reconstructions on the InAs(1 0 0) surface, Surf. Sci., 2005, 598, L361.
22. P. Laukkanen, J. Pakarinen, M. Ahola-Tuomi, M. Kuzmin, R. E. Perälä, I. J. Väyrynen, A. Tukiainen, J. Konttinen, P. Tuomisto and M. Pessa, Structural and electronic properties of Bi-adsorbate-stabilized reconstructions on the InP(100) and GaAsxN1−x(100) surfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 155302.
23. P. Laukkanen, M. P. J. Punkkinen, H.-P. Komsa, M. Ahola-Tuomi, K. Kokko, M. Kuzmin, J. Adell, J. Sadowski, R. E. Perälä, M. Ropo, T. T. Rantala, I. J. Väyrynen, M. Pessa, L. Vitos, J. Kollár, S. Mirbt and B. Johansson, Anomalous Bismuth-Stabilized (2×1) Reconstructions on GaAs(100) and InP(100) Surfaces, Phys. Rev. Lett., 2008, 100, 086101.
24. M. P. J. Punkkinen, P. Laukkanen, H.-P. Komsa, M. Ahola-Tuomi, N. Räsänen, K. Kokko, M. Kuzmin, J. Adell, J. Sadowski, R. E. Perälä, M. Ropo, T. T. Rantala, I. J. Väyrynen, M. Pessa, L. Vitos, J. Kollár, S. Mirbt and B. Johansson, Bismuth-stabilized (2×1) and (2×4) reconstructions on GaAs(100) surfaces: Combined first-principles, photoemission, and scanning tunneling microscopy study, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 195304.
25. M. Ahola-Tuomi, P. Laukkanen, M. P. J. Punkkinen, R. E. Perälä, I. J. Väyrynen, M. Kuzmin, K. Schulte and M. Pessa, Formation of an ordered pattern of Bi nanolines on InAs(100) by self-assembly, Appl. Phys. Lett., 2008, 92, 011926.
26. M. Ahola-Tuomi, M. P. J. Punkkinen, P. Laukkanen, M. Kuzmin, J. Lång, K. Schulte, A. Pietzsch, R. E. Perälä, N. Räsänen and I. J. Väyrynen, Properties of self-assembled Bi nanolines on InAs(100) studied by core-level and valence-band photoemission, and first-principles calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 245401.
27. J. Kishi, Y. Ohtsubo, T. Nakamura, K. Yaji, A. Harasawa, F. Komori, S. Shin, J. E. Rault, P. Le Fèvre, F. Bertran, A. Taleb-Ibrahimi, M. Nurmamat, H. Yamane, S.-I. Ideta, K. Tanaka and S.-I. Kimura, Spin-polarized quasi-one-dimensional state with finite band gap on the Bi/InSb(001) surface, Phys. Rev. Mater., 2017, 1, 064602.
28. T. Nakamura, Y. Ohtsubo, Y. Yamashita, S.-I. Ideta, K. Tanaka, K. Yaji, A. Harasawa, S. Shin, F. Komori, R. Yukawa, K. Horiba, H. Kumigashira and S.-I. Kimura, Giant Rashba splitting of quasi-one-dimensional surface states on Bi/InAs(110)-(2×1), Phys. Rev. B, 2018, 98, 075431.
29. O. Heckmann, M. Christine Richter, J.-M. Mariot, L. Nicolaï, I. Vobornik, W. Wang, U. Djukic and K. Hricovini, Quasi 1D structures at the Bi/InAs(100) surface, AIP Conf. Proc., 2018, 1996, 020017.
30. T. Nakamura, Y. Ohtsubo, N. Tokumasu, P. Le Fèvre, F. Bertran, S.-I. Ideta, K. Tanaka, K. Kuroda, K. Yaji, A. Harasawa, S. Shin, F. Komori and S.-I. Kimura, Giant Rashba system on a semiconductor substrate with tunable Fermi level: Bi/GaSb(110)–(2×1), Phys. Rev. Mater., 2019, 3, 126001.
31. Y. Ohtsubo, N. Tokumasu, H. Watanabe, T. Nakamura, P. Le Fèvre, F. Bertran, M. Imamura, I. Yamamoto, J. Azuma, K. Takahashi and S.-I. Kimura, One-dimensionality of the spin-polarized surface conduction and valence bands of quasi-one-dimensional Bi chains on GaSb(110)-(2×1), Phys. Rev. B, 2020, 101, 235306.
32. T. Nakamura, Y. Ohtsubo, A. Harasawa, K. Yaji, S. Shin, F. Komori and S. Kimura, Fluctuating spin-orbital texture of Rashba-split surface states in real and reciprocal space, Phys. Rev. B, 2022, 105, 235141.
33. D. Nafday, C. Richter, O. Heckmann, W. Wang, J.-M. Mariot, U. Djukic, I. Vobornik, P. Lefevre, A. Taleb-Ibrahimi, F. Bertran, J. Rault, L. Nicolaï, C. S. Ong, P. Thunström, K. Hricovini, J. Minár and I. Di Marco, Electronic structure of Bi nanolines on InAs(100), Electronic structure of Bi nanolines on InAs(100), Appl. Surf. Sci., 2023, 611, 155436.
34. A. N. Mihalyuk, L. V. Bondarenko, A. Y. Tupchaya, D. V. Gruznev, N. Yu. Solovova, V. A. Golyashov, O. E. Tereshchenko, T. Okuda, A. Kimura, S. V. Eremeev, A. V. Zotov and A. A. Saranin, Emergence of quasi-1D spin-polarized states in ultrathin Bi films on InAs(111)A for spintronics applications, Nanoscale, 2024, 16, 1272–1281.
35. L. Zhang, E. G. Wang, Q. K. Xue, S. B. Zhang and Z. Zhang, Generalized Electron Counting in Determination of Metal-Induced Reconstruction of Compound Semiconductor Surfaces, Phys. Rev. Lett., 2006, 97, 126103.
36. A. Duzik, J. C. Thomas, A. van der Ven and J. M. Millunchick, Surface reconstruction stability and configurational disorder on Bi-terminated GaAs(001), Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 035313.
37. P. De Padova, C. Quaresima, P. Perfetti, R. Larciprete, R. Brochier, C. Richter, V. Ilakovac, P. Bencok, C. Teodorescu, V. Y. Aristov, R. L. Johnson and K. Hricovini, Electron accumulation layer on clean In-terminated InAs(0 0 1)(4×2)-c(8×2) surface, Surf. Sci., 2001, 482485, 587.
38. G. Goryl, D. Toton, M. Goryl, N. Tomaszewska and J. J. Kolodziej, Structure of the In-rich InAs (001) surface, Surf. Sci., 2011, 605, 2073.
39. L. Petaccia, P. Vilmercati, S. Gorovikov, M. Barnaba, A. Bianco, D. Cocco, C. Masciovecchio and A. Goldoni, BaD ElPh: A 4 m normal-incidence monochromator beamline at Elettra, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 606, 780.
40. C. Schneider, C. Wiemann, M. Patt, V. Feyer, L. Plucinski, I. Krug, M. Escher, N. Weber, M. Merkel, O. Renault and N. Barrett, Expanding the view into complex material systems: From micro-ARPES to nanoscale HAXPES, J. Electron Spectrosc. Relat. Phenom., 2012, 185, 330.
41. C. Tusche, M. Ellguth, A. A. Ünal, C.-T. Chiang, A. Winkelmann, A. Krasyuk, M. Hahn, G. Schönhense and J. Kirschner, Spin resolved photoelectron microscopy using a two-dimensional spin-polarizing electron mirror, Appl. Phys. Lett., 2011, 99, 032505.
42. C. Tusche, M. Ellguth, A. Krasyuk, A. Winkelmann, D. Kutnyakhov, P. Lushchyk, K. Medjanik, G. Schönhense and J. Kirschner, Quantitative spin polarization analysis in photoelectron emission microscopy with an imaging spin filter, Ultramicroscopy, 2013, 130, 70.
43. S. H. Vosko, L. Wilk and M. Nusair, Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis, Can. J. Phys., 1980, 58, 1200.
44. https://zenodo.org/records/7576163,  DOI:10.5281/ZENODO.7576163.
45. Z. M. Fang, K. Y. Ma, D. H. Jaw, R. M. Cohen and G. B. Stringfellow, Photoluminescence of InSb, InAs, and InAsSb grown by organometallic vapor phase epitaxy, J. Appl. Phys., 1990, 67, 7034.
46. J. J. Yeh and I. Lindau, Atomic subshell photoionization cross sections and asymmetry parameters: 1 ≤ Z ≤ 103, At. Data Nucl. Data Tables, 1985, 32, 1.
47. T. Conard, R. Sporken, J. Ghijsen, L. M. Yu, R. Caudano, R. Seemann and R. L. Johnson, Photoemission study of the Interface, Surf. Sci., 1996, 369, 177.
48. S. Doniach and M. Sunjic, Many-electron singularity in X-ray photoemission and X-ray line spectra from metals, J. Phys. C: Solid State Phys., 1970, 3, 285.
49. P. Moras and C. Carbone, Quantum well band formation in Ag films on InSb(111), J. Phys.: Condens. Matter, 2009, 21, 355502.
50. N. Tomaszewska, L. Walczak, J. Lis and J. J. Kolodziej, Surface states and charge accumulation states on reconstructed InAs(001) surfaces, Surf. Sci., 2015, 632, 103.
51. K. Ishizaka, M. Bahramy, H. Murakawa, M. Sakano, T. Shimojima, T. Sonobe, K. Koizumi, S. Shin, H. Miyahara, A. Kimura, K. Miyamoto, T. Okuda, H. Namatame, M. Taniguchi, R. Arita, N. Nagaosa, K. Kobayashi, Y. Murakami, R. Kumai, Y. Kaneko, Y. Onose and Y. Tokura, Giant Rashba-type spin splitting in bulk BiTeI, Nat. Mater., 2011, 10, 521–526.
52. J. Han, A. Zhang, M. Chen, W. Gao and Q. Jiang, Giant Rashba splitting in one-dimensional atomic tellurium chains, Nanoscale, 2020, 12, 10277.
53. J. Park, S. W. Jung, M.-C. Jung, H. Yamane, N. Kosugi and H. Woong Yeom, Self-Assembled Nanowires with Giant Rashba Split Bands, Phys. Rev. Lett., 2013, 110, 036801.
54. A. Takayama, T. Sato, S. Souma, T. Oguchi and T. Takahashi, One-Dimensional Edge States with Giant Spin Splitting in a Bismuth Thin Film, Phys. Rev. Lett., 2015, 114, 066402.
55. V. Edelstein, Spin polarization of conduction electrons induced by electric current in two-dimensional asymmetric electron systems, Solid State Commun., 1990, 73, 233.
56. K. Kondou and Y. Otani, Emergence of spin–charge conversion functionalities due to spatial and time-reversal asymmetries and chiral symmetry, Front. Phys., 2023, 11, 1140286.
57. W. Han, Y. Otani and S. Maekawa, Quantum materials for spin and charge conversion, npj Quantum Mater., 2018, 3, 27.
58. A. W. Holleitner, V. Sih, R. C. Myers, A. C. Gossard and D. D. Awschalom, Dimensionally constrained D'yakonov–Perel’ spin relaxation in n-InGaAs channels: transition from 2D to 1D, New J. Phys., 2007, 9, 342.
59. D. Lükermann, M. Gauch, M. Czubanowski, H. Pfnür and C. Tegenkamp, Magnetotransport in anisotropic Pb films and monolayers, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125429.
60. M. Kopciuszyński, M. Krawiec, R. Zdyb and M. Jałochowski, Purely one-dimensional bands with a giant spin-orbit splitting: Pb nanoribbons on Si(553) surface, Sci. Rep., 2017, 7, 46215.
61. N. Sedlmayr, J. M. Aguiar-Hualde and C. Bena, Majorana bound states in open quasi-one-dimensional and two-dimensional systems with transverse Rashba coupling, Phys. Rev. B, 2016, 93, 155425.
62. B. Braunecker, G. I. Japaridze, J. Klinovaja and D. Loss, Spin-selective Peierls transition in interacting one-dimensional conductors with spin-orbit interaction, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 045127.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr01591f

---