Understanding and tuning magnetism in van der Waals-type metal thiophosphates

Abstract

Over the past two decades, significant progress in two-dimensional (2D) materials has invigorated research in condensed matter and material physics in low dimensions. While traditionally studied in three-dimensional systems, magnetism has now been extended to the 2D realm. Recent breakthroughs in 2D magnetism have attracted substantial interest from the scientific community, owing to the stable magnetic order achievable in atomically thin layers of the van der Waals (vdW)-type layered magnetic materials. These advances offer an exciting platform for investigating related phenomena in low dimensions and hold promise for spintronic applications. Consequently, vdW magnetic materials with tunable magnetism have attracted significant attention. Specifically, antiferromagnetic metal thiophosphates MPX₃ (M = transition metal, P = phosphorus, X = chalcogen) have been investigated extensively. These materials exhibit long-range magnetic order spanning from bulk to the 2D limit. The magnetism in MPX₃ arises from localized moments associated with transition metal ions, making it tunable via substitutions and intercalations. In this review, we focus on such tuning by providing a comprehensive summary of various metal- and chalcogen-substitution and intercalation studies, along with the mechanism of magnetism modulation, and a perspective on the development of this emergent material family.

---

Rabindra Basnet

Dr Rabindra Basnet is currently a postdoctoral scholar in the Department of Chemistry and Physics at the University of Arkansas at Pine Bluff (UAPB). His research focuses on the synthesis and characterization (structural, electronic, magnetic, and thermodynamic properties) of a wide range of quantum materials including magnetic, topological, strongly correlated materials, and superconductors. He received a MS degree in Physics from Tribhuvan University, Nepal in 2016 and a Ph.D. in Physics from the University of Arkansas in 2023 before starting his current postdoc position at UAPB.

Jin Hu

Dr Jin Hu is currently an associate professor in the Department of Physics at the University of Arkansas. His research focuses on discovering novel materials with exotic properties or advanced functionalities, and understanding the physics behind the properties. He received a BS degree in Applied Physics from the University of Science and Technology of China in 2008, and a Ph.D. in Physics from Tulane University in 2013. He established the Quantum Material Research group at the University of Arkansas in 2017, and has been awarded the DOE Early Career Award and the NSF Career award.

---

1. Introduction

Since the discovery of graphene,¹ numerous two-dimensional (2D) materials have been theoretically predicted and experimentally realized. For a long time, 2D material research was mainly centralized around graphene and transition metal dichalcogenides (TMDs) in terms of their electronic properties because they display almost all functionalities of solid-state systems such as metal, semimetal, semiconductor, and insulator as well as exotic quantum phases and phenomena such as superconductivity, charge density wave, and topological quantum phases. In addition to these properties, magnetism in 2D materials has also attracted intensive attention due to fundamental scientific interest in low dimensional orders and technological demands such as spintronics. Graphene² and TMDs^3–5 have been found to exhibit magnetism. However, owing to the non/weak-magnetic nature of the constituted atoms/ions, magnetism in these materials mainly arises from extrinsic factors such as defects or doping of guest atoms. Therefore, there has been an intensive search for 2D materials with intrinsic magnetism. Recently, there have been breakthroughs in discovering intrinsic magnetic orders in atomically thin layers of FePS₃,⁶ CrI₃,⁷ CrGeTe₃,⁸ CrBr₃,⁹ VI₃,¹⁰ Fe₃GeTe₂ ¹¹ and Fe₃GaTe₂,¹² which greatly expand the realm of the 2D magnetism and provide material platforms not only for gaining deep insight into low dimensional magnetism but also for spintronic applications.^13–25 These developments have motivated the search for additional novel magnetic van der Waals (vdW) materials, resulting in a blossoming of magnetic vdW materials that can be broadly categorized into two groups: (1) transition metal halides (including both dihalides and trihalides), and (2) transition metal chalcogenides (both binary and ternary) involving transition metals from V to Ni in the periodic table (i.e., V, Cr, Mn, Fe, Co, and Ni). Magnetism in those vdW magnets arises from the magnetic moment of the 3d electrons of the transition metal cations. The metal ions in these compounds are mostly arranged in honeycomb lattices, except for a few compounds such as transition metal dihalides that is characterized by triangular networks of metal ions.²⁶

Metal thiophosphates are some of the model systems among various 2D magnetic materials. Those materials were discovered in the late 1800s,^27,28 usually represented by a chemical formula of MPX₃ or M₂P₂X₆, where M, P, and X denote transition metal, phosphorus, and chalcogen elements, respectively. Since their discovery, MPX₃ compounds have been studied in various fields including magnetism,^6,29–43 magneto-optics,^44–50 optoelectronics,^{27,28,51–53} Li-ion batteries,^27,28,54,55 and ferroelectricity.^{27,28,56–59}Their layered structures allow for mechanical exfoliations down to atomically thin layers,^{6,29,41–43,60} creating pathways to study 2D physics. The magnetic members of the MPX₃ (M = V, Cr, Mn, Fe, Co, and Ni) family are antiferromagnets in which the M ions carry localized magnetic moments in a layered honeycomb lattice. Antiferromagnetic (AFM) orders have been found to persist down to atomically thin layers and even to the monolayer limit in some MPX₃,^6,42,43 thus these materials have been established as important candidates for 2D magnets.^{6,29,41–43,60} The MPX₃ compounds exhibit semiconducting⁶¹ or insulating^62,63 behavior with band gaps ranging from 1.3 to 3.5 eV. Interestingly, applying high pressure can induce insulator-to-metal transitions^64–71 and even superconductivity⁷² in some MPX₃ compounds. Furthermore, these compounds also offer platforms to study correlated electrons in 2D magnetic materials.^45,64,73 Recent studies have revealed a strong coupling between optically active excitons and magnetism in MPX₃.^44–49 For example, in NiPS₃, a novel coherent spin–orbit entangled excitonic state stabilized by AFM order⁴⁴ as well as the correlation between emitted photon and spins⁴⁵ have been reported. Such coupling can lead to an all-optical control of magnetic anisotropy.⁵⁰ In addition, a strong correlation of magnons and phonons that generates phonon spin through the transfer of spin angular momentum has been demonstrated in FePS₃.^42,74 Such intertwined degrees of freedom provide a unique opportunity to explore the interplay between magnetism, strong correlation, and light–matter interactions in 2D magnets.

In addition to fundamental research, this material family also offers a large material pool for potential technological applications. The feasibility of obtaining atomically thin layers enables nanodevices and heterostructures fabrication and integration, opening opportunities for utilization in electronics and spintronics. Moreover, in MPX₃, the band gaps ranging from 1.3 to 3.5 eV cover near-infrared to the UV region, enabling the optoelectronic applications in a broad wavelength horizon.^27,28 Additionally, the unusual intercalation–reduction behavior and higher ionic conductivity of these materials facilitate potential applications in Li-ion batteries.^27,28,54,55 Furthermore, their unusual ferroelectricity could lead to new energy and data storage devices and sensors.^27,28

Given such versatility, MPX₃ materials have recently gained intensive attention. In particular, magnetism in those materials has been established as an important research topic.⁷⁵ The magnetic properties in MPX₃ strongly depend on the choice of the transition metal M and chalcogen X elements. Not only the AFM transition temperature (Néel temperature, T_N) that changes upon substituting M and X,^30–39 but also various AFM structures can be obtained through M^76–93 and X^{30–32,94,95} substitutions. Such tuning of magnetism by altering M and X has led to the study of a series of polymetallic^76–93 and polychalcogenide^{30–32,94,95} “mixed” MPX₃ compounds. Tunable magnetism has been observed in these mixed compounds, providing promising candidates to explore novel phenomena originating from 2D magnetism. In addition to substitution, the layered structure of MPX₃ allows for another doping strategy i.e., the inter-layer intercalation of guest ions. Intercalating various guest species has been reported to cause AFM to ferrimagnetic (FIM)^96–100 and ferromagnetic (FM)¹⁰¹ transitions in MPX₃. This suggests that the intercalation could be a promising route to achieve additional magnetic phases in MPX₃ that may not be accessible by substitution.

Thus far, a wide range of magnetic, electronic, vibrational, optical, and ferroelectric properties of pristine MPX₃ compounds have already been summarized by a few excellent review articles.^27,28,75 Therefore, the focus of this review will be put on engineering magnetic properties through various doping strategies: metal substitution, chalcogen substitution, and inter-layer intercalation, aiming to provide a comprehensive summary with sufficient depth and width for deeper understanding of magnetism in MPX₃ based on magnetic exchanges and anisotropies. This review is organized as follows: summarizing the crystal growth methods and lattice structures, an overall theoretical framework for understanding magnetism in MPX₃, experimental efforts in engineering the magnetism, and the perspective of the development of this field. We hope this review can provide the community with comprehensive information on the existing discoveries in doping studies and an in-depth understanding of magnetism, which serves as an important guideline for further exploring the exciting materials physics in MPX₃ as well as other 2D magnets and their property tuning. We wish to cover all relevant studies in this review. However, given the rapid development of MPX₃ materials, the emerging new discoveries may not be included but can be introduced by future review articles.

2. Crystal growth

The studies on functional materials, their properties, and applications, greatly rely on the development of convenient and reliable synthesis methods to produce high-quality crystals. For solid state systems, single crystals are highly desired because a single crystal possesses well-defined crystalline axes so that the intrinsic anisotropic magnetic, electronic transport and optical properties can be experimentally determined, which are critical to understanding the fundamental physics principles that govern the material properties. In addition, well-defined surfaces and edges of a single crystal enables the surface-sensitive measurements such as angle resolved photoemission spectroscopy (ARPES), scanning tunneling microscopy/spectroscopy (STM/S), etc. which provide valuable information. Conventional single-crystal synthesis techniques include chemical vapor transport (CVT), flux, Bridgman, floating zone (FZ), and Czocharalski methods. The synthesis of MPX₃ compounds goes back to the late 19^th century when Friedel obtained FePS₃ by heating a weighed amount of phosphorus pentasulfide with iron.^27,28 This technique was later used by Ferrand^27,28 to synthesize other sibling compounds ZnPS₃, CdPS₃, and NiPS₃. Nowadays, CVT and flux have become the main techniques to grow the bulk single crystals of MPX₃, which have proven to be effective methods to yield large single crystals for physical characterizations.

A CVT method has been widely used to synthesize pristine, metal-, and chalcogen-substituted MPX₃ compounds as summarized in Table 1. As shown in Fig. 1(a), this method is based on the vaporization of source materials at the hot end of the growth chamber (usually a quartz ampoule), transportation of the vapor along some temperature gradient, and condensation of vapor at the cold end. For MPX₃, a mixture of elementary powders of M, P, and X, or pre-synthesized polycrystal precursors prepared by solid-state reaction, can be used as source materials for CVT. For CVT growth, a transport agent such as I₂, TeCl₄, SeCl₄, etc., is usually added to the source material to aid the vapor transportation process. For MPX₃, CVT growth using these transport agents has been reported.^{31,40,71,87–91,102–106} On the other hand, owing to the volatile elements P and S or Se, CVT growth without a transport agent^{33,41,107–112} has also been successfully used to synthesize the single crystals of MPX₃. Experimentally, the source materials (elementary powders with proper molar ratio or pre-reacted polycrystal precursors) along with the transport agent (if used) are sealed in an evacuated quartz ampoule. The ampoule should be sufficiently long (usually ∼10–15 cm) to create a proper temperature gradient between the source and sink to facilitate the vapor transport. Then, the ampoule is placed in a two-zone furnace [Fig. 1(a)] which provides the needed temperatures and temperature gradient and heated at a certain duration required for the formation of the desired MPX₃ phase. The source end is kept at a higher temperature (T_hot) than the sink end (T_cold) to establish the thermal gradient, as summarized in Table 1. The heating process must be slow to avoid excessive pressure due to volatile elements P and X. Upon the completion of the growth, the furnace either slowly cools at a controlled slow cooling rate or naturally cools to room temperature, and single crystals can be found at the cold end. Single crystals harvested by quenching in ice water (i.e., very rapid cooling) have also been reported.¹¹³ The optical images of single crystals of some pristine and substituted (both metal- and chalcogen-substituted) MPX₃ compounds synthesized using the CVT technique are shown in Fig. 1(b–d).

Fig. 1 Crystal growth of MPX₃. (a) Schematic of chemical vapor transport (CVT) growth. Optical microscope images of (b) pristine, (c) metal (M)-, (d) chalcogen (X)-substituted MPX₃ single crystals synthesized by CVT methods. (e) Optical images of single crystals of MPX₃ compounds synthesized by using the reactive P₂S₅ flux method. Reprinted (adapted) with permission.¹¹⁵ Copyright 2021, American Chemical Society.

Table 1 Summary of crystal growth of MPX₃ compounds

Materials	Growth method	Temperature (°C)		Duration (days)	Ref.
		T hot	T cold
VPS3	CVT	600	500–350	7–30	71 and 106
MnPS3	CVT	780–650	720–600	7	31, 41, 87, 104 and 238
	P2S5 flux	650	—	2	115
FePS3	CVT	750–700	730–600	9–21	6, 72, 88, 91, 104, 107 and 239
	P2S5 flux	650	—	3	114–116
CoPS3	CVT	600	550–500	7–8	108 and 240
	P2S5 flux	580	—	2	114–116
NiPS3	CVT	760–670	690–550	7–21	31, 88, 89, 91 and 123
	P2S5 flux	650	—	2	115
ZnPS3	CVT	600	550	7	151
	P2S5 flux	650	—	2	115
CdPS3	CVT	630	600	5	104
	P2S5 flux	650	—	2	115
MgPS3	CVT	670	550–800	90	124
	P2S5 flux	650	—	2	115
PdPS3		500	450–500	7	124
SnPS3		630	600	3–5	104 and 105
HgPS3	CVT	350	320–500	3	124
	P2S5 flux	400	—	2	118
PbPS3		650	620	3–5	105
CrPSe3		800	700	10	103
MnPSe3		650	600	7	31 and 241
FePSe3		720–700	700–600	7–10	72 and 242
NiPSe3		530	500–560	90	124
ZnPSe3		370	—	10	243
CdPSe3		610	650–550	30	124
MgPSe3		620	480–690	90	124
HgPSe3		400	300	5	244
PbPSe3		750	710	3–5	105
CuCrP2S6		750–720	700–680	5–8	153 and 154
CuInP2S6	CVT	800	700	7	245
	P2S5 flux	650	—	4	115
AgCrP2S6		750	690	5	156
AgInP2S6		750–680	610–600	7–9	246 and 247
Mn1−xFexPS3		730	700–630	5	81
Fe1−xNixPS3		760–700	690–600	9	88 and 91
Ni1−xMnxPS3		750–720	670–550	7–12	87, 89 and 152
Mn1−xCoxPS3	P2S5 flux	540	—	3	117
Fe1−xCoxPS3	P2S5 flux	580	—	4	114–116
Ni1−xCoxPS3		625	550	21	90
Ni1−xCrxPS3		750	550	7	177
Mn1−xZnxPS3		700–650	680–600	7	77, 78, 85 and 151
Fe1−xZnxPS3		700	650	7	93
Fe1−xCuxPS3		597	577	15	187
Fe1−xCdxPS3
Mn1−xFexPSe3		750	550	7	122
(Mn,Fe,Ni,Co)PS3		650	-	18	113
(V,Mn,Fe,Ni,Co)PS3		610	-	3	113
(Zn,Mn,Fe,Ni,Co)PS3		610	-	3	113
(Mg,Mn,Fe,Ni,Co)PS3		610	-	3	113
(Fe,Mn,Cd,In)PSe3		627	377	7	121
CuxNi2(1−x)CrxP2S6		750	550	7	181
MnPS3−xSex		650	600	7	31 and 32
NiPS3−xSex		750	550	7	31
FePS3−xSex		750	550	7	122

---

In addition to CVT, the reactive flux technique has been recently reported to synthesize pristine and metal-substituted MPX₃ single crystals. This method adopts P₂X₅ (X = S^114–118 or Se¹¹⁹) flux and metal precursors, as summarized in Table 1. First, the metal and P₂X₅ powders in a ratio of 2 : 3 for monometallic or 1 : 1 : 3 for bimetallic compounds is sealed in an evacuated silica tube inside a glove box. The mixture is then heated and maintained at a certain temperature with different heating profiles depending on the target compounds.¹¹⁵ The excess P₂S₅ (melting point ∼285 °C)^114–118 and P₂Se₅ (melting point ∼214 °C)¹¹⁹ act as a reactive flux that oxidizes the metal element and enhances solubility to reduce reaction times and increase crystallite sizes. Upon the completion of the growth, the excess P₂S₅ flux is then removed with a 1 : 1 mixture of ethanol and water followed by a subsequent treatment using deionized water and acetone.^114–118 On the other hand, the excess P₂Se₅ flux is removed by the distillation process at a temperature gradient between 400 °C and room temperature.¹¹⁹ This method can result in sizable single crystals in a relatively shorter synthesis time as compared to a traditional CVT technique, as shown in Fig. 1(e).

3. Crystal structure

The crystal lattice structures and symmetries are critical in determining magnetic properties, as has been theoretically predicted for MPX₃.¹²⁰ Varying lattice parameters have been found to strongly affect the magnetic properties.¹²⁰ So, understanding crystal structure is essential for gaining deeper insights into magnetism. At first glance, all MPX₃ materials exhibit very similar layered structures [Fig. 2(a)]. Careful structure characterizations have revealed monoclinic, rhombohedral, and triclinic structures for various MPX₃, as summarized in Table 2. Despite three different lattice structures, MPX₃ materials exhibit common structural characteristics. As shown in Fig. 2(b), metal atoms M are arranged in a honeycomb lattice. Each P displays a tetrahedral coordination, which is covalently bonded with one P to form P–P (P₂) dimers perpendicular to the hexagonal plane and three X featuring a (P₂X₆)⁴⁻ bipyramid structure unit. Such P–P dimer forming (P₂X₆)⁴⁻ bipyramids fill the center of the M honeycomb lattice. Therefore, these compounds have also been referred to as M₂P₂X₆ in the literature. For chalcogen atoms X that sandwich the metal honeycomb layer, they form almost close-packed surfaces of the layer with an array of octahedral coordinated sites [Fig. 2(c)]. The monolayer MPX₃ can be considered as the monolayer MX₂ where the one-third of M sites are substituted by P–P dimers. Thus, in MPX₃, two-thirds of the octahedral centers are filled by M²⁺ cations while the P–P dimers occupy the remaining one-third [Fig. 2(c), P–P dimer in the center is not shown].

Fig. 2 Crystal structures of MPX₃. (a) The layered structure of van der Waals material MPX₃. (b) The (P₂X₆)⁴⁻ (X = S or Se) anion sublattice in each layer. Metal M is arranged in a honeycomb lattice around the (P₂X₆)⁴⁻ bipyramids. (c) MX₆ octahedron of MPX₃. Such MX₆ octahedra possesses a trigonal distortion that is characterized by the angle θ between the trigonal axis (perpendicular to the ab-plane) and the M–X bond. (d) Splitting of five 3d orbitals of transition metal cations into three t_2g and two e_g levels under an octahedral crystal field. (e) Schematic of direct exchange interaction between magnetic ions, and superexchange interactions between two cations through anion. (f) Schematic of nearest-neighbor (J₁), second nearest-neighbor (J₂), and third nearest-neighbor (J₃₎ interactions in MPX₃.

Table 2 Crystal structures of MPX₃ compounds

Materials	Crystal structure	Space group	Ref.
VPS3	Monoclinic	C2/m	71 and 106
MnPS3	Monoclinic	C2/m	31, 41, 87, 104 and 238
FePS3	Monoclinic	C2/m	6, 72, 88, 91, 104, 107 and 239
CoPS3	Monoclinic	C2/m	108, 240
NiPS3	Monoclinic	C2/m	31, 88, 89, 91 and 123
ZnPS3	Monoclinic	C2/m	151
CdPS3	Monoclinic	C2/m	104
MgPS3	Monoclinic	C2/m	124
PdPS3	Monoclinic	C2/m	124
SnPS3	Monoclinic	C2/m	104 and 105
HgPS3	Triclinic	P1̄	124
PbPS3	Monoclinic	P21/c	105
CrPSe3	Monoclinic	C2/m	103
MnPSe3	Rhombohedral	R3̄	31 and 241
FePSe3	Rhombohedral	R3̄	72 and 242
NiPSe3	Monoclinic	C2/m	124
ZnPSe3	Rhombohedral	R3̄	243
CdPSe3	Rhombohedral	R3̄	124
MgPSe3	Rhombohedral	R3̄	124
HgPSe3	Monoclinic	C2/m	244
PbPSe3	Monoclinic	P21/c	105
CuCrP2S6	Monoclinic	C2/c	153 and 154
CuInP2S6	Trigonal	P3̄1c	245
AgCrP2S6	Monoclinic	P2/a	156
AgInP2S6	Trigonal	P31c	246 and 247
Mn1−xFexPS3	Monoclinic	C2/m	81
Fe1−xNixPS3	Monoclinic	C2/m	88
Ni1−xMnxPS3	Monoclinic	C2/m	87, 89 and 152
Mn1−xCoxPS3	Monoclinic	C2/m	117
Fe1−xCoxPS3	Monoclinic	C2/m	114–116
Ni1−xCoxPS3	Monoclinic	C2/m	90
Ni1−xCrxPS3	Monoclinic	C2/m	177
Mn1−xZnxPS3	Monoclinic	C2/m	151
Fe1−xZnxPS3	Monoclinic	C2/m	93
Mn1−xFexPSe3	Rhombohedral	R3̄	86
(Mn,Fe,Ni,Co)PS3	Monoclinic	C2/m	113
(V,Mn,Fe,Ni,Co)PS3	Monoclinic	C2/m	113
(Zn,Mn,Fe,Ni,Co)PS3	Monoclinic	C2/m	113
(Mg,Mn,Fe,Ni,Co)PS3	Monoclinic	C2/m	113
(Fe,Mn,Cd,In)PSe3	Rhombohedral	R3̄	121
CuxNi2(1−x)CrxP2S6	Monoclinic	C2/m	181
MnPS3−xSex	Mono → Rhom	C2/m → R3̄	32
NiPS3−xSex	Monoclinic	C2/m	31
FePS3−xSex	Mono → Rhom	C2/m → R3̄	122

---

As seen in Fig. 2(a), a finite vdW gap of about 3.22–3.24 Å is present in MPX₃.^27,28,75 Various metal ions M²⁺ with different ionic radii slightly modify the slab size. The two flat pyramids formed by bonding between a P and three X atoms at the top and bottom of the (P₂X₆)⁴⁻ structural unit [shown in Fig. 2(b)] remain invariable, but the P–P distance is slightly adjusted to accommodate the changes in metal cations. For example, the P–P distance elongates from 2.148 Å in NiPS₃ to 2.222 Å in CdPS₃,²⁷ which is accompanied by increases of the layer thickness.

Although the individual lamella is similar for all MPX₃ compounds, their symmetry, and layer stacking to form a bulk lattice structure can vary depending on M and X, as summarized in Table 2. In particular, the symmetries and crystal structures for sulfides and selenides of MPX₃ materials are distinct. Generally, almost all the known sulfides MPS₃ exhibit monoclinic crystal structures with a C2/m space group, except for PbPS₃¹⁰⁵ which has been reported to crystalize in a P21/c monoclinic structure as its selenide counterpart, and for HgPS₃¹¹⁸ which is triclinic with a P1̄ space group symmetry. In sulfides, the monoclinic angle β depends on the metal cation, ranging from 106.97° for MgPS₃ to 107.35° for MnPS₃. On the other hand, as summarized in Table 2, selenides MPSe₃ process larger P–Se bond lengths and Se–P–Se bond angles as compared to their sulfide counterparts, and mostly crystallize in rhombohedral structures with a R3̄ space group. The exceptions are NiPSe₃, CrPSe₃, HgPSe₃, and PbPSe₃ which exhibit monoclinic crystal structures.

Therefore, the lattice structure of MPX₃ appears to be more sensitive to chalcogen rather than metal. This is further confirmed by substitution studies. As summarized in Table 2, substituting metal atoms M does not change the lattice structure in MPX₃.^{76–92,114,116,117} Most known metal-substituted sulfide compounds exhibit monoclinic structure with a C2/m space group in the entire substitutional range. For selenides, previous works on a bimetallic compound Mn_1−xFe_xPSe₃ ⁸⁶ and a high entropy compound Fe_{1−x−y−z}Mn_xCd_yIn_zSe₃ ¹²¹ also found unchanged lattice with rhombohedral R3̄ structures. On the other hand, chalcogen S–Se substitution can induce structure transition from monoclinic (C2/m) to rhombohedral (R3̄) in MnPS_3−xSe_x ³² and FePS_3−xSe_x,¹²² which is consistent with the different lattice structures for their sulfide and selenide end compounds. One exception is NiPS_3−xSe_x which displays unchanged monoclinic C2/m structure, which is also in line with the identical C2/m space group for NiPS₃ ^{31,88,89,91,123} and NiPSe₃ ¹²⁴.

4. Magnetism

4.1. Theoretical background

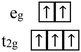
Owing to the insulating nature of MPX₃ compounds, their magnetism can be described by local moment pictures. Magnetism in vdW magnetic materials arises from the magnetic moment of the spin and orbital momenta of the 3d electrons of the transition metal cations. Thus, the choice of transition metal cations plays a vital role in determining magnetism. In the presence of a crystal electric field from the octahedral coordination of the transition metal cations [Fig. 2(c)], the d_x²−y² and d_z² orbitals among the five d-orbitals of the transition metal point in the direction of the ligands, thereby the electrons in these orbitals experience greater repulsion with ligands and increase the energy of these orbitals. Thus, these two d-orbitals are pushed to higher energy levels in the band structure and referred to as two-fold degenerate high-energy e_g orbitals. On the other hand, the remaining three d-orbitals d_xz, d_yz, and d_xy do not directly align towards ligands leading to a weaker repulsion and stabilized to a lower energy level than two e_g orbitals. Therefore, these three orbitals lie below e_g orbitals (d_x²−y² and d_z²) in term of energy and constitute three-fold degenerate low-energy t_2g orbitals.^125,126 The splitting of five 3d orbitals of transition metal ions under an octahedral crystal field is depicted in the schematic in Fig. 2(d). Then, the d electrons of various transition metal cations fill these orbitals following Hund's rule, as presented in Table 3.¹²⁷ The occupancy of these orbitals determines the total magnetic moment of the 3d transition metal cations, with the total magnetic moment given by g_J[j(j + 1)]^1/2μ_B where |j|, g_J, and μ_B are the total angular momentum quantum number (= spin + orbital angular momentum), Landé g-factor, and Bohr magneton, respectively. When orbital angular momentum is quenched (i.e., L = 0), only the spin magnetic moment contributes to the total magnetic moment, resulting in a total magnetic moment of 2[s(s + 1)]^1/2μ_B where s is the total spin quantum number, which is generally the case for transition metals.¹²⁵

Table 3 Orbital occupancy for 3d valence electrons of various transition metal cations under octahedral crystal field

Transition metal ions	3d orbital occupancy
V^2+ (3d^3)
V^3+ (3d^2)
Cr^2+ (3d^4)
Cr^3+ (3d^3)
Mn^2+(3d^5)
Fe^2+ (3d^6)
Fe^3+ (3d^5)
Co^2+ (3d^7)
Ni^2+ (3d^8)

---

In the classic Heisenberg model, the magnetism can be explained within the framework of isotropic Heisenberg Hamiltonian: H = −2Σ(JS_i·S_j), where J is the exchange coupling, which is considered to be isotropic, the summation is over all pairs of magnetic ions in the lattice and the spins are treated as three-component vectors where S_i and S_j are spin magnetic moments of the atomic site i and j respectively. The Heisenberg model provides an accurate account of the interactions between the localized magnetic moments that govern the magnetic properties in insulators (such as MPX₃). In vdW materials, magnetic interactions can be anisotropic and are described by a Heisenberg Hamiltonian with anisotropic exchange: H = −2Σ(J_xS_iS_j + J_yS_iS_j + J_zS_iS_j), where J_x, J_y, and J_z are exchange couplings along the crystallographic axes. In layered MPX₃, magnetic exchanges within the layer are much stronger than inter-layer interactions,^128–130 hence the long-range magnetic ordering is believed to be mainly governed by intralayer exchange interactions. The interactions between localized moments in insulating MPX₃ compounds are mainly mediated through direct and superexchange interactions, as shown in Fig. 2(e). The direct exchanges between neighboring magnetic moments, which result from the overlapping wavefunctions, mainly depend on their spatial separation, and contribute to the nearest neighbor interaction J₁. Despite the fact that the distances between magnetic cations are large (in the order of 3–4 Å), such direct exchange has been found to be important or even dominate the magnetic interactions in some MPX₃ compounds such as MnPS₃.¹²⁸ On the other hand, in many other MPX₃ materials such as NiPS₃, the long-range magnetic coupling between moments is dominated by metal–chalcogen–metal (M–X–M) superexchange interactions mediated through non-magnetic chalcogen X.¹²⁸ The superexchange couplings contribute to both the nearest-neighbor interaction (J₁) and the interactions between further neighbors such as second nearest-neighbor (J₂), and third nearest-neighbor (J₃) interactions.¹²⁸ The magnetic interactions J₁, J₂, and J₃ are depicted in Fig. 2(f). The nature and strength of superexchange interactions are determined by M–X–M bonding angle, d-orbital occupancy of M²⁺ ions, and orbital overlap between M²⁺ cation and X²⁻ anion:^40,128 According to Goodenough–Kanamori rules,^131,132 the superexchange interaction is ferromagnetic (FM) if M–X–M bond angle is close to 90° and AFM when M–X–M bond angle is 180°. The occupancy of d orbitals is important. For example, CoPS₃ and NiPS₃ share the same magnetic structure but possess different strengths for superexchange due to their distinct occupancy of d orbitals for Co²⁺ (d⁷) and Ni²⁺ (d⁸) ions.¹²⁹ Such differences could be important in designing different strategies to tune magnetism in CoPS₃ and NiPS₃. The overlap of atomic orbitals also affects the superexchange interaction. Usually, stronger orbital overlap strengthens the superexchange, therefore substituting Se for S in MPX₃ leads to enhanced superexchange because of the extended orbital overlap due to more extended atom orbitals of Se than S.³¹

Furthermore, structural distortions also affect the magnetism in MPX₃.^40,128,129 As illustrated in Fig. 2(c) and mentioned above, every metal atom M in MPX₃ is located at the center of an octahedron formed by six X atoms. Such MX₆ octahedra, however, possess a trigonal distortion that is characterized by the angle θ between the trigonal axis (perpendicular to the ab-plane) and the M–X bond [Fig. 2(c)]. The experimental θ values for various MPX₃ compounds are presented in Table 4. An ideal octahedral possesses the ideal octahedral angle θ ≈ 54.75°. The deviation of θ angle from this ideal value characterizes the trigonal distortion. The crystal field arising from trigonal distortion of MX₆ octahedra together with spin–orbit coupling (SOC) of the M²⁺ cations introduce anisotropy in an otherwise isotropic system. Now, with an additional anisotropy term, the full Hamiltonian becomes H = −2 ∑(J_ijS_i·S_j) − A∑(S_i^z)², where J_ij is exchange interaction between neighboring i^th and j^th moments and A is single-ion anisotropy parameter that defines the magnetic anisotropy of the system. The strengths of various J's and A determine the magnetism in MPX₃. Table 4 summarizes the experimental values of J and A parameters obtained by neutron scattering experiments for various MPX₃ materials,^{35,94,107,128,129} together with theoretical calculated values for VPS₃.¹³³ These distinct J and A values for different MPX₃ compounds result in diverse AFM structures for this material family, as shown in Fig. 3. When J ≫ A (for very small A), the magnetism is weakly anisotropic and can be explained by the 3D isotropic Heisenberg Hamiltonian, such as MnPS₃.^35,40 For large A values, on the other hand, the magnetism becomes rather anisotropic and corresponds to XY (such as NiPS₃ ^40,123 and CoPS₃ ¹²⁹) or Ising-type (such as FePS₃ ⁴⁰ and FePSe₃ ³⁰) magnetism depending on the sign and magnitudes of A. In Mn and Ni systems, the orbital angular momentum (L) is quenched for Mn²⁺ (d⁵) and Ni²⁺ (d⁸) ions because of their half and fully-filled t_2g orbitals respectively, leading to negligible SOC for magnetic ions.⁴⁰ In MnPS₃ which possesses relative weak trigonal distortion (octahedral angle θ ≈ 51.67°), the effect of both spin–orbit splitting and trigonal distortion is found to be negligible for the high spin ground state of Mn²⁺,⁴⁰ so the magnetism in MnPS₃ is governed by the dipolar anisotropy^35,134,135 which results in an out-of-plane moment orientation with a small tilt towards the a-axis (Fig. 3). On the other hand, NiPS₃ exhibits greater trigonal distortion characterized by octahedral angle, θ ≈ 51.05° from the undistorted octahedral angle of 54.75°. This leads to remarkable single-ion anisotropy A ≈ 0.3 meV in NiPS₃, which is much stronger than that of 0.0086 meV in MnPS₃ (Table 4).^35,128,129 Consequently, Ni moments are aligned within the basal plane perpendicular to the trigonal axis (Fig. 3),^36,40,135 and this system can be modeled by the anisotropic Heisenberg Hamiltonian with XY-type anisotropy. The situation is different for FePS₃, which exhibits a substantial magnetic anisotropy with a much higher A (≈2.66 meV) in comparison to MnPS₃ and NiPS₃.^107,128 Thus, FePS₃ is best described by the Ising Hamiltonian corresponding to the highly anisotropic Ising-type magnetic ordering with magnetic moments aligned along the out-of-plane direction.^40,107 In FePS₃, the degenerate t_2g orbitals for the high-spin Fe²⁺ (d⁶) state lead to a stronger trigonal distortion of the FeS₆ octahedra (θ ≈ 51.28° (ref. 107 and 129)) that causes a significant splitting of t_2g orbitals to lift the degeneracy while the e_g orbitals remain doubly degenerate.¹³⁶ In addition, the lack of half- or fully-filled t_2g orbitals for high-spin Fe²⁺ ions also contribute to the net orbital moment and consequently enhances the SOC. Although, a recent X-ray photoemission electron microscopy study has demonstrated that the spin–orbit entanglement for Fe²⁺ under trigonal elongation plays a key role behind the significant magnetic anisotropy in FePS₃,¹³⁷ the SOC alone may not be a dominant factor behind strong magnetic anisotropy in FePS₃ because the SOC for Ni²⁺ (d⁸) ion is larger than Fe²⁺ (d⁶) ion but the resulting compound NiPS₃ is less anisotropic than FePS₃.⁴⁰ The large crystal electric field arising from the strong trigonal distortion of the FeS₆ octahedra might also be attributed to a substantial magnetic anisotropy in FePS₃, which has been confirmed by a recent X-ray absorption spectroscopy experiment.¹³⁶ In fact, the strong anisotropy due to crystal electrical field i.e., crystal-field anisotropy has been ascribed to Fe²⁺ (d⁶) ion in different Fe-based compounds.^138,139

Fig. 3 Experimentally determined magnetic structures of various MPX₃ materials. For CuCrP₂S₆, the low-temperature structure is shown. Magnetic structures for (V,Co,Ni)PSe₃ and CuCrP₂Se₆ have not been experimentally determined.

Table 4 Magnetic exchange and anisotropy parameters for MPX₃ materials. Here, negative and positive signs denote AFM and FM interactions, respectively. θ is defined as the angle between the z-axis and the vector that joins the metal M²⁺ ion and any particular nearest-neighbor chalcogen ligand [Fig. 3(e)]. Without trigonal distortion, θ becomes 54.7°

Parameters	VPS3 ^a ^133	MnPS3 ^35	FePS3 ^107	CoPS3 ^129	NiPS3 ^248	MnPSe3 ^94
a Theoretical study.
S	3/2	5/2	2	3/2	1	5/2
T N (K)	56 (ref. 106)	78	118	120	155	74
J 1 (meV)	−7.387	−0.77(9)	1.46(1)	2.04	1.9(1)	−0.45
J 2 (meV)	−0.068	−0.07(7)	−0.04(4)	0.26	−0.1(1)	−0.03
J 3 (meV)	−0.223	−0.18(1)	−0.96(5)	−4.21	−6.90(5)	−0.19
J c (meV)	—	0.0019(2)	−0.0073(3)	—	0.32(3) (ref. 130)	−0.031(5)
A (meV)	—	0.0086(9)	2.66(8)	2.06	0.3(1)	—
θ (°)	—	51.67 (ref. 129)	51.28 (ref. 129)	51.38 (ref. 129)	51.05 (ref. 129)	—

---

4.2. Engineering magnetism in MPX₃

Engineering magnetism in layered magnetic materials not only optimizes properties for technological applications (such as high transition temperature, wider hysteresis loop, and various types of FM and AFM structures) but also provides an effective approach to clarify the mechanism for the magnetism by identifying the parameters that govern magnetism. Several strategies such as doping,^{30–32,76–91,94,95,97–99,140–146} high pressure,^147–150 and electrostatic gating^14,16 have been adopted to tune the magnetic properties in layered magnets. These techniques have been successful in controlling the spin orientation in vdW magnetic materials, which leads to novel magnetic phenomenon arising from 2D magnetism. Tuning magnetic properties has been one major focus and studied for a long time in the MPX₃ family.^77,78,85 Doping, including metal M and chalcogen X substitutions, and inter-layer intercalation, has been demonstrated as a powerful technique to modulate magnetism in MPX₃, which will be the focus of this review as discussed below.

4.2.1. Metal (M) substitution. Metal substitution has been adopted as an important method to manipulate the magnetic properties in MPX₃. Owing to the structural similarity of the MPX₃ materials, a divalent metal M²⁺ ion can be substituted with another divalent metal ion to create a polymetallic “mixed” compound such as (Mn,Ni)_xFe_1−xPS₃, Ni_1−xMn_xPS₃, (Mn,Fe)_1−xZn_xPS₃, (Mn,Fe,Ni)_1−xCo_xPS₃ and Mn_1−xFe_xPSe₃ ^{76–91,93,114,116,117,151,152} where two different metal atoms are mixed in a honeycomb lattice as shown in Fig. 4(a). In addition to these bimetallic substitutions, the metal substitution in MPX₃ has recently been extended to mixing of more than two divalent metal M²⁺ ions creating medium¹²¹ and high entropy¹¹³ vdW materials. In addition to these bi- and poly-metallic compounds based on isovalent M²⁺ ion substitutions, the non-isovalent substitution of monovalent and trivalent ions that leads to a series of quaternary compounds (M₁)¹⁺(M₂)³⁺P₂X₆ (M₁ = Li, Cu, Ag, etc.; M₂ = V, Cr, In, Bi, etc.; X = S and Se)^{119,153–161} have also been reported in this material family. Although the focus of this review is the divalent metal substitutions, we have also briefly summarized the magnetic properties of a few magnetic quaternary compounds (Cu,Ag)¹⁺(V,Cr)³⁺P₂(S,Se)₆ that have been formed by mixing trivalent ions such as Cr³⁺ or V³⁺ with monovalent metal ions such as Cu¹⁺ or Ag¹⁺.^153–157 The magnetic exchange J and single-ion anisotropy A parameters are found to be effectively modulated with metal substitutions that lead to efficient control of magnetic properties. Tunable magnetism arising from competing magnetic interactions, magnetic anisotropies, and spin fluctuations has been observed in metal-substituted MPX₃ compounds, which will be discussed in the following sections.

Fig. 4 Conceptual schematic of (a) metal (M) substitution, (b) chalcogen (X) substitution, and (c) Li intercalation in MPX₃.

4.2.1.1. Isovalent substitution.
4.2.1.1.1. Mn_1−xFe_xPS₃. As shown in Fig. 3, MnPS₃ and FePS₃ exhibit out-of-plane magnetic moment but different Néel¹³⁴ and zig-zag¹⁰⁷ type AFM structures for each layer, respectively. Therefore, the tuning of magnetic properties arising from the competition between two different AFM interactions is expected when Mn²⁺ and Fe²⁺ ions are mixed, which has been studied by Masubuchi et al.⁸¹ Single crystals of Mn_1−xFe_xPS₃ (0 ≤ x ≤ 1) were synthesized using a CVT technique as detailed in ref. 81.

As shown in Fig. 5, the magnetic properties were characterized by the temperature dependence of magnetization under various magnetic fields along the easy axis (the c* axis in Fig. 5 is perpendicular to the ab-plane. i.e., the out-of-plane direction).⁸¹ A few magnetic phases have been identified: AFM order for 0 ≤ x ≤ 0.2 and 0.8 ≤ x ≤ 1 composition, which is characterized by a clear AFM transition in susceptibility without remarkable difference between zero-field-cooling (ZFC) and field-cooling (FC). A broad hump in susceptibility occurs above the AFM ordering temperature T_N in end compounds [Fig. 5(a)]. This is a generic feature in many MPX₃ compounds, which has been attributed to a short-range 2D or quasi-2D magnetic correlation owing to the layered structures. The broad hump is suppressed by substitution, leading to a sharper peak at T_N [Fig. 5(a)], which has been ascribed to the weakening of a short-range magnetic correlation due to randomness introduced by Fe substitution.

Fig. 5 (a and b) Temperature dependence of zero-field cooled (ZFC) susceptibility with the magnetic field applied parallel to the magnetic easy axis (c*-axis) of Mn_1−xFe_xPS₃ (x = 0.0, 0.1, 0.2, 0.8, 0.9, 1.0). (c) Magnetic phase diagram of the Mn_1−xFe_xPS₃. SG, RSG, AF, and Para indicate a spin glass phase, a reentrant spin glass phase, an antiferromagnetic ordered phase, and a paramagnetic phase, respectively. Reprinted (adapted) with permission.⁸¹ Copyright 2008, Elsevier.

Samples in 0.5 ≤ x ≤ 0.6 compositions display significant irreversibility [Fig. 5(b)] and are ascribed to a spin glass phase, which might be attributed to the competition between dominant exchange interactions in MnPS₃ and FePS₃ phases, namely AFM Mn²⁺–Mn²⁺J₁ interaction and FM Fe²⁺–Fe²⁺J₁ interaction, respectively^35,107 (Table 4). This is further confirmed by AC susceptibility.⁸¹ The glass temperature, defined as the temperature where susceptibility displays irreversibility between ZFC and FC measurement, is found to enhance with the frequency in AC susceptibility measurements. The remaining composition regions, i.e., 0.3 ≤ x ≤ 0.45 and 0.6 < x ≤ 0.7, are characterized by an AFM-like transition without irreversibility at T_N. However, irreversibility occurs at a lower temperature. This has been ascribed by a reentrant spin glass transition [RSG in the phase diagram in Fig. 5(c)]. Considering equal Mn–Fe substitutions in both end compounds, the reentrant spin glass phase is found to be stronger towards Fe-rich compositions as compared to Mn-rich compositions, which is manifested by the higher reentrant spin glass transition temperature for x = 0.7 than x = 0.3.⁸¹ Such behavior could stem from much larger single-ion anisotropy A for FePS₃ (Table 4) as compared to MnPS₃, as has been proposed in dilute alloys.¹⁶²

Overall, Mn_1−xFe_xPS₃ displays a non-monotonic doping dependence of T_N with a minimum of around x ≈ 0.5. Such behavior is widely seen in other metal-substituted MPX₃ and is usually interpreted by spin frustration due to the mixing of two types of magnetic ions compounds (MnPS₃ and FePS₃) with significantly distinct magnetic exchange interactions J₁, J₂, and J₃ ^35,107 as summarized in Table 4.

4.2.1.1.2. Fe_1−xNi_xPS₃. For Fe_1−xNi_xPS₃, the distinct XY- and Ising-like antiferromagnetism for the end members NiPS₃ and FePS₃ respectively makes it rather interesting to investigate the evolution between those two magnetic orders with distinct magnetic anisotropies.

Fe_1−xNi_xPS₃ single crystals were grown using CVT with a temperature gradient from (760–700) to (690–600) °C for 200 hours.^88,91 The magnetic properties of Fe_1−xNi_xPS₃ were characterized using temperature and field dependence of magnetization. Fig. 6(a) presents the temperature dependence of susceptibility (χ = M/H) with the magnetic field of 1 T along a, b, and c*. Here, c* represents the direction that is perpendicular to the crystallographic ab-plane, which is slightly deviated from the crystallographic c axis in a monoclinic unit cell. For end compounds FePS₃ (x = 0) and NiPS₃ (x = 1), susceptibility first increases upon cooling, forming a broad maximum at around temperature T_max, followed with the AFM transition temperature T_N below T_max. On increasing Ni content x, T_N is found to slightly reduce up to x = 0.3, followed by systematic increase with further increasing Ni content [Fig. 6(b)]. Judging from magnetic exchange interaction, such T_N increase can be explained by stronger magnetic exchange interactions J₁ and J₃ for NiPS₃ ¹²⁸ than FePS₃ ¹⁰⁷ (Table 4). Composition dependence for T_max follows a similar non-monotonic trend, but T_max increases more remarkably with Ni content in Ni-rich compositions [Fig. 6(b)]. As mentioned in the previous section on Mn_1−xFe_xPS₃, the broad maximum exists in pristine MPX₃ and has been ascribed to the strong low-dimensional dynamic magnetism pertaining to short-range correlated spins. Similarly, in Fe_1−xNi_xPS₃ this broad maximum is also suppressed by substitution, leading to sharper susceptibility transition at T_N in substituted samples. This suggests the suppression of the short-range magnetic correlation by substitution in this system. However, the Raman spectroscopy results based on two-magnon Raman scattering reveal that the short-range dynamic magnetism does not quickly quench but rather persists to compositions much below x = 0.9.⁹¹ Therefore, more efforts are needed to clarify the nature of such a broad maximum above T_N.

Fig. 6 (a) Temperature dependencies of magnetization divided by magnetic field MH⁻¹ for Fe₂P₂S₆, (Fe_0.7Ni_0.3)₂P₂S₆, (Fe_0.5Ni_0.5)₂P₂S₆, (Fe_0.3Ni_0.7)₂P₂S₆, (Fe_0.1Ni_0.9)₂P₂S₆, and Ni₂P₂S₆, measured with a field of 1 T applied along three different crystallographic directions. T_N and T_max denote Néel temperature and the maximum magnetization temperature. (b) Evolution of T_N and T_max with composition for (Fe_1−xNi_x)₂P₂S₆. Reprinted (adapted) with permission.⁸⁸ Copyright 2021, American Physical Society.

The rapid suppression of a broad maximum with Fe substitution in NiPS₃ also suggests the modification of XY-type magnetism. In fact, the evolution from XY- to Ising-type anisotropy below x < 0.9 is clearly manifested in susceptibility. For pristine NiPS₃ (x = 1), susceptibility measured with field along a (χ_a), b (χ_b), and c* (χ_c*) axes overlaps above T_N but display significant anisotropy below T_N [Fig. 6(a)], implying a moment orientation along the a-axis and consistent with the reported magnetic structure.¹²³ However, by adding Fe, the x ≤ 0.9 (i.e., Fe content ≥ 10%) samples display anisotropy even above T_N, and χ_c* exhibits much stronger temperature dependence. Those observations are characters for highly anisotropic Ising-type magnetism with out-of-plane moment orientation of the end compound FePS₃ (x = 0).¹⁰⁷ Therefore, a transition from XY- to Ising-type anisotropy may start with only 10% Fe substitution in NiPS₃. Such sensitive tuning of magnetic anisotropy in NiPS₃ by just 10% Fe substitution might be attributed to a much stronger (≈9 times) single-ion anisotropy (A) for FePS₃ ¹⁰⁷ than NiPS₃ ¹²⁸ (Table 4).

4.2.1.1.3. Ni_1−xMn_xPS₃. Ni_1−xMn_xPS₃ provides a platform to study spin-flop transitions under relatively low magnetic fields. In AFM systems, a magnetic field along the easy axis exceeding a critical spin-flop field H_SF drives the magnetic moments to rotate to a canted configuration with a component perpendicular to the field direction, resulting in a net moment along the easy axis.^163,164 Such field-driven moment reorientation from AFM to SF state is known as the spin-flop (SF) transition, which manifests into a super-linear behavior in field-dependent magnetization measurements (i.e., magnetization upturn). This is different from the spin–flip transition in which the moments are polarized to the magnetic field direction under a strong field and is characterized by a magnetization saturation-like behavior. For MnPS₃ with magnetic moment along the out-of-plane direction (Fig. 3),^78,134 a SF transition in the isothermal magnetization has been observed under out-of-plane magnetic field (H⊥ab) but is absent under in-plane field (H∥ab) [Fig. 7(a)–(c)].^{10,28,65,119,146} During this SF transition, the magnetic moments undergo continuous rotation towards the ab-plane.¹³⁴ Although the SF transition was discovered a long time ago¹⁶⁵ and widely studied from bulk to atomically thin MnPS₃,²⁹ it has been reported only recently in NiPS₃.⁸⁹ NiPS₃ displays an SF transition under the in-plane field of ∼6 T at 2 K [Fig. 7(c)], which is consistent with the almost in-plane moment orientation of this compound (Fig. 3),^33,111,166 as shown by a black arrow in Fig. 7(c). Also, the zig-zag AFM structure with moments oriented along a-axis leads to an anisotropic SF transition that is sensitive to the in-plane field orientations.⁸⁹

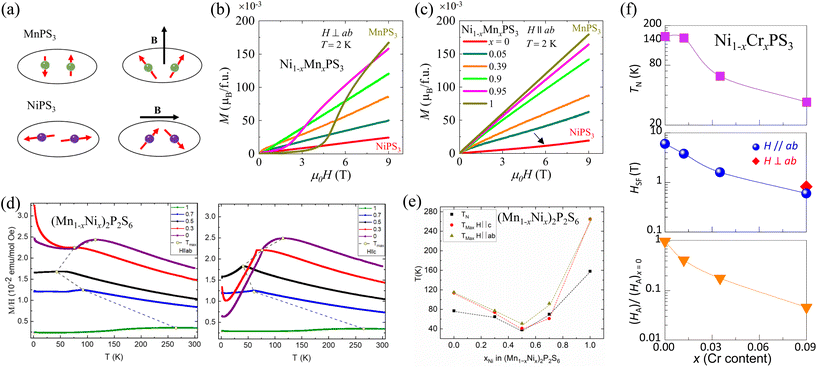Fig. 7 (a) Schematics of spin-flop transition for MnPS₃ and NiPS₃.⁸⁹ (b and c) Magnetic field dependence of magnetization for Ni_1−xMn_xPS₃ under in-plane (H∥ab) and out-of-plane (H⊥ab) magnetic fields.⁸⁹ Reprinted (adapted) with permission.⁸⁹ Copyright 2021, American Physical Society. (d) Temperature dependence of magnetization for (Mn_1−xNi_x)₂P₂S₆ under in-plane (H∥ab) and out-of-plane (H∥c) magnetic fields.⁸⁷ (e) Evolution of T_N and T_max with composition for (Mn_1−xNi_x)₂P₂S₆.⁸⁷ (f) Doping dependence of Néel temperature (T_N), spin-flop field (H_SF), and the effective magnetic anisotropy field (H_A) of Ni_1−xCr_xPS₃.¹⁷⁷

The distinct SF behavior in NiPS₃ and MnPS₃ indicates an evolution of SF transition with composition in “mixed” compounds Ni_1−xMn_xPS₃. Indeed, magnetism is found to be highly tunable with composition. Fig. 7(b) and (c) show that the in-plane and out-of-plane magnetizations exhibit a systematic enhancement upon increasing Mn content x, consistent with the greater magnetic moment of Mn²⁺ than Ni²⁺. Interestingly, the SF transitions are also extremely sensitive to composition variation.⁸⁹ The SF transition in NiPS₃ under an in-plane field disappears up to 5% Mn substitution (i.e., x = 0.05 in Ni_1−xMn_xPS₃, Fig. 7(c)). Similarly, the H_SF for the out-of-plane field in MnPS₃ is reduced by half with 5% Ni substitution (i.e., x = 0.95) and disappears upon 10% substitution (x = 0.9) [Fig. 7(b)]. Such highly sensitive nature of SF transition to light substitution of magnetic atoms is very different from that of non-magnetic substitution. It has been found that 20% substitution is needed to reduce H_SF by half in Zn-substituted MnPS₃.^78,85 In Ni-substituted MnPS₃, the substantially different single-ion anisotropy (Table 4) may explain the efficient suppression of SF transition. A similar mechanism has also been proposed for the suppression of H_SF in MnPS₃ under pressure.¹³⁵ In addition, Ni–Mn substitution can also be viewed as inducing magnetic impurities, especially in low-substitution levels. Hence, it is necessary to consider the magnetic interaction to understand the observed sensitive doping dependence in Ni_1−xMn_xPS₃. The magnetic ordering temperature T_N characterizes the strengths of magnetic interactions. For lightly substituted samples with x close to 0 or 1, the T_N is found to only change slightly as compared to the parent compounds NiPS₃ and MnPS₃, which is interesting given that the light Ni–Mn substitution drastically suppresses the SF transitions. This suggests that the efficient suppression of the SF transition with light magnetic substitution in Ni_1−xMn_xPS₃ can be attributed to the tuning of single ion isotropy rather than exchange interaction.

The modification of magnetic anisotropy with Ni–Mn substitution in Mn_1−xNi_xPS₃ ⁸⁷ is further demonstrated by the temperature dependence of susceptibility (χ = M/H) [Fig. 7(d)]. For compositions 0 ≤ x ≤ 0.5, the out-of-plane susceptibility (χ_c, measured under an out-of-plane field) is significantly reduced below T_N in comparison to in-plane susceptibility (χ_ab, measured under an in-plane field), implying moment orientation along the c axis, consistent with the reported magnetic structure of pristine MnPS₃.^78,134 This susceptibility trend is reversed on further increasing Ni content above x > 0.5 in which χ_ab < χ_c below T_N,⁸⁷ suggesting switching of magnetic easy axis from out-of-plane to in-plane direction above x > 0.5. These results agree well with a theoretical study that predicts the magnetic transition from Néel-type (where all nearest-neighbor spins are aligned antiparallel as shown in Fig. 3) in pristine MnPS₃ to zigzag-type in pristine NiPS₃ (Fig. 3) at around x = 0.25–0.5.¹⁵²

In addition, the T_N and T_max (broad maximum temperature) in susceptibility also provide useful information. As shown in Fig. 7(e), both T_N and T_max undergo non-monotonic dependence on Ni–Mn substitution with a minimum around x = 0.5 (ref. 87, 89 and 152) that can be ascribed to the attenuation of the magnetic interaction due to magnetic disorder in such a magnetically substituted system. T_max is much larger than T_N for both MnPS₃ and NiPS₃, but is comparable with increasing substitution levels [Fig. 7(e)], reminiscent to the observation for Fe_1−xNi_xPS₃ ^88,91 described above. Furthermore, for x = 0.5 composition, the PM to AFM transition at T_N = 42 K is followed by the emergence of a reentrant spin glass state at low temperature,¹⁵² which is manifested by the irreversibility between ZFC and FC below T = 30 K similar to the case of Mn_1−xFe_xPS₃ described above.⁸¹

4.2.1.1.4. Ni_1−xCr_xPS₃. The Cr-based layered compounds, such as CrI₃, Cr₂Ge₂Te₆, CrCl₃, and CrPS₄, have recently gained intensive attention because of their robust magnetic order persisting in the 2D limit.^{7,8,167–169} Surprisingly, the study of Cr-based MPX₃ compounds has been very limited. So far, only CrPSe₃ ¹⁷⁰ and Cr_2/3PS₃ ¹⁷¹ have been reported while the stoichiometric CrPS₃ has not been experimentally realized. This has been attributed to the weakened P–P dimerization that favors the formation of Cr³⁺ cation instead of the +2 metal valence required to stabilize the MPX₃ lattice.¹⁷² The direct substitution of Cr³⁺ for M²⁺ ion in MPX₃ is challenging from a chemical valence balance perspective, which may eventually lead to vacancies at metal sites. A similar issue also occurs for V_xPS₃ (x = 0.78 (ref. 173 and 174) and 0.9 (ref. 71)) in which V²⁺ and V³⁺ ions coexist and lead to V vacancies. Indeed, Cr substitution in MPX₃ has been found to be challenging in comparison to other divalent metal ion substitutions.^{87–89,91,175,176}

So far, light substitution of up to 9% without inducing a clear signature of vacancies in NiPS₃ has been recently reported.¹⁷⁷ The lack of vacancies from composition analyses implies an isovalent substitution of +2 valence for Cr ions. Interestingly, a low Cr amount already can efficiently modulate the magnetism in NiPS₃. As shown in Fig. 7(f), first, the magnetic transition temperature T_N is found to reduce significantly from 155 K in NiPS₃ to 34 K in the x = 0.09 sample. Second, the SF transition under an in-plane magnetic field in NiPS₃ is significantly suppressed [Fig. 7(f)]. Also, the SF transition starts to occur even under a weak out-of-plane magnetic field of <1 T in the x = 0.09 sample, which strongly implies moment reorientation upon Cr substitution. Evaluating the characteristic field for spin flop, magnetic exchange, and magnetic anisotropy also reveals that the magnetic anisotropy is significantly suppressed by Cr substitution. Furthermore, in addition to SF transition, a moment polarization-like behavior has been observed under both in-plane and out-of-plane fields, with a similar polarization field of ∼8 T and a small saturation moment of 0.24μ_B per formula unit.

Suppressed SF transition and more isotropic magnetization are consistent with a suppression of magnetic anisotropy upon Cr substitution, which gives rise to more controllable moment orientations and eventually the moment polarization in the x = 0.09 sample. Indeed, similar field-induced moment polarization at relatively low magnetic fields have also been seen in quite a few Cr-based AFM compounds such as CuCrP₂S₆,^153,154 CrPS₄,¹⁷⁸ CrCl₃,¹⁷⁹ and CrSBr.¹⁸⁰ However, owing to the 3+ valence of Cr ions instead of the 2+ metal valence expected in MPX₃, substituting Cr is limited to only 9% in NiPS₃, as discussed above. This makes it difficult to explore the potential of this route.

Therefore, recently, an alternative approach that balances the valence by co-substituting mono-valent metal ions together with the tri-valent Cr ions has been reported, through which all M²⁺ ions can be replaced to tune the magnetism more efficiently.¹⁸¹ This work provides a new doping strategy in the MPX₃ family, which successfully substitutes an equal Cu and Cr for Ni leading to a wide range of medium-entropy compositions Cu_xNi_2(1−x)Cr_xP₂S₆ (0 ≤ x ≤ 1).

4.2.1.1.5. Mn_1−xCo_xPS₃. Compared to other metal substitutions, Co substitution has been fairly elusive in MPX₃ with only a few recent studies.^114,116,117 This might be due to the challenges in crystal growth for CoPS₃¹¹⁷ which causes this compound and its derivatives to be less-explored.^{36,108,129,182} A recent breakthrough in reactive flux technique using P₂S₅ and metal precursors offers an opportunity to study Co-substituted MPX₃ compounds,^114–118 as described in section 2. The Mn_xCo_2−xP₂S₆ single crystals can be obtained by annealing the stoichiometric mixture of Mn, Co, and P₂S₅ powders at 540 °C for 72 hours.¹¹⁷

The two parent compounds Mn₂P₂S₆ (Néel-type AFM with out-of-plane easy axis) and Co₂P₂S₆ (zig-zag type AFM with in-plane easy axis) exhibit distinct AFM ordering, so magnetism is expected to be tunable with substituting. As shown in Fig. 8(a), the magnetic susceptibility of Mn_xCo_2−xP₂S₆ lacks significant irreversibility between ZFC and FC in the entire temperature range, suggesting AFM ordering below T_N without spin-glass state that is also seen in Fe-⁸¹ and Ni-substituted¹⁵² Mn₂P₂S₆. Similar to many other metal substituted MPX₃,^{81,85,87,89,152}T_N also exhibits a non-monotonic composition dependence, showing maximum values for the two end compounds (x = 0 and 1) and reduces upon mixing the metal atoms. In addition, the broad maximum temperature T_max observed just above T_N also displays a similar variation with substitution, except that the broad maximum in susceptibility is completely suppressed for the x = 1 (50% Mn and 50% Co) sample, as shown in Fig. 8(a). Such suppression is also observed in thin flakes of Mn₂P₂S₆, which has been ascribed to the reorientation of Mn²⁺ moments that gives rise to a weak FM state.¹⁸³ Similar weak ferromagnetism may also be responsible to the rapid rise in the susceptibility at low temperature below T < 30 K [Fig. 8(a)] and non-linear isothermal magnetization at T = 2 K [Fig. 8(b)] for this x = 1 sample. Nevertheless, one should always be caution about the presence of trace FM impurities in doped materials.

Fig. 8 (a) Field-cooled (FC) magnetic susceptibility of Mn_xCo_2−xP₂S₆ measured with H = 1000 Oe.¹¹⁷ (b) Magnetization for MnCoP₂S₆ at 2 K and 150 K.¹¹⁷ Reprinted (adapted) with permission.¹¹⁷ Copyright 2022, American Chemical Society. (c) SEM images of nanosheet (NS) of NiPS₃, Ni_0.88Co_0.12PS₃, Ni_0.68Co_0.32PS₃, and Ni_0.60Co_0.40PS₃.⁹⁰ (d) Magnetization at 5 K for Ni_1−xCo_xPS₃ NS and single crystal samples.⁹⁰

The evolution of Curie–Weiss temperature θ_cw extracted from the linear fit of the high temperature (T > 200 K) paramagnetic (PM) region of the inverse susceptibility also provides useful information.¹¹⁷θ_cw is negative for AFM Mn_xCo_2−xP₂S₆, which undergoes a non-monotonic variation with Mn–Co substitution and reaches the maximal (i.e., less negative) at x = 1, indicating the attenuation of AFM interaction around this composition. This is probably due to magnetic frustration owing to the competition between distinct AFM exchange interactions J₁, J₂, and J₃ for Mn₂P₂S₆ ³⁵ and Co₂P₂S₆.¹²⁹

4.2.1.1.6. Ni_1−xCo_xPS₃. Magnetic properties of Co-substituted NiPS₃ (Ni_1−xCo_xPS₃) have been investigated in both single crystals and nanosheet (NS) samples.⁹⁰ Ni_1−xCo_xPS₃ single crystals were grown using a CVT technique as shown in Table 1. For NS samples, Ni_1−xCo_xPS₃ (0 ≤ x < 0.5) NS of average thickness of 8 nm (around 10 layers) were grown by a chemical vapor conversion method via a two-step process: first, the metal hydroxide NS precursor containing various Ni : Co ratios were synthesized on carbon cloth through a wet chemical method. Second, these metal hydroxide precursors were loaded downstream of an evacuated custom-designed fused silica socket tube with a mixture of P and S positioned on the other side. Ultrathin Ni_1−xCo_xPS₃ NS can be evenly grown on carbon cloth over a reaction time of 90 min at 480° to 490 °C with an argon gas flow [Fig. 8(c)].⁹⁰

Magnetization measurements with the background from carbon cloth removed are shown in Fig. 8(d). T_N ≈ 155 K for pristine NiPS₃ is suppressed by Co substitution for both single crystals and NS, which is in line with the general trend of metal substitution in MPX₃ as described above. In contrast to bulk single crystals, susceptibility for all Ni_1−xCo_xPS₃ (0 ≤ x ≤ 0.4) NS samples display low-temperature upturns, suggesting the rise of weak ferromagnetism. Field dependence of magnetization [Fig. 8(d)] also reveals magnetic hysteresis over a low field region (|H| < 300 Oe), which becomes more obvious with increasing Co content.

Providing similar lattice parameters and zig-zag type AFM structures for pristine NiPS₃ and CoPS₃, it is not surprising that Co–Ni substitution does not cause significant modification in magnetic properties. The low-temperature magnetization upturn and magnetic hysteresis occur in NS samples, which might be attributed to the sulfur vacancy in NSs. Electron spin resonance (ESR) spectroscopy measurements⁹⁰ have revealed that the sulfur vacancy formation, which is in line with the rise of ferromagnetism with Co substitution. Defect-induced ferromagnetism has been observed in the atomically thin layers of non-magnetic 2D materials such as graphene^2,184 and MoS₂.^4,185 As mentioned earlier in section 4.1, in NiPS₃, the magnetic interactions are mainly governed by the Ni–S–Ni superexchange interactions, occurring through the overlapping of half-filled Ni e_g and S 3p orbitals that mediates the effective electron hopping between neighboring Ni sites.¹²⁸ Therefore, tuning of magnetic states due to sulfur vacancy is plausible in Ni_1−xCo_xPS₃ NS. In fact, the theoretical calculations have demonstrated the disruption of anion-mediated superexchange interaction between Ni moments due to sulfur vacancy.⁹⁰ Furthermore, the calculated electronic structure has revealed unoccupied in-gap-like states that could serve as a carrier trap site and hinder the charge transfer process, further suppressing superexchange interaction and might facilitate other competing magnetic phases in NiPS₃.

4.2.1.1.7. Non-magnetic dopant: Mn_xZn_1−xPS₃. Magnetic properties of Zn-substituted MnPS₃ have been widely studied using magnetization^77,78,85 and Raman¹⁵¹ measurements. Up on replacing Mn by non-magnetic Zn, the broad maximum immediately above T_N in susceptibility measured with in-plane field starts to vanish with increasing Zn substitution, leading to a sharp susceptibility peak at magnetic transition T_N.⁸⁵ This suggests a breakdown of short-range correlation, as expected for metal substitution in MPX₃.^81,87,88,91 In addition, for Zn-rich samples (Zn content ≥ 0.5), the low-temperature susceptibility displays an abrupt enhancement, which has been ascribed to a weak PM behavior of the significant number of isolated spins due to magnetic dilution by Zn.^85,151

Suppression of transition temperature T_N by Zn substitution is seen in both susceptibility⁸⁵ and Raman¹⁵¹ experiments. Unlike magnetic ion substitutions that always lead to a U-shape non-monotonic composition dependency of T_N, non-magnetic Zn substitution gradually suppresses T_N to zero temperature up to 50% substitution level in magnetization measurements^77,85 [Fig. 9(a)], or even to 70% from extrapolating the results from Raman spectroscopy¹⁵¹ [Fig. 9(b)]. This is surprising given the critical concentration for site dilution in a honeycomb lattice with nearest-neighbor interactions (J₁) is x = 0.7.¹⁸⁶ Therefore, J₁ alone may not explain the behavior of Mn_xZn_1−xPS₃, and the second (J₂) and the third (J₃) nearest-neighbor interactions, though weaker than J₁ in MnPS₃ (see Table 4), might be ascribed for the magnetic stability below x < 0.7.⁸⁵ Of course, measurements on the addition of high-Zn samples would provide a better estimate of the critical composition, which was determined by linear extrapolation of a few compositions¹⁵¹ as shown in Fig. 9(b).

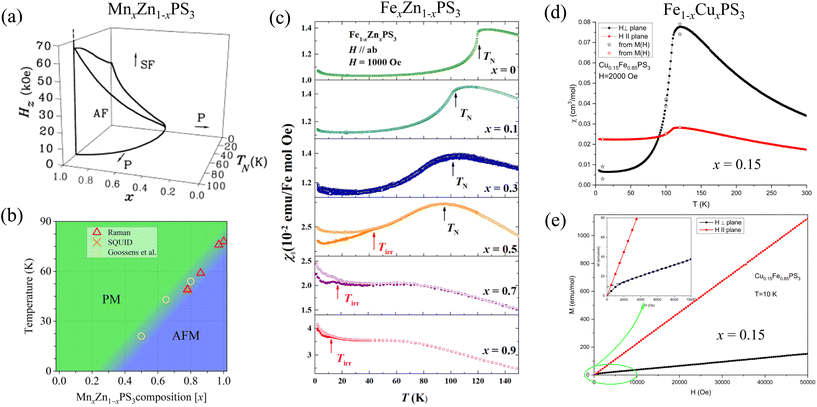Fig. 9 (a and b) Magnetic phase diagrams for Mn_xZn_1−xPS₃. Field dependence of phases is also shown in (a).^85,151 Reprinted (adapted) with permission.⁸⁵ Copyright 1998, IOP Publishing. Reprinted (adapted) with permission.¹⁵¹ Copyright 2023, American Physical Society. (c) Temperature dependence of magnetic susceptibilities of Fe_1−xZn_xPS₃ under an in-plane magnetic field of 1000 Oe.⁹³ (d) Temperature dependence of the magnetic susceptibility for Cu_0.15Fe_0.85PS₃ measured under in-plane (H||plane) and out-of-plane (H⊥plane) field of 2000 Oe. (e) Field dependence of magnetization for Cu_0.15Fe_0.85PS₃ at T = 10 K.¹⁸⁷

The impact of Zn substitution in MnPS₃ is further manifested as reduced SF transition field H_SF.⁷⁸ Substituting Zn for Mn breaks down the long-range magnetic order, resulting in “weakly bound” Mn moments aligned along the out-of-plane direction. For MnPS₃ in which the dipolar anisotropy dominates, the local dipole field along the out-of-plane direction may be attenuated by these weakly bound moments. Furthermore, replacing a Mn with a non-magnetic Zn is accompanied by a vanishing moment at the substitute site, which affects the nearby Mn moments and causes them to be canted.⁷⁷ On a larger scale, this leads to an average staggered magnetic moment which consequently suppresses the magnetic anisotropy of the system, which eventually suppresses H_SF.⁷⁸

4.2.1.1.8. Non-magnetic dopant: Fe_1−xZn_xPS₃. Magnetic dilution by non-magnetic Zn substitution has also been studied in Ising-type antiferromagnet FePS₃.⁹³ Substituting Zn in FePS₃ is reported to induce weak ferromagnetism associated with spin/cluster spin glass.⁹³ As shown in Fig. 9(c), substituting Fe with non-magnetic Zn suppresses T_N. For Zn content x greater than 0.3, significant irreversibility between ZFC and FC measurements starts to occur at temperatures below T_N, which has been ascribed to weak ferromagnetism associated with glassy behavior.⁹³ For high Zn samples (0.7 ≤ x ≤ 0.9), susceptibility upturn appears at low temperatures, which has been attributed to the emergence of FM order with an out-of-plane easy axis.⁹³ This conclusion is also supported by the Curie–Weiss temperature (θ_CW), which becomes less negative with increasing Zn substitution and even attains positive values for χ_⊥ of x = 0.7 and 0.9 samples, suggesting the attenuation of AFM interactions and development of FM correlation with Zn substitution in FePS₃.⁹³

The rise of ferromagnetism is further supported by the field dependence of magnetization. The in-plane magnetization displays linear field dependence for all compositions and temperature ranges. However, under H⊥ab magnetic field, the x = 0.9 sample displays magnetic hysteresis and saturation behavior with saturation moment reaching ∼4μ_B/Fe, which is consistent with the S = 2 Fe²⁺.⁹³ The theoretical study further reveals the key role played by hole doping to stabilize ferromagnetism in Zn-substituted FePS₃.⁹³ In highly Zn-substituted samples x = 0.7 and 0.9,⁹³ the XPS result reveals the presence of Fe³⁺ ion in addition to Fe²⁺ ion, leading to hole doping and the subsequent rising of FM interactions mediated by bound magnetic polarons induced impurity-band-exchange in such diluted environment induced by Zn substitution in FePS₃.

4.2.1.1.9. Non-magnetic dopant: Fe_1−xCu_xPS₃. In addition to Zn, magnetic dilution in FePS₃ has also been realized by Cu substitution.¹⁸⁷ Cu substitution up to 15% is found to suppress T_N to ≈108 K from that of 120 K in pristine FePS₃ [Fig. 9(d)],¹⁸⁷ consistent with the result obtained for Zn-substituted FePS₃ ⁹³ and can be attributed to the suppression of magnetic exchange interactions, as discussed in the previous section. Other than that, the susceptibility for the substituted sample is highly similar to that of the pristine FePS₃: the out-of-plane susceptibility measured with a magnetic field perpendicular to the basal plane displays a much stronger temperature dependence below T_N than in-plane susceptibility. In addition, in the PM state, susceptibility displays strong anisotropy, with a much higher value for the out-of-plane susceptibility that is similar to undoped FePS₃ [Fig. 9(d)]. These observations suggest that magnetic anisotropy is not strongly modified upon Cu substitution up to 15%.

In field-dependent magnetization, the 10% Cu-substituted sample displays a weak non-linearity under an out-of-plane magnetic field [Fig. 9(e)], which was claimed to be a signature of weak ferromagnetism due to the reorientation of canted moments, and has also been observed in Zn-⁷⁸ and Ni-substituted⁸⁹ MnPS₃. In addition to a moment canting scenario, other mechanisms, such as sulfur vacancy which has been seen in Co-substituted NiPS₃ nanoflakes⁹⁰ (see section 4.2.1.1.5) and the presence of the finite clusters of uncompensated spins¹⁸⁷ might also give rise to weak ferromagnetism in Cu_0.15Fe_0.85PS₃.

4.2.1.1.10. Non-magnetic dopant: Fe_1−xCd_xPS₃. Cd as another non-magnetic dopant has been studied a long time ago on a 50% Cd-substituted Fe_0.5Cd_0.5PS₃ sample.¹⁸⁸ Magnetic phase transition is not observed in susceptibility measurements down to 57 K. The Curie–Weiss temperature displays positive values, decreasing from 104 K for pristine FePS₃ to 40 K for Fe_0.5Cd_0.5PS₃. The positive Curie–Weiss temperature even in pristine FePS₃ appears interesting given it well defined AFM ground state. It might be ascribed to the competition between the direct FM J₁ and indirect AFM J₂ interactions.¹⁸⁸ The suppression of Curie–Weiss temperature upon introduction of Cd in FePS₃ can be attributed to the attenuation of direct J₁ owing to the expanded lattice due to Cd substitution, which increases the nearest neighbor distance of Fe²⁺ by 1.95%.¹⁸⁸ A more concrete understanding may be obtained by future substitution studies covering more Cd compositions.
4.2.1.1.11. Metal substitution in selenides: Fe_1−xMn_xPSe₃. Most of the metal substitutions were performed on sulfides as summarized above, whereas the selenide MPSe₃ compounds are relatively less explored. Mn–Fe substitution has been reported in selenide compounds MnPSe₃ and FePSe₃,⁸⁶ which are characterized by Néel-type and Ising-type magnetic structures with in-plane and out-of-plane moments, respectively (Fig. 3). Similar to sulfide FePS₃ stated above, anisotropy between out-of-plane susceptibility χ_⊥ and in-plane susceptibility χ_∥above T_N is a character of Ising-type magnetism in FePSe₃. Such anisotropy is suppressed by Mn substitution for Fe [Fig. 10(a)],¹²² which is expected since the end compounds FePSe₃ and MnPSe₃ possess different magnetic structures with different easy axes. Interestingly, the susceptibility anisotropy below T_N suggests that the out-of-plane magnetic easy axis for FePSe₃ is robust against Mn-substitution up to 90%, which is also supported by the emergence and evolution of the SF transition. SF transition is not observed up to 9 T in FePSe₃ due to the strong magnetic anisotropy for Ising-type magnetism. Heavy Mn substitution leads the SF to occur in out-of-plane magnetization only, and further increased Mn content beyond 90% causes the SF transition to appear in in-plane magnetization, implying the switching of easy axis from out-of-plane to in-plane when Mn content x > 0.9 [Fig. 10(b)]. The rotation of the magnetic easy axis occurring only above 90% Mn for Fe substitution suggests a highly anisotropic magnetic order in FePSe₃. This can be estimated from the relative magnitudes of single-ion anisotropy (A) for the two end compounds FePSe₃ and MnPSe₃. Though the experimental value of A is still lacking for FePSe₃, in sulfide counterparts FePS₃ ¹⁰⁷ possesses much higher A by >300 times than that of MnPS₃ ³⁵ (Table 4). Expecting a similar scenario in selenide samples, the robust magnetic easy axis against up to 90% Mn substitution in FePSe₃ can be understood.

Fig. 10 (a) Temperature dependencies susceptibility for Fe_1−xMn_xPSe₃ measured under a magnetic field of 0.1 T.¹²² (b) Isothermal magnetization at 2 K for Fe_1−xMn_xPSe₃ under out-of-plane (H⊥ab, red) and in-plane (H||ab, blue) magnetic fields. Insets show spin-flop transition at low fields.¹²² (c and d) Magnetic phase diagrams of Mn_1−xFe_xPSe₃ obtained from (c) single crystals¹²² and (d) polycrystals.⁸⁶ Reprinted (adapted) with permission.⁸⁶ Copyright 2020, American Physical Society.

Because both end compounds FePSe₃ ⁴² and MnPSe₃ ⁴³ exhibit 2D magnetism down to the monolayer limit, exploring possible 2D magnetism in their mixed compounds (Fe_1−xMn_xPSe₃) is interesting. Having said that, the strong frustration arising from mixing two different magnetic metal ions may destabilize magnetic order in the 2D limit. Indeed, such mixing suppresses T_N and leads it to reach a minimum for 50% substitution in studies using both single crystals¹²² [Fig. 10(c)] and polycrystals⁸⁶ [Fig. 10(d)]. This appears to be a generic behavior for all polymetallic MPX₃.^81,85,87,89 In addition, a mixed phase consisting of both Fe²⁺- and Mn²⁺-type ordering, forming nano-sized chemically disordered clusters in intermediate compositions (0.25 < x < 0.875) has also been discovered⁸⁶ [Fig. 10(d)].

4.2.1.1.12. HEPX₃ (HE = high entropy; X = S or Se). High entropy (HE) alloy involves the mixing of five or more elements each with a composition of 5–35 atomic percentage. The composition of HE compounds can be greatly varied by adjusting the ratios of constituent elements. Such flexible composition stoichiometry allows for property tuning with a wide compositions range. Incorporating multiple elements also offers various valence states and spin states in a system. Depending on the choices of elements, the distribution of charges and spin interactions may vary significantly. Furthermore, the presence of multiple elements results in a complex and disordered atomic structure. Hence, with the added complexity, HE compounds provides an opportunity to investigate the interplay between charge, spin, and composition degrees of freedom. Recently, the bimetallic substitution in MPX₃ has been extended to the realm of HE compounds.^113,121,189 Providing various anisotropy of ions and diverse magnetic structures for different MPX₃ compounds, such a strategy is expected to lead to rich magnetic properties and phases.

For Mn_0.25Fe_0.25Co_0.25Ni_0.27P_1.04S₃ ^113,189 with equal molar ratio of metal atoms, a well-defined PM to AFM transition at T_N = 70 K is found in susceptibility measurements¹¹³ [Fig. 11(a)]. Deviation from this equal metal concentration results in broader or less-obvious AFM transition, as observed in Mn_0.2Fe_0.3Co_0.25Ni_0.25PS₃.¹⁸⁹ In Mn_0.25Fe_0.25Co_0.25Ni_0.27P_1.04S₃, the magnetic moments are likely to be aligned perpendicular to the basal plan, providing a weaker temperature dependence for susceptibility under an in-plane field. A spin-glass state is also proposed due to the emergence of irreversibility between ZFC and FC susceptibility at a temperature below T_N [Fig. 11(b)]. Similarly, the spin-glass phase has also been observed in a few other HEPS₃ compounds at different glass temperatures,^113,189 as summarized in Table 5. In addition to sulfides, selenide-based HE compounds have also been studied in Fe–Mn–Cd–In-based HE MPSe₃.¹²¹ The comparison study on FePSe₃, Fe_0.8Mn_0.1Cd_0.05In_0.05PSe₃, Fe_0.7(MnCd)_0.1In_0.1PSe₃, and (FeMnCd)_0.25In_0.17PSe₃ has revealed decreased T_N with reducing Fe amount [Fig. 11(c)]. The AFM transition disappears in (FeMnCd)_0.25In_0.17PSe₃, leaving a substantial susceptibility irreversibility around 15 K [Fig. 11(c)] that implies a glass state, which is further confirmed by the frequency-dependent peak in AC susceptibility measurements.¹²¹

Fig. 11 (a and b) Magnetization of (Mn,Fe,Co,Ni)PS₃ under the external magnetic field of 500 Oe along different directions. The antiferromagnetic transition (T_N) and spin glass transition temperature (T_g) are indicated.¹¹³ Reprinted (adapted) with permission.¹¹³ Copyright 2021, American Chemical Society. (c) Susceptibility (χ) of pristine FePSe₃ and (Fe,Mn,Cd,In)PS₃.¹²¹ Reprinted (adapted) with permission.¹²¹ Copyright 2022, American Physical Society.

Table 5 Summary of magnetic properties of high-entropy MPX₃ compounds

HEPX3 compounds	Magnetic properties	Ref.
Mn0.25Fe0.25Co0.25Ni0.27P1.04S3	AFM (TN = 70 K) and spin-glass (Tg1 = 35 K, Tg2 = 56 K)	113
Zn0.29Mn0.14Fe0.17Co0.18Ni0.24PS2.61	Spin-glass (Tg = 30 K), Tkink = 120 K	113
Mg0.19Mn0.18Fe0.19Co0.26Ni0.28P1.08S3	Multikinks in MT at 8 K, 42 K, 60, and 120 K	113
V0.16Mn0.18Fe0.21Co0.23Ni0.24PS2.62	Spin-glass (Tg = 37 K), Tkink = 150 K	113
(FeMnCd)0.25In0.17PSe3	Spin-glass (Tg = 15 K)	121

---

4.2.1.2. Non-isovalent substitution.
4.2.1.2.1. CuCrP₂X₆ (X = S or Se). The metal substitution in M₂P₂X₆ has been extended to the mixing of monovalent M₁¹⁺ (M₁ = Cu or Ag) and trivalent M₂³⁺ (M₂ = V or Cr) ions to from (M₁¹⁺)(M₂³⁺)P₂X₆.^{153–157,190–192} Chemical valence is balanced by maintaining an equal amount of monovalent and trivalent ions. While these compounds have been discovered a long time ago,^{155,157,190,193} there have been only a few studies on magnetic properties.^{154,155,157,190,193,194} CuCrP₂S₆ ^153,154 has recently gained increased attention. In contrast to the random distribution of dissimilar metal ions in isovalent metal-substituted M₂P₂X₆,^76–91 weak repulsive Coulomb interactions and substantial size difference between Cu¹⁺ and Cr³⁺ cations¹⁵⁶ favor an alternating arrangements of them in CuCrP₂S₆:^153,154 as shown in Fig. 12(a), Cr³⁺ ions are located almost at the center in the vdW layer, whereas Cu+ ions are slightly displaced from the center at the alternative positions above and below the Cr³⁺ layers.¹⁵⁴ This further leads to broken inversion symmetry and ferroelectricity up to room temperature.^58,59,195

Fig. 12 (a) Crystal structure of CuCrP₂S₆. (b and c) Temperature and magnetic field dependencies of magnetic susceptibility of CuCrP₂S₆. (d) Spin-flop transition when the field is applied along the a-axis.¹⁵⁴

Regarding the magnetic properties which is the focus of this review, CuCrP₂S₆ displays an AFM order below T_N = 32 K (ref. 154) [Fig. 12(b)]. On the other hand, CuCrP₂Se₆ has a slightly higher T_N (= 40 K) than that of CuCrP₂S₆, which is likely attributed to a stronger Cr–Se–Se–Cr superexchange interaction due to enhanced covalency arising from greater atomic orbitals for Se.¹⁹⁶ The much sharper drop in susceptibility measured with the field along the a-axis in comparison to other field directions suggests the magnetic moment orientation along the a-axis. The linear fit of inverse susceptibility yielded a positive Curie–Weiss temperature θ_cw = 24 K [Fig. 12(b)], implying in-plane FM interaction that may be attributed to an A-type AFM order¹⁵⁴ (see Fig. 3). The effective moments of μ_eff = (3.78 ± 0.05)μ_B f.u.⁻¹ for H∥ab and μ_eff = (3.89 ± 0.05)μ_B f.u.⁻¹ for H⊥ab¹⁵³ match with the theoretical value of 3.87μ_B for Cr³⁺. Like many other Cr-based van der Waals magnets such as CrPS₄,¹⁷⁸ CrCl₃,¹⁷⁹ and CrSBr,¹⁸⁰ as well as Cr-substitute NiPS₃ mentioned above (section 4.2.1.1.6), a field-driven AFM to FM transition has been observed in magnetization measurements with a saturation moment of ≈3μ_B/Cr [Fig. 12(c)]. Consistent with the easy-axis along the a-axis, an SF transition appears in magnetization with low H_SF ≈ 0.4 T [Fig. 12(d)].

As mentioned above in section 4.2.1.1.4, the mono- and tri-valent of Cu⁺ and Cr³⁺ allows for co-substitute other bi-valent ions such as Ni²⁺ to form Cu_xNi_2(1−x)Cr_xP₂S₆ (0 ≤ x ≤ 1).¹⁸¹ This doping strategy provides further tuning of magnetism in the MPX₃ family and leads to a wide range of medium-entropy compositions.

4.2.1.2.2. AgMP₂X₆ (M = V or Cr; X = S or Se). AgVP₂S₆ and AgCrP₂S₆ have been studied a long time ago.^191,192 Structurally, these materials form a zig-zag chain of V³⁺ (S = 1) and Cr³⁺ (S = 3/2) ions respectively along the a-axis [Fig. 13(a)], which is distinct from other MPX₃ compounds. Long-range AFM order is absent in AgVP₂S₆ from 5 to 200 K in susceptibility measurements¹⁹¹ [Fig. 13(b)]. In contrast, AgCrP₂S₆ is reported to be AFM below T_N ≈ 7 K (ref. 192) [Fig. 13(c)]. Such T_N from susceptibility is lower than T_N ≈ 20 K obtained from powder neutron diffraction experiment.¹⁵⁵ Both compositions display enhanced susceptibility at low temperatures, but AgVP₂S₆ ¹⁹¹ is characterized by isotropic susceptibility for magnetic field directions along and perpendicular to the zig-zag chain direction [Fig. 13(a)], while AgCrP₂S₆ features a small anisotropy at low temperatures¹⁹² [Fig. 13(b)].

Fig. 13 (a) Crystal structure of AgVP₂S₆ and AgCrP₂S₆. (b and c) Temperature dependence of the susceptibility for AgVP₂S₆ ¹⁹¹ and AgCrP₂S₆.¹⁹² Reprinted (adapted) with permission.¹⁹¹ Copyright 1994, Elsevier. Reprinted (adapted) with permission.¹⁹² Copyright 1990, Elsevier. (d) Crystal structure (top and side views) of AgVP₂Se₆. (e) Temperature (left) and magnetic field (right) dependencies of magnetization for AgVP₂Se₆.¹⁹⁷

A more recent study has expanded to selenide counterpart AgVP₂Se₆ ¹⁹⁷ and AgCrP₂Se₆.¹⁹⁸ These compounds are structurally slightly different from the above AgVP₂S₆ and AgCrP₂S₆ [Fig. 13(d)]. Interestingly, susceptibility irreversibility and magnetization saturation of AgVP₂S₆ ¹⁹⁷ [Fig. 13(e)] implies ferromagnetism with a T_c ∼ 18.5 K, which is distinct from the AFM ground state for other MPX₃. On the other hand, AgCrP₂Se₆ ¹⁹⁸ exhibits AFM ground state below T_N ∼ 42 K, which features field-driven moment polarization under the high field of B ∼ 3–6 T. Furthermore, polar-reflective magnetic circular dichroism (RMCD) experiments on AgVP₂Se₆ ¹⁹⁷ found a growing hysteresis loop with reducing thickness in thin flakes, which persist down to 6.7 nm flake thickness with unchanged T_c.

4.2.2. Chalcogen (X) substitution. As discussed in section 3, transition metal atoms M are surrounded by P₂X₆ clusters in each layer of MPX₃ (Fig. 2). So, substituting chalcogen X modifies the local environment of M²⁺ ion within honeycomb layers with the magnetic plane intact [Fig. 4(b)]. Therefore, chalcogen substitution offers a relatively clean approach to modifying magnetic exchange interactions. This approach has been demonstrated to be effective in other vdW magnets such as chromium halides,^145,146 in which the magnetism can be efficiently controlled by non-magnetic ligand substitution. Although the syntheses and structural characterizations of chalcogen-substituted MPX₃ have been reported a long time ago,^199–201 their magnetic properties were studied recently in a few Mn-, Fe-, and Ni-based MPX₃ compounds,^31,32 as described below.
4.2.2.1. MnPS_3−xSe_x. In MnPS_3−xSe_x, the successful substitution can be readily seen by the colors of the crystal. Upon increasing the Se content, these relatively transparent crystals gradually change color from green to wine red [Fig. 14(a)], indicating the variation of the optical gap.³¹ Upon Se substitution, T_N displays a monotonic, slight reduction from 78.5 K for MnPS₃ to 74 K for MnPSe₃ ^31,32 [Fig. 14(b)], which is drastically different from non-monotonic composition dependence seen in metal-substituted MnPS₃.^81,85,87,89 This is found to be caused by the suppressed exchange interaction.³¹ Magnetism in MnPS₃ is governed by the nearest-neighbor exchange interaction (J₁) from the Mn–Mn direct exchange,^39,128,129 and the third nearest-neighbor interaction (J₃) is also considerable (Table 5). Se substitution for S expands in-plane lattice^202,203 and elongates Mn–Mn distance, which attenuates the direct exchange and consequently reduces T_N.^31,32

Fig. 14 (a) Images of MnPS_3−xSe_x single crystals. Doping dependence of (b) Néel temperature (T_N) and (c) spin-flop (SF) field for MnPS_3−xSe_x. (d) Images of NiPS_3−xSe_x single crystals (0 ≤ x ≤ 1.3). (e) Doping dependence of T_N for NiPS_3−xSe_x. (f) Field dependence of magnetization of NiPS_3−xSe_x at T = 2 K.³¹ Reprinted (adapted) with permission.³¹ Copyright 2022, American Physical Society.

In addition to magnetic exchange interactions, chalcogen S–Se substitution also modifies magnetic anisotropy.³¹ This is expected because the two end compounds MnPS₃ and MnPSe₃, though both possess Néel-type AFM structure within each vdW layer where all nearest-neighbor spins are aligned antiparallel, feature different magnetic out-of-plane^78,134 and almost-in-plane^30,86,94,95 easy axis, respectively^{30,78,86,94,95,134} (Fig. 3). The modification of magnetic anisotropy is reflected by the evolution of SF transition. SF transition in MnPS₃ occurs under an in-plane field. The SF field H_SF is gradually suppressed to zero upon increasing Se content near x = 1 (MnPSSe₂). On the other hand, the SF transition re-appears but under an out-of-plane field for x > 1 samples. Since SF transition in AFM material is driven by magnetic field component along the magnetic moment direction (i.e., easy axis), this implies the rotation of easy axis from out-of-plane towards the in-plane direction with Se substitution, which can be attributed to the enhanced single-ion anisotropy upon Se substitution that usually favors the in-plane moment orientation in MPX₃. The switching of the easy axis is found to happen closer to the MnPS₃ side i.e., between x = 0.7 and 1.2 [Fig. 14(c)], implying the magnetism in MnPS₃ is softer than MnPSe₃, which is also consistent with the results obtained from the theoretical calculations that reveal much smaller anisotropy between the in-plane and out-of-plane directions of the spins in MnPS₃ than MnPSe₃.³¹

4.2.2.2. NiPS_3−xSe_x. The study on Ni-based NiPS_3−xSe_x faces difficulty in synthesizing single crystals for Se-rich compositions. Indeed, the studies on NiPSe₃ are very limited³⁹ as compared to the sulfide counterpart NiPS₃. A recent investigation on NiPS_3−xSe_x ³¹ combining single crystal with Se content up to x = 1.3 [Fig. 14(d)] and polycrystals up to x = 3 have revealed monotonic enhancement in T_N with increasing Se content, from ∼155 K for NiPS₃ to ∼210 K for NiPSe₃ [Fig. 14(e)]. This observation is distinct from the reduced T_N due to metal substitution in NiPS₃.^87,89 Interestingly, compared to MnPS_3−xSe_x in which Se substitution slightly reduces T_N,^31,32 in NiPS₃ the similar Se substitution causes strong T_N enhancement.³¹ Such results have been ascribed to different governing exchanges in Mn- and Ni-based systems.³¹ Magnetism of both systems are determined by the nearest J₁ and third nearest J₃ while the second nearest-neighbor interaction J₂ is negligible (Table 4). Unlike MnPS₃ in which the direct exchange between the neighboring metal ions contributes to J as described in the previous section, neutron scattering experiments^39,128 have demonstrated that the magnetic interactions in NiPS₃ are superexchange in nature. The direct exchange between Ni²⁺, however, does not exist due to the filled t_2g orbitals for Ni²⁺.^39,128 Therefore, compared to S, Se with extended 4p-orbitals favors orbital overlap and enhances superexchange between Ni²⁺ through chalcogen, giving rise to enhanced T_N.

Similar to the case of MnPS₃, Se substitution also tunes SF transitions in NiPS₃.³¹ The SF transition under an in-plane field of ∼6 T for NiPS₃ (x = 0) occurs at a higher in-plane field of ∼8 T for x = 0.25 [Fig. 14(f)]. Further increasing Se content up to 1.3 results in essentially linear magnetization under both in-plane (H∥ab) and out-of-plane (H⊥ab) fields up to 9 T. This is consistent with enhanced exchange interactions with Se substitution, based on evaluating the SF field, where H_E and H_A are effective exchange and magnetic anisotropy fields, respectively.²⁰⁴ SF transition also provides a measure of magnetic anisotropy. When SF transition switches from one magnetic field direction to another, it suggests rotation of magnetic easy axis as seen in aforementioned MnPS_3−xSe_x. For NiPS_3−xSe_x, however, unavailable single crystals for Se-rich compositions, and the lack of experimentally determined magnetic structure for end compound NiPSe₃, make it difficult to judge the evolution of magnetic anisotropy based on magnetization study.

4.2.2.3. FeP(S_1−xSe_x)₃. In the MPX₃ family, FePS₃ has been identified as a representative material that displays Ising-type magnetism characterized by out-of-plane magnetic moments (Fig. 3).^6,40,107 Such Ising-type magnetism in FePS₃ has been proposed to originate from the combination of the strong spin–orbit coupling (SOC) of the high-spin Fe²⁺ (d⁶) state and the trigonal distortion of FeS₆ octahedra.⁴⁰ Another Fe-based MPX₃ compound FePSe₃ which was discovered a few decades ago^30,100 has so far received surprisingly less attention than FePS₃ despite the fact that both FePS₃ ^6,40,107 and FePSe₃ ^30,42 exhibit similar Ising-type zig-zag AFM ordering from bulk to the monolayer limit. This is in stark contrast to the distinct magnetic structures (experimentally or theoretically determined) for sulfide and selenide compounds in some other known MPX₃ such as MnP(S,Se)₃ and NiP(S,Se)₃.^31,205 Such lack of change in magnetic structure in FeP(S,Se)₃ naturally raises a question of whether chalcogen substitution may play any role in modifying magnetic properties, which has been investigated in ref. 122. For the entire composition range, magnetic susceptibility displays strong anisotropy both below and above T_N, with the in-plane susceptibility measured under the in-plane field (H∥ab) showing much weaker temperature dependence as compared to the out-of-plane susceptibility [Fig. 15(a)], implying the persistence of the Ising-type magnetism up on Se substitution. In Mn- and Ni-based MPX₃, the magnetic anisotropy mainly originate from anisotropic superexchange interaction that arises from SOC of non-magnetic ligands.^206,207 However, in FeP(Se_1−xS_x)₃, magnetic anisotropy predominantly stems from the strong crystal electric field on Fe²⁺ ion (discussed in section 4.1.),^138,139 and thus S–Se substitution does not substantially change magnetic anisotropy and consequently maintains the robust Ising-type magnetic ordering in FeP(Se_1−xS_x)₃.¹²²

Fig. 15 (a) Temperature dependencies of susceptibility of FeP(Se_1−xS_x)₃ measured under a magnetic field of 0.1 T. Doping dependence of (b) T_N and (c) Fe–Fe distance for FeP(Se_1−xS_x)₃.¹²²

The evolution of T_N with Se substitution is also interesting. Unlike Mn- and Ni-based MPX₃ in which chalcogen substitution leads to monotonic decrease or increase in T_N, respectively (see sections 4.2.2.1 and 4.2.2.2), in Fe-based system, a non-monotonic dependent is observed¹²² [Fig. 15(b)]. This has been attributed to the evolution of magnetic exchange:¹²² previous neutron scattering measurement has revealed dominant J₁ in FePS₃ ¹⁰⁷ (Table 4), which is FM in nature and sensitive to Fe–Fe distance due to direct exchange interaction of the nearest-neighbor Fe moments.^128,188 A similar direct exchange scenario occurs for MnPS_3−xSe_x except J₁ is AFM in nature (see sections 4.2.2.1). With the consideration that the competition between FM and AFM correlations determines the magnetic ordering type and transition temperature, the evolution of T_N can be understood in terms of the nearest-neighbor Fe–Fe distance that governs the FM J₁ in FeP(Se_1−xS_x)₃. As shown in Fig. 15(c), the nearest-neighbor Fe–Fe distance in FeP(Se_1−xS_x)₃ first reduces with S substitution up to x = 0.5. Further increasing S content slightly modifies the lattice structure and leads to elongated Fe–Fe distance. This causes a non-monotonic composition dependence for J₁ and eventually results in non-monotonic evolution for T_N.

4.2.3. Inter-layer intercalation. In addition to metal and chalcogen substitutions, the layered structure of MPX₃ allows for another doping strategy – inter-layer intercalation of guest ions, as shown in the schematic in Fig. 4(c). The metal and chalcogen substitutions are all based on the direct mixing of dopants and source materials during synthesis such as flux and chemical vapor transport (CVT). On the other side, the intercalation technique is usually applied to post-grown crystals, involving the insertion of guest ions into inter-layer spaces of the material. So, this method is relatively clean and does not strongly modify the host layers. Generally, intercalation to vdW materials is expected to modulate the inter-layer spacing and may also lead to carrier doping. Therefore, compared to metal M and chalcogen X substitutions, intercalation offers a new approach to tuning the magnetic properties of MPX₃ materials, which may create new magnetic phenomena and novel magnetic phases in MPX₃ that are not accessible by substitution. Intercalation of Li^{54,98,100,208,209} and various organic-ions^96,97,99,101 have been reported in MPX₃, which were achieved by electrochemical^{54,97–99,208,209} and wet chemical^96,100,101 techniques.
4.2.3.1. Lithium intercalation. Lithium (Li) intercalation in MPX₃ has been reported a long time ago.^{54,100,208,209} Earlier work mainly focused on the electrical, optical, and electrochemical properties of Li-intercalated MPX₃. Regarding magnetic properties, the effects of Li intercalation on NiPS₃, FePS₃, FePSe₃, and MnPSe₃ compounds were first studied four decades ago.¹⁰⁰ The intercalation was achieved by reacting MPX₃-powered samples and n-butyllithium solution in hexane at room temperature in a dry, oxygen-free environment for 10–15 days. The duration of the reaction and concentration of n-butyllithium was found to affect the amount of intercalated Li. In this work,¹⁰⁰ resistivity reduction in those powered samples implies successful intercalation. However, magnetic properties including transition temperature, effective moment, and Weiss temperature extracted from temperature-dependent magnetic susceptibility measurements do not display notable changes [Fig. 16(a)].

Fig. 16 (a) Magnetic properties for Li_xMnPSe₃, Li_xFePSe₃, Li_xFePS₃, and Li_xNiPS₃.¹⁰⁰ Reprinted (adapted) with permission.¹⁰⁰ Copyright 1979, American Chemical Society. (b) Conceptual schematic of electrochemical intercalation process and the coin cell setup for intercalation.⁹⁸ (c) Non-linear field dependence of magnetization of Li_xNiPS₃ at T = 2 K after removing the linear magnetization background.⁹⁸ (d) Evolution of saturation moment (μ_sat) and coercive fields (H_c) with Li content.⁹⁸

Recent studies adopting electrochemical interaction to intercalate Li in single crystalline samples reveal modified magnetic properties in Li_xNiPS₃ ⁹⁸ and Li_xFePS₃.²¹⁰ The intercalation in both studies was performed using a battery setup [Fig. 16(b)] and the expanded c-axis implies successful intercalation. For NiPS₃, samples with Li content up to x = 0.4 are air-stable and maintain good crystallinity based on X-ray diffraction and scanning electron microscope imaging, though non-magnetic Li₃PS₄ impurity starts to occur for x ≥ 0.3. It is worth noting that the Li amount is the nominal content calculated based on the intercalation duration and electrical current because neither X-ray diffraction nor energy dispersive X-ray spectroscopy can directly probe Li. Similar to the earlier study using n-butyllithium solution for Li intercalation,¹⁰⁰ the electrochemically intercalated Li_xNiPS₃ (x = 0–0.4) samples do not display clear changes in T_N. However, the development of non-linear field dependence for magnetization, and its saturation-like behavior after removing the linear background [Fig. 16(c)], and the rise of the hysteresis loop and tiny magnetic moment [Fig. 16(d)] have been ascribed to ferrimagnetism due to uncompensated antiparallel magnetic moments.⁹⁸ For FePS₃,²¹⁰ in contrast, T_N is found to be reduced with the expansion of the c-axis by Li-intercalation, suggesting a possible role of inter-layer magnetic exchange. The Ising-type magnetism characterized by strong anisotropy in magnetic susceptibility in the high-temperature paramagnetic state remains robust. At low temperatures, non-linear field dependence for magnetization is also observed, similar to Li-intercalated NiPS₃.

4.2.3.2. Organic-ion intercalation. The vdW gap allows for not only the intercalation of small Li atoms or ions but also the much larger organic molecules or ions.^{96,97,99,211,212} Organic ion intercalation has been mainly performed on NiPS₃.^96,97,99 Intercalating tetraheptyl ammonium (THA⁺),⁹⁷ tetrabutylammonium (TBA⁺),⁹⁹ cobaltocenium ions [Co(Cp)₂⁺, where Cp is a cyclopentadienyl ring C₅H₅⁻],⁹⁹ and 1,10-phenanthroline⁹⁶ using electrochemical^97,99 and solution reaction⁹⁶ have been performed. Compared to Li-intercalation, intercalating large organic ions results in a much more significant elongation of inter-layer spacing.^96,97,99 It has also been found that the intralayer lattice structure does not display remarkable change upon intercalation.⁹⁶

Organic-ions intercalation in NiPS₃ is found to drastically modify the magnetic properties,^96,97,99 mainly giving rise to a low-temperature FIM state^97,99 that is also reported in Li-intercalated NiPS₃ ⁹⁸ described in the previous section. The conclusion has been drawn based on the transition-like sharp susceptibility upturn around and below 100 K [Fig. 17(a) and (c)], as well as magnetic hysteresis loops in THA⁺-,⁹⁷ TBA⁺-,⁹⁹ and Co(Cp)₂⁺ (ref. 99)-intercalated NiPS₃ [Fig. 17(b) and (d)]. It has been proposed⁹⁹ that the cation intercalation causes the reduction of certain Ni from the Ni²⁺ to the Ni⁰ state, together with its displacement from the O_h to the T_d lattice site. Such transition from high spin Ni²⁺–O_h atoms ([Ar]3d⁸s⁰) to zero-spin Ni⁰–T_d ([Ar]3d¹⁰s⁰) leads to uncompensated antiferromagnetism, i.e. a FIM state. An alternative mechanism based on the Stoner effect has also been proposed:⁹⁷ the charge doping due to organic-ion intercalation enhances the density of states (DOS) at the Fermi level and eventually triggers the inter-chain Stoner splitting of the itinerant electrons, resulting in the higher electron concentration in one Ni chain to create net magnetic moment which gives rise to ferrimagnetism.

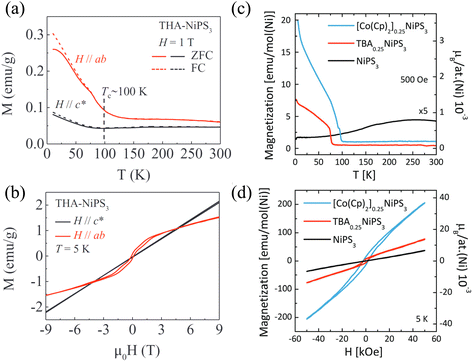Fig. 17 (a) Temperature and (b) field dependencies of magnetization of intercalated THA-NiPS₃.⁹⁷ (c) Field-cooled temperature-dependent magnetization and (d) magnetic hysteresis for NiPS₃, TBA_0.25NiPS₃, and [Co(Cp)₂]_0.25NiPS₃.⁹⁹

Recently, a new method using iron dopant as reaction active sites to intercalating organic-ion in NiPS₃ has been reported.⁹⁶ In this method, light Fe-substituted NiPS₃ (i.e., Fe_0.02Ni_0.98PS₃) single crystals are synthesized, which is followed by intercalation of a complexing agent 1,10-phenanthroline by solution reaction with aniline chloride.⁹⁶ In this process, 1,10-phenthroline removes Fe²⁺ ions into the solution, creating metal-ion vacancies. The aniline chloride provides a proton to 1,10-phenthroline, and such protonated 1,10-phenanthroline is attracted towards the vacant metal sites, forcing intercalation of 1,10-phenanthroline into inter-layer spacing. The intercalated samples also display the signature of ferrimagnetism.

5. Engineering magnetism through pressure

In addition to chemical doping, pressure has also been established as an efficient external stimulus to tune magnetic properties. In MPX₃, high pressure has been found to effectively modulate electronic properties.^64–72 Recently, pressure has also been used to control magnetism in this material family.^213–216 A recent review article has extensively summarized the theoretical and experimental progress of the structural, electronic, magnetic, and optical properties tuning of MPX₃ under pressure.²¹⁷ In this review, we focus on engineering magnetism in MPX₃ materials. Since pressure generally tunes lattice structures and possibly induces structure transitions, it also sheds light on tuning magnetism through changing magnetic exchange and anisotropy. Therefore, here we briefly describe the pressure-driven modification of magnetism in MPX₃. The magnetic properties of MPX₃ are found to be sensitive to high pressure. T_N systematically increases with the pressure for MnPS₃ ^213,216 and FePS₃,²¹⁴ which can be explained by the enhanced magnetic interactions under pressure. In particular, compressing the crystal planes closer strengthens the inter-layer interaction.^214,216 For MnPS₃, the T_N also enhances with applying pressure, with different reported rates of 6.7 K GPa⁻¹ (ref. 213) and 13 K GPa⁻¹ (ref. 216) depending on the type of samples (polycrystal or single crystal). In addition, SF transition is tunable by pressure. In MnPS₃,²¹⁶ the SF field decreases at a rate of 4.0 × 10³ Oe GPa⁻¹, which is likely due to the reduction of magnetic anisotropy under pressure. Furthermore, the magnetic structure for MnPS₃ remains unchanged up to ∼3.6 GPa (ref. 213) but changes at ∼2 GPa for FePS₃ ²¹⁴ and ∼4 GPa for NiPSe₃.²¹⁵ Such changes in magnetic structures are accompanied by the insulator-to-metal transition and even superconductivity in FePSe₃ ⁷² and NiPSe₃.²¹⁵ Therefore, high pressure, as well as strain, are excellent tools that can be combined with chemical tuning (substitution and intercalation) to achieve additional properties, such as the combination of the desired magnetic structure and electrical conductivity.

6. Summary and perspectives

In this review article, we provide a summary covering the crystal growth, structure, and magnetic properties of the vdW-type AFM MPX₃ material family, with a focus on property tuning by various doping scenarios. Metal substitution, chalcogen substitution, and inter-layer intercalation are highly effective in tuning the magnetic properties in MPX₃, including magnetic ordering, exchange interactions, magnetic anisotropy, etc. Generally, AFM ground states are robust, and most of those metal and chalcogen substitution tune properties within antiferromagnetism, except for a few cases such as Fe_1−xZn_xPS₃ and AgVP₂Se₆ that display FM-like behaviors such as irreversibility, hysteresis, and saturation magnetization. However, magnetization is not a bulk measurement as a tiny number of magnetic impurities may give rise to a strong magnetization signal. Also, quite a few FM-like signatures may originate from a spin–flip transition or a canted AFM state, as seen in AFM CuCrP₂S₆ and Ni_1−xCr_xPS₃. Therefore, other bulk measurements such as neutron diffraction are needed to clarify the magnetic ground state as well as any field-induced phase transitions. Indeed, the rapid development of MPX₃ and its derivatives calls for more neutron resource allocations on these interesting vdW magnetic compounds.

On the other hand, intercalations of a few guest species have been reported to result in a FIM state at low temperatures. The differences in substitution and intercalation might be attributed to different consequences: substitution within each individual layer plays a role mainly in altering magnetic anisotropy and exchange interactions while intercalation in the inter-layer spacing might lead to carrier doping or reductive reaction for metal ions. Also, intercalation is efficient in tuning inter-layer distance, especially when intercalating large ions such as organic intercalation. This effectively reduces interlayer interaction and may push the magnetism approach to a 2D limit. Therefore, intercalation might be a good tool to engineering magnetism for compounds in which the interlayer exchange J_z is important. So far, there are not many reported intercalation studies, therefore more efforts toward this direction are needed to fully explore this promising material tuning approach. Similarly, a direct probe for magnetic ordering such as neutron diffraction is also highly desired in this direction. Another urgent need is an accurate and convenient approach to determine the amount of Li for Li-intercalated samples.

High-entropy (HE) MPX₃ is an emerging field with great opportunities owing to the expanded degrees of freedom. The combination of multiple elements in HE compounds offers greater versatility and tunability of material properties as compared to conventional bi-metallic and bi-chalcogenide alloys by varying the composition of M and X elements. Incorporating multiple components in an HE compound could induce a severe lattice distortion due to the difference in their atomic sizes, which provides opportunities for crystal structure and symmetry engineering for possible novel functional properties. The HE alloys are expected to generate unusual magnetic orderings due to competing magnetic interactions enabled by the interplay between spin, charge, and orbital degrees of freedom.²¹⁸ On the other side, the randomness introduced by high entropy may also quench the magnetic order and simultaneously facilitate the insulator-to-metal transition and subsequent emergence of superconductivity, which may be extremely challenging but has been observed in FePSe₃-based HE compounds under external pressure.¹²¹ Further exploring HE MPX₃ compounds could provide pathways to realize enhanced conductivity and even superconductivity at an ambient pressure or much lower pressure. Understanding the effect of entropy on the structural stability and material properties of complex HE compounds is critical for their optimal design and utilization in practical applications. However, the controlled synthesis of the alloy composition, and the large parameter space, pose significant challenges for controlled study (e.g., fixing the content of one or more metals) to clarify the mechanism behind the property changes. More effort, especially in synthesis and applying additional experimental tools, would be beneficial.

One driving force of the study of MPX₃ is the feasibility of obtaining their atomically thin layers that provide invaluable opportunities for studying new phenomena originating from 2D magnetism and future device applications. The tunable magnetism summarized in this review further demonstrates the great potential of this material platform. Despite their well-established magnetic orders in bulk materials and the fact of being one of a few first demonstrated 2D magnets in the atomically thin layer form, the study of 2D magnetism in MPX₃ is still in an early stage with only a few pristine compositions being investigated, as summarized in Table 6. It has been found that the long-range magnetic orders in atomically mono- or bi-layers only exist in a few MPX₃ compounds such as MnPS₃,^29,109 FePS₃,⁶ NiPS₃,⁶⁰ CoPS₃,¹⁰⁸ MnPSe₃,⁴³ and FePSe₃.⁴² Whereas the 2D magnetism in substituted and intercalated MPX₃ compounds remains elusive. So far, few challenges to exploring magnetism in 2D have been identified in the MPX₃ family. First, because of the absence of net magnetization, direct probe of AFM states in 2D layers of MPX₃ is challenging by using nanoscale magnetic characterization techniques such as scanning single-spin magnetometry,²¹⁹ magneto-optical Kerr effect microscopy,^7,8 polar reflective magnetic circular dichroism (RMCD),¹⁰ X-ray magnetic dichroism (XMCD),¹⁶⁷ and optical linear dichroism (LD).^48,220 In addition to developing more experimental techniques for probing AFM state in nanoscale, inducing ferromagnetism in MPX₃ can be a shortcut for 2D magnetism study. We hope the various doping techniques summarized in this review can provide some insight into creating FM ground states for field-driven polarized FM states in these materials. Another advantage of inducing ferromagnetism is the breaking of time-reversal symmetry that may bring in other exotic phenomena. Recent studies have predicted the non-trivial topological states in the FM phase of MPX₃,^221,222 providing a rare platform for investigating the interplay between magnetism and band topology in the 2D limit.

Table 6 Summary of magnetic ordering in atomically thin layers of MPX₃ compounds

Compounds	Magnetic ordering temperature (K)			Ref.
	Monolayer	Bilayer	Bulk
a Magnetic order not stable in the monolayer.
MnPS3	—^a	78	78	29 and 109
FePS3	118	118	118	6
NiPS3	—^a	130	155	60
CoPS3	100	100	120	108 and 129
MnPSe3	40	56	74	43
FePSe3	98	102	111	42

---

Although this review mainly focuses on magnetism, we wish to take this opportunity to comment on the electronic properties of MPX₃. Those materials are well-known wide band gap insulators and electronic transport measurements in bulk materials are almost impossible or only possible in the high-temperature range.^71,197 Enabling electronic studies in vdW-type magnetic MPX₃ could be an important direction. Exploiting the coupling between magnetic and electronic properties would provide a platform for tunable electrical properties to develop quantum materials and devices with multifunctional magnetic and electronic properties. Therefore, though applying high pressure has been demonstrated to be effective,^64–72 further development in approaches or materials that are compatible with 2D magnetism and device integration is critical, which calls for synergistic efforts in material modeling, high-throughput calculations, synthesis, characterization, and device study.

The vdW structure of MPX₃ materials is naturally advantageous for fabricating devices for electronic and optoelectronic applications. However, the highly insulating nature of MPX₃ materials has somewhat hindered the rapid development of device applications. To the best of our knowledge, so far the field-effect transistors (FET) using atomically thin layers of only a few MPX₃ compounds such as NiPS₃ ²²³ and MnPS₃ ⁵³ have been reported. The FET based on NiPS₃ ²²³ and MnPS₃ ⁵³ thin flakes have been found to exhibit n-type and p-type semiconducting behavior with on/off ratios of ∼10³–10⁵ and ∼10²–10³ respectively at room temperature, with low charge carrier mobilities of ∼0.5–1 cm² V⁻¹ s⁻¹ and 8.3 × 10⁻³ cm² V⁻¹ s⁻¹ respectively. On the other hand, recent works have mainly focused on optoelectronic devices such as photodetectors,^52,224–226 phototransistors,^227,228 and sensors²²⁹ based on a few layers of MPX₃. High-performance and sensitive photodetectors working in a wide frequency range from near-infrared²²⁶ to ultraviolet⁵² have been successfully fabricated using the thin layers of MnPS₃,⁵³ FePS₃,^52,224 MnPSe₃,²²⁵ and FePSe₃.²²⁶ The few layers NiPS₃ ²²⁸ and MnPSe₃ ²²⁷ have also been integrated into phototransistors for ultrasensitive light detection. Furthermore, the MnPS₃ thin flakes²²⁹ has been demonstrated as sensors for sensitive and selective moisture sensing. Providing this progress, efficiently tuning the magnetism would possibly lead to new optoelectronic and photonic applications, especially the light polarization-based applications for which magnetism can play a role. Furthermore, metalizing MPX₃via combined chemical and strain may pave a way for electronic applications.

Finally, more attention should be given to atomic ordering in these substituted and intercalated compounds. The distribution of the dopants and possibly the associated vacancies may play important roles in mediating properties. The ultimate examples are well-defined atomic orderings such as superlattice or Peierls transition, which can be relatively easily probed by high-resolution structure characterization tools such as High-resolution/Scanning transmission electron microscopy (HRTEM/STEM) and synchrotron XRD. However, chemical short-range order, which is another ultimate example, is difficult to characterize and has not been widely studied in crystalline solids. Such chemical short-range order is distinct from the well-known short-range order in condensed matter physics that is defined from the long-range ordering. Roughly speaking, the long-range order is based on periodic ordering with long-range correlation length, while the short-range order is normally referred to as similar ordering but with much-shortened correlation length, which usually occurs with the disturbance of the long-range order by doping or increasing the temperature to around the phase transition temperature. In contrast, chemical short-range order occurs in a doped system and characterizes the deviation of the atomic distribution from the perfect random distributions. The study started from the III–V semiconductor alloys decades ago which mainly focused on long-range order,²³⁰ and has been recently extended to chemical short-range order in other systems such as group-IV semiconductors,^231,232 metal alloys,^233,234 thermoelectric materials,^235,236 and oxides.²³⁷ Thus far, chemical short-range order remains to be an extremely less-explored topic in condensed matter physics, probably owing to the lack of efficient experimental tools to probe it. In doped MPX₃ systems, chemical short-range order should also occur and may affect the magnetic properties. Providing rich and tunable magnetism, the doped MPX₃ compounds provide an ideal platform for studying the nature of the possible various chemical short-range orders in vdW materials and their impacts on magnetism, which is a new field awaiting exploration.

Author contributions

R. B. and J. H. designed, wrote, and edited this manuscript.

Data availability

No primary research results, software or code have been included and no new data were generated as part of this review.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

R. B. acknowledges the support from μ-ATOMS, an Energy Frontier Research Center funded by DOE, Office of Science, Basic Energy Sciences, under Award DE-SC0023412. J. H. acknowledges the support from the U.S. Department of Energy, Office of Science, Basic Energy Sciences program under Grant No. DE-SC0022006. The authors are grateful to T. Li at George Washington University for informative discussions.

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
2. W. Han, R. K. Kawakami, M. Gmitra and J. Fabian, Nat. Nanotechnol., 2014, 9, 794–807.
3. B. Li, T. Xing, M. Zhong, L. Huang, N. Lei, J. Zhang, J. Li and Z. Wei, Nat. Commun., 2017, 8, 1958.
4. Z. Guguchia, A. Kerelsky, D. Edelberg, S. Banerjee, F. von Rohr, D. Scullion, M. Augustin, M. Scully, D. A. Rhodes, Z. Shermadini, H. Luetkens, A. Shengelaya, C. Baines, E. Morenzoni, A. Amato, J. C. Hone, R. Khasanov, S. J. L. Billinge, E. Santos, A. N. Pasupathy and Y. J. Uemura, Sci. Adv., 2018, 4, eaat3672.
5. K.-T. Ko, K. Kim, S. B. Kim, H.-D. Kim, J.-Y. Kim, B. I. Min, J.-H. Park, F.-H. Chang, H.-J. Lin, A. Tanaka and S.-W. Cheong, Phys. Rev. Lett., 2011, 107, 247201.
6. J.-U. Lee, S. Lee, J. H. Ryoo, S. Kang, T. Y. Kim, P. Kim, C.-H. Park, J.-G. Park and H. Cheong, Nano Lett., 2016, 16, 7433–7438.
7. B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270–273.
8. C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265–269.
9. Z. Zhang, J. Shang, C. Jiang, A. Rasmita, W. Gao and T. Yu, Nano Lett., 2019, 19, 3138–3142.
10. Z. Lin, B. Huang, K. Hwangbo, Q. Jiang, Q. Zhang, Z. Liu, Z. Fei, H. Lv, A. Millis, M. McGuire, D. Xiao, J.-H. Chu and X. Xu, Nano Lett., 2021, 21, 9180–9186.
11. Z. Fei, B. Huang, P. Malinowski, W. Wang, T. Song, J. Sanchez, W. Yao, D. Xiao, X. Zhu, A. F. May, W. Wu, D. H. Cobden, J.-H. Chu and X. Xu, Nat. Mater., 2018, 17, 778–782.
12. G. Zhang, F. Guo, H. Wu, X. Wen, L. Yang, W. Jin, W. Zhang and H. Chang, Nat. Commun., 2022, 13, 5067.
13. S. Albarakati, C. Tan, Z.-J. Chen, J. G. Partridge, G. Zheng, L. Farrar, E. L. H. Mayes, M. R. Field, C. Lee, Y. Wang, Y. Xiong, M. Tian, F. Xiang, A. R. Hamilton, O. A. Tretiakov, D. Culcer, Y.-J. Zhao and L. Wang, Sci. Adv., 2019, 5, eaaw0409.
14. S. Jiang, L. Li, Z. Wang, K. F. Mak and J. Shan, Nat. Nanotechnol., 2018, 13, 549–553.
15. Z. Wang, T. Zhang, M. Ding, B. Dong, Y. Li, M. Chen, X. Li, J. Huang, H. Wang, X. Zhao, Y. Li, D. Li, C. Jia, L. Sun, H. Guo, Y. Ye, D. Sun, Y. Chen, T. Yang, J. Zhang, S. Ono, Z. Han and Z. Zhang, Nat. Nanotechnol., 2018, 13, 554–559.
16. B. Huang, G. Clark, D. R. Klein, D. MacNeill, E. Navarro-Moratalla, K. L. Seyler, N. Wilson, M. A. McGuire, D. H. Cobden, D. Xiao, W. Yao, P. Jarillo-Herrero and X. Xu, Nat. Nanotechnol., 2018, 13, 544–548.
17. Y. Deng, Y. Yu, Y. Song, J. Zhang, N. Z. Wang, Z. Sun, Y. Yi, Y. Z. Wu, S. Wu, J. Zhu, J. Wang, X. H. Chen and Y. Zhang, Nature, 2018, 563, 94–99.
18. T. Song, X. Cai, M. W.-Y. Tu, X. Zhang, B. Huang, N. P. Wilson, K. L. Seyler, L. Zhu, T. Taniguchi, K. Watanabe, M. A. McGuire, D. H. Cobden, D. Xiao, W. Yao and X. Xu, Science, 2018, 360, 1214–1218.
19. Y. Wu, S. Zhang, J. Zhang, W. Wang, Y. L. Zhu, J. Hu, G. Yin, K. Wong, C. Fang, C. Wan, X. Han, Q. Shao, T. Taniguchi, K. Watanabe, J. Zang, Z. Mao, X. Zhang and K. L. Wang, Nat. Commun., 2020, 11, 3860.
20. D. R. Klein, D. MacNeill, J. L. Lado, D. Soriano, E. Navarro-Moratalla, K. Watanabe, T. Taniguchi, S. Manni, P. Canfield, J. Fernández-Rossier and P. Jarillo-Herrero, Science, 2018, 360, 1218–1222.
21. J. Shang, X. Tang, X. Tan, A. Du, T. Liao, S. C. Smith, Y. Gu, C. Li and L. Kou, ACS Appl. Nano Mater., 2020, 3, 1282–1288.
22. D. Zhong, K. L. Seyler, X. Linpeng, R. Cheng, N. Sivadas, B. Huang, E. Schmidgall, T. Taniguchi, K. Watanabe, M. A. McGuire, W. Yao, D. Xiao, K.-M. C. Fu and X. Xu, Sci. Adv., 2017, 3, e1603113.
23. Z. Wang, I. Gutiérrez-Lezama, N. Ubrig, M. Kroner, M. Gibertini, T. Taniguchi, K. Watanabe, A. Imamoğlu, E. Giannini and A. F. Morpurgo, Nat. Commun., 2018, 9, 2516.
24. T. Song, M. W.-Y. Tu, C. Carnahan, X. Cai, T. Taniguchi, K. Watanabe, M. A. McGuire, D. H. Cobden, D. Xiao, W. Yao and X. Xu, Nano Lett., 2019, 19, 915–920.
25. Y. Wang, J. Balgley, E. Gerber, M. Gray, N. Kumar, X. Lu, J.-Q. Yan, A. Fereidouni, R. Basnet, S. J. Yun, D. Suri, H. Kitadai, T. Taniguchi, K. Watanabe, X. Ling, J. Moodera, Y. H. Lee, H. O. H. Churchill, J. Hu, L. Yang, E.-A. Kim, D. G. Mandrus, E. A. Henriksen and K. S. Burch, Nano Lett., 2020, 20, 8446–8452.
26. K. F. Mak, J. Shan and D. C. Ralph, Nat. Rev. Phys., 2019, 1, 646–661.
27. F. Wang, T. A. Shifa, P. Yu, P. He, Y. Liu, F. Wang, Z. Wang, X. Zhan, X. Lou, F. Xia and J. He, Adv. Funct. Mater., 2018, 28, 1802151.
28. R. Samal, G. Sanyal, B. Chakraborty and C. S. Rout, J. Mater. Chem. A, 2021, 9, 2560–2591.
29. G. Long, H. Henck, M. Gibertini, D. Dumcenco, Z. Wang, T. Taniguchi, K. Watanabe, E. Giannini and A. F. Morpurgo, Nano Lett., 2020, 20, 2452–2459.
30. A. Wiedenmann, J. Rossat-Mignod, A. Louisy, R. Brec and J. Rouxel, Solid State Commun., 1981, 40, 1067–1072.
31. R. Basnet, K. M. Kotur, M. Rybak, C. Stephenson, S. Bishop, C. Autieri, M. Birowska and J. Hu, Phys. Rev. Res., 2022, 4, 023256.
32. H. Han, H. Lin, W. Gan, Y. Liu, R. Xiao, L. Zhang, Y. Li, C. Zhang and H. Li, Appl. Phys. Lett., 2023, 122, 033101.
33. A. R. Wildes, V. Simonet, E. Ressouche, G. J. Mcintyre, M. Avdeev, E. Suard, S. A. Kimber, D. Lançon, G. Pepe and B. Moubaraki, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 224408.
34. A. R. Wildes, H. M. Rønnow, B. Roessli, M. J. Harris and K. W. Godfrey, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 094422.
35. A. R. Wildes, B. Roessli, B. Lebech and K. W. Godfrey, J. Phys.: Condens. Matter, 1998, 10, 6417–6428.
36. A. R. Wildes, V. Simonet, E. Ressouche, R. Ballou and G. J. McIntyre, J. Phys.: Condens. Matter, 2017, 29, 455801.
37. T. Sekine, M. Jouanne, C. Julien and M. Balkanski, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 8382–8393.
38. Y. Takano, N. Arai, A. Arai, Y. Takahashi, K. Takase and K. Sekizawa, J. Magn. Magn. Mater., 2004, 272–276, E593–E595.
39. G. Le Flem, R. Brec, G. Ouvard, A. Louisy and P. Segransan, J. Phys. Chem. Solids, 1982, 43, 455–461.
40. P. A. Joy and S. Vasudevan, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 5425–5433.
41. G. Long, T. Zhang, X. Cai, J. Hu, C. Cho, S. Xu, J. Shen, Z. Wu, T. Han, J. Lin, J. Wang, Y. Cai, R. Lortz, Z. Mao and N. Wang, ACS Nano, 2017, 11, 11330–11336.
42. J. Luo, S. Li, Z. Ye, R. Xu, H. Yan, J. Zhang, G. Ye, L. Chen, D. Hu, X. Teng, W. A. Smith, B. I. Yakobson, P. Dai, A. H. Nevidomskyy, R. He and H. Zhu, Nano Lett., 2023, 23, 2023–2030.
43. Z. Ni, A. V. Haglund, H. Wang, B. Xu, C. Bernhard, D. G. Mandrus, X. Qian, E. J. Mele, C. L. Kane and L. Wu, Nat. Nanotechnol., 2021, 16, 782–787.
44. S. Kang, K. Kim, B. H. Kim, J. Kim, K. I. Sim, J.-U. Lee, S. Lee, K. Park, S. Yun, T. Kim, A. Nag, A. Walters, M. Garcia-Fernandez, J. Li, L. Chapon, K.-J. Zhou, Y.-W. Son, J. H. Kim, H. Cheong and J.-G. Park, Nature, 2020, 583, 785–789.
45. X. Wang, J. Cao, Z. Lu, A. Cohen, H. Kitadai, T. Li, Q. Tan, M. Wilson, C. H. Lui, D. Smirnov, S. Sharifzadeh and X. Ling, Nat. Mater., 2021, 20, 964–970.
46. F. Dirnberger, R. Bushati, B. Datta, A. Kumar, A. H. MacDonald, E. Baldini and V. M. Menon, Nat. Nanotechnol., 2022, 17, 1060–1064.
47. K. Hwangbo, Q. Zhang, Q. Jiang, Y. Wang, J. Fonseca, C. Wang, G. M. Diederich, D. R. Gamelin, D. Xiao, J.-H. Chu, W. Yao and X. Xu, Nat. Nanotechnol., 2021, 16, 655–660.
48. H. Zhang, Z. Ni, C. E. Stevens, A. Bai, F. Peiris, J. R. Hendrickson, L. Wu and D. Jariwala, Nat. Photonics, 2022, 16, 311–317.
49. C. A. Belvin, E. Baldini, I. O. Ozel, D. Mao, H. C. Po, C. J. Allington, S. Son, B. H. Kim, J. Kim, I. Hwang, J. H. Kim, J.-G. Park, T. Senthil and N. Gedik, Nat. Commun., 2021, 12, 4837.
50. D. Afanasiev, J. R. Hortensius, M. Matthiesen, S. Mañas-Valero, M. Šiškins, M. Lee, E. Lesne, H. S. J. van der Zant, P. G. Steeneken, B. A. Ivanov, E. Coronado and A. D. Caviglia, Sci. Adv., 2021, 7, eabf3096.
51. J. Chu, F. Wang, L. Yin, L. Lei, C. Yan, F. Wang, Y. Wen, Z. Wang, C. Jiang, L. Feng, J. Xiong, Y. Li and J. He, Adv. Funct. Mater., 2017, 27, 1701342.
52. Y. Gao, S. Lei, T. Kang, L. Fei, C.-L. Mak, J. Yuan, M. Zhang, S. Li, Q. Bao, Z. Zeng, Z. Wang, H. Gu and K. Zhang, Nanotechnology, 2018, 29, 244001.
53. R. Kumar, R. N. Jenjeti, M. P. Austeria and S. Sampath, J. Mater. Chem. C, 2019, 7, 324–329.
54. A. H. Thompson and M. S. Whittingham, Mater. Res. Bull., 1977, 12, 741–744.
55. P. J. S. Foot, T. Katz, S. N. Patel, B. A. Nevett, A. R. Pieecy and A. A. Balchin, Phys. Status Solidi A, 1987, 100, 11–29.
56. F. Liu, L. You, K. L. Seyler, X. Li, P. Yu, J. Lin, X. Wang, J. Zhou, H. Wang, H. He, S. T. Pantelides, W. Zhou, P. Sharma, X. Xu, P. M. Ajayan, J. Wang and Z. Liu, Nat. Commun., 2016, 7, 12357.
57. A. Belianinov, Q. He, A. Dziaugys, P. Maksymovych, E. Eliseev, A. Borisevich, A. Morozovska, J. Banys, Y. Vysochanskii and S. V. Kalinin, Nano Lett., 2015, 15, 3808–3814.
58. W. F. Io, S.-Y. Pang, L. W. Wong, Y. Zhao, R. Ding, J. Mao, Y. Zhao, F. Guo, S. Yuan, J. Zhao, J. Yi and J. Hao, Nat. Commun., 2023, 14, 7304.
59. C. B. Park, A. Shahee, K.-T. Kim, D. R. Patil, S. A. Guda, N. Ter-Oganessian and K. H. Kim, Adv. Electron. Mater., 2022, 8, 2101072.
60. K. Kim, S. Y. Lim, J.-U. Lee, S. Lee, T. Y. Kim, K. Park, G. S. Jeon, C.-H. Park, J.-G. Park and H. Cheong, Nat. Commun., 2019, 10, 345.
61. K. Du, X. Wang, Y. Liu, P. Hu, M. I. B. Utama, C. K. Gan, Q. Xiong and C. Kloc, ACS Nano, 2016, 10, 1738–1743.
62. Y. Jin, M. Yan, T. Kremer, E. Voloshina and Y. Dedkov, Sci. Rep., 2022, 12, 735.
63. A. Kamata, K. Noguchi, K. Suzuki, H. Tezuka, T. Kashiwakura, Y. Ohno and S. Nakai, J. Phys. Soc. Jpn., 1997, 66, 401–407.
64. H.-S. Kim, K. Haule and D. Vanderbilt, Phys. Rev. Lett., 2019, 123, 236401.
65. Y. Wang, Z. Zhou, T. Wen, Y. Zhou, N. Li, F. Han, Y. Xiao, P. Chow, J. Sun, M. Pravica, A. L. Cornelius, W. Yang and Y. Zhao, J. Am. Chem. Soc., 2016, 138, 15751–15757.
66. R. A. Evarestov and A. Kuzmin, J. Comput. Chem., 2020, 41, 1337–1344.
67. M. Tsurubayashi, K. Kodama, M. Kano, K. Ishigaki, Y. Uwatoko, T. Watanabe, K. Takase and Y. Takano, AIP Adv., 2018, 8, 101307.
68. C. R. S. Haines, M. J. Coak, A. R. Wildes, G. I. Lampronti, C. Liu, P. Nahai-Williamson, H. Hamidov, D. Daisenberger and S. S. Saxena, Phys. Rev. Lett., 2018, 121, 266801.
69. M. J. Coak, D. M. Jarvis, H. Hamidov, C. R. S. Haines, P. L. Alireza, C. Liu, S. Son, I. Hwang, G. I. Lampronti, D. Daisenberger, P. Nahai-Williamson, A. R. Wildes, S. S. Saxena and J.-G. Park, J. Phys.: Condens. Matter, 2019, 32, 124003.
70. X. Ma, Y. Wang, Y. Yin, B. Yue, J. Dai, J. Cheng, J. Ji, F. Jin, F. Hong, J.-T. Wang, Q. Zhang and X. Yu, Sci. China: Phys., Mech. Astron., 2021, 64, 297011.
71. M. J. Coak, S. Son, D. Daisenberger, H. Hamidov, C. R. S. Haines, P. L. Alireza, A. R. Wildes, C. Liu, S. S. Saxena and J.-G. Park, npj Quantum Mater., 2019, 4, 1–6.
72. Y. Wang, J. Ying, Z. Zhou, J. Sun, T. Wen, Y. Zhou, N. Li, Q. Zhang, F. Han, Y. Xiao, P. Chow, W. Yang, V. V. Struzhkin, Y. Zhao and H. Mao, Nat. Commun., 2018, 9, 1914.
73. S. Y. Kim, T. Y. Kim, L. J. Sandilands, S. Sinn, M.-C. Lee, J. Son, S. Lee, K.-Y. Choi, W. Kim, B.-G. Park, C. Jeon, H.-D. Kim, C.-H. Park, J.-G. Park, S. J. Moon and T. W. Noh, Phys. Rev. Lett., 2018, 120, 136402.
74. S. Liu, A. Granados del Águila, D. Bhowmick, C. K. Gan, T. Thu Ha Do, M. A. Prosnikov, D. Sedmidubský, Z. Sofer, P. C. M. Christianen, P. Sengupta and Q. Xiong, Phys. Rev. Lett., 2021, 127, 097401.
75. M. A. Susner, M. Chyasnavichyus, M. A. McGuire, P. Ganesh and P. Maksymovych, Adv. Mater., 2017, 29, 1602852.
76. N. Chandrasekharan and S. Vasudevan, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 14903–14906.
77. D. J. Goossens, A. J. Studer, S. J. Kennedy and T. J. Hicks, J. Phys.: Condens. Matter, 2000, 12, 4233–4242.
78. A. M. Mulders, J. C. P. Klaasse, D. J. Goossens, J. Chadwick and T. J. Hicks, J. Phys.: Condens. Matter, 2002, 14, 8697–8705.
79. Y. Takano, A. Arai, Y. Takahashi, K. Takase and K. Sekizawa, J. Appl. Phys., 2003, 93, 8197–8199.
80. J. N. Graham, M. J. Coak, S. Son, E. Suard, J.-G. Park, L. Clark and A. R. Wildes, Phys. Rev. Mater., 2020, 4, 084401.
81. T. Masubuchi, H. Hoya, T. Watanabe, Y. Takahashi, S. Ban, N. Ohkubo, K. Takase and Y. Takano, J. Alloys Compd., 2008, 460, 668–674.
82. V. Manríquez, P. Barahona and O. Peña, Mater. Res. Bull., 2000, 35, 1889–1895.
83. D. J. Goossens, S. Brazier-Hollins, D. R. James, W. D. Hutchison and J. R. Hester, J. Magn. Magn. Mater., 2013, 334, 82–86.
84. Y. He, Y.-D. Dai, H. Huang, J. Lin and Y. Hsia, J. Alloys Compd., 2003, 359, 41–45.
85. D. J. Goossens and T. J. Hicks, J. Phys.: Condens. Matter, 1998, 10, 7643–7652.
86. A. Bhutani, J. L. Zuo, R. D. McAuliffe, C. R. dela Cruz and D. P. Shoemaker, Phys. Rev. Mater., 2020, 4, 034411.
87. Y. Shemerliuk, Y. Zhou, Z. Yang, G. Cao, A. U. B. Wolter, B. Büchner and S. Aswartham, Electron. Mater, 2021, 2, 284–298.
88. S. Selter, Y. Shemerliuk, M.-I. Sturza, A. U. B. Wolter, B. Büchner and S. Aswartham, Phys. Rev. Mater., 2021, 5, 073401.
89. R. Basnet, A. Wegner, K. Pandey, S. Storment and J. Hu, Phys. Rev. Mater., 2021, 5, 064413.
90. F. Wang, N. Mathur, A. N. Janes, H. Sheng, P. He, X. Zheng, P. Yu, A. J. DeRuiter, J. R. Schmidt, J. He and S. Jin, Sci. Adv., 2000, 7, eabj4086.
91. S. Lee, J. Park, Y. Choi, K. Raju, W.-T. Chen, R. Sankar and K.-Y. Choi, Phys. Rev. B, 2021, 104, 174412.
92. J. P. Odile, J. J. Steger and A. Wold, Inorg. Chem., 1975, 14, 2400–2402.
93. J. Peng, X. Yang, Z. Lu, L. Huang, X. Chen, M. He, J. Shen, Y. Xing, M. Liu, Z. Qu, Z. Wang, L. Li, S. Dong and J.-M. Liu, Adv. Quantum Technol., 2023, 6, 2200105.
94. S. Calder, A. V. Haglund, A. I. Kolesnikov and D. Mandrus, Phys. Rev. B, 2021, 103, 024414.
95. P. Jeevanandam and S. Vasudevan, J. Phys.: Condens. Matter, 1999, 11, 3563–3570.
96. X. Ma, L. Zhang, C. Xu, Q. Dong, R. I. Walton, Z. Li, H. Shi, G. Chen, J. Hu, J. Li and H. Yang, Chem. Commun., 2020, 56, 4603–4606.
97. M. Mi, X. Zheng, S. Wang, Y. Zhou, L. Yu, H. Xiao, H. Song, B. Shen, F. Li, L. Bai, Y. Chen, S. Wang, X. Liu and Y. Wang, Adv. Funct. Mater., 2022, 32, 2112750.
98. R. Basnet, D. Ford, K. TenBarge, J. Lochala and J. Hu, J. Phys.: Condens. Matter, 2022, 34, 434002.
99. D. Tezze, J. M. Pereira, Y. Asensio, M. Ipatov, F. Calavalle, F. Casanova, A. M. Bittner, M. Ormaza, B. Martín-García, L. E. Hueso and M. Gobbi, Nanoscale, 2022, 14, 1165–1173.
100. R. Brec, D. M. Schleich, G. Ouvrard, A. Louisy and J. Rouxel, Inorg. Chem., 1979, 18, 1814–1818.
101. E. Manova, A. Leaustic, I. Mitov, D. Gonbeau and R. Clement, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1998, 311, 155–160.
102. J. J. Abraham, Y. Senyk, Y. Shemerliuk, S. Selter, S. Aswartham, B. Büchner, V. Kataev and A. Alfonsov, Phys. Rev. B, 2023, 107, 165141.
103. M. Baithi, N. T. Dang, T. A. Tran, J. P. Fix, D. H. Luong, K. P. Dhakal, D. Yoon, A. V. Rutkauskas, S. E. Kichanov, I. Y. Zel, J. Kim, N. J. Borys, D. P. Kozlenko, Y. H. Lee and D. L. Duong, Inorg. Chem., 2023, 62, 12674–12682.
104. R. Nitsche and P. Wild, Mater. Res. Bull., 1970, 5, 419–423.
105. C. D. Carpentier and R. Nitsche, Mater. Res. Bull., 1974, 9, 401–410.
106. C. Liu, Z. Li, J. Hu, H. Duan, C. Wang, L. Cai, S. Feng, Y. Wang, R. Liu, D. Hou, C. Liu, R. Zhang, L. Zhu, Y. Niu, A. A. Zakharov, Z. Sheng and W. Yan, Adv. Mater., 2023, 35, 2300247.
107. D. Lançon, H. C. Walker, E. Ressouche, B. Ouladdiaf, K. C. Rule, G. J. McIntyre, T. J. Hicks, H. M. Rønnow and A. R. Wildes, Phys. Rev. B, 2016, 94, 214407.
108. Q. Liu, L. Wang, Y. Fu, X. Zhang, L. Huang, H. Su, J. Lin, X. Chen, D. Yu, X. Cui, J.-W. Mei and J.-F. Dai, Phys. Rev. B, 2021, 103, 235411.
109. K. Kim, S. Y. Lim, J. Kim, J.-U. Lee, S. Lee, P. Kim, K. Park, S. Son, C.-H. Park, J.-G. Park and H. Cheong, 2D Mater., 2019, 6, 041001.
110. C.-T. Kuo, M. Neumann, K. Balamurugan, H. J. Park, S. Kang, H. W. Shiu, J. H. Kang, B. H. Hong, M. Han, T. W. Noh and J.-G. Park, Sci. Rep., 2016, 6, 20904.
111. H. Chu, C. J. Roh, J. O. Island, C. Li, S. Lee, J. Chen, J.-G. Park, A. F. Young, J. S. Lee and D. Hsieh, Phys. Rev. Lett., 2020, 124, 027601.
112. S. Lee, K.-Y. Choi, S. Lee, B. H. Park and J.-G. Park, APL Mater., 2016, 4, 086108.
113. T. Ying, T. Yu, Y.-S. Shiah, C. Li, J. Li, Y. Qi and H. Hosono, J. Am. Chem. Soc., 2021, 143, 7042–7049.
114. M. Cheng, Y.-S. Lee, A. K. Iyer, D. G. Chica, E. K. Qian, M. A. Shehzad, R. dos Reis, M. G. Kanatzidis and V. P. Dravid, Inorg. Chem., 2021, 60, 17268–17275.
115. D. G. Chica, A. K. Iyer, M. Cheng, K. M. Ryan, P. Krantz, C. Laing, R. dos Reis, V. Chandrasekhar, V. P. Dravid and M. G. Kanatzidis, Inorg. Chem., 2021, 60, 3502–3513.
116. M. Cheng, A. K. Iyer, A. P. Douvalis, S. M. Ribet, M. G. Kanatzidis and V. P. Dravid, Chem. Mater., 2023, 35, 1458–1465.
117. M. Cheng, A. K. Iyer, X. Zhou, A. Tyner, Y. Liu, M. A. Shehzad, P. Goswami, D. Y. Chung, M. G. Kanatzidis and V. P. Dravid, Inorg. Chem., 2022, 61, 13719–13727.
118. L.-J. Yao, C.-L. Hu, Z. Fang and J.-G. Mao, J. Solid State Chem., 2022, 315, 123433.
119. E. K. Qian, A. K. Iyer, M. Cheng, K. M. Ryan, L. Jirousek, D. G. Chica, P. Krantz, Y.-S. Lee, V. Chandrasekhar, V. P. Dravid and M. G. Kanatzidis, Chem. Mater., 2023, 35, 3671–3685.
120. B. L. Chittari, Y. Park, D. Lee, M. Han, A. H. MacDonald, E. Hwang and J. Jung, Phys. Rev. B, 2016, 94, 184428.
121. X. Chen, J. Wang, T. Ying, D. Huang, H. Gou, Q. Zhang, Y. Li, H. Hosono, J. Guo and X. Chen, Phys. Rev. B, 2022, 106, 184502.
122. R. Basnet, T. Patel, J. Wang, D. Upreti, S. K. Chhetri, G. Acharya, M. R. U. Nabi, J. Sakon and J. Hu, Adv. Electron. Mater., 2024, 10, 2300738.
123. A. R. Wildes, V. Simonet, E. Ressouche, G. J. McIntyre, M. Avdeev, E. Suard, S. A. J. Kimber, D. Lançon, G. Pepe, B. Moubaraki and T. J. Hicks, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 224408.
124. W. Klingen, R. Ott and H. Hahn, Z. Anorg. Allg. Chem., 1973, 396, 271–278.
125. D. Khomskii, Transition Metal Compounds, Cambridge University Press, 2014.
126. M. Dalal, A Textbook of Inorganic Chemistry – Volume 1, Dalal Institute, 2017.
127. R. Basnet, Understanding and Tuning Magnetism in van der Waals Magnetic Compounds, Doctoral dissertation, University of Arkansas, 2023.
128. D. Lançon, R. A. Ewings, T. Guidi, F. Formisano and A. R. Wildes, Phys. Rev. B, 2018, 98, 134414.
129. C. Kim, J. Jeong, P. Park, T. Masuda, S. Asai, S. Itoh, H.-S. Kim, A. Wildes and J.-G. Park, Phys. Rev. B, 2020, 102, 184429.
130. A. R. Wildes, J. R. Stewart, M. D. Le, R. A. Ewings, K. C. Rule, G. Deng and K. Anand, Phys. Rev. B, 2022, 106, 174422.
131. J. B. Goodenough, Phys. Rev., 1955, 100, 564–573.
132. J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98.
133. N. Bazazzadeh, M. Hamdi, F. Haddadi, A. Khavasi, A. Sadeghi and S. M. Mohseni, Phys. Rev. B, 2021, 103, 014425.
134. D. J. Goossens, A. R. Wildes, C. Ritter and T. J. Hicks, J. Phys.: Condens. Matter, 2000, 12, 1845–1854.
135. D. J. Goossens, Eur. Phys. J. B, 2010, 78, 305–309.
136. A. G. Chang, L.-W. Lan, Y.-J. Chan, C.-N. Kuo, T. Chen, C.-H. Huang, T.-H. Chuang, D.-H. Wei, C.-S. Lue and C.-C. Kuo, Phys. Rev. B, 2022, 106, 125412.
137. Y. Lee, S. Son, C. Kim, S. Kang, J. Shen, M. Kenzelmann, B. Delley, T. Savchenko, S. Parchenko, W. Na, K.-Y. Choi, W. Kim, H. Cheong, P. M. Derlet, A. Kleibert and J.-G. Park, Adv. Electron. Mater., 2023, 9, 2200650.
138. R. R. Rao and A. K. Raychaudhuri, J. Phys. Chem. Solids, 1992, 53, 577–583.
139. L. Bevaart, E. Frikkee and L. J. de Jongh, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 4741–4756.
140. C.-K. Tian, C. Wang, W. Ji, J.-C. Wang, T.-L. Xia, L. Wang, J.-J. Liu, H.-X. Zhang and P. Cheng, Phys. Rev. B, 2019, 99, 184428.
141. X. Hu, D.-X. Yao and K. Cao, Phys. Rev. B, 2022, 106, 224423.
142. C. Tian, F. Pan, S. Xu, K. Ai, T. Xia and P. Cheng, Appl. Phys. Lett., 2020, 116, 202402.
143. G. Drachuck, Z. Salman, M. W. Masters, V. Taufour, T. N. Lamichhane, Q. Lin, W. E. Straszheim, S. L. Bud'ko and P. C. Canfield, Phys. Rev. B, 2018, 98, 144434.
144. S. Pan, Y. Bai, J. Tang, P. Wang, Y. You, G. Xu and F. Xu, J. Alloys Compd., 2022, 908, 164573.
145. M. Abramchuk, S. Jaszewski, K. R. Metz, G. B. Osterhoudt, Y. Wang, K. S. Burch and F. Tafti, Adv. Mater., 2018, 30, 1801325.
146. T. A. Tartaglia, J. N. Tang, J. L. Lado, F. Bahrami, M. Abramchuk, G. T. McCandless, M. C. Doyle, K. S. Burch, Y. Ran, J. Y. Chan and F. Tafti, Sci. Adv., 2020, 6, eabb9379.
147. T. Masubuchi, X. Jin, K. Koyama, Y. Takahashi, K. Takase, Y. Uwatoko, Y. Takano and K. Sekizawa, AIP Conf. Proc., 2006, 850, 1279–1280.
148. T. Li, S. Jiang, N. Sivadas, Z. Wang, Y. Xu, D. Weber, J. E. Goldberger, K. Watanabe, T. Taniguchi, C. J. Fennie, K. Fai Mak and J. Shan, Nat. Mater., 2019, 18, 1303–1308.
149. S. Mondal, M. Kannan, M. Das, L. Govindaraj, R. Singha, B. Satpati, S. Arumugam and P. Mandal, Phys. Rev. B, 2019, 99, 180407.
150. Y. Peng, Z. Lin, G. Tian, J. Yang, P. Zhang, F. Wang, P. Gu, X. Liu, C.-W. Wang, M. Avdeev, F. Liu, D. Zhou, R. Han, P. Shen, W. Yang, S. Liu, Y. Ye and J. Yang, Adv. Funct. Mater., 2022, 32, 2106592.
151. R. Oliva, E. Ritov, F. Horani, I. Etxebarria, A. K. Budniak, Y. Amouyal, E. Lifshitz and M. Guennou, Phys. Rev. B, 2023, 107, 104415.
152. Z. Lu, X. Yang, L. Huang, X. Chen, M. Liu, J. Peng, S. Dong and J.-M. Liu, J. Phys.: Condens. Matter, 2022, 34, 354005.
153. S. Selter, K. K. Bestha, P. Bhattacharyya, B. Özer, Y. Shemerliuk, M. Roslova, E. Vinokurova, L. T. Corredor, L. Veyrat, A. U. B. Wolter, L. Hozoi, B. Büchner and S. Aswartham, Phys. Rev. Mater., 2023, 7, 033402.
154. X. Wang, Z. Shang, C. Zhang, J. Kang, T. Liu, X. Wang, S. Chen, H. Liu, W. Tang, Y.-J. Zeng, J. Guo, Z. Cheng, L. Liu, D. Pan, S. Tong, B. Wu, Y. Xie, G. Wang, J. Deng, T. Zhai, H.-X. Deng, J. Hong and J. Zhao, Nat. Commun., 2023, 14, 840.
155. C. Payen, H. Mutka, J. L. Soubeyroux, P. Molinié and P. Colombet, J. Magn. Magn. Mater., 1992, 104–107, 797–798.
156. S. Selter, Y. Shemerliuk, B. Büchner and S. Aswartham, Crystals, 2021, 11, 500.
157. H. Mutka, C. Payen, P. Molinié, J. L. Soubeyroux, P. Colombet and A. D. Taylor, Phys. Rev. Lett., 1991, 67, 497–500.
158. M. A. Gave, D. Bilc, S. D. Mahanti, J. D. Breshears and M. G. Kanatzidis, Inorg. Chem., 2005, 44, 5293–5303.
159. D. Kim, E. K. Qian, D. G. Chica, Y.-H. Chiang, M. G. Kanatzidis and Q. Tu, ACS Appl. Nano Mater., 2023, 6, 8214–8221.
160. A. Kargar, H. Hong, J. Tower, P. Guggenheim, E. Qian, C. Brown, M. Breen, J. F. Christian, K. Shah, E. Lukosi, R. Golduber, J. Gallagher, A. Benkechkache, M. Kanatzidis and M. R. Squillante, in Hard X-Ray, Gamma-Ray, and Neutron Detector Physics XXIV, SPIE, 2022, vol. 12241, pp. 59–12268.
161. D. G. Chica, Y. He, K. M. McCall, D. Y. Chung, R. O. Pak, G. Trimarchi, Z. Liu, P. M. De Lurgio, B. W. Wessels and M. G. Kanatzidis, Nature, 2020, 577, 346–349.
162. A. del Moral, J. I. Arnaudas and P. M. Gehring, J. Phys.: Condens. Matter, 1994, 6, 4779.
163. F. B. Anderson and H. B. Callen, Phys. Rev., 1964, 136, A1068–A1087.
164. L. J. D. Jongh and A. R. Miedema, Adv. Phys., 2001, 50, 947–1170.
165. K. Okuda, K. Kurosawa, S. Saito, M. Honda, Z. Yu and M. Date, J. Phys. Soc. Jpn., 1986, 55, 4456–4463.
166. A. P. Dioguardi, S. Selter, U. Peeck, S. Aswartham, M.-I. Sturza, R. Murugesan, M. S. Eldeeb, L. Hozoi, B. Büchner and H.-J. Grafe, Phys. Rev. B, 2020, 102, 064429.
167. A. Bedoya-Pinto, J.-R. Ji, A. K. Pandeya, P. Gargiani, M. Valvidares, P. Sessi, J. M. Taylor, F. Radu, K. Chang and S. S. P. Parkin, Science, 2021, 374, 616–620.
168. X. Cai, T. Song, N. P. Wilson, G. Clark, M. He, X. Zhang, T. Taniguchi, K. Watanabe, W. Yao, D. Xiao, M. A. McGuire, D. H. Cobden and X. Xu, Nano Lett., 2019, 19, 3993–3998.
169. J. Son, S. Son, P. Park, M. Kim, Z. Tao, J. Oh, T. Lee, S. Lee, J. Kim, K. Zhang, K. Cho, T. Kamiyama, J. H. Lee, K. F. Mak, J. Shan, M. Kim, J.-G. Park and J. Lee, ACS Nano, 2021, 15, 16904–16912.
170. M. Baithi, N. T. Dang, T. A. Tran, J. P. Fix, D. H. Luong, K. P. Dhakal, D. Yoon, A. V. Rutkauskas, S. E. Kichanov, I. Y. Zel, J. Kim, N. J. Borys, D. P. Kozlenko, Y. H. Lee and D. L. Duong, Inorg. Chem., 2023, 62, 12674–12682.
171. Z.-L. Huang, J.-T. Zhao, J.-X. Mi, S.-Y. Mao and L.-S. Zheng, J. Solid State Chem., 1999, 144, 388–391.
172. D. Sen and T. Saha-Dasgupta, Phys. Rev. Mater., 2023, 7, 064008.
173. G. Ouvrard, R. Fréour, R. Brec and J. Rouxel, Mater. Res. Bull., 1985, 20, 1053–1062.
174. K. Ichimura and M. Sano, Synth. Met., 1991, 45, 203–211.
175. D. J. Goossens, D. James, J. Dong, R. E. Whitfield, L. Norén and R. L. Withers, J. Phys.: Condens. Matter, 2011, 23, 065401.
176. P. Fuentealba, C. Olea, H. Aguilar-Bolados, N. Audebrand, R. C. de Santana, C. Doerenkamp, H. Eckert, C. J. Magon and E. Spodine, Phys. Chem. Chem. Phys., 2020, 22, 8315–8324.
177. R. Basnet, D. Upreti, T. Patel, S. Karki Chhetri, G. Acharya, M. R. U. Nabi, M. M. Sharma, J. Sakon, M. Mortazavi and J. Hu, Phys. Rev. B, 2024, 109, 184405.
178. Y. Peng, S. Ding, M. Cheng, Q. Hu, J. Yang, F. Wang, M. Xue, Z. Liu, Z. Lin, M. Avdeev, Y. Hou, W. Yang, Y. Zheng and J. Yang, Adv. Mater., 2020, 32, 2001200.
179. M. A. McGuire, G. Clark, S. KC, W. M. Chance, G. E. Jellison, V. R. Cooper, X. Xu and B. C. Sales, Phys. Rev. Mater., 2017, 1, 014001.
180. E. J. Telford, A. H. Dismukes, K. Lee, M. Cheng, A. Wieteska, A. K. Bartholomew, Y.-S. Chen, X. Xu, A. N. Pasupathy, X. Zhu, C. R. Dean and X. Roy, Adv. Mater., 2020, 32, 2003240.
181. D. Upreti, R. Basnet, M. M. Sharma, S. K. Chhetri, G. Acharya, M. R. U. Nabi, J. Sakon, M. Mortazavi and J. Hu, 2024, arXiv:2408.02858.  DOI:10.48550/arXiv.2408.02858.
182. T. Matsuoka, R. Rao, M. A. Susner, B. S. Conner, D. Zhang and D. Mandrus, Phys. Rev. B, 2023, 107, 165125.
183. W. Bai, Z. Hu, C. Xiao, J. Guo, Z. Li, Y. Zou, X. Liu, J. Zhao, W. Tong, W. Yan, Z. Qu, B. Ye and Y. Xie, J. Am. Chem. Soc., 2020, 142, 10849–10855.
184. O. V. Yazyev and L. Helm, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 125408.
185. L. Cai, J. He, Q. Liu, T. Yao, L. Chen, W. Yan, F. Hu, Y. Jiang, Y. Zhao, T. Hu, Z. Sun and S. Wei, J. Am. Chem. Soc., 2015, 137, 2622–2627.
186. V. K. S. Shante and S. Kirkpatrick, Adv. Phys., 1971, 20, 325–357.
187. V. Pashchenko, O. Bludov, D. Baltrunas, K. Mazeika, S. Motria, K. Glukhov and Yu. Vysochanskii, Condens. Matter Phys., 2022, 25, 43701.
188. A. Bhowmick, B. Bal, S. Ganguly, M. Bhattacharya and M. L. Kundu, J. Phys. Chem. Solids, 1992, 53, 1279–1284.
189. T. Ying, T. Yu, Y. Qi, X. Chen and H. Hosono, Adv. Sci., 2022, 9, 2203219.
190. P. Colombet, A. Leblanc, M. Danot and J. Rouxel, J. Solid State Chem., 1982, 41, 174–184.
191. T. Asano, Y. Ajiro, M. Mekata, H. Yamazaki, N. Hosoito, T. Shinjo and H. Kikuchi, Solid State Commun., 1994, 90, 125–128.
192. C. Payen, P. Molinie, P. Colombet and G. Fillion, J. Magn. Magn. Mater., 1990, 84, 95–101.
193. S. Lee, P. Colombet, G. Ouvrard and R. Brec, Mater. Res. Bull., 1986, 21, 917–928.
194. S. Selter, K. K. Bestha, P. Bhattacharyya, B. Özer, Y. Shemerliuk, L. T. Corredor, L. Veyrat, A. U. B. Wolter, L. Hozoi, B. Büchner and S. Aswartham, Phys. Rev. Mater., 2022, 7, 033402.
195. Y. Ma, Y. Yan, L. Luo, S. Pazos, C. Zhang, X. Lv, M. Chen, C. Liu, Y. Wang, A. Chen, Y. Li, D. Zheng, R. Lin, H. Algaidi, M. Sun, J. Z. Liu, S. Tu, H. N. Alshareef, C. Gong, M. Lanza, F. Xue and X. Zhang, Nat. Commun., 2023, 14, 7891.
196. X. Bourdon, V. Maisonneuve, V. B. Cajipe, C. Payen and J. E. Fischer, J. Alloys Compd., 1999, 283, 122–127.
197. Y. Peng, X. Cheng, P. Gu, F. Wang, J. Yang, M. Xue, W. Yang, C. Wang, S. Liu, K. Watanabe, T. Taniguchi, Y. Ye and J. Yang, Adv. Funct. Mater., 2020, 30, 1910036.
198. M. A. Susner, B. S. Conner, E. Rowe, R. Siebenaller, A. Giordano, M. V. McLeod, C. R. Ebbing, T. J. Bullard, R. Selhorst, T. J. Haugan, J. Jiang, R. Pachter and R. Rao, J. Phys. Chem. C, 2024, 128, 4265–4276.
199. X. Yan, X. Chen and J. Qin, Mater. Res. Bull., 2011, 46, 235–238.
200. G. Kliche, Z. Naturforsch., A: Astrophys., Phys. Phys. Chem., 1983, 38, 1133–1137.
201. B. Zapeka, M. Kostyrko, I. Martynyuk-Lototska and R. Vlokh, Philos. Mag., 2015, 95, 382–393.
202. B. Hillman, L. Noren and D. J. Goossens, in Proceedings of the 35th Annual Australia/New Zealand Condensed Matter and Materials Meeting, (Australian Institute of Physics, 2011), p. 50.
203. Y. Gu, Q. Zhang, C. Le, Y. Li, T. Xiang and J. Hu, Phys. Rev. B, 2019, 100, 165405.
204. Y. Yu, G. Deng, Y. Cao, G. J. McIntyre, R. Li, N. Yuan, Z. Feng, J.-Y. Ge, J. Zhang and S. Cao, Ceram. Int., 2019, 45, 1093–1097.
205. A. M. Ruiz, D. L. Esteras, A. Rybakov and J. J. Baldoví, Dalton Trans., 2022, 51, 16816–16823.
206. J. L. Lado and J. Fernández-Rossier, 2D Mater., 2017, 4, 035002.
207. G. Wang, K. Yang, Y. Ma, L. Liu, D. Lu, Y. Zhou and H. Wu, Chin. Phys. Lett., 2023, 40, 077301.
208. A. Le Méhauté, G. Ouvrard, R. Brec and J. Rouxel, Mater. Res. Bull., 1977, 12, 1191–1197.
209. P. J. S. Foot and B. A. Nevett, Solid State Ionics, 1983, 8, 169–172.
210. D. Upreti, R. Basnet, M. M. Sharma, S. K. Chhetri, G. Acharya, M. R. U. Nabi, J. Sakon, B. Da, M. Mortazavi and J. Hu, 2024,  DOI:10.48550/arXiv.2407.12662.
211. C. Yang, X. Chen, J. Qin, K. Yakushi, Y. Nakazawa and K. Ichimura, J. Solid State Chem., 2000, 150, 281–285.
212. J. S. O. Evans, D. O'Hare, R. Clement, A. Leaustic and P. Thuéry, Adv. Mater., 1995, 7, 735–739.
213. D. P. Kozlenko, O. N. Lis, N. T. Dang, M. Coak, J.-G. Park, E. V. Lukin, S. E. Kichanov, N. O. Golosova, I. Yu. Zel and B. N. Savenko, Phys. Rev. Mater., 2024, 8, 024402.
214. M. J. Coak, D. M. Jarvis, H. Hamidov, A. R. Wildes, J. A. M. Paddison, C. Liu, C. R. S. Haines, N. T. Dang, S. E. Kichanov, B. N. Savenko, S. Lee, M. Kratochvílová, S. Klotz, T. C. Hansen, D. P. Kozlenko, J.-G. Park and S. S. Saxena, Phys. Rev. X, 2021, 11, 011024.
215. H. Sun, L. Qiu, Y. Han, E. Yi, J. Li, M. Huo, C. Huang, H. Liu, M. Li, W. Wang, D.-X. Yao, B. A. Frandsen, B. Shen, Y. Hou and M. Wang, Mater. Today Phys., 2023, 36, 101188.
216. W. Toyoshima, T. Masubuchi, T. Watanabe, K. Takase, K. Matsubayashi, Y. Uwatoko and Y. Takano, J. Phys.: Conf. Ser., 2009, 150, 042215.
217. T. Matsuoka, H.-S. Kim, S. Samanta, J. L. Musfeldt and D. G. Mandrus, Front. Mater., 2024, 11, 1362744.
218. L. Min, M. Sretenovic, T. W. Heitmann, T. W. Valentine, R. Zu, V. Gopalan, C. M. Rost, X. Ke and Z. Mao, Commun. Phys., 2022, 5, 1–7.
219. L. Thiel, Z. Wang, M. A. Tschudin, D. Rohner, I. Gutiérrez-Lezama, N. Ubrig, M. Gibertini, E. Giannini, A. F. Morpurgo and P. Maletinsky, Science, 2019, 364, 973–976.
220. Q. Zhang, K. Hwangbo, C. Wang, Q. Jiang, J.-H. Chu, H. Wen, D. Xiao and X. Xu, Nano Lett., 2021, 21, 6938–6945.
221. J. Yang, Y. Zhou, Y. Dedkov and E. Voloshina, Adv. Theory Simul., 2020, 3, 2000228.
222. N. Sheremetyeva, I. Na, A. Saraf, S. M. Griffin and G. Hautier, Phys. Rev. B, 2023, 107, 115104.
223. R. N. Jenjeti, R. Kumar, M. P. Austeria and S. Sampath, Sci. Rep., 2018, 8, 8586.
224. J. Duan, P. Chava, M. Ghorbani-Asl, Y. Lu, D. Erb, L. Hu, A. Echresh, L. Rebohle, A. Erbe, A. V. Krasheninnikov, M. Helm, Y.-J. Zeng, S. Zhou and S. Prucnal, ACS Appl. Mater. Interfaces, 2022, 14, 11927–11936.
225. P. Liu and Y. Pu, Results Phys., 2021, 29, 104750.
226. T. Xu, M. Luo, N. Shen, Y. Yu, Z. Wang, Z. Cui, J. Qin, F. Liang, Y. Chen, Y. Zhou, F. Zhong, M. Peng, M. Zubair, N. Li, J. Miao, W. Lu, C. Yu and W. Hu, Adv. Electron. Mater., 2021, 7, 2100207.
227. X. Han, P. Song, J. Xing, Z. Chen, D. Li, G. Xu, X. Zhao, F. Ma, D. Rong, Y. Shi, Md. R. Islam, K. Liu and Y. Huang, ACS Appl. Mater. Interfaces, 2021, 13, 2836–2844.
228. Y. Liu and X. Sun, Magnetochemistry, 2022, 8, 101.
229. R. Kumar, R. N. Jenjeti and S. Sampath, Adv. Mater. Interfaces, 2019, 6, 1900666.
230. Spontaneous Ordering in Semiconductor Alloys, ed. A. Mascarenhas, Springer US, Boston, MA, 2002.
231. B. Cao, S. Chen, X. Jin, J. Liu and T. Li, ACS Appl. Mater. Interfaces, 2020, 12, 57245–57253.
232. X. Jin, S. Chen and T. Li, Commun. Mater., 2022, 3, 1–9.
233. R. Zhang, S. Zhao, J. Ding, Y. Chong, T. Jia, C. Ophus, M. Asta, R. O. Ritchie and A. M. Minor, Nature, 2020, 581, 283–287.
234. J. Ding, Q. Yu, M. Asta and R. O. Ritchie, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 8919–8924.
235. B. Jiang, Y. Yu, J. Cui, X. Liu, L. Xie, J. Liao, Q. Zhang, Y. Huang, S. Ning, B. Jia, B. Zhu, S. Bai, L. Chen, S. J. Pennycook and J. He, Science, 2021, 371, 830–834.
236. S. Roychowdhury, T. Ghosh, R. Arora, M. Samanta, L. Xie, N. K. Singh, A. Soni, J. He, U. V. Waghmare and K. Biswas, Science, 2021, 371, 722–727.
237. H. Ji, A. Urban, D. A. Kitchaev, D.-H. Kwon, N. Artrith, C. Ophus, W. Huang, Z. Cai, T. Shi, J. C. Kim, H. Kim and G. Ceder, Nat. Commun., 2019, 10, 592.
238. K. Kim, S. Y. Lim, J. Kim, J.-U. Lee, S. Lee, P. Kim, K. Park, S. Son, C.-H. Park, J.-G. Park and H. Cheong, 2D Mater., 2019, 6, 041001.
239. K. C. Rule, G. J. McIntyre, S. J. Kennedy and T. J. Hicks, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 134402.
240. Y. Jin, Y. Jin, K. Li, M. Yan, Y. Guo, Y. Zhou, A. Preobrajenski, Y. Dedkov and E. Voloshina, J. Phys. Chem. Lett., 2022, 13, 10486–10493.
241. T. T. Mai, K. F. Garrity, A. McCreary, J. Argo, J. R. Simpson, V. Doan-Nguyen, R. V. Aguilar and A. R. H. Walker, Sci. Adv., 2021, 7, eabj3106.
242. D. Jana, P. Kapuscinski, A. Pawbake, A. Papavasileiou, Z. Sofer, I. Breslavetz, M. Orlita, M. Potemski and C. Faugeras, Phys. Rev. B, 2023, 108, 144415.
243. R. Gusmão, Z. Sofer, D. Sedmidubský, Š. Huber and M. Pumera, ACS Catal., 2017, 7, 8159–8170.
244. L. Liao, E. Kovalska, V. Mazanek, L. Valdman, L. Dekanovsky, W. Bing, D. Sedmidubský, J. Luxa, Š. Huber, A. P. Herman, R. Kudrawiec and Z. Sofer, J. Mater. Chem. C, 2022, 10, 8834–8844.
245. J. Zhang, W. Xu, L. Wang, Z. Zheng, F. Liu, P. Yu and G. Yang, Cryst. Growth Des., 2023, 23, 1259–1268.
246. X. Zhao, X. Yin, D. Liu, C. Huo, G.-Z. Dong, S. Chen, Z.-B. Liu, X.-Q. Yan and J.-G. Tian, J. Phys. Chem. C, 2022, 126, 6837–6846.
247. X. Wang, K. Du, W. Liu, P. Hu, X. Lu, W. Xu, C. Kloc and Q. Xiong, Appl. Phys. Lett., 2016, 109, 123103.
248. D. Lançon, R. A. Ewings, T. Guidi, F. Formisano and A. R. Wildes, Phys. Rev. B, 2018, 98, 134414.

---