 Open Access Article
Open Access ArticleMagnetic clusters as efficient EY-like spin-scattering centres in graphene†
Wout
Keijers
 a,
Ramasamy
Murugesan
a,
Ramasamy
Murugesan
 b,
Guillaume
Libeert
b,
Guillaume
Libeert
 a,
Bart
Raes
a,
Bart
Raes
 c,
Steven
Brems
c,
Steven
Brems
 c,
Stefan
De Gendt
c,
Stefan
De Gendt
 c,
Michel
Houssa
c,
Michel
Houssa
 b,
Ewald
Janssens
b,
Ewald
Janssens
 *a and
Joris
Van de Vondel
*a and
Joris
Van de Vondel
 *a
*a
aQuantum Solid-State Physics, Department of Physics and Astronomy, KU Leuven, Celestijnenlaan 200D, B-3001 Leuven, Belgium. E-mail: ewald.janssens@kuleuven.be; joris.vandevondel@kuleuven.be
bSemiconductor Physics Laboratory, Department of Physics and Astronomy, KU Leuven, Celestijnenlaan 200D, Leuven, B-3001, Belgium
cIMEC, Kapeldreef 75, Leuven, B-3001, Belgium
First published on 23rd July 2024
Abstract
The spin scattering induced by magnetic adsorbates on graphene was studied using a combination of transport measurements on a graphene field effect transistor decorated with atomically precise nickel clusters and first principles calculations. A comparative study before and after deposition of Ni4 clusters unambiguously corroborated the contribution of the added scatterers. An investigation of the spin scattering parameters as a function of the applied voltage indicated a cluster-induced Elliot–Yafet like spin scattering mechanism. Density functional theory calculations were used in combination with a tight-binding model to quantify the strength of the spin–orbit coupling terms induced by the adsorbed clusters.
1 Introduction
Controlled doping by impurities can provide semiconducting materials with the desired properties. In the case of two-dimensional materials, the adsorption of metal atoms and nanoparticles offers a similar platform to extend functionalities. For example, to transform graphene into a spin active material, a strong Rashba spin–orbit coupling can be induced by the proximity effect. Transition metal dichalcogenides (TMDs) and adatoms have the potential to enhance spin–orbit coupling (SOC),1–3 thereby inducing spin anisotropy4–7 and robust quantum spin Hall states, enabling gate manipulation of spin transport and the conversion of electrical currents into spin currents via the spin Hall effect (SHE) or vice versa (iSHE).8–11 However, fundamental questions remain on the spin relaxation mechanisms in graphene. Both experimental and theoretical studies dealing with the influence of impurities and adatoms on spin scattering yield contradictory results on the dominant spin scattering mechanism.12–16 In a recent proof-of-principle experiment, we investigated the spin transport parameters of graphene spin valves decorated with soft-landed, size-selected, few-atom Aun clusters.17 A study as a function of cluster density allowed the derivation of cluster-size dependent spin and momentum scattering times.Exploiting the material flexibility of cluster beam deposition, we redirect our attention to magnetic clusters to identify their impact on the spin transport of the hybrid structure. We focus on nickel clusters due to their relatively high intrinsic magnetic moments,18 which are predicted to not be completely quenched when adsorbed on perfect graphene.19 In order to select the most appropriate cluster size, the electronic structure of Nin (n = 2–5) clusters adsorbed on graphene was calculated. These calculations pinpoint Ni4 as an interesting candidate to enhance the spin properties of the Nin/graphene system. Firstly, the Dirac cone is almost undistorted, preserving graphene's high carrier mobilities. Secondly, the Ni4 cluster has a large doping efficiency, implying a strong charge transfer to graphene. Finally, non-collinear spin-polarized calculations of the Ni4/graphene system indicate that the Ni4 cluster gives rise to sizable spin splitting of the Dirac bands due to the induced spin–orbit coupling and exchange interaction.
To investigate the impact of the magnetic clusters on (spin) transport, a graphene spin valve is decorated with Ni4 clusters at a density of 5.7 × 1012 clusters per cm2. Following the example by Zomer et al.,20 we study the spin relaxation mechanism by characterizing the spin transport parameters at different values of applied backgate voltages before and after cluster deposition. As the spin scattering mechanism in pristine graphene (i.e. the virgin state) is debated in the literature,4 only a comparative study can unambiguously corroborate the contribution of the added scatterers. By performing Hanle spin precession measurements at different applied backgate voltages, the spin scattering time, τs, and the momentum scattering time, τp, are obtained. By comparing the ‘before’ and ‘after’ states of the device, the induced effects of the clusters are identified as an Elliot–Yafet (EY) like spin scattering mechanism.
2 DFT calculations of Nin/graphene
First-principles calculations were performed using the Vienna ab initio simulation package (VASP) with plane wave basis sets and projected-augmented wave (PAW) potentials.21–23 First, the ground state geometrical configurations of the Nin clusters adsorbed on graphene were obtained by performing simulations with non-local vdW-DF2 exchange and correlation functionals.24,25 The clusters were placed at different possible adsorption sites in the 5 × 5 graphene supercell with an interlayer spacing of 20 Å. This corresponds to a cluster density of 7.6 × 1013 cm−2. The systems were relaxed until the forces between the atoms were less than 25 meV Å−1 using a 5 × 5 × 1 k-point mesh with an energy cutoff of 520 eV. Furthermore, electronic structure calculations were performed on a denser mesh of 11 × 11 × 1 k-points. For Ni3 and Ni5 adsorbed on graphene, the Ni d-states are close to the Dirac point, resulting in a distortion of the Dirac cone in the spin-polarised band structure. As discussed below, the Ni4 cluster preserves the Dirac cone and thus the high carrier mobility, while it has at the same time a large doping efficiency per cluster, implying a stronger charge transfer to graphene, with a high mobility and strong localized magnetic moment. Therefore, we direct our attention to Ni4 clusters as a test bed to explore the physics at play when magnetic clusters are adsorbed on graphene.The resultant total energies were compared to obtain the most stable configuration, which is shown in Fig. 1(a). The isolated Ni4 cluster is tetrahedrally shaped and it prefers to adsorb with a single Ni atom on the bridge position (between two carbon atoms) with bond lengths of 2.119 Å and 2.299 Å. The Ni4 adsorption energy is calculated to be −1.05 eV, indicating a stronger interaction than physisorption (a few hundred meV), but too weak for a real chemical bond. It can be seen from electronic structure calculations that Ni4 donates electrons to graphene, resulting in a (Ni+C−) charge state type of attraction at the adsorption site. The adsorption of the Ni4 cluster leads to the elongation of the C–C bond length by ∼0.01 Å. The adsorbed Ni4 has a localised magnetic moment of 3.3μB, which is slightly reduced when compared to the magnetic moment of the isolated cluster (3.7μB).
The doping characteristics of the cluster are studied by performing open-shell electronic structure calculations. From the band structure of the Ni4/graphene system, the Dirac cone is almost undistorted (see Fig. 1(b)) and the adsorption of the Ni4 cluster preserves the high carrier mobility of graphene. The resultant band structure yields an n-type doping, as can be observed from the apparent shift of the Dirac cone below the Fermi level, which is consistent with the experimental results that are presented in section 3. From the shift of the Dirac point, one can compute the charge carrier doping density,26 which corresponds to a doping efficiency of about 0.09 electrons per cluster. While the electron transfer was found to be independent of the supercell size, its absolute value does vary slightly with the size of the supercell (see the ESI† for details).
In the next step, we studied the induced spin-dependent effects of the Ni4 cluster on the graphene layer. The induced spin splitting is estimated from the band splitting along the graphene band lines (i.e., only the C-projected band states are considered) around the Dirac point. The band gap amounts to 25 meV and the obtained values of the band line splitting vary along the M → K → Γ path with an average value of 48.5 meV for the valence band and 29.9 meV for the conduction band. These values vary slightly with the size of the supercell that is used in the computations, as discussed in the ESI.† The average value is computed by calculating the absolute energy difference between the spin-split C-projected band in the −0.6 eV to 0 eV energy range. The origin of the induced spin-splitting is discussed below.
To qualitatively study the strength of different SOC terms, we constructed a tight binding Hamiltonian model to reproduce the electronic structure of the Ni4/graphene system close to the Dirac point. From the DFT band structure, four Ni states are located close to the band extrema. These states are indicated by blue arrows in Fig. 1(b). A simple model was constructed dealing only with the interaction between the Ni anchor atom (with four spin states) and the two graphene C atoms (with two spin states per site). The Hamiltonian is given by
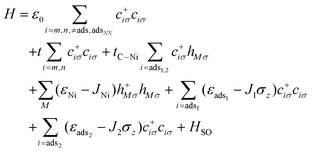 | (1) |
Here, c+iσ(ciσ) and h+Mσ(hMσ) correspond to the creation (annihilation) operator for an electron with spin σ at graphene lattice site i and cluster site M, respectively. ε0 and t represent on-site and nearest-neighbor hopping energies between the carbon atoms. The onsite energy and local Zeeman coupling of the Ni atom are given by εNi and JNi respectively. The adsorption of the Ni cluster modifies the onsite potential (εads1) and induces a local magnetic interaction (J1) at the closest (2.119 Å) adsorption site and its two nearest neighboring sites. J2 corresponds to the Zeeman coupling at the carbon site 2.299 Å from the Ni4 cluster. This C site is the third nearest neighbor of the closest adsorption site, but due to the bonding with the Ni atom, the on-site potential (εads2) is slightly modified. The hopping from C to Ni (tC–Ni) was set to 0.5 eV to fit the DFT band structure. The spin–orbit coupling Hamiltonian is derived based on ref. 27–29 as follows:
 | (2) |
The first term represents spin-conserving next nearest neighbor hopping, with the intrinsic (λi) and valley-Zeeman (λVZ) spin–orbit terms, where  and
and  . The second term in eqn (2) represents the spin mixing nearest neighbor hopping, with λBR being the Bychkov–Rashba spin–orbit coupling term. The third term in eqn (2) corresponds to the spin mixing next nearest neighbor hopping, where λA/BPIA is the strength of the pseudospin inversion asymmetry induced spin–orbit coupling, due to the sublattice symmetry breaking. In the above Hamiltonian, ξi is +1 (−1) for sublattice A (B), υmn is +1 (−1) for the clockwise (counterclockwise) hopping path to the next nearest neighbor site, and dmn (Dmn) is the unit vector from site n to its nearest (next-nearest) site m. The single (double) bracket represents the sum of the first (second) nearest neighbor sites.
. The second term in eqn (2) represents the spin mixing nearest neighbor hopping, with λBR being the Bychkov–Rashba spin–orbit coupling term. The third term in eqn (2) corresponds to the spin mixing next nearest neighbor hopping, where λA/BPIA is the strength of the pseudospin inversion asymmetry induced spin–orbit coupling, due to the sublattice symmetry breaking. In the above Hamiltonian, ξi is +1 (−1) for sublattice A (B), υmn is +1 (−1) for the clockwise (counterclockwise) hopping path to the next nearest neighbor site, and dmn (Dmn) is the unit vector from site n to its nearest (next-nearest) site m. The single (double) bracket represents the sum of the first (second) nearest neighbor sites.
The tight binding model was fitted to the spin-split conduction and valence Dirac cones of the Ni4/graphene system. The parameters were obtained by minimizing the energy difference in the DFT computed band lines and are provided in Table 1. The strength of the SOC is given by the magnitude of λ, and its sign corresponds to the direction of the spin splitting. The calculated electronic band structure, obtained from the tight binding model, is compared with the DFT simulations in Fig. 2. The tight binding model reproduces the DFT spin–orbit band structure close to the Dirac point. The tight-binding analysis suggests that the spin conserving valley-Zeeman-type SOC, represented by a large value of λVZ, dominates the SOC interaction in the Ni4/graphene system.
| Orbital parameters (eV) | |||||||
|---|---|---|---|---|---|---|---|
| ε 0 | t | ε ads1 | ε ads2 | ε Ni | J Ni | J 1 | J 2 |
| −2.16 | −2.53 | −5.94 | −6.82 | −2.79, −2.30 | 0.030, 0.023 | −0.056 | 0.082 |
| Spin–orbit parameters (meV) | ||||
|---|---|---|---|---|
| λ i | λ VZ | λ BR | λ APIA | λ BPIA |
| 16.9 | −59.8 | 4.22 | 1.60 | −8.06 |
3 Experimental results
3.1 Device characteristics
The device used as a starting point to fabricate the Ni4/graphene hybrid is presented in Fig. 3. A more in-depth discussion of the sample fabrication process can be found in ref. 17. The graphene layer resides on a highly doped Si substrate terminated with a 300 nm SiO2 top layer. The graphene is grown using platinum-based chemical vapor deposition (Pt-CVD) and subsequently transferred to the substrate.30 The graphene's area of interest lies between the two magnetic contacts indicated by the width (W) and length (L) of the probed area, both of which are 10 μm. A backgate voltage Vg can be applied between the highly doped Si electrode and the graphene channel. To ensure a difference in magnetization reversal of the two Co electrodes at the center, the widths of these Co bars are set at 290 nm and 320 nm, respectively. The interface between these Co electrodes and graphene is made of 1 nm TiOx to facilitate the spin injection and measurement. These left and right barriers behave as ohmic contacts in the applied voltage range and are roughly 425 Ω and 280 Ω, respectively. Conductivity measurements are performed by applying a current from #1 to #4 while measuring voltage over #2 and #3. Nonlocal measurements, i.e. the Hanle spin precession measurement, are carried out by applying a current from #2 to #1, while a nonlocal voltage is measured over #4 and #3. Both the conductivity and non-local transport measurements are performed at room temperature and a current of 10 μA is used. For such a low current, the effect of heating in these graphene devices can be ignored.31 During the Hanle spin precession measurements, after aligning the magnetization of the central Co electrodes, a magnetic field is applied perpendicular to the plane of the graphene. The measurements are done for field strengths ranging from −120 mT to +120 mT.Using a magnetron sputtering gas aggregation cluster source,32 a molecular beam of nickel clusters is formed. Ni4+ clusters are selected with atomic precision using a quadrupole mass filter and finally soft-landed on graphene devices. With a retarding field, the average kinetic energy of the Ni4+ clusters was determined to be 5.1 eV.33 During deposition, the device was supplied a repelling voltage of +2.5 V, reducing the average landing energy of the clusters to 2.6 eV. Therefore, the cluster energy is tuned to the soft-landing regime (1 eV per atom (ref. 34)). The beam current IB was recorded during the deposition, and after integration, the total cluster density was found to be nc = 5.7 × 1012 clusters per cm2.
3.2 Impact of Ni4 on charge transport properties
Fig. 3(b) presents the backgate dependent conductivity measurements of graphene in the virgin state and after Ni4 cluster deposition. For the virgin state, these measurements indicate a charge neutrality point, VCNP, of +0.5 V and an average mobility μav = (μe + μh)/2 of 2.7 × 103 cm2 V−1 s−1. The electron and hole mobilities (μe and μh, respectively) are extracted from linear least-squares fitting procedures with a 2 V interval around the steepest part of the conductivity curve σS(Vg).35 The VCNP becomes −18 V after cluster deposition. The shift of VCNP corresponds to a doping efficiency of 0.15–0.25 electrons per Ni4 cluster taking into account the 5.7 × 1012 clusters per cm2 deposited density. The hole mobility after cluster deposition decreased to 1.9 × 103 cm2 V−1 s−1, while the electron mobility became 2.3 × 103 cm2 V−1 s−1. The different influence of the Ni4 clusters on the electron and hole mobilities, which is reflected in the enhanced asymmetry of the sheet conductivity curve after cluster deposition, can be attributed to the stronger Ni–graphene interaction in the hole Dirac cone than in the electron Dirac cone. This aligns with the calculated band structure (Fig. 1), where the energy difference of Ni states in the valence band with the Dirac point (∼0.2 eV) is slightly smaller than the corresponding energy difference of Ni states in the conduction band. Compared to the cases of Au3 and Au6,17 the results correspond to each other in a qualitative sense, where a decrease in mobility was seen as well following cluster deposition. However, quantitatively, the electron donation per cluster is larger than that of the Au6 cluster by a factor of ∼3 and almost two orders of magnitude compared to the Au3 cluster. Considering the Pauling electronegativity of Au and Ni (2.4 and 1.8), compared to 2.5 for C, Ni has a lower tendency to attract electrons and it therefore donates more electrons to graphene. Compared to the simulations, the experimentally obtained doping efficiency is twice as large. This discrepancy could be due to the fact that DFT simulations are performed on ideal free-standing graphene monolayers, i.e. neither defects nor substrate effects are taken into account. Next, the spintronic properties of the device are evaluated, both in the virgin state and after Ni4 deposition.3.3 Spin transport characteristics of the virgin state
 | ||
| Fig. 4 (a) Hanle spin precession measurements, after background subtraction, at backgate voltages Vg = −50 V, 0 V and 50 V in the virgin state. (b) Repeat of the measurement in panel (a) after Ni4 deposition. (c) Amplitude of the nonlocal resistance at zero field, after background subtraction, as a function of backgate voltage. All data are corrected for back-gate creep (see the ESI of ref. 17 for details). | ||
 | ||
| Fig. 5 Spin transport parameters of the graphene spin valve. (a) Spin lifetime τs and (c) diffusion constant D as a function of Vg for the device in the virgin state. (b) Spin lifetime τs and (d) diffusion constant D as a function of Vg for the device after Ni4 deposition. All data shown are averaged for the gate up and down measurements after VCNP creep correction.17 | ||
Since the Elliot–Yafet (EY) and D'yakonov Perel (DP) mechanisms have very different dependencies on the Fermi level EF and the momentum scattering lifetime τp, studying the spin transport parameters at different Vg values provides information about the scattering mechanism at play. As introduced by Zomer et al.,20 the spin scattering rate can be written as Matthiessen's rule of summation of the scattering rates caused by EY and DP simultaneously: τs−1 = τs,EY−1 + τs,DP−1, assuming that individual scattering probabilities are independent of each other. Inserting the formulas for EY and DP, with ΔEY being the spin–orbit coupling strength of the EY interaction38 and ΔDP being the spin–orbit coupling strength of the DP interaction,39
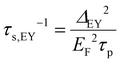 | (3) |
 | (4) |
 | (5) |
Fig. 6 presents the left hand side term,  , as a function of EF2τp2. τs is directly obtained from the Hanle fit, EF is measured from VCNP and the applied gate voltage, and τp is calculated from the Hanle fit-parameter D using the relation D = vF2τp/2, where vF ≈ 106 m s−1. Using this presentation of the data, eqn (5) implies that a linear fit estimates the slope as 4ΔDP2/ħ2 and the offset as ΔEY2. It should be noted that not all data extracted from the Hanle fit are presented here. Although the S/N ratio close to the VCNP is still reasonable for the characterization of the virgin state, the signal decreased too much after deposition in order to obtain reliable fitting parameters. Therefore, for consistency, the data close to the VCNP that could not be measured in the decorated state also was left out of the fit and figure in the virgin state.
, as a function of EF2τp2. τs is directly obtained from the Hanle fit, EF is measured from VCNP and the applied gate voltage, and τp is calculated from the Hanle fit-parameter D using the relation D = vF2τp/2, where vF ≈ 106 m s−1. Using this presentation of the data, eqn (5) implies that a linear fit estimates the slope as 4ΔDP2/ħ2 and the offset as ΔEY2. It should be noted that not all data extracted from the Hanle fit are presented here. Although the S/N ratio close to the VCNP is still reasonable for the characterization of the virgin state, the signal decreased too much after deposition in order to obtain reliable fitting parameters. Therefore, for consistency, the data close to the VCNP that could not be measured in the decorated state also was left out of the fit and figure in the virgin state.
 | ||
| Fig. 6 Hanle fit parameters (τs and τp = 2D/vF2) before and after Ni4 cluster deposition presented according to eqn (5) as the blue and red circles for the virgin and Ni4 decorated device, respectively. The offset and slope of the linear fits plotted are related to the ΔEY and ΔDP coupling strengths. | ||
The linear fit performed on the virgin state measurement provides an EY SOC ΔEY = 0.97 ± 0.17 meV and a DP SOC ΔDP = 0.053 ± 0.002 meV. It can be seen from these values that both scattering mechanisms have a non-zero contribution to the total spin scattering. Compared to the exfoliated graphene samples measured in Zomer et al.,20 where the EY coupling strength lies in a range of 1–2 meV and DP in a range of 0.05–0.1 meV, the experimental values obtained here are of similar magnitude. Graphene devices on a SiO2 substrate also showed similar coupling strengths.15 Using the EY and DP scattering strengths measured from the linear fit on the virgin state data (Fig. 6), the spin scattering rates of the two mechanisms can be compared directly. For example, at 50 V from the charge neutrality point (EF = 0.22 eV), the scattering rate of DP is 1.5 ns−1, while that of the EY mechanism is 0.35 ns−1. While for the largest applied backgate voltages, Vg = ±75 V, corresponding to |EF| ≈ 0.27 eV, the DP induced scattering rate is almost an order of magnitude higher than the EY induced scattering rate. This difference in the spin scattering rate can be calculated from eqn (3) and (4) using the SOC obtained from the fit and a typical τp of 50 fs. Only when |EF| ≲ 0.13 eV (Vg − VCNP ≲ 18 V), the EY induced scattering rate is larger than the DP induced scattering rate. However, in contrast to the Fermi level regimes away from the Dirac point, where the measured τs (Fig. 5(a and b)) corresponds to the sum of both scattering mechanisms, this sum fails to capture the behaviour around the Dirac point. As the EY spin scattering rate is proportional to EF−2, the scattering rate tends to infinity as EF → 0. Thermal broadening and charge puddles are not taken into account in this formula, which could explain the discrepancy with the experimental data.
3.4 Spin transport characteristics of the Ni4 cluster decorated state
3.5 Ni4 cluster-induced SOC in graphene
A comparison of the experimentally obtained SOC strengths with those found in the DFT calculations in section 2 requires isolating the Ni4 contribution from the total coupling strength. We estimate the value for ΔEY,Ni4, representing the SOC strength associated with the Ni4 clusters at certain backgate voltages. Two highly doped regimes are chosen: high p-doping and high n-doping, evaluated at Vg − VCNP = −50 V and Vg − VCNP = +50 V. In these high doping regimes, the spin lifetime could be extracted from the Hanle spin precession experiments with low uncertainty. The carrier densities in these regimes are n = 3.59 × 1012 holes per cm2 and n = 3.59 × 1012 electrons per cm2, respectively. In order to obtain ΔEY,Ni4, we consider eqn (6), representing the terms contributing to the total spin scattering rate: | (6) |
The first term on the right hand side represents the spin scattering contribution due to the virgin scatterers in the EY mechanism. The second term expresses the Ni4 cluster EY scattering contribution. The last term represents the DP scattering contribution. The required data extracted from the measurements are collected in Table 2. Finally, inserting these quantities and their errors in the equations, the Ni4 cluster induced SOC EY coupling strength is ΔEY,Ni4 = 4.0 ± 0.5 meV evaluated at Vg − VCNP = −50 V and ΔEY,Ni4 = 4.3 ± 0.5 meV at Vg − VCNP = +50 V (or −/+0.21 eV from the Dirac point, respectively).
 with vF ≈ 106 m s−1
with vF ≈ 106 m s−1
| n c | Virgin state | Ni4 cluster decorated state |
| V CNP | 0.5 V | −18 V |
| n | 3.59 × 1012 holes per cm2 | |
| E F | −0.221 eV | |
| V g | −49.5 V | −68 V |
| σ S(n) | 1.38 mS | 1.13 mS |
| τ p(σS,n) | 53 ± 1 fs | 43 ± 1 fs |
| τ s | 560 ± 60 ps | 330 ± 70 ps |
| n | 3.59 × 1012 electrons per cm2 | |
| E F | 0.221 eV | |
| V g | 50.5 V | 32 V |
| σ S(n) | 1.51 mS | 1.30 mS |
| τ p(σS,n) | 58 ± 1 fs | 50 ± 1 fs |
| τ s | 500 ± 50 ps | 360 ± 60 ps |
For an intuitive way to understand eqn (6) and how the obtained ΔEY,Ni4 relates to the ΔEY, one has to consider the complete (spin) scattering picture of our device. When it scatters due to a scattering centre already present in the virgin sample there is about a 1 in 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 chance that the spin will scatter as well, since
000 chance that the spin will scatter as well, since  . When there is a momentum scattering event with the Ni4 cluster, this probability is much higher: about 1 in 3000 as
. When there is a momentum scattering event with the Ni4 cluster, this probability is much higher: about 1 in 3000 as  , with the coupling strength taken in the hole regime. In this picture, the ΔEY provided by the linear regression in Fig. 6 can be regarded as the ‘average’ scattering probability behaving like the EY mechanism, weighted over the clusters and the other momentum scatterers. As seen in Table 2, the momentum lifetime decreases from τp,0 = 53 fs to τp = 43 fs after Ni4 deposition in the hole dominated regime and from τp,0 = 58 fs to τp = 50 fs in the electron dominated regime. The relative contribution of the cluster momentum scatterers to the total momentum scattering equals τp,Ni4−1/τp−1 = (τp−1 − τp,0−1)/τp−1 = 19% in the hole doped regime and 14% in the electron doped regime. This indicates that about 1 in 6 momentum scattering events are caused by the Ni4 cluster. Therefore, the measured increase from ΔEY = 0.97 ± 0.17 meV to ΔEY = 1.68 ± 0.09 meV can be attributed to a Ni4 EY coupling strength of ΔEY,Ni4 = 4.0 ± 0.5 meV and ΔEY,Ni4 = 4.3 ± 0.5 meV for the hole and electron charge carrier regimes, respectively.
, with the coupling strength taken in the hole regime. In this picture, the ΔEY provided by the linear regression in Fig. 6 can be regarded as the ‘average’ scattering probability behaving like the EY mechanism, weighted over the clusters and the other momentum scatterers. As seen in Table 2, the momentum lifetime decreases from τp,0 = 53 fs to τp = 43 fs after Ni4 deposition in the hole dominated regime and from τp,0 = 58 fs to τp = 50 fs in the electron dominated regime. The relative contribution of the cluster momentum scatterers to the total momentum scattering equals τp,Ni4−1/τp−1 = (τp−1 − τp,0−1)/τp−1 = 19% in the hole doped regime and 14% in the electron doped regime. This indicates that about 1 in 6 momentum scattering events are caused by the Ni4 cluster. Therefore, the measured increase from ΔEY = 0.97 ± 0.17 meV to ΔEY = 1.68 ± 0.09 meV can be attributed to a Ni4 EY coupling strength of ΔEY,Ni4 = 4.0 ± 0.5 meV and ΔEY,Ni4 = 4.3 ± 0.5 meV for the hole and electron charge carrier regimes, respectively.
The spin–orbit coupling strengths obtained from the tight binding model for the spin-mixing terms λBR and λA/BPIA (which act like a second-order Rashba SOC) are in close agreement with the experimental values obtained for ΔEY,Ni4. It should be noted that the presence of magnetic impurities can lead to an efficient spin relaxation mechanism due to resonant spin scattering induced by impurities, as shown by Kochan et al.40 The presence of a larger spin–orbit coupling and exchange interaction induced by the adsorbed Ni4 cluster could thus turn the clusters into local spin scatterers, which enhances the spin flip probability for each scattering event. Consequently, Ni4 clusters act as charge and magnetic dopants in graphene, having a strong impact on its spin transport properties while possibly maintaining graphene's high charge carrier mobility due to the weak distortion of the Dirac cone induced by the adsorbed clusters.
4 Conclusions
We performed an in-depth analysis of Ni4 clusters on graphene using both DFT calculations and spin transport experiments. Before and after deposition analysis reveals an EY-like spin scattering mechanism induced by the Ni4 clusters with an EY SOC strength of ΔEY,Ni4 = 4.0 ± 0.5 meV. The overall SOC can only be ‘engineered’ up to a maximum of 4.0 ± 0.5 meV due to the nature of the EY mechanism by decorating graphene with Ni4 clusters. When the cluster density is increased, the contribution of the cluster to the total momentum scattering moves closer towards 100%. The experimental values obtained for ΔEY,Au3 and ΔEY,Au6 were 5.7 meV and 3.9 meV.17 These values are comparable to the one obtained for ΔEY,Ni4 in the current work and as such, the magnetic character of nickel cannot be pinpointed as a much stronger source of spin scattering. In order to increase the SOC, different sizes or elements need to be examined and the experimental protocol presented in this work is ideally suited for performing such studies.Data availability
The data that support the findings of this study are available from corresponding author JVdV upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Research Foundation-Flanders (FWO, Belgium), grant no. G0D5619N.References
- A. H. Castro Neto and F. Guinea, Phys. Rev. Lett., 2009, 103, 026804 CrossRef CAS PubMed.
- J. Katoch, Synth. Met., 2015, 210, 68–79 CrossRef CAS.
- G. Jian-Lei, W. Tian-Ru, G. Ming, B. Zhan-Bin, C. Lu, W. Xue-Feng, Q. Yu-Yuan and S. Feng-Qi, Front. Phys., 2017, 12, 127210 CrossRef.
- B. Raes, J. E. Scheerder, M. V. Costache, F. Bonell, J. F. Sierra, J. Cuppens, J. Van De Vondel and S. O. Valenzuela, Nat. Commun., 2016, 7, 11444 CrossRef CAS PubMed.
- T. S. Ghiasi, J. Ingla-Aynés, A. A. Kaverzin and B. J. Van Wees, Nano Lett., 2017, 17, 7528–7532 CrossRef CAS PubMed.
- J. Bundesmann, D. Kochan, F. Tkatschenko, J. Fabian and K. Richter, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 081403 CrossRef.
- L. A. Benítez, J. F. Sierra, W. Savero Torres, A. Arrighi, F. Bonell, M. V. Costache and S. O. Valenzuela, Nat. Phys., 2018, 14, 303–308 Search PubMed.
- A. Ferreira, T. G. Rappoport, M. A. Cazalilla and A. H. Castro Neto, Phys. Rev. Lett., 2014, 112, 066601 CrossRef PubMed.
- D. Van Tuan, J. M. Marmolejo-Tejada, X. Waintal, B. K. Nikolić, S. O. Valenzuela and S. Roche, Phys. Rev. Lett., 2016, 117, 176602 CrossRef CAS PubMed.
- Z. Jia, B. Yan, J. Niu, Q. Han, R. Zhu, D. Yu and X. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 085411 CrossRef.
- C. K. Safeer, J. Ingla-Aynés, F. Herling, J. H. Garcia, M. Vila, N. Ontoso, M. R. Calvo, S. Roche, L. E. Hueso and F. Casanova, Nano Lett., 2019, 19, 1074–1082 CrossRef CAS PubMed.
- P. Zhang and M. W. Wu, New J. Phys., 2012, 14, 033015 CrossRef.
- A. G. Swartz, J. R. Chen, K. M. McCreary, P. M. Odenthal, W. Han and R. K. Kawakami, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 20–23 CrossRef.
- K. Pi, W. Han, K. M. McCreary, A. G. Swartz, Y. Li and R. K. Kawakami, Phys. Rev. Lett., 2010, 104, 187201 CrossRef CAS PubMed.
- C. Józsa, T. Maassen, M. Popinciuc, P. J. Zomer, A. Veligura, H. T. Jonkman and B. J. Van Wees, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 1–4 CrossRef.
- W. Han and R. K. Kawakami, Phys. Rev. Lett., 2011, 107, 047207 CrossRef PubMed.
- W. Keijers, R. Murugesan, G. Libeert, J. E. Scheerder, B. Raes, S. Brems, S. D. Gendt, M. Houssa, E. Janssens and J. V. de Vondel, J. Phys.: Mater., 2021, 4, 045005 CAS.
- S. E. Apsel, J. W. Emmert, J. Deng and L. A. Bloomfield, Phys. Rev. Lett., 1996, 76, 1441–1444 CrossRef CAS PubMed.
- R. Ambrusi, V. Orazi, J. Marchetti and M. Pronsato, J. Phys. Chem. Solids, 2020, 138, 109258 CrossRef CAS.
- P. J. Zomer, M. H. D. Guimarães, N. Tombros and B. J. van Wees, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 161416 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- K. Lee, É. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101 CrossRef.
- M. S. Lundstrom and C. Jeong, Near-equilibrium transport: fundamentals and applications, World Scientific Publishing Company, 2013, vol. 2, p. 252 Search PubMed.
- A. W. Cummings, J. H. Garcia, J. Fabian and S. Roche, Phys. Rev. Lett., 2017, 119, 206601 CrossRef PubMed.
- M. Gmitra, D. Kochan and J. Fabian, Phys. Rev. Lett., 2013, 110, 246602 CrossRef PubMed.
- K. Song, D. Soriano, A. W. Cummings, R. Robles, P. Ordejón and S. Roche, Nano Lett., 2018, 18, 2033–2039 CrossRef CAS PubMed.
- K. Verguts, Y. Defossez, A. Leonhardt, J. D. Messemaeker, K. Schouteden, C. V. Haesendonck, C. Huyghebaert, S. D. Gendt and S. Brems, ECS J. Solid State Sci. Technol., 2018, 7, 195–200 CrossRef.
- G. Libeert, R. Murugesan, M. Guba, W. Keijers, S. Collienne, B. Raes, S. Brems, S. De Gendt, A. V. Silhanek, T. Höltzl, M. Houssa, J. Van de Vondel and E. Janssens, Nanoscale, 2022, 14, 12437–12446 RSC.
- Z. Li, H.-Y. T. Chen, K. Schouteden, T. Picot, K. Houben, T.-W. Liao, C. Van Haesendonck, G. Pacchioni, P. Lievens and E. Janssens, Nano Lett., 2016, 16, 3063–3070 CrossRef CAS PubMed.
- J. E. Scheerder, T. Picot, N. Reckinger, T. Sneyder, V. S. Zharinov, J.-F. Colomer, E. Janssens and J. Van de Vondel, Nanoscale, 2017, 9, 10494–10501 RSC.
- S. R. Plant, L. Cao, F. Yin, Z. W. Wang and R. E. Palmer, Nanoscale, 2014, 6, 1258–1263 RSC.
- J. H. Chen, C. Jang, S. Adam, M. S. Fuhrer, E. D. Williams and M. Ishigami, Nat. Phys., 2008, 4, 377–381 Search PubMed.
- W. Han, K. Pi, K. M. McCreary, Y. Li, J. J. I. Wong, A. G. Swartz and R. K. Kawakami, Phys. Rev. Lett., 2010, 105, 3–6 CrossRef PubMed.
- F. Volmer, M. Drögeler, T. Pohlmann, G. Güntherodt, C. Stampfer and B. Beschoten, 2D Mater., 2015, 2, 024001 CrossRef.
- H. Ochoa, A. H. Castro Neto and F. Guinea, Phys. Rev. Lett., 2012, 108, 206808 CrossRef CAS PubMed.
- M. D'Yakonov and V. Perel’, Soviet J. Exp. Theor. Phys., 1971, 33, 1053 Search PubMed.
- D. Kochan, M. Gmitra and J. Fabian, Phys. Rev. Lett., 2014, 112, 116602 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr01478b |
| This journal is © The Royal Society of Chemistry 2024 |



