Seeding the vertical growth of laterally coherent coordination polymers on the rutile-TiO₂(110) surface

Abstract

Coordination polymers may be synthesized by linear bridging ligands to metal ions with conventional chemistry methods (e.g. in solution). Such complexes can be hardly brought onto a substrate with the chemical, spatial and geometrical homogeneity required for device integration. Instead, we follow an in situ synthesis approach, where the anchoring points are provided by a monolayer of metal(II)-tetraphenylporphyrin (M-TPP, M = Cu, Zn, Co) grown in vacuum on the rutile-TiO₂(110) surface. We probed the metal affinity to axial coordination by further deposition of symmetric dipyridyl-naphthalenediimide (DPNDI). By NEXAFS linear polarization dichroism, we show that DPNDI stands up on Zn- and Co-TPP thanks to axial coordination, whereas it lies down on the substrate for Cu-TPP. Calculations for a model pyridine ligand predict strong binding to Zn and Co cations, whose interaction with the O anions underneath is disrupted by surface trans effect. The weaker interactions between pyridine and Cu-TPP are then overcome by the strong attraction between TiO₂ and DPNDI. The binding sites exposed by the homeotropic alignment of the ditopic DPNDI ligand on Zn- and Co-TPP are the foundations to grow coordination polymers preserving the lateral coherence of the basal layer.

---

Introduction

The tetrapyrrolic macrocycle of porphyrins and phthalocyanines is able to chelate most metal ions, thus yielding a class of compounds with easily tunable optical properties and (photo-) chemical reactivity. Depending on the electronic configuration, the metal center in planar tetra-coordination may have one or two additional out of plane coordination sites (yielding a square pyramidal or octahedral coordination, respectively) for linking further molecules in a controlled, possibly recursive, geometry.^1–3 The on-surface assembly by axial coordination of vertically stacked donor–acceptor bilayers would be highly desirable, because it would shift the description of the interfacial properties from a layer-on-layer effective medium picture to a molecule-on-molecule model.⁴

Simple donor–acceptor dyads formed by axial coordination to the porphyrin macrocycle of pyridyl-terminated perylene derivatives may be prepared in solution. Then, they can be brought onto inert surfaces by simple dropcasting. Accommodation of dyads at specific sites, may be achieved by pre-patterning the surface with suitable self-assembled monolayers.^5,6 Such chemical protocols yield a poor surface homogeneity, as well as a low degree of purity. For applications in organoelectronic devices, one would rather need to control also the lateral coherence (transverse to the coordination axis direction) in order to grow recursively 2D + 1 hetero-stacked homogeneous layers. In-vacuum molecular deposition meets the requisites of purity and spatial homogeneity, provided the interaction with the surface does not hinder the axial (vertical) chemical coordination ability of the deposited species. In fact, metal porphyrins adsorb on most of technologically relevant metals and semiconductors with the appropriate flat orientation, but their axial coordination site is often saturated by charge transfer.⁷ A few methods of passivating metal substrates have been shown to suppress to some extent the charge transfer from the substrates to aromatic molecules, while preserving the flat molecular orientation. These include predeposition of a KCl insulating layer on Ag,⁸ deposition of Sn submonolayers on Cu,⁹ and surface oxidation of Fe.^10–12 On the latter system, which is particularly relevant for the study of magnetic properties of metal–organic molecules, we have recently demonstrated that Zn-TPP molecules in the monolayer phase preserve their single axial coordination site, where pyridyl-terminated molecules deposited in vacuum may directly link. By using a dipyridyl-naphthalenediimide (DPNDI), the out-of-plane dangling pyridyl group may further coordinate to the axial site of a next layer porphyrin. If this is in turn made of Co-TPP, which displays two axial sites, the columnar growth of parallel porphyrins and vertical DPNDI can be continued for several bilayers, still preserving the original phase symmetry and ordering of the contact layer.¹³ Thanks to the rigid spacing of the basal layer, such a supramolecular assembly mimics the lateral coherence of a coordination polymer network, even in absence of specific intralayer bonds among the molecules.¹⁴

From a technological point of view, a substrate of choice to tailor the growth, stacking and orientation of porphyrins is certainly the rutile-TiO₂(110) surface.¹⁵ In particular, achieving the 2D coherent columnar growth of multiple porphyrin layers and/or donor–acceptor bilayers would improve the electron transfer to the substrate upon excitation, thanks to the direct intermolecular interaction along the vertical path. The possibility of intercalating homogeneous heterolayers of porphyrins would increase the degrees of freedom for tailoring the (photo)electronic properties of a stacked multilayer, e.g. for tuning the optical window, exciton spatial confinement, etc. In addition, one might envisage the 2D confinement of an array of molecular magnets (e.g. Co-, Fe-TPP) entirely decoupled from the substrate, or even to exploit the pyridine axial coordination for tuning the spin state of the chelated metal atom. However, one must beware of the high reactivity of the TiO₂(110) surface, which may prevent the axial coordination of porphyrins. Very recently, we have shown that metal(II)-tetraphenylporphyrins, M(II)-TPP (M = Co, Ni, Cu, Zn), share the same adsorption orientation and ordering on the TiO₂(110) surface.¹⁶ These porphyrins adsorb on the protruding rows of oxygen atoms (O_br) yielding a commensurate (2 × 4)-oblique phase, like that observed also for 2H-TPP and its titanyl counterparts.^17,18 According to DFT calculations, the adsorption site of Co- and Zn-TPP is driven by direct linking of their metal atom atop one O_br atom. In the case of Ni- and Cu-TPP, the adsorption is only driven by the network of weak hydrogen bonds among the C–H phenyl moieties and the adjacent O_br rows, while the central metal atom (and its heteroaromatic macrocycle) floats unperturbed above the O_br rows with no direct interaction. These porphyrin overlayers are thus ideal candidates to probe the docking of molecular acceptors by in-vacuum pyridyl to metal axial coordination.

Results and discussion

Here we focus on Zn-, Co-, and Cu-TPP, which are representative of three different coordinative configurations (as depicted in Fig. 1): Zn(II) and Co(II) in planar tetra-coordination display one and two free additional axial coordination sites, respectively (square pyramidal and octahedral coordination); Cu(II) in planar tetra-coordination has no axial sites, but its coordination geometry is subject to Jahn–Teller effects, hence the specific perturbation produced by an out of plane ligand can trigger tetragonal coordination (in this case, the axial sites are expected to be at a much larger distance than the in-plane ones).¹⁹ As a linker, we used DPNDI, which has the advantage of being sublimable in vacuum and, thanks to its double pyridyl terminations, was demonstrated to link M(II)-TPP at both ends, yielding a coordination network made of several bilayers.¹³ We compared experiments with DFT calculations (PBE functional²⁰ with D2 Grimme dispersion^21,22 and Vanderbilt pseudopotentials²³), where we modeled the DPNDI ligand with a simple pyridine (Py) molecule to reduce the computational costs imposed by (i) the large size of the supercells associated with adsorbed M-TPPs, and (ii) the large thickness of the TiO₂ slab required to describe the interaction of M-TPPs with the substrate (section S1 of ESI†).

Fig. 1 Right: schematic representation of pyridine coordination to the axial site of Co-, Zn- and Cu-TPP (from top to bottom, respectively). Top right: topview of the molecular structure of N,N′-di(4-pyridyl)-1,4,5,8-naphthalenetetracarboxdiimide (DPNDI) (the imide and pyridyl N atoms are indicated). Bottom right: 3D side view of the rutile-TiO₂(110) surface (Ti and O atoms in green and red, respectively), highlighting the protruding rows of undercoordinated oxygen-bridge (O_br) atoms.

We performed preliminary theoretical investigations of the Py/M-TPP adducts in the gas phase (section S2 of ESI†). At equilibrium, the pyridine molecular plane is predicted to stand perpendicular to that of the porphyrin M–N₄ chromophore, with the pyridyl N atom on top of the chelated metal atom for M = Zn, Co, Cu and Ni, as previously found for similar molecular complexes.²⁴ We computed binding energies of 0.8–1.0 eV for Py coordination to Zn- and Co-TPP, and much lower values of 0.3–0.5 eV for Ni- and Cu-TPP, in good agreement with former B3LYP calculations for pyridine coordination to Cu- and Zn-Porphyrin complexes.²⁵ The corresponding M(II)–N(Py) bond lengths span from 2.1 to 2.5 Å; when compared to the tetrapyrrolic pocket size, which depends on the specific metal ions,²⁶ the axial site distance is found to be only 7% larger than the pristine in-plane M(II)–N₄ bond length for Zn- and Co-TPP,^27–29 and about 20% larger for Cu- and Ni-TPP,^27,30 as expected by coordination chemistry rules.¹⁹

Experimentally, the effective docking of DPNDI at the metal-porphyrin was probed by measuring the average DPNDI orientation with respect to the surface. According to theoretical models, a standing up DPNDI orientation is expected in case of axial coordination to flat laying M-TPPs, as opposed to random or laying down orientation in absence of it. We remark that such a homeotropic orientation can be hardly imaged by scanning tunneling microscopy (STM) at the solid/vacuum interface because of the vibrational smearing of widely spaced (isolated) DPNDI. Even STM imaging in solution is hampered by the tip interaction with the upward dangling termination of the coordinated molecule, as formerly shown by a comparative topographic study of perylene derivatives coordinated either vertically or coplanarly to Zn-tetrapyrroles.⁶ Conventional Raman infrared spectroscopy may detect the vibrational modes of a free standing molecule,⁵ but lacks quantitativeness (in terms of molecular population and orientation), as well as chemical sensitivity.

The average tilt angle of DPNDI can be determined from the linear dichroism of near edge X-ray absorption fine structure (NEXAFS) at the N K-edge ionization threshold: the N 1s → π* transitions of the corresponding unoccupied molecular orbitals, UMOs, yield maximum intensity (zero intensity) when the electric field of a linearly polarized photon beam is perpendicular to (parallel to) the corresponding heteroaromatic plane. Assuming a common molecular orientation, the average molecular tilt can thus be determined from the intensity ratio between the NEXAFS spectra measured with the surface oriented either parallel or perpendicular to the electric field (s- and p-polarization, respectively).³¹ In the present case, absence of dichroism, corresponding to a nominal orientation of 45° for the two-fold TiO₂(110) surface, may be rather assumed as an indication of random molecular orientation.

In order to disentangle the NEXAFS contribution of the DPNDI top layer from that of the M-TPPs layer beneath, we have separately characterized the monolayer phases of each molecular complex (details in sections S5 and S6 of ESI†). Compared to our former spectroscopic study on the passivated Fe(001)–p(1 × 1)O surface, the reactive TiO₂(110) surface displays a direct interaction with DPNDI. The N 1s photoemission spectrum of DPNDI multilayer is characterized by two well separated peaks at 399.5 and 401.1 eV, corresponding to the pyridyl and imide nitrogen atoms, respectively (see Fig. 2a). A single spectral line at ∼400.4 eV rather dominates the N 1s XPS at a coverage lower than 1 ML. We may exclude a chemical bonding of the pyridyl terminations to the substrate from comparison with deposition of 4,4′-bipyridine (section S7 of ESI†), whose ML film at RT displays a N 1s binding energy within 0.1 eV from the multilayer value of 399.8 eV.³² We rather attribute the DPNDI spectral feature to a charge transfer from the substrate into the molecule, which shifts the imide N 1s core level towards the pyridyl one and vice versa, consistently with the effects observed for the sister molecule PTCDI, perylenediimide (−1.7 binding energy shift of the imide peak).³³

Fig. 2 XPS of the N 1s peak measured at 515 eV for a sequence of molecular depositions; (a) DPNDI deposited at RT on TiO₂(110) at increasing coverage; (b) DPNDI (1.9 Å) deposited on Zn-TPP; (c) DPNDI (1.8 Å) on Cu-TPP; (d) DPNDI (1.5 Å) on Co-TPP. All the M-TPPs films have the same nominal coverage of 2.8 Å. The difference spectra between the DPNDI/M-TPP bilayer and the corresponding M-TPP layer are shown at the bottom of panels (b), (c), (d). All the spectra of panels (b), (c), (d) are rescaled to the same intensity range.

We took advantage of our former studies on the FeO substrate,¹³ for an appropriate calibration of the molecular coverage and stoichiometric ratio, which is made even simpler by the close matching of molecular density for the (5 × 5) and (2 × 4)-oblique monolayer phases formed by M-TPPs on FeO and TiO₂: 0.49 and 0.52 mol nm⁻², respectively (details in section S5 of ESI†). In order to avoid second layer porphyrins, that would automatically coordinate DPNDI at their out of plane axial site, the M-TPP coverage was limited to ∼0.95 ML (corresponding to a nominal thickness of 2.8 Å from the microbalance reading), even if this will yield a small amount of uncoordinated DPNDI. We recall that the conventional protocol of achieving M-TPP monolayer saturation by thermal desorption of a multilayer film, like on Fe(001)–p(1 × 1)O,¹³ is not viable on TiO₂(110). In fact, post growth annealing of M-TPPs on TiO₂(110) may lead to unwanted chemical reactions, as reported for free porphyrins beyond 370 K (from extraction of Ti interstitials^17,34 to cyclo-dehydrogenation¹⁷). In the monolayer range, M-TPPs are characterized by a single N 1s photoemission peak at a slightly variable binding energy of 398.1–398.5 eV, depending on the specific metal atom.¹⁶ We observed the presence of a residual N 1s component at ∼400.2 eV, corresponding to a pyrrolic contribution from contaminants (largest for Co-TPP), possibly associated with free-porphyrins residuals in the powders (more details in section S5 of ESI†). In the latter case, they would assume their diacidic form (4H-TPP) on TiO₂(110) and no iminic peak (∼398 eV) would be detected in the N 1s XPS.³⁵ Independently on their nature, such contaminants cannot bear coordination to pyridyl groups.

When depositing DPNDI, we aimed at a 1 : 1 stoichiometric ratio with the M-TPP amount in the overlayer, hence the nominal thickness was changed accordingly, as detailed in the caption of Fig. 2. The DPNDI overlayer yields a major peak in the N 1s spectrum, whose binding energy depends on the nature of the metal-porphyrin film. These core level shifts are accompanied by a change of shape of the superimposed DPNDI contribution, which is well evidenced by operating a simple difference between the DNPDI/M-TPP spectra and the corresponding M-TPP ones (shown at the bottom of panels (b), (c), (d) of Fig. 2). The difference spectra for Zn- and Co-TPP clearly show the presence of two well separated peaks, strongly resembling the imide and pyridyl peaks of the DPNDI multilayer. The difference spectra for Cu-TPP rather displays a majority component closely matching the single component observed in low coverage DPNDI films deposited directly on TiO₂(110). These evidences suggest a preferential DPNDI interaction with the surface when deposited on Cu-TPP, whereas Zn- and Co-TPP effectively decouple the DPNDI overlayer from the substrate.

The NEXAFS measurements at the N K-edge of the M-TPPs monolayer phase are shown in the panel (a) of Fig. 3, where the resonances corresponding to the π*-symmetry orbitals can be easily recognized in the p-polarization spectra: the lowest UMO (LUMO) at ∼398.5 eV and the characteristic porphyrin doublet at 400.5–401.5 eV. They display an almost perfect linear dichroism, where their intensities almost vanish in s-polarization, indicating a macrocycle orientation closely parallel to the surface. The reverse dichroism is observed for the main σ*-symmetry resonance at ∼406.5 eV, which is maximum in s-polarization. We remark that the small resonance observed in s-polarization at ∼398.5 eV for Co- and Cu-TPP is not a residual intensity of their π*-symmetry LUMO (as due to molecular distortion/tilt), but it is associated with a true σ*-symmetry resonance, characteristic of the planar tetra-coordination to nitrogen of the Cu(II) and Co(II) ions.^36–38

Fig. 3 NEXAFS at the N K-edge measured in p- and s-polarization (solid and dashed lines, respectively) with the surface [100] direction (the O_br rows) oriented parallel to the incoming photon beam. (a) The energy calibrated partial electron yield spectra are shown for the three M-TPP systems (red, green and blue lines for Cu-, Co- and Zn-TPP), and after DPNDI deposition (brown); the spectra are to scale and rigidly offset for a better comparison. (b) Reference NEXAFS of DPNDI directly grown on TiO₂(110) at two different thicknesses (2 and 20 Å) with the same color code of Fig. 2a; the spectra of the multilayer (black curves) have been multiplied by a factor 0.2 for better visual comparison; the corresponding DPNDI orientation is shown in the 3D drawings on the right side. (c) The DPNDI difference spectra obtained by subtraction of each M-TPP spectrum from the corresponding DPNDI/M-TPP one (same color code); all spectra are to scale and rigidly offset; the corresponding DPNDI orientation is represented in the 3D drawings on the right side.

In panel (b) of Fig. 3, we show the NEXAFS measured on a reference DPNDI multilayer that is dominated by a sharp π*-symmetry resonance at an energy of ∼398.7 eV, slightly larger than that of M-TPPs LUMO. This resonance may be associated with a molecular orbital localized on the pyridyl N atoms, while the imide N atom is in a nodal plane of the LUMO.³⁹ Two additional π*-symmetry resonances are clearly discriminated at 401.3 and 402.5 eV; these may be associated with the characteristic doublet predicted for PTCDI derivatives,⁴⁰ in good agreement with experimental reports of ∼401.5 eV for the leading NEXAFS resonance of PTCDI.³⁹ The poor linear dichroism of the DPNDI multilayer may be associated with a tendency to disordering rather than to a homogeneous tilt value of molecules (also see section S6 of ESI†). In the ML range, the NEXAFS is strongly modified by the large charge transfer from the substrate, which quenches the LUMO and shifts to lower energy the higher order UMO resonances. The corresponding linear dichroism indicates that DPNDI lays down on the surface with a small tilt angle. In addition, the residual intensity of the main resonance at ∼399 eV in s-polarization vanishes when measured with the electric field oriented along the substrate [001] direction, indicating that the molecular axis is strictly oriented along the O_br rows (section S6 of ESI†). This is a common orientation for polyconjugated (hetero)aromatic hydrocarbons on TiO₂(110), indeed (e.g. pentacene,⁴¹ PTCDA,⁴² PTCDI,⁴³ perylene^44,45).

When DPNDI is deposited on the Zn-TPP overlayer, the NEXAFS displays a dramatic change in s-polarization, where now a resonance peak can be detected, as intense as the Zn-TPP LUMO in p-polarization, but at slightly higher energy. Because of the close 1 : 1 stoichiometry, this experimental evidence indicates that DPNDI molecules are mostly oriented normal to surface, i.e. one pyridyl termination is coordinated to the Zn center with the DPNDI backbone standing up, as originally observed on the FeO substrate.¹³ The DPNDI/Co-TPP system also behaves similarly, but the corresponding linear dichroism is not as sharp as for DPNDI/Zn-TPP, likely due to the aforementioned larger amount of non-coordinating contaminants. In contrast to the above cases, only a minor increase of the low energy resonance in s-polarization is observed for the DPNDI/Cu-TPP pair, which excludes a standing up orientation, as well as the N_Py–Cu coordination.

For a better evaluation of the reversed DPNDI orientation on Cu-TPP with respect to Zn- and Co-TPP, we have normalized the NEXAFS spectra to the pre-edge linear background. Then we have subtracted the normalized M-TPP spectra from the normalized DPNDI/M-TPP ones, which yields the effective NEXAFS spectrum of the DPNDI overlayer (panel c) of Fig. 3. The average tilt angle obtained from these spectra cannot be directly associated with the actual orientation of coordinated DPNDI. In fact, apart from the indetermination associated with the spectra normalization and subtraction, even a small concentration of defects (such as the aforementioned contaminants and M-TPP coverage of ∼0.95 ML) on an otherwise flat molecular orientation may yield a nominal average tilt of 20–25°.⁴⁶ In the present case, deviation from a perfect dichroism should be rather considered as a measure of the degree of order. In this regard, we can get important physical information on the DPNDI overlayer from comparison of its NEXAFS lineshape with the reference DPNDI multilayer and ML spectra. First, the DPNDI overlayer on Zn-TPP displays in s-polarization the same spectral fine structure (satellite resonances) of the multilayer in p-polarization, consistently with the corresponding XPS difference spectra. On the contrary, the DPNDI overlayer on Cu-TPP rather resembles that of DPNDI ML (with characteristic satellite at ∼400.5 eV), and with the same dichroism: we can conclude that DPNDI does not adsorb on the Cu-TPP overlayer, but it is directly adsorbed on the TiO₂(110) surface, likely intercalated among porphyrins, in full agreement with indication from the photoemission difference spectra. Last, the DPNDI/Co-TPP spectra, which contain the largest fraction of non-coordinating pyrrolic contaminants, present a mix of both configurations: a DPNDI multilayer fine structure is clearly observed in s-polarization, as due to DPNDI molecules axially coordinated to Co-TPP; conversely, the fine structure of DPNDI ML is rather exhibited in p-polarization, as due to uncoordinated DPNDI adsorbed on the surface, instead of above metal-free porphyrins.

We investigated in better detail the mechanism of pyridyl ligand to metal ion coordination at the surface by DFT calculations of the equilibrium configuration of model Pyridine/M-TPP adducts on the TiO₂(110). As formerly found, M(II)-TPPs (M = Co, Zn, Cu, Ni) offer the computational advantage of adopting the same (2 × 4)-oblique phase symmetry and molecular orientation as 2H/4H-TPP (with two opposite nitrogen atoms aligned on the O_br rows, hereafter labelled R0°).¹⁶ Thus, we adopted the same supercell used in ref. 34 for modeling the Py/M-TPP^ads interaction (10 unit cells with 6-layers slab).

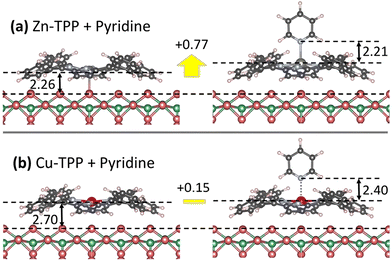
When compared to isolated M-TPPs (21 unit cells), the present results show a slight stabilization for adsorption on O_br rows (section S3 of ESI†), which are ascribed to stronger/additional surface-ligand and/or ligand–ligand van der Waals interactions. The stabilization is larger for the O_br top site, which remains the preferred one for Co- and Zn-TPP, whereas no clear site preference can now be predicted for Ni-TPP and Cu-TPP (the O_br bridge site was rather preferred for isolated molecules). For the sake of simplicity, we considered adsorption on the top site also for Cu- and Ni-TPP, even though no significant Cu–O_br and Ni–O_br interactions are present. A study of the azimuthal orientation of the pyridine plane (R = 0°, 45°, 90°) on the (2 × 4)-oblique adsorbed phase of Zn-TPP (hereafter denominated Zn-TPP^ads phase) yielded a slight preference (0.01–0.02 eV) for the R0° case, which was then adopted also for the other pyridine/M-TPP^ads systems. Results, reported in Table 1, show that pyridine interacts more strongly with Co- and Zn-TPP^ads with respect to the Ni- and Cu-TPP^ads ones by 0.2–0.3 eV. Remarkably, the net interaction with the adsorbed species Co- and Zn-TPP^ads is slightly lower with respect to what found in the gas phase, the opposite is true for Ni- and Cu-TPP^ads.

Table 1 Pyridine/M-TPP binding energy and axial site distances

	E b(Py/M-TPP) [eV]		d(M–Obr) [Å]		d(M–N^Py) [Å]
	Ads.^a	Gas phase	Py/M-TPP^a	M-TPP^a	Ads.^a	Gas phase
a Calculated for the (2 × 4)-oblique phase.
Co-TPP	−0.86	−0.99	2.92	2.29	2.23	2.11
Zn-TPP	−0.77	−0.78	3.03	2.26	2.21	2.19
Cu-TPP	−0.57	−0.45	2.85	2.70	2.40	2.33
Ni-TPP	−0.52	−0.26	2.87	2.71	2.38	2.48

---

A rationale for the above findings can be proposed by comparing the structural data of Table 1, which show that the formation of the pyridine/M-TPP^ads adducts causes a large elongation (0.7–0.8 Å) of the pristine M–O_br distance in the case of Co- and Zn-TPP^ads, whereas the distance is much less affected for the Ni- and Cu-TPP^ads cases (see drawings in Fig. 4). This shows that the formation of the Py–M bond causes a disruption of the M–O_br bond by a surface trans effect,⁴⁷ which explains the net reduction of the formation energy computed for the pyridine/M-TPP adduct. This effect is counterbalanced by a general increase of the other interactions (e.g. van der Waals) between pyridine and M-TTP, when passing from the unsupported to the supported species, as revealed by a comparison of the E_b and ^adsE_b for the Ni and Cu compounds. This may be due to the saddle deformation of the porphyrin structure, which shortens the distances between pyridine and some parts of the TPP ligand. These two opposite effects nearly compensate in the cases of Co- and Zn-TPP^ads, whereas the ^adsE_b increase observed in the Cu- and Ni-TPP^ads systems is due to the weakness of the M–O_br interactions.

Fig. 4 Side views of (a) Zn-TPP^ads before (left) and after (right) coordination to pyridine, (b) same for Cu-TPP^ads; the yellow arrow in (a) highlights the lifting of Zn by surface trans effect, which is absent for Cu in (b). Distances are in Ångstrom.

The pyridine model is no longer appropriate to account for the van der Waals interactions of the DPNDI scaffold, which displays a preferential coupling to the TiO₂(110) surface, witnessed by the charge transfer into the LUMO of contact molecules. On the contrary, DPNDI hanging up at Zn- and Co-TPP^ads displays the pristine electronic structure of molecules in a multilayer (close to the gas phase ones), with one additional pyridyl termination protruding vertically out of the surface for further M-TPP axial coordination, like originally found on the passivated Fe(100)–p(1 × 1)O surface. As formerly demonstrated for Zn-TPP on FeO,¹³ as well as for Fe-octaethylporphyrin on Au(111),⁴⁸ the axial coordination of either a pyridinic or an aminic linker does not affect the lateral molecular ordering. By appropriate choice of the metal in the next layer macrocycles (with one or two axial sites), one may add further units to the laterally coherent film or terminate the film with a capping Zn-TPP layer.¹³ In comparison with growth from solution, our in-vacuum layer-by-layer approach can yield coordination polymers only extending for a few bilayers. However, it combines the advantage of vertical growth with that of spatial coherence. We may draw a parallelism with conventional heteroepitaxial growth, where the strength of either covalent or metallic bonding allows to compensate the accumulation of in-plane energy strain for hundreds (semiconductors) or tens (metals) of layers. Here, the same arguments may be translated into a local (molecular) perspective, where the in-plane steric repulsion among peripheral terminations is opposed to the axial coordination bond, much weaker than the covalent/metallic one.

Conclusions

We have demonstrated that it is possible to grow in vacuum vertically coordinated DPNDI on a few selected M-TPPs (namely Zn- and Co-TPP), even when adsorbed on a very reactive substrate like TiO₂(110). One pyridine end is bound to the N-chelated metal cation, while the dangling symmetric N-ligand provides the coordination site to achieve a step-by-step vertical growth of coordination polymers with laterally homogeneous layer composition, as well as regular lateral spacing thanks to the long range order of the M-TPP^ads basal planes. The molecule-on-molecule chemical link also simplifies the theoretical modeling of the film and the corresponding calculation of charge transport properties. One may further envisage the intercalation of different metal-porphyrins (even Cu- and Ni-TPP, once decoupled from the substrate), as well as different bifunctional molecular compounds. Most importantly, the intra-layer periodicity may trigger the coherent enhancement of specific electronic properties and transitions. Finally, alternative functionalization at the dangling end of the docking molecule might be exploited to develop specific interaction with third layer molecules, providing a high density of reaction sites. In this regard, the porphyrin–TiO₂ interface represents an optimal substrate for integration into sensor devices, especially in ambient and bio-related environments. In perspective, the substitution of the porphyrin peripheral terminations may allow to exploit steric effects to drive an azimuthal reorientation of the macrocycle in the termination layer, or to tailor its axial site for further reactions.

Author contributions

LS, GB: methodology, investigation, data analysis, writing-review & editing. CG, CO: investigation. AG: conceptualization. AC: methodology, writing-review & editing. AB: methodology. GB, AOB: conceptualization, writing-review & editing. AV: supervision, conceptualization, validation, methodology, formal analysis, writing-original draft. LF: supervision, conceptualization, validation, methodology, data analysis, writing-original draft. All authors have read and agreed to the published version of the manuscript.

Data availability

XPS and NEXAFS spectral data are available at Open Science Framework at https://osf.io/9qsut/?view_only=baba4a94e0624e11b31d6cb4f99fa639.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

AC gratefully acknowledge the financial support from the European Union – Next Generation EU, PNRR - M4C2, investment 1.1, and Fondo PRIN 2022, within project ‘Functionalized Surfaces by True Molecular Bottom-Up Growth’ (FUTURO), ID 2022FWZCHK, CUP D53D23009110006. AOB acknowledges support from the Ministero dell'Università e della Ricerca (MUR) and the University of Pavia through the program “Dipartimenti di Eccellenza 2023–2027”. AV acknowledges the financial support from Next Generation EU from the Italian Ministry of Environment and Energy Security POR H2 AdP MMES/ENEA with involvement of CNR and RSE, PNRR - Mission 2, Component 2, Investment 3.5 “Ricerca e sviluppo sull'idrogeno”, CUP: B93C22000630006. AV acknowledges the computational resources of the C3P (Computational Chemistry Community in Padua) HPC facility of the Department of Chemical Sciences of the University of Padua.

References

1. T. Kojima, T. Honda, K. Ohkubo, M. Shiro, T. Kusukawa, T. Fukuda, N. Kobayashi and S. Fukuzumi, Angew. Chem., Int. Ed., 2008, 47, 6712–6716.
2. S. Fukuzumi, T. Honda, K. Ohkubo and T. Kojima, Dalton Trans., 2009, 3880–3889.
3. M. E. El-Khouly, A. M. Gutiérrez, Á. Sastre-Santos, F. Fernández-Lázaro and S. Fukuzumi, Phys. Chem. Chem. Phys., 2012, 14, 3612–3621.
4. N. Xin, J. Guan, C. Zhou, X. Chen, C. Gu, Y. Li, M. A. Ratner, A. Nitzan, J. F. Stoddart and X. Guo, Nat. Rev. Phys., 2019, 1, 211–230.
5. B. Kim, C. Cho, I. Arfaoui, C. Paris, C. Petit, T. Le Bahers, E. Kim and A. J. Attias, Mater. Horiz., 2020, 7, 2741–2748.
6. Q. Fernez, S. Moradmand, M. Mattera, W. Djampa-Tapi, C. Fiorini-Debuisschert, F. Charra, D. Kreher, F. Mathevet, I. Arfaoui and L. S. Vargas, J. Mater. Chem. C, 2022, 10, 13981–13988.
7. J. M. Gottfried, Surf. Sci. Rep., 2015, 70, 259–379.
8. M. Müller, J. Ikonomov and M. Sokolowski, Surf. Sci., 2011, 605, 1090–1094.
9. A. Carrera, L. J. Cristina, S. Bengió, A. Cossaro, A. Verdini, L. Floreano, J. D. Fuhr, J. E. Gayone and H. Ascolani, J. Phys. Chem. C, 2013, 117, 17058–17065.
10. G. Bussetti, A. Calloni, M. Celeri, R. Yivlialin, M. Finazzi, F. Bottegoni, L. Duò and F. Ciccacci, Appl. Surf. Sci., 2016, 390, 856–862.
11. A. Picone, D. Giannotti, A. Brambilla, G. Bussetti, A. Calloni, R. Yivlialin, M. Finazzi, L. Duò, F. Ciccacci, A. Goldoni, A. Verdini and L. Floreano, Appl. Surf. Sci., 2018, 435, 841–847.
12. G. Fratesi, S. Achilli, A. Ugolotti, A. Lodesani, A. Picone, A. Brambilla, L. Floreano, A. Calloni and G. Bussetti, Appl. Surf. Sci., 2020, 530, 147085.
13. A. Orbelli Biroli, A. Calloni, A. Bossi, M. S. Jagadeesh, G. Albani, L. Duò, F. Ciccacci, A. Goldoni, A. Verdini, L. Schio, L. Floreano and G. Bussetti, Adv. Funct. Mater., 2021, 31, 1–7.
14. A. Y. Robin and K. M. Fromm, Coord. Chem. Rev., 2006, 250, 2127–2157.
15. M. Urbani, M. Grätzel, M. K. Nazeeruddin and T. Torres, Chem. Rev., 2014, 114, 12330–12396.
16. L. Schio, G. Bavdek, C. Grazioli, C. Gutiérrez Bolaños, A. Goldoni, A. Vittadini, M. Tormen and L. Floreano, Appl. Surf. Sci., 2023, 616, 156548.
17. G. Lovat, D. Forrer, M. Abadia, M. Dominguez, M. Casarin, C. Rogero, A. Vittadini and L. Floreano, J. Phys. Chem. C, 2017, 121, 13738–13746.
18. L. Schio, D. Forrer, M. Casarin, A. Goldoni, C. Rogero, A. Vittadini and L. Floreano, Phys. Chem. Chem. Phys., 2022, 24, 12719–12744.
19. A. Greenwood and N. N. Earnshaw, Chemistry of the Elements, Elsevier, 1997.
20. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
21. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
22. V. Barone, M. Casarin, D. Forrer, M. Pavone, M. Sambi and A. Vittadini, J. Comput. Chem., 2009, 30, 934–939.
23. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
24. D. V. Konarev, A. L. Litvinov, I. S. Neretin, N. V. Drichko, Y. L. Slovokhotov, R. N. Lyubovskaya, J. A. K. Howard and D. S. Yufit, Cryst. Growth Des., 2004, 4, 10–13.
25. J. Cremers, S. Richert, D. V. Kondratuk, T. D. W. Claridge, C. R. Timmel and H. L. Anderson, Chem. Sci., 2016, 7, 6961–6968.
26. C. J. Kingsbury and M. O. Senge, Coord. Chem. Rev., 2021, 431, 152–160.
27. E. B. Fleischer, C. K. Miller and L. E. Webb, J. Am. Chem. Soc., 1964, 86, 2342–2347.
28. P. Madura and W. R. Scheldt, Inorg. Chem., 1976, 15, 3182–3184.
29. E. D. Stevens, J. Am. Chem. Soc., 1981, 103, 5087–5095.
30. W. R. Scheidt and I. Turowska-tyrk, Inorg. Chem., 1994, 33, 1314–1318.
31. J. Stöhr, NEXAFS Spectroscopy, Springer Berlin Heidelberg, Berlin, Heidelberg, 1992, vol. 25.
32. A. Ravikumar, G. Kladnik, M. Müller, A. Cossaro, G. Bavdek, L. L. Patera, D. Sánchez-Portal, L. Venkataraman, A. Morgante, G. P. Brivio, D. Cvetko and G. Fratesi, Nanoscale, 2018, 10, 8014–8022.
33. V. Lanzilotto, G. Lovat, G. Fratesi, G. Bavdek, G. P. Brivio and L. Floreano, J. Phys. Chem. Lett., 2015, 6, 308–313.
34. M. K. Kremer, D. Forrer, C. Rogero, L. Floreano and A. Vittadini, Appl. Surf. Sci., 2021, 564, 150403.
35. G. Lovat, D. Forrer, M. Abadia, M. Dominguez, M. Casarin, C. Rogero, A. Vittadini and L. Floreano, Phys. Chem. Chem. Phys., 2015, 17, 30119–30124.
36. D. G. De Oteyza, A. Sakko, A. El-Sayed, E. Goiri, L. Floreano, A. Cossaro, J. M. Garcia-Lastra, A. Rubio and J. E. Ortega, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075469.
37. M. V. Nardi, F. Detto, L. Aversa, R. Verucchi, G. Salviati, S. Iannotta and M. Casarin, Phys. Chem. Chem. Phys., 2013, 15, 12864–12881.
38. A. Calloni, M. S. Jagadeesh, G. Bussetti, G. Fratesi, S. Achilli, A. Picone, A. Lodesani, A. Brambilla, C. Goletti, F. Ciccacci, L. Duò, M. Finazzi, A. Goldoni, A. Verdini and L. Floreano, Appl. Surf. Sci., 2020, 505, 144213.
39. J. Taborski, P. Väterlein, H. Dietz, U. Zimmermann and E. Umbach, J. Electron Spectrosc. Relat. Phenom., 1995, 75, 129–147.
40. B. Mukherjee and M. Mukherjee, ACS Omega, 2017, 2, 9181–9190.
41. V. Lanzilotto, C. Sanchez-Sanchez, G. Bavdek, D. Cvetko, M. F. Lopez, J. A. Martin-Gago and L. Floreano, J. Phys. Chem. C, 2011, 115, 4664–4672.
42. L. Cao, Y. Wang, J. Zhong, Y. Han, W. Zhang, X. Yu, F. Xu, D. C. Qi and A. T. S. Wee, J. Phys. Chem. C, 2011, 115, 24880–24887.
43. V. Lanzilotto, G. Lovat, G. Otero, L. Sanchez, M. F. López, J. Méndez, J. A. Martín-Gago, G. Bavdek and L. Floreano, J. Phys. Chem. C, 2013, 117, 12639–12647.
44. G. Fratesi, V. Lanzilotto, S. Stranges, M. Alagia, G. P. Brivio and L. Floreano, Phys. Chem. Chem. Phys., 2014, 16, 14834–14844.
45. G. Otero-Irurueta, J. I. Martínez, G. Lovat, V. Lanzilotto, J. Méndez, M. F. López, L. Floreano and J. A. Martín-Gago, J. Phys. Chem. C, 2015, 119, 7809–7816.
46. L. Floreano, A. Cossaro, R. Gotter, A. Verdini, G. Bavdek, F. Evangelista, A. Ruocco, A. Morgante and D. Cvetko, J. Phys. Chem. C, 2008, 112, 10794–10802.
47. W. Hieringer, K. Flechtner, A. Kretschmann, K. Seufert, W. Auwärter, J. V. Barth, A. Görling, H. P. Steinrück and J. M. Gottfried, J. Am. Chem. Soc., 2011, 133, 6206–6222.
48. Z. Wang, K. Qian, M. A. Öner, P. S. Deimel, Y. Wang, S. Zhang, X. Zhang, V. Gupta, J. Li, H. J. Gao, D. A. Duncan, J. V. Barth, X. Lin, F. Allegretti, S. Du and C. A. Palma, ACS Appl. Nano Mater., 2020, 3, 11752–11759.

---

Footnotes

† Electronic supplementary information (ESI) available: A single pdf file is provided with sections: S1. DFT calculations; S2. pyridine/M-TPP adducts in Gas phase; S3. M-TPP^ads in the (2 × 4)-oblique phase; S4. experimental methods: XPS and NEXAFS; S5. sample preparation; S6. characterization of DPNDI on TiO₂(110); S7. characterization of bipyridine on TiO₂(110). See DOI: https://doi.org/10.1039/d4nr01309c

‡ These two authors contributed equally to the manuscript.

---