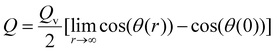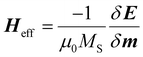DOI:
10.1039/D4NR01003E
(Paper)
Nanoscale, 2024,
16, 12431-12444
Multilayer ferromagnetic spintronic devices for neuromorphic computing applications†
Received
9th March 2024
, Accepted 3rd June 2024
First published on 3rd June 2024
Abstract
Based on ferromagnetic thin film systems, spintronic devices show substantial prospects for energy-efficient memory, logic, and unconventional computing paradigms. This paper presents a multilayer ferromagnetic spintronic device's experimental and micromagnetic simulation-based realization for neuromorphic computing applications. The device exhibits a temperature-dependent magnetic field and current-controlled multilevel resistance state switching. To study the scalability of the multilayer spintronic devices for neuromorphic applications, we further simulated the scaled version of the multilayer system read using the magnetic tunnel junction (MTJ) configuration down to 64 nm width. We show the device applications in hardware neural networks using the multiple resistance states as the synaptic weights. A varying pulse amplitude scheme is also proposed to improve the device's weight linearity. The simulated device shows an energy dissipation of 1.23 fJ for a complete potentiation/depression. The neural network based on these devices was trained and tested on the MNIST dataset using a supervised learning algorithm. When integrated as a weight into a 3-layer, fully connected neural network, these devices achieve recognition accuracy above 90% on the MNIST dataset. Thus, the proposed device demonstrates significant potential for neuromorphic computing applications.
Introduction
Spintronic devices have gained a lot of interest for their application in high-integration data storage and energy-efficient computing applications.1–6 In particular, owing to different operating behaviors such as binary deterministic,7–9 stochastic,10–13 and analog resistance,14,15 these devices are proving to be quite promising for neuromorphic computing applications. Magnetic domain wall and skyrmion devices as alternate analog memory16–18 and logic technology19,20 have been explored for their applications in neuromorphic computing.21–23 To stabilize room temperature skyrmions and domains, spintronic perpendicular magnetic anisotropy PMA-based magnetic multilayer systems have been extensively studied from materials and physical perspectives.24–27 These systems are used to study the domain wall and skyrmions dynamics in different magnetic materials and their interface with other heavy metals.28–30 Also, recently, some of the works have shown discrete resistance in different ferromagnetic systems31–34 Considering the interesting physical phenomenon in these systems and, thus, the associated emerging device characteristics, it becomes interesting to explore these systems’ magnetic and electrical characteristics for unconventional computing and memory applications. This paper presents a spintronic device's experimental and micromagnetic realization exhibiting discrete resistance states. The discreteness of the device behavior increases as we lower the temperature, and for 100 K temperature, 15 resistance states are observed. We attribute this discrete resistance behavior to the magnetic domain wall pinning/depinning and gradual switching of different magnetic layers at low temperatures. The discrete resistance behavior is also observed in the micromagnetic simulations of similar crossbars of different widths. Furthermore, we show the multi-step resistance switching with current pulses, which generate the spin transfer and spin–orbit torque on the domain walls. Using the multi-level resistance state of the device, we propose its applications as a synaptic device in hardware neural networks and study the linearity performance of the synaptic devices. We map these resistance states to the weights of a neural network architecture. The network based on these devices was trained and tested on the MNIST dataset using a supervised learning algorithm. The system shows accuracy performance up to 90%, comparable to most beyond CMOS synaptic devices. Furthermore, the discrete resistance states at low temperatures also open the possibility of these devices being applied in cryogenic electronics for quantum computers.
Results and discussion
The fabricated crossbar spintronic devices based on the magnetic heterostructure are shown in Fig. 1(a). The device consists of the [Ta(2)/CoFeBt(0.9)/MgO(2)]20-based multilayer magnetic hall bar devices patterned on Si/SiO2 with gold contacts. The area of these fabricated devices is in the 2 μm × 50 μm–3 μm × 50 μm range. The contacts were put on the lateral sides of the magnetic crossbar to provide the voltage from the pulse generator into one of the crossbar legs. At the same time, the resistance was measured across the transverse arm using a standard PPMS set-up and an oscilloscope. The 2 nm thick MgO dielectric allows a tiny tunneling current. The multilayer device structure can be considered 20 magnetization-dependent resistors in parallel, as shown by the equivalent resistor model in Fig. 1(b). The scanning electron microscopy image of the Hall bar is shown in Fig. 1(c). The magnetization of the magnetic layers is changed by the external magnetic ranging from −650 mT to 650 mT. Fig. 1(d) shows the MFM image of the device at room temperature and 0 Oe field; we observed an unperturbed multi-domain magnetic texture with stripe domains. Since the width of the Hall bar is 2 μm and based on the thin film magnetic stack, we expect stabilization of the Néel-type domain wall having a width of around 20 nm as revealed by micromagnetic simulations shown in Fig. 4. MFM was performed on the full stack, but we believe that in Fig. 1(d), the major contribution to the observed magnetization texture is coming predominantly from the top layer, which is closer to the MFM tip. Hall measurements were performed using the standard lock-in technique. As shown in Fig. 2, we observed discrete anomalous Hall resistance. The magnetic anisotropy and saturation magnetization are small for room temperature samples. Thus, all magnetic layers switch at lower fields. At 300 K, the magnetization switches at 21 mT for the positive and 19 mT for the negative magnetic fields.
 |
| | Fig. 1 (a) Domain wall crossbar devices. (b) Equivalent resistor model. (c) Scanning electron microscopy (SEM) image of the device. (d) Magnetic force microscopy (MFM) image at 0 Oe and 300 K. | |
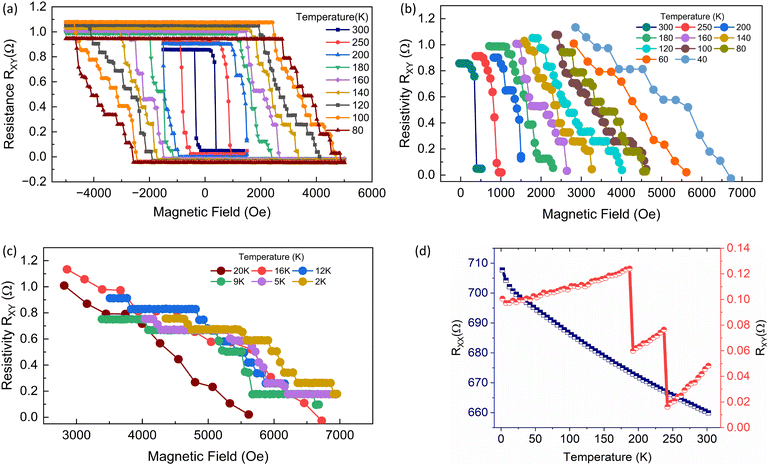 |
| | Fig. 2 (a–c) Discrete anomalous Hall resistances at different temperatures (2 K to 300 K). (d) Longitudinal and anomalous Hall resistances at different temperatures. | |
As the temperature is lowered, the switching field increases, and switching becomes more gradual, with each resistance state separated by discrete steps. The discrete behavior and gradual switching are attributed to the saturation magnetization and anisotropy increases upon lowering the temperature. This increases the stray field effects and the domain wall pinning to the edges. The thermal effects are high, which reduces the domain wall pinning effect at this temperature. We observed discrete resistance states as all magnetic layers switch simultaneously at a 40 mT magnetic field. As we lower the temperature, the anisotropy and saturation magnetization increase, which increases the switching field and the stray field effect on different layers. Moreover, the thermally activated depinning is lowered, resulting in more discrete states, as shown in Fig. 2(a–c). For the temperature T = 120 K, we obtained 11 discrete resistance states, as shown in Fig. 2(b). In the anomalous Hall measurement technique, the ON/OFF ratio or memory window obtained for the devices is around 66, which is quite better compared to other spintronic devices where the ON/OFF ratio is around 3.
In Fig. 2(a–c), we show the magnetic hysteresis loop measurement at varying temperatures with a magnetic field step size of 60 Oe. The measurements reveal interesting temperature-dependent characteristics; the discrete resistance states increase with lowering temperature. At 300 K, 2 binary resistance states are observed; at 250 K, 3 resistance states were observed; 4 states at 200 K, 8 states at 150 K, and 11 states at 120 K were observed. Below 120 K temperature, the value of net Hall resistance decreases significantly; thus, the number of resistance states decreases. However, the resistance step width is increased at lower temperatures, making the states more stable. We measured 8 states for 80 K, then again 11 states for 20 K and 6 for 2 K, as shown in Fig. 2(c and d). This behavior can be explained by lowering temperatures that lower the thermal effects and increase saturation magnetization. This results in discrete switching due to pinning/depinning effects added to individual layers switching independently. However, anisotropy is also found to increase; thus, on the one hand, the number of states should increase, but the increased anisotropy stabilizes the multilayer structure; therefore, magnetic layers start switching together, which results in a reduced number of states as observed in Fig. 2(c). In Fig. 2(d), the temperature dependence of Rxx and Rxy is shown. In Fig. 2(d), we have shown the temperature dependence of the longitudinal resistivity Rxx and Hall resistivity Rxy. The resistivities were measured by passing a current (70 μA) through the longitudinal arm of the device, and the Hall voltage/resistance was measured simultaneously across both the arms (Rxx and Rxy). The magnetic field was kept at 1000 Oe and the temperature was varied from 2 K to 300 K. This measurement helps in determining the role of different physical scatterings in the anomalous Hall conductivity of the sample. The approximate σxx ≅ 4.22 kΩ cm−1 indicates a bad metal behavior. Furthermore, in our device measurements, Rxx increases with lowering temperature, which is expected in Ta/CoFeB/MgO systems, but the temperature vs. Rxy characteristics are different from normal single Ta/CoFeB/MgO systems. Overall, we observed that Rxy increases with lowering temperature, which is expected as shown in ref. 35. In addition to normal characteristics, we observed this increasing trend in discrete steps. We attribute this behavior to the increasing stray field effects with lowering temperature, which results in strong DW pinning, as also observed in Fig. 2(a–c). Please note that apart from the DW pinning effects, we can't rule out other localization and scattering effects in the system.
To investigate the scalability of the proposed device for neuromorphic computing applications. We furthermore simulated similar and scaled crossbars in the micromagnetic software MuMax.36,37 The simulation parameters, such as saturation magnetization and anisotropy, were taken from the experimental results (VSM). Table 1 in the Methods section gives the parameters and simulation details, we considered the crossbar nanotrack width from 100 nm to 300 nm in intervals of 50 nm. When perturbed by an external magnetic field ranging from −5000 Oe to 5000 Oe, we observed discrete magnetization switching for all the nanotrack widths. The discrete magnetization behavior is most dominant for the lowest width W = 100 nm. Five stable discrete magnetization states were observed for the nano track length L = 1 μm, as shown in Fig. 3(a). As the width increases, the magnetization discrete switching behavior starts fading. Although four discrete states are observed for W = 250 nm, the switching field gap between the states is reduced. In 250 nm, the magnetization switching is gradual, whereas in the 100 nm nanotrack, the magnetization switches in sharp steps, as shown in Fig. 3(a).
 |
| | Fig. 3 (a) Discrete magnetization switching of the crossbar of different widths. (b) MFM images showing DW pinning to edges. | |
Table 1 Details of simulated parameters
| Grid size |
Cell size (nm) |
Anisotropy, 
(J m−2) |
Saturation mag, Ms (A m−1) |
Exchange stiffness, 
(J m−1) |
DMI, 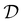
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41 (J m−2) 41 (J m−2) |
IEC, 
(J m−2) |
α
H
|
|
X is the number of layers. |
| 256, 64, X1 |
2, 2, 0.8 |
0.9 × 106 |
0.8 × 106 |
1.5 × 10−11 |
1.0 × 10−12 |
5 × 10−13 |
0.15 |
In the corresponding magnetization textures obtained from the simulations, we observed switching from stipe domains to stable skyrmions as the field changes. Fig. 4(a) shows the magnetization profile of the single FM layer at the different switching points. At zero magnetic field, the stripe domains are pinned to the track edges; by applying the external magnetic field in the Z-axis, we observed the depinning and stabilization of the skyrmions. The numbers [(1)–(6)] show the discrete switching points, as shown in Fig. 4(a). For cases (1), (2), and (3), we see normalized magnetization switching from 0 to 0.7, while from (4) to (6), the normalized magnetization reaches a value of 0.9. Corresponding to switching points (1), (2), and (3), we observed the depinning and conversion of stripe domains into the skyrmions. This accounts for the maximum change (about 77%) in the magnetization of the device. After switching point (3), the skyrmions are stable, and the external field reduces the size of the skyrmions as seen in the corresponding texture in Fig. 4(a)[(4)–(6)] and (b). This increases the magnetization linearly, and the overall change is about 23%. The skyrmion radius calculated using nearest linear interpolation reduces gradually from R = 10.92 nm to R = 4.64 nm.
 |
| | Fig. 4 (a) Repeatability of the discrete magnetization behavior with applying one ns magnetic field pulses. (b) Magnetization texture through the hysteresis loop shows switching occurring via stripe domain conversion into skyrmions. | |
A magnetic field ranging from −5000 Oe to 5000 Oe was applied perpendicular to the device. The Néel skyrmions with polarity +1 are stabilized from the stripe domain phase in the favorable field regime. While reducing the field from high to low, skyrmioniums are stabilized in the Hall bar, stabilizing to skyrmion polarity −1 as we increase the field in the z-direction. Depending on the direction of the magnetic field, the skyrmions change the polarity from +1 to −1 and vice versa (see ESI SV1† and Fig. 4). The experimental MFM images of the fabricated device and the micromagnetic MFM images of the scaled device are shown in Fig. 3(b) (bottom). Clearly skyrmion/domains are pinned to the device's edges in both cases.
Multilayer spintronic synapse
We repeated the hysteresis simulation to check the feasibility of using these multilayer spintronic devices as synapses. As shown in Fig. 5, the measurement was repeated three times for different temperatures to check the repeatability of the discrete resistance behavior shown by the crossbar. We observed the pinning/depinning behavior; thus, discrete resistance states are shown in Fig. 6(a) for temperatures 300 K, 250 K, and 120 K. Apart from a minor deviation in the value of depinning fields, discrete states are observed during all the measurement cycles. In neuromorphic computing applications, repeated potentiation/depression of a synaptic device is needed. For temperature T = 120 K, Fig. 6(b and c) shows a repeated increase (depression) or decrease (potentiation) of device resistance by the magnetic field. We observed the repeated and reliable discrete resistance switching. These results show the possibility of employing this device as a multi-bit memory or synapse for neuromorphic computing applications. However, controlling a spintronic device with a magnetic field is not scalable. Thus, realizing a device with current-controlled resistance states for circuit and system-level neuromorphic computing implementation becomes imperative. In Fig. 6(d), we show the magnetic field-assisted current-controlled switching of the multilayer stack. We applied the current pulses with a pulse width of 500 μs across the terminals T1 and T2. After each current pulse, the resistance was measured 4 times during each cycle across the terminals T3 and T4. We obtained up to 4 discrete resistance states at 300 K by biasing the device at a particular point on RH hysteresis. Thus, the device provides transistor-like behavior, qualifying it as a memtransistor. Combining the dual (field and current) control ability allows the device to be used as a memristor with transistor properties in a crossbar array. We also simulated the repeatability measurement for the nano-track width W = 100 nm in MuMax. The measurement was repeated six times when the magnetic field was limited to 0 to 3000 Oe, and the discrete behavior was observed throughout six cycles. The devices show hysteresis, indicating a memory effect, but we observed some randomness in the hysteresis cycles as shown in ESI (a)† [cycles 1 to 6].
 |
| | Fig. 5 (a) Micromagnetic texture of the 20-layer stack. | |
 |
| | Fig. 6 (a) Anomalous Hall resistance for T = 300 K, 250 K, and 120 K (repeated three times). (b and c) Discrete resistances at positive and negative field ranges (T = 120 K) and (d) field-assisted current-controlled multi-level resistance switching. | |
The repeatability of the discrete resistance indicates the potential application of the device as a synapse in neural networks. Where the probability of the stochastic behavior is controlled by the (a) temperature, (b) pinning distribution, and (c) external field/current. We also show the evolution of skyrmion topological charge during the different phases. For the first two cycles of pulse number (50), the topological charge increases from 0 to −28; skyrmion density varies between −28 and −20. This shows the magnetization contribution from the skyrmions during the potentiation/depression. We observed the conversion of labyrinth domains into skyrmions throughout the cycles, as shown in the ESI video [SV1].† For a futuristic application in neuromorphic computing, the scalability of these devices will play a crucial role in increasing storage density and simultaneously reducing energy consumption. Also, to increase the output signal, the best reading method is tunnel magnetoresistance. So, to demonstrate these devices’ scalability and improve the output signal, we further simulated the current response of the multilayer devices with 15 layers and 20 layers. The device was pulsed with current pulses of a width of 1 ns and a current density of 5 × 1011 A m−2. The SOT generated by these pulses drives the domain wall motion, resulting in the free layer magnetization switching. We observed the synaptic potentiation/depression emulated by the device regarding the magnetization profile. The resistance of the device depends on the magnetization profile
| | | ρxy = ρ0 + ρA + ρT = ROB + RSμ0MZ + ROPBemZ | (1) |
where
ρ0 is the ordinary Hall resistivity, which has negligible contribution in the magnetic materials, and the second is the anomalous Hall resistivity. The third term represents the topological Hall resistivity added by the skyrmions and it can be considered to have a minimal contribution.
The emergent magnetic field is given by,38
| |  | (2) |
leading to topological resistivity
| |  | (3) |
The other method of reading the device is by tunnel magnetoresistance TMR. Depending on the magnetization profile, the resistance of the MTJ is given by39
| |  | (4) |
where
RAP/
RP are the antiparallel/parallel resistances and
![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif)
/
![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) P
P is the free layer/pinned layer normalized magnetization.
In micromagnetic simulations, the current pulses with amplitude Jc = −5 × 1011 A m−2 push the domain wall in the +x direction, whereas the DW motion direction is reversed for Jc = +5 × 1011 A m−2. Depending on the DW position, the device's net magnetization varies, leading to a variation in its resistance. Depending on the reading mechanism AHE [eqn (1)], we computed the resistance by mapping magnetization to the measured resistance. We further consider the TMR [eqn (4)] reading to compute the synapse conductance evolution. The magnetization potentiation/depression of the 15-layer and 20-layer synaptic device with current pulses is shown in Fig. 7(a and b). When the DW starts moving away from the left edge, we observed fast magnetization evolution at the beginning because the DW is going away from the edge, which results in reduced demagnetization energy density, thus increasing the DW velocity. As the DW reaches the center it reaches a minimum and with a more current pulse, the demagnetization energy starts gradually increasing until we reverse the current; this results in a sudden decrease in the demagnetization energy due to the formation of a full Bloch DW in the perpendicular direction, as shown in Fig. 7(d and e). On the application of Jc = −5 × 1011 A m−2, the demagnetization energy is minimized by the twist in the perpendicular axis, and we observed that the bottom 10 layers are stable. In contrast, the top 10 layers form an incomplete Bloch DW. For Jc = +5 × 1011 A m−2, the DW gains full rotation, and more layers flip such that the first 6–7 bottom layers are stable and the remaining 13 layers form a full Bloch DW, as clearly depicted in the contour plot of the cross-section in Fig. 8.
 |
| | Fig. 7 (a) Normalized magnetization evolution and associated demagnetization energy explaining the behavior of DW motion. (b) SOT-controlled DW synapse: magnetization profile (potentiation/depression) in 15-layer and 20-layer devices (micromagnetic). (c) DW shape during negative and positive currents explains the sudden drop in demagnetization energy on current reversal. (d)–(f) Current-controlled synapse (measured). | |
 |
| | Fig. 8 Contour depiction of the magnetization vector within the magnified cross-sectional region of (a) 10 layers and (b) 20 layers. | |
This results in a reduced demagnetization energy and an increased DW velocity. Furthermore, for the 20-layer device, we observed fast switching, which indicates increased DW velocity, in comparison with the 15-layer device [see Fig. 7(b)]. This phenomenon is explained by the inset Fig. 7(b); interestingly, we observed the lowering of the demagnetization energy with increasing number of FM layers. Due to the increased number of layers, the spins vertically rotate almost by π, thus forming the Bloch domain wall, which reduces the demagnetization energy. Compared to the case of 15 layers, the rotation is by about 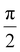 , resulting in higher demagnetization energy. Fig. 7(c) shows the measured current-controlled device operation; here, we applied 200 μs voltage pulses with an amplitude of 5 V and a time period of 500 μs across the length of the device. The oscilloscope collects the signal generated across the transverse arm. We observed potentiation of the transverse voltage, which we attribute to the change in the magnetization due to the SOT and STT. The anomalous Hall resistance and planner Hall resistance depend on the net magnetic moment of the device. As shown in Fig. 7(c) and 9(d), the resistance change leads to a variation in the voltage drop across the device. We observed an increasing voltage drop with respect to the number of current pulses (200 μs) being applied across the X-axis. As shown in Fig. 1(b), the observed resistance can be seen as the combined effect of AHE (lateral), planar Hall effect PHE (lateral), and tunnel magnetoresistance (TMR) (vertical).
, resulting in higher demagnetization energy. Fig. 7(c) shows the measured current-controlled device operation; here, we applied 200 μs voltage pulses with an amplitude of 5 V and a time period of 500 μs across the length of the device. The oscilloscope collects the signal generated across the transverse arm. We observed potentiation of the transverse voltage, which we attribute to the change in the magnetization due to the SOT and STT. The anomalous Hall resistance and planner Hall resistance depend on the net magnetic moment of the device. As shown in Fig. 7(c) and 9(d), the resistance change leads to a variation in the voltage drop across the device. We observed an increasing voltage drop with respect to the number of current pulses (200 μs) being applied across the X-axis. As shown in Fig. 1(b), the observed resistance can be seen as the combined effect of AHE (lateral), planar Hall effect PHE (lateral), and tunnel magnetoresistance (TMR) (vertical).
Fig. 9(a) shows the synaptic conductance potentiation/depression by applying current pulses in 15-layer and 20-layer devices. As discussed above, compared to the 15-layer device, the conductance evolves faster for the 20-layer device due to reduced demagnetization energy. For the same writing current density and time, the performance of a 20-layer device is better. Thus, the demagnetization energy can reduce the dissipation of writing energy in these multilayer devices. As seen in Fig. 9(a), the conductance/resistance switches sharply at the beginning of the positive current due to reduced demagnetization energy density, followed by gradual switching as the DW approaches the edges. This leads to an increased non-linearity NL of the synapse. We computed the NL by using the following methodology:
| | | GLTP(Vg, Vd) = β[1 − e−(P/α)] + Gmin(Vg, Vd) | (5) |
| |  | (6) |
| |  | (7) |
where
GLTP is the synaptic conductance,
Gmin is the minimum conductance,
Gmax is the maximum conductance achieved by the device,
α is the non-linearity fitting parameter,
PM is the maximum pulse number, and
a is the function of
Gmin,
Gmax,
α and
PM. To improve the linearity of the device, we propose varying pulse schemes as shown in
Fig. 9(b). The current density is reduced during the depression cycle, for
JC = +2 × 10
11 A m
−2, the non-linearity (NL)
α = −3.19, for
JC = +3 × 10
11 A m
−2, the NL
α = −3.36, for
JC = +5 × 10
11 A m
−2, the NL
α = −3.8 and for
JC = ∓9 × 10
11 A m
−2, the NL
α = +2.29/−3.19. Thus, we can reduce the NL by either reducing the write current density during the resistance depression or increasing the current density to a much higher value where it dominates the demagnetization effect as seen for
JC = ∓9 × 10
11 A m
−2.
Fig. 9(c) shows the scaling of the synapse behavior with the scaling nanotrack width; the magnetization potentiation/depression for the 64 nm device shows better linearity compared to the 128 nm device due to reduced demagnetization energy. We believe that the devices could be scaled below 64 × 100 nm nanowires. Especially with advanced EBL techniques, there is scope for even 10 nm wide nanotracks. The measured potentiation of multilayer devices is shown in
Fig. 9(d). The application of a 5 V (200 μs) voltage pulse results in a voltage drop
Vxy across the transverse arm (short-term potentiation (STP)). The voltage drop relaxes back to 0V without the
Vxx pulse. As the device is stressed with more voltage pulses, we observed gradual long-term potentiation (LTP). This phenomenon is linked to the magnetization switching and relaxation in the device. The pinning of DWs during the relaxation phase can account for the long-term potentiation. These measured and simulated results promise the potential of multilayer device-based neuromorphic computing. Please note that there are two possible ways to integrate the proposed ferromagnetic multilayer device in a crossbar array: (1) the array of Hall bars as shown in the following ref.
40; however, we need extra circuitry to amplify the weak Hall signal and summing amplifiers as shown in ref.
40 and (2) in the DW-MTJ configuration, we can consider the multilayer stack as a single free layer and add MgO and a fixed layer CoFeB. The writing can be done laterally while reading vertically. However, to realize this MTJ, we might have to reduce the Ta and MgO thickness to below 1 nm. We can consider a full stack to be a synthetic ferromagnet.
 |
| | Fig. 9 (a) SOT-controlled multilayer DW synapse: conductance (potentiation/depression) in 15 layer and 20 layer devices (micromagnetic). (b) Writing pulse scheme for synaptic linearity improvement. (c) Magnetization evolution for different nano-track widths. (d).Current pulses vs. Vxy measured using the oscilloscope. | |
Multilayer spintronics synapse ANN for MNIST data recognition
The performance of the FM multilayer synapse was evaluated using the MLPNeuroSim34 integrated framework for on-chip training and inference. The simulator provides the benchmark from the device to the circuit level. We considered a simple 3-layer feedforward neural network (FNN) having 784 input neurons, 100 hidden neurons, and 10 output neurons, as shown in Fig. 10(a). The architecture was trained and tested to classify the handwritten MNIST digits using the stochastic gradient descent (SGD) algorithm. The input to the network is the pixel value from the 28 × 28 matrix representing the handwritten digit. The synaptic conductance values act as the weight of the neural network. Here, the weights are mapped to the devices’ conductance values. Fig. 10(b) shows the crossbar matrix of the DW devices and the peripheral circuitry, such as the read circuit, adder, and shift registers.
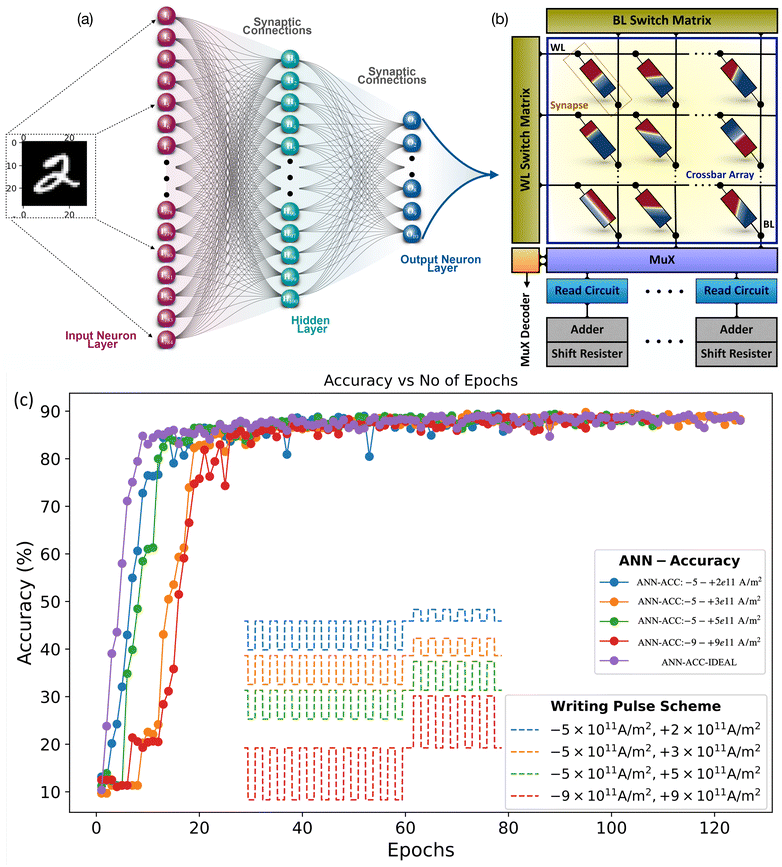 |
| | Fig. 10 (a) Illustration of the 3-layer FCNN architecture for MNIST data recognition. (b) Crossbar array in a circuit. (c) Recognition accuracy for 125 epochs and different write pulse schemes is above 89% for all cases. | |
As shown in Fig. 10(c), the classification accuracy of the devices with different write pulse schemes indicates that the proposed devices can learn and recognize the MNIST dataset with up to 90% accuracy. Which is very well in the range for acceptable recognition performance benchmarked for other memristors and ideal software-based 3-layer FCNN. The system level read and write energies are 1.47 × 10−4 J and 4.8 × 10−3 J. The read latency and write latency are 1.98 × 10−2 s and 2.38 × 10−1 s. These results provide a clear benchmark for realizing hardware neural accelerators based on the DW-MTJ devices. Lastly, the MNIST dataset for classification performance evaluation is more convenient for the presented devices. At this stage, for a realistic integration of the measured devices in a hardware neural network, it is important to visualize how the devices will operate in the neural network. So, a 3-layer feedforward network for MNIST data classification is the best choice with 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 devices. Additionally, the training and testing of the 3-layer neural network with the presented devices is quite clear and intuitive compared to the more data-intensive datasets such as CIFAR-10.
400 devices. Additionally, the training and testing of the 3-layer neural network with the presented devices is quite clear and intuitive compared to the more data-intensive datasets such as CIFAR-10.
Fabrication and characterization
The Rotaris magnetron sputtering system deposited the magnetic thin films at room temperature on a 4-inch thermally oxidized Si wafer. A 300 nm bottom layer of SiO2 was deposited before stack deposition by using thermal oxidation. Then, the multilayer stack was grown using ultrahigh vacuum magnetron sputtering at room temperature in 5 × 10−8 mbar. The multilayer structure consists of, from the substrate side, a 300 nm SiO2 insulating layer. Finally, a stack of SiO2 (300 nm)/[Ta (5 nm)/CoFeB (x)/MgO (2 nm)] × 20 was formed, where MgO layers were deposited by RF magnetron sputtering, and the other layers were deposited by DC magnetron sputtering. After the film deposition, we spin-coated an AZ5214 photoresist with a thickness of 1.6 μm and performed a hard bake for 2 min at 110 °C for positive tone use. We then patterned the crossbars on the resist using conventional photolithography. Ion beam etching using Ar gas removed the exposed magnetic stacks outside the resist mask. During the etching, we monitored the conductivity of the etched region and stopped the etching when the signal from the 300 nm thick silicon oxide layer appeared. To form electrical contacts, Ti (10 nm)/Au (100 nm) was deposited on the sides of the crossbars through sputtering at a rate of 0.8 nm s−1. The electrical contact pads were defined using photolithography and lifted off by immersion in acetone with ultrasonic processing for 5 min.
Characterization and imaging
The magnetic characterization of the samples for thickness optimization was performed using normal vibrating sample magnetometry (VSM) at room temperature. After VSM, we performed imaging of the samples with multi-domain magnetic characteristics using magnetic force microscopy (MFM) based on dimension icon SPM. We used the CoIr-coated MFM tip provided by Bruker Inc. for probing. Hall measurements were performed using a standard Hall measurement system, quantum design PPMS, capable of applying DC magnetic fields. We measured the crossbar devices at temperatures ranging from 2 K to 300 K and at different magnetic fields depending on the temperature. To measure the electrical characteristics, such as pulse current response, we used a standard 4-probe station with external magnetic field capability. The current pulses were applied using a Keithley 6221 current source and voltage was measured using a Keithley 2182A nanovoltmeter. Lastly, a signal generator was used to supply voltage pulses through the MTJ, and an oscilloscope was used to measure the output voltage response of the devices.
Micromagnetics
Micromagnetic simulations were performed using the micromagnetic software framework MuMax.37 Two devices with 15 ferromagnetic layers and 20 ferromagnetic layers coupled with ferromagnetic inter-layer exchange coupling IEC were simulated. We varied the current amplitude, pulse width, and nano track width to study the linearity and scalability of the devices. The free layer was discretized considering varying grid sizes from 128, 64, and 1 to 256, 128, and 1 and cell sizes of 2, 1, and 0.8. The simulation parameters are given in Table 1. For synaptic device simulation, DWs were initiated in each of the ferromagnetic layers, and energy minimization was performed on eqn (13), followed by the time integration of the LLG equation (eqn (11)). Magnetic skyrmions are described using their topological or skyrmion number Q calculated as follows:| |  | (8) |
The spins projected on the XY-plane and the normalized magnetization vector m can be determined by the radial function θ, vorticity Qv and helicity Qh:
| | | m(r) = [sin(θ)cos(Qvφ + Qh), sin(θ)sin(Qvφ + Qh), cos(θ)] | (9) |
The vorticity number is related to the skyrmion number as follows:
| | 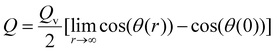 | (10) |
The LLG equation describes the magnetization evolution as follows:
| |  | (11) |
where
m is the normalized magnetization vector,
γ is the gyromagnetic ratio,
α is the Gilbert damping coefficient, and
| | 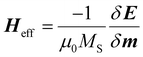 | (12) |
is the effective MF around which the magnetization process occurs. The total magnetic energy of the free layer includes exchange, Zeeman, uniaxial anisotropy, demagnetization, and DMI energies.
| |  | (13) |
where
A is the exchange stiffness,
μ0 is the permeability,
Ku is the anisotropy energy density,
Hd is the demagnetization field, and
Hext is the external field; moreover, the DMI energy density was then computed as follows:
| | | εDM = D[mz(∇·m) − (m·∇)·m] | (14) |
The spin–orbit torque was then added as a modified STT term to the LLG equation as:
| |  | (15) |
where
θSH is the spin Hall coefficient of the material,
j is the current density, and
d is the free layer thickness. The resistance of the proposed skyrmion MTJ synapse was then computed using the compact model presented in the main discussion (
eqn (4)). We then consider the magnetization profile of the free layer and feed it to our model, which computes the resistance of the MTJ device as follows:
| |  | (16) |
Author contributions
A. H. Lone conceived the idea and fabricated the devices along with X. Zou. A. H. Lone performed the characterization of the devices with support from V. S. The micromagnetic and neural network simulations were carried out by A. L. K. M. helped in editing and data plotting. A. H. Lone wrote the paper with support from G. Setti and H. Fariborzi. R Sbiaa provided the feedback. The project was supervised by H. Fariborzi and G. Setti.
Conflicts of interest
The authors declare no conflict of interest.
References
- D. Marković, A. Mizrahi, D. Querlioz and J. Grollier, Physics for neuromorphic computing, Nat. Rev. Phys., 2020, 2, 499–510 CrossRef.
- A. Fert, N. Reyren and V. Cros, Magnetic skyrmions: advances in physics and potential applications, Nat. Rev. Mater., 2017, 2, 17031 CrossRef CAS.
- B. Dieny, I. L. Prejbeanu, K. Garello, P. Gambardella, P. Freitas, R. Lehndorff, W. Raberg, U. Ebels, S. O. Demokritov, J. Akerman, A. Deac, P. Pirro, C. Adelmann, A. Anane, A. V. Chumak, A. Hirohata, S. Mangin, S. O. Valenzuela, M. C. M. d'Aquino, G. Prenat, G. Finocchio, L. Lopez-Diaz, R. Chantrell, O. Chubykalo-Fesenko and P. Bortolotti, Opportunities and challenges for spintronics in the microelectronics industry, Nat. Electron., 2020, 3, 446–459 CrossRef.
- G. Finocchio, M. Di Ventra, K. Y. Camsari, K. Everschor-Sitte, P. Khalili Amiri and Z. Zeng, The promise of spintronics for unconventional computing, J. Magn. Magn. Mater., 2021, 521, 167506 CrossRef CAS.
- S.-H. Yang, R. Naaman, Y. Paltiel and S. S. P. Parkin, Chiral spintronics, Nat. Rev. Phys., 2021, 3, 328–343 CrossRef.
- K. Asifuzzaman, N. R. Miniskar, A. R. Young, F. Liu and J. S. Vetter, A survey on processing-in-memory techniques: Advances and challenges, Mem. – Mater., Devices, Circuits Syst., 2023, 4, 100022 Search PubMed.
- G. Srinivasan, A. Sengupta and K. Roy, Magnetic Tunnel Junction Based Long-Term Short-Term Stochastic Synapse for a Spiking Neural Network with On-Chip STDP Learning, Sci. Rep., 2016, 6, 29545 CrossRef CAS PubMed.
- M. A. Azam, D. Bhattacharya, D. Querlioz and J. Atulasimha, Resonate and fire neuron with fixed magnetic skyrmions, J. Appl. Phys., 2018, 124, 152122 CrossRef.
- A. Sengupta, Z. Al Azim, X. Fong and K. Roy, Spin-orbit torque induced spike-timing dependent plasticity, Appl. Phys. Lett., 2015, 106, 093704 CrossRef.
- A. H. Lone, S. Amara and H. Fariborzi, Voltage-Controlled Domain Wall Motion-Based Neuron and Stochastic Magnetic Tunnel Junction Synapse for Neuromorphic Computing Applications, IEEE J. Explor. Solid-State Comput. Devices Circuits, 2022, 8, 1–9 Search PubMed.
- J. Deng, V. P. K. Miriyala, Z. Zhu, X. Fong and G. Liang, Voltage-Controlled Spintronic Stochastic Neuron for Restricted Boltzmann Machine With Weight Sparsity, IEEE Electron Device Lett., 2020, 41, 1102–1105 Search PubMed.
- B. Sutton, K. Y. Camsari, B. Behin-Aein and S. Datta, Intrinsic optimization using stochastic nanomagnets, Sci. Rep., 2017, 7, 44370 CrossRef PubMed.
- S. Chowdhury, A. Grimaldi, N. A. Aadit, S. Niazi, M. Mohseni, S. Kanai, H. Ohno, S. Fukami, L. Theogarajan, G. Finocchio, S. Datta and K. Y. Camsari, A Full-Stack View of Probabilistic Computing With p-Bits: Devices, Architectures, and Algorithms, IEEE J. Explor. Solid-State Comput. Devices Circuits, 2023, 9, 1–11 Search PubMed.
- D. Bhowmik, U. Saxena, A. Dankar, A. Verma, D. Kaushik, S. Chatterjee and U. Singh, On-chip learning for domain wall synapse based Fully Connected Neural Network, J. Magn. Magn. Mater., 2019, 489, 165434 CrossRef CAS.
- A. H. Lone, S. Amara and H. Fariborzi, Magnetic tunnel junction based implementation of spike time dependent plasticity learning for pattern recognition, Neuromorph. Comput. Eng., 2022, 2, 024003 CrossRef.
- A. Jaiswal, A. Agrawal, P. Panda and K. Roy, Neural Computing With Magnetoelectric Domain-Wall-Based Neurosynaptic Devices, IEEE Trans. Magn., 2021, 57, 1–9 Search PubMed.
- A. Sengupta, Z. Al Azim, X. Fong and K. Roy, Spin-orbit torque induced spike-timing dependent plasticity, Appl. Phys. Lett., 2015, 106, 093704 CrossRef.
- S. S. P. Parkin, M. Hayashi and L. Thomas, Magnetic Domain-Wall Racetrack Memory, Science, 2008, 320, 190–194 CrossRef CAS PubMed.
- Z. Luo, A. Hrabec, T. P. Dao, G. Sala, S. Finizio, J. Feng, S. Mayr, J. Raabe, P. Gambardella and L. J. Heyderman, Current-driven magnetic domain-wall logic, Nature, 2020, 579, 214–218 CrossRef CAS PubMed.
- W. Wang, Y. Sheng, Y. Zheng, Y. Ji and K. Wang, All-Electrical Programmable Domain-Wall Spin Logic-In-Memory Device, Adv. Electron. Mater., 2022, 8, 2200412 CrossRef CAS.
- A. H. Lone and H. Fariborzi, Skyrmion-Magnetic Tunnel Junction Synapse With Long-Term and Short-Term Plasticity for Neuromorphic Computing, IEEE Trans. Electron Devices, 2023, 70, 371–378 CAS.
- K. Everschor-Sitte, J. Masell, R. M. Reeve and M. Kläui, Perspective: Magnetic skyrmions—Overview of recent progress in an active research field, J. Appl. Phys., 2018, 124, 240901 CrossRef.
- K. M. Song, J.-S. Jeong, B. Pan, X. Zhang, J. Xia, S. Cha, T.-E. Park, K. Kim, S. Finizio, J. Raabe, J. Chang, Y. Zhou, W. Zhao, W. Kang, H. Ju and S. Woo, Skyrmion-based artificial synapses for neuromorphic computing, Nat. Electron., 2020, 3, 148–155 CrossRef.
- S. Azzawi, A. T. Hindmarch and D. Atkinson, Magnetic damping phenomena in ferromagnetic thin-films and multilayers, J. Phys. D: Appl. Phys., 2017, 50, 473001 CrossRef.
- S. Woo, K. M. Song, X. Zhang, Y. Zhou, M. Ezawa, X. Liu, S. Finizio, J. Raabe, N. J. Lee, S.-I. Kim, S.-Y. Park, Y. Kim, J.-Y. Kim, D. Lee, O. Lee, J. W. Choi, B.-C. Min, H. C. Koo and J. Chang, Current-driven dynamics and inhibition of the skyrmion Hall effect of ferrimagnetic skyrmions in GdFeCo films, Nat. Commun., 2018, 9, 959 CrossRef PubMed.
- F. Büttner, B. Krüger, S. Eisebitt and M. Kläui, Accurate calculation of the transverse anisotropy of a magnetic domain wall in perpendicularly magnetized multilayers, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 054408 CrossRef.
- I. Lemesh and G. S. D. Beach, Twisted domain walls and skyrmions in perpendicularly magnetized multilayers, Phys. Rev. B, 2018, 98, 104402 CrossRef CAS.
- M. Kuepferling, A. Casiraghi, G. Soares, G. Durin, F. Garcia-Sanchez, L. Chen, C. Back, C. Marrows, S. Tacchi and G. Carlotti, Measuring interfacial Dzyaloshinskii-Moriya interaction in ultrathin magnetic films, Rev. Mod. Phys., 2023, 95, 015003 CrossRef.
- R. Tomasello, Z. Wang, E. Raimondo, S. Je, M. Im, M. Carpentieri, W. Jiang and G. Finocchio, Field-driven collapsing dynamics of skyrmions in magnetic multilayers, Phys. Rev. B, 2023, 107, 184416 CrossRef CAS.
- J. Fullerton, A. Hierro-Rodriguez, C. Donnelly, D. Sanz-Hernández, L. Skoric, D. A. MacLaren and A. Fernández-Pacheco, Controlled evolution of three-dimensional magnetic states in strongly coupled cylindrical nanowire
pairs, Nanotechnology, 2023, 34, 125301 CrossRef PubMed.
- B. Zhang, W. Lv, Y. Guo, B. Wang, K. Luo, W. Li and J. Cao, Realization of Multi-Level State and Artificial Synapses Function in Stacked (Ta/CoFeB/MgO)N Structures, Adv. Electron. Mater., 2023, 9, 2200939 CrossRef CAS.
- J. Cai, B. Fang, C. Wang and Z. Zeng, Multilevel storage device based on domain-wall motion in a magnetic tunnel junction, Appl. Phys. Lett., 2017, 111, 182410 CrossRef.
- S. Zhang, Y. Su, X. Li, R. Li, W. Tian, J. Hong and L. You, Spin-orbit-torque-driven multilevel switching in Ta/CoFeB/MgO structures without initialization, Appl. Phys. Lett., 2019, 114, 042401 CrossRef.
- S. Zhang, S. Luo, N. Xu, Q. Zou, M. Song, J. Yun, Q. Luo, Z. Guo, R. Li, W. Tian, X. Li, H. Zhou, H. Chen, Y. Zhang, X. Yang, W. Jiang, K. Shen, J. Hong, Z. Yuan, L. Xi, K. Xia, S. Salahuddin, B. Dieny and L. You, Memristors: A Spin-Orbit-Torque Memristive Device (Adv. Electron. Mater. 4/2019), Adv. Electron. Mater., 2019, 5, 1970022 CrossRef.
- S. B. Wu, T. Zhu, X. F. Yang and S. Chen, The anomalous Hall effect in the perpendicular Ta/CoFeB/MgO thin films, J. Appl. Phys., 2013, 113, 17C717 CrossRef.
- J. Leliaert, M. Dvornik, J. Mulkers, J. De Clercq, M. V. Milošević and B. Van Waeyenberge, Fast micromagnetic simulations on GPU–recent advances made with $\mathsf{mumax}^3$, J. Phys. D: Appl. Phys., 2018, 51, 123002 CrossRef.
- A. Vansteenkiste, J. Leliaert, M. Dvornik, M. Helsen, F. Garcia-Sanchez and B. Van Waeyenberge, The design and verification of MuMax3, AIP Adv., 2014, 4, 107133 CrossRef.
- N. Nagaosa and Y. Tokura, Topological properties and dynamics of magnetic skyrmions, Nat. Nanotechnol., 2013, 8, 899–911 CrossRef CAS PubMed.
-
P.-Y. Chen, X. Peng and S. Yu, 2017 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 2017, pp. 6.1.1–6.1.4.
- L. Yang, W. Li, C. Zuo, Y. Tao, F. Jin, H. Li, R. Tang and K. Dong, Field-Free Memristive Spin–Orbit Torque Switching in A1 CoPt Single Layer for Image Edge Detection, Adv. Electron. Mater., 2024, 2300885 CrossRef.
- R. Chen, X. Wang, H. Cheng, K.-J. Lee, D. Xiong, J.-Y. Kim, S. Li, H. Yang, H. Zhang, K. Cao, M. Kläui, S. Peng, X. Zhang and W. Zhao, Large Dzyaloshinskii-Moriya interaction and room-temperature nanoscale skyrmions in CoFeB/MgO heterostructures, Cell Rep. Phys. Sci., 2021, 2, 100618 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Xuecui
Zou
a,
Kishan K.
Mishra
*a,
Xuecui
Zou
a,
Kishan K.
Mishra
 a,
Venkatesh
Singaravelu
b,
R.
Sbiaa
a,
Venkatesh
Singaravelu
b,
R.
Sbiaa
 c,
Hossein
Fariborzi
*a and
Gianluca
Setti
*a
c,
Hossein
Fariborzi
*a and
Gianluca
Setti
*a






![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) /
/![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) P is the free layer/pinned layer normalized magnetization.
P is the free layer/pinned layer normalized magnetization.

 , resulting in higher demagnetization energy. Fig. 7(c) shows the measured current-controlled device operation; here, we applied 200 μs voltage pulses with an amplitude of 5 V and a time period of 500 μs across the length of the device. The oscilloscope collects the signal generated across the transverse arm. We observed potentiation of the transverse voltage, which we attribute to the change in the magnetization due to the SOT and STT. The anomalous Hall resistance and planner Hall resistance depend on the net magnetic moment of the device. As shown in Fig. 7(c) and 9(d), the resistance change leads to a variation in the voltage drop across the device. We observed an increasing voltage drop with respect to the number of current pulses (200 μs) being applied across the X-axis. As shown in Fig. 1(b), the observed resistance can be seen as the combined effect of AHE (lateral), planar Hall effect PHE (lateral), and tunnel magnetoresistance (TMR) (vertical).
, resulting in higher demagnetization energy. Fig. 7(c) shows the measured current-controlled device operation; here, we applied 200 μs voltage pulses with an amplitude of 5 V and a time period of 500 μs across the length of the device. The oscilloscope collects the signal generated across the transverse arm. We observed potentiation of the transverse voltage, which we attribute to the change in the magnetization due to the SOT and STT. The anomalous Hall resistance and planner Hall resistance depend on the net magnetic moment of the device. As shown in Fig. 7(c) and 9(d), the resistance change leads to a variation in the voltage drop across the device. We observed an increasing voltage drop with respect to the number of current pulses (200 μs) being applied across the X-axis. As shown in Fig. 1(b), the observed resistance can be seen as the combined effect of AHE (lateral), planar Hall effect PHE (lateral), and tunnel magnetoresistance (TMR) (vertical).

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 devices. Additionally, the training and testing of the 3-layer neural network with the presented devices is quite clear and intuitive compared to the more data-intensive datasets such as CIFAR-10.
400 devices. Additionally, the training and testing of the 3-layer neural network with the presented devices is quite clear and intuitive compared to the more data-intensive datasets such as CIFAR-10.