 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Strong sequence–dependence in RNA/DNA hybrid strand displacement kinetics†
Francesca G.
Smith
ab,
John P.
Goertz
a,
Križan
Jurinović
bc,
Molly M.
Stevens
 *ac and
Thomas E.
Ouldridge
*ac and
Thomas E.
Ouldridge
 *bc
*bc
aDepartment of Materials, Imperial College London, London, SW7 2AZ, UK
bImperial College Centre for Synthetic Biology, Imperial College London, London, SW7 2AZ, UK
cDepartment of Bioengineering, Imperial College London, London, SW7 2AZ, UK. E-mail: t.ouldridge@imperial.ac.uk; molly.stevens@dpag.ox.ac.uk
First published on 5th September 2024
Abstract
Strand displacement reactions underlie dynamic nucleic acid nanotechnology. The kinetic and thermodynamic features of DNA-based displacement reactions are well understood and well predicted by current computational models. By contrast, understanding of RNA/DNA hybrid strand displacement kinetics is limited, restricting the design of increasingly complex RNA/DNA hybrid reaction networks with more tightly regulated dynamics. Given the importance of RNA as a diagnostic biomarker, and its critical role in intracellular processes, this shortfall is particularly limiting for the development of strand displacement-based therapeutics and diagnostics. Herein, we characterise 22 RNA/DNA hybrid strand displacement systems, alongside 11 DNA/DNA systems, varying a range of common design parameters including toehold length and branch migration domain length. We observe that differences in stability between RNA–DNA hybrids and DNA–DNA duplexes have large effects on strand displacement rates, with rates for equivalent sequences differing by up to 3 orders of magnitude. Crucially, however, this effect is strongly sequence-dependent, with RNA invaders strongly favoured in a system with RNA strands of high purine content, and disfavoured in a system when the RNA strands have low purine content. These results lay the groundwork for more general design principles, allowing for creation of de novo reaction networks with novel complexity while maintaining predictable reaction kinetics.
Introduction
Strand displacement reactions form the basis of most dynamic nucleic acid reaction networks and are fundamental to the field of DNA nanotechnology.1–3 Strand displacement is a nucleic acid-based process in which an incumbent strand (Inc) is replaced by an invader strand (Inv) within a complex (SInc) with a substrate strand (S). Specifically, toehold-mediated strand displacement (TMSD) reactions are a subset of strand displacement reactions that repeatedly appear in nucleic acid circuits due to their relatively high reaction rates. The presence of an overhang or ‘toehold’ motif on the substrate strand to which the invader can bind, known as the invader toehold (γ), provides the thermodynamic drive for forward strand displacement (Fig. 1A). Hybridisation of the invader strand to the invader toehold is followed by branch migration, in which displacement of the incumbent strand occurs by a random walk process. Completion of branch migration results in two nucleic acid products: a single-stranded incumbent strand (Inc) and fully complementary invader–substrate complex (SInv).The highly efficient and specific nature of TMSD reactions makes this mechanism a critical tool within dynamic nucleic acid reaction circuit designs. Moreover, the kinetic and thermodynamic properties of DNA-based (or DNA > DNA) TMSD reactions have been extensively and systemically characterised.4,5 Zhang and Winfree (2009) pioneered systematic investigations into the effect of toehold length on the rate of TMSD. This foundational work revealed that the rate of strand displacement increases exponentially with a linear increase in toehold length up to approximately 6–7nt, above which the rate of strand displacement plateaus. The understanding obtained from this seminal work has enabled development of increasingly complex de novo reaction networks with predictable reaction kinetics, implemented across broad range of applications including digital nucleic acid computation,1,2,6 molecular motors,7 and diagnostic biosensors.3,8,9
Since the foundational work by Zhang and Winfree (2009), further studies have explored the kinetics of DNA > DNA strand displacement in more detail to harness more fine-tuned kinetic control within this reaction motif. The introduction of mismatched base pairs in the branch migration domain of the invader–substrate complex has been found to decrease the rate of strand displacement by up to 4 orders of magnitude.10,11 On the other hand, elimination of an existing mismatch in the branch migration domain of the incumbent–substrate complex can increase in the rate of strand displacement by up to 2 orders of magnitude.10,12 Fine-tuned programmable control has equally been realised through introduction of a spacer between the invader toehold and branch migration domain, known as a remote toehold.13 This kinetic variability offers improved system flexibility and has facilitated circuit design with more regulated dynamics.
Building on the experimental work towards understanding DNA > DNA TMSD, a number of predictive models have been developed to capture strand displacement kinetics. Within the second-order limit, TMSD kinetics can be effectively described as an instantaneous, bimolecular reaction, with two products formed from two reactants via a single reaction step. Zhang and Winfree employed a simple, two-intermediate model to describe TMSD reaction kinetics.5 While this phenomenological model was able to successfully explain the exponential increase in rate with toehold length as well as the presence of a rate plateau, it was unable to provide insight into why the rate plateaued for toehold lengths of approximately 6–7nt. Subsequently, Srinivas et al. (2013) developed an ‘Intuitive Energy Landscape’ (IEL) model for TMSD, which provides a nucleotide-level understanding of strand displacement kinetics and offers useful insights from a biophysical perspective. The IEL model has since been expanded to successfully capture the effect of introduction or elimination of mismatches on reaction kinetics, supporting the previous experimental data.10
While TMSD is frequently employed in nucleic acid reaction networks, it is limited in its use due to its irreversibility. When reversible displacement reactions are desired, the toehold exchange reaction motif is often used as an alternative. Toehold exchange involves a second toehold, known as the incumbent toehold (ε), that is initially sequestered in the incumbent–substrate complex but is exposed following incumbent displacement. This toehold facilitates hybridisation of the incumbent strand to the invader–substrate complex and as such allows effective reversibility5 (Fig. 1B). The second toehold enables construction of more flexible, reversible reaction networks by weakening the coupling between the thermodynamics and kinetics of such systems. There are numerous examples in which this property of toehold exchange has been exploited to achieve novel functionality including reversible logic gates14,15 and regulated molecular switches.16,17
The kinetics of toehold exchange have also been studied in depth. Systematic characterisation showed that the rate of strand displacement is effectively independent of the length of the incumbent toehold within the limit that the incumbent toehold (ε) is shorter than the invader toehold (γ). However, for ε > γ, the rate of toehold exchange decays sharply with increasing ε.5
While DNA remains a critical building block in nucleic acid nanotechnology, recent years have seen increased interest in RNA-based or RNA/DNA hybrid nucleic acid nanodevices and reaction circuits.3,9,18–21 Despite being less stable and more costly than DNA, the structural and catalytic properties of RNA open up the field of nucleic acid nanotechnology to novel functionalities and design capabilities. Furthermore, RNA has vital roles within the cell, with direct functions in gene regulation, protein-coding, structural scaffolding and catalysis. The fundamental role for RNA in the correct functioning of cells makes it a highly informative biomarker for many diseases and developmental disorders including cancers, heart disease and neurological disorders.22–27 As such, it is unsurprising that many novel nucleic acid reaction schemes have been geared towards RNA biosensing applications in recent years.3,9,28,29 Additionally, RNA–DNA hybrids have been shown to hold important roles in chromosome segregation, telomere regulation and replication regulation.30–32 These observations emphasise the importance of effectively interfacing RNA within hybrid nucleic acid reaction circuits and networks with a view to diagnostic and therapeutic applications. Moreover, in vivo studies have also revealed that RNA/DNA strand displacement reactions (in which RNA displaces DNA or equally DNA displaces RNA) appear to play a critical role within numerous intracellular processes including RNA transcription; genome repair, and the operation of the CRISPR/Cas machinery, highlighting the importance of gaining a clear understanding of the kinetics of this reaction in particular.33–35
At a fundamental level, RNA > DNA (RNA displacement of DNA from a DNA–DNA duplex) strand displacement involves the separation of DNA–DNA complexes and the production of RNA–DNA hybrid complexes and vice versa in the case of DNA > RNA (DNA displacement of RNA from an RNA–DNA hybrid complex) strand displacement. The kinetics of RNA > DNA and DNA > RNA strand displacement are therefore likely to be highly dependent on the stability of RNA–DNA complexes relative to DNA–DNA complexes, a consideration that does not arise in DNA > DNA and RNA > RNA strand displacement. Moreover, it is likely that the properties of the displacement domain will play a much more important role in hybrid strand displacement than the DNA > DNA context, in which branch migration along the displacement domain replace base pairs in one duplex with identical base pairs in another.
Previous hybridisation studies of RNA–DNA hybrids point to a dependence on the purine (G/A) content within the RNA sequence. The consensus suggests that, for low purine content in the RNA strand of the hybrid, RNA–DNA hybrids are less stable than the corresponding DNA–DNA complexes. In contrast, RNA–DNA hybrids show greater stability than the equivalent DNA–DNA complex when there is a high purine content in the RNA sequence of the hybrid.36–39 Notably, many of these studies only tested short oligonucleotides and a relatively limited number of sequences were considered.36,37 TMSD reactions allow us to effectively probe this purine dependence and quantify its effect on the thermodynamics and reaction kinetics.
Despite the importance of RNA/DNA hybrid (RNA > DNA and DNA > RNA) TMSD, and its potential complexity with respect to the DNA-based analog, understanding of RNA/DNA hybrid strand displacement kinetics remains limited. Some initial studies into RNA/DNA hybrid strand displacement have been performed,40 however thus far there is insufficient experimental data to draw consistent conclusions about the kinetics of these systems and to exploit for further computational modelling. Moreover, no studies have explicitly addressed the role of purine content on the kinetics of RNA/DNA hybrid strand displacement.
In this work we characterise RNA/DNA hybrid strand displacement reactions across a range of common design parameters including invader toehold length and branch migration domain length. We extract rate constants for each system and reveal distinct differences in strand displacement kinetics between DNA > DNA and RNA/DNA hybrid systems. We highlight the importance of the sequence composition and specifically purine content of the branch migration domain in determining the rate of hybrid strand displacement reactions, which lies in contrast to DNA > DNA strand displacement. Finally, we interpret this experimental rate data by parameterising a continuous-time Markov chain model of RNA/DNA hybrid strand displacement. This model can describe strand displacement rates for RNA/DNA hybrid systems in terms of toehold length, branch migration domain length and, critically, includes a sequence-dependent parameter for the relative stability of RNA–DNA and DNA–DNA complexes as dictated by sequence composition.
Materials and methods
Reagents and sequence design
All sequences used in the low RNA purine content experiments (DNApy > DNApy, RNApy > DNApy, DNApy > RNApy) were designed in NUPACK (https://www.nupack.org).41 Sequences were designed with minimal secondary structure. All sequences used in the high RNA purine content experiments (DNApu > DNApu, RNApu > DNApu, DNApu > RNApu) were adapted from Yao et al. (2015). All DNA and RNA strands were ordered from Integrated DNA Technologies (IDT, Coralville, Iowa) with HPLC purification, and normalised to 100 μM in LabReady 1× IDTE buffer (pH 8.0). For labelled strands a TTT spacer was introduced between the fluorophore/quencher and the sequence of interest. All sequences were designed to have between 40% and 60% GC content. All sequences used in this work are given in Tables S1 & S2.† Table S3† lists all strands required to recreate each figure in this work.Annealing complexes
Strands were combined and heated to 95 °C for 5 minutes and then cooled to 20 °C at a constant rate of 1 °C min−1 to form complexes. For reporter (FQ) complexes, F and Q strands were combined for a final concentration of 300 nM and 360 nM, respectively. For SInc complexes, S and Inc strands were combined for a final concentration of 200 nM and 240 nM, respectively. We used a 20% excess of Inc and Q strands in order to ensure that all S and F strands were bound into complexes. All annealing was performed at 1 M NaCl in 1× TAE (Tris–Acetate–EDTA) buffer.Fluorescence spectroscopy
All fluorescence measurements were performed using the BMG CLARIOstar® microplate reader. Reactions were performed in clear, flat bottom 96-well plates from Greiner Bio-One. All measurements were taken from the bottom of the wells. For all measurements, each read was an average of 20 flashes. Flashes were taken in a spiral configuration in the well with a 4 mm diameter, to account for any heterogeneity within each well. For fast (well mode) reactions measurements were not taken in a spiral but at a single point at the centre of each well. Plates were maintained at the reaction temperature (25 °C) for 30 minutes prior to the first measurement to ensure that the reaction mixtures were at the correct temperature. Injection of the relevant trigger strand for each reaction was performed using the automatic injection feature of the CLARIOstar® microplate reader at a pump speed of 430 μL s−1. After each injection, samples were shaken for 6 s at a speed of 400 rpm in a double-orbital configuration. The injectors were passivated with 5% BSA for 20 minutes prior to being loaded with DNA or RNA samples to minimise loss of the nucleic acid and maximise reproducibility. Plates were sealed using Thermo Fisher Adhesive PCR Plate Seals and kept for up to a month in a shaking incubator at the reaction temperature and 70 rpm to allow the reaction to reach equilibrium. F was labelled with AlexaFluor488 (excitation: 488 nm; emission: 496 nm) and Q was labelled with IowaBlack FQ®. An excitation window of 488-14 and emission window of 535-30 were used. The same focal height (5.9 mm) was used across all experiments to allow for comparison between experiments. The gain was set to the same value as that used for calibration curve measurements to ensure comparability (the gains used for each calibration curve are given in Fig. S2†).General procedure for experimental strand displacement characterisation
Experimental protocols were adapted from ref. 42. All experiments had a final reaction volume of 200 μL, and used a monovalent salt concentration of 1 M NaCl unless otherwise stated. All experiments were composed of multiple measurements that each captured either the reaction kinetics or allowed for estimation of reactant or product concentrations. All experiments included a positive control with 15 nM FQ and an excess (20 nM) Inc; and a buffer-only negative control. All reactions were measured in at least triplicate to obtain an estimate of the error within our measurements. Of note, the concentrations given are intended concentrations of reactants, however for fitting purposes we determined the exact concentrations for each reactant based on fluorescence output after calibration. | (1) |
 | (2) |
For these experiments we used [FQ] = 15 nM and [Inc] = 4–12 nM. The majority of FQ complexes used herein were designed with a 6nt toehold (RNA > DNA and DNA > DNA strand displacement reactions for the high RNA purine content system used an FQ reporter toehold of 8nt). All reactions were saturated with an excess concentration of Inc after reaction kinetics were completed to determine [FQ] at time t = 0. An additional negative control was included with [FQ] = 15 nM and [Inc] = 0 nM. Further details of experimental protocol for reporter characterisation are given in ESI Note 7.1† (full protocol in Table S6,† illustrative fluorescent data in Fig. S3†). Further details of the normalisation and estimation of krep are given in ESI Notes 7.2 and 7.3,† respectively. All fluorescent traces for reporter characterisation are given in Fig. S4,† fits of the ODE model to the fluorescent traces are given in Fig. S5 & S6† and estimated krep values are given in Tables S7 & S8.†
 | (3) |
We combine both the toehold exchange and reporter displacement reactions to generate a system of ODEs. Using conservation laws this series of reactions can be well described by 3 ODEs
 | (4) |
 | (5) |
 | (6) |
Note that eqn (6) is equivalent to eqn (2) above.
For each design we estimated keff for DNA > DNA, RNA > DNA and DNA > RNA displacement reactions. These experiments were performed by combining [FQ] = 15 nM, [SInc] = 10 nM and [Inv] = 4–8 nM (for DNApu > RNApu strand displacement reactions we used [Inv] = 40–80 nM). We used an excess of [FQ] and [SInc], unless specified otherwise, to ensure that all [Inv] reacted and we were able to effectively estimate [Inv] at time, t = 0, [Inv]0. For these experiments we used 3 different [Inv] concentrations to confirm the robustness of the second-order assumption and each reaction was performed in triplicate. All reactions were saturated with an excess concentration of Inv after reactions kinetics were complete to determine [SInc] at time t = 0. Reactions were next saturated with an excess concentration of Inc to determine [FQ] at time t = 0. An additional negative control was included with [FQ] = 15 nM, [SInc] = 10 nM and [Inv] = 0 nM. Further details of the experimental protocol for toehold exchange characterisation are given in ESI Note 8.1† (full protocol in Tables S9 & S10,† illustrative fluorescent data in Fig. S7 & S8†). Further details of the normalisation and estimation of keff are given in ESI Notes 8.2 and 8.3,† respectively. All fluorescent traces for toehold exchange characterisation are given in Fig. S10–S12,† fits of the ODE model to the fluorescent traces are given in Fig. S13–S18† and fitted keff values are given in Tables S12 & S13.†
 | (7) |
For these strand displacement reactions we adapted the experimental protocol to effectively estimate keff despite the presence of the leak reaction. These experiments were performed by combining [FQ] = 15 nM, [SInc] = 10 nM and [Inv] = 40–80 nM. An excess of Inc is also present from formation of the SInc complexes. All reactions were performed in triplicate. All reactions were subsequently saturated with a further large excess concentration of Inv to ensure all SInc complexes were dissociated and therefore determine [SInc] at time t = 0. Reactions were next saturated with an excess concentration of Inc to determine [FQ] at time t = 0. An additional negative control was included with [FQ] = 15 nM, [SInc] = 10 nM and [Inv] = 0 nM. We first estimated the leak reaction rate constant, kleak, from this negative control reaction using the following ODEs
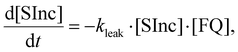 | (8) |
 | (9) |
 | (10) |
Note that the right hand side of eqn (9) is equivalent to eqn (2) and (6) above. We include the ODE describing the reporter displacement reaction due to the presence of excess Inc.
For the toehold exchange reactions of interest we then estimated keff while keeping the corresponding kleak estimate fixed. We adapted the ODE model in eqn (4) and (5) to account for the undesired leak reaction observed for DNA > RNA strand displacement
 | (11) |
 | (12) |
 | (13) |
 | (14) |
Note that the right hand side of eqn (11) is equivalent to eqn (4) above and the right hand side of eqn (14) is equivalent to eqn (10) above.
Further details of experimental protocol for toehold exchange characterisation for these leak reactions are given in ESI Note 8.1† (full protocol in Table S11,† illustrative fluorescent data in Fig. S9†). Further details of the normalisation are given in ESI Note 8.3.† Further details of kleak and keff estimation are given in ESI Note 8.4.† All fluorescent traces for toehold exchange characterisation for systems with a leak are given in Fig. S12,† fits of the ODE model to the fluorescent traces are given in Fig. S19 & S20† and fitted kleak and keff values are given in Tables S14 and S15,† respectively.
General fitting procedure
All fitting was performed in Python version 3.8.8. First, kinetic traces for fluorescence in afu were converted to [FInc] in nM using the calibration results, then least-squares fitting of the ODE model was used to estimate relevant rate constants. Initial reactant concentration parameters, which may deviate from intended values due to experimental imperfections, were calculated prior to fitting using the calibration results.For reporter characterisation data we estimated the rate constant krep. For each experiment we derived a single, global estimate of krep across all replicates and each initial concentration of Inc at time t = 0 ([Inc]0). [Inc]0 and [FQ]0 were fixed values in the fitting protocol. The krep values estimated in the reporter characterisation experiments were fixed for fitting the corresponding toehold exchange reactions. Similarly, the values of kleak obtained from preliminary experiments (see ESI Note 8.4†) were fixed for fitting the corresponding DNApu > RNApu strand displacement reactions.
We estimated keff for each toehold exchange system that we tested in the standard 1 M NaCl buffer. [Inv]0, [SInc]0 and [FQ]0 were fixed values in the fitting protocol. Unless otherwise specified, for each experiment we estimated a single, global estimate for keff across all replicates and [Inv]0.
For DNApu > RNApu strand displacement reactions we were unable to estimate global keff values. In this case, for each experiment we assumed that [Inv]0 matched the intended concentration and calculated the individual estimates of keff for each experimental trace. We report the mean of these keff values instead of a global fit of keff. Fitting individual estimates of keff for each experimental trace for all other sets of experiments produced results that agreed well with the global fits. ESI Note 7.3† contains a detailed description of the fitting procedures for reporter characterisation experiments. ESI Notes 8.3 and 8.4† contain a detailed description of the fitting procedures for full strand displacement experiments.
Initial rate predictions using IEL model
Initial predictions from the IEL model were based on previous parameters for DNA > DNA strand displacement taken from ref. 10: ΔGassoc = 2.5kBT, ΔGbp = –2.52kBT, ΔGp = 3.5kBT, ΔGbm = 7.4kBT and kbp = 5.9 × 107 s−1. For initial perdicitions ΔGrd, the relative stability of RNA/DNA and DNA/DNA duplexes, is a flexible parameter. For these predictions we used an initial invader concentration of 6 nM, with γ = 4nt, β = 26nt and ε = 4nt (Fig. S1†). We assumed a reaction temperature of 25 °C (298 K). Full details of the IEL model are given in ESI Notes 1–3.† Detailed explanation of these initial predictions are given in ESI Note 4.†Parameterisation of IEL model for RNA/DNA hybrid strand displacement
Parameterisation of the free-energy landscape model was performed in Python version 3.8.8. For parameterisation based on the low RNA purine content (DNApy > DNApy, RNApy > DNApy, DNApy > RNApy) kinetic data ΔGassoc, ΔGp and ΔGbp were fixed at the previously estimated values given in Table 1, while ΔGbm, kbp and ΔGrd were estimated. For parameterisation using the high RNA purine content (DNApu > DNApu, RNApu > DNApu, DNApu > RNApu) kinetic data ΔGassoc, ΔGp, ΔGbp and ΔGbm were fixed at the values predicted from the low RNA purine content kinetic data, while kbp and ΔGrd were flexible parameters. For parameterisation the reaction temperature was set to 25 °C (298 K). Parameterisation was performed by minimising the squared residuals between the model-predicted and the experimentally-derived values of keff. The details of the parameterisation protocol are given in ESI Note 9.†| Data set | ΔGbp (kBT) | ΔGassoc (kBT) | ΔGp (kBT) | ΔGbm (kBT) | k bp (s−1) | ΔGrd (kBT) |
|---|---|---|---|---|---|---|
| This study | −2.52* | 2.5* | 3.5* | 9.3 ± 1.2 | 6.4 (CI: 2.3; 18.3) × 107 | 0.16 ± 0.04 |
| Irmisch | −2.52 | 2.5 ± 0.2 | 3.5 ± 0.2 | 7.4 ± 0.2 | (5.9 ± 1.1) × 107 | — |
| Machinek | −2.51 | 4.0 ± 0.2 | 5.4 ± 0.4 | 8.5 ± 0.3 | (20.6 ± 0.6) × 107 | — |
Results and discussion
RNA/DNA hybrid free-energy landscape model
In this work we have developed a continuous-time, Markov chain model to describe the rate of strand displacement for RNA/DNA hybrid systems. This model has been adapted from the Intuitive Energy Landscape (IEL) model developed by Srinivas et al. (2013). The IEL model was initially introduced to explain DNA > DNA strand displacement reaction kinetics.43 More recently it has been expanded to capture the effect of mismatches in strand displacement systems.10 We further expand on the IEL model as described by Irmisch et al. (2020) to allow a description of RNA > DNA and DNA > RNA strand displacement kinetics. For all systems referred to here the substrate strand (S) was composed of DNA.Our free-energy landscape model is shown in Fig. 2A. This model contains a number of distinct states which represent each step in the strand displacement reaction, from state −γ through to state N. State −γ refers to the stage in which the invader is unbound from the incumbent–substrate complex. Completion of toehold hybridisation is defined as state 0, in which in the invader is bound to the incumbent–substrate complex via the toehold but branch migration has not been initiated. Branch migration proceeds through to state β in which the incumbent has been successfully displaced by the invader strand. For systems with no incumbent toehold state β, is equivalent to state N. For systems in which the incumbent toehold length is non-zero (ε > 0 as in Fig. 1B), state N refers to the complete dissociation of the incumbent strand from the incumbent toehold of the invader–substrate complex.
 | ||
| Fig. 2 Free-energy landscape model for toehold exchange. (A) Simplified free-energy landscape of a toehold exchange reaction, based on the IEL.10 The substrate has length N + γ, with invader toehold length γ, branch migration domain length β and incumbent toehold length ε. Within the diagram, the states represented by blue dots are defined by the number of invader base pairs formed; large barriers inhibit transitions between these states during branch migration. (I) Unbound invader and incumbent–substrate complex; (II) single invader nucleotide hybridised to the invader toehold; (III) invader strand fully hybridised to the invader toehold; (IV) invader strand fully displaced incumbent strand in branch migration domain; (V) single incumbent nucleotide bound to the incumbent toehold; (VI) unbound incumbent and invader–substrate complex. Curved, red arrows represent spontaneous invader and incumbent dissociation, and straight, double-headed red arrows reflect free-energy changes. (B) ΔGrd determines the gradient of the landscape within the branch migration domain. For RNA > DNA strand displacement, negative ΔGrd values produce a downhill landscape and positive ΔGrd values produce an uphill landscape. (C) For RNA > DNA toehold exchange, we predict the rate constant (keff) for an increase in β = 11nt to β = 26nt, across a range of ΔGrd = −0.4kBT to ΔGrd = 0.4kBT for γ = 4nt and ε = 4nt. Increasing ΔGrd increases the dependence of rate on branch migration domain length. | ||
The IEL model as defined by Irmisch et al. (2020) fully describes non-mismatched DNA > DNA strand displacement reactions with 4 free-energy parameters and a single rate parameter: ΔGassoc, ΔGbp, ΔGp, ΔGbm and kbp.10 ΔGassoc is the free-energy penalty caused by the initial association of the invader to incumbent–substrate complex within the toehold resulting in reduced orientational and translational freedom of the single strand at the standard 1 M reference concentration. ΔGbp corresponds to the free-energy change resulting from formation of a single additional DNA–DNA base pair within a duplex. Therefore, toehold hybridisation can be expressed as a free-energy reduction by ΔGbp for each base pair formed in this process. For simplicity, within this model we ignore the individual contribution of the different nucleotides and assume a sequence-average value for ΔGbp. ΔGp defines the free-energy penalty associated with the initiation of branch migration due to the presence of two single-stranded overhangs as the incumbent strand starts to be displaced. ΔGbm is the free-energy barrier associated with each branch migration step. This parameter can be thought of as the transition barrier to breaking a single incumbent–substrate base pair and formation of a single invader–substrate base pair, due to the rearrangement of invader and incumbent strands involved in displacement.43 We assume that for DNA > DNA strand displacement reactions there is no net free-energy change between adjacent states during branch migration. These 4 free-energy parameters describe a one-dimensional free-energy landscape for a non-mismatched DNA > DNA strand displacement reaction. Notably, the IEL model as described by Irmisch et al. (2020) also accounts for spontaneous incumbent dissociation before state N is reached. The probability of spontaneous detachment of the incumbent strand is assumed to drop off exponentially with an increase in the number of remaining base pairs with the substrate strand. Expanding the one-dimensional landscape model to include spontaneous incumbent dissociation has been shown to improve predictions of experimental strand displacement kinetic data.10,11
In this study we introduce an additional free-energy parameter, ΔGrd, which describes the free-energy difference between DNA–DNA and RNA–DNA base pairs. Using these 5 free-energy parameters the free-energy change between each state was calculated in order to construct complete free-energy landscapes for DNA > DNA, RNA > DNA and DNA > RNA strand displacement reactions. We stress that using a single parameter to describe the asymmetry between DNA/DNA and DNA/RNA duplexes is the simplest possible way to adjust the landscape, and the effective ΔGrd is expected to be sequence dependent. We will use fits of ΔGrd to experimental data as a useful way to quantify the relative advantage of RNA or DNA strands in a given context.
Using an analytical solution of our model we calculated the predicted rate of reaction from the free-energy landscape for each system (ESI Note 3†). We first calculated the first passage time t, which is defined as the time taken to pass from state −γ through to state N for each system. Within the second order limit the first passage time is related to the effective second-order rate constant (keff) according to
 | (15) |
We made preliminary keff predictions for RNA > DNA and DNA > RNA toehold exchange reactions across a range of toehold lengths and branch migration domain lengths. For initial predictions we made use of free-energy parameter values extracted from previous work of DNA > DNA strand displacement kinetics and allowed ΔGrd to remain a flexible parameter.10 The IEL model suggests that for strand displacement reactions with no net free-energy change between states during branch migration (ΔGrd = 0kBT) the rate of strand displacement decreases with an increase in the branch migration domain length, β, according to
 | (16) |
Previous studies of hybridisation within the literature suggest that RNA–DNA hybrids are less stable than the corresponding DNA–DNA complexes for systems with a low purine content in the RNA strand of the hybrid, while a high RNA purine content produces the opposite thermodynamic trend.36–39 Under this assumption, we would expect RNA displacing DNA (RNA > DNA) and DNA displacing RNA (DNA > RNA) to exhibit an overall uphill free-energy landscape for low and high RNA purine content systems, respectively (Fig. 2B). Within these limits, our initial predictions suggest an approximately exponential decrease in effective rate constant with a linear increase in β (Fig. 2C). By contrast, we anticipate RNA > DNA and DNA > RNA strand displacement reactions to exhibit an overall downhill free-energy landscape for high and low RNA purine content systems, respectively. In this case preliminary predictions indicate a very weak dependence of the effective rate constant on β for branch migration domain lengths greater than 10nt. These initial predictions suggest that the branch migration domain length is a critical parameter in effectively extracting ΔGrd, displaying significantly different trends between uphill and downhill landscapes (Fig. S1†). Therefore, we focussed on systems with differing branch migration domain lengths to probe the relative stability of RNA–DNA and DNA–DNA base pairs, and extract a useful estimate for ΔGrd for RNA > DNA and DNA > RNA strand displacement reactions across systems of purine content extremes.
Experimental characterisation of RNA/DNA hybrid strand displacement reactions
We designed a toehold exchange reaction network to probe the reaction rates for RNA > DNA and DNA > RNA strand displacement systems. These toehold exchange reactions were monitored over time by assessing the concentration of released incumbent strand over the course of the reaction. We made use of a distinct fluorescent reporter detection system (Fig. 3A) to assess the concentration of released incumbent to avoid directly labelling the strands within the reaction of interest, which may otherwise influence the kinetics of strand displacement.44 The reporter complex was composed of a fluorescently (AlexaFluor488)-labelled strand (F) which was partially complementary to a quencher (IowaBlack-FQ)-associated strand (Q). The reporter complex was designed such that F had a 5′ overhang of 6nt or 8nt, which acted as the reporter toehold (δ). The released incumbent strand (Inc) possessed a domain complementary to the toehold δ, allowing the incumbent to displace the quencher-associated strand, resulting in a detectable fluorescent product (FInc). Across all the systems, we designed the reporter reaction to be effectively instantaneous compared to the toehold exchange reaction of interest such that the reporter acted as an effective readout for the toehold exchange kinetics.For each design we assessed RNA and DNA counterparts of invader and incumbent strands, however for all systems herein only DNA substrate strand and DNA–DNA reporter complexes were used. Importantly, all sequences were designed to minimise secondary structure which may otherwise have affected the strand displacement rate, and confounded estimation of keff. In this work, we designed one system with low purine content in the invader strand (17% G/A) and designed a second system with high purine content in the invader strand (78% G/A). For these two independently-designed systems we aimed to extract the effective rate constant for DNA > DNA, RNA > DNA and DNA > RNA strand displacement reactions across a range of invader toehold lengths (4–10nt) and branch migration domain lengths (11–26nt) or (11–21nt for the high RNA purine content design). We refer to RNA > DNA strand displacement for the design with high purine content in the RNA invader strand (and thus high purine content in the incumbent strand) as RNApu > DNApu and equivalently for DNA > RNA strand displacement as DNApu > RNApu. For systems with low purine content in the invader (and thus high pyrimidine content), we use RNApy > DNApy and DNApy > RNApy. In order to minimise interaction and limit potential sequestration of the reporter toehold by the invader we ensured that only 4nt of the invader strand overlapped with the reporter toehold. We also introduced a GC-rich clamp in both the incumbent–substrate and reporter complexes to minimise undesired leak reactions. This design resulted in an incumbent toehold (ε) of 4nt for all systems.
To minimise cost we designed our system such that only two RNA or DNA invaders were required across all toehold length and branch migration domain length combinations: one for the low RNA purine content design and one for the high RNA purine content design. For the low RNA purine content design an invader with γ = 10nt and β = 26nt was used, while the toehold length and branch migration domain length of the substrate and incumbent strands were adjusted. For the high RNA purine content design an invader with γ = 6nt and β = 21nt was used, while the branch migration domain length of the substrate and incumbent strands were adjusted to achieve the desired domain lengths.
We initially performed a series of reporter characterisation reactions to estimate the rate of TMSD for the reporter reaction (krep). For these experiments we combined the 15 nM of FQ with Inc at a range of concentrations (Fig. 3B). Across all the reporters that were tested we showed that the reporter strand displacement reaction was sufficiently rapid to act as an effective readout for the reaction of interest, confirming the suitability of these designs. We estimated krep for each reporter reaction by fitting an ODE model to the fluorescence data (ESI Note 7.3 and Fig. S6†). Final estimates of krep for all designs are given in Table S8.†
We next monitored the fluorescence for the complete strand displacement network for the low purine content design (Fig. 4A). We initially assessed the effect on keff of changing the invader toehold length (410nt) for a fixed branch migration domain length of 26nt. Reactions were initiated by combining 4 nM, 6 nM or 8 nM of Inv with 10 nM of SInc and 15 nM of FQ. We then estimated keff by fitting a simple ODE model to the fluorescent traces using a non-linear least-squares approach (ESI Note 8.3, Fig. S16–S18†) (Fig. 4B). We found that the estimated keff values (Fig. 4C) for DNApy > DNApy toehold exchange were in good agreement with experimental data from previous studies, with the rate appearing to plateau at an invader toehold length between 6nt and 7nt.5,10 Both DNApy > RNApy and RNApy > DNApy toehold exchange systems appeared to follow the same general trend as DNApy > DNApy toehold exchange. However, RNApy > DNApy and DNApy > RNApy strand displacement rates plateaued at toehold lengths closer to 7nt and 6nt, respectively. These results also reveal that RNApy > DNApy strand displacement is up to an order of magnitude slower than the corresponding DNApy > DNApy strand displacement reaction. In contrast, DNApy > RNApy strand displacement is up to an order of magnitude faster than DNApy > DNApy strand displacement and up to two orders of magnitude faster than RNApy > DNApy strand displacement. Numerical estimates of keff for RNApy > DNApy, DNApy > DNApy and DNApy > RNApy strand displacement reactions are given in Table S13.†
Subsequently, we investigated the effect of branch migration domain length on the rate of strand displacement. A 4nt invader toehold was used and a total of 4 branch migration domain lengths (11nt, 16nt, 21nt and 26nt) were explored (Fig. 4D). A fixed invader toehold of 4nt was selected as our initial model predictions suggested this toehold length would provide the most obvious rate differences between systems with uphill and downhill free-energy landscapes (ESI Note 4 and Fig. S1†). We found that for DNApy > DNApy strand displacement reactions, keff decreased by a factor of 15 for an approximate 2.5-fold increase in branch migration domain length. This fold-change is slightly larger than we would predict by eqn (16), although this is likely explained by variability between sequences. More importantly, keff for DNApy > RNApy strand displacement only decreased by a factor of 5.7 between 11nt and 26nt, suggesting that keff is less dependent on the length of the branch migration domain as compared to DNApy > DNApy strand displacement. Finally, the rate of RNApy > DNApy strand displacement decreased by a factor of 54 for an increase in the branch migration domain length between 11nt and 26nt, which is significantly larger than for DNApy > DNApy strand displacement.
Using the experimental data for RNApy > DNApy, DNApy > DNApy and DNApy > RNApy strand displacement systems we were able to parameterise our adapted IEL model and estimate ΔGrd. The available kinetic data did not strongly constrain all IEL parameters (Table S16†), as such we performed a 3-parameter fit to 24 rate constants. The predicted keff values obtained from the fully parameterised model showed good fit to the experimental kinetic data across both toehold length and branch migration domain length (Fig. 4E and F). The estimated free-energy parameters and rate parameter are given in Table 1. These parameters are in good agreement with previous values of DNA > DNA strand displacement reactions.10,11 For the low RNA purine content system we extracted a ΔGrd value of 0.16kBT. This value of ΔGrd for RNApy > DNApy strand displacement predicts an overall uphill (although notably shallow) free-energy landscape during branch migration. In contrast, our model predicts an overall downhill free-energy landscape for DNApy > RNApy branch migration with a ΔGrd value of the same magnitude.
Next we probed the rate of strand displacement for an independent design with alternative sequence composition. Specifically, we investigated the effect of high purine content (78%) within the RNA invader strand (Fig. 5A). We studied 3 different branch migration domain lengths (11nt, 16nt and 21nt) for a fixed invader toehold length of 4nt. As above, we estimated keff for each system by fitting an ODE model to the fluorescence traces (Fig. 5B). In complete contrast to the low RNA purine content design, we found that RNApu > DNApu strand displacement was up to an order of magnitude faster than DNApu > DNApu strand displacement, while DNApu > RNApu strand displacement was over an order of magnitude slower than DNApu > DNApu strand displacement (Fig. 5C). For DNApu > DNApu strand displacement we see a reduction in keff by a factor of 1.7 between branch migration domain lengths of 11nt and 21nt, in accordance with eqn (16). For an approximate doubling in the branch migration domain length, we observe no decrease or even a slight increase in keff for RNApu > DNApu strand displacement (keff = 9.670 × 104 M−1 s−1 for β = 11nt and keff = 1.640 × 105 M−1 s−1 for β = 21nt), indicating that keff is effectively independent of branch migration domain length across this range. Finally, we observe a reduction in keff by a factor of 4.8 for DNApu > RNApu strand displacement for an increase in β between 11nt and 16nt. Notably, we were unable to explicitly estimate keff for β = 21nt because the reaction speed was slow enough for an undesired leak reaction to obfuscate the reaction kinetics of interest. Numerical estimates of keff for RNApu > DNApu, DNApu > DNApu and DNApu > RNApu strand displacement reactions are given in Tables S13 and S15.†
Using the experimental data from the high purine content design, we reparameterised the IEL model using the same approach as above. We fixed values for ΔGbp, ΔGassoc and ΔGp as above. We also fixed ΔGbm at the value predicted from experimental rate data of the low RNA purine content design (Table 1). We allowed both kbp and ΔGrd to be flexible parameters and extracted estimates of 3.0 (CI: 1.9; 4.5) × 107 s−1 and −0.25 ± 0.07kBT for these parameters, respectively. This parameterisation provided keff predictions that were in line with the experimental kinetic data for RNApu > DNApu and DNApu > DNApu strand displacement (Fig. 5D). However, for DNApu > RNApu strand displacement the model predicts higher keff values, although the trend across branch migration domain length is correctly predicted. Notably, the estimated value of |ΔGrd| is slightly larger than that predicted from the low RNA purine content experimental data, but in this case ΔGrd is negative. We identified alternative fits and ΔGrd estimates by fixing different free-energy parameters but importantly ΔGrd is estimated to be negative across all parameterisations (Fig. S21 and Table S17†). In contrast to the low RNA purine content design, these estimates of ΔGrd predict an overall downhill (although again notably shallow) free-energy landscape during branch migration for RNApu > DNApu strand displacement. Meanwhile, this model parameterisation predicts an overall uphill free-energy landscape for DNApu > RNApu branch migration.
It is interesting to ask whether the observed behaviour is robust to changes in experimental conditions. In particular, while high monovalent salt is common in nanotechnological settings, lower salt concentrations may be relevant to biological or biologically-derived systems, and high divalent salt concentrations are typically employed if large nanostructures such as DNA origami are present. In ESI Note 10, Fig. S22 and S23,† we show results for DNApy > DNApy, DNApy > RNApu, RNApy > DNApy, DNApu > DNApu, DNApu > RNApu and RNApu > DNApu reactions for systems with γ = 4nt, ε = 4nt and β = 11nt at both 100 mM NaCl and 10 mM MgCl2. Although we have not performed a complete set of carefully calibrated experiments under these conditions, the results in ESI Note 10† are consistent with a picture in which RNA > DNA is relatively favoured for low purine content in the RNA strand, and relatively disfavoured for high purine content. At 10 mM MgCl2, however, we observe that DNA > RNA reactions are suppressed in general, and that all reactions are slowed in 100 mM NaCl relative to 1 M NaCl.
Conclusions
In this work we experimentally characterised RNA > DNA and DNA > RNA strand displacement systems, which revealed notable differences in kinetics between DNA > DNA and RNA/DNA hybrid strand displacement systems, with important implications for the rational design of hybrid reaction networks. We have developed a parameterised free-energy landscape model which accurately predicts strand displacement kinetics for the test hybrid systems employed herein, given a fixed branch migration domain purine content. Most importantly, we demonstrate a strong sequence–dependence for the RNA > DNA and DNA > RNA strand displacement reactions that we tested. We highlight the importance of purine content within the RNA strand in determining the relative stability of RNA–DNA hybrids compared to DNA–DNA duplexes. We found that between high (78%) and low (17%) purine content within the RNA strand, estimated ΔGrd values shifted from −0.25kBT to 0.16kBT. These results support conclusions from previous thermodynamic studies into RNA–DNA hybridisation, which suggest that a high purine content in the RNA strand of an RNA–DNA complex results in increased stability compared to DNA–DNA duplexes while low RNA purine content results in reduced stability of RNA–DNA complexes.36–39Banerjee et al.36 report RNA–DNA hybrid nearest neighbour (NN) parameters at 1 M NaCl. These can be compared to the DNA–DNA NN parameters of SantaLucia.45 To get a rough idea of the relative stability of duplexes, one can average over the contribution of each base pair step at 298 K, weighted so as to produce the correct proportion of purine/pyrimidine bases in each strand. Doing so predicts ΔGrd values of +0.24kBT for 17% purine content in the RNA strand and −0.51kBT for 78% purine content in the RNA strand. These values are larger than those predicted in this work and would therefore predict more extreme kinetic behaviour for hybrid systems. It is worth noting that only a limited number of data points were used to derive these hybrid NN parameters and as such extreme behaviour is likely not well accounted for. Importantly, these NN parameters indicate that high purine content within the RNA strand should give a larger effect than low purine content in the RNA strand,36 which is also predicted from our experiments. Notably, there is some suggestion that the relative stability of RNA–DNA hybrids as compared to DNA–DNA complexes is also dependent on the G/C content of the displacement domain, particularly for sequences with high G/C content.39 Our study was limited to systems with approximately 50% GC content within the branch migration domain so future work should investigate how these sequence composition factors interact to determine the kinetics of strand displacement reactions.
Although the estimated ΔGrd values of −0.25kBT and 0.16kBT are relatively small, our results suggest these free-energy differences per base pair can compound over the whole landscape giving orders of magnitude differences in the rate of RNA > DNA strand displacement compared to DNA > RNA strand displacement. Moreover, changing the sequence composition of the RNA from 17% purine content to 78% purine content resulted in a difference in rate of up to 3 orders of magnitude, suggesting that this factor could be a critical parameter in the rational design of RNA/DNA hybrid strand displacement systems and facilitate tuneable reaction kinetics. Indeed, requesting minimal secondary structure within NUPACK typically yields sequence designs excluding G or C nucleotides,41 and therefore by default these sequences exhibit extremes in purine content. As such our work is particularly relevant to synthetic designs within the low secondary structure constraint.
With knowledge of the underlying free-energy landscapes of hybrid strand displacement, other tools, including use of mismatches, could be exploited for further fine-tuned kinetic control.11,12 Given that the predicted ΔGrd values are relatively small, elimination of mismatches within the incumbent–substrate complex could be employed to counter the observed uphill free-energy landscapes. We also suggest that future studies could explicitly investigate the effect of mismatches within hybrid systems to gain a better understanding how this might differ from DNA > DNA strand displacement reactions.
The vital role of RNA in the correct functioning of intracellular processes makes RNA a critical target for both diagnostics and therapeutics. Putative detection or therapeutic systems based on strand displacement by RNA may be compromised by the sequence-dependent biases for and against RNA invasion of DNA duplexes observed here. On the one hand, if an RNA strand struggles to complete displacement, it will be difficult to detect. On the other, if the RNA strand completes displacement too easily, it will be more difficult to distinguish perfectly matching sequences from single nucleotide mutants. While real, clinically relevant RNA sequences may not fall into the purine content extremes, we propose that our work may provide informative limits on the possible behaviours of these systems.
Future work should focus on exploring the sequence dependence of RNA/DNA strand displacement, further looking to confirm whether the behaviour revealed here applies across all sequences and experimental conditions. We note that, consistent with our preliminary data, nearest neighbour models predict a qualitatively similar sequence dependence of ΔGrd at 100 mM and 1 M NaCl.36,45 Indeed, the key question is whether nearest neighbour models of DNA/DNA and DNA/RNA duplexes, in their current parameterisation, are sufficient to provide either quantitative or semi-quantitative predictions for the sequence dependence of hybrid strand displacement rates. If so, relatively few experiments would be needed to establish a useful predictive tool, based on the free-energy landscape model with a slope determined by the nearest neighbour models. If not, a far larger set of experiments will be necessary to characterise the range of possible behaviour.
Author contributions
F. G. S., J. P. G., M. M. S. and T. E. O. devised the project. F. G. S. performed the experiments (except experiments performed at 100 mM NaCl and 10 mM MgCl2, which were performed by K. J.). F. G. S. performed the data fitting, and with support from J. P. G. and T. E. O., analysed the data. F. G. S., J. P. G., K. J., M. M. S. and T. E. O. wrote the manuscript.Data availability
All raw data, fitting and parameterisation code are freely available at https://doi.org/10.5281/zenodo.10090783.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by UK Engineering and Physical Sciences Research Council (EPSRC) [EP/S022856/1 to F. G. S.]; the Royal Academy of Engineering Chair in Emerging Technologies award [CiET2021\94 to M. M. S.]; a Royal Society PhD studentship to K. J., and a Royal Society University Research Fellowship to T. E. O. The authors would like to acknowledge Dr Rakesh Mukherjee for his assistance in checking the data and code associated with this work.References
- K. M. Cherry and L. Qian, Nature, 2018, 559, 370–376 CrossRef CAS PubMed.
- H. Su, J. Xu, Q. Wang, F. Wang and X. Zhou, Nat. Commun., 2019, 10, 5390 CrossRef PubMed.
- J. K. Jung, C. M. Archuleta, K. K. Alam and J. B. Lucks, Nat. Chem. Biol., 2022, 18, 385–393 CrossRef CAS PubMed.
- D. Y. Zhang, A. J. Turberfield, B. Yurke and E. Winfree, Science, 2007, 318, 1121–1125 CrossRef CAS PubMed.
- D. Y. Zhang and E. Winfree, J. Am. Chem. Soc., 2009, 131, 17303–17314 CrossRef CAS PubMed.
- L. Oesinghaus and F. C. Simmel, Nat. Commun., 2019, 10, 2092 CrossRef PubMed.
- S. F. J. Wickham, J. Bath, Y. Katsuda, M. Endo, K. Hidaka, H. Sugiyama and A. J. Turberfield, Nat. Nanotechnol., 2012, 7, 169–173 CrossRef CAS PubMed.
- Y. Guo, M. Wang, F. Shen, Z. Hu, H. Ding, W. Yao and H. Qian, Anal. Methods, 2021, 13, 447–452 RSC.
- M. Mohammadniaei, M. Zhang, J. Ashley, U. B. Christensen, L. J. Friis-Hansen, R. Gregersen, J. G. Lisby, T. L. Benfield, F. E. Nielsen, J. Henning Rasmussen, E. B. Pedersen, A. C. R. Olinger, L. T. Kolding, M. Naseri, T. Zheng, W. Wang, J. Gorodkin and Y. Sun, Nat. Commun., 2021, 12, 5089 CrossRef CAS PubMed.
- P. Irmisch, T. E. Ouldridge and R. Seidel, J. Am. Chem. Soc., 2020, 142, 11451–11463 CrossRef CAS PubMed.
- R. R. F. Machinek, T. E. Ouldridge, N. E. C. Haley, J. Bath and A. J. Turberfield, Nat. Commun., 2014, 5, 1–9 Search PubMed.
- N. E. C. Haley, T. E. Ouldridge, I. Mullor Ruiz, A. Geraldini, A. A. Louis, J. Bath and A. J. Turberfield, Nat. Commun., 2020, 11, 2562 CrossRef CAS PubMed.
- A. J. Genot, D. Y. Zhang, J. Bath and A. J. Turberfield, J. Am. Chem. Soc., 2011, 133, 2177–2182 CrossRef CAS PubMed.
- W. Deng, J. Y. Xu, H. Peng, C. Z. Huang, X. C. Le and H. Zhang, Biosens. Bioelectron., 2022, 217, 114704 CrossRef CAS PubMed.
- A. J. Genot, J. Bath and A. J. Turberfield, J. Am. Chem. Soc., 2011, 133, 20080–20083 CrossRef CAS PubMed.
- G. A. Wang, X. Wu, F. Chen, C. Shen, Q. Yang and F. Li, J. Am. Chem. Soc., 2023, 145, 2750–2753 CrossRef CAS PubMed.
- F. Wang, H. Lv, Q. Li, J. Li, X. Zhang, J. Shi, L. Wang and C. Fan, Nat. Commun., 2020, 11, 121 CrossRef CAS PubMed.
- G. Chatterjee, Y.-J. Chen and G. Seelig, ACS Synth. Biol., 2018, 7, 2737–2741 CrossRef CAS PubMed.
- S. Chen and T. Hermann, J. Am. Chem. Soc., 2021, 143, 20356–20362 CrossRef CAS PubMed.
- W.-J. Wang, J. Lin, C.-Q. Wu, A.-L. Luo, X. Xing and L. Xu, Nucleic Acids Res., 2023, 51, 7691–7703 CrossRef CAS PubMed.
- R. Lopez, R. Wang and G. Seelig, Nat. Chem., 2018, 10, 746–754 CrossRef CAS PubMed.
- A. Bayés-Genis, D. E. Lanfear, M. W. J. de Ronde, J. Lupón, J. J. Leenders, Z. Liu, N. P. A. Zuithoff, M. J. C. Eijkemans, E. Zamora, M. De Antonio, A. H. Zwinderman, S.-J. Pinto-Sietsma and Y. M. Pinto, Eur. J. Heart Failure, 2018, 20, 67–75 CrossRef PubMed.
- H. Fang, J. Xie, M. Zhang, Z. Zhao, Y. Wan and Y. Yao, Am. J. Transl. Res., 2017, 9, 953–961 CAS.
- R. Hernández, E. Sánchez-Jiménez, C. Melguizo, J. Prados and A. R. Rama, BMB Rep., 2018, 51, 563–571 CrossRef PubMed.
- N. van Boven, I. Kardys, L. C. van Vark, K. M. Akkerhuis, M. W. J. de Ronde, M. A. F. Khan, D. Merkus, Z. Liu, A. A. Voors, F. W. Asselbergs, E.-J. van den Bos, E. Boersma, H. Hillege, D. J. Duncker, Y. M. Pinto and D. Postmus, Eur. J. Heart Failure, 2018, 20, 89–96 CrossRef CAS PubMed.
- Z. Zhou, H. Xiong, F. Xie, Z. Wu and Y. Feng, Front. Neurol., 2020, 11, 132 CrossRef PubMed.
- S. Paik, S. Shak, G. Tang, C. Kim, J. Baker, M. Cronin, F. L. Baehner, M. G. Walker, D. Watson, T. Park, W. Hiller, E. R. Fisher, D. L. Wickerham, J. Bryant and N. Wolmark, N. Engl. J. Med., 2004, 351, 2817–2826 CrossRef CAS PubMed.
- X. Tang, Y. Wang, L. Zhou, W. Zhang, S. Yang, L. Yu, S. Zhao, K. Chang and M. Chen, Microchim. Acta, 2020, 187, 172 CrossRef CAS PubMed.
- Y.-Y. Zhou, G.-F. Li, R.-X. Ma, Y. Lin, J.-W. Wu, Y.-Y. Wu, J. Yan, S.-G. Liu, X.-C. Tan and K.-J. Huang, Anal. Chem., 2023, 95, 14052–14060 CrossRef CAS PubMed.
- P. B. Chen, H. V. Chen, D. Acharya, O. J. Rando and T. G. Fazzio, Nat. Struct. Mol. Biol., 2015, 22, 999–1007 CrossRef CAS PubMed.
- T. G. Fazzio, Transcription, 2016, 7, 121–126 CrossRef CAS PubMed.
- S. Toubiana and S. Selig, FEBS J., 2018, 285, 2552–2566 CrossRef CAS PubMed.
- A. Brambati, L. Zardoni, E. Nardini, A. Pellicioli and G. Liberi, Mutat. Res., Rev. Mutat. Res., 2020, 784, 108300 CrossRef CAS PubMed.
- F. Hong and P. Šulc, J. Struct. Biol., 2019, 207, 241–249 CrossRef CAS PubMed.
- M. Klein, B. Eslami-Mossallam, D. G. Arroyo and M. Depken, Cell Rep., 2018, 22, 1413–1423 CrossRef CAS PubMed.
- D. Banerjee, H. Tateishi-Karimata, T. Ohyama, S. Ghosh, T. Endoh, S. Takahashi and N. Sugimoto, Nucleic Acids Res., 2020, 48, 12042–12054 CrossRef CAS PubMed.
- J. I. Gyi, A. N. Lane, G. L. Conn and T. Brown, Biochemistry, 1998, 37, 73–80 CrossRef CAS PubMed.
- E. Hantz, V. Larue, P. Ladam, L. Le Moyec, C. Gouyette and T. Huynh Dinh, Int. J. Biol. Macromol., 2001, 28, 273–284 CrossRef CAS PubMed.
- E. A. Lesnik and S. M. Freier, Biochemistry, 1995, 34, 10807–10815 CrossRef CAS PubMed.
- H. Liu, F. Hong, F. Smith, J. Goertz, T. Ouldridge, M. M. Stevens, H. Yan and P. Šulc, ACS Synth. Biol., 2021, 10, 3066–3073 CrossRef CAS PubMed.
- J. N. Zadeh, C. D. Steenberg, J. S. Bois, B. R. Wolfe, M. B. Pierce, A. R. Khan, R. M. Dirks and N. A. Pierce, J. Comput. Chem., 2011, 32, 170–173 CrossRef CAS PubMed.
- J. Cabello-Garcia, W. Bae, G.-B. V. Stan and T. E. Ouldridge, ACS Nano, 2021, 15, 3272–3283 CrossRef CAS PubMed.
- N. Srinivas, T. E. Ouldridge, P. Šulc, J. M. Schaeffer, B. Yurke, A. A. Louis, J. P. K. Doye and E. Winfree, Nucleic Acids Res., 2013, 41, 10641–10658 CrossRef CAS PubMed.
- C. Li, Z. Li, W. Han, X. Yin, X. Liu, S. Xiao and H. Liang, Chem. Commun., 2022, 58, 5849–5852 RSC.
- J. SantaLucia Jr and D. Hicks, Annu. Rev. Biophys. Biomol. Struct., 2004, 33, 415–440 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr00542b |
| This journal is © The Royal Society of Chemistry 2024 |




