Optical gain and entanglement through dielectric confinement and electric field in InP quantum dots

Abstract

Quantum dots are widely recognized for their advantageous light-emitting properties. Their excitonic fine structure along with the high quantum yields offers a wide range of possibilities for technological applications. However, especially for the case of colloidal QDs, there are still characteristics and properties which are not adequately controlled and downgrade their performance for applications which go far beyond the simple light emission. Such a challenging task is the ability to manipulate the energetic ordering of exciton and biexciton emission and subsequently control phenomena such as Auger recombination, optical gain and photon entanglement. In the present work we attempt to engineer this ordering for the case of InP QDs embedded in polymer matrix, by means of their size, the dielectric confinement and external electric fields. We employ well tested, state of the art theoretical methods, in order to explore the conditions under which the exciton–biexciton configuration creates the desired conditions either for optical gain or photon entanglement. Indeed, this appears to be feasible for QDs with small diameters (1 nm, 1.5 nm) embedded in a host material with high dielectric constant and additional external electric fields. These findings offer a new design principle which might be complementary to the well-established type II core–shell QDs approach for achieving electron–hole separation.

---

1. Introduction

The phenomenon of transferring the recombination energy of an exciton to an additional charge carrier instead of its conversion to a photon is called Auger recombination and is quite common in semiconductors that are subjected to optical or electrical excitation.¹ When multiple excitons per particle are generated, Auger recombination emerges as the primary factor that restricts the overall quantum efficiency of optoelectronic processes in colloidal QDs.² Additionally, it is responsible for the efficiency roll-off (efficiency droop) in light-emitting diodes.³ In the meantime, the Auger recombination of charged excitons would also result in an effect called photoluminescence blinking which is very common in the case of single colloidal QDs. The blinking is particularly harmful to bio-related applications such as single-molecule labeling and imaging.^4,5

Various techniques have been employed in order to decrease the Auger rates. The most promising efforts include either the utilization of elongated quantum dots (QDs)⁶ of core/shell hetero-QDs,⁷ and the application of external electric fields.⁸ These approaches favor the reduction of exciton–exciton coupling while in the same time they retain the advantages of strong confinement. The most innovative approach to address the issue of Auger decay involves the introduction of techniques and/or configurations which allow for optical-gain in the single-exciton regime, wherein Auger recombination is rendered inactive. A successful implementation of this idea has been achieved by Klimov et al.,⁹ by taking advantage of the band alignment in type-II core/shell hetero-quantum dots. Another successful approach to suppress Auger recombination is to use large QDs where the wave function overlap between electron and holes is reduced and non-local effects appear.¹⁰

In this particular case, the electrons and holes are confined in different parts of the nanostructure. The electrons remain at the core while the holes are confined in the shell. The resulting spatial separation between the two charge distributions leads to the emergence of a strong local field, which affects the lowest energy transitions by means of a Stark shift. If E_X and E_XX are the exciton (X) and biexciton (XX) total energies and ħω_XX and ħω_X denote the energy of the XX → X and X → 0 transitions, then the energy difference between these peaks, is represented by the symbol Δ_XX = ħω_XX − ħω_X = J_ee + J_hh − 2J_eh. The sign of this quantity plays an important role in the optical gain of nanocrystals since it indicates the relative positions between exciton and biexciton peaks. A negative value of Δ_XX implies that the X–X interaction is attractive in nature forcing the XX → X transition to shift towards a lower energy. Such an effect can potentially increase the absorption probability of a photon emitted from transition (i.e. X → 0) that lies energetically just above the biexciton absorption peak (i.e. X → XX), having a negative impact on the possible existence of any lasing properties. On the other hand, a positive value of Δ_XX would indicate a X–X repulsion which, if comparable to or greater than the transition line width, would enhance the lasing properties since the photon emitted by the X → 0 transition has lower energy than the one required for the X → XX transition.⁹ Positive values of Δ_XX have been observed for small strained self-organized InAs/GaAs QDs.¹¹

In parallel, it is widely recognized that the creation of a photon source that produces polarization entangled photons on demand is a vital prerequisite for applications in the fields of quantum information and quantum optics.^12,13 To this end, QDs offer the possibility to take advantage of the biexciton–exciton transitions^14,15 and create such entangled photon pairs. However, the favorable conditions for entanglement are destroyed by the fine structure splitting (FSS) which is present in the intermediate exciton state and significantly affects the radiative cascade. Various approaches have been successfully employed to mitigate the FSS, including the application of suitable electric,¹⁶ magnetic¹⁷ or strain¹⁸ as well as a combination of electric and strain fields,¹⁹ engineering of QD size and composition^20,21 and controlling the growth process in order to produce highly symmetric QDs.²²

An alternative way which could help to overcome the FSS and lead to the generation of entangled photon pairs, involves the fine tuning of the biexciton binding energy to zero.^23,24 This has been experimentally achieved with techniques which include the introduction of lateral strain in the material²⁵ or suitable electric fields.^24,26

Motivated by the aforementioned open issues in the field and our recent findings regarding the ways that the dielectric confinement affects the exciton properties in wurtzite colloidal ZnO quantum dots,²⁷ we chose to investigate possible routes to address the challenges mentioned above. In particular, it has been previously found²⁷ that for the case of ZnO QDs embedded in a host material the exciton energy increases and the exciton binding energy decreases as the dielectric constant of the surrounding material becomes larger. This behavior is induced by the presence of a self-polarization potential due to the dielectric mismatch on the QD's surface. Specifically, this potential primarily affects the localization of the hole charge density, causing it to migrate towards the center of the QD, while in the same time the electron density appears to be almost unaffected. This different behavior leads to a subsequent reduction of the overlap between the electron and hole and inevitably reduces the exciton binding energy. The self canceling arrangement of positive and negative densities is destroyed by this charge separations and the emerging internal local field modifies the conditions for the biexciton creation. As a result, the exciton and biexciton properties of QDs might be manipulated by suitably engineering their host environment and their dielectric mismatch. This provides us with an extra degree of freedom which, when complemented with the additional application of external fields, can greatly enhance our capabilities to fine tune the exciton and biexciton ordering as desired.

Following this line of work, we turn our attention to zinc blende InP quantum dots and investigate the impact of the surrounding host material and the externally applied electric field on the exciton and biexciton fine structure. Actually InP QDs/polymer nanocomposites have been widely used as a means to improve the stability of InP QDs against heat and moisture²⁸ and improve their quantum yield.²⁹ To this purpose we employ large-scale atomistic pseudopotential calculations which incorporate the effects of multiband coupling, multivalley coupling, spin–orbit interaction, and excitonic correlation via the configuration interaction method.^27,30–33 The primary objective is to explore the possible existence of favorable conditions (QD size, host material and external electric fields) which may actually allow us to control the exciton–biexciton ordering. The accuracy of the observed trends through the described computational approach is also tested against a small set of benchmark calculations performed with Density Fuctional Theory (DFT) methods coupled to our own CI package.

2. Method

The computational modeling of the systems under consideration is based on solving the following single-particle Schrödinger equation in the framework of the empirical pseudopotential method (EPM).^27,30–33

In this formula, the QD potential is represented by a superposition of screened atomic pseudopotentials centered at atom sites and v^SO_α represents the spin–orbit term. E is the applied electric field and |q| is the electron charge in atomic units (i.e. |q| = 1). In general the atomic pseudopotentials used in the EPM are thoroughly optimized in order to accurately reproduce the band structure of the bulk material, including the values of the hole and electron effective masses. In the particular case the adopted potentials for InP have been taken from literature.³⁴ Furthermore, in order to consider the dielectric confinement and the external electric field, the model Hamiltonian has been complemented by the terms V_s (self-polarization) and (electric field) respectively. The analytic form of the self-energy term can be found in our previous work.²⁷

Once the eigenfunctions of the system have been calculated, a screened configuration interaction (CI) scheme is employed in order to obtain the excitations of the QD. The excitonic wavefunctions are expanded in terms of singly excited Slater determinants constructed from the single-particle wavefunctions produced by the solution of the corresponding Schrödinger equation. Since the CI expansion is limited only to single excitations and the active space includes only a small number of electron and hole states, it is necessary to screen all the Coulomb interactions.³⁰ As for the exchange interactions, it has been argued³⁵ that in the limiting case where transitions are considered over a wide energy range, they should be unscreened. However, in our case where only a few lowest energy transitions are considered, the interaction should be screened by the full dielectric function. Thus, in the present work we will employ the previously used approximation,²⁷ in which the inverse dielectric constant consists of an electronic high-frequency contribution³⁶ and an ionic low-frequency contribution.^37,38

In order to find the optimal size and composition of the active space, an initial set of benchmark calculations was performed. The results indicated that the required accuracy as well as the desired computational efficiency can be achieved by including in our CI treatment the 10 highest occupied states and 8 lowest unoccupied states.

For the case of biexciton calculations the CI expansion includes only doubly excited determinants (i.e. two electrons and two holes). The optical transitions are calculated within the dipole approximation.

Although the adopted computational scheme has been proved extremely accurate for a wide range of materials and properties throughout the years, it has been considered necessary to further validate its trends by means of selective first principles calculations. For this reason we have performed some additional benchmark DFT calculations for the smallest QDs in order to verify that the ordering change in the position of exciton and biexciton peaks is validated by a completely different methodology. In particular, all structures considered in this step were optimized at a PBE/def2-SVP^39,40 level of theory. In the relaxed geometries, the solvation effects (with the desired dielectric constants) were taken into consideration using the COnductor-like Screening MOdel (COSMO) model.⁴¹ On top of this, we carried out two-component, single-point calculations^42,43 using the x2c-SVPall-2c basis set⁴⁴ and the PBE0 hybrid functional.^45–49 The excited states were then calculated using the same screened CI methodology⁵⁰ used for the EPM calculations.²⁷

3. Results and discussion

For the purposes of the current study a total number of six InP QDs has been created with diameters 1.0, 1.5, 2.0, 3.0, 4.0 and 5.0 nm respectively using the experimental lattice constants of bulk InP. The resulting structures were passivated by embedding them in an artificial material with wider gap and suitable band offsets. An additional dielectric confinement is imposed by assigning a desired dielectric constant ε to the surrounding material. In the present work, four different values have been used ε = 4 (M4), ε = 15 (M15), ε = 40 (M40) and ε = 80 (M80). These values are considered realistic since they correspond to actual materials which have been (or can be) used as hosts for InP QDs. Such examples could be poly(methyl-methylacrylate)-PMMA, polyvinyl alcohol–PVA and cyanoethylated cellulose polymer with 20% to 40% volume fracture of BaTiO₃ filler.⁵¹ In such cases, the ligands of the QDs can be syntheticaly exchanged with the polymers thus making the QDs being in direct contact with the host.^28,29 For the screening of the CI calculations, the following parameter set was also adopted ω_LO = 344.5 cm⁻¹, , , 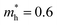ε(∞) = 9.61, ε(0) = 12.5.

The exciton energy obtained through the CI method for various quantum dot diameters across four different dielectric matrices is displayed in Fig. 1a. The anticipated trend of the exciton energy decreasing as a function of the quantum dot (QD) diameter is consistently observed in all scenarios, irrespective of the surrounding environment. Furthermore, it is evident that the dielectric constant of the host material causes a shift in the exciton energy towards higher values across all size ranges. The observed trend can be safely attributed to the self-polarization potential, as has been found both experimentally^52–54 and theoretically^55,56 in the case of InP quantum dots. The variation of the exciton binding energy across the various quantum dot (QD) diameters within the four distinct dielectric matrices is illustrated in Fig. 1b. The exciton binding energy exhibits a decreasing behavior as the quantum dot diameter increases across all host matrices as expected from quantum confinement. However, the most interesting feature so far, is related to the dependence of the binding energy of the excitons on the dielectric constant of the surrounding material. As the ε of the host increases the binding energy decreases significantly (initially) but then it seems as if it saturates. For example as we move from small values (e.g. M4) to larger ones (e.g. M15) the change is quite prominent but as we keep increasing ε (e.g. from M15 to M40 or M80) the shift of the curve seem to converge to a specific limit.

Fig. 1 (a) Exciton energy as a function of QD diameter for all the host materials considered. (b) Dependence of the exciton binding energy on size and surrounding material.

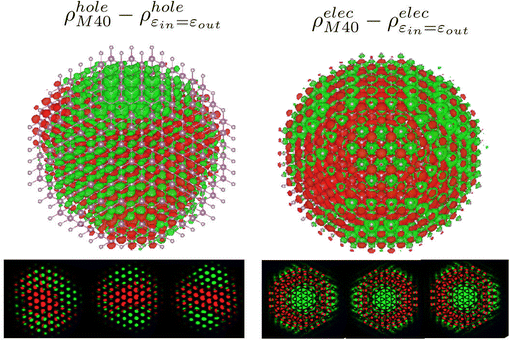
In order to gain some insight into this behavior, we constructed density difference isosurfaces for the holes and electrons participating in the formation of excitons and focus on the charge redistribution induced by the presence of the matrix material, as described in ref. 26. The density differences defined by the formula ρ_diff = ρ_{(εin≠εout)} − ρ_(εin=εout) can give us a visual representation of any rearrangement of the hole or electron charge distributions. In particular, areas of the ρ_diff isosurface with positive values correspond to charge accumulation areas while the negative ones to charge depletion (see Fig. 2). Interestingly it is found that only the hole density is significantly affected by the presence of the host material (with increased ε_out) resulting in a charge migration towards the center of the QD. On the other hand, the electron density exhibits migration towards the surface but with a very small percentage. After all, it would seem that the dielectric mismatch at the dot's interface with the host material induces some mild charge separation within the dot, which in turn reduces the Coulomb interaction and accordingly the exciton binding energy. Moreover, this effect appears to quickly reach saturation, and from a certain point onward, an increase in the value of ε does not result in any additional charge separation or decrease in the exciton's binding energy.

Fig. 2 Charge migration due to the presence of the host material (M40 in this particular case). On the left side is the density difference between the hole densities (in the excitonic state) with and without the presence of the dielectric mismatch. On the right side is the same plot for the electron densities. The green color corresponds to charge depletion areas while the red color to charge accumulation. Since the presented isosurfaces are quite complicated we also provide some density slices on planes which pass through the center of the dot and they are perpendicular to the directions of the lattice vectors. For the case of the hole a 14% of the total charge is moved while for the electron the percentage is limited to 1%. The corresponding values for hole movement in the cases of M15 and M80 are ∼13% and ∼14% respectively. The color mapping in the two figures is different and it has been arbitrarily adjusted in order to clearly highlight the charge depletion and accumulation areas.

The biexciton energy behaves similarly to the exciton energy and decreased with increasing QD size and with decreasing ε_out (see Fig. 3a). In the same time, Δ_XX appears to increase as we move to hosts with larger ε and interestingly, when the value of ε is adequately large, it might even change sign (see Fig. 3b). This is actually the case for the smallest diameters (i.e. D = 1.0 nm and D = 1.5 nm). Actually the same behavior has also been observed for small strained self-organized InAs/GaAs QDs.¹¹ This is rather intriguing for two reasons: the first one is that as it has already been stated, positive values of Δ_XX imply optical gain while zero values of Δ_XX fulfill the condition for photon entanglement.²⁴ It is noteworthy that in Fig. 3b the M4 plot exhibits a non-monotonic behavior. This can be attributed to the relative values of ε_in and ε_out. In particular, the value of ε_in varies from approximately 2.9 to almost 5 (for the specific size ranges). As a result, the difference ε_in–ε_out for the case of M4 changes sign as the size of the QDs increases. Since this difference is important for the self-polarization effects²⁷ induced by the matrix environment, we deduce that it is tightly connected with the observed behavior. In all other matrices the ε_out is significantly larger than ε_in and as a result this trend does not appear.

Fig. 3 (a) Variation of ħω_XX as a function of size. (b) Δ_XX = ħω_XX − ħω_X as a function of the QD diameter in different host materials.

This behavior can be understood if one considers explicitly the terms which contribute to the Δ_XX: Δ_XX = J_ee + J_hh − 2J_eh. The values of all right hand terms depend on the localization patterns of the hole and electron charge densities. Fig. 4 makes this point very clear: when there is a dielectric mismatch, the hole density moves towards the center of the QD, but the electron density is essentially insensitive (moves very slightly towards the surface). As a result, the effect of the host material on the charge distribution of the carriers indicates that although J_ee is only marginally affected, the term J_hh increases as expected (since the holes tend to localize to the center) and the term J_eh decreases since the average e–h distance increases. As is also clearly seen from Fig. 3b, above a specific threshold diameter (e.g. D = 3 nm for M4 and M15, D = 4 nm for M40, M80) the biexciton binding energy decreases with decreasing confinement. Actually the radius which defines the onset of this threshold diameter moves to higher values as the dielectric constant of the host materials increases.

Fig. 4 Biexciton charge polarization due to the presence of dielectric mismatch. The color coding and the description is similar to the one of Fig. 2. In the specific case the percentage of hole charge movement towards the center is ∼13% while the corresponding value for the electron (towards the surface) is 1%.

This means that, as it could be expected, for smaller dots the repulsive term V_hh is significantly enhanced due to the combined effects of strong spatial confinement and hole migration towards the center of the QD, hence affecting the binding characteristics of the biexciton. As the size of the QD increases this combined effect becomes looser and the attractive term V_eh takes the leading role.

Due to the fact that the observed changes in the ordering of exciton and biexciton peaks (i.e. Δ_XX > 0 or Δ_XX < 0) is a rather important finding, we chose to verify the trend by means of a completely different computational approach. In particular, we performed some benchmark DFT calculations, as described in the previous section, for the smallest nanoparticles with different dielectric constants using the COSMO solvation model. Indeed it was verified that the ordering change of exciton and biexciton peaks takes place for small QDs and large values of ε (e.g. for QD diameter equal to 1 nm, Δ_XX = 18.8 meV for M40 and Δ_XX = 19.7 meV for M80).

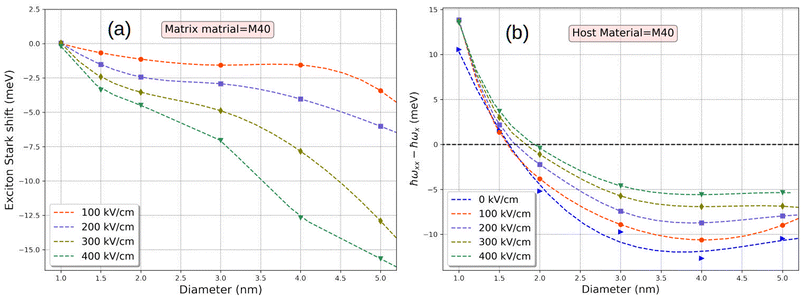
As a means to further increase our ability to manipulate the relative position of the X and XX peaks, the application of external electric field was also considered. This was achieved by incorporating into the Hamiltonian of eqn (1), the last term. The electric field was applied along the [001] direction, and set to 100, 200, 300 and 400 kV cm⁻¹. Its impact on the exciton can be expressed by means of the induced Stark shift (see Fig. 5a which depicts its dependence on the QD diameter and the strength of the field). As is clearly shown the absolute value of the shift is an increasing function of both the QD diameter and the field strength. Beyond that, our results revealed that, indeed, the application of an external electric field offers some extra ability to manipulate the relative peak positions. This can be clearly seen in Fig. 5b, where the field seems to shift the whole Δ_XX curve towards larger values. In this way even the initially bound biexciton of the 2.0 nm dot appears to move close to the zero binding energy threshold. Moreover, for the smaller dot, the field induced enhancement of Δ_XX (for the specific host) appears to become as large as 14 meV, which is quite close to the experimental line widths of fluorescence line narrowing (FLN) spectra (15–30 meV) of InP quantum dots.⁵⁷

Fig. 5 (a) Stark shift of the exciton as a function of the QD diameter for different electric fields. (b) Dependence of the biexciton binding energy on the size of the QD and the strength of the external field. In both figures the matrix material is M40.

4. Conclusions

Using large scale empiric pseudopotential calculations coupled with the configuration interaction method, we demonstrate that by a suitable embedding of InP QDs in a host material and the application of an external electric field, the exciton and biexciton properties can be engineered to suit specific requirements. The presence of dielectric confinement affects the properties of both excitons and biexcitons by inducing a mild charge separation between holes and electrons, which in turn affects the binding behavior of excitons and biexcitons. As a result, by controlling the size of InP QDs, their surrounding environment and possible external fields, we can effectively manipulate the details of excitonic emission and determine the relative position of X and XX peaks. This is extremely important since the ordering of these two peaks is critical in phenomena like optical gain and photon entanglement.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the Horizon-2020 research and innovation program of the European Union (grant no. 952335, NanoQIQO project). The authors thank Dr Nika Akopian for the fruitful discussions. GB acknowledges funding by the Cluster of Excellence “Advanced Imaging of Matter” of the Deutsche Forschungsgemeinschaft (DFG). EXC 2056-Project 390715994.

References

1. Recombination In Semiconductors, ed. P. T. Landsberg, Cambridge University Press, 2003.
2. D. Harankahage, et al., Quantum Shell in a Shell: Engineering Colloidal Nanocrystals for a High-Intensity Excitation Regime, J. Am. Chem. Soc., 2023, 145, 13326–13334.
3. W. K. Bae, Y.-S. Park, J. Lim, D. Lee, L. A. Padilha, H. McDaniel, I. Robel, C. Lee, J. M. Pietryga and V. I. Klimov, Controlling the influence of Auger recombination on the performance of quantum-dot light-emitting diodes, Nat. Commun., 2013, 4, 2661.
4. C. Galland, Y. Ghosh, A. Steinbrück, M. Sykora, J. A. Hollingsworth, V. I. Klimov and H. Htoon, Two types of luminescence blinking revealed by spectroelectrochemistry of single quantum dots, Nature, 2011, 479, 203–207.
5. F. Pinaud, S. Clarke, A. Sittner and M. Dahan, Probing cellular events, one quantum dot at a time, Nat. Methods, 2010, 7, 275–285.
6. H. Htoon, J. A. Hollingsworth, R. Dickerson and V. I. Klimov, Effect of Zero- to One-Dimensional Transformation on Multiparticle Auger Recombination in Semiconductor Quantum Rods, Phys. Rev. Lett., 2003, 91, 227401.
7. J. Nanda, S. A. Ivanov, H. Htoon, I. Bezel, A. Piryatinski, S. Tretiak and V. I. Klimov, Absorption cross sections and Auger recombination lifetimes in inverted core-shell nanocrystals: Implications for lasing performance, J. Appl. Phys., 2006, 99, 034309.
8. Y. Tang, Q. Qin, H. Yang, S. Feng, C. Zhang, J. Zhang, M. Xiao and X. Wang, Electrical control of biexciton Auger recombination in single CdSe/CdS nanocrystals, Nanoscale, 2022, 14, 7674–7681.
9. V. I. Klimov, S. A. Ivanov, J. Nanda, M. Achermann, I. Bezel, J. A. McGuire and A. Piryatinski, Single-exciton optical gain in semiconductor nanocrystals, Nature, 2007, 447, 441–446.
10. P. Huang, S. Sun, H. Lei, Y. Zhang, H. Qin and H. Zhong, Nonlocal interaction enhanced biexciton emission in large CsPbBr₃ nanocrystals, eLight, 2023, 3, 10.
11. S. Rodt, R. Heitz, A. Schliwa, R. L. Sellin, F. Guffarth and D. Bimberg, Repulsive exciton-exciton interaction in quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 035331.
12. A. J. Shields, Semiconductor quantum light sources, Nat. Photonics, 2007, 1, 215–223.
13. N. Gisin and R. Thew, Quantum communication, Nat. Photonics, 2007, 1, 165–171.
14. O. Benson, C. Santori, M. Pelton and Y. Yamamoto, Regulated and Entangled Photons from a Single Quantum Dot, Phys. Rev. Lett., 2000, 84, 2513–2516.
15. R. Singh and G. Bester, Nanowire Quantum Dots as an Ideal Source of Entangled Photon Pairs, Phys. Rev. Lett., 2009, 103, 063601.
16. B. D. Gerardot, S. Seidl, P. A. Dalgarno, R. J. Warburton, D. Granados, J. M. Garcia, K. Kowalik, O. Krebs, K. Karrai, A. Badolato and P. M. Petroff, Manipulating exciton fine structure in quantum dots with a lateral electric field, Appl. Phys. Lett., 2007, 90, 041101.
17. R. M. Stevenson, R. J. Young, P. Atkinson, K. Cooper, D. A. Ritchie and A. J. Shields, A semiconductor source of triggered entangled photon pairs, Nature, 2006, 439, 179–182.
18. R. Trotta, J. Martín-Sánchez, J. S. Wildmann, G. Piredda, M. Reindl, C. Schimpf, E. Zallo, S. Stroj, J. Edlinger and A. Rastelli, Wavelength-tunable sources of entangled photons interfaced with atomic vapours, Nat. Commun., 2016, 7, 10375.
19. R. Trotta, P. Atkinson, J. D. Plumhof, E. Zallo, R. O. Rezaev, S. Kumar, S. Baunack, J. R. Schröter, A. Rastelli and O. G. Schmidt, Nanomembrane Quantum-Light-Emitting Diodes Integrated onto Piezoelectric Actuators, Adv. Mater., 2012, 24, 2668–2672.
20. R. Hafenbrak, S. M. Ulrich, P. Michler, L. Wang, A. Rastelli and O. G. Schmidt, Triggered polarization-entangled photon pairs from a single quantum dot up to 30K, New J. Phys., 2007, 9, 315.
21. G. Pirard, F. B. Basset, S. Bietti, S. Sanguinetti, R. Trotta and G. Bester, Effects of random alloy disorder, shape deformation, and substrate misorientation on the exciton lifetime and fine structure splitting of GaAs/Al_x,Ga_1−xAs(111) quantum dots, Phys. Rev. B, 2023, 107, 205417.
22. A. Mohan, M. Felici, P. Gallo, B. Dwir, A. Rudra, J. Faist and E. Kapon, Polarization-entangled photons produced with high-symmetry site-controlled quantum dots, Nat. Photonics, 2010, 4, 302–306.
23. M. Korkusinski, M. E. Reimer, R. L. Williams and P. Hawrylak, Engineering photon cascades from multiexciton complexes in a self-assembled quantum dot by a lateral electric field, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 035309.
24. M. E. Reimer, M. P. van Kouwen, A. W. Hidma, M. H. M. van Weert, E. P. A. M. Bakkers, L. P. Kouwenhoven and V. Zwiller, Electric Field Induced Removal of the Biexciton Binding Energy in a Single Quantum Dot, Nano Lett., 2011, 11, 645–650.
25. F. Ding, R. Singh, J. D. Plumhof, T. Zander, V. Křápek, Y. H. Chen, M. Benyoucef, V. Zwiller, K. Dörr, G. Bester, A. Rastelli and O. G. Schmidt, Tuning the Exciton Binding Energies in Single Self-Assembled InGaAs/GaAs Quantum Dots by Piezoelectric-Induced Biaxial Stress, Phys. Rev. Lett., 2010, 104, 067405.
26. M. E. Reimer, M. Korkusiński, D. Dalacu, J. Lefebvre, J. Lapointe, P. J. Poole, G. C. Aers, W. R. McKinnon, P. Hawrylak and R. L. Williams, Prepositioned single quantum dot in a lateral electric field, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 195301.
27. C. S. Garoufalis, Z. Zeng, G. Bester, I. Galanakis, D. Hayrapetyan, E. Paspalakis and S. Baskoutas, Excitons in ZnO Quantum Dots: The Role of Dielectric Confinement, J. Phys. Chem. C, 2022, 126, 2833–2838.
28. J. H. Jo, S. J. Lee, H. S. Heo and K. Lee, Stability enhancement of InP quantum dot/poly(methyl methacrylate) nanocomposites for light-emitting diode applications by grafting thermoresponsive poly(N-isopropylacrylamide), J. Mater. Chem. C, 2021, 9, 14606–14612.
29. S. N. Sharma, A. Singh and S. Jain, Development of InP-based polymer nanocomposites by wet route for optoelectronic devices, Colloid Polym. Sci., 2017, 295, 985–993.
30. G. Bester, Electronic excitations in nanostructures: an empirical pseudopotential based approach, J. Phys.: Condens. Matter, 2009, 21, 023202.
31. L. Wang and A. Zunger, Solving Schrödinger's equation around a desired energy: Application to silicon quantum dots, J. Chem. Phys., 1994, 100, 2394–2397.
32. Z. Zeng, C. S. Garoufalis, S. Baskoutas, Y. Jia and G. Bester, Realization of linearly polarized exciton emission in wurtzite zinc oxide quantum dots, Phys. Rev. B, 2018, 98, 235410.
33. S. Baskoutas, Z. Zeng, C. S. Garoufalis and G. Bester, Morphology control of exciton fine structure in polar and nonpolar zinc sulfide nanorods, Sci. Rep., 2017, 7, 9366.
34. L. Zhang, J.-W. Luo, A. Zunger, N. Akopian, V. Zwiller and J.-C. Harmand, Wide InP Nanowires with Wurtzite/Zincblende Superlattice Segments Are Type-II whereas Narrower Nanowires Become Type-I: An Atomistic Pseudopotential Calculation, Nano Lett., 2010, 10, 4055–4060.
35. A. Franceschetti, H. Fu, L. W. Wang and A. Zunger, Many-body pseudopotential theory of excitons in InP and CdSe quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 1819.
36. R. Resta, Thomas-Fermi dielectric screening in semiconductors, Phys. Rev. B: Solid State, 1977, 16, 2717–2722 . Cited by: 241.
37. H. Haken, Kopplung nichtrelativistischer teilchen mit einem quantisierten feld, Lett. Nuovo Cimento, 1956, 10, 1230.
38. A. Franceschetti, H. Fu, L. Wang and A. Zunger, Many-body pseudopotential theory of excitons in InP and CdSe quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 1819.
39. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
40. F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
41. A. Klamt and G. Schüürmann, COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
42. D. Peng, N. Middendorf, F. Weigend and M. Reiher, An efficient implementation of two-component relativistic exact-decoupling methods for large molecules, J. Chem. Phys., 2013, 138, 184105.
43. D. Peng and M. Reiher, Local relativistic exact decoupling, J. Chem. Phys., 2012, 136, 244108.
44. P. Pollak and F. Weigend, Segmented contracted error-consistent basis sets of double-and triple-ζ valence quality for one-and two-component relativistic all-electron calculations, J. Chem. Theory Comput., 2017, 13, 3696–3705.
45. P. A. M. Dirac, Quantum mechanics of many-electron systems, Proc. R. Soc. London, Ser. A, 1929, 123, 714–733.
46. J. C. Slater, A simplification of the Hartree-Fock method, Phys. Rev., 1951, 81, 385.
47. J. P. Perdew and Y. Wang, Accurate and simple analytic representation of the electron-gas correlation energy, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244.
48. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865.
49. J. P. Perdew, M. Ernzerhof and K. Burke, Rationale for mixing exact exchange with density functional approximations, J. Chem. Phys., 1996, 105, 9982–9985.
50. A. R. Ziefuss, T. Steenbock and D. Benner, et al., Photoluminescence of Fully Inorganic Colloidal Gold Nanocluster and Their Manipuation Using Surface Charge Effects, Adv. Mater., 2021, 33, 2101549.
51. C. K. Chiang and R. Popielarz, Polymer Composites with High Dielectric Constant, Ferroelectrics, 2002, 275, 1–9.
52. A. Karpulevich, H. Bui, Z. Wang, S. Hapke, C. Palencia Ramírez, H. Weller and G. Bester, Dielectric response function for colloidal semiconductor quantum dots, J. Chem. Phys., 2019, 151, 224103.
53. O. I. Mićić, S. P. Ahrenkiel and A. J. Nozik, Synthesis of extremely small InP quantum dots and electronic coupling in their disordered solid films, Appl. Phys. Lett., 2001, 78, 4022–4024.
54. E. Cho, H. Jang, J. Lee and E. Jang, Modeling on the size dependent properties of InP quantum dots: a hybrid functional study, Nanotechnology, 2013, 24, 215201.
55. B. Sklénard, G. Mugny, B. Chehaibou, C. Delerue, A. Arnaud and J. Li, Size and Solvation Effects on Electronic and Optical Properties of PbS Quantum Dots, J. Phys. Chem. Lett., 2022, 13, 9044–9050.
56. D. F. Macias-Pinilla, J. Planelles and J. I. Climente, Biexcitons in CdSe nanoplatelets: geometry, binding energy and radiative rate, Nanoscale, 2022, 14, 8493–8500.
57. O. I. Micic, H. F. Cheong, A. Zunger, J. R. Sprague, A. Mascarenhas and A. Nozik, Size-Dependent Spectroscopy of InP Quantum Dots, J. Phys. Chem. B, 1997, 101, 4904–4912.

---