Study of a charge transition-driven resistive switching mechanism in TiO₂-based random access memory via density functional theory

Abstract

The nature of the conducting filament (CF) with a high concentration of oxygen vacancies (V_Os) in oxide thin film-based resistive random access memory (RRAM) remains unclear. The V_Os in the CF have been assumed to be positively charged (V_O²⁺) to explain the field-driven switching of RRAM, but V_O²⁺ clusters in high concentration encounter Coulomb repulsion, rendering the CF unstable. Therefore, this study examined the oxidation state of V_Os in the CF and their effects on the switching behavior via density functional theory calculations using a Pt/TiO₂/Ti model system. It was concluded that the V_Os in the CF are in a low oxidation state but are transformed to V_O²⁺ immediately after release from the CF. In addition, the short-range interactions between V_Os were confirmed to facilitate the rupture and rejuvenation of the CF by reducing the required activation energy. Finally, an improved switching model was proposed by considering the charge transition of V_Os, providing a plausible explanation for the reported coexistence of two opposite bipolar switching polarities: the eight-wise and the counter-eight-wise polarities.

---

1. Introduction

Metal–oxide-based resistive random-access memory (RRAM) is a promising next-generation memory device due to its low power consumption, high performance, and compatibility with current complementary metal oxide semiconductor technology. RRAM is currently applied to state-of-the-art applications such as process-in-memory and neuromorphic computing.^1–3 However, its operation mechanism is not fully understood yet, hampering systematic research on RRAM.

For valence-change type memory (VCM), the redistribution of oxygen vacancies (V_Os) in the conducting filament (CF) in response to applied bias is widely accepted as the major source of resistive switching.^4,5 However, there is still controversy about the charge state of V_Os in the CF. Based on their field-driven characteristic, it has been argued that the V_Os should be positively charged (that is, V_O²⁺). On the other hand, other recent studies questioned the V_O²⁺ argument because the CF with a high V_O²⁺ concentration would be unstable due to the Coulomb repulsion.^6–8 Lee et al. suggested that the CF consists of V_O⁰s rather than V_O²⁺s.⁷ They experimentally observed the acceleration of CF destruction once devices are illuminated by a green-light laser, enhancing a charge transition from V_O⁰ to V_O²⁺. They argued that this finding indicates that the original CF was composed of V_O⁰s. They also confirmed that the CF composed of V_O⁰s is more stable than the one composed of V_O²⁺s through density functional theory (DFT) calculations. Furthermore, Park et al. proposed a modified physical model that incorporated the charge transition from V_O²⁺ to V_O⁰ when the concentration of V_O exceeds a threshold value.⁸ The model allowed them to explain secondary set and retention failure, which the conventional model could not explain. Nevertheless, a theoretical study dealing with the evolution in oxidation number (ON) of V_O during the switching process is required to elucidate the effects of the charge transition of V_Os on the switching behavior.

Meanwhile, in bipolar-type resistive switching (BRS) devices, two opposing switching polarities were reported: the counter-eight-wise (c8w) and the eight-wise (8w) polarities. The c8w polarity is more general and corresponds to the case where the set and reset occur by applying negative and positive voltages to the active electrode, respectively.⁹ The active electrode refers to the electrode where switching occurs in the nearby switching film and is usually identified as the electrode with a higher work function. For VCM devices, the c8w BRS mode is well understood via a field-driven drift of V_O²⁺s. In contrast, the 8w BRS mode, an abnormal case where the set and reset occur by positive and negative voltages applied to the active electrode, respectively, has occasionally been observed in various oxides such as TiO₂, HfO₂, and SrTiO₃.^10–16 However, its origin is still under debate. Furthermore, both BRS modes can simultaneously appear in several VCM devices, as shown in Fig. 1, where the red and green lines represent the c8w and 8w BRS modes. This unusual I–V curve has been reported in TiO₂, Ta₂O₅, and Al₂O₃-based devices.^{10–12,17,18} For TiO₂ systems, there is no common consensus for the origin of the 8w BRS mode. For Pt/TiO₂/Ti devices, Yin et al. attributed this abnormal BRS mode to the electron trapping/detrapping effects at the interfacial states.¹⁰ Zhang et al., on the other hand, argued that the 8w BRS mode arises from the exchange of oxygen ions between the Pt electrode and TiO₂ layer at the Pt/TiO₂ interface.¹¹ For Pt/TiO₂/Pt devices, Miao et al. suggested that the switching polarity is determined by which electrode, top or bottom, dominantly participates in the switching process,¹² while Kim et al. explained that the switching mode depends on the shape of the CF.¹³ Accordingly, the mechanism of the 8w BRS mode in TiO₂-based devices remains controversial, especially when two opposite BRS modes coexist.

Fig. 1 Characteristic I–V curve exhibiting the coexistence of the c8w polarity (red) and the 8w polarity (green). LRS and HRS represent the low resistance state and high resistance state, respectively. The asterisks indicate that they are involved in the 8w polarity.

Therefore, this work shows the comprehensive DFT calculation results for a Pt/TiO₂/Ti model system with two main objectives: (1) elucidating the evolution in ON of V_O during switching and (2) proposing an improved mechanism encompassing both the c8w and 8w BRS modes. The Pt electrode was chosen as the active electrode due to its high work function. In this paper, the voltage is assumed to be applied to the Pt electrode while the Ti electrode is grounded. The 8w BRS mode of the Pt/TiO₂/Ti device was assumed to be filamentary type, based on the observation that the resistance value of the low resistance state (LRS) of the 8w BRS mode does not show area-dependency.¹¹ The Results and discussion of this paper are organized as follows: section A investigates the interaction between V_Os considering their ON; section B examines a suitable CF structure and its preference for the oxidation state; finally, section C provides a comprehensive explanation of the charge transition of the V_O and suggests a plausible origin for the coexistence of the two BRS modes in Pt/TiO₂/Ti devices.

2. Computational methods

The Vienna ab initio simulation package (VASP) was adopted for all DFT calculations using local density approximation (LDA) parameterized by Ceperley and Alder for the exchange–correlation functional.^19–22 The plane wave cutoff energy of 500 eV and Monkhorst–Pack 4 × 4 × 6 k-points were used for the conventional rutile unit cell of TiO₂. The k-points for supercells were scaled to keep the same k-point density as the unit cell. The atomic structures were relaxed until the Hellmann–Feynman forces were below 0.02 eV Å⁻¹. The 3s, 3p, 3d, and 4s orbitals of Ti and the 2s and 2p orbitals of O were treated as valence electrons. In order to mitigate a well-known bandgap underestimation of the conventional LDA calculations, the LDA+U approach suggested by Dudarev et al. was implemented to correct the on-site Coulomb interactions, with the U parameter for Ti 3d orbitals, U_d, of 4.0 eV and that for O 2p orbitals, U_p, of 9.0 eV.²³ The J parameter for Hund's coupling was fixed at 0 eV. All calculations included the spin polarization effects. The calculated lattice parameters of rutile TiO₂ were (a, b, c) = (4.543 Å, 4.543 Å, 2.957 Å), indicating good agreement with the experimental values within 1%.²⁴ The calculated bandgap of 2.51 eV, closer to the experimental bandgap of 3.0 eV than that obtained by the conventional LDA calculations of 1.81 eV, did not completely mitigate the bandgap underestimation problem.²⁵ However, the calculated defect states and formation energies of a V_O^q+ (q = 0, 1, 2) showed feasible agreements with previous Heyd–Scuseria–Ernzerhof (HSE) or DFT+GW studies, as described in Fig. S1,† demonstrating the reliability of our calculation conditions.^26,27

To simulate the various arrangements of V_Os, such as in the CF, they were introduced into the 3 × 3 × 6 supercells of rutile TiO₂ while keeping the lattice parameters fixed. This supercell was confirmed to sufficiently prevent unintended interactions between image cells, even if there are multiple V_Os inside. The formation energy (E_f) of a charged V_O was calculated as follows:

E_f(V_O^q+) = E_tot(V_O^q+) − E_tot(TiO₂) + μ_O + q(VBM + PA + ε_f), (1)

where E_tot(V_O^q+) indicates the total energy of a defective supercell containing one V_O^q+, and E_tot(TiO₂) is the total energy of the defect-free rutile supercell whose size is the same as that of the defective supercell. The third term, μ_O, is the chemical potential of oxygen, which was obtained from the equilibrium condition that μ_Ti of the TiO₂ layer should be identical to μ_Ti of the Ti electrode that is in contact. The last term corresponds to the electron chemical potential, where the VBM, PA, and ε_f are the valence band maximum of the rutile, potential alignment for a charged system, and the Fermi level with respect to the VBM, respectively. The high dielectric constant (ε_r) of rutile (∼100) makes the correction for electrostatic interaction between periodic images negligible, and thus, the correction was neglected as in the previous report.²⁶ For the E_f values of supercells containing more than one V_O^q+, eqn (1) was adequately modified.

To clarify the discussion, the ON was classified into average oxidation number (AON) and individual oxidation number (ION). AON represents the average ON of all V_Os within a supercell and is determined by dividing the total charge by the number of V_Os in the supercell. In this study, the AON was considered for all instances in which the number of electrons in the supercell is an integer. For example, for a supercell containing two V_Os, four electrons can be removed since each V_O can accommodate up to two electrons. Accordingly, five AONs (0, +0.5, +1, +1.5, +2) can be considered. Meanwhile, in a supercell where V_O sites are not symmetrically equivalent, individual V_Os may have distinct ONs that are different from the AON. This specific ON for each V_O is termed ION. To the authors’ knowledge, the ION of V_O has not been estimated, presumably due to the difficulties in its direct calculation. The conventional ON calculation methodologies, such as Bader charge (BC) analysis, apply only to ions but not to vacancies. Accordingly, this study devised an alternative approach to estimate the ION. It was revealed that, in rutile TiO₂, the sum of BC values of three neighboring Ti ions (∑BC) surrounding a certain V_O is determined by the ION of the V_O and the coordination numbers (CNs) of these three Ti ions. Other nearby V_Os hardly affect the ∑BC value, as shown in Fig. S2.† Consequently, the ION of each V_O can be estimated via the ∑BC value and CN distribution of neighboring Ti ions. The full description of this approach is provided in the ESI and Fig. S2–S6.† The sum of IONs obtained from the approach was compared with the actual total charge of the supercell to validate this proposed approach. These two values are sufficiently identical within an error of less than 3%, as shown in Table S1.†

For both the BC analysis and the activation energy (E_a) calculations, open-source codes were implemented.^28–30 A default setting was used for the BC analysis. For the E_a calculations, on the other hand, the climbing nudged elastic band (cNEB) method was used, and the images were stabilized until the forces were less than 0.05 eV Å⁻¹.

3. Results and discussion

A. Interaction between V_Os

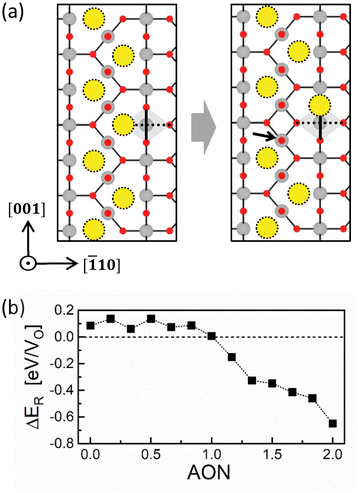
The long-range interaction between two charged vacancies can be understood through the Coulomb interaction. Besides, other factors, such as lattice distortion caused by vacancies, may also play a role in the short-range interaction, which is non-negligible in CFs with a high concentration of V_Os. For comprehending the short-range interaction, the cohesive energy (E_coh) was calculated as follows:

E_coh(V_O^q+) = E_f(two V_O^q+, d) − 2E_f(V_O^q+) (2)

The first term on the right-hand side is the E_f of two V_O^q+s separated by a distance of d, while the second term is that of an isolated V_O^q+ multiplied by a factor of 2. Fig. 2a shows the calculated results, where five AONs from 0 to +2 with increments of +0.5 were considered. For supercells containing two V_Os, their sites are symmetrically equivalent irrespective of d since all O sites in rutile are symmetrically equivalent. Accordingly, the two V_Os must exhibit an identical ION (i.e., q+ = ION = AON).

Fig. 2 (a) E_coh as a function of the distance between two V_O^q+s (q = 0, 0.5, 1, 1.5, and 2) in rutile TiO₂. (b) Atomic structure of rutile TiO₂ viewing along the [110] direction (left panel) and size of the Ti–O octahedron constituting the rutile TiO₂ (right panel). The bold rectangle (and line) and dotted line represent the equatorial plane and the vertical axis of the Ti–O octahedron, respectively. The numerical values adjacent to the blue lines indicate the distances between two oxygen ions in units of Å. Grey, red, and yellow circles indicate Ti, O, and V_O, respectively. This color notation is maintained throughout this paper. Electron clouds for (c) an isolated V_O⁰, (d) two V_O⁰s separated by a distance of 3.88 Å, and (e) two V_O⁰s separated by a distance of 4.42 Å, respectively (isosurface = 0.005 e Å⁻¹). The two electron clouds in (e) are located in two immediately adjacent (110) planes.

For V_O²⁺, the overall trend of the E_coh deviates from the Coulomb interaction (∼1/d), implying that other factors affect the short-range interaction. In particular, the E_coh reaches a maximum at distances of 3.88 Å and 3.91 Å, while it decreases significantly at the closer distances of 2.52 Å and 2.76 Å. This tendency is related to the atomic structure of rutile TiO₂, as shown in Fig. 2b, which consists of the Ti–O octahedral (right panel) columns stacked along the [001] direction and perpendicular to their neighbors. The bold rectangle (and line) and dotted line indicate the equatorial plane and the vertical axis of the Ti–O octahedron, respectively, while the blue lines indicate the distances between oxygen ions in units of Å. Once two V_O²⁺s are generated, the surrounding Ti ions tend to move further away from the two V_O²⁺s due to Coulomb repulsion between the positively charged Ti ions and V_O²⁺s. However, when the distance between the V_O²⁺s is 3.88 Å or 3.91 Å, the symmetrical position of these two V_O²⁺s in the Ti–O octahedron induces two Coulomb repulsions of equal magnitude and opposite directions on the central Ti ion, hindering this Ti ion from being further displaced. Accordingly, the system does not adequately mitigate the Coulomb repulsion, resulting in abnormally high E_coh values at distances of 3.88 Å and 3.91 Å. In contrast, at shorter distances of 2.52 Å and 2.76 Å, the central Ti ion can easily move away from the two V_O²⁺s since the two Coulomb repulsions are not canceled out, mitigating the repulsion between the Ti ion and the V_O²⁺s. The atomic structures before and after relaxation in each case are shown in Fig. S7.† The E_coh trend at close distance depends on which is predominant: either the mitigation effect by displacing the central Ti ion or the Coulomb repulsion between two vacancies. For V_O²⁺, the former dominates, resulting in a decrease in E_coh at the distance of 2.52 Å and 2.76 Å compared to 3.88 Å. Meanwhile, for V_O^1.5+, the latter dominates, leading to an increase in E_coh.

On the other hand, the E_coh of V_O²⁺ is not negligible even at a distance farther than 7.75 Å, the maximum distance examined. The corresponding composition to this distance is TiO_1.93 (or 2.15 × 10²¹ cm⁻³ in concentration). Considering that the Magnéli phase Ti₄O₇ (=TiO_1.75), a well-known CF structure in the TiO₂ system,³¹ is more oxygen-deficient, the distance between V_Os in an actual CF is certainly shorter than 7.75 Å. Consequently, the CF composed of V_O²⁺s will largely be affected by the short-range interaction and become unstable.

For V_O⁰, where Coulomb interaction is absent, the E_coh remains nearly zero at distances ≥4.42 Å. However, at distances shorter than 4.42 Å, specifically at 3.88 Å and 3.91 Å, the E_coh exhibits significant negative values, implying non-negligible effects of the short-range attraction between V_O⁰s. Fig. 2c shows the electron cloud for an isolated V_O⁰, revealing a symmetrical distribution around the V_O⁰. Fig. 2d illustrates the electron clouds of two V_O⁰s separated by 3.88 Å, clearly showing the overlap of the two electron clouds at the 4-coordinated Ti ion indicated by an arrow. The electron clouds are more concentrated at the 4-coordinated Ti ion, indicating that the electrons stabilize around the 4-coordinated Ti ion. The defect states in Fig. 2d are located at a depth of 1.01 eV below the conduction band minimum (CBM), which is much deeper than that of an isolated V_O⁰ (0.49 eV from the CBM; see Fig. S8a and b†). Considering that each state accommodates two electrons, this depth difference in the defect states leads to an energy gain of 1.04 eV, twice that of the defect level difference. This value is comparable to the corresponding E_coh of −0.83 eV, demonstrating that the charge redistribution by the electron cloud overlap is the primary cause of the short-range attraction. As the distance becomes <3.88 Å (2.52 Å and 2.76 Å in Fig. S8c and d†), on the other hand, the defect states become shallower, resulting in smaller magnitude E_coh values. On the other hand, the electron clouds of two V_O⁰s separated by a distance ≥4.42 Å do not overlap, as shown in Fig. 2e, resulting in nearly zero E_coh.

The most intriguing observation is that V_O^0.5+ and V_O¹⁺ exhibit similar trends in E_coh with V_O⁰ despite their positive charges. It is presumably due to a high ε_r value of rutile TiO₂, which effectively screens the electric field within the crystal. Further investigations on the effect of AON on the E_coh were conducted using virtual AONs of +0.25, +0.75, +1.25, and +1.75, as shown in Fig. S9.† The term ‘virtual’ was used since the number of electrons in the supercell with these AONs is a non-integer, making them physically infeasible. Nevertheless, the AONs ranging from 0 to +1 show similar negative E_coh trends, indicating an attractive force; hence, they are called the low oxidation state (LO state). In contrast, the AONs exceeding +1 exhibit significant increases in E_coh towards positive values, indicating a repulsive force, especially at distances of 3.88 Å and 3.91 Å. Hence, they are called the high oxidation state (HO state). Consequently, the V_Os belonging to the LO and HO states tend to attract and repel each other at a close distance, respectively.

B. Characteristics of the CF

In TiO₂-based RRAMs, the 8w BRS mode appears only when low electric power proceeds the electroforming.^12,13 The low-power electroforming may lead to two consequences. (1) Formation of the Magnéli phase Ti₄O₇-type CF is unlikely since it requires substantial thermal energy to overcome the large structural mismatch with the parent rutile TiO₂ phase.³² Hence, an alternative CF structure suitable for a low-power electroformed device is introduced in section B.1. (2) Insufficient electric power results in immature CF growth, creating a tunneling gap between the CF and the active electrode (Pt electrode) after the electroforming process.³³ The role of this tunneling gap in resistive switching is discussed in section C.

B.1. CF structure in the low-power electroformed device. The CF structure was constructed by arranging V_Os at intervals of 3.88 Å along the diagonal direction on the equatorial planes of the Ti–O octahedra, based on the E_coh analyses. The atomic structure of the CF was created using a 3 × 3 × 6 supercell with six V_Os, corresponding to a composition of TiO_1.94, as shown in Fig. 3a. The V_Os are aligned in a zigzag manner along the [001] direction. All V_O sites in our CF are symmetrically equivalent, ensuring that the ION of each V_O is identical to the AON. Although the concentration of V_Os in the proposed CF is considerably lower than that of the CF composed of the Magnéli phase Ti₄O₇, the V_Os can be well aligned with the assistance of a temperature gradient and the short-range interaction between V_Os. During the electroforming step, the V_Os comprising the CF will be reduced by electrons injected from the Ti electrode. This reduction reaction results in a decrease in AON to the LO state, promoting the alignment of V_Os by short-range attraction.

Fig. 3 (a) Atomic structure of the CF employed in this study. Due to the periodic boundary conditions, the V_O at the top is identical to the V_O at the bottom, resulting in six V_Os within the 3 × 3 × 6 supercell. For clarity, only the vicinity of the V_Os was shown. E_f distributions for various configurations of V_O with AONs of (b) 0, (c) +1, and (d) +2, respectively. Two CF structures previously proposed (green pentagon and red star) are also included. The dashed lines indicate the E_f of an isolated V_O in each case. The ε_f is set to zero for AONs of +1 and +2. (e) Atom-resolved DOS of the CF composed of V_O⁰s (blue areas), obtained by the projection onto the Ti atom marked by an arrow in (a). For comparison, the DOS projected on the furthest Ti atom from the V_O⁰s, standing for the perfect rutile TiO₂, is shown together as grey areas.

The proposed CF structure is consistent with a previous experiment that observed a spontaneous alignment of V_Os along the [001] direction in a rutile single crystal at temperatures between 200 and 500 °C using the in situ synchrotron X-ray Laue diffraction.³⁴ This temperature range is much lower than the threshold temperature, 900 °C, for the Magnéli phase Ti₄O₇ formation reported by Domaschke et al., supporting the suitability of the suggested CF structure for low-power electroformed devices.³⁵

The energetic stability of the suggested CF structure was validated by comparing its E_f with 100 other random CF configurations with symmetrically different V_O distributions in the same composition generated using DBmaker in the Lattice Configuration Simulation (LACOS) package.³⁶ Two CF structures proposed previously in rutile TiO₂ were also considered.^37,38 These two previously proposed CF structures were determined by examining randomly generated arrangements of V_Os, in contrast to the present approach of constructing the CF based on the interaction between V_Os. Due to the vast number of possible arrangements of 6 V_Os in a 3 × 3 × 6 supercell (exceeding 100 billion, without considering symmetry), finding a CF structure from random structures might be inefficient. Fig. 3b, c, and d show the E_f values of the examined structures for the AONs of 0, +1 and +2, respectively. In the E_f calculations with AONs of +1 and +2, the ε_f was set to zero, which does not affect the relative E_f values. The dashed lines represent the E_f value of an isolated V_O. When AON is 0, the suggested CF is the most stable with a significant energy margin. This stability originates from all the V_O spacings within the CF being 3.88 Å, the distance at which E_coh reaches a minimum. Considering that V_Os in the LO state exhibit a similar E_coh value, all the CFs in the LO state are expected to be the zigzag structure, such that the suggested CF remains the most stable even when AON is +1. In addition, the stability of the CF in the LO state was verified in compositions with higher V_O concentrations (TiO_1.88, TiO_1.83, and TiO_1.75), as shown in Fig. S10.† At these concentrations, the arrangements of V_Os are the same as those shown in Fig. 3a, with reductions in the spacing between the zigzag strings of V_O. When AON is +2, all examined configurations, on the other hand, have a higher E_f value than that containing an isolated V_O²⁺. This finding indicates that V_O²⁺ prefers to remain isolated rather than agglomerated due to its positive E_coh.

Fig. 3e shows the atom-resolved electronic density of states (DOS) of the CF composed of V_O⁰s, obtained by projecting onto the Ti ion indicated by an arrow in Fig. 3a. Broad defect states were observed down to about 2.0 eV below the CBM. However, due to the relatively low density of defect states, the CF structure is expected to be semi-metallic rather than fully metallic. For comparison, the DOS projected on the Ti ion furthest from the V_Os, standing for the perfect TiO₂, is also represented as grey areas.

B.2. Initiation process of the CF rupture. Fig. 4a shows the initiation of the CF rupture process, where one of the V_Os constituting the CF is released from it. For better understanding, one Ti–O octahedron is represented as a grey diamond, with the bold solid and dotted lines denoting the equatorial plane and vertical axis of the octahedron, respectively. From the viewpoint of this grey octahedron, the released V_O can move from the axial site to any of the four sites on the equatorial plane, where these four paths are symmetrically equivalent. In order to investigate the spontaneity of this process, the rupture energy (ΔE_R) was calculated as:

ΔE_R = E_f(RCF) − E_f(CF) (3)

Fig. 4 (a) Atomic-scale view of an initiation of the CF rupture process. The grey diamond represents the Ti–O octahedron, with the bold solid and dotted lines indicating the equatorial plane and the octahedral axis, respectively. For clarity, only the vicinity of the V_Os is shown. (b) ΔE_R with respect to AON. Positive (negative) ΔE_R means that the rupture process is non-spontaneous (spontaneous).

The first term on the right-hand side is the E_f for the ruptured CF (RCF, right panel of Fig. 4a), while the second is the E_f for the CF (left panel of Fig. 4a). Fig. 4b shows the variation of the ΔE_R as a function of AON. Thirteen AON values from 0 to +2 were considered with increments of 1/6, ensuring that the number of electrons in the supercell remains an integer. The sign of ΔE_R depends on the oxidation state and is positive up to AON of +1, which means that the rupture is not favored in the LO state. Conversely, the ΔE_R value becomes negative in the HO state (AON > +1), indicating the spontaneous rupture of the CF due to the repulsion between highly positively charged V_Os.

To examine the charge distribution within the CF and RCF in the equilibrium state (no external bias is applied), the transition level diagrams (TLDs) were calculated, presenting the most stable AON as a function of the ε_f. Fig. 5a shows a schematic band diagram of a Pt/TiO₂/Ti device based on the experimental values of the work functions of Pt (5.35 eV) and Ti (4.33 eV) and the electron affinity of TiO₂ (4.0 eV).^39–41 The range of ε_f available within a device is primarily influenced by the electrode materials. Accordingly, the possible range of ε_f values spans from 1.65 eV (near the Pt electrode) to 2.67 eV (near the Ti electrode).

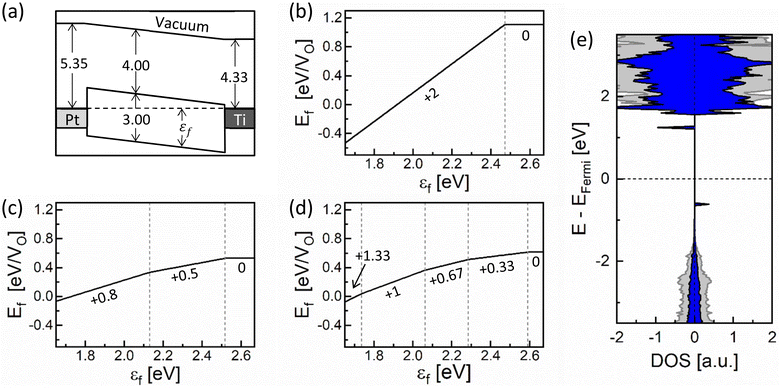Fig. 5 (a) Schematic band diagram of a Pt/TiO₂/Ti system. The work function of Pt and Ti and the electron affinity of TiO₂ are set to the experimental values. TLDs for (b) an isolated V_O, (c) V_Os in the CF, and (d) V_Os in the RCF, where the x-axes are confined to the available range of ε_f in the Pt/TiO₂/Ti system. (e) Atom-resolved DOS of the RCF (blue areas) when the AON is +1.33, obtained by the projection onto the Ti atom marked by an arrow in the right panel of Fig. 4a. For comparison, the DOS projected on the furthest Ti atom from the V_Os, standing for the perfect rutile TiO₂, is shown together as grey areas.

Fig. 5b–d show the TLDs of an isolated V_O, the CF, and the RCF, respectively, with the x-axes set to the available range of ε_f for this device. For the isolated V_O, V_O²⁺ is preferred across most ε_f regions, particularly in film regions near the Pt electrode, probably because oxygen ions prefer to be O²⁻. On the other hand, V_O⁰ becomes predominant around the Ti electrode, which can supply additional V_O⁰s to the nearby TiO₂ from the Ti oxidation reaction. (See supplementary note 2 in the ESI† for oxygen ion exchange at the TiO₂/Ti interface.) Considering that V_O⁰s in proximity attract each other as described in section A, CF can readily be initiated at the TiO₂/Ti interface, which may further grow toward the Pt electrode upon the set switching voltage application. For the CF in Fig. 5c, the LO state is preferred throughout all regions, indicating its stability across the film thickness. For the RCF in Fig. 5d, on the other hand, the HO state (AON = +1.33) becomes stable around the Pt electrode, while the LO state remains in other regions. Therefore, it can be inferred that the CF rupture may occur at the Pt/TiO₂ interface when the reset voltage is applied. Meanwhile, the RCF in the LO state will spontaneously revert to the CF, following the energetic preference shown in Fig. 4b, preventing the CF from being wholly ruptured. Therefore, only a tiny portion of the CF near the Pt electrode, which prefers the HO state in the RCF, may play a crucial role in resistive switching. This finding is consistent with several high-resolution transmission electron microscopy (HRTEM) studies revealing that the CF of only a few nanometers in thickness participates in resistive switching.^14,31,42 This local region involved in the resistive switching is called a CF tip in the remainder of this paper. These tendencies in TLDs demonstrate that the resistive switching is accompanied by charge transition of V_Os: a decrease in AON during the CF formation and an increase in AON during the CF rupture process, as described in detail in the next section.

Fig. 5e shows the atom-resolved DOS of the RCF whose AON is +1.33, obtained by projecting onto the Ti ion marked by an arrow in Fig. 4a. The DOS projected on the Ti ion furthest from the V_Os, standing for the perfect TiO₂, was also represented as grey areas. Upon comparing with the DOS of the CF in Fig. 3e, the RCF is more resistive than the CF since there is no state crossing the Fermi level. This finding suggests that even a minor alternation of the arrangement of V_Os can induce a significant change in the resistance.

C. Charge transition of V_Os during the switching process

The source of the charge transition of V_Os during the resistive switching is the charge injection by the applied bias (V). Fig. 6a represents the post-electroformed state with a tunneling gap between the Pt electrode and the CF (yellow trapezoid) when the device was electroformed with low electric power. When the Pt electrode is negatively biased, the injection of electrons (e⁻) from the Pt electrode is limited due to the tunneling gap with a high Schottky barrier height (SBH) at the Pt/TiO₂ interface. In contrast, injecting holes (h⁺) from the Ti electrode is facilitated by the metallic contact between the CF and the Ti electrode. The charge transfer between the CF and the Ti electrode must be fluent since the Fermi level of the Ti electrode (0.33 eV under the CBM of TiO₂) is located within the consecutive defect states of the CF (see Fig. 3e). Consequently, the h⁺ will accumulate at the CF tip, further oxidizing the V_Os. This process was named h⁺-injection. Conversely, when the Pt electrode is positively biased, the e⁻ will be injected from the Ti interface to the CF and accumulate at the CF tip, causing the reduction of V_Os, which is named e⁻-injection.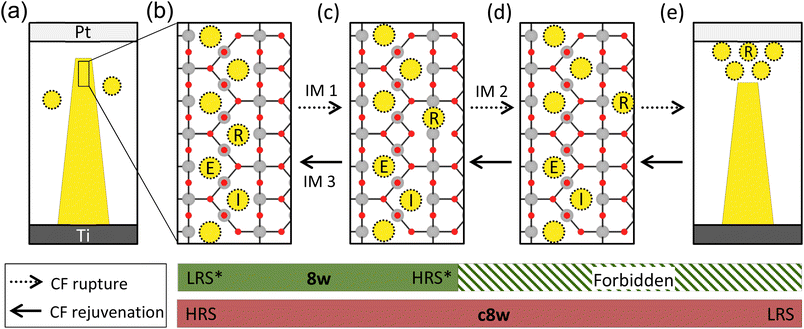

Fig. 6 Overview of the switching process in the Pt/TiO₂/Ti device. (a) The post-electroforming state characterized by a CF represented by the yellow trapezoid, along with a thin tunneling gap between the Pt electrode and the CF due to insufficient electric power. The dotted yellow circles represent the remaining V_Os after the electroforming process. (b) Atomic structure of the CF tip in the pre-charge injection state. R, E, and I denote the released V_O, V_O located at the edge of the residual CF, and V_O inside the residual CF, respectively. (c) Atomic structure of the CF tip after one movement of V_O,R, corresponding to the RCF. Therefore, IM 1 represents the initiation of the CF rupture process from the structure in (b) to that in (c) (the same as Fig. 4a). (d) Atomic structure of the CF tip after subsequent movement of the V_O,R. The V_O,R drifts toward the upper right in response to the electric field and the concentration gradient of V_O. (e) LRS of the device, where the V_O²⁺s are located beneath the Pt electrode. The horizontal dotted arrows denote the CF rupture process, and the solid arrows indicate the CF rejuvenation process. The green and red bars at the bottom of the figure represent the ranges of the 8w and c8w BRS modes, respectively.

The amount of charge carriers accumulated by V is determined by the capacitance (C) of the device. The upper limit of C was roughly estimated by assuming that the CFs are uniformly distributed across the entire cross-sectional area. In this case, the device geometry is a parallel plate capacitor whose electrodes are the CF and the Pt electrode; hence, C becomes ε_rε₀A/t, where ε₀, A, and t are the permittivity of vacuum, CF cross-sectional area, and spacing between the CF and the Pt electrode, respectively. As a result, the density of charge carriers (n) accumulated in the CF is given by n = Q/eΩ_CF, where Q is the total accumulated charge, given as ε_rε₀AV/t, and Ω_CF is the CF volume, given as A(l − t), where l is the total thickness of the TiO₂ layer and e is the elementary charge. Therefore, we have n = ε_rε₀V/et(l − t). Assuming that ε_r and l are the typical values of 100 and 10 nm, and V and t are 2 V and 1.5 nm based on an experiment by Zhang et al., the resulting n is estimated to be 8.67 × 10²⁰ cm⁻³, which is about half the V_O concentration of the suggested CF (1.82 × 10²¹ cm⁻³).¹¹ Given that this n value is the upper limit, the actual change in the AON of the V_Os by the charge injection will be modest. Therefore, the maximum change of AON due to charge injection from the equilibrium state was assumed to be ±0.5.

In this section, the effects of the charge injection on the switching behavior are addressed by examining the atomic kinetics and the evolution in the ION of each V_O. With this purpose, the resistive switching process was simulated, where the evolution in the atomic structure of the CF tip is shown from Fig. 6b–d. Here, the IM indicates an ionic movement, and the dotted and solid arrows represent the rupture and the rejuvenation processes of the CF, respectively. During the rupture process indicated by IM 1 and IM 2, one V_O denoted as R escapes and moves away from the CF. The remaining portion of the CF after releasing the V_O is called residual CF. The rejuvenation process is the reverse process of the rupture. The three V_Os, denoted as R, E, and I, are focused, where V_O,R, V_O,E, and V_O,I indicate the released V_O, the V_O located at the edge of residual CF, and the V_O inside the residual CF, respectively. The green and red bars at the bottom of the figure represent the ranges of the 8w and c8w BRS modes, which are discussed in sections C.1 and C.2, respectively.

C.1. 8w BRS mode.
C.1.1. 8w reset process. The CF exists in the LO state in an equilibrium state without an external bias, as depicted in Fig. 5c. However, when the Pt electrode is negatively biased, the V_Os within the CF undergo additional oxidation by h⁺-injection. If the AON of the CF reaches the HO state, the CF will spontaneously rupture, as described in Fig. 6b and c (which are the same as that described in Fig. 4a), increasing the device resistance (reset switching). This charge transition-driven rupture process is triggered by a repulsive force between V_Os in the HO state, distinguishing it from the conventional thermally induced rupture process. This charge transition-driven rupture process corresponds to the 8w reset process, as a negative voltage resets the device.

The AON of the CF tip was assumed to increase from the equilibrium state of +0.83 to +1.33 by h⁺-injection to simulate the charge transition-driven rupture process. The upper panel of Table 1 provides the energy gain (ΔE) and activation energy (E_a) for the rupture process (IM 1 and IM 2). The corresponding values for the diffusion of an isolated V_O²⁺ are also shown together for comparison. (See Fig. S14† for a description of the V_O²⁺ diffusion.) The IM 1 is expected to readily occur due to the large negative ΔE and the significantly lower E_a of 0.21 eV compared to V_O²⁺ diffusion, 1.31 eV. After IM 1, the V_O,R drifts toward the upper right direction in response to both the electric field and the concentration gradient of V_O, as represented by IM 2 in Fig. 6. However, the E_a for IM 2, 1.34 eV, is much higher than that of IM 1. Considering the lack of operation power of the 8w BRS mode, IM 2 is unlikely to occur in the 8w BRS mode, making the 8w reset a two-step process consisting of the h⁺-injection and IM 1. Consequently, the device states in Fig. 6b and c become the low resistance state (LRS*) and the high resistance state (HRS*), respectively, of the 8w BRS mode. The asterisk is used to emphasize the involvement in the 8w BRS mode.

Table 1 The energy gain (ΔE), activation barrier (E_a), and evolution in ION during the CF rupture process, when the AON increases from +0.83 to +1.33 due to the h⁺-injection

Kinetic parameters
	VO^2+ diffusion	IM 1	IM 2
ΔE [eV]	0.00	−2.15	0.00
E a [eV]	1.31	0.21	1.34

---

Evolution in ION
	h^+-injection		IM 1	IM 2
	Pre-	Post-
VO,R	+0.83	+1.33	+2.03	+2.07
VO,E	+0.83	+1.33	+1.49	+1.53
VO,I	+0.83	+1.33	+0.93	+0.96

---

The lower panel of Table 1 shows the evolution in IONs of three representative V_Os. The whole dataset, including that of other V_Os, is available in Table S1.† Before the h⁺-injection, the IONs are +0.83, corresponding to the equilibrium state of the CF near the Pt electrode, or the CF tip region, as shown in Fig. 5c. It increases to +1.33 after the h⁺-injection, as assumed. The IONs are the same because all V_O-sites in the CF are symmetrically equivalent.

However, the IONs become dissimilar after IM 1. Most notably, the ION of V_O,I changes from +1.33 to +0.93, indicating that the inside of the residual CF becomes the LO state from the HO state. Accordingly, the residual CF is expected to be stable. The following two events induce this charge transition. First, the excessive charge inside the CF is discharged by releasing V_O,R in the further oxidized states. Note that the ION of V_O,R becomes +2.03 after IM 1, then remains almost intact after IM 2. Furthermore, the kinetic parameters (ΔE and E_a) of V_O,R for IM 2 are almost identical to those of V_O²⁺ diffusion, suggesting that the V_O,R behaves like an isolated V_O²⁺ immediately after IM 1. Indeed, the cNEB profiles of these two processes are almost identical, as shown in Fig. S15.† For these reasons, IM 2 is identified with the V_O²⁺ diffusion in this study. Consequently, it is concluded that the V_O becomes V_O²⁺ as soon as it is released from the CF. Second, charge redistribution occurs within the residual CF. Upon comparing the ION values of V_O,E, and V_O,I after IM 1, the remaining charge after releasing V_O,R is concentrated at the edge of residual CF, reducing the charge inside the CF. This behavior is metal-like, which probably originates from the semi-metallic characteristic of the CF. However, the net charge remains inside because free carriers are insufficient to neutralize the internal charge due to the CF's relatively low density of defect states near the Fermi level, which differs from that of metal with zero internal charge. It should be noted that the charge transition-driven rupture process cannot be applied to the CF composed of the Magnéli phase Ti₄O₇ because no net charge exists within the Magnéli phase due to its fully metallic characteristic. In this case, the CF will be thermally ruptured, which requires high power consumption to overcome its superior stability.

Another 8w reset process was also simulated with the lower AON of +1.17. As shown in Table 2, similar results were obtained in both aspects that the V_O,R behaves like an isolated V_O²⁺ and that the charge redistribution within the residual CF occurs to reduce the internal charge. For IM 1, however, both ΔE and E_a are higher than the case of AON = +1.33, presumably due to the weaker repulsion between V_O^1.17+s compared to V_O^1.33+s. Nonetheless, the E_a value is still considerably lower than that for V_O²⁺ diffusion, which accords with the low operation power of the 8w BRS mode.

Table 2 The energy gain (ΔE), activation barrier (E_a), and evolution in ION during the CF rupture process, when the AON increases from +0.83 to +1.17 due to the h⁺-injection

Kinetic parameters
	VO^2+ diffusion	IM 1	IM 2
ΔE [eV]	0.00	−1.21	−0.05
E a [eV]	1.31	0.78	1.30

---

Evolution in ION
	h^+-injection		IM 1	IM 2
	Pre-	Post-
VO,R	+0.83	+1.17	+2.02	+2.07
VO,E	+0.83	+1.17	+1.51	+1.52
VO,I	+0.83	+1.17	+0.87	+0.93

---

C.1.2. 8w set process. The atomic structure of the CF tip in HRS* is the same as that in the RCF. Hence, the AON of the ruptured CF tip is +1.33 (HO state) in an equilibrium state, as shown in Fig. 5d. However, when the Pt electrode is positively biased, the AON can decrease to the LO state due to e⁻-injection, resulting in spontaneous rejuvenation of the RCF to the CF, as represented by IM 3 in Fig. 6. This transition corresponds to the 8w set process (transition from HRS* to LRS*) since the positive voltage sets the device.

To simulate the charge transition-driven rejuvenation process, the AON of V_Os in the ruptured CF tip was assumed to decrease from the equilibrium state of +1.33 to +0.83 by the e⁻-injection. Table 3 provides kinetic parameters for IM 3 (upper panel) in comparison with the diffusion of an isolated V_O²⁺ and the evolution in IONs during the 8w set process (lower panel). The ION distribution before e⁻-injection is identical to that in IM 1 of Table 1. For the IM 3, ΔE is negative, and E_a is 0.66 eV, considerably lower than that of the V_O²⁺ diffusion. Therefore, the 8w set can be driven with low electric power. Meanwhile, upon comparing IONs before and after the e⁻-injection, the ION of V_O,R decreases from +2.03 to +1.03, and the ION of V_O,E also decreases from +1.49 to +0.95. Since these two IONs are close to +1, an attractive force is expected between V_O,R and V_O,E after the e⁻-injection. Consequently, the main driving force of this rejuvenation process is the short-range attraction between V_Os in the LO state rather than the Soret force induced by a temperature gradient, as conventionally explained.

Table 3 Energy gain (ΔE), activation barrier (E_a), and ION during the 8w set process, when the AON decreases from +1.33 to +0.83 due to the e⁻-injection

Kinetic parameters
	VO^2+ diffusion	IM 3
ΔE [eV]	0.00	−0.45
E a [eV]	1.31	0.66

---

Evolution in ION
	e^−-injection		IM 3
	Pre-	Post-
VO,R	+2.03	+1.03	+0.83
VO,E	+1.49	+0.95	+0.83
VO,I	+0.93	+0.86	+0.83

---

C.2. c8w BRS mode. The V_O²⁺ diffusion, including IM 2, is unlikely to occur in the 8w BRS mode due to the high activation energy. In the c8w BRS mode driven at high electric power, in contrast, the V_O²⁺ diffusion becomes feasible. When a high negative voltage is applied to the Pt electrode, not only V_O,R but also isolated V_O²⁺s around the CF (dotted circles in Fig. 6a) will drift toward the Pt electrode, as shown in Fig. 6e. This induces a decrease in resistance, commonly attributed to the Schottky barrier modulation model.⁴³ This model explains that the presence of V_O²⁺s near the electrode promotes electrical conduction by lowering the SBH. This process corresponds to the c8w set process, where the resistance decreases with a negative bias. Hence, the state of Fig. 6e is the low resistance state of the c8w BRS mode (LRS).

Conversely, when a high positive voltage is applied to the Pt electrode, the reverse process, the c8w reset process, occurs, inducing V_O²⁺s near the Pt electrode to move away from the electrode and drift toward the residual CF along the electric field. Subsequently, the ruptured CF will be rejuvenated by e⁻-injection, and the device will become the state of Fig. 6a. Due to the presence of the tunneling gap with a high SBH, the state of Fig. 6a is expected to be more resistive than LRS, and accordingly, this state corresponds to the high resistance state of the c8w polarity (HRS). Note that HRS is identical to LRS*, as shown in Fig. 1.

However, the explanations above still involve two ambiguous points. First, the CF rupture by h⁺-injection must precede the SBH lowering during the c8w set process, implying a temporary increase in resistance before it decreases. Indeed, this phenomenon was experimentally reported by Miao et al.,¹² as discussed in the next section. Second, no quantitative explanation is provided for why the LRS in Fig. 6e is less resistive than the HRS in Fig. 6a. The change in resistance is determined by the competition between the tunneling gap thickening (increasing resistance) and the SBH lowering (decreasing resistance). However, the simulations of this variation are beyond the scope of DFT calculations due to the scale limitation. Qualitatively, according to the Schottky conduction equation in logarithmic form, ln(I) is proportional to t^−1/2 but decreases linearly by SBH, indicating that the influence of the SBH lowering might be predominant over the thickening effect.⁴⁴ Furthermore, the actual increase in thickness of the tunneling gap was insignificant, with a scale of 0.5 nm, based on the experiment of Zhang et al.¹¹ Meanwhile, the additional contribution of V_O²⁺s from the surroundings of the CF to the SBH lowering facilitates the decrease in resistance. Hence, the SBH lowering effect is expected to be predominant in the c8w set process, but a follow-up study is required to clarify this further.

C.3. Summary of the proposed switching mechanism. Fig. 7 summarizes the overall switching mechanism encompassing the 8w (green bar) and c8w (red bar) BRS modes. Three E_a values corresponding to IM 1 (0.21 eV), IM 3 (0.66 eV), and the V_O²⁺ diffusion (1.31 eV) are represented by the arrows. The 8w BRS mode is a charge transition-driven switching, where the 8w reset arises from the repulsion between V_Os in the HO state and the 8w set results from the attraction between V_Os in the LO state. These interactions between V_Os reduce E_a for switching, enabling the 8w BRS mode to be driven by low power. On the other hand, the c8w BRS mode is akin to conventional field-driven switching, with a distinction that the CF comprises V_Os in the LO state rather than V_O²⁺s. The charge transition of V_O occurs only in a highly localized region around the CF tip since the V_Os released from the CF transform into V_O²⁺s with just one movement (lower panels of Tables 1 and 2). Therefore, in the c8w BRS mode, the impact of charge transition on switching behavior is expected to be negligible, and the c8w BRS mode is primarily governed by the diffusion and drift of V_O²⁺. Accordingly, the assumption that fixes the ION of V_O to +2, frequently employed in previous studies, might provide plausible outcomes only to the c8w BRS mode.

Fig. 7 Summary of the proposed mechanism encompassing the 8w BRS mode (green bar) and the c8w BRS mode (red bar). The numerical values represent the E_a for the corresponding process in the unit of eV. The 8w BRS mode arises from the local redistribution of V_Os within the CF tip, while the c8w BRS mode is caused by the mesoscopic redistribution of V_Os between the Pt electrode and the CF tip. The 8w BRS mode can be driven by low electric power due to its significantly low E_as compared to the c8w BRS mode.

The estimated E_a values support the experimental results that two direct transitions from HRS to LRS and from LRS to HRS* were not experimentally observed.¹² In the former case, HRS was indirectly transformed to LRS, passing through HRS*. According to Fig. 7, the transition from HRS to LRS (from left to right panel) involves two sequential barriers of 0.21 eV and 1.31 eV. Since the first barrier is significantly lower than the second one, the device can easily overcome the first barrier but will remain in HRS* by the higher second barrier. For the transition from the LRS to HRS* (from right to middle panel), on the other hand, the device in HRS*, which has surpassed the barrier of 1.31 eV, can easily overcome the subsequent barrier of 0.66 eV, resulting in an immediate transition to HRS. Hence, the transition from the LRS to HRS* is not observable.

It should be noted that these claims are based on a straightforward observation that attractive and repulsive forces occur between V_Os in the LO and HO states, respectively. Accordingly, these findings may hold for other materials showing similar behaviors. Indeed, similar tendencies in the interaction between V_Os were reported in various VCM materials, such as Ta₂O₅, HfO₂, and Al₂O₃.^7,46,47 Consequently, these findings are expected to apply to various VCM devices.

While this study focused only on rutile TiO₂, TiO₂ films in real devices are commonly polycrystalline or amorphous. To address this limitation, the E_coh in anatase TiO₂, another major phase, was also calculated, as shown in Fig. S16.† The tendency in E_coh is similar to rutile TiO₂, implying that the findings can be similarly applied to anatase TiO₂.⁴⁵

4. Conclusion

An improved resistive switching mechanism considering the charge transition and the atomic kinetics of V_O is suggested to explain the coexistence of the 8w and c8w BRS modes in the Pt/TiO₂/Ti model device. The suggested mechanism gives enhanced insights into the resistive switching process as follows. First, the CF prefers to be composed of V_Os in the low oxidation state (LO state) rather than those in the high oxidation state (HO state), which contrasts with the prior simulation studies that considered the CF an aggregation of V_O²⁺s. The stability of the CF in the LO state arises from a short-range attraction between V_Os in the LO state. Second, the 8w BRS mode is charge transition-driven switching, where the attraction at the LO state and repulsion at the HO state cause the CF rejuvenation (8w set) and rupture (8w reset) processes, respectively. These charge transition-driven switchings exhibit lower activation barriers ranging from 0.21 eV–0.78 eV (depending on the oxidation number (ON)) compared to the conventional field-driven switching, whose activation barrier is 1.31 eV. It enables the 8w BRS mode to operate with low electric power. Lastly, a V_O released from the CF becomes V_O²⁺ only by one ionic movement, indicating that the charge transition of V_O occurs within a localized region near the CF. Given that the c8w BRS mode occurs throughout a broad region compared to the 8w BRS mode, the influence of the charge transition of V_O on the switching behavior of c8w polarity is negligible. Therefore, limited to the c8w BRS mode, fixing ON of V_O to +2, as in previous studies, can provide a plausible interpretation for resistive switching.

Author contributions

Taeyoung Jeong: formal analysis, investigation, methodology, and writing – original draft; In Won Yeu: formal analysis and writing – review & editing; Kun Hee Ye: formal analysis and writing – review & editing; Seungjae Yoon: formal analysis and writing – review & editing; Dohyun Kim: writing – review & editing; Cheol Seong Hwang: supervision and writing – review & editing; Jung-Hae Choi: conceptualization, funding acquisition, project administration, supervision, and writing – review & editing.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

J.-H. C. was supported by the National Research Foundation of Korea (NRF) grant funded by MSIT [Next Generation Intelligence Semiconductor Foundation 2022M3F3A2A01076569], and by the Institutional Research Program of Korea Institute of Science and Technology (KIST) [2E32491 and 2E33223]. C. S. H. was supported by the National Research Foundation of Korea [2020R1A3B2079882]. The authors would also like to acknowledge the support from the KISTI Supercomputing Center through a Strategic Support Program for Supercomputing Application Research [KSC-2022-CRE-0378].

References

1. Y. H. Jang, S. H. Lee, J. Han, W. Kim, S. K. Shim, S. Cheong, K. S. Woo, J.-K. Han and C. S. Hwang, Adv. Mater., 2023, 2309314.
2. T. Stecconi, R. Guido, L. Berchialla, A. L. Porta, J. Weiss, Y. Popoff, M. Halter, M. Sousa, F. Horst, D. Dávila, U. Drechsler, R. Dittmann, B. J. Offrein and V. Bragaglia, Adv. Electron. Mater., 2022, 8, 2200448.
3. D. S. Jeong, K. M. Kim, S. Kim, B. J. Choi and C. S. Hwang, Adv. Electron. Mater., 2016, 2, 1600090.
4. R. Waser, R. Dittmann, G. Staikov and K. Szot, Adv. Mater., 2009, 21, 2632–2663.
5. K. M. Kim, B. J. Choi, Y. C. Shin, S. Choi and C. S. Hwang, Appl. Phys. Lett., 2007, 91, 012907.
6. K. Kamiya, M. Y. Yang, S.-G. Park, B. Magyari-Köpe, Y. Nishi, M. Niwa and K. Shiraishi, Appl. Phys. Lett., 2012, 100, 073502.
7. J. Lee, W. Schell, X. Zhu, E. Kioupakis and W. D. Lu, ACS Appl. Mater. Interfaces, 2019, 11, 11579–11586.
8. J. Park, J. Choi, G. Kim, G. Kim, G. S. Kim, H. Song, Y. S. Kim, Y. Lee, H. Rhee, H. M. Lee, C. S. Hwang and K. M. Kim, ACS Appl. Mater. Interfaces, 2022, 14, 35949–35958.
9. R. Muenstermann, T. Menke, R. Dittmann and R. Waser, Adv. Mater., 2010, 22, 4819–4822.
10. X.-B. Yin, K. Tian, Z.-H. Tan, R. Yang and X. Guo, J. Electrochem. Soc., 2015, 162(10), E271–E275.
11. H. Zhang, S. Yoo, S. Menzel, C. Funck, F. Cüppers, D. J. Wouters, C. S. Hwang, R. Waser and S. Hoffmann-Eifert, ACS Appl. Mater. Interfaces, 2018, 10, 29766–29778.
12. F. Miao, J. J. Yang, J. Borghetti, G. Medeiros-Ribeiro and R. S. Williams, Nanotechology, 2011, 22, 254007.
13. K. M. Kim, G. H. Kim, S. J. Song, J. Y. Seok, M. H. Lee, J. H. Yoon and C. S. Hwang, Nanotechology, 2010, 21, 305203.
14. Y. Zhang, G.-Q. Mao, X. Zhao, Y. Li, M. Zhang, Z. Wu, W. Wu, H. Sun, Y. Guo, L. Wang, X. Zhang, Q. Liu, H. Lv, K.-H. Xue, G. Xu, X. Miao, S. Long and M. Liu, Nat. Commun., 2021, 12, 7232.
15. D. Cooper, C. Baeumer, N. Bernier, A. Marchewka, C. L. Torre, R. E. Dunin-Borkowski, S. Menzel, R. Waser and R. Dittmann, Adv. Mater., 2017, 29, 1700212.
16. T. Heisig, C. Baeumer, U. N. Gries, M. P. Mueller, C. L. Torre, M. Luebben, N. Raab, H. Du, S. Menzel, D. N. Mueller, C.-L. Jia, J. Mayer, R. Waser, I. Valov, R. A. D. Souza and R. Dittmann, Adv. Mater., 2018, 30, 1800957.
17. A. Schönhals, C. M. M. Rosário, S. Hoffmann-Eifert, R. Waser, S. Menzel and D. J. Wouters, Adv. Electron. Mater., 2018, 4, 1700243.
18. H. Ryu and S. Kim, Nanomaterials, 2020, 10, 2055.
19. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
20. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
21. D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566–569.
22. J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079.
23. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505.
24. D. T. Cromer and K. Herrington, J. Am. Chem. Soc., 1955, 77, 4708–4709.
25. D. Reyes-Coronado, G. Rodríguez-Gattorno, M. E. Espinosa-Pesqueira, C. Cab, R. d. Coss and G. Oskam, Nanotechnology, 2008, 19, 145605.
26. A. Janotti, J. B. Varley, P. Rinke, N. Umezawa, G. Kresse and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 0852121.
27. A. Malashevich, M. Jain and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 075205.
28. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354.
29. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
30. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985.
31. D.-H. Kwon, K. M. Kim, J. H. Jang, J. M. Jeon, M. H. Lee, G. H. Kim, X.-S. Li, G.-S. Park, B. Lee, S. Han, M. Kim and C. S. Hwang, Nat. Nanotechnol., 2010, 5, 148–153.
32. Y. M. Lu, M. Noman, Y. N. Picard, J. A. Bain, P. A. Salvador and M. Skowronski, J. Appl. Phys., 2013, 113, 163703.
33. K. Zhang, Y. Ren, P. Ganesh and Y. Cao, npj Comput. Mater., 2022, 8, 76.
34. T. Li, F. Hong, K. Yang, B. Yue, N. Tamura, H. Wu, Z. Cheng and C. Wang, Sci. Bull., 2020, 65, 631–639.
35. M. Domaschke, X. Zhou, L. Wergen, S. Romeis, M. E. Miehlich, K. Meyer, W. Peukert and P. Schmuki, ACS Catal., 2019, 9, 3627–3632.
36. M. Chandran, Comput. Mater. Sci., 2015, 108, 192–204.
37. W. Heckel, M. Wehlau, S. B. Maisel, T. Frauenheim, J. M. Knaup and S. Müller, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 214104.
38. B. Magyari-Köpe, S. G. Park, H.-D. Lee and Y. Nishi, J. Mater. Sci., 2012, 47, 7498–7514.
39. R. Vanselow and X. Q. D. Li, Surf. Sci. Lett., 1992, 264, L200–L206.
40. D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press, Boca Raton, FL, 2014, pp. 12–124.
41. X. Yin, C. Battaglia, Y. Lin, K. Chen, M. Hettick, M. Zheng, C.-Y. Chen, D. Kiriya and A. Javey, ACS Photonics, 2014, 1, 1245–1250.
42. J.-Y. Chen, C.-L. Hsin, C.-W. Huang, C.-H. Chiu, Y.-T. Huang, S.-J. Lin, W.-W. Wu and L.-J. Chen, Nano Lett., 2013, 13, 3671–3677.
43. J. J. Yang, J. Borghetti, D. Murphy, D. R. Stewart and R. S. Williams, Adv. Mater., 2009, 21, 3754–3758.
44. C.-R. Cheng, M.-H. Tsai, T.-H. Hsu, M.-J. Li and C.-L. Huang, J. Alloys Compd., 2023, 930, 167487.
45. T. Lee and A. Selloni, J. Phys. Chem. C, 2023, 127(1), 627–634.
46. K. Kamiya, M. Y. Yang, T. Nagata, S.-G. Park, B. Magyari-Köpe, T. Chikyow, K. Yamada, M. Niwa, Y. Nishi and K. Shiraishi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 155201.
47. M. Y. Yang, K. Kamiya, B. Magyari-Köpe, H. Momida, T. Ohno, M. Niwa, Y. Nishi and K. Shiraishi, Jpn. J. Appl. Phys., 2013, 52, 04CD11.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr06614b

---