A multiscale approach to assess thermomechanical performance and force generation in nanorobotic microgels

Abstract

We present a multiscale approach to characterize the performance of photothermally powered, nanorobotic 3D microgels. Optically triggered nanoactuators, consisting of a gold nanorod core and thermoresponsive pNIPMAM shell, are used as building blocks to generate the nanorobotic 3D microgels. We use microfluidic encapsulation to physically embed the nanoactuators in an alginate network, to form the microgel droplets. The nanoactuators respond to near-infrared light owing to the synergistic effects of plasmonic and thermoresponsive components, and the nanorobotic 3D microgels generate compressive force under the same light stimulus. We use a multiscale approach to characterize this behavior for both the nanoactuators and the assembled microgels via dynamic light scattering and fluorescence microscopy, respectively. A thermoresponsive fluorescent molecule, Rhodamine B, is integrated into alginate chains to monitor the temperature of the microgels (22–59 °C) during actuation at laser intensities up to 6.4 μW μm⁻². Our findings show that nanoactuators and the microgels exhibit reversible deformation above the lower critical solution temperature of the thermoresponsive polymer at 42 °C. 785 nm laser light triggers the generation of 2D radial strain in nanoactuators at a maximum of 44%, which translates to an average 2D radial strain of 2.1% in the nanorobotic microgels at 26.4 vol% nanoactuator loading. We then use a semi-experimental approach to quantify the photothermally generated forces in the microgels. Finite element modeling coupled with experimental measurements shows that nanorobotic microgels generate up to 8.5 nN of force over encapsulated single cells. Overall, our method provides a comprehensive approach to characterizing the mechanical performance of nanorobotic hydrogel networks.

---

1 Introduction

Introducing small-scale robots into cell culture systems has yielded a new class of biomanipulation tools with versatile capabilities. Wirelessly controlled tiny actuators have been particularly useful in probing cellular responses to locally applied stimuli, due to their outstanding ability to generate tunable forces ranging from several pNs to tens of μN.^1–6 Owing to their mobility, small-scale machines have enabled targeting single cells in biological 3D environments, without interfering with cell culture conditions.^7–10 Moreover, force-generating microrobots have demonstrated their potential as effective tools for biomechanical characterization in vitro and tissue regeneration in vivo, further highlighting their versatility.^11–16

Among the emerging active cell culture technologies, those that rely on optically driven microactuators have received considerable attention due to high spatiotemporal resolution, low power attenuation, precise control over force magnitude and frequency, and excellent biocompatibility.¹⁷ Relying on the synergistic effect of plasmonic nanoparticles and thermoresponsive polymers, optically responsive soft microdevices have been demonstrated as efficient tools in converting light into mechanical work, in a highly localized manner.^18–22 Moreover, biocompatible and stimuli-responsive polymers have allowed smooth biointegration of the engineered devices into cell culture conditions.^23,24 Combined with microscopy, optomechanically active cell culture systems have enabled investigations into integrin-mediated mechanotransduction, cell migration, and stretch-activated calcium channels in single cells.^1,4,6,25,26

An essential feature of optically triggered active cell culture systems is force modulation, which requires precise characterization of actuator performance. In most cases, photothermally generated strains are directly measured using microscopy techniques, which are converted into force values using the mechanical properties of the microdevice in question.^25,26 With this approach, forces within a range of a few nN up to 100 μN have been quantified in strain-regulated optical systems.² Theoretical investigations relying on finite element modeling have been used to support experimental findings and to quantitatively assess the mechanical performance of force-generating networks in a multiparametric manner.^3,5,6,13 Combining numerical simulations with experimental approaches has allowed rapid and versatile solutions for assessing the actuation performance of mechanically active cell culture systems. This approach enabled investigations into the influence of geometrical and mechanical properties of 3D hydrogel networks, which have been used to design active biomaterials in an efficient manner by significantly reducing the number of experimental parameters to be tested.^3,5,6

On the other hand, integrating photothermally powered actuators in cell culture systems requires tuning of generated heat loads to avoid excessive heating, which may cause cell damage in extreme cases. At the millimeter scale, the temperature output of optical actuators could be directly measured using infrared imaging and standard thermometry.^27–30 The ability to regulate the optically generated heat dose over distance and time, has enabled precise control over actuator strain.^25,26 Specialized imaging methods, such as fluorescence-based thermometry, have allowed photothermal characterization in microsystems, providing indirect control over temperature at the microscale with the precision of direct measurement techniques.^10,31–33 With these approaches, the overall temperature of the optical actuator has been measured, while the photothermal performance of the individual plasmonic building blocks has often been only analyzed with finite element modeling.^1,7,34 Correlating the photothermal performance of the individual plasmonic building blocks and the assembled microactuator with the generated strain and the force could achieve superior mechanical control in active cell culture systems. However, it remains a challenge to accurately characterize the thermomechanical performance of small-scale machines within the three-dimensional (3D) workspace.

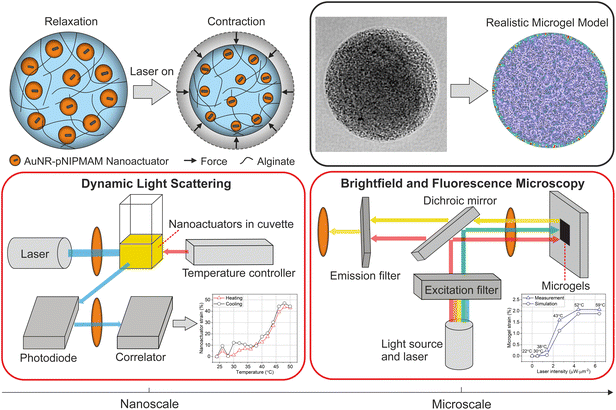
In this work, we present a multiscale approach to characterize the thermomechanical performance and force output of nanorobotic 3D microgels. Our mechanically active microgel system relies on optically triggered nanoactuators dispersed in an alginate-based hydrogel network, which is capable of generating spatiotemporally controlled strains and compressive forces (Fig. 1). Building on our previously reported work, we use nanoactuators consisting of plasmonic gold nanorods, coated with a thin layer of the thermoresponsive polymer, poly(N-isopropylmethacrylamide) (pNIPMAM) as force generators in alginate microgels. We present a new three-channel microfluidic device to physically encapsulate nanoactuators within alginate chains homogeneously. The temperature sensitive fluorescent dye, Rhodamine B, is used as a microthermometer, providing immediate temperature feedback during microgel actuation.¹⁰ We characterize the thermomechanical behavior of both the nanoactuators and the assembled nanorobotic 3D microgels using dynamic light scattering (DLS) and fluorescence-based thermometry via an optical microscope (Fig. 1). By tracking the change in fluorescence intensity of Rhodamine-B, we track the temperature changes in nanorobotic microgels during laser activation. We correlate the laser intensity to microgel strain and temperature, which allows precise control over photothermal actuation and the generated heat loads. We implement finite element modeling to quantify artificially generated forces within the nanorobotic 3D microgels. For this purpose, the geometrical and mechanical properties of our nanorobotic system are experimentally characterized and utilized as input parameters to ensure modeling accuracy. We experimentally verify the accuracy of the models, by encapsulating single stem cells in nanorobotic hydrogels and measuring the generated compressive forces over the cell circumference. Force values received from the simulations (4.2 nN) are in approximate agreement with the experimentally determined force values (8.5 nN) under the same conditions. Our work provides a comprehensive approach for characterizing the thermomechanical performance of optical microactuators in cell culture conditions, while enabling fast and reliable quantification of artificially generated forces.

Fig. 1 Schematic overview of the methodology for thermomechanical characterization and force estimation in nanorobotic microgels. Nanoactuators exhibit a core–shell structure where the plasmonic gold nanorod core (black) converts light into localized heat, causing the thermoresponsive polymer shell (orange) to reversibly shrink. Nanoactuator contraction leads to the overall deformation of the nanorobotic microgel. Nanoactuator performance is characterized by DLS and correlated with nanorobotic microgel behavior using fluorescence-based thermometry via an optical microscope. Finite element modeling is used to calculate generated forces using the realistic microgel model, which accurately represents the spatial orientation of the nanoactuators in the microgels.

2 Results and discussion

2.1 Fabrication of nanorobotic microgels via microfluidic encapsulation

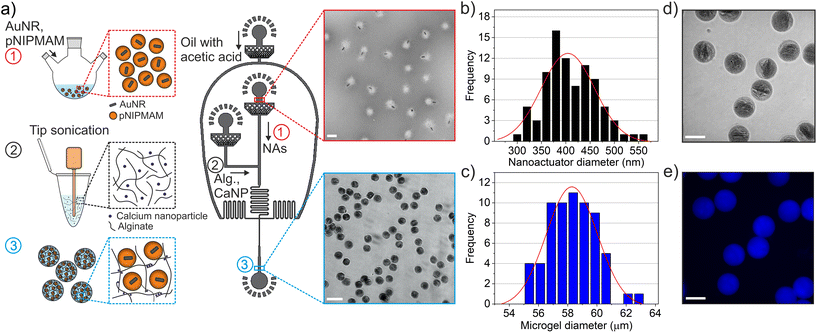
We developed nanorobotic microgels that are capable of mechanical deformation using photothermally activated small-scale actuators encapsulated into an alginate network. For this purpose, nanoactuators composed of a gold nanorod core and a thermoresponsive pNIPMAM shell were selected as the force-generating, active components. The coupling between plasmonic nanoparticles and thermoresponsive polymers allows efficient conversion of near-infrared light into local heat, which triggers physical deformation and force generation in nanoactuators.^1,6 We selected alginate as the static element to enable cell integration in later stages, due to its outstanding biochemical properties and suitability for cell culture.^35,36 A thermosensitive fluorescent dye, Rhodamine B, was integrated into alginate chains to allow real-time monitoring of light-induced temperature changes.¹⁰

We chose microfluidic encapsulation to integrate all components into a functional structure, which allows high-throughput production of multicomponent microgels.^37–42 An important consideration when designing the microfluidic encapsulation device was ensuring the homogenous distribution of nanoactuators within the alginate network. We conjectured that homogenous nanorobotic microgels would perform reliably, without exhibiting significant differences in actuation performance among a batch of microgels. Towards this goal, a flow-focusing microfluidic device with three independent flow inlets was developed (Fig. 2a). Having two separate aqueous phases for alginate-crosslinker and nanoactuator solutions allowed easy handling of viscous components (e.g. 2 wt% alginate), and efficient mixing on the chip.³⁸ This approach prevented device failure due to the undesirable agglomeration of nanoactuators and calcium carbonate nanoparticles, which we observed in microfluidic devices with a single aqueous inlet. This was particularly important considering the size of the nanoactuators (410.4 ± 52.9 nm, Fig. 2b) and the high concentration of nanoactuators (40 mg mL⁻¹) in the pre-gel mixture. A T-junction followed by a serpentine channel allowed proper mixing of nanoactuators, alginate, and calcium carbonate nanoparticles prior to droplet formation (Fig. 2a). The acetic acid (0.04 vol%) in the fluorinated oil phase was sufficient in dissolving calcium carbonate nanoparticles to ionically crosslink alginate (Fig. 2a).⁶ The resulting microgels were collected and centrifuged to remove the remaining oil phase, following demulsification. Our approach revealed homogenous nanorobotic microgels with very low variation in average size at 58.1 ± 2.0 μm (Fig. 2c). The nanorobotic microgel is estimated to contain 747 370 nanoactuators, calculated by the corresponding nanoactuator concentration in the pre-microgel mixture (40 mg mL⁻¹, 26.4 vol%), assuming 100% encapsulation efficiency. Brightfield microscopy and scanning electron microscopy images confirmed the uniform distribution of nanoactuators, which were physically encapsulated in the alginate microgel network (Fig. 2d and Fig. S1†). We found that the three-channel microfluidic design with the 40 μm wide T-junction produced the most homogeneous microgels with equally distributed nanoactuators. Any deviation from this design led to nanoactuator agglomerations in the microgels, resulting in spatial variations within the microgels (Fig. S2†). These observations were further validated by measuring the fluorescence intensity of the Rhodamine B labeled alginate network, which was constant along the radius of the microgels when encapsulated nanoactuators were homogeneously distributed (Fig. 2e and Fig. S2†).

Fig. 2 Nanorobotic microgel fabrication and morphological characterization. (a) Step-by-step fabrication of nanorobotic microgels showing, (1) the production of nanoactuators made up of gold nanorod (AuNR) core and pNIPMAM shell, (2) the preparation of alginate and calcium nanoparticle mixture via tip sonication, and (3) integration of nanoactuators in alginate networks via microfluidics. Nanoactuators (NAs) are physically encapsulated in alginate (Alg.) microgels using a three-channel device, where calcium carbonate nanoparticles (CaNP) act as the crosslinker. The inset images show nanoactuators (top) and assembled microgels (bottom). The transmission electron microscopy (TEM) image shows core–shell structure of nanoactuators indicated by the corona around the gold nanorods with an overall average size of 410.4 ± 52.9 nm (scale bar: 500 nm). Brightfield image shows nanorobotic microgels with an average size of 58.1 ± 2.0 μm (scale bar: 100 μm). Size distribution of (b) nanoactuators (n = 67) and (c) nanorobotic microgels (n = 87). (d) Brightfield and (e) fluorescent images of a group of nanorobotic microgels are shown (scale bar: 50 μm). Blue indicates Rhodamine B intensity in the nanorobotic microgels.

2.2 Thermomechanical characterization of actuation performance

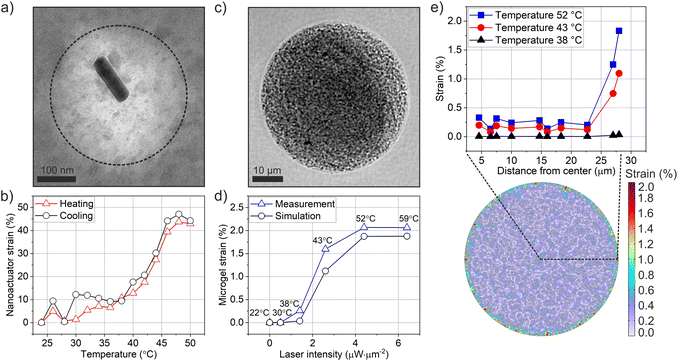
After constructing the nanorobotic microgels, we set out to characterize their actuation performance using a multiscale approach. We first experimentally quantified the generated strain and induced photothermal heat load from nanoscale to microstructural level, as depicted in Fig. 3. The nanoactuators (Fig. 3a) undergo a rapid volume change upon near-infrared light illumination due to the synergistic effect of surface plasmon resonance on polymer phase transition (Fig. 3b).^4,24,43 We used radial strain ε_r (%) to assess the strain performance of both nanoactuators and the nanorobotic microgels.^2,44Here, r₀ and r refer to the radii at the initial relaxed and contracted states, respectively. We used DLS to quantify the heat-induced strain behavior of the nanoactuators (Fig. 3b), which showed a dramatic increase in nanoactuator strain at temperatures above 40 °C. The rapid rise in strain was due to the hydrophilic–hydrophobic pNIPMAM phase change past its lower critical solution temperature (LCST) at around 42 °C (Fig. 3b), which aligns well with previous reports.^6,44,45 Nanoactuator strain stayed constant at 44% above 45 °C, and it was fully reversed to 0% when cooled to room temperature, allowing repeatable nanoactuator deformation in an untethered manner.

Fig. 3 Thermomechanical characterization of nanoactuators and the nanorobotic microgels. (a) TEM image of a single nanoactuator is presented, showing the core–shell structure (scale bar: 100 nm). The dotted line represents the boundary of the pNIPMAM shell. (b) Nanoactuator strain versus temperature is shown for a population of nanoactuators. Hydrodynamic size of nanoactuators was determined via DLS from 24 °C to 50 °C at intervals of 2 °C. Red (triangle) and black (circle) lines represent heating and cooling cycles, respectively. (c) Brightfield image of a single microgel is illustrated, showing randomly distributed nanoactuators inside the microgel. Scale bar: 10 μm. (d) Microgel strain versus laser intensity is shown for different local temperatures. Microgel strain is quantified by determining the radial displacement over initial radius. Blue (triangle) and black (circle) lines refer to measurement and simulation data, respectively. Average values (n = 10) are calculated for both simulation and measurement profiles. The duration of laser light application was 2 seconds for all intensities. (e) Microgel strain over microgel radius is simulated via realistic microgel model in random spatial distribution of nanoactuators. The simulation cross-section consists of a total of 4925 nanoactuators. Each white circle in the 2D radial strain simulation indicates one single nanoactuator. Blue (rectangle), red (circle) and black (triangle) represent the various local temperatures of 52 °C, 43 °C and 38 °C, respectively. 2D map visualizes the overall strain distribution inside the microgel at temperature 52 °C.

To track strain behavior in nanorobotic microgels, we used 785 nm laser light to actuate the microgels during live imaging (Fig. 1). Radial 2D strain was calculated based on relaxed and contracted microgel states during laser off and on phases, respectively, which were acquired via post-actuation image processing. The nanorobotic microgels presented a homogeneous distribution of contractile elements at 40 mg mL⁻¹ loading concentration (Fig. 3c and S1†) and contracted isotropically when illuminated with uniform near-infrared (NIR) light. We systematically varied the laser intensity from 0 to 6.4 μW μm⁻² and recorded the microgel response. Photothermally generated microgel strain increased up to 2.1% with increasing laser intensity (Fig. 3d). The duration of laser application was fixed to 2 s for all conditions to reach saturation strain, based on our previously reported measurements.⁶ Continuous laser application over 1 s ensured maximum strain generation, where laser intensity was the only variable influencing strain performance for constant material properties (e.g. nanoactuator concentration, microgel size). The evolution of strain in microgels at the selected laser intensities demonstrated that microgel strain was saturated within 2 s of laser actuation (Fig. S3†).

To be able to correlate the strain profile of microgels with nanoactuators, we converted laser intensity into temperature values using fluorescence-based microthermometry.¹⁰ For this purpose, we integrated the thermosensitive fluorescent probe, Rhodamine B, into nanorobotic microgels by covalently coupling it onto alginate chains prior to microfluidic encapsulation. Using a stage top heater, we measured Rhodamine B signal at increasing temperatures from 22 to 60 °C to establish a calibration curve (Fig. S4†). Fluorescence signal recordings were then performed during laser actuation on the same nanorobotic microgels to correlate applied laser intensity with corresponding changes in local temperature (Fig. S4†). Our measurements indicate an LCST of 42 °C for nanorobotic microgels (Fig. 3d), which is comparable to the transition temperature of the nanoactuators, obtained from DLS measurements (Fig. 3b). These observations are in line with our previously reported findings for actuated 3D microgels with physically encapsulated nanoactuators.⁶

We next sought to develop a semi-experimental method to reliably estimate generated forces in nanorobotic microgels. To this end, we used a computational framework to estimate the thermomechanical behavior of nanorobotic microgels via finite-element modeling. We were particularly interested in strain transmission from the physically encapsulated nanoactuators to the alginate network, and how estimations determined by finite element modeling (FEM) correlated to the measured behavior. We built a mechanical model to observe the transmission of radial strain from the nanoactuators to the rest of the microgel network over 2D cross-sections. A total of 4925 nanoactuators were placed in the microgel cross-section, corresponding to a concentration of 26.4 vol% (40 mg mL⁻¹). The nanoactuators were activated at increasing radial strain, and deformation at the cell–material interface was computed. Both the nanoactuators and the alginate network were modeled as linearly elastic solids, which accurately describes the material system for strains less than 15% and short, non-repetitive actuation durations, as we previously demonstrated.^2,6 To ensure modeling accuracy, the geometrical and mechanical properties of the microgels were experimentally determined and used to build the simulations (Table 1). In the 2D model, nanoactuators were distributed within the alginate network either randomly or in an equidistant manner (Fig. S5†), which allowed us to investigate the influence of the spatial distribution of nanoactuators on strain generation efficiency of the nanorobotic microgels. Microgel strain was computed in the models using experimentally measured nanoactuator strains determined by DLS, and we correlated nanoactuator strain to the laser-induced temperature changes using the calibration curve established with microthermometry (Fig. S4 and S6†).

Table 1 Mechanical and geometrical properties used in FEM. The parameters were experimentally determined

Mechanical properties
Name	Young's modulus/kPa	Poisson's ratio
Cell	1.41	0.49
Microgel	1.24	0.49
Nanoactuator	4.8	0.49

---

Geometrical properties
Name	Symbol	Value
Cell radius	r c	7.5 μm
Microgel radius	r m	28 μm
Nanoactuator radius	r n	205 nm
Nanoactuator distance	nd	614 nm
Hydrogel droplet size	hs	2168 μm
Laser size	ls	88 μm

---

The realistic microgel model (RMM), where nanoactuators were randomly distributed, exhibited a maximum strain of 1.9% at 52 °C (Fig. 3d and e). As expected, microgel strain increased noticeably at temperatures past the LCST of 42 °C and along the direction of the microgel radius (Fig. 3e). Interestingly, the highest strain values in our 2D simulations were observed at the circumference of the microgel, while the inner regions of the nanorobotic microgels exhibited lower strain. This result is likely because the deformation at the edges is not constrained, and most of the deformation generated by the nanoactuators in the inner section of the microgels canceled each other out. Similarly, we established the ideal representative model consisting of uniformly distributed nanoactuators, arranged in a circular pattern with an equidistant spacing of 614 nm (Fig. S5†). Uniformly distributed nanoactuators could generate uniform deformations within the microgel network (Fig. S7†), however this inherently caused a significant loss of strain performance in the 2D model, reducing the overall strain by 2.4 times (Fig. S8†). Our mechanical model enabled analysis of the correlation between nanoactuator strain and microgel performance. We found that the realistic microgel model accurately described the experimentally generated nanorobotic microgels, based on excellent matching of simulated and measured strain profiles at a nanoactuator concentration of 40 mg mL⁻¹ in both cases (Fig. 3d). Moreover, scanning electron microscopy confirmed the random distribution of nanoactuators without any distinct, repetitive patterns (Fig. S1†).

2.3 Force estimation in cell-encapsulated nanorobotic microgels

Our main goal was to develop a fast and low-cost method to accurately quantify compressive forces generated within the nanorobotic microgels, specifically at the cell–material interface. To do so, we introduced cells into the realistic microgel model and calculated the generated forces at varying microgel strains. The nanoactuators were modeled as spherical particles with an average radius of 205 nm, which was experimentally determined via TEM and DLS (Table 1). Hydrodynamic radius measurements of the nanoactuators confirmed the spherical shape, given the single peak observed in DLS scans (Fig. S9†). The microgel radius was fixed at 28 μm, determined via brightfield microscopy and subsequent image analysis using the open-source Fiji software.

The theoretical quantification of artificially generated forces required precise determination of Young's moduli for the encapsulated cell and the elements of the nanorobotics microgels. For this purpose, we used nanoindentation to determine the Young's modulus for microgels and murine mesenchymal stem cells, which we previously showed to be responsive to isotropic compression.⁶ Measurements were conducted using a microscope-compatible, modular nanoindentor (Chiaro, Optics11), which yielded average Young's moduli of 1.24 kPa for alginate microgels (n = 20) and 1.41 kPa for cells (n = 20), (Fig. S10†). In 2D models, the Young's modulus of nanoactuators, cells, and microgels were inserted separately. The Young's modulus of nanoactuators was set to 4.8 kPa based on previous measurements.² The cell was modeled as a spherical particle with a radius of 7.5 μm, determined by brightfield images, and placed into the microgel center, while nanoactuators at 26.4 vol% concentration (40 mg mL⁻¹) were randomly distributed within the microgel shell.

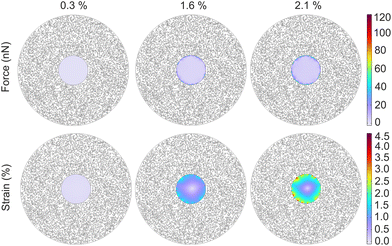
The artificially generated forces acting on a single cell, encapsulated within the nanorobotic microgel, was predicted using the realistic microgel model as shown in Fig. 4. The 2D model allowed the simulation of overall microgel strain based on input nanoactuator strain, which we had experimentally characterized. The lowest force output (0.1 nN) was observed at 0.3% microgel strain corresponding to 38 °C input temperature. As expected, the generated force acting on the encapsulated cell increased as the microgel strain increased reaching a total of 7.7 nN at a microgel strain of 2.1% (Fig. 4). For the medium microgel strain case at 1.6%, the generated compressive force was calculated as 4.6 nN, which was almost uniformly exerted to the cell circumference despite the random distribution of nanoactuators (Fig. 4). However, the implications of nanoactuator distribution on the force pattern became much more pronounced at the higher microgel strain of 2.1% (Fig. 4). Moreover, the model allowed estimation of mechanical performance in multicellular microgels, further demonstrating its versatility (Fig. S11†).

Fig. 4 Nanorobotic microgel performance is estimated using the realistic microgel model. A single cell (r_c = 7.5 μm) is located at the center of the nanorobotic microgel (r_m = 28 μm). Distribution maps of strains and forces acting on the encapsulated cell are simulated for three cases, where estimates are predicted with regard to the overall strains of microgels. Nanoactuator concentration (black circles): 26.4 vol% (40 mg mL⁻¹), corresponds to 4572 nanoactuators around the cell.

2.4. Experimental validation of generated forces

To be able to reliably use the computational framework for future experiments, we next validated the model using an experimental approach to measure the generated force. For this purpose, we fabricated 3D alginate networks loaded with cells and physically encapsulated nanoactuators at 26.4 vol% concentration. Mechanically active hydrogels containing single mesenchymal stem cells were formed using calcium carbonate nanoparticles to crosslink the alginate chains, while physically entrapping the nanoactuators in the network (Fig. 5a). Cells were fluorescently tagged using Calcium AM prior to encapsulation in order to track changes at the cell–material interface during optomechanical actuation (Fig. 5a).

Fig. 5 Experimental validation of the realistic model with cell encapsulated, nanorobotic hydrogel droplets. (a) A brightfield image of a nanorobotic hydrogel droplet, with an encapsulated mesenchymal stem cell shown in green (insets). Isotropic compression on the single cell is triggered via photothermal actuation at 2.6 μW μm⁻², leading to deformation of the encapsulated cell. Relaxed (laser off) and actuated (laser on) states of the encapsulated cell are shown in the insets (scale bar: 10 μm). (b) A nanorobotic hydrogel model was built to validate force measurements, where nanoactuators were randomly distributed around the cell. The experimentally measured laser beam area was used to determine the overall size of the actuated area. The geometrical parameters hs and ls refer to the diameters of the nanorobotic hydrogel droplet (2168 μm) and the laser beam (88 μm), measured experimentally. (c) 2D force map showing the magnitude and distribution of generated forces acting on the surface of the encapsulated cell, and (d) comparison of cell strains and forces between different quantification approaches. Each black circle in the model cross-section indicates one nanoactuator.

We used the 785 nm laser at an intensity of 2.6 μW μm⁻² to photothermally actuate the hydrogel network around the encapsulated cell, and to apply isotropic compression on the cell in question for 1.5 s (Fig. 5a, inset). The actuation duration of 1.5 s was chosen to ensure maximum microgel strain, which reached its saturation point at the end of 1 s (Fig. S3†). Radial strain of the encapsulated cell was calculated according to eqn (1), using the cell radii in relaxed and actuated states. For this purpose, relaxed and strained cell images were collected and processed using Fiji, resulting in an overall strain of 3.4%. Using the Young's modulus of the cell and the measured strain value, we calculated the corresponding force over the cell circumference, resulting in a value of 8.5 nN. We established a hydrogel model based on the actual geometrical parameters of the fabricated hydrogel droplet and the laser beam (Fig. 5b). Only the nanoactuators within the laser beam area were considered to generate compressive force, therefore nanoactuators outside the beam area were not actuated in this simulation (Fig. 5b). The sizes of the laser beam and the nanorobotic hydrogel droplet were quantified via microscopy. The mechanical properties of nanoactuators, cells, and alginate remained constant, and we used the identical Young's modulus and Poisson's ratio utilized in microgel models. We obtained a force value of 4.2 nN (Fig. 5c), exerted on a single encapsulated cell with the corresponding strain of 3.2%. Our findings indicate a great match between the estimated and measured forces, proving the reliability of our model (Fig. 5d).

3 Experimental

3.1 Synthesis of nanoactuators

Nanoactuators consisting of a gold nanorod core and a thermoresponsive polymer shell were synthesized using an established approach. For this purpose, gold(III) chloride trihydrate (HAuCl₄, 99.99%), hexadecyltrimethylammonium bromide (CTAB, 98%), sodium borohydride (99.99%), sodium oleate (95%), silver nitrate (99.0%), hydrochloric acid (HCl, 37%), L-ascorbic acid, N-isopropylmethacrylamide (NIPMAM), N,N′-methylenebisacrylamide, 2,2′ azobis(2-methylpropionamidine) dihydrochloride (AAPH), allylamine, and N,N′-bis(acryloyl)cystamine were all purchased from Sigma Aldrich and used as received. Based on our previously published work, we first synthesized gold nanorods using CTAB capped seed nanoparticles in the presence of silver nitrate and sodium oelate as the secondary surfactant.^2,6 Briefly, a growth solution containing sodium oleate and CTAB was prepared, while silver nitrate and gold(III) chloride trihydrate were sequentially added. A seed solution was simultaneously prepared, where sodium borohydride was used as the reducing agent. Finally, 320 μL of seed solution and 2.4 mL of ascorbic acid (64 mM) were injected into the growth solution, and the reaction was then left undisturbed at 30 °C for 15 hours. A ligand exchange was then performed using N,N′-bis(acryloyl)cystamine as previously reported.^1,2,6

Gold nanorods were coated with the thermoresponsive polymer using an in situ free radical polymerization process. For this purpose, 90 mL of ultra-pure water was heated to 70 °C under constant stirring (700 rpm) and purged with N₂ for 30 minutes. A reflux column was inserted, and 0.6 g NIPMAM followed by 0.06 g N,N’-methylenebisacrylamide was added while stirring. The stirring speed was increased to 1400 rpm and 6 mL of gold nanorod solution was directly injected into the solution. After 1 minute of stirring, 480 μL of 0.1 M AAPH was added, and the reaction was allowed to proceed for 120 minutes under continuous N₂ purging while stirring at 1400 rpm. A hazy solution with a whitish-pink color was visible within the first 30 minutes of the reaction, indicating a successful polymerization process, after which 60 μL allylamine diluted in 1 mL of ultra-pure water was added to the mixture. The solution was removed at the end of 120 minutes and allowed to cool down to room temperature while stirring. The resulting nanoparticle solution was centrifuged at 11 000 rpm for 15 minutes at 20 °C. The supernatant was removed, and the pellet was re-dispersed in ultra-pure water. The washing steps were repeated three times, and the solution was concentrated to 5 mg mL⁻¹, which was used as the stock solution for further steps.

3.2 Microfluidic fabrication of nanorobotic microgels

Microfluidic devices were fabricated via conventional soft photolithography. A thin layer (25 μm) of SU8-3050 photoresist (Kayaku Advanced Materials) was spin-coated onto a silicon wafer. UV-exposure was performed at a dose of 250 μJ cm⁻² using a tabletop maskless aligner system (μM LA, Heidelberg Instruments). Post-baking and development were then performed according to manufacturer instructions. Following photoresist development, a degassed mixture of polydimethylsiloxane (PDMS) and the crosslinker at 10 : 1 ratio, was poured on the wafer. The wafer was again degassed and cured in the oven at 65 °C for at least one hour. The PDMS mold was then carefully removed from the wafer and bonded to a glass slide by peeling off from the master and oxidizing both surfaces via a compact handheld plasma device (Piezobrush® PZ3, Relyon Plasma GmbH). Inlet and outlet holes were removed from the PDMS mold using a biopsy punch, prior to bonding.

Microgel fabrication was performed using the prepared microfluidic devices at a flow rate of 1.7 μL min⁻¹. For this purpose, a mixture containing 60 μL of Rhodamine B tagged alginate (2 wt%), 40 μL of calcium carbonate nanoparticles (10 mg mL⁻¹) and 20 μL bead buffer (130 mM NaCl, 25 mM HEPES, 2 mM CaCl₂) was prepared, while a second mixture contained 60 μL of nanoactuators (40 mg mL⁻¹) and 60 μL of Rhodamine B tagged alginate (2 wt%). The mixture of alginate and calcium carbonate nanoparticles was treated with a tip sonicator for homogeneous mixing. The second mixture containing nanoactuators and Rhodamine B labelled alginate was mixed via vortexing and pipetting repeatedly. Both solutions were vigorously stirred prior to microfluidics to ensure homogeneity. Before this step, high molecular weight alginate (IG1, KIMICA) was functionalized with Rhodamine B (DS 2) using EDC-NHS carbodiimide chemistry, and the resulting alginate was dialyzed against sodium chloride over 3 days. Rhodamine B functionalized alginate was then dried using a freeze-dryer for a week, after which it was reconstituted at 2 wt%. The two aqueous phase mixtures were loaded into separate 0.5 mL Luer-Lok syringes. The oil phase containing the fluorinated oil HFE 7500 (Novec 750 engineered fluid, 3 M), the fluorinated surfactant Pico-Surf (Dolomite Microfluidics), and 0.04 vol% acetic acid was loaded into a 3 mL syringe. The syringes were connected to the microfluidic device via a syringe pump (Darwin Microfluidics) and microgel fabrication was initiated. The collected emulsion was treated with PFO for 5 minutes and washed three times to remove any remaining oil.

3.3 Thermomechanical characterization of nanoactuators and nanorobotic microgels

The nanoactuators were imaged via transmission electron microscopy (TEM, FEI Tecnai) at 120 kV, using negative staining, to determine the overall size. A total of 67 nanoactuators were analyzed using image processing via the open-source software, Fiji and an average diameter was calculated. Changes in nanoactuator size were determined via dynamic light scattering (DLS, Litesizer 500, Anton Paar) in aqueous media, within a temperature range of 24 °C to 50 °C using increments of 2 °C. To ensure sample homogenization, a waiting time of 3 minutes was introduced at each temperature step.

Microgel size was determined using brightfield images of 87 nanorobotic microgels under quiescent conditions via the thresholding method with Fiji image analysis tools. The mechanical performance of nanorobotic microgels was measured using an inverted fluorescence microscope (Thunder Imager, Leica Microsystem), equipped with a 785 nm laser diode (200 mW, Thorlabs) controlled externally. Imaging during actuation was performed to capture changes in radial strain of microgels in situ, at 10× magnification with varying laser intensity from 0 to 6.4 μW μm⁻². Laser intensity was measured using a photometer at the objective, while the effective area of the laser beam was determined using the NIR light sensitive fluorescent dye, Indocyanine Green. During actuation, microgels were illuminated with the laser for 2 s, followed by a 10 s period of relaxation. Local temperatures in microgels were quantified by recording changes in fluorescence intensity, which were converted to temperature using the calibration function in Fig. S4.† All captured images were normalized to the starting temperature of 22 °C.

3.4 Nanoindentation measurements

The Young's modulus of microgels and cells were measured using a microscope-compatible nanoindentor (Chiaro, Optics11 Life). A cantilever probe with a tip radius of 3 μm and stiffness of 0.047 N m⁻¹ was used, while an indentation depth of 2 μm with a loading speed of 5000 nm s⁻¹ was used during measurements for 20 individual microgels. For microgels, 0.45 mg mL⁻¹ poly-D-lysine hydrobromide (Sigma-Aldrich) was used to anchor microgels onto the substrate prior to measurements. Similarly, 20 cells were measured via nanoindentation using an indentation depth of 2 μm and a loading speed of 5000 nm s⁻¹.

3.5 Cell culture and formation of large-scale, cell-loaded hydrogel scaffolds

Murine mesenchymal stem cells (D1s, ATCC) were cultured in 10% fetal bovine serum containing high-glucose Dulbecco's Modified Eagle Serum (DMEM) with 1% penicillin/streptomycin at sub-confluency. Viability assessment was performed via live-dead cell staining using calcein AM and ethidium homodimer-1. All reagents were purchased from Thermo Fisher Scientific. Hydrogel scaffolds were prepared by suspending cells in a mixture of 12 μL of Rhodamine B labeled alginate, 6 μL of nanoactuators, and 4 μL of calcium carbonate nanoparticles. The mixture was pipetted in 0.5 μL volume droplets and left undisturbed for 40 minutes to fully crosslink. Finally, 2 mL of cell culture media was added to suspend hydrogel droplets for actuation and imaging.

3.6 Finite element modeling

All numerical simulations were conducted using finite element modeling software COMSOL Multiphysics 6.0. For small-scale microgel models, cells and alginate microgels were modeled as linear elastic materials, where the stress–strain relationship was described via Duhamel–Hooke's theory through two governing parameters: Young's modulus and Poisson's ratio. The Young's moduli of cells (1.41 kPa) and alginate microgels (1.24 kPa) were determined via nanoindentation measurement as described before. The Young's modulus of the nanoactuator was used as 4.8 kPa based on our previous work.² The Poisson's ratio for all materials was set to 0.49. We assumed nanoactuators shrank isotropically normal to their surfaces when actuated. The thermomechanical effect on strain generation of nanoactuators was considered in simulations by defining corresponding nanoactuator strains as input, based on the characterized temperature-strain profile of nanoactuators (Fig. S6†). The nanoactuator strain (44%) was parameterized as isotropic compression on its surface boundary. Nanoactuators were arranged equidistantly with a mutual distance of 150 nm for the ideal representative model. In contrast, they were randomly distributed in the alginate network via COMSOL Application Builder for the realistic microgel model. The cell radius was set to 7.5 μm determined via brightfield microscopy.

The large-scale hydrogel model was set up under the assumption that the mechanical behavior of the alginate scaffold is only influenced by the nanoactuators that are stimulated by the laser beam, so the response of nanoactuators outside the beam area was omitted. The mechanical properties of nanoactuators, cells, and alginate scaffold were set using Young's moduli and Poisson's ratio as in microgel models. The diameter of the laser beam area and the nanorobotic hydrogel droplet were defined to be 88 μm and 2168 μm respectively, which were experimentally quantified via microscopy. A single cell was placed in the nanorobotic hydrogel droplet, where 26.4 vol% nanoactuators were randomly distributed.

4 Conclusions

In this work, we propose a new semi-experimental approach to characterizing the photothermal performance of nanorobotic 3D microgels. The active microgel network is effectively fabricated through a three-channel flow-focusing microfluidic device. Multiscale mechanical characterization of optically regulated nanorobotic microgels is achieved via DLS and brightfield microscopy, where fluorescence-based thermometry accurately visualizes the thermal effects. The nanoactuators shrink by 44% past LCST and significantly contribute to strain generation in microgels, which contract by 2.1%. Supported by experimentally determined microgel properties, our simulations provide reliable quantification of photothermally generated forces. With this approach, the nanorobotic microgels are transitioned from a strain-regulated to a force-controlled system.

In sum, our work enables the quantification of thermomechanical performance in force-regulated cell-laden biosystems. This approach can be further applied to multicellular nanorobotic microgels to study mechanosensitive cell–cell signaling. Future work will focus on developing multicellular active microgels via microfluidics and visualizing the correlation between thermomechanical effects and force-sensitive cellular behavior. Furthermore, simulations can be utilized to optimize the design of nanorobotic microsystems by regulating the governing parameters and providing guidelines for the desired geometry and performance. Future work will simulate the effects of chemical crosslinking and expand the current 2D models to 3D versions.

Author contributions

C. W. conducted the experiments and analyzed the data. B. O. conceived the research idea. P. H. contributed to the thermomechanical analysis. N. I. helped the preparation of cell-loaded nanorobotic hydrogel. B. L. contributed to the simulation modeling. L. H. and B. W. contributed to the fabrication of microfluidic devices. B. O. and C. W. wrote the manuscript with contributions from all authors.

Conflicts of interest

No conflict of interest from any of the authors.

Acknowledgements

We gratefully acknowledge the Bavarian High-Tech Agenda for funding. The authors would furthermore like to thank Christine Benning for conducting Scanning Electron Microscopy on nanorobotic microgels, and colleagues Ece Özelçi, Yimin Yang, and Dr Sabine Zips for their valuable input on the simulations.

References

1. Z. Liu, Y. Liu, Y. Chang, H. R. Seyf, A. Henry, A. L. Mattheyses, K. Yehl, Y. Zhang, Z. Huang and K. Salaita, Nat. Methods, 2016, 13, 143–146.
2. B. Özkale, R. Parreira, A. Bekdemir, L. Pancaldi, E. Özelçi, C. Amadio, M. Kaynak, F. Stellacci, D. J. Mooney and M. S. Sakar, Lab Chip, 2019, 19, 778–788.
3. F. E. Uslu, C. D. Davidson, E. Mailand, N. Bouklas, B. M. Baker and M. S. Sakar, Adv. Mater., 2021, 33, 2102641.
4. A. N. Ramey-Ward, H. Su and K. Salaita, ACS Appl. Mater. Interfaces, 2020, 12, 35903–35917.
5. T. Andersen, D. Wörthmüller, D. Probst, I. Wang, P. Moreau, V. Fitzpatrick, T. Boudou, U. Schwarz and M. Balland, Biophys. J., 2023, 122, 684–696.
6. B. Özkale, J. Lou, E. Özelçi, A. Elosegui-Artola, C. M. Tringides, A. S. Mao, M. S. Sakar and D. J. Mooney, Lab Chip, 2022, 22, 1962–1970.
7. L. Liu, J. Wu, B. Chen, J. Gao, T. Li, Y. Ye, H. Tian, S. Wang, F. Wang, J. Jiang, J. Ou, F. Tong, F. Peng and Y. Tu, ACS Nano, 2022, 16, 6515–6526.
8. S. Schuerle, I. A. Vizcarra, J. Moeller, M. S. Sakar, B. Özkale, A. M. Lindo, F. Mushtaq, I. Schoen, S. Pané, V. Vogel and B. J. Nelson, Sci. Robot, 2017, 2, eaah6094.
9. M. B. Akolpoglu, Y. Alapan, N. O. Dogan, S. F. Baltaci, O. Yasa, G. Aybar Tural and M. Sitti, Sci. Adv., 2022, 8, eabo6163.
10. P. Harder, N. İyisan, C. Wang, F. Kohler, I. Neb, H. Lahm, M. Dreßen, M. Krane, H. Dietz and B. Özkale, Adv. Healthcare Mater., 2023, 2300904.
11. E. Mohagheghian, J. Luo, F. M. Yavitt, F. Wei, P. Bhala, K. Amar, F. Rashid, Y. Wang, X. Liu, C. Ji, J. Chen, D. P. Arnold, Z. Liu, K. S. Anseth and N. Wang, Sci. Robot, 2023, 8, eadc9800.
12. D. O. Asgeirsson, M. G. Christiansen, T. Valentin, L. Somm, N. Mirkhani, A. H. Nami, V. Hosseini and S. Schuerle, Lab Chip, 2021, 21, 3850–3862.
13. Y. Li, G. Huang, B. Gao, M. Li, G. M. Genin, T. J. Lu and F. Xu, NPG Asia Mater., 2016, 8, e238–e238.
14. S. Nam, B. R. Seo, A. J. Najibi, S. L. McNamara and D. J. Mooney, Nat. Mater., 2023, 22, 249–259.
15. A. Méry, A. Ruppel, J. Revilloud, M. Balland, G. Cappello and T. Boudou, Nat. Commun., 2023, 14, 717.
16. J. Chen, P. Gu, G. Ran, Y. Zhang, M. Li, B. Chen, H. Lu, Y.-Z. Han, W. Zhang, Z. Tang, Q. Yan, R. Sun, X. Fu, G. Chen, Z. Shi, S. Wang, X. Liu, J. Li, L. Wang, Y. Zhu, J. Shen, B. Z. Tang and C. Fan, Nat. Mater., 2023, 1–10.
17. I. Pastoriza-Santos, C. Kinnear, J. Pérez-Juste, P. Mulvaney and L. M. Liz-Marzán, Nat. Rev. Mater., 2018, 3, 375–391.
18. M. Karg, I. Pastoriza-Santos, J. Pérez-Juste, T. Hellweg and L. M. Liz-Marzán, Small, 2007, 3, 1222–1229.
19. R. Contreras-Cáceres, J. Pacifico, I. Pastoriza-Santos, J. Pérez-Juste, A. Fernández-Barbero and L. M. Liz-Marzán, Adv. Funct. Mater., 2009, 19, 3070–3076.
20. T. Ding, V. K. Valev, A. R. Salmon, C. J. Forman, S. K. Smoukov, O. A. Scherman, D. Frenkel and J. J. Baumberg, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5503–5507.
21. Y. Zeng and J. Q. Lu, ACS Nano, 2014, 8, 11695–11706.
22. C. Yang, D. Xu, W. Peng, Y. Li, G. Zhang, F. Zhang and X. Fan, Nanoscale, 2018, 10, 15387–15392.
23. M. Das, N. Sanson, D. Fava and E. Kumacheva, Langmuir, 2007, 23, 196–201.
24. B. Özkale, M. S. Sakar and D. J. Mooney, Biomaterials, 2021, 267, 120497.
25. A. Sutton, T. Shirman, J. V. Timonen, G. T. England, P. Kim, M. Kolle, T. Ferrante, L. D. Zarzar, E. Strong and J. Aizenberg, Nat. Commun., 2017, 8, 14700.
26. Y. Chandorkar, A. Castro Nava, S. Schweizerhof, M. Van Dongen, T. Haraszti, J. Köhler, H. Zhang, R. Windoffer, A. Mourran, M. Möller and L. De Laporte, Nat. Commun., 2019, 10, 4027.
27. M. Lu, S. Li, X. Xiong, Z. Huang, B. Xu, Y. Liu, Q. Wu, N. Wu, H. Liu and D. Zhou, Adv. Funct. Mater., 2022, 32, 2208061.
28. T. D. Cong, Z. Wang, M. Hu, Q. Han and B. Xing, ACS Nano, 2020, 14, 5836–5844.
29. J. Wang, B. Hao, K. Xue, H. Fu, M. Xiao, Y. Zhang, L. Shi and C. Zhu, Adv. Mater., 2022, 34, 2205653.
30. A. Mourran, H. Zhang, R. Vinokur and M. Möller, Adv. Mater., 2017, 29, 1604825.
31. J. Zhou, B. Del Rosal, D. Jaque, S. Uchiyama and D. Jin, Nat. Methods, 2020, 17, 967–980.
32. W. Yu, O. Deschaume, L. Dedroog, C. J. Garcia Abrego, P. Zhang, J. Wellens, Y. de Coene, S. Jooken, K. Clays, W. Thielemans, C. Glorieux and C. Bartic, Adv. Funct. Mater., 2022, 32, 2108234.
33. M. Zhu, G. Baffou, N. Meyerbroker and J. Polleux, ACS Nano, 2012, 6, 7227–7233.
34. C. M. Maier, M. A. Huergo, S. Milosevic, C. Pernpeintner, M. Li, D. P. Singh, D. Walker, P. Fischer, J. Feldmann and T. Lohmüller, Nano Lett., 2018, 18, 7935–7941.
35. K. Y. Lee and D. J. Mooney, Prog. Polym. Sci., 2012, 37, 106–126.
36. K. Teng, Q. An, Y. Chen, Y. Zhang and Y. Zhao, ACS Biomater. Sci. Eng., 2021, 7, 1302–1337.
37. L. P. Guerzoni, J. C. Rose, D. B. Gehlen, A. Jans, T. Haraszti, M. Wessling, A. J. Kuehne and L. De Laporte, Small, 2019, 15, 1900692.
38. A. Mora-Boza, L. M. M. Castro, R. S. Schneider, W. M. Han, A. J. García, B. Vázquez-Lasa and J. San Román, Mater. Sci. Eng., C, 2021, 120, 111716.
39. A. J. Krüger, O. Bakirman, L. P. Guerzoni, A. Jans, D. B. Gehlen, D. Rommel, T. Haraszti, A. J. Kuehne and L. De Laporte, Adv. Mater., 2019, 31, 1903668.
40. D. M. Headen, J. R. García and A. J. García, Microsyst. Nanoeng., 2018, 4, 1–9.
41. R. Dubay, J. N. Urban and E. M. Darling, Adv. Funct. Mater., 2021, 31, 2009946.
42. R. Ding, K.-C. Hung, A. Mitra, L. W. Ung, D. Lightwood, R. Tu, D. Starkie, L. Cai, L. Mazutis, S. Chong, D. A. Weitz and J. A. Heyman, RSC Adv., 2020, 10, 27006–27013.
43. J. Zhao, H. Su, G. E. Vansuch, Z. Liu, K. Salaita and R. B. Dyer, ACS Nano, 2018, 13, 515–525.
44. R. Parreira, E. Özelçi and M. S. Sakar, Adv. Intell. Syst., 2020, 2, 2000062.
45. S. Deshpande, S. Sharma, V. Koul and N. Singh, ACS Omega, 2017, 2, 6455–6463.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr06485a

---