Unraveling the formation of oxygen vacancies on the surface of transition metal-doped ceria utilizing artificial intelligence

Abstract

Ceria has been extensively utilized in different fields, with surface oxygen vacancies playing a central role. However, versatile oxygen vacancy regulation is still in its infancy. In this work, we propose an effective strategy to manipulate the oxygen vacancy formation energy via transition metal doping by combining first-principles calculations and analytical learning. We elucidate the underlying mechanism driving the formation of oxygen vacancies using combined symbolic regression and data analytics techniques. The results show that the Fermi level of the system and the electronegativity of the dopants are the paramount parameters (features) influencing the formation of oxygen vacancies. These insights not only enhance our understanding of the oxygen vacancy formation mechanism in ceria-based materials to improve their functionality but also potentially lay the groundwork for future strategies in the rational design of other transition metal oxide-based catalysts.

---

Zhong-Kang Han

Zhong-Kang Han is presently a researcher at the School of Materials Science and Engineering, Zhejiang University, Hangzhou, China. He earned his PhD degree from the University of Chinese Academy of Sciences in 2018. Subsequently, he pursued postdoctoral research at the Fritz Haber Institute of the Max Planck Society and at the Skolkovo Institute of Science and Technology from 2019 to 2021. His research interests encompass the surface phase diagram of elemental and alloy transition metals under realistic conditions, the design of high-performance heterogeneous catalysts for water–gas shift and CO oxidation reactions, and machine learning-guided high-performance materials design.

---

1. Introduction

Ceria-based materials are the key components in catalysts used for automotive exhaust treatment and hydrogen purification, as well as in many other functional materials, such as oxide-ion conductors and sensors.^1–5 In all such applications, the formation of oxygen vacancies (O_vs) is a critical step. These O_vs serve as anchor sites to stabilize small transition metal (TM) clusters and prevent them from aggregating in ceria-supported TM catalysts.^6–8 Two electrons remaining after the removal of one neutral oxygen localize in the empty 4f orbital of Ce,^9,10 resulting in the reduction of two Ce cations from the +4 oxidation state to the +3 oxidation state; this reduction changes the surface chemistry of the ceria and consequently its catalytic performance.^11,12 Thus, the effective regulation of the O_v formation energy is extremely important, especially in catalytic applications.

In recent decades, tremendous efforts have been devoted to designing and synthesizing TM oxides with optimized O_v populations and distributions. Some examples of such efforts include modifying the O_v dynamic behavior and concentration of CeO₂ by suitable doping and strong metal–support interactions,^13–18 tuning the oxygen storage capacity and O_v formation energy of CeO₂ through a large biaxial strain,¹⁹ and altering the formation, distribution, and mobility of O_vs and ion defects of CeO₂via dislocation.²⁰ TM doping has been thoroughly utilized to manipulate the surface chemistry and O_v behavior of ceria-based catalysts.^21–23 Ke and coworkers proposed a robust approach for tuning the CO oxidation activity over CeO₂ nanowires through careful modulation of the local structure and surface states by doping lanthanides with continuous variation in the ionic radii.²¹ Zhang et al. successfully synthesized CeO₂ solid solutions with an ultrahigh manganese doping concentration and found that highly reducible Mn⁴⁺ ions strongly facilitate the migration of O_vs from the bulk to the surface.²² Jiang and coworkers found that cobalt-doped ceria nanosheets possess high efficiency toward the hydrogen evolution reaction due to the increased concentration of O_vs and the increased number of active sites.²³

Theoretical calculations also play an essential role in investigating the origins of the increased performance of TM-doped ceria materials.^24–28 Guo et al. investigated the effects of Pd, Ru, and Cu dopants on the reduction selectivity of CO₂ on CeO₂(111) and found that the doped metals distorted the local geometry of the ceria surface by weakening the Ce–O bond and thus generating highly active O_v sites.²⁴ Yang et al. investigated the CO oxidation reaction on Cu-adsorbed and Cu-doped ceria systems and found that the Cu-adsorbed system inhibited the formation of O_vs, while the Cu-doped system facilitated the formation of O_vs.²⁶ Krcha and coworkers systematically calculated the O_v formation energies and reaction activity for hydrocarbon conversion on various TM-doped CeO₂(111) surfaces, and clear periodic trends in the O_v formation energies and C–H bond activations were observed.²⁵ Despite extensive efforts, the mechanisms underlying the changes in the dopant-induced O_v formation energy remain unclear.

In this work, we performed systematic calculations on the stabilities and surface O_v formation energies for 97 TM-doped ceria systems, with dopants occupying the surface cerium sites. An in-depth analysis was conducted to explore the correlations between the properties of these systems (including stabilities and surface O_v formation energies) and the features of the dopants, employing a combined approach of sure independence screening and sparsifying operator (SISSO)²⁹ and subgroup discovery (SGD) methodologies.^30–35 These techniques facilitated the unveiling of the underlying mechanisms that drive the observed trends in the data.

2. Methods

Spin-polarized DFT calculations were carried out using the generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE) as implemented in the Vienna ab initio Simulation Package (VASP).^36,37 A Hubbard-type term U = 5.0 eV was used for the Ce 4f states to describe the localization of the excess charges, which is within the range of suitable values to describe reduced ceria-based systems.³⁸ The Kohn–Sham valence states were expanded in a plane-wave basis set with a cutoff energy of 400 eV. The core–valence interactions were represented using the projector augmented wave (PAW) approach,³⁹ where the (4f, 5s, 5p, 5d, 6s) and (2s, 2p) states of the Ce and O atoms were treated as valence states. A periodic slab with a (4 × 4), (3 × 4), and (4 × 4) surface unit cell was employed to model the CeO₂(100), CeO₂(110), and CeO₂(111) surfaces, respectively. The slabs consisted of nine, five, and twelve atomic layers, respectively, with an additional vacuum layer of 15 Å. During the geometry optimization, the bottom two layers (O–Ce), three layers (O–Ce–O), and three layers (O–Ce–O) were held fixed at their bulk positions for CeO₂(100), CeO₂(110), and CeO₂(111) surfaces, respectively. Due to the large supercell dimensions, the k-point sampling was restricted to the Γ point. Structures were fully relaxed until the maximum force on each atom becomes less than 0.05 eV/Å. The surface energies for CeO₂(100), CeO₂(110), and CeO₂(111) are collected in Table S1† and benchmarked against the existing literature values.

The formation energy (ΔE_F) of the TM-doped CeO₂ surfaces was calculated using formula (1):

where E_TM-slab is the total energy of the whole system, E_slab is the energy of the clean CeO₂ surfaces, E^Ce_bulk is the energy of the conventional cell of ceria, N^Ce_bulk is the number of Ce atoms in the conventional cell, E^TM_bulk is the energy of the conventional cell of TM, and N^TM_bulk is the number of TM atoms in the conventional cell.

The O_v formation energy of the TM-doped CeO₂ surfaces was calculated by means of formula (2):

where E_Ov, E_TM-slab, and E_O2 are the total energies of the TM-doped CeO₂ surfaces with oxygen vacancies, the TM-doped CeO₂ surfaces, and the gas-phase O₂ molecule, respectively.

Subgroup discovery (SGD) was performed using the RealKD package.⁴⁰ Each feature was split into 14 subsets using a 14-means clustering algorithm.⁴¹ The candidate subgroups were built as conjunctions of the obtained simple inequalities. The main idea of SGD is that the subgroups are unique if the distribution of the data they contain is as different as possible from the data distribution in the whole sample. Detailed information about the SGD approach can be found in the ESI.†

3. Results and discussion

3.1 Sure independence screening and sparsifying operator

The stability of catalysts is as significant as their catalytic performance. To begin, we conducted a comprehensive investigation into the stabilities of 97 TM-doped ceria systems, including those of CeO₂(100), CeO₂(110), and CeO₂(111). We considered 30 different d-block TM dopants. As shown in Fig. 1, the TM dopants were positioned at the surface cerium sites of the ceria substrates. The formation energies of the TM-doped ceria systems are collected in Tables S2–S4.† Given the existence of multiple localizations of Ce³⁺ polarons,⁴² we have taken care to include a variety of Ce³⁺ polaron configurations in our dataset to ensure that our analytical learning approaches adequately capture these features (refer to Fig. S1†).

Fig. 1 Structural models of the TM-doped ceria systems. The dopant is positioned at the top cerium site of the (a) CeO₂(100), (b) CeO₂(110), and (c) CeO₂(111) surfaces. The oxygen vacancy sites under consideration are highlighted with dashed circles.

To evaluate the impact of TM dopants on the stability of various TM-doped ceria systems, we systematically explored the correlations between the formation energies of the TM-doped ceria systems (the property) and the characteristics of the dopants (the features) using analytical learning techniques. The proper selection of initial features is of paramount importance in analytical learning. The guiding principles for initial feature selection are as follows: (a) the features can be obtained or calculated in convenient ways and (b) the features are already evaluated and shown to have close correlations with properties investigated either experimentally or theoretically. We considered two classes of features: fourteen atomic features and five system-based features, and the selection of features is based on their relevance to the properties and simplicity,^43–49 as detailed in Table 1. The Pearson's correlation coefficient matrix among the considered features of the TM-doped ceria systems was checked first, with the results summarized in Fig. 2a–d. The results reveal that certain features, including Ndsm, Ndm, Mm, and Rm, are closely correlated with each other for the subgroup data set encompassing 3d-, 4d-, and 5d-block metals (Fig. 2a–c). However, their correlation significantly diminished for the entire data set comprising all d-block metals (Fig. 2d). This observation suggests a high degree of diversity within the primary feature space, which is well-suited for subsequent analytical learning analyses.

Fig. 2 Heat map of the Pearson's correlation coefficient matrix among the nineteen features of the (a) 3d-, (b) 4d-, (c) 5d-, and (d) total d-block transition metals for the TM-doped ceria systems.

Table 1 The nineteen considered features of the TM dopants

Class	Name	Abbreviation
Atomic	First ionization energy (eV)	EIm
	Highest occupied molecular orbital (eV)	Hm
	Lowest unoccupied molecular orbital (eV)	Lm
	Atomic radius (empirical) (Å)	Rm
	Bond dissociation energy of homo-diatomic molecules (eV)	BDEm
	Cohesive energy (eV)	ECm
	Radius of the s-orbital (Å)	RSm
	Radius of the d-orbital (Å)	RDm
	Electronegativity	ENm
	Number of d valence electrons	Ndm
	Total number of d and s valence electrons	Ndsm
	Miedema parameters (volt)	MdLm
	Miedema parameters (density unit)	MdNm
	Relative atomic mass (a.m.u.)	Mm
System	Bader charge of the dopant (e^−)	q
	Fermi level (eV)	FL
	Work function (eV)	WF
	d-band center of the dopant (eV)	DC
	p-band center of oxygen (eV)	PC

---

An in-depth investigation was conducted to explore the correlations between the primary features and the formation energies of the TM-doped ceria systems. The findings are presented in Fig. 3 and Fig. S2,† which reveal that the formation energies exhibit a continuous distribution within a wide energy range (−12.0 eV to 3.0 eV) and display clear periodic trends that are associated with the number of d electrons (Ndm, refer to Fig. 3a) and the radius of d-orbitals (RDm, refer to Fig. 3b) of the TM dopants.⁵⁰ The discerned linear relationship between Ndm and ΔE_F can be interpreted based on the significant influence the d-orbitals of TM atoms exert on their interaction with oxygen. Transition metals are characterized by their distinct numbers of d-electrons, and those with fewer d-electrons tend to have less strong correlations within their d-orbitals. This reduced correlation promotes the delocalization of the d-orbitals, which in turn makes it easier for other atoms to extract electrons and consequently form bonds. Furthermore, the formation of a covalent bond necessitates an effective overlap of orbitals with matching energies. Transition metals with fewer d-electrons generally have d-orbitals with energy levels closer to the 2p-orbitals of oxygen. This facilitates the formation of stronger covalent bonds due to the enhanced orbital overlap. These combined factors contribute to the strong binding between TM dopants with a small number of d-electrons and the lattice oxygen within ceria. This, in turn, stabilizes the TM-doped ceria systems. Similarly, an increase in the size of d-orbitals can lead to an enhanced orbital overlap with the p-orbitals of oxygen. If the d-orbitals of a metal atom are larger, they hold greater potential for overlapping with the p-orbitals of the oxygen atom, leading to the creation of a stronger covalent bond. These observations provide a crucial understanding of the key factors contributing to the stabilities of TM-doped ceria systems.

Fig. 3 Correlation between the formation energies (ΔE_F) of TM-doped ceria systems and features of transition metal dopants. (a) The correlation between ΔE_F and Ndm and (b) the correlation between ΔE_F and RDm.

We further explored the correlation between the surface O_v formation energies of the TM-doped ceria systems and the primary features. The corresponding results are shown in Fig. S3.†It is evident that the surface O_v formation energies of the TM-doped ceria systems exhibit much weaker correlations with the primary features than the formation energies of the TM-doped ceria systems. Thus, more complex features are required to describe the O_v formation energies of the TM-doped ceria systems. To identify the key descriptive features, we employed the state-of-the-art multi-task SISSO approach. The multi-task SISSO approach enables us to identify the best low-dimensional descriptor in an immensity of offered candidates. The model is a linear combination of a few derived features, which are typically non-linear expressions created from mathematical operations on the primary features or between them. In the multi-task SISSO, we divided the entire dataset into three groups based on different surface cuts. While the best low-dimensional descriptors have the same features across these groups, they have different feature coefficients. These derived features are selected from a massive set of more than one billion candidate-derived features, with feature complexity (the number of operators in each derived feature) of up to five in this work. Fig. S4† illustrates that the five-dimensional (5D) SISSO model, which incorporates five derived features, demonstrates a high level of accuracy and predictive power, as validated through 10 iterations of a leave-5%-out validation method (Table S5†). Therefore, to maintain the simplicity of the model and to prevent overfitting, we decided not to explore higher-dimensional models. Interestingly, throughout the 10 iterations of the leave-5%-out validation, a similar set of primary features was consistently identified, especially the primary features WF, ECm, FL, PC, Hm, and BDEm, all of which were consistently selected (Table S6†). It's not surprising that the system-based features WF, FL, and PC were chosen, considering their strong correlation with the redox abilities of the systems, a factor that directly influences the formation and healing of O_vs. Moreover, features like ECm and BDEm encapsulate the interaction characteristics of the TM dopant with other species, while Hm captures the electron-sharing capacity of the TM dopants with other species. All these features were consistently selected throughout the validation process, indicating the SISSO model's capability to capture the underlying physics that governs the formation of O_vs. The frequent selection of these descriptor components, despite changes in system size and composition, underscores the robustness of the model, affirming its reliability in comprehending such complex systems.

3.2 Subgroup discovery

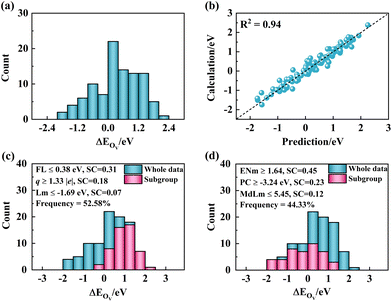
The components of the optimal model identified by the SISSO approach are presented in Table 2. Additionally, Fig. 4 displays the error distribution of the O_v formation energies as predicted by the optimal SISSO model (Fig. 4b), alongside the distribution of the O_v formation energies themselves (Fig. 4a). While the SISSO model provides mathematical formulas, gaining a deeper understanding of the mechanisms underlying the formation of O_vs in various TM-doped ceria systems using the SISSO model remains a challenging task. In an attempt to identify the key descriptive parameters and facilitate a physical understanding of the actuating mechanisms, we applied the SGD local artificial intelligence approach.³² SGD is a method designed to identify local patterns in data that maximize a specific quality function. The identified pattern/subgroup is defined as an intersection of simple inequalities involving provided features.⁵⁰ The so-called quality function measures the degree of distinctiveness of a pattern/subgroup in comparison to the entire data set (further details about the implementation of the SGD approach can be found in the ESI†).

Fig. 4 Analytical learning of surface O_v formation energies of the TM-doped ceria systems. (a) The histogram distribution of data samples for O_v formation energies of the TM-doped ceria systems, (b) the error distribution between the SISSO model predicted energies and DFT calculated energies for the TM-doped ceria systems, and the results of the SGD by maximizing (c) and minimizing (d) the surface O_v formation energies.

Table 2 Components of descriptors and their coefficient (C) of the multi-task SISSO-identified best model. The intercept values are −1.20 for CeO₂(100), 2.84 for CeO₂(110), and −3.96 for CeO₂(111)

Descriptor	CeO2(100)	CeO2(110)	CeO2(111)
	(Task 1)	(Task 2)	(Task 3)
	C1	C2	C3
(MdLm − WF)/(q × ENm) − (WF/MdLm)	−0.19 × 10^1	0.32 × 10^1	−0.53 × 10^1
(Mm/(DC + BDEm))/(FL + (MdLm/ECm))	−0.20 × 10^−4	0.58 × 10^−5	−0.40 × 10^−3
(WF/Lm)/((Rm × MdLm) − (WF/RDm))	0.71	−0.16	0.38 × 10^−1
(q + Ndm)/(MdLm − EIm − (Ndm/q))	−0.19 × 10^−1	−0.74 × 10^−1	−0.27 × 10^−1
(MdNm/(MdNm − RSm))/(DC + WF − RSm)	0.47 × 10^−2	0.32 × 10^−2	−0.66 × 10^−3

---

To gain better insight into the factors and mechanisms that facilitate the formation of O_vs on various TM-doped ceria systems, we utilized the SGD approach. Starting with the identification of subgroups that maximize the O_v formation energies, one specific subgroup was singled out. This subgroup, which consists of 51 data points or 52.58% of the total dataset as depicted in Fig. 4c, was distinguished by the conditions FL ≤ 0.38 eV, q ≥ 1.33 |e|, and Lm ≤ −1.69 eV. On the other hand, the identification of subgroups that minimize O_v formation energies led to the discovery of another subgroup. This subgroup contained 43 data points or 44.33% of the total dataset as shown in Fig. 4d, and was characterized by the conditions ENm ≥ 1.64, PC ≥ −3.24 eV, and MdLm ≤ 5.45. The importance of each feature was determined by its respective support score (SC), which is derived from the quality function value (Q). A score of 0 suggests that removing this specific feature does not affect the value of Q, indicating that this feature does not influence the SGD result. Among these features, FL ≤ 0.38 eV and q ≥ 1.33 |e| stood out for their relatively high SCs, which the SGD approach identified as key in inhibiting O_v formation. In contrast, features ENm ≥ 1.64 and PC ≥ −3.24 eV were noted to facilitate O_v formation. In a physical context, a lower Fermi level (FL ≤ 0.38 eV) implies that the highest occupied 2p orbitals of lattice oxygen should be situated at relatively low energy levels. As a result, electron transfer from the removed neutral oxygen to the empty d-orbitals of the TM dopants or the f-orbitals of the lattice cerium site becomes less feasible, inhibiting surface O_v formation. Similarly, the condition q ≥ 1.33 |e| can be interpreted from the fact that four positive charges (4e⁺) are retained when one neutral cerium atom is removed. If these positive charges are not adequately compensated by the TM dopant (as can occur when the q is small), the remaining positive charges will form empty hole states that can combine with the electrons left after oxygen removal, thereby facilitating O_v formation. Thus, a larger q is crucial to suppress O_v formation. Furthermore, a larger dopant electronegativity (ENm ≥ 1.64) and a larger p-orbital center (PC ≥ −3.24 eV) of the lattice oxygen can facilitate O_v formation. Dopants with lower electronegativity, due to their large electronegativity difference, bind strongly with the lattice oxygen, inhibiting O_v formation. On the other hand, a higher p-orbital center eases the electron transfer from oxygen to TM sites upon oxygen removal, promoting O_v formation. In addition, the insights gleaned from the SGD analysis are applicable to other transition metal-doped metal oxides as well (Table S7†). With the help of SGD, a sophisticated understanding was developed that would have been challenging to achieve without local artificial intelligence. SGD has proven useful in identifying multiple alternative subgroups, each corresponding to different mechanisms affecting the target properties. The target properties with the desired values that lie in a specific range are also factors affecting the identified subgroups.⁵¹ Exploring the role of different factors can significantly improve the interpretability of the subgroups.

The interpretation of SGD results is sometimes limited by our domain knowledge. To validate the abovementioned explanations, we further analyzed the species projected density of states of three representative CeO₂(111) systems with low (Cu-doped), moderate (La-doped), and high (Nb-doped) O_v formation energies (Fig. 5). For the Cu-doped surface, pronounced 3d empty states of Cu exist near the Fermi level due to the relatively large q of Cu (−1.10 e⁻) (Fig. 5a). These empty states will be occupied by extra electrons to facilitate the removal of neutral oxygen and the formation of O_vs. For the Nb-doped surface, there are no empty d-orbitals near the Fermi level due to the relatively small q of Nb (−2.58 e⁻). The electrons remaining after the removal of neutral oxygen must occupy the 4f states of the cerium atoms, splitting from the stable unoccupied 4f states of cerium atoms, which makes O_v formation difficult (Fig. 5c). The density of empty states decreases in the order of Cu-doped > La-doped (Fig. 5b) > Nb-doped surfaces, resulting in O_v formation energies that increase in the order of Cu-doped < La-doped < Nb-doped surfaces. Similar findings were observed for both the CeO₂(100) and CeO₂(110) systems.

Fig. 5 Species projected density of states for surface doped CeO₂(111) surfaces. The TM-doped CeO₂(111) surfaces with low O_v formation energy (a, Cu doping), moderate O_v formation energy (b, La doping), and high O_v formation energy (c, Nb doping).

4. Conclusions

In summary, by synergistically utilizing first-principles calculations and an interpretable artificial intelligence approach, we have successfully identified the key descriptive features and mechanisms that facilitate the formation of oxygen vacancies in various transition metal-doped CeO₂ systems. The Fermi level of the system and the electronegativity of the dopants are the paramount parameters (features) influencing the formation of oxygen vacancies. By integrating domain knowledge, symbolic regression, subgroup discovery, and electronic structure analysis, the facilitated formation mechanism of oxygen vacancies was attributed to the distributions and behaviors of the occupied 2p states of lattice oxygen and the empty states of the transition metal dopants near the Fermi level. Our methodology can be easily adapted to other transition metal oxide-based functional materials. It demonstrates the powerful potential of artificial intelligence to provide new understanding and insights into the physical principles underlying data.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge the financial support of the National Key Research and Development Program (2022YFA1505500), the Fundamental Research Funds for the Central Universities, and the National Research Foundation of Korea (NRF) grants funded by the Korean government (Grant RS-2023-00243788).

References

1. Q. Fu, H. Saltsburg and M. Flytzani-Stephanopoulos, Science, 2003, 301, 935–938.
2. G. A. Deluga, J. R. Salge, L. D. Schmidt and X. E. Verykios, Science, 2004, 303, 993–997.
3. C. T. Campbell and C. H. F. Peden, Science, 2005, 309, 713–714.
4. J. A. Rodriguez, S. Ma, P. Liu, J. Hrbek, J. Evans and M. Pérez, Science, 2007, 318, 1757–1760.
5. S. Park, J. M. Vohs and R. J. Gorte, Nature, 2000, 404, 265–267.
6. A. Bruix, J. A. Rodriguez, P. J. Ramírez, S. D. Senanayake, J. Evans, J. B. Park, D. Stacchiola, P. Liu, J. Hrbek and F. Illas, J. Am. Chem. Soc., 2012, 134, 8968–8974.
7. J. Carrasco, D. López-Durán, Z. Liu, T. Duchoň, J. Evans, S. D. Senanayake, E. J. Crumlin, V. Matolín, J. A. Rodríguez and M. V. Ganduglia-Pirovano, Angew. Chem., Int. Ed., 2015, 54, 3917–3921.
8. S. Zhang, Z. Xia, T. Ni, Z. Zhang, Y. Ma and Y. Qu, J. Catal., 2018, 359, 101–111.
9. M. V. Ganduglia-Pirovano, J. L. F. Da Silva and J. Sauer, Phys. Rev. Lett., 2009, 102, 026101.
10. H.-Y. Li, H.-F. Wang, X.-Q. Gong, Y.-L. Guo, Y. Guo, G. Lu and P. Hu, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 193401.
11. Q. Gao, J. Hao, Y. Qiu, S. Hu and Z. Hu, Appl. Surf. Sci., 2019, 497, 143732.
12. K. B. Sravan Kumar and P. A. Deshpande, J. Phys. Chem. C, 2015, 119, 8692–8702.
13. S. Sen, T. Edwards, S. K. Kim and S. Kim, Chem. Mater., 2014, 26, 1918–1924.
14. Z. Wang, H. Fu, Z. Tian, D. Han and F. Gu, Nanoscale, 2016, 8, 5865–5872.
15. Y. Zheng, H. Xiao, K. Li, Y. Wang, Y. Li, Y. Wei, X. Zhu, H.-W. Li, D. Matsumura, B. Guo, F. He, X. Chen and H. Wang, ACS Appl. Mater. Interfaces, 2020, 12, 42274–42284.
16. Z.-K. Han, Y.-G. Wang and Y. Gao, ChemComm, 2017, 53, 9125–9128.
17. E. W. McFarland and H. Metiu, Chem. Rev., 2013, 113, 4391–4427.
18. M. Nolan, J. Mater. Chem., 2011, 21, 9160.
19. C. Balaji Gopal, M. García-Melchor, S. C. Lee, Y. Shi, A. Shavorskiy, M. Monti, Z. Guan, R. Sinclair, H. Bluhm, A. Vojvodic and W. C. Chueh, Nat. Commun., 2017, 8, 15360.
20. L. Sun, D. Marrocchelli and B. Yildiz, Nat. Commun., 2015, 6, 6294.
21. J. Ke, J.-W. Xiao, W. Zhu, H. Liu, R. Si, Y.-W. Zhang and C.-H. Yan, J. Am. Chem. Soc., 2013, 135, 15191–15200.
22. P. Zhang, H. Lu, Y. Zhou, L. Zhang, Z. Wu, S. Yang, H. Shi, Q. Zhu, Y. Chen and S. Dai, Nat. Commun., 2015, 6, 8446.
23. S. Jiang, R. Zhang, H. Liu, Y. Rao, Y. Yu, S. Chen, Q. Yue, Y. Zhang and Y. Kang, J. Am. Chem. Soc., 2020, 142, 6461–6466.
24. C. Guo, S. Wei, S. Zhou, T. Zhang, Z. Wang, S.-P. Ng, X. Lu, C.-M. L. Wu and W. Guo, ACS Appl. Mater. Interfaces, 2017, 9, 26107–26117.
25. M. D. Krcha, A. D. Mayernick and M. J. Janik, J. Catal., 2012, 293, 103–115.
26. Z. Yang, B. He, Z. Lu and K. Hermansson, J. Phys. Chem. C, 2010, 114, 4486–4494.
27. C. Riley, S. Zhou, D. Kunwar, A. De La Riva, E. Peterson, R. Payne, L. Gao, S. Lin, H. Guo and A. Datye, J. Am. Chem. Soc., 2018, 140, 12964–12973.
28. S. Zhao, D. Kang, Y. Liu, Y. Wen, X. Xie, H. Yi and X. Tang, ACS Catal., 2020, 10, 11739–11750.
29. R. Ouyang, S. Curtarolo, E. Ahmetcik, M. Scheffler and L. M. Ghiringhelli, Phys. Rev. Mater., 2018, 2, 083802.
30. S. Wrobel, in Principles of Data Mining and Knowledge Discovery, ed. J. Komorowski and J. Zytkow, Springer Berlin Heidelberg, Berlin, Heidelberg, 1997, vol. 1263, pp. 78–87.
31. J. H. Friedman and N. I. Fisher, Stat. Comput., 1999, 9, 123–143.
32. M. Atzmueller, WIREs Data Min. Knowl. Discov., 2015, 5, 35–49.
33. M. Boley, B. R. Goldsmith, L. M. Ghiringhelli and J. Vreeken, Data Min. Knowl. Disc., 2017, 31, 1391–1418.
34. B. R. Goldsmith, M. Boley, J. Vreeken, M. Scheffler and L. M. Ghiringhelli, New J. Phys., 2017, 19, 013031.
35. A. Mazheika, Y.-G. Wang, R. Valero, F. Viñes, F. Illas, L. M. Ghiringhelli, S. V. Levchenko and M. Scheffler, Nat. Commun., 2022, 13, 419.
36. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
37. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
38. C. W. M. Castleton, J. Kullgren and K. Hermansson, J. Chem. Phys., 2007, 127, 244704.
39. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
40. C. Sutton, M. Boley, L. M. Ghiringhelli, M. Rupp, J. Vreeken and M. Scheffler, Nat. Commun., 2020, 11, 4428.
41. T. Kanungo, D. M. Mount, N. S. Netanyahu, C. D. Piatko, R. Silverman and A. Y. Wu, IEEE Trans. Pattern Anal. Mach. Intell., 2002, 24, 881–892.
42. G. S. Otero, P. G. Lustemberg, F. Prado and M. V. Ganduglia-Pirovano, J. Phys. Chem. C, 2020, 124, 625–638.
43. H. Zhuang, A. J. Tkalych and E. A. Carter, J. Phys. Chem. C, 2016, 120, 23698–23706.
44. V. Subramanian, E. E. Wolf and P. V. Kamat, J. Am. Chem. Soc., 2004, 126, 4943–4950.
45. B. Hammer and J. K. Norskov, Nature, 1995, 376, 238–240.
46. L. Gong, D. Zhang, C. Y. Lin, Y. Zhu, Y. Shen, J. Zhang, X. Han, L. Zhang and Z. Xia, Adv. Energy Mater., 2019, 9, 1902625.
47. C. G. Vayenas, S. Bebelis and S. Ladas, Nature, 1990, 343, 625–627.
48. Y. Liu, C. Wen, Y. Guo, G. Lu and Y. Wang, J. Phys. Chem. C, 2010, 114, 9889–9897.
49. S. Zha, Z. J. Zhao, S. Chen, S. Liu, T. Liu, F. Studt and J. Gong, CCS Chem., 2020, 2, 262–270.
50. Z. Hu and H. Metiu, J. Phys. Chem. C, 2011, 115, 17898–17909.
51. Z.-K. Han, D. Sarker, R. Ouyang, A. Mazheika, Y. Gao and S. V. Levchenko, Nat. Commun., 2021, 12, 1833.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr05950b

‡ These authors contributed equally to this work.

---