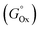Open Access Article
Open Access ArticlePhysical and chemical parameters determining the formation of gold–sp metal (Al, Ga, In, and Pb) nanoalloys
Vito
Coviello
 a,
Daniel
Forrer
a,
Daniel
Forrer
 ab,
Patrizia
Canton
ab,
Patrizia
Canton
 c and
Vincenzo
Amendola
c and
Vincenzo
Amendola
 *a
*a
aDepartment of Chemical Sciences, Università di Padova, via Marzolo 1, I-35131 Padova, Italy
bCNR – ICMATE, Padova, I-35131, Italy
cDepartment of Molecular Sciences and Nanosystems, University Ca’ Foscari of Venice, Via Torino 155, 30172 Venice, Italy. E-mail: vincenzo.amendola@unipd.it
First published on 11th January 2024
Abstract
Alloying is a key step towards the fabrication of advanced and unique nanomaterials demanded by the next generation of nanotechnology solutions. In particular, the alloys of Au with the sp-metals are expected to have several appealing plasmonic and electronic properties for a wide range of applications in optics, catalysis, nanomedicine, sensing and quantum devices. However, little is known about the thermodynamic and synthetic factors leading to the successful alloying of Au and sp-metals at the nanoscale. In this work, Au–M nanoalloys, with M = Al, Ga, In, or Pb, have been synthesized by a green and single step laser ablation in liquid (LAL) approach in two environments (pure ethanol and anhydrous acetone). To delve deeper into the key parameters leading to successful alloying under the typical operating conditions of LAL, a multiparametric analysis was performed considering the mixing enthalpy from DFT calculations and other alloying descriptors such as the Hume-Rothery parameters. The results showed that the dominant factors for alloying change dramatically with the oxidative ability of the synthesis environment. In this way, the tendency of the four sp metals to alloy with gold was accurately predicted (R2 > 0.99) using only two and three parameters in anhydrous and non-anhydrous environments, respectively. These results are important to produce nanoalloys using LAL and other physical methods because they contribute to the understanding of factors leading to element mixing at the nanoscale under real synthetic conditions, which is crucial for guiding the realization of next-generation multifunctional metallic nanostructures.
Introduction
In the bulk and at the nanoscale, alloying is one of the most convenient and ancient strategies to combine the properties of different elements of the periodic table in a single multifunctional material.1,2 The research of new nanoalloys is in part motivated by the unique properties exhibited by nanoparticles (NPs), such as a high surface-to-volume ratio and the presence of physicochemical processes specific to nanostructures. In part, new nanoalloys are sought for the range of electronic, magnetic, optical, catalytic, structural, environmental and economic advantages brought about by the synergy of different elements alloyed at the nanoscale.2,3 Ideally, by looking at the periodic table, one can identify a proper combination of elements for any specific physical or chemical property. This means that the potential range of applications for nanoalloys is broad and multi-sectorial.1,2,4–6 Despite the remarkable progress in the synthesis of nanoalloys with complex structures, such as a mesoporous surface,7 or with unconventional compositions, such as multinary high entropy alloys,8 the number of unexplored compositions remains extremely high.2,3,9–11 Besides, obtaining multimetallic nanomaterials with a well-defined composition, size and shape is in most cases difficult.2,3,9–11 For instance, there are significant issues related to the structural stability over time and in the operating environments, and in many cases it is necessary to overcome the thermodynamic miscibility limits to achieve the desired composition.3,12,13 Furthermore, obtaining homogeneous structures, such as solid solution (SS) or intermetallic nanoalloys, may be hampered by segregation due to immiscibility and/or by passivation due to different chemical reactivities of one of the elements with the surrounding environment, leading to heterostructures (i.e. core–shell, Janus) or even amorphous NPs.9,14–18The prediction of alloying versus dealloying or passivation is still under debate, for instance concerning the preferential tendency of one specific element to create a shell or to segregate, and important results were obtained in describing the behaviors of various nanoalloys.19–22 Guisbiers et al. proposed two general rules to identify the element that segregates in a bimetallic alloy based on the melting temperature and surface energy in the pure elemental state.21 The first rule states that the element with the highest bulk melting point will segregate to the surface if the difference between the melting temperatures of the two bulk elements is larger than 10% of the highest melting point. If the difference is <10%, the surface segregation depends on the surface energy of the massive material, leading to surface segregation of the element with the lowest surface energy.21,23 Despite multiple pieces of evidence about their applicability, these rules are not valid for all possible nanoalloys, and some exceptions have also been demonstrated,23,24 as expected, considering the complexity of the problem. Regarding the morphology and topology of bimetallic NPs, intense computational efforts have been devoted to understanding the chemical ordering and the structural evolution by using DFT calculations and Monte Carlo simulations.19,20,22,25–27 These efforts received several experimental confirmations, indicating the good accuracy of the theoretical results.19,20,22,25–27 Clearly, not all real-world features can be considered, such as the presence and types of solvents in colloidal synthesis or the oxidation path promoted by the environment. Accounting for these aspects is challenging or impossible in terms of computational capabilities and identification of an accurate multiscale modelling framework for the complex synthetic methods.2,3,19,20,22,25–28 Consequently, much uncertainty remains about the predictability of nanoalloy formation under real synthetic conditions, and it is still not well understood how the latter introduce additional variables and other competitive processes against alloying.
Contributing to the predictability of nanoalloy formation under real synthetic conditions is especially important for the alloys of noble metals like Au with other non-noble elements. The alloys of Au with other coinage or noble metals have found a wide range of applications in optics, catalysis, nanomedicine, sensing and quantum devices.3,6,29,30 To date, gold NPs have been a hotspot of research endeavors due to their properties and applications, but Au is also listed among the rare metals due to its limited Earth abundance, and limiting its use by partial replacement with Earth-abundant materials, as in a nanoalloy, is a necessity nowadays.31 Beyond the well-known bimetallic NPs with coinage metals such as Cu32,33 and Ag21,34–36 or noble metals such as Pt25,37 and Pd,25,38 many studies have also considered Au alloys with d-metals such as Fe,12,13 Co,16,39 and Ni.40,41 These nanoalloys are interesting for plasmon-enhanced photocatalysis,6 magneto-optics,42 or theranostics,13 but they suffer from the strong damping of the localized surface plasmon resonance (LSPR), which limits their optical properties with the exception of Au–Ag and Au-rich Cu NPs.3,43 Identifying new Au alloys that reduce the content of the precious metal in favor of Earth-abundant compounds, while retaining appreciable optical and plasmonic properties or introducing even new or improved features, is still challenging. To this end, the sp-metals are good candidates44,45 because aluminum,46,47 gallium,48–50 and indium48,51 are already well-known for their good plasmonic properties and quality factors.43,45 Recently, due to the low melting point of Ga and In, Clarysse et al. proposed an amalgamation-seeded growth to synthesize intermetallic nanocrystals of Au–Ga, Ag–Ga, Cu–Ga, Ni–Ga, Pd–Ga, Pd–In, and Pd–Zn with good size and compositional control.11 They display a particular control toward the production of Au–Ga intermetallics with a predetermined composition and a narrow size distribution. Fonseca Guzman et al. exploited, instead, the seed-mediated method to produce Au–Ga and Au–In NPs.10 They were able to obtain Au–In alloy NPs with ∼9% In and with detectable traces of Ga. Despite the low amount of these metals in the NPs, the shift of the LSPR position towards the UV region was observed, confirming the interest in these binary NPs for the study of optical properties.
In this work, the synthesis of four alloy nanosystems (Au–Al, Au–Ga, Au–In, and Au–Pb) using a single-step procedure based on laser ablation in liquid (LAL) is investigated. The purpose of employing this series of metals is to study their effect on the composition, structure and morphology of the products as we move along the 13th group. Lead is preferred over thallium to avoid the use of a highly toxic material with scarce interest for real applications,52 while maintaining the most similar size, weight, and electronic configuration. LAL is currently one of the reference techniques for the green and straightforward preparation of colloids of nanoalloys with conventional (e.g. Au–Ag53 and Au–Cu54) or unconventional (e.g., immiscible elements such as Au–Fe,12,13,55,56 Ag–Fe,57 Ag–Co,58 and Au–Co16,39) composition. In addition, LAL has other advantages such as being a green, low-cost and self-standing process.15,59,60 Regarding Al, Ga, In, and Pb, these elements form intermetallic phases or are miscible with Au,61 but also form stable oxides with a strongly negative standard formation enthalpy.62 Therefore, oxidation and passivation at the surface of NPs, as well as segregation due to the oxidation of the sp metal during the synthesis, may occur. This aspect is elucidated in our study by using anhydrous (acetone) and non-anhydrous (ethanol) liquid environments routinely exploited for the LAL of nanoalloys.12,16–18,55,58,63,64 The different results in the composition and size of the Au–M nanoalloys have been studied with a multiparametric analysis to identify the leading physical and chemical descriptors for the synthesis process. In this way, important indications emerged on the production of nanoalloys by LAL and other physical methods with similar conditions such as pulsed laser deposition or sputtering techniques in reactive gaseous environments. In addition, our study contributes to the understanding of factors leading to element mixing at the nanoscale under real synthetic conditions, which will be crucial for guiding the realization of next-generation multifunctional metallic nanostructures.
Experimental methods
Synthesis
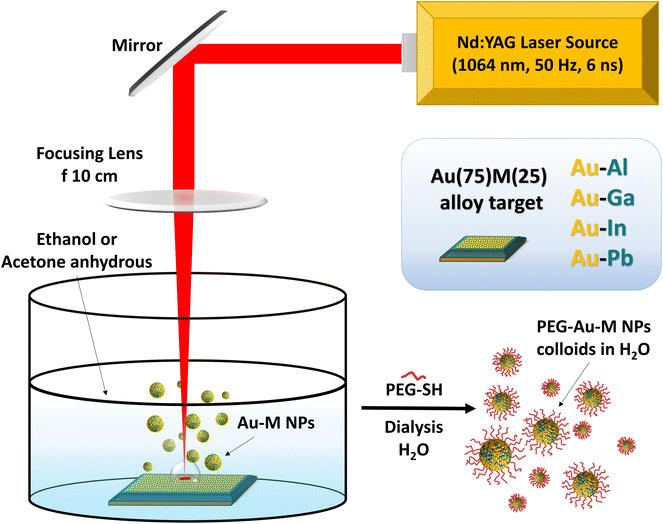
Au NPs and Au–M (M = Al, Ga, In, or Pb) alloy NPs have been obtained by LAL synthesis according to a previously established procedure.58 In brief, pulses generated from a 1064 nm Nd-YAG laser (50 Hz, 6 ns) have been focused with a lens (f 10 cm) at a fluence of 9.5 J cm−2 on the bimetallic Au–M 75–25 at% alloy targets (from Mateck GmbH, purity >99.9%). The target compositions were as follows: for Au–Al: AlAu4 40.2 ± 1.0 wt% and Al3Au8 59.8 ± 1.0 wt%; for Au–Ga: Au2Ga 9.3 ± 1.0 wt%, Au7Ga2 12.4 ± 1.0 wt%, and Au9Ga 78.3 ± 1.0 wt%; for Au–In: Au7In3 21.8 ± 1.0 wt%, Au3In 30.9 ± 1.0 wt%, Au10In3 27.6 ± 1.0 wt%; and Au9In 19.7 ± 1.0 wt%; and for Au–Pb: AuPb2 15.7 ± 1.0 wt%, Au2Pb 58.4 ± 1.0 wt%, and Au 25.9 ± 1.0 wt% (assessed by Rietveld refinement of the X-ray diffraction patterns; see below).All syntheses were conducted in either ethanol (HPLC grade, purity ≥99.8%, water ≤0.2%, from Sigma Aldrich) or anhydrous acetone (purity ≥99.8%, water ≤0.01%, from VWR) under a constant Ar atmosphere. The ablation cell was mounted on a motorized XY scanning stage (Standa) equipped with a 2-axis stepper and a DC motor controller, and the targets were moved in a spiral path with a 6 mm diameter during the synthesis, which lasted 90′ in all cases. Then, 7 mg of thiolated polyethylene glycol (PEG-SH, 2000 Da, Sigma-Aldrich) were added to the batch colloidal solution to improve the stability of NPs, and the mixture was placed in an ultrasonic bath for 30′ to ensure NPs coating with PEG-SH. Afterwards, the colloidal solution was concentrated at a volume of ∼5 mL using a rotavapor at 40 °C. The concentrated colloid was transferred into water and excess PEG was removed by dialysis with 10 kDa concentration membranes (Sartorius) at 750 rcf. The water environment is chosen to ensure optimal colloidal stability for the PEG-coated NPs. A schematic illustration of the synthetic procedure is provided in Fig. 1.
Characterization
Standard transmission electron microscopy (TEM) analysis was performed using an FEI Tecnai G2 12 transmission electron microscope operating at 100 kV and equipped with a TVIPS CCD camera.High-resolution TEM (HRTEM) and electron diffraction analyses were performed using a JEOL JEM-F200 TEM equipped with a cold FEG gun and operating at 200 kV in HREM and diffraction modes. Diffraction patterns were collected in both selected area electron diffraction mode (SAED), sampling a wide area in the specimen, and nano beam diffraction mode (NBD) when collecting diffraction data from a single particle or a group made of a few particles.
To prepare the sample, a drop of the colloidal solutions was deposited on a copper TEM grid coated with an amorphous carbon holey film. The size histograms of all samples were obtained by analyzing the TEM images with the automatic script particlesizer implemented in the Fiji software.65 A minimum of 500 NPs were counted from at least 10 different images per sample, with a convexity threshold value set at 0.99 and a size threshold value at 1.5 nm, i.e., just above the resolution of the TEM for standard imaging.
Additional morphological inspection and elemental analyses were performed with scanning electron microscopy (SEM) coupled with energy dispersive X-ray analysis (EDX) using a Zeiss HD microscope equipped with an FEG source operating at 5 keV (to avoid melting of the samples during the analysis), an Oxford Instrument EDX detector, and working in energy dispersive mode for X-ray microanalysis. The spectra were collected on the same samples deposited on the TEM grids.
UV-vis spectra were obtained using a Jasco V-770 spectrophotometer, employing a quartz cuvette with a 2 mm optical path. X-Ray powder diffraction (XRD) analyses were performed on the samples deposited on silicon substrates by drop-casting followed by drying at room temperature. The diffractograms were recorded using a Panalytical XPERT-3 diffractometer equipped with a Cu anode (40 kV, 40 mA). The crystalline phases were identified by the Rietveld refinement of the XRD diffractograms using the TOPAS V6 software and the COD database.
DFT calculations
Density functional theory (DFT) calculations were performed in order to compute the mixing enthalpy of the alloys. Calculations were performed with a plane-wave-pseudopotential approach using the Quantum ESPRESSO66 package. The PBE67 exchange–correlation functional was adopted and ultra-soft pseudopotentials from the GBRV library68 were used. Plane waves and electron density cut-offs were set to 35 and 300 Ry, respectively. All structures were relaxed until total energies were converged within 10−4 Ry, forces were lower than 10−3 Ry Bohr−1, and stress was lower than 0.5 kbar. Alloys were modelled using a 2 × 2 × 2 supercell containing 32 FCC sites, where sp atoms occupied sites with only Au atoms as nearest neighbors. A fixed composition of 12.5 at% of the sp element was chosen. The mixing enthalpy was calculated as follows| ΔHmix = EAunXm − nEAu − mEX |
Results
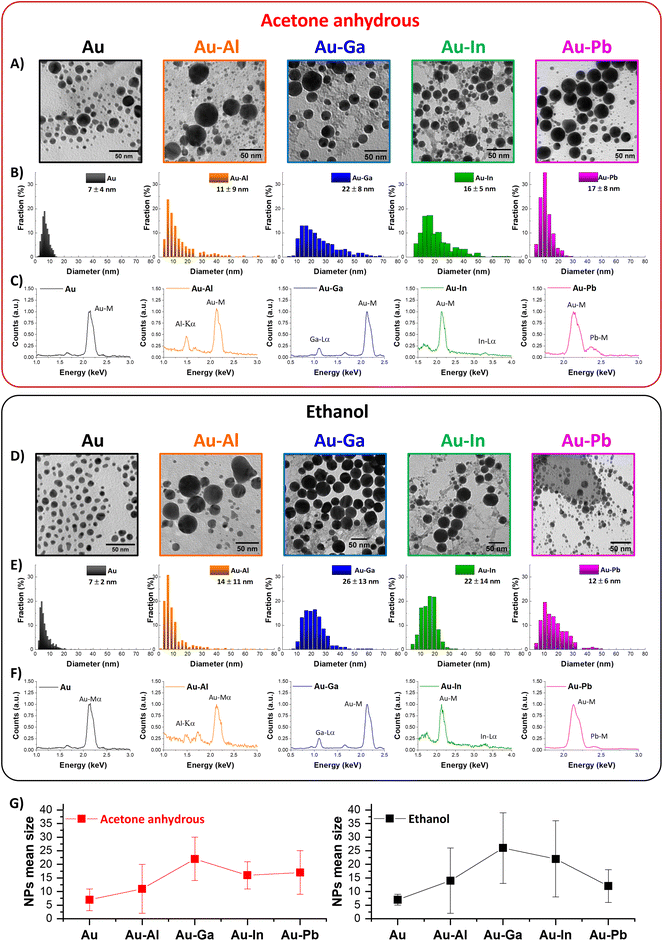
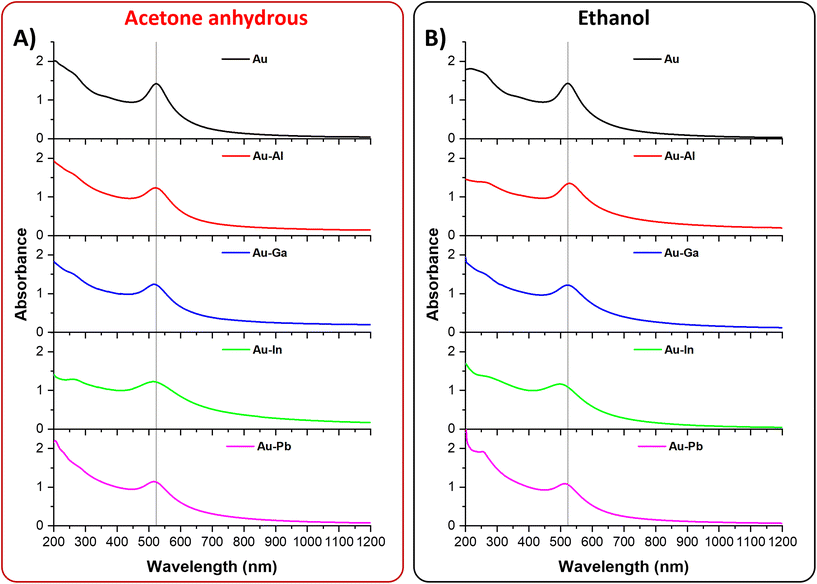
It is well known that the nanosecond LAL of alloy targets in liquid usually produces NPs with composition different from the ablated target.12,16–18,55,63,64,69 In the NPs obtained from gold alloy targets, this is associated with the depletion of the non-noble metal, as a result of its reactivity with oxidizing species, even at trace levels in the solution, and immiscibility with Au in the case of metastable alloys.39,55,56,58 In these cases, metal NPs are mixed with non-metallic compounds (less electron opaque),55 which are usually eliminated after the LAL with dedicated washing procedures.39,56,58 To this end, Au nanoalloys with Al, Ga, In or Pb have been synthesized in two standard solvents (ethanol and anhydrous acetone) for LAL of multimetallic NPs, with comparable physical and chemical properties70,71 but with a different content of water (≤0.2% for ethanol and ≤0.01% for anhydrous acetone). In this way, the role of sp metal oxidation can be better elucidated, because it is evident from the morphology of the nanostructures in the TEM images of the ten samples (Fig. 2). A majority of the NPs have a spherical shape (Fig. 2A and D), although some elongated particles are observed, with a higher frequency in the Au samples. Several submicrometric (∼500 nm) non-metallic particles are found in the sample of Au–Pb NPs obtained in ethanol, while these particles are less frequent in the Au–Pb sample obtained in acetone. Monomodal size distributions have been obtained for all samples (Fig. 2B and E) and these results are consistent with the use of nanosecond lasers, indicating that the ablation mechanism is the same for all alloys and in both solvents.15,17,55,59,60,64,72 The NPs are larger in ethanol for Au–Al, Au–Ga and Au–In but not for Au–Pb, while the size of Au NPs obtained in the two liquids is the same. The mean sizes obtained from the size histograms for the NPs synthesized in acetone are respectively 7 ± 4 nm (Au), 11 ± 9 nm (Au–Al), 22 ± 8 nm (Au–Ga), 16 ± 5 nm (Au–In), and 17 ± 8 nm (Au–Pb), and in ethanol, the sizes are respectively 7 ± 2 nm (Au), 14 ± 11 nm (Au–Al), 26 ± 13 nm (Au–Ga), 22 ± 14 nm (Au–In), and 12 ± 6 nm (Au–Pb). To better visualize these results, a comparison of the mean size with the standard deviation is shown in Fig. 2G, depicting that the size trend is increasing from Au to Au–Ga and decreasing from Au–Ga to Au–Pb in both anhydrous acetone and ethanol. According to this finding, the average size of the NPs generated by LAL seems primarily dependent on the sp metal mixed with Au. SEM-EDX spectra (Fig. 2C and F) of the same deposited NPs analyzed via TEM consistently show a clear Au M-line peak and the characteristic emission lines of the sp alloying metal (Al-Kα, Ga-Lα, In-Lα, Pb-M-line).It is well known that the composition of Au alloys affects the LSPR intensity and position compared to that of pure Au NPs, usually causing the damping of the plasmon band and its blue- or red-shift.3,12,39,43 Hence, taking advantage of the PEG coating and the stability in aqueous solution, the optical properties of the ten samples were measured and reported in the range of 200–1200 nm to obtain evidence of alloying (Fig. 3). It is worth noting that the absorption spectra of the nanoalloys extend also to the UV region without any overlap with the intense UV absorption bands of other organic compounds, such as acetone used for LAL or stabilizing agents and byproducts usually adopted in wet-chemistry approaches. In fact, the LAL synthetic procedure allowed the transfer of the NPs to water by dialysis just after coating with a non-absorbing polymer. On the other hand, the near-zero absorbance of all samples in the near infrared range (Fig. 3) demonstrates that LAL avoided irreversible NP agglomeration, which is a common drawback of physical synthesis methods.3 The LSPR of the bimetallic NPs is always less intense compared to those of the Au NPs. This is indicative of alloying because the Au NPs are small compared to the nanoalloys (Au ∼7 nm versus alloys ∼12–27 nm), and the LSPR intensity is known to increase with size in pure gold NPs.73 In addition, the LSPR position is often shifted in the bimetallic NPs obtained in acetone (Au: 523.5 nm; Au–Al: 521 nm; Au–Ga: 516 nm; Au–In: 512 nm; and Au–Pb: 516 nm) and in ethanol (Au: 522.5 nm; Au–Al: 528 nm; Au–Ga: 522 nm; Au–In: 497.5 nm; and Au–Pb: 513 nm), with a remarkable blue shift of 25 nm observed for the Au–In NPs in ethanol.
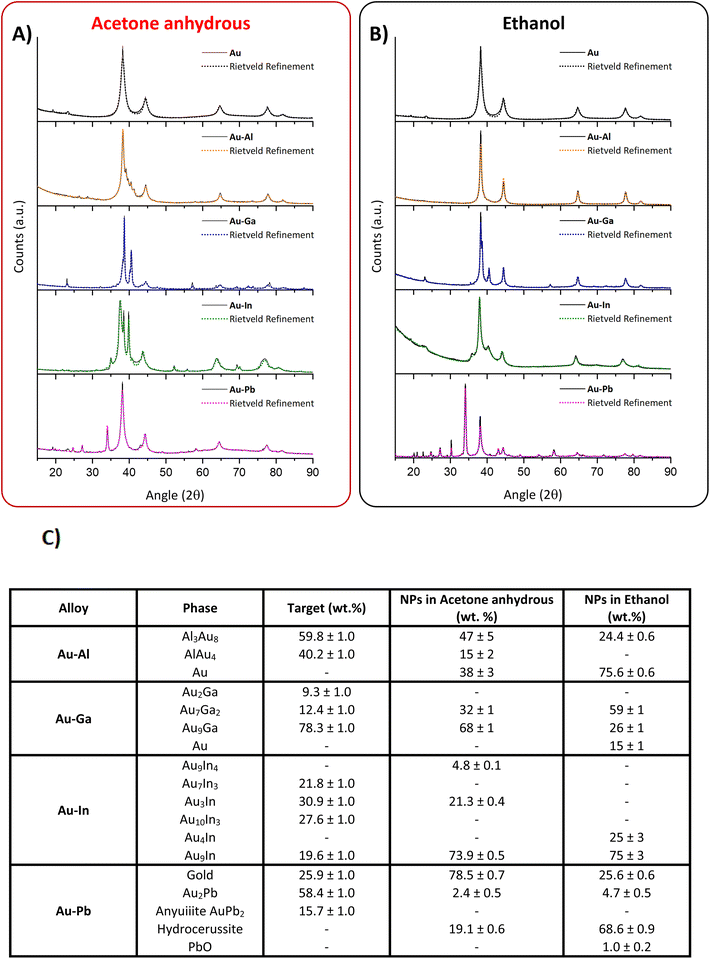
To further confirm that the sp metals are alloyed with gold and identify the alloy phase among the various possibilities (substitutional SS, intermetallic compound, or phase-segregated), the XRD patterns of the ten dried colloids were collected and the phases were identified through the Rietveld refinement (Fig. 4). In all samples, at least one substitutional alloy or intermetallic phase was detected, confirming the presence of the nanoalloys. However, the composition of each Au–sp metal alloy was different in anhydrous acetone and in ethanol. For the Au–Al NPs in acetone, the diffractogram shows a good fit with the FCC Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase of pure Au (38 ± 3%), the cubic P213 phase of AlAu4 (15 ± 2%), and the trigonal R
m phase of pure Au (38 ± 3%), the cubic P213 phase of AlAu4 (15 ± 2%), and the trigonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c phase of Al3Au8 (47 ± 5%); in ethanol, instead, only the pure Au FCC (75.6 ± 0.6%) and the trigonal R
c phase of Al3Au8 (47 ± 5%); in ethanol, instead, only the pure Au FCC (75.6 ± 0.6%) and the trigonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c phase of Al3Au8 (24.4 ± 0.6%) are found. The XRD pattern of Au–Ga NPs in acetone shows a good fit with the intermetallic hexagonal p62m phase Au7Ga2 (32 ± 1%) and the cubic substitutional Fm
c phase of Al3Au8 (24.4 ± 0.6%) are found. The XRD pattern of Au–Ga NPs in acetone shows a good fit with the intermetallic hexagonal p62m phase Au7Ga2 (32 ± 1%) and the cubic substitutional Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase Au9Ga (68 ± 1%); for ethanol, instead, the same two phases (Au7Ga2: 59 ± 1%; Au90Ga10: 26 ± 1%) are present together with pure gold (15 ± 1%). The samples of Au–In NPs are the only ones without pure gold phases in both solvents, since the XRD pattern for acetone was fitted with the FCC Fm
m phase Au9Ga (68 ± 1%); for ethanol, instead, the same two phases (Au7Ga2: 59 ± 1%; Au90Ga10: 26 ± 1%) are present together with pure gold (15 ± 1%). The samples of Au–In NPs are the only ones without pure gold phases in both solvents, since the XRD pattern for acetone was fitted with the FCC Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase Au9In (73.9 ± 0.5%), the orthorhombic Pmmn intermetallic phase Au3In (21.3 ± 0.4%), and the cubic P
m phase Au9In (73.9 ± 0.5%), the orthorhombic Pmmn intermetallic phase Au3In (21.3 ± 0.4%), and the cubic P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m phase Au9In4 (4.8 ± 0.1%), while the phases identified in the Au–In NPs synthesized in ethanol are the FCC Fm
3m phase Au9In4 (4.8 ± 0.1%), while the phases identified in the Au–In NPs synthesized in ethanol are the FCC Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase of Au9In (75 ± 3%) and the hexagonal P63/mmc phase of Au4In (25 ± 3%). Lastly, the XRD pattern of Au–Pb NPs in acetone is composed of pure Au (78.5 ± 0.7%), the trigonal R
m phase of Au9In (75 ± 3%) and the hexagonal P63/mmc phase of Au4In (25 ± 3%). Lastly, the XRD pattern of Au–Pb NPs in acetone is composed of pure Au (78.5 ± 0.7%), the trigonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase of hydrocerussite (19.1 ± 0.6%), and the cubic Fd
m phase of hydrocerussite (19.1 ± 0.6%), and the cubic Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase of Au2Pb (2.4 ± 0.5%), while in ethanol the refinement identified Au (25.6 ± 0.9%), hydrocerussite (68.6 ± 0.9%), Au2Pb (4.7 ± 0.5%), and also traces of the orthorhombic Pbcm phase of PbO (1.0 ± 0.2). It should be noted that the various SS and intermetallic phases are partly present also in the original targets used for LAL, as shown in Fig. 4C. The comparison between the target and the NP composition indicates a higher tendency toward oxidation and dealloying in the Au–Al and Au–Pb NPs in ethanol than in anhydrous acetone, while the Au–Ga and Au–In NPs appear less sensitive to the solvent type. In particular, the analysis of the XRD patterns confirmed the presence of submicron non-metallic particles observed from TEM images of Au–Pb samples, which can now be ascribed to hydrocerussite (Pb3(CO3)2(OH)2). During LAL, Pb(II) ions form lead carbonate (cerussite) with the CO2 dissolved in the solvents despite the Ar atmosphere, and the cerussite converts into hydrocerussite when the samples are transferred to water. The interaction of metal NPs with hydrocerussite and PbO can have an effect also on the optical properties, as shown in Fig. 3.
m phase of Au2Pb (2.4 ± 0.5%), while in ethanol the refinement identified Au (25.6 ± 0.9%), hydrocerussite (68.6 ± 0.9%), Au2Pb (4.7 ± 0.5%), and also traces of the orthorhombic Pbcm phase of PbO (1.0 ± 0.2). It should be noted that the various SS and intermetallic phases are partly present also in the original targets used for LAL, as shown in Fig. 4C. The comparison between the target and the NP composition indicates a higher tendency toward oxidation and dealloying in the Au–Al and Au–Pb NPs in ethanol than in anhydrous acetone, while the Au–Ga and Au–In NPs appear less sensitive to the solvent type. In particular, the analysis of the XRD patterns confirmed the presence of submicron non-metallic particles observed from TEM images of Au–Pb samples, which can now be ascribed to hydrocerussite (Pb3(CO3)2(OH)2). During LAL, Pb(II) ions form lead carbonate (cerussite) with the CO2 dissolved in the solvents despite the Ar atmosphere, and the cerussite converts into hydrocerussite when the samples are transferred to water. The interaction of metal NPs with hydrocerussite and PbO can have an effect also on the optical properties, as shown in Fig. 3.
It is worth noting that the NPs obtained by LAL have a relatively broad size distribution; hence, the composition obtained from the XRD analysis is the average composition of the sample, while it does not give information about the possibility that the chemical composition changes with the size of the NPs.
Therefore, alloying was also assessed at the nanoscale using SAED (Fig. 5A), NBD (Fig. 5B) and HRTEM (Fig. 5C) on the samples obtained in anhydrous acetone, which are those with the highest fraction of Au–sp metal phases. HRTEM analysis evidenced the polycrystalline structure of the NPs, which is also systematically observed in single-element metal particles obtained by LAL.15,59,60 Consequently, the SAED patterns on groups of NPs are rich in reflections coming from different crystalline domains, even inside the same particle. Nonetheless, it was possible to identify the reflections of the various Au–sp metal alloys previously identified using XRD analysis, where there is no ambiguity about the discrimination from the pure Au FCC reflections. This includes the AlAu4 phase with space group P213, the Au7Ga2 phase with space group P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) 2m, and reflections compatible with both the Au3In phase with space group Pmmn and the Au9In4 phase with space group P
2m, and reflections compatible with both the Au3In phase with space group Pmmn and the Au9In4 phase with space group P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m. In the case of the Au–Pb sample, the very low abundance of the alloy compared to that of pure Au and hydrocerussite does not allow for the unambiguous identification of the Au2Pb phase in the SAED and NBD patterns, but it was possible to find a match with HRTEM of a single Au–Pb NP, exhibiting the interplanar distance and the Hanning masked FFT pattern of the Au2Pb phase with space group Fd
3m. In the case of the Au–Pb sample, the very low abundance of the alloy compared to that of pure Au and hydrocerussite does not allow for the unambiguous identification of the Au2Pb phase in the SAED and NBD patterns, but it was possible to find a match with HRTEM of a single Au–Pb NP, exhibiting the interplanar distance and the Hanning masked FFT pattern of the Au2Pb phase with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. Overall, the NBD and HRTEM results, along with the Hanning masked FFT patterns on selected nanometric regions, further confirmed, at the single NP level (Fig. 5B and C), all results obtained by SAED on groups of NPs and by XRD on the powder samples.
m. Overall, the NBD and HRTEM results, along with the Hanning masked FFT patterns on selected nanometric regions, further confirmed, at the single NP level (Fig. 5B and C), all results obtained by SAED on groups of NPs and by XRD on the powder samples.
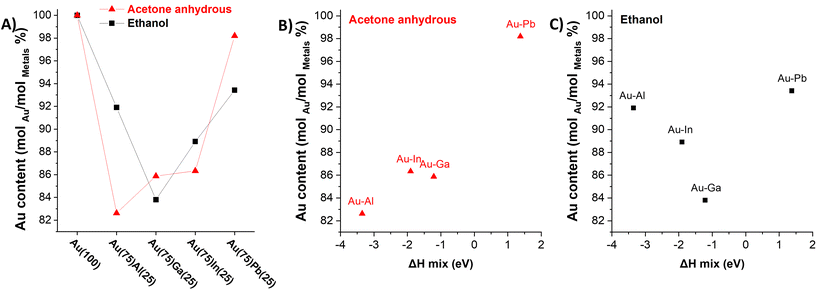
To better summarize the efficacy of alloying inferred from the quantitative analysis of the XRD results, the molar ratio between Au and the other sp metal in the metallic state is presented in Fig. 6A. The molar fraction of Au has been calculated by summing the mols derived from the pure gold phase and from the intermetallic and the SS phases. The calculated average elemental compositions of the bimetallic NP samples are Au(83)Al(17), Au(86)Ga(14), Au(86)In(13), and Au(98)Pb(2) in anhydrous acetone and Au(91)Al(9), Au(84)Ga(16), Au(89)In(11), and Au(93)Pb(7) in ethanol. The results show a trend in the gold content versus the sp metal. In acetone, the composition becomes more gold-rich going from Au–Al to Au–Pb NPs. A different trend appears in ethanol, where the gold content increases from Au–Ga to Au–Pb NPs, with the exception of Au–Al NPs where the gold content is higher than in Au–Ga and Au–In NPs. As summarized in Fig. 6A, in all cases starting from a target with 75 at% of gold and 25 at% of the sp metal, nanoalloys with a higher content of gold are obtained.
Discussion
Au–sp metal alloy NPs with different sizes, compositions and yields have been obtained by LAL of Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M 75
M 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 at% (M = Al, Ga, In, Pb) bulk metal targets. The deviation of the NP composition with respect to that of the target is indicative of the different tendency of the sp metals to alloy with Au. As a first attempt, the tendency to alloying can be interpreted on the basis of the Hume-Rothery and other alloying rules, which are valid in the ideal case where no other chemical reactions occur with the surrounding environment, such as in inert gases.21,74 The first rule states that, to obtain a substitutional SS in a bimetallic alloy, the atomic radius of one element should not differ by more than 15% from the other. If the atomic radius of one element is smaller than the 60% of the other, an interstitial alloy can form. Looking at the four sp metals, one can observe that the atomic sizes of Au and Pb differ by almost 20%, while the difference is lower for Al (8%), Ga (4%) and In (12%).75,76 Therefore, despite sharing the same Bravais lattice (FCC), important distortions are expected when alloying Au with Pb. According to the second rule, a larger solubility is reached in both SS and interstitial alloys when the two elements have similar crystalline structures in their pure form. The third rule states that the tendency to form intermetallic compounds instead of solid solutions increases with the difference in electronegativity of the two elements. The formation of intermetallics between Au and the sp metals is, in fact, favored by the large difference in electronegativity (2.54 for Au and, respectively, 1.61, 1.81, and 1.78 for Al, Ga, and In).74,75 The importance of the difference in electronegativity in the formation of alloys was already discussed by Miedema.77 The heat of formation of a series of binary alloys was plotted as a function of the difference in electronegativity and the difference in electronic density, revealing a good correlation with the experimental results. In the majority of the cases, if the difference in electronegativity was higher than the difference in the electron density at the boundary of the Wigner–Seitz cell multiplied by 0.48, the two metals formed alloys by either producing new compounds in the phase diagrams or by mixing for at least 10%.77
25 at% (M = Al, Ga, In, Pb) bulk metal targets. The deviation of the NP composition with respect to that of the target is indicative of the different tendency of the sp metals to alloy with Au. As a first attempt, the tendency to alloying can be interpreted on the basis of the Hume-Rothery and other alloying rules, which are valid in the ideal case where no other chemical reactions occur with the surrounding environment, such as in inert gases.21,74 The first rule states that, to obtain a substitutional SS in a bimetallic alloy, the atomic radius of one element should not differ by more than 15% from the other. If the atomic radius of one element is smaller than the 60% of the other, an interstitial alloy can form. Looking at the four sp metals, one can observe that the atomic sizes of Au and Pb differ by almost 20%, while the difference is lower for Al (8%), Ga (4%) and In (12%).75,76 Therefore, despite sharing the same Bravais lattice (FCC), important distortions are expected when alloying Au with Pb. According to the second rule, a larger solubility is reached in both SS and interstitial alloys when the two elements have similar crystalline structures in their pure form. The third rule states that the tendency to form intermetallic compounds instead of solid solutions increases with the difference in electronegativity of the two elements. The formation of intermetallics between Au and the sp metals is, in fact, favored by the large difference in electronegativity (2.54 for Au and, respectively, 1.61, 1.81, and 1.78 for Al, Ga, and In).74,75 The importance of the difference in electronegativity in the formation of alloys was already discussed by Miedema.77 The heat of formation of a series of binary alloys was plotted as a function of the difference in electronegativity and the difference in electronic density, revealing a good correlation with the experimental results. In the majority of the cases, if the difference in electronegativity was higher than the difference in the electron density at the boundary of the Wigner–Seitz cell multiplied by 0.48, the two metals formed alloys by either producing new compounds in the phase diagrams or by mixing for at least 10%.77
The fourth rule of Hume-Rothery identifies the valence, or more precisely, the number of itinerant electrons per atom (e/a) in the alloy,78 as a relevant parameter for a metal to be able to dissolve in another. At parity of other parameters, two elements have the maximum capability to alloy as a SS when they have the same number of itinerant electrons per atom. If e/a differs, it is the element with the higher value that has the larger solubility in the lattice of the other metal.79
The four Hume-Rothery rules are intrinsically accounted for in the DFT calculations of the mixing enthalpy (ΔHmix) for the four Au–sp metal alloys, which have been applied to the representative cases of 87.5 at% of gold with its FCC cell. The ΔHmix is plotted in Fig. 5B–Cversus the molar fraction of Au in the NPs obtained by LAL. The mixing enthalpy is negative for all nanoalloys except for Au–Pb, which is not thermodynamically stable. Overall, the trend is well described for the samples in acetone, although the prediction is not accurate enough for the Ga and In nanoalloys. Conversely, the correlation between ΔHmix and the Au content is not satisfactory for the samples obtained in ethanol. Although it is well known that the entropy of the alloy has a non-negligible role in the stabilization of solid solutions and can become dominant in high-entropy alloys,78 in this study it was not considered. In fact, the mixing entropy of an ideal solid solution can be expressed as 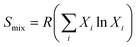 , with Xi the molar fractions of the alloy components. Thus, the entropic term −TS will depend only on the composition and will be the same for all sp metals at parity of Au fraction in the alloy.
, with Xi the molar fractions of the alloy components. Thus, the entropic term −TS will depend only on the composition and will be the same for all sp metals at parity of Au fraction in the alloy.
Instead, the compositional variations between the NPs and the original target, as well as the differences between anhydrous acetone and ethanol, are compatible with nanosecond LAL when the chemical interaction with the liquid solution is also considered.15,55,56,60,80 During LAL, the extreme synthetic conditions lead to the generation of redox species due to solvent decomposition. Reactive gaseous compounds such as reactive oxygen species (ROS), O2, solvent pyrolysis products, or H2 can form, depending on the experimental conditions.81,82 Likewise, it has been recently demonstrated how different gas concentrations are obtained by ablating different metallic targets in water.82 Hence, various redox reactions can occur at different rates depending on the redox potential of the elements in the ablated target.81 By translating these findings to the relative composition of the bimetallic NPs, it becomes evident that the liquid environment plays a role in either promoting or limiting the oxidation of one of the elements in the alloy. This feature, combined with the rules for alloying valid in the absence of specific chemical interactions with the environment, will determine the final NP composition. To account for these aspects and delve deeper into the factors leading to the successful or unsuccessful synthesis of nanoalloys, a list of physical and chemical parameters that describe the sp metal was correlated with the average gold atomic fraction in the NPs.
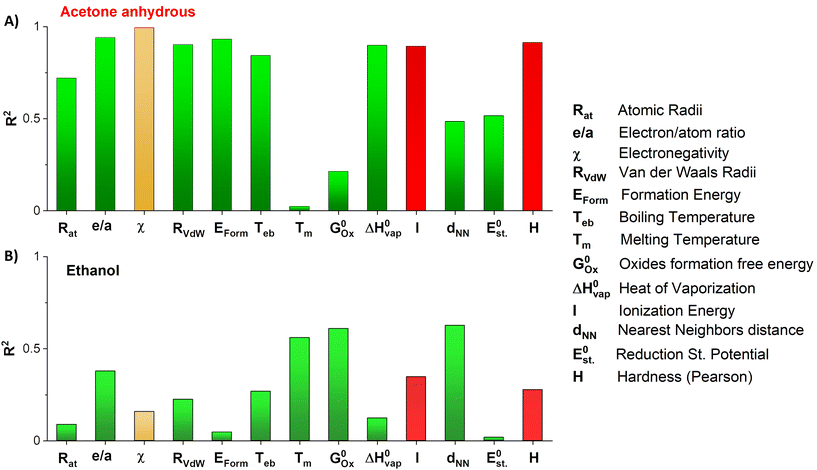
First, each single parameter was related to the gold atomic fraction in the synthesized metal NPs. The coefficient of determination (R2) was chosen as the indicator of how well each parameter correlates linearly with the gold atomic fraction, as shown in Fig. 7. Besides the abovementioned parameters of the Hume-Rothery rules (atomic radius, Rat; number of itinerant electrons per atom, e/a; and electronegativity, c), the melting (Tm) and boiling (Teb) temperature, the heat of vaporization 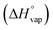 , the mixing enthalpy (ΔHmix), the standard Gibbs free energy of formation of the oxide
, the mixing enthalpy (ΔHmix), the standard Gibbs free energy of formation of the oxide 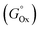 , the ionization energy (I), the van der Waals radius (RvdW), the distance between nearest neighbors (dNN), and the standard reduction potential
, the ionization energy (I), the van der Waals radius (RvdW), the distance between nearest neighbors (dNN), and the standard reduction potential 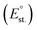 were also considered. Moreover, the Pearson hardness (H) was added to the set of parameters. H describes the behavior of Lewis acids and bases and is defined as the half of the second derivative of the total energy curve of an atom versus the number of its electrons. In the finite domain, it can be calculated as the semi-difference between the ionization energy and the electron affinity.83 The rule states that hard acids prefer to associate with hard bases and vice versa or, in other words, the closer the hardness of two elements, the larger is their affinity.83 Although the value of R2 shown in Fig. 7 for each parameter is not always close to 1, in the majority of cases it confirms that the parameters have a role in alloying. In Fig. 7, green columns are used when the efficacy of alloying is as expected from the literature, i.e. the slope has the expected sign, which is the case in the majority of instances. However, the values for I and H are depicted as red columns, since the alloying efficacy decreased for sp metals having I and H similar to those of Au, while the rule states the opposite. For this reason, they can be considered as scarcely important parameters. The column associated with electronegativity is depicted in yellow because there is not a specific slope expected from the rule, which states that SS or intermetallic alloys may form in the case of similarities or differences in electronegativity between the sp metals and gold.
were also considered. Moreover, the Pearson hardness (H) was added to the set of parameters. H describes the behavior of Lewis acids and bases and is defined as the half of the second derivative of the total energy curve of an atom versus the number of its electrons. In the finite domain, it can be calculated as the semi-difference between the ionization energy and the electron affinity.83 The rule states that hard acids prefer to associate with hard bases and vice versa or, in other words, the closer the hardness of two elements, the larger is their affinity.83 Although the value of R2 shown in Fig. 7 for each parameter is not always close to 1, in the majority of cases it confirms that the parameters have a role in alloying. In Fig. 7, green columns are used when the efficacy of alloying is as expected from the literature, i.e. the slope has the expected sign, which is the case in the majority of instances. However, the values for I and H are depicted as red columns, since the alloying efficacy decreased for sp metals having I and H similar to those of Au, while the rule states the opposite. For this reason, they can be considered as scarcely important parameters. The column associated with electronegativity is depicted in yellow because there is not a specific slope expected from the rule, which states that SS or intermetallic alloys may form in the case of similarities or differences in electronegativity between the sp metals and gold.
The R2 values are generally larger in the case of anhydrous acetone than in ethanol. In particular, the Hume-Rothery parameters (atomic size, electronegativity, number of itinerant electrons per atom, van der Waals radii) are linearly correlated with the atomic gold fraction with R2 between 0.72008 and 0.99384. This reflects the trend of these parameters in the periodic table when going from Al to Pb. The alloy mixing enthalpy (R2: 0.93118), the boiling temperature (R2: 0.84253), and the heat of vaporization (R2: 0.89847) are also highly correlated with the gold fraction in acetone. The mixing enthalpy has been discussed above, while the heat of vaporization and the boiling temperature are thought to be involved in the laser ablation process.59,60,84 The heat of vaporization of Au (334.4 kJ mol−1) is closer to that of Al (293.4 kJ mol−1) than to those of Ga, In, and Pb.85–88 A similar trend is found for the boiling points, with the Teb of Au of 2780 °C being closer to those of Al of 2470 °C and Ga of 2400 °C, followed by In with 2072 °C and Pb with 1749 °C.62 These trends may indicate that the ablation of Au and Al has similar thresholds and, in fact, the NPs obtained in acetone have a higher content of Al than of Ga, In, and Pb.
Notably, the plot in Fig. 7 shows that some of the parameters with the largest R2 in acetone have the lowest R2 in ethanol. In particular, the melting temperature, Tm (R2: 0.02242), and the Gibbs free energy related to the formation of the corresponding sp metal oxides, 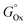 (R2: 0.21241), have the lowest correlation in acetone but the 2nd and 3rd best correlation with the gold fraction of the NPs obtained in ethanol (respectively,
(R2: 0.21241), have the lowest correlation in acetone but the 2nd and 3rd best correlation with the gold fraction of the NPs obtained in ethanol (respectively, 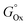 , R2: 0.60855 and Tm, R2: 0.55903). This suggests that the formation of the nanoalloys in anhydrous acetone and ethanol involves different processes, thus leading to a different content of gold in the synthesized NPs. This difference is well described by the Gibbs free energy of the most common oxides formed by the sp metals, which are Al2O3, Ga2O3, ln2O3, and PbO. Al2O3 (−1582.3 kJ mol−1) and PbO (−1705 kJ mol−1) have lower Gibbs free energy of formation than Ga2O3 (−998.3 kJ mol−1) and ln2O3I (−830.7 kJ mol−1).62 Accordingly, the gold atomic fraction for the NPs obtained in ethanol is larger in the Al and Pb cases and smaller in the Ga and In cases. This suggests that Al preferentially forms amorphous alumina in ethanol, and Pb may form oxidized species that subsequently evolves into cerussite by interaction with atmospheric CO2. Hence, the fraction of water contained in ethanol (≤0.2%) is enough to affect the efficiency of alloy formation during LAL, due to the strong tendency of Al and Pb to undergo oxidation. It has also been reported that the presence of 0.2% of water in ethanol drastically affects the composition and structure of Au–Fe NPs produced with nanosecond LAL.56
, R2: 0.60855 and Tm, R2: 0.55903). This suggests that the formation of the nanoalloys in anhydrous acetone and ethanol involves different processes, thus leading to a different content of gold in the synthesized NPs. This difference is well described by the Gibbs free energy of the most common oxides formed by the sp metals, which are Al2O3, Ga2O3, ln2O3, and PbO. Al2O3 (−1582.3 kJ mol−1) and PbO (−1705 kJ mol−1) have lower Gibbs free energy of formation than Ga2O3 (−998.3 kJ mol−1) and ln2O3I (−830.7 kJ mol−1).62 Accordingly, the gold atomic fraction for the NPs obtained in ethanol is larger in the Al and Pb cases and smaller in the Ga and In cases. This suggests that Al preferentially forms amorphous alumina in ethanol, and Pb may form oxidized species that subsequently evolves into cerussite by interaction with atmospheric CO2. Hence, the fraction of water contained in ethanol (≤0.2%) is enough to affect the efficiency of alloy formation during LAL, due to the strong tendency of Al and Pb to undergo oxidation. It has also been reported that the presence of 0.2% of water in ethanol drastically affects the composition and structure of Au–Fe NPs produced with nanosecond LAL.56
Yet, the LAL of Au–Pb nanoalloys was not efficient even in acetone, and it is unclear from this analysis if a specific set of parameters can predict the efficacy of nanoalloy formation during LAL in the two liquid environments. Hence, a multiparametric analysis was performed to identify the best subset of parameters that correlates with the gold fraction.
A collective parameter YM was defined:
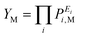 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 594
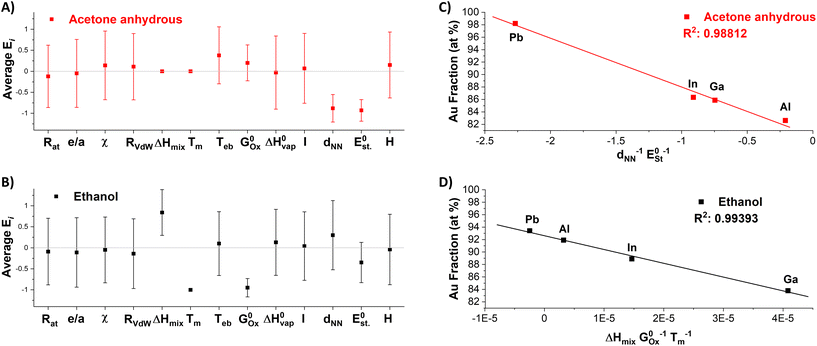
594![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 323 permutations. The correlation of each YM with the Au content in the NPs obtained in either anhydrous acetone or ethanol was evaluated through the calculation of R2, as done above for the single parameters. Subsequently, for each solvent, the 100 combinations with the highest R2 were selected, and the average exponent Ei was calculated for each of the 13 Pi,M parameters (Fig. 8A and B). It is remarkable that the average Ei significantly deviates from zero only for a few parameters in both solvents, which are considered those with the highest significance for predicting the formation of nanoalloys of Au and sp metals by LAL. As a further check, the top 50 and 25 combinations were also considered, and the average Ei was found to be very similar to that of the top 100 combinations. The significant parameters in acetone are the distance between nearest neighbors (dNN) and the standard reduction potential
323 permutations. The correlation of each YM with the Au content in the NPs obtained in either anhydrous acetone or ethanol was evaluated through the calculation of R2, as done above for the single parameters. Subsequently, for each solvent, the 100 combinations with the highest R2 were selected, and the average exponent Ei was calculated for each of the 13 Pi,M parameters (Fig. 8A and B). It is remarkable that the average Ei significantly deviates from zero only for a few parameters in both solvents, which are considered those with the highest significance for predicting the formation of nanoalloys of Au and sp metals by LAL. As a further check, the top 50 and 25 combinations were also considered, and the average Ei was found to be very similar to that of the top 100 combinations. The significant parameters in acetone are the distance between nearest neighbors (dNN) and the standard reduction potential 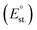 , while in ethanol they are the mixing enthalpy (ΔHmix), the melting temperature (Tm), and the free energy of formation of oxides
, while in ethanol they are the mixing enthalpy (ΔHmix), the melting temperature (Tm), and the free energy of formation of oxides 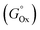 . Hence, the relative Au content in the NPs was plotted versus the product YM of these parameters, each elevated to the resulting average exponent (approximated to the closest integer), resulting in an R2 of 0.98812 in anhydrous acetone (Fig. 8C) and of 0.99393 in ethanol (Fig. 8D). This excellent agreement in ethanol confirms that the melting temperature, which is directly related to the cohesive energy of the metals,89 and the free energy of formation of oxides are the relevant parameters for the nanoalloy formation processes that happen during LAL in this liquid. The rationale behind this model can be discussed in terms of general chemistry reasoning. Concerning the dependence on
. Hence, the relative Au content in the NPs was plotted versus the product YM of these parameters, each elevated to the resulting average exponent (approximated to the closest integer), resulting in an R2 of 0.98812 in anhydrous acetone (Fig. 8C) and of 0.99393 in ethanol (Fig. 8D). This excellent agreement in ethanol confirms that the melting temperature, which is directly related to the cohesive energy of the metals,89 and the free energy of formation of oxides are the relevant parameters for the nanoalloy formation processes that happen during LAL in this liquid. The rationale behind this model can be discussed in terms of general chemistry reasoning. Concerning the dependence on 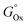 , the more exergonic is the formation of the oxide, the more likely the sp metal is oxidized during synthesis, thus depleting the resulting NP of the sp element. Accordingly,
, the more exergonic is the formation of the oxide, the more likely the sp metal is oxidized during synthesis, thus depleting the resulting NP of the sp element. Accordingly, 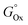 becomes more negative in the order In–Ga–Al–Pb. The ratio ΔHmix/Tm combines information on the heteroatomic Au–X (X = Ga, In, Al, Pb) bond in alloys and the homoatomic bond in pure elements. A strong Au–X bond (a more negative ΔHmix) will favor the alloy formation, while a strong X–X bond (larger Tm) will favor segregation. Interestingly enough, Al possesses a much higher Tm than the other metals in the series, which is however balanced by the most negative ΔHmix. In acetone, the presence of dNN, which is related to the similarity in the crystalline structure and the atomic size of the elements, indicates that the standard alloying rules apply to the LAL under anhydrous and non-oxidizing conditions. Concerning the standard reduction potential, this refers to the reduction from the most stable cation to the metallic form (Al3+ → Al, Ga3+ → Ga, In3+ → In, and Pb2+ → Pb), indicating a correlation between the propensity of the sp element to remain in the metallic state during LAL and the ability of forming the nanoalloy. Overall, the formation of alloy NPs in acetone is guided by dynamical effects, whereas in ethanol thermodynamics seems more relevant.
becomes more negative in the order In–Ga–Al–Pb. The ratio ΔHmix/Tm combines information on the heteroatomic Au–X (X = Ga, In, Al, Pb) bond in alloys and the homoatomic bond in pure elements. A strong Au–X bond (a more negative ΔHmix) will favor the alloy formation, while a strong X–X bond (larger Tm) will favor segregation. Interestingly enough, Al possesses a much higher Tm than the other metals in the series, which is however balanced by the most negative ΔHmix. In acetone, the presence of dNN, which is related to the similarity in the crystalline structure and the atomic size of the elements, indicates that the standard alloying rules apply to the LAL under anhydrous and non-oxidizing conditions. Concerning the standard reduction potential, this refers to the reduction from the most stable cation to the metallic form (Al3+ → Al, Ga3+ → Ga, In3+ → In, and Pb2+ → Pb), indicating a correlation between the propensity of the sp element to remain in the metallic state during LAL and the ability of forming the nanoalloy. Overall, the formation of alloy NPs in acetone is guided by dynamical effects, whereas in ethanol thermodynamics seems more relevant.
Conclusions
The physical and chemical parameters determining the formation of gold–sp metal nanoalloys were studied as a function of the sp metal period, moving from Al to Ga, In and Pb, and under real synthetic conditions involved in the nanosecond laser ablation of bimetallic targets in two different liquid environments (anhydrous acetone and ethanol). The successful formation of Au nanoalloys with sp metals has been demonstrated in most cases and the LAL is confirmed to be a versatile approach for the production of innovative nanoalloys, provided that appropriate synthesis parameters are adopted. Especially relevant is the oxidizing capability of the solvent which must be balanced with the tendency of the metals to undergo oxidation, to avoid phase segregation and byproduct formation. To clarify these aspects, the physical and chemical parameters leading to the formation of alloyed versus phase segregated NPs were analyzed systematically. Good agreement with the typical rules for alloying is found only in the absence of remarkable chemical interactions with the metals; otherwise, the tendency to undergo oxidation prevails. Through a multiparametric analysis, the efficacy of alloying Au with the sp metals was described with only two parameters (the distance between nearest neighbors and the standard reduction potential) with an R2 of 0.98812 in anhydrous acetone and only three parameters (mixing enthalpy, melting temperature, and the free energy of formation of oxides) with an R2 0.99393 in ethanol. The nanoscale structural analysis did not reveal a clear variation of the composition of the nanoalloys with their size, although a more systematic investigation would be required to investigate this aspect in the future, through the analysis of size fractionated samples. These findings lead to an immediate and deeper understanding of the phenomena that affect the composition of nanoalloys under real physical synthetic conditions. This will provide a crucial support for guiding the realization of next-generation multifunctional metallic nanostructures with remarkable applicative potential in optics, catalysis, nanomedicine, sensing and quantum devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by the University of Padova P-DiSC project “DYNAMO”. We acknowledge the C3P computer facility at the University of Padova.References
- R. Ferrando, J. Jellinek and R. L. Johnston, Chem. Rev., 2008, 108, 845–910 CrossRef CAS PubMed.
- K. Loza, M. Heggen and M. Epple, Adv. Funct. Mater., 2020, 30, 1909260 CrossRef CAS.
- V. Coviello, D. Forrer and V. Amendola, ChemPhysChem, 2022, 23, e202200136 CrossRef CAS PubMed.
- M. Jahn, S. Patze, I. J. Hidi, R. Knipper, A. I. Radu, A. Mühlig, S. Yüksel, V. Peksa, K. Weber and T. Mayerhöfer, Analyst, 2016, 141, 756–793 RSC.
- K. H. Huynh, X. H. Pham, J. Kim, S. H. Lee, H. Chang, W. Y. Rho and B. H. Jun, Int. J. Mol. Sci., 2020, 21, 1–29 Search PubMed.
- K. Sytwu, M. Vadai and J. A. Dionne, Adv. Phys.: X, 2019, 4, 1619480 CAS.
- A. S. Nugraha, M. Han, A. Ashok, Y. Kang, J. Kim, S. M. Alshehri, T. Ahamad, Y. Bando and Y. Yamauchi, Nano Energy, 2023, 116, 108770 CrossRef CAS.
- S. L. A. Bueno, A. Leonardi, N. Kar, K. Chatterjee, X. Zhan, C. Chen, Z. Wang, M. Engel, V. Fung and S. E. Skrabalak, ACS Nano, 2022, 16, 18873–18885 CrossRef CAS PubMed.
- C. B. Wahl, M. Aykol, J. H. Swisher, J. H. Montoya, S. K. Suram and C. A. Mirkin, Sci. Adv., 2021, 7, eabj5505 CrossRef CAS PubMed.
- M. V. Fonseca Guzman, M. E. King, N. L. Mason, C. S. Sullivan, S. Jeong and M. B. Ross, Matter, 2023, 6, 838–854 CrossRef CAS.
- J. Clarysse, A. Moser, O. Yarema, V. Wood and M. Yarema, Sci. Adv., 2021, 7, eabg1934 CrossRef CAS PubMed.
- D. T. L. Alexander, D. Forrer, E. Rossi, E. Lidorikis, S. Agnoli, G. D. Bernasconi, J. Butet, O. J. F. Martin and V. Amendola, Nano Lett., 2019, 19, 5754–5761 CrossRef CAS PubMed.
- V. Torresan, D. Forrer, A. Guadagnini, D. Badocco, P. Pastore, M. Casarin, A. Selloni, D. Coral, M. Ceolin, M. B. Fernández van Raap, A. Busato, P. Marzola, A. E. Spinelli and V. Amendola, ACS Nano, 2020, 14, 12840–12853 CrossRef CAS PubMed.
- É. Camus, M. Pellarin, N. Blanchard, O. Boisron, M. Hillenkamp, L. Roiban, P. Andreazza and E. Cottancin, Faraday Discuss., 2023, 242, 478–498 RSC.
- V. Amendola, D. Amans, Y. Ishikawa, N. Koshizaki, S. Scirè, G. Compagnini, S. Reichenberger and S. Barcikowski, Chem. – Eur. J., 2020, 26, 9206–9242 CrossRef CAS PubMed.
- J. Johny, M. Kamp, O. Prymak, A. Tymoczko, U. Wiedwald, C. Rehbock, U. Schürmann, R. Popescu, D. Gerthsen, L. Kienle, S. Shaji and S. Barcikowski, J. Phys. Chem. C, 2021, 125, 9534–9549 CrossRef CAS.
- A. Tymoczko, M. Kamp, C. Rehbock, L. Kienle, E. Cattaruzza, S. Barcikowski and V. Amendola, Nanoscale Horiz., 2019, 4, 1326–1332 RSC.
- S. X. Liang, L. C. Zhang, S. Reichenberger and S. Barcikowski, Phys. Chem. Chem. Phys., 2021, 23, 11121–11154 RSC.
- D. Nelli and R. Ferrando, Nanoscale, 2019, 11, 13040–13050 RSC.
- P. Andreazza, A. Lemoine, A. Coati, D. Nelli, R. Ferrando, Y. Garreau, J. Creuze and C. Andreazza-Vignolle, Nanoscale, 2021, 13, 6096–6104 RSC.
- G. Guisbiers, R. Mendoza-Cruz, L. Bazán-Díaz, J. J. Velázquez-Salazar, R. Mendoza-Perez, J. A. Robledo-Torres, J. L. Rodriguez-Lopez, J. M. Montejano-Carrizales, R. L. Whetten and M. José-Yacamán, ACS Nano, 2016, 10, 188–198 CrossRef CAS PubMed.
- J. M. Rahm and P. Erhart, J. Phys. Chem. C, 2018, 122, 28439–28445 CrossRef CAS.
- G. Guisbiers, R. Mendoza-Cruz, L. Bazán-Díaz, J. J. Velázquez-Salazar, R. Mendoza-Perez, J. A. Robledo-Torres, J. L. Rodríguez-López, J. M. Montejano-Carrizales, R. L. Whetten and M. José-Yacamán, ACS Nano, 2016, 10, 10620–10622 CrossRef CAS PubMed.
- M. Cui, H. Lu, H. Jiang and X. Meng, ACS Nano, 2016, 10, 10618–10619 CrossRef CAS PubMed.
- N. Danielis, L. Vega, G. Fronzoni, M. Stener, A. Bruix and K. M. Neyman, J. Phys. Chem. C, 2021, 125, 17372–17384 CrossRef CAS PubMed.
- D. Nelli, C. Mottet and R. Ferrando, Faraday Discuss., 2023, 242, 52–68 RSC.
- M. Moreira, L. C. Felix, E. Cottancin, M. Pellarin, D. Ugarte, M. Hillenkamp, D. S. Galvao and V. Rodrigues, J. Phys. Chem. C, 2023, 127, 1944–1954 CrossRef CAS.
- V. Nominé, N. Tarasenka, A. Nevar, M. Nedel'Ko, H. Kabbara, A. Nominé, S. Bruy re, J. Ghanbaja, C. Noel, A. Krasilin, G. Zograf, V. Milichko, N. Kulachenkov, S. Makarov, N. Tarasenko and T. Belmonte, Plasma Phys. Controlled Fusion, 2021, 64, 014003 CrossRef.
- A. Loiseau, V. Asila, G. Boitel-Aullen, M. Lam, M. Salmain and S. Boujday, Biosensors, 2019, 9, 78 CrossRef CAS PubMed.
- P. Srinoi, Y. T. Chen, V. Vittur, M. D. Marquez and T. R. Lee, Appl. Sci., 2018, 8, 1106 CrossRef.
- D. Raabe, Chem. Rev., 2023, 123, 2436–2608 CrossRef CAS PubMed.
- N. E. Motl, E. Ewusi-Annan, I. T. Sines, L. Jensen and R. E. Schaak, J. Phys. Chem. C, 2010, 114, 19263–19269 CrossRef CAS.
- V. Mkhitaryan, K. March, E. N. Tseng, X. Li, L. Scarabelli, L. M. Liz-Marzán, S.-Y. Chen, L. H. G. Tizei, O. Stéphan, J.-M. Song, M. Kociak, F. J. G. de Abajo and A. Gloter, Nano Lett., 2021, 21, 2444–2452 CrossRef CAS PubMed.
- C. Gong and M. S. Leite, ACS Photonics, 2016, 3, 507–513 CrossRef CAS.
- R. Borah and S. W. Verbruggen, J. Phys. Chem. C, 2020, 124, 12081–12094 CrossRef CAS.
- A. N. Hidayah and Y. Herbani, J. Phys.: Conf. Ser., 2020, 1436, 12107 CrossRef CAS.
- M. Sui, S. Kunwar, P. Pandey and J. Lee, Sci. Rep., 2019, 9, 16582 CrossRef PubMed.
- M. Sahoo, S. Mansingh, S. Subudhi, P. Mohapatra and K. Parida, Catal. Sci. Technol., 2019, 9, 4678–4692 RSC.
- A. Guadagnini, S. Agnoli, D. Badocco, P. Pastore, R. Pilot, R. Ravelle-Chapuis, M. B. F. Raap and V. Amendola, ChemPhysChem, 2021, 22, 657–664 CrossRef CAS PubMed.
- D. J. McPherson, S. Supansomboon, B. Zwan, V. J. Keast, D. L. Cortie, A. Gentle, A. Dowd and M. B. Cortie, Thin Solid Films, 2014, 551, 200–204 CrossRef CAS.
- J. N. G. Stanley, I. García-García, T. Perfrement, E. C. Lovell, T. W. Schmidt, J. Scott and R. Amal, Chem. Eng. Sci., 2019, 194, 94–104 CrossRef CAS.
- G. Armelles, A. Cebollada, A. García-Martín and M. U. González, Adv. Opt. Mater., 2013, 1, 10–35 CrossRef.
- M. G. Blaber, M. D. Arnold and M. J. Ford, J. Phys.: Condens. Matter, 2010, 22, 143201 CrossRef CAS PubMed.
- J. M. Sanz, D. Ortiz, R. Alcaraz De La Osa, J. M. Saiz, F. González, A. S. Brown, M. Losurdo, H. O. Everitt and F. Moreno, J. Phys. Chem. C, 2013, 117, 19606–19615 CrossRef CAS.
- Y. Gutiérrez, A. S. Brown, F. Moreno and M. Losurdo, J. Appl. Phys., 2020, 128, 080901 CrossRef.
- M. W. Knight, N. S. King, L. Liu, H. O. Everitt, P. Nordlander and N. J. Halas, ACS Nano, 2013, 8, 834–840 CrossRef PubMed.
- E. Shiles, T. Sasaki, M. Inokuti and D. Y. Smith, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 22, 1612–1628 CrossRef CAS.
- J. Mingear, Z. Farrell, D. Hartl and C. Tabor, Nanoscale, 2021, 13, 730–738 RSC.
- P. C. Wu, T. Kim, A. Suvorova, M. Giangregorio, M. Saunders, G. Bruno, A. S. Brown and M. Losurdo, Small, 2011, 7, 751–756 CrossRef CAS PubMed.
- C. Yi, T. Kim, W. Jiao, Y. Yang, A. Lazarides, K. Hingerl, G. Bruno, A. Brown and M. Losurdo, Small, 2012, 8, 2721–2730 CrossRef CAS PubMed.
- Y. Kumamoto, A. Taguchi, M. Honda, K. Watanabe, Y. Saito and S. Kawata, ACS Photonics, 2014, 1, 598–603 CrossRef CAS.
- S. Galván-Arzate, A. Santamaría and A. Santamaría, Toxicol. Lett., 1998, 99, 1–13 CrossRef PubMed.
- D. Tiedemann, U. Taylor, C. Rehbock, J. Jakobi, S. Klein, W. A. Kues, S. Barcikowski and D. Rath, Analyst, 2014, 139, 931–942 RSC.
- E. B. Gordon, A. V. Karabulin, V. I. Matyushenko, T. N. Rostovshchikova, S. A. Nikolaev, E. S. Lokteva and E. V. Golubina, Gold Bull., 2015, 48, 119–125 CrossRef CAS.
- V. Amendola, S. Scaramuzza, F. Carraro and E. Cattaruzza, J. Colloid Interface Sci., 2017, 489, 18–27 CrossRef CAS PubMed.
- S. Scaramuzza, S. Agnoli and V. Amendola, Phys. Chem. Chem. Phys., 2015, 17, 28076–28087 RSC.
- V. Amendola, A. Guadagnini, S. Agnoli, D. Badocco, P. Pastore, G. Fracasso, M. Gerosa, F. Vurro, A. Busato and P. Marzola, J. Colloid Interface Sci., 2021, 596, 332–341 CrossRef CAS PubMed.
- A. Guadagnini, S. Agnoli, D. Badocco, P. Pastore, D. Coral, M. B. Fernàndez van Raap, D. Forrer and V. Amendola, J. Colloid Interface Sci., 2021, 585, 267–275 CrossRef CAS PubMed.
- D. Zhang, B. Gökce and S. Barcikowski, Chem. Rev., 2017, 117, 3990–4103 CrossRef CAS PubMed.
- D. Zhang, J. Liu and C. Liang, Sci. China: Phys., Mech. Astron., 2017, 60, 74201 Search PubMed.
- H. Okamoto, M. E. Schlesinger and E. M. Mueller, in Alloy Phase Diagrams, ASM International, 2016, 3, 89–89 Search PubMed.
- D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press, 85th edn, 2004 Search PubMed.
- V. Torresan, A. Guadagnini, D. Badocco, P. Pastore, G. A. Muñoz Medina, M. B. Fernàndez van Raap, I. Postuma, S. Bortolussi, M. Bekić, M. Čolić, M. Gerosa, A. Busato, P. Marzola and V. Amendola, Adv. Healthcare Mater., 2020, 10, 2001632 CrossRef PubMed.
- C. Y. Shih, C. Chen, C. Rehbock, A. Tymoczko, U. Wiedwald, M. Kamp, U. Schuermann, L. Kienle, S. Barcikowski and L. V. Zhigilei, J. Phys. Chem. C, 2021, 125, 2132–2155 CrossRef CAS.
- T. Wagner and J. Eglinger, 2017, https://github.com/thorstenwagner/ij-particlesizer/releases/tag/v1.0.9-SNAPSHOT.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- K. F. Garrity, J. W. Bennett, K. M. Rabe and D. Vanderbilt, Comput. Mater. Sci., 2014, 81, 446–452 CrossRef CAS.
- C. X. Wang, P. Liu, H. Cui and G. W. Yang, Appl. Phys. Lett., 2005, 87, 201913 CrossRef.
- G. Cristoforetti, E. Pitzalis, R. Spiniello, R. Ishak, F. Giammanco, M. Muniz-Miranda and S. Caporali, Appl. Surf. Sci., 2012, 258, 3289–3297 CrossRef CAS.
- Y. Han, S. Wu, E. Dai, Y. Ye, J. Liu, Z. Tian, Y. Cai, X. Zhu and C. Liang, ChemPhysChem, 2017, 18, 1133–1139 CrossRef CAS PubMed.
- C.-Y. Shih, M. V. Shugaev, C. Wu and L. V. Zhigilei, Phys. Chem. Chem. Phys., 2020, 22, 7077–7099 RSC.
- V. Amendola, R. Pilot, M. Frasconi, O. M. Maragò and M. A. Iatì, J. Phys.: Condens. Matter, 2017, 29, 203002 CrossRef PubMed.
- W. D. Callister Jr. and D. G. Rethwisch, Materials Science and Engineering - An Introduction, 10th edn, 2018 Search PubMed.
- C. Kittel, Introduction to solid state physics, Wiley, 8th edn, 2005 Search PubMed.
- J. C. Slater, J. Chem. Phys., 1964, 41, 3199–3204 CrossRef CAS.
- A. R. Miedema, J. Less-Common Met., 1973, 32, 117–136 CrossRef CAS.
- A. Lehr, J. J. Velázquez-Salazar, J. M. Montejano-Carrizales, S. Mejia-Rosales, R. Mendoza-Cruz, L. Bazan-Diaz and M. J. Yacaman, Faraday Discuss., 2023, 242, 10–22 RSC.
- D. A. Goodman, L. H. Bennett and R. E. Watson, MRS Proc., 1982, 19, 43 CrossRef.
- I. Y. Khairani, Q. Lin, J. Landers, S. Salamon, C. Doñate-Buendía, E. Karapetrova, H. Wende, G. Zangari and B. Gökce, Nanomaterials, 2023, 13, 227 CrossRef CAS PubMed.
- T. Fromme, L. K. Tintrop, S. Reichenberger, T. C. Schmidt and S. Barcikowski, ChemPhysChem, 2023, 24, e202300089 CrossRef CAS PubMed.
- M. R. Kalus, R. Lanyumba, N. Lorenzo-Parodi, M. A. Jochmann, K. Kerpen, U. Hagemann, T. C. Schmidt, S. Barcikowski and B. Gökce, Phys. Chem. Chem. Phys., 2019, 21, 18636–18651 RSC.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- J. Jakobi, S. Petersen, A. Menéndez-Manjón, P. Wagener and S. Barcikowski, Langmuir, 2010, 26, 6892–6897 CrossRef CAS PubMed.
- M. L. Williams, Occup. Environ. Med., 1996, 53, 504–504 CrossRef.
- O. Kubaschewski and O. von Goldbeck, Gold Bull., 1975, 8, 80–85 CrossRef CAS.
- P. D. Desai, Int. J. Thermophys., 1987, 8, 621–638 CrossRef CAS.
- E. B. Amitin, Y. F. Minenkov, O. A. Nabutovskaya, I. E. Paukov and S. I. Sokolova, J. Chem. Thermodyn., 1984, 16, 431–436 CrossRef CAS.
- W. Qi, Acc. Chem. Res., 2016, 49, 1587–1595 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2024 |