Elucidating the role of diverse mineralisation paradigms on bone biomechanics – a coarse-grained molecular dynamics investigation

Abstract

Bone as a hierarchical composite structure plays a myriad of roles in vertebrate skeletons including providing the structural stability of the body. Despite this critical role, the mechanical behaviour at the sub-micron levels of bone's hierarchy remains poorly understood. At this scale, bone is composed of Mineralised Collagen Fibrils (MCF) embedded within an extra-fibrillar matrix that consists of hydroxyapatite minerals and non-collagenous proteins. Recent experimental studies hint at the significance of the extra-fibrillar matrix in providing the bone with the stiffness and ductility needed to serve its structural roles. However, due to limited resolution of experimental tools, it is not clear how the arrangement of minerals, and in particular their relative distribution between the intra- and extra-fibrillar space contribute to bone's remarkable mechanical properties. In this study, a Coarse Grained Molecular Dynamics (CGMD) framework was developed to study the mechanical properties of MCFs embedded within an extra-fibrillar mineral matrix and the precise roles extra- and intra-fibrillar mineralisation on the load-deformation response was investigated. It was found that the presence of extra-fibrillar mineral resulted in the development of substantial residual stress in the system, by limiting MCF shortening that took place during intra-fibrillar mineralisation, resulting in substantial compressive residual stresses in the extra-fibrillar mineral phase. The simulation results also revealed the crucial role of extra-fibrillar mineralisation in determining the elastic response of the Extrafibrillar mineralised MCF (EFM-MCF) system up to the yield point, while the fibrillar collagen affected the post-yield behaviour. When physiological levels of mineralisation were considered, the mechanical response of the EFM-MCF systems was characterised by high ductility and toughness, with micro-cracks being distributed across the extra-fibrillar matrix, and MCFs effectively bridging these cracks leading to an excellent combination of strength and toughness. Together, these results provide novel insight into the deformation mechanisms of an EFM-MCF system and highlight that this universal building block, which forms the basis for lamellar bone, can provide an excellent balance of stiffness, strength and toughness, achieving mechanical properties that are far beyond the capabilities of the individual constituents acting alone.

---

Introduction

Bone is a naturally occurring composite material that combines organic proteins with Hydroxyapatite (HAp) mineral crystals to form a mineralised tissue that exhibits high stiffness and excellent resistance to fracture.^1,2 Tropocollagen proteins at the nanoscale level of the bone structure are made of three collagen molecules wrapped around each other to provide a helical protein with an overall radius ∼1.5 nm and length of ∼300 nm.³ At the next level of hierarchy, tropocollagens are assembled into collagen fibrils that are several micro-meters in length and have diameters in the range of 50–200 nm.² The staggered arrangement of collagen molecules in the fibrils results in high and low density collagen, creating what are termed overlap and gap regions that repeat throughout the structure at a periodic length of D = 67 nm.^2,4 Mineralisation of collagen fibrils gives rise to Mineralised Collagen Fibrils (MCFs). Even though higher-order structures of bones may differ, MCFs are present across the majority of bone types, anatomies and species and are considered a universal building block of bone tissue.^2,4 For many years, the mineral phase of bone was thought to be concentrated in these regions in the intra-fibrillar structure.^5–7 However, it has become evident that the volume available within the gap and overlap zones is relatively limited and these regions cannot accommodate the overall mineral content in the tissue.^8,9 This implies that mineralisation must extend beyond the gap and overlap regions^5,9,10 to the extra-fibrillar space.^11–13 However, the implications of various intra and extra-fibrillar mineralisation patterns on mechanical properties of MCFs and the load-deformation response of bone tissue remains poorly understood.

A major challenge in understanding the mechanics of MCFs is the inherent difficulty in isolating and testing intricate micron-scale fibrillar structures, with only a limited number of experimental studies specifically addressing roles of intra- and extra-fibrillar mineralisation.^12,14 For example, Karunaratne et al. showed that mouse bone with impaired extra-fibrillar mineralisation had lower stiffness and higher extensibility compered to healthy bone.¹² A range of models have sought to uncover the relative roles of intra- and extra-fibrillar mineral on tissue biomechanics through theoretical^15,16 and finite element based^15–18 approaches. Reisinger et al.¹⁹ demonstrated through a theoretical homogenisation approach that the extra-fibrillar mineral is the phase that makes the primary contribution towards the tissue stiffness. Subsequent models that have been developed using the finite element method have confirmed this, with these models providing additional information on the role of arrangement and organization of constituents on tissue-level behaviour.^15–18 However, to date, the vast majority of these models have only considered behaviour in the elastic regime, with a wide variation of Young's modulus for collagen fibrils being prescribed.^14,20 More recently, molecular dynamics modelling has been used to provide mechanistic insight into the mechanics of mineralised collagen fibrils themselves.^21,22 These frameworks have provided a platform to understand deformation and mechanics of individual proteins and interactions between proteins and mineral phases.²³ With this, while the extra-fibrillar matrix is known to be a key determinant of elastic properties,^16,19 our recent coarse grained molecular dynamics (CGMD) study has shown that intra-fibrillar mineralisation is essential in providing MCFs both high strength and ductility.²³ Furthermore, these results show that MCFs have fracture strains that are far higher than tissue-level fracture strains.²³ These observations suggest that MCFs could play an important role in extrinsic toughening to crack propagation at this scale. However, all of the models that have been developed to date have only considered a single MCF,^21–26,27 in the absence of any extra-fibrillar matrix, which represents a highly idealised system. While MCFs are considered as one of the universal building blocks of bone tissue, these structures do not physically exist in isolation of the extra-fibrillar matrix in bone tissue structures. Therefore, to fully understand the mechanical behaviour of lamellar bone at this scale, the performance of MCFs in the presence of the extra-fibrillar matrix must be considered.

In this study, a CGMD framework is used to investigate the effect of extra-fibrillar mineralisation on the load-deformation response of MCFs. This framework builds on our previous CGMD study on a single MCF system²³ and introduces a matrix of extra-fibrillar minerals around an array of four MCFs to predict the uniaxial mechanical properties of these extra-fibrillar mineral-mineralised collagen fibril (EFM-MCF) systems. Through systematic investigation, we provide new insight into the relative roles of intra- and extra-fibrillar mineralisation on the fracture behaviour of EFM-MCF systems, highlighting the importance of the extra-fibrillar mineralisation on the mechanical properties of bone tissue.

Results

Mechanical properties of MCFs with various extra-fibrillar mineralisation

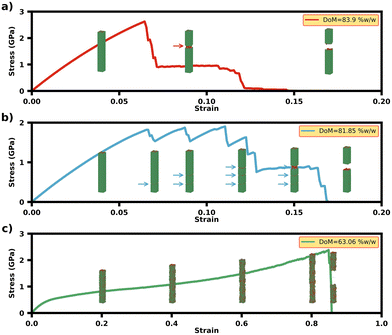
Fig. 1 shows the stress–strain plots for the EFM-MCF systems for various levels of extra-fibrillar mineralisation and a constant level of intra-fibrillar mineral (iDoM = 35% w/w). Here, the importance of extra-fibrillar mineralisation on the load-deformation response of the EFM-MCF system (Fig. 1a) is evident, with several different characteristic shapes observed in the stress–strain plots depending on the level of extra-fibrillar mineralisation. Highly mineralised systems (DoM = 81.85–83.90% w/w) were characterised with high initial stiffness and low fracture strain, with a high sensitivity in the pre-yield mechanical response depending on the amount of extra-fibrillar mineral present. For intermediate levels of mineralisation (DoM = 43.36–80.17% w/w), the fracture strain was higher, with less variation in the pre-yield mechanical properties. Finally, for systems without extra-fibrillar mineralisation (DoM = 35.05% w/w), there were initial toe and heel regions (Fig. 1a) in the response and the loading regime was characterised by lower stiffness and high fracture strain and ultimate tensile strength (UTS) values, with a work hardening region evident before the final fracture. Our previous study evaluated the performance of an MCF in absence of extra-fibrillar mineral in detail,²³ and the load-deformation mechanisms associated with these cases will not be discussed in detail here.

Fig. 1 Mechanical properties of EFM-MCF systems with 35% w/w intra-fibrillar mineralization and various degrees of extra-fibrillar mineralization illustrating the importance of extra-fibrillar mineralization. (a) Stress–strain plots for different degrees of mineralization showing the effect of extra-fibrillar mineralization on the MCF mechanical behaviour. (b) Young modulus and UTS and (c) Fracture strain, residual strain and Toughness (GPa) for various mineralisation degrees for MCF systems with 35% w/w intra-fibrillar mineralization. The mineralization amount of 35.05% w/w corresponds to the system without extra-fibrillar mineralization, while 83.90% w/w refers to the maximum amount of extra-fibrillar mineralization possible.

For the highly mineralised regime, where the total degree of mineralisation ranged between DoM = 81.85–83.90% w/w, the initial stress–strain response prior to the UTS was heavily dependent on the amount of extra-fibrillar mineral. Both the Young's modulus and UTS increased linearly with the amount of extra-fibrillar mineral present (Fig. 1b) and there was a slight decrease in the toughness (the thumbnail in Fig. 1c), while the fracture strain and residual strain were largely similar across these regimes (the thumbnail in Fig. 1c). Fig. 2a shows simulation snapshots of this regime with DoM = 83.85 ± 0.03% w/w, where it is shown that both the extra-fibrillar mineral and the MCFs were under loading (Fig. 2a). Once the UTS is reached, the stress initially drops to a fixed value for a short range of strains before the final fracture. From the simulation snapshots, the UTS is reached at 8% strain, at which point fracture takes place in the extra-fibrillar matrix and the loading is re-distributed to the MCFs and a crack bridging mechanism is clearly observed (Fig. S2†), which contributes to the load plateau in stress–strain response until the final fracture takes place through fracture in the individual MCFs components themselves.

Fig. 2 The representative simulation snapshots for uniaxial pulling of different extra-fibrillar mineralisation regimes of MCFs showing different deformation mechanisms. (a) Simulation snapshots for the system with 83.90% w/w mineralised system as a representative for the system with highly mineralised extra-fibrillar matrix shows that until the strain of 8 percent there is no crack in the system and both the extra-fibrillar matrix and collagen fibrils carry the external loading and after the strain of 8% a crack is formed in the sample and the external loading is exerted into the fibrils until the final fracture event which also occurs in the fibrils. (b) The system with 81.85% w/w mineralisation which is considered as a handshake between the systems with highly mineralised and medium mineralised extra-fibrillar matrix which is characterized by consecutive drops in the stress value each concomitant with the formation of a new crack in the system. (c) Simulation snapshots for the system with mineralisation of 63.06% w/w representing the slight mineralisation of the extra-fibrillar matrix which is characterized by the gradual deformation of both the matrix and the collagen fibrils and the lack of crack growth. The cracks in the matrix are shown with arrows.

For medium levels of extra-fibrillar mineralisation, where the total degree of mineralisation range between DoM = 43.36–80.17% w/w, the mechanical response was characterised by higher ductility and toughness, higher fracture strains and lower stiffness than the highly mineralised regime (Fig. 1c). However, the UTS remains almost fixed for various DoM values, while the Young's modulus only showed modest increases compared to the highly mineralised regime (Fig. 1b). The simulation snapshot for the system with DoM = 81.85% w/w (Fig. 2b) shows that each drop in the stress value corresponds to the formation of a new transverse crack in the extra-fibrillar mineral (identified in Fig. 2b with arrows), with one dominant crack path emerging in the extra-fibrillar mineral in the later stages of loading. The simulation snapshots for other cases in this regime (Fig. 2c) show similar transverse cracks initiating in the extra-fibrillar mineral matrix, although these do not result in failure of the EFM-MCF system. Here, some longitudinal cracks are gradually formed, but these do not grow beyond the length of an overlap or a gap region. In this case, failure is dominated by the MCF array whereby the UTS strain corresponds to the final fracture strain, which is when the MCFs break.

The role of collagen, intra and extra fibrillar minerals in the load deformation response of EFM-MCFs

Fig. 3a–c shows the stress in the collagen and intra- and extra-fibrillar mineral components under uniaxial tension for various degrees of mineralisation, and Fig. 3d shows the residual stress in each of these components for each degree of mineralisation. Prior to loading, Fig. 3d shows the residual stress values in each of the EFM-MCF components, where the intra-fibrillar mineral always has tensile residual stress present. Collagen generally had compressive residual stresses, up until the DoM = 63.06% w/w case (start of highly mineralised regime). Finally, the extra-fibrillar mineral had tensile stresses at low mineralisation, which gradually decreased with increasing mineralisation, until these eventually became compressive at DoM = 63.06% w/w. Fig. 3d shows that the residual stress in the EFM-MCF system for the highest level of mineralisation provides tensile and compressive residual stresses in the intra- and extra-fibrillar regions, respectively. Our previous simulations on individual MCFs showed that intra-fibrillar mineralisation causes MCFs to shorten (see Fig. 6c), which is characterised by an increase in the residual strain.²³ However, the presence of the extra-fibrillar mineral limits the shortening of the MCFs, which induces tensile residual stress in the MCF components (collagen and the intra-fibrillar mineral) and substantial compressive residual stress in the extra-fibrillar mineral. Different residual stress values are the reason for different mechanical properties observed in the various mineralisation regimes observed in (Fig. 1a) which is explained in the following paragraph.

Fig. 3 The role of individual components of extra-fibrillar mineralized MCF with intra-fibrillar mineralisation of 35% w/w and various degrees of extra-fibrillar mineralization showing the significance of collagen and intra-fibrillar minerals in carrying the external loading in tension. The stress carried by collagen, intra-fibrillar and extra-fibrillar minerals for MCFs with mineralisation of (a) 63.06% w/w, (b) 74.19% w/w and (c) 83.90% w/w. The zoomed in views shown in the thumbnails of panels a and b illustrated residual stress in all the three components of the system. (d) The residual stress for the various components of the system. In all the panels the legend is the same as panel a legend. In panels a and b the stress–strain plots for small deformation are shown in the inset.

In the small deformation regime (strain < 0.04), the extra-fibrillar mineral content directly influences the relative contributions of collagen, intra- and extra-fibrillar minerals on the response of the system, while in larger deformation regime the brittle behaviour of hydroxyapatite is the reason why the collagen takes the external loading. For the lower mineralised case of DoM = 63.06% w/w, the collagen molecule is initially under compression due to the presence of residual stress (inset in Fig. 3a), while both the intra- and extra-fibrillar minerals are under pre-tension. As a result, in small deformation, the external loading is applied mainly to the minerals until the strain of ∼0.15, at which point it is exceeded by the stress applied to the collagen fibril. For DoM = 74.19% w/w mineralisation (inset in Fig. 3b), the residual stress in the extra-fibrillar mineral becomes compressive, while there is a tensile residual stress on the collagen and intra-fibrillar minerals. Thus, the external loading is initially mainly carried by the collagen and the intra-fibrillar minerals in the small deformation regime, while the collagen itself becomes dominant in the large deformation regime. Finally, in the highly mineralised case of DoM = 83.85% w/w (Fig. 3c), the residual tensile stress in the collagen is larger than minerals, which is the reason why it has larger stress than other two phases in the whole strain range studied here, and again is dominant in the large deformation regime. Decreasing the mineralisation from DoM = 83.85% w/w to 83.27% w/w, 82.59% w/w and 81.85% w/w, the stress carried by the intra-fibrillar minerals in the MCFs decreases by 1.97%, 5.83% and 11.03%, while the same changes leads to decrease of 26.55%, 50.83% and 74.30% in the extra-fibrillar matrix, respectively.

Effect of intra-fibrillar mineralisation on the EFM-MCF mechanical properties

In addition to the extra-fibrillar mineralisation, the degree of intra-fibrillar mineralisation (iDoM) also affects the mechanical properties of the EFM-MCF system. Fig. 4a shows the stress–strain plots for EFM-MCF systems with iDoM = 5% w/w, which can be compared to the corresponding plots for iDoM = 35% w/w (Fig. 1a). Lower levels of intra-fibrillar mineralisation in the fixed extra-fibrillar mineral amount brings about less mineral in the system and lower stiffness as a result. Thus, lower levels of intra-fibrillar mineralisation exhibited reduced stress values for the same extra-fibrillar mineral amount, until matrix fracture occurred with three distinct regimes observed, as before (Fig. 4b and c). In highly mineralised systems, the stress drops to an independent value after reaching UTS upon matrix fracture. However, in the case of iDoM = 5% w/w, stress gradually declines following UTS.

Fig. 4 The mechanical properties of EFM-MCF with 5% w/w intra-fibrillar mineralization and various degrees of extra-fibrillar mineralisation illustrating the effect of extra-fibrillar minerals in the MCF mechanical properties. (a) stress–strain plots, (b) Young modulus, UTS and (c) residual strain and toughness values for MCFs with various degrees of extra-fibrillar mineralization and 5% w/w intra-fibrillar mineralization. The inset in panel a shows the stress values in the strain of 5%.

Fig. 5a compares the toughness values for iDoM = 5% w/w with iDoM = 35% w/w for various extra-fibrillar mineral content (eDoM). For highly mineralised EFM-MCFs, lower intra-fibrillar mineralisation (iDoM = 5% w/w) had higher toughness than higher levels intra-fibrillar mineralisation (iDoM = 35% w/w). In these cases, after the extra-fibrillar mineral matrix fractures, the lower intra-fibrillar mineralised MCFs provides the collagen fibrils with the ability to withstand larger strain values without breaking due to the higher sliding capacity of the collagen molecules. For extra-fibrillar mineralisation (eDoM) of smaller than 50% w/w (Fig. 5a, eDoM < 50% w/w), the length of post-yield region in the stress–strain plot is not long enough to counteract the lower stress in this intra-fibrillar mineralisation density. Thus, the toughness in this range of extra-fibrillar mineralisation is lower for EFM-MCFs with iDoM = 5% w/w.

Fig. 5 Mechanical properties of MCFs with 5% and 35% w/w intra-fibrillar mineralisation and various degrees of extra-fibrillar mineralisation illustrate more significant effect of extra-fibrillar mineralisation on the MCF mechanical properties. (a) Toughness values show that an increase in the intra-fibrillar mineralisation decreases the MCF toughness. (b) Young modulus (blue colored line and the left axis) and UTS (orange colored line and the right axis) showing that the intra-fibrillar mineralisation slightly affects the MCF mechanical properties while the extra-fibrillar mineral amount significantly influences both the parameters. (c) Residual stress values for MCF with various intra-fibrillar and extra-fibrillar mineral amounts depicting smaller residual stress for lower intra-fibrillar mineralisation. In all the panels the 5% w/w and 35% w/w intra-fibrillar mineralized MCFs are depicted with dashed and solid lines, respectively.

Fig. 5b presents the Young's modulus and UTS for EFM-MCF systems with low (iDoM = 5% w/w) and high (iDoM = 35% w/w) intra-fibrillar mineralisation regimes, illustrating a slight increase in Young modulus and UTS with an increase in intra-fibrillar mineral content. However, it is notable that, for the same amount of total mineral content, the 5% w/w intra-fibrillar mineralised system have larger Young's modulus (Fig. 4 and 1). This implies that, while the total mineral content directly contributes to both the UTS and Young modulus values, the presence of mineral in the extra-fibrillar matrix provides a greater contribution to these properties in the elastic regime. The residual stress shows a similar trend. The residual stress is larger for 35% w/w for the same extra-fibrillar mineralisation, while for the same total number of minerals 5% w/w case have larger residual stress (Fig. 5c).

Discussion

This study used a CGMD framework to investigate the effect of extra-fibrillar mineralisation on the load-deformation response of EFM-MCF systems. Prior to loading, it was found that substantial compressive residual stresses (60–70 MPa at biologically relevant DoM = 60%–70%) were present in the extra-fibrillar mineral phase once (intra-fibrillar) mineralisation of the MCFs had taken place. These arose as the stiff extra-fibrillar matrix phases limited the amount of shortening that could take place in the fibrillar collagen components due to intrafibrillar mineralisation. Depending on the amount and the position of the mineral (intra vs. extra-fibrillar), the residual stress on the collagen and the extrafibrillar mineral can be compressive or tensile. Under loading, several characteristic behaviours were observed depending on the amount of extra-fibrillar mineral present. For high amounts of extra-fibrillar mineral, the EFM-MCF system showed high stiffness and immediately after the UTS was reached, there was a brittle fracture in the extra-fibrillar matrix, with MCFs showing subsequent load take-up and a crack-bridging mechanism. For intermediate levels of extra-fibrillar mineral, the mechanical response was characterised by higher ductility and toughness, with micro-cracks being distributed across the extra-fibrillar matrix, and MCFs effectively bridging these cracks leading to an excellent combination of strength and toughness. On the other hand, for low amounts of extra-fibrillar mineral, the stiffness and stress values were substantially lower, with the stress–strain response of the system resembling previous isolated representations of MCF systems without a surrounding extra-fibrillar matrix,²³ showing a response that was similar to a characteristic tendon stress–strain curve. Together, these results provide novel insight into the deformation mechanisms of an EFM-MCF system and highlight that this universal building block, which forms the basis for lamellar bone, can provide an excellent balance of stiffness, strength and toughness, achieving mechanical properties that are far beyond the capabilities of the individual constituents acting alone.

Even though extra-fibrillar mineral may account for up to 60–70% of the total mineral content in bone tissue,¹³ there remains a lack of understanding on how both intra- and extra-fibrillar mineralisation contribute to the mechanical properties of bone tissue.^12,15,18,28 Our simulation results show that the extra-fibrillar mineral provides an important contribution to the stiffness of bone tissue, with the predicted Young's moduli of the EFM-MCF systems directly dependent on extra-fibrillar mineral content. On the other hand, the amount of intra-fibrillar mineral content had little influence on the stiffness of the EFM-MCF system. Other theoretical¹⁹ and finite element-based^15–18 approaches have made similar observations on the dominant role of the extra-fibrillar mineral on the tissue stiffness. Considering that physiological levels of mineralisation would range between 60–70% w/w,^8,29 the predicted range of Young's moduli predicted across the this mineralisation range (9.6–12.27 GPa) were in a comparable range to previously measured tissue-level values for bone through experiments,^7,30 while the wider predicted range of Young's moduli across these EFM-MCF systems (2–45 GPa) were in a similar range to previously measured tissue-level values for mice bones with various degrees of impaired extrafibrillar mineralisation.¹² Our previous computational study²³ showed that isolated MCFs, in the absence of extra-fibrillar mineralisation, had fracture strains that were in the range of 100%, which were much higher than experimentally measured values of mineralised fibrillar systems. However, the current simulations showed that introducing extra-fibrillar mineralisation to an MCF system resulted in yield strains of the order of ∼7% for highly mineralised EFM-MCF systems, which are much closer to experimentally-measured values of 5.14–6.72%, which have been observed for highly mineralised antler bone.¹⁴ A major difficulty in conducting experiments on MCFs in mineralised fibrillar systems is that it is difficult to physically isolate and test MCFs in the absence of any extra-fibrillar mineral and therefore the EFM-MCF system that we have simulated here may better represent previous microscale experimental studies on mineralised fibrillar systems. Also, the calculated extra-fibrillar shear stress values of 21.94 ± 2.89 MPa and 20.28 ± 4.03 MPa for mineralisation for this system (see ESI† section) were in a good agreement with the value of 18.2 MPa from experiments conducted on hydrated multiple lamellas.⁵ The CGMD model presented here represents a significant advance on previous MD frameworks that considered single MCFs in isolation,^{21,22,24–26,27,31} and is the first to explicitly consider the presence of extra-fibrillar mineral. These findings highlight the critical importance of extra-fibrillar mineral in both elastic and post-yield behaviour of the tissue, with the EFM-MCF system providing much better agreement with experimental observations of bone's mechanical properties compared to isolated MCF models.^{21,22,24–26,27,31}

Our simulation results showed a wide range of load-deformation behaviour for EFM-MCF systems, depending on the relative amounts of intra- and extra-fibrillar mineralisation. In our previous study, we showed that several features of the load-deformation behaviour of MCFs including the initial toe region arose due to the partial release of residual strains, which were generated upon mineralisation of the system.²³ In the absence of extra-fibrillar mineral, there is a large build-up of residual strain in MCFs upon intra-fibrillar mineralisation, with considerable shortening of the MCF taking place.²³ In considering an extra-fibrillar region, we based our EFM-MCF simulations on the recent evidence for the initiation of mineralisation from the extra-fibrillar matrix obtained in recent experimental work by Macías-Sánchez et al.³² In the case that opposite mineralisation path from intra to extra-fibrillar space was considered the EFM-MCF would have behaved like a traditional composite due to less residual stress in the extrafibrillar matrix. However, in the current study with the hypothesis of mineralisation pathway from extra to intra-fibrillar matrix according to the finding of Macías-Sánchez et al.,³² the extra-fibrillar mineral was added to the system before equilibrating the whole system to reflect that finding‡ and this resulted in substantial residual stresses being generated. The effects of these residual stresses were most evident when the response of MCFs with and without extra-fibrillar mineralisation were considered. In particular, the presence of the extra-fibrillar mineral limited the shortening of the MCFs that takes place upon intra-fibrillar mineralisation, which resulted in lower residual strains in the EFM-MCF system, but instead generated higher residual stresses in the system. The predicted magnitudes of residual stresses were in agreement with experimental findings of Almer and Stocks,³³ who observed compressive residual stresses on the order of −100 MPa, which was similar to our model predictions of compressive stresses in the extra-fibrillar phase for highly mineralised systems (which are lower than intra-fibrillar mineralised MCFs). Interestingly, the presence of extra-fibrillar mineral also plays an important role in determining the characteristic load-deformation response for the EFM-MCF system. In the absence of extra-fibrillar mineral, MCFs typically have a toe region in the stress–strain curve, which would be a typical characteristic response of tendon-like tissues. This toe region is caused by the partial release of the collagen residual strain in the non-mineralised length of collagen components of an MCF.²³ However, this is prevented due to the lack of non-mineralised length in the EFM-MCF system. Thus, the presence of the extra-fibrillar limits partial release of its lower residual strains resulting in a stress–strain profile similar to those of bone tissue, which does not typically have an initial toe-region. The presence of residual strains in the intra-fibrillar region also results in various dependence of the elastic response on the mineral amount which is discussed in more detail below.

Comparing various simulations in this study and our previous study,²³ the mechanical response of MCF and EFM-MCF systems depended on overall mineral content and its distribution between either the intra- or extra-fibrillar space. Firstly, in the absence of extra-fibrillar mineralisation, higher levels of intra-fibrillar mineralisation in MCFs actually decreases the effective elastic modulus of an MCF, due to the higher levels of residual strain that are generated upon mineralisation. Meanwhile, for fixed amounts of extra-fibrillar mineral, increasing the amount of intra-fibrillar mineral has little effect on the effective elastic modulus of the system, which suggests that the mechanical properties of the tissue might not change greatly as the mineralisation proceeds from extra-fibrillar to intra-fibrillar region.³² For fixed levels of intra-fibrillar mineralisation, it was found that higher levels of extra-fibrillar mineralisation directly resulted in higher effective Young's moduli in EFM-MCF systems in the elastic regime. For highly mineralised regimes (>80% w/w), both the extra-fibrillar mineral and the MCFs carry the external loading. The stress in the intrafibrillar mineralised MCF is dependent on both its load-deformation response and the load transferred to it through shear transfer from extrafibrillar matrix. However, the load-deformation response of the intra-fibrillar mineralised MCF²³ only shows slight changes in the highly mineralised regime, while the extra-fibrillar matrix shear stress does not change prior to the yield point. Therefore, the applied load on the intra-fibrillar mineralised MCF does not experience any meaningful changes with the mineral amount, explaining only slight changes in its stress. However, the extra-fibrillar matrix stress is heavily dependent on the extra-fibrillar mineral content, with the stress carried by extra-fibrillar mineral increasing with higher mineral content (see Fig. S1†). While increasing amounts of mineralisation result in a very high stiffness response, and therefore good load-bearing properties, these systems show drastic reductions in the overall toughness of the EFM-MCF system due to the fact that the extra-fibrillar matrix is dominating the loading regime. For medium levels of extra-fibrillar mineralisation (60–70% w/w), the effective elastic properties seems to be independent of the mineral content, which might be the reason why the bone mineral amount is tightly regulated in this range. In this physiological range, it would seem that the best balance of mechanical properties is achieved, with substantially higher toughness values than the highly mineralised regime, with good stiffness and UTS values also predicted.

Thus, the current study provided novel insights into the mechanical properties of MCFs with different intra and extra-fibrillar mineralisation amounts. This effort was not devoid of limitations. Since drying affects the mechanical properties of bone, the lack of solvation in the current study is the first limitation enumerated here. However, for the high extra-fibrillar mineralisation regime which was the main focus of the current study the water molecules are replaced with minerals. The other shortcoming is the lack of crosslinks in the current model. Crosslink breaking might happen before the MCF breaking in medium extra-fibrillar mineralisation EFM-MCF which might explain large fracture strains reported in the current study for this regime. Finally, a more accurate representation of extra-fibrillar matrix is needed which might be possible in future with advent of more accurate experimental methods.

Concluding remarks

This study used a CGMD framework to investigate the effect of extra-fibrillar mineralisation on the load-deformation response of EFM-MCF systems. It was found that the extra-fibrillar mineral provides an important contribution to the stiffness of bone tissue, with the predicted Young's moduli of the EFM-MCF systems directly dependent on extra-fibrillar mineral content. It was also found that the presence of extra-fibrillar mineral significantly affected the development of residual strains in MCFs, limiting the amount of shortening that takes place during intra-fibrillar mineralisation, resulting in higher levels of residual stresses in a full EFM-MCF system. The presence of these residual stresses subsequently affected the load-deformation response of fibrillar systems. When physiological levels of mineralisation were considered, the mechanical response of the EFM-MCF systems was characterised by high ductility and toughness, with micro-cracks being distributed across the extra-fibrillar matrix, and MCFs effectively bridging these cracks leading to an excellent combination of strength and toughness. Together, these results provide novel insight into the deformation mechanisms of an EFM-MCF system and highlight that this universal building block, which forms the basis for lamellar bone, can provide an excellent balance of stiffness, strength and toughness, achieving mechanical properties that are far beyond the capabilities of the individual constituents acting alone.

Methods

Coarse grained model framework

This study considers the uniaxial load-deformation and fracture behaviour of an array of MCFs that were embedded within an extra-fibrillar mineral matrix. Fig. 6a shows the EFM-MCF model arrangement whereby, four MCFs with a diameter of 20 nm were arranged in a 2 × 2 configuration, with a gap distance of d = 2 nm between them,⁷ unless stated otherwise. Since the length of one collagen molecule is equal to 300 nm and the periodic length (D) of collagen fibrils is D = 67 nm (Fig. 6), the length of MCFs was chosen as L = 5D = 0.335 μm to eliminate periodic boundary effects.²¹ Using this arrangement, several systems were considered such that the amount of intra-fibrillar mineralisation of MCFs was considered as 0% w/w, 5% w/w (Fig. 6b) and 35% w/w (Fig. 6c), while various extra-fibrillar mineralisation patterns were also generated.

Fig. 6 The initial setup for the current system under study with different distribution of minerals in the intra and extra-fibrillar spaces. (a) The system with 35% w/w intra-fibrillar mineralisation, no porosity in the extra-fibrillar matrix and total mineralisation of 83.85 ± 0.03 w/w. The length of 5D distance was chosen to eliminate interaction of each collagen molecule with its period image and the radius was selected since the mechanical properties of an individual MCF are not dependent on its diameter. The d distance is equal to 2 nm unless stated otherwise. Various extra-fibrillar mineralisation patterns for MCF systems with (b) 5% and (c) 35% extra-fibrillar mineralisation. The sliced view of each system is shown beside it and the intra-fibrillar mineralisation is considered only in the gap region.

For the collagen components in the CGMD model, the atoms along the collagen molecule central axis were replaced by 14Å equidistance beads.^21,22 The coordinates of the collagen central axis were taken from the Protein Data Bank code³⁴ of “3hr2”, which was the structure resolved by Orgel et al.³⁵ Mapping the all-atom resolution to the CG resolution was done through a python code³⁶ that used the symmetry information provided with the structure to build collagen fibrils with the chosen radius and mineralisation patterns (explained below). A C++ code was developed to add bond and angle information to the atomic coordinates and transform it to the LAMMPS input file.³⁷

To mineralise the system, intra-fibrillar mineralisation of MCFs was considered by using an in-house tcl code implemented in VMD software³⁸ similar to our previous study.²³ The entire mineralisation region, which is the gap region in the current study, was filled with minerals arranged in a Face Centered Cubic (FCC) lattice. However, those minerals that were within a specific cut-off distance to a collagen bead were removed. This cut-off distance was adapted to get the desired intra-fibrillar mineral amount (see Table S1†). The procedure was carried out several times with various intra-fibrillar cut-off values to assure that there is no bias towards the initial random pattern. The intra-fibrillar Mineral Volume Fraction (iMVF) for MCF was calculated through eqn (1),

where n_IFM, n_collagen, r_mineral and r_collagen represent the number of intra-fibrillar mineral beads, number of collagen beads, radius of mineral and collagen beads, respectively. The radius values for all beads were considered equal to the van der Waals radius from the forcefield.³⁹ The iMVFs of 0%, 1.54% and 13.88% corresponded to the intra-fibrillar Degree of Mineralisation (iDoM) of 0% w/w, 5% w/w and 35% w/w, which were chosen since the maximum intra-fibrillar bone mineral weight concentration is ∼40% w/w according to experimental studies.²⁷

For extra-fibrillar mineralisation, the region was modelled as a matrix of HAp minerals that has various degrees of porosity to represent a porous material structure.⁴⁰ Different percentages of extra-fibrillar minerals ranging from 100% to 0% were randomly removed from the extra-fibrillar region to obtain the various extra-fibrillar mineral amounts. This procedure was carried out multiple times with various random seeds to ensure there is no bias towards the initial random pattern (see Table S1†). The extra-fibrillar Mineral Volume Fraction (eMVF) was calculated with eqn (2)

where the parameters were the same as the eqn (1), with an extra parameter of n_EFM introduced to represent the number of extra-fibrillar minerals. Filling the whole extra-fibrillar matrix with minerals led to the maximum values of eMVF = 54.59 ± 0.07% and eMVF = 58.00 ± 0.05% for iMVF = 13.88% and iMVF = 1.54%, respectively. The degree of mineralisation was defined as the mass of the minerals divided by the mass of the system with units of % w/w according to Eqn 3, 4 and 5where DoM, iDoM, eDoM, m_mineral and m_collagen represent the total degree of mineralisation, intra-fibrillar degree of mineralisation, extra-fibrillar degree of mineralisation, mass of mineral beads and mass of collagen beads, respectively. In the text, the total amount of mineralisation is described as the total Degree of mineralisation (DoM).

Coarse grained model forcefields

A reactive CGMD framework was employed that was based on the forcefield developed by Buehler^21,24,25,39 since the conventional non-reactive all atom forcefields such as CHARMM⁴¹ do not reach the time and length scales²⁴ required to predict breaking of covalent bonds^24,42 at large deformation. Reactive bonds with a bilinear function (eqn (6)) connecting two neighbouring collagen beads belonging to the same molecule were considered, while a harmonic angle was considered between three consecutive beads. The coefficients of bonds and angles were calibrated through simulation of a uniaxial tension test on the single collagen molecule with a reactive all-atom MD simulation.²⁴ A new bilinear bond style similar to²¹ was added to LAMMPS to model the bond interaction between beads. Non-bonded collagen beads interacted through non-bonded Lennard-Jones interactions calibrated based on the all-atom simulation of one collagen fibril being pulled from two adjacent fibrils.²⁴ A Lennard-Jones potential was used to calculate mineral-mineral interactions, which was calibrated based on the HAp bulk modulus and Poisson's ratio which are K = 90 GPa and υ = 0.28, respectively. The mineral beads interacted with collagen beads through the similar potential function, with coefficients calibrated based on collagen-HAp adhesion energy obtained through all-atom simulations.²²eqn (6) describes the variables of the potential function for the bonded interaction (U_bond), small (k⁽⁰⁾) and large deformation (k⁽⁰⁾) spring constants, bead-bead distance (r), the equilibrium distances for small (r₀) and large deformation regimes (r̄₁), the distance at which the potential function switches (r₁) and the cut-off distance (r₂). eqn (7) describes the relation between the Lennard-Jones non-bonded potential function (U_non-bonded), the distance at which the potential energy is zero (σ), depth of potential well (ε), bead–bead distance (r) and the cut-off distance (r_cutoff).

Uniaxial tensile test simulation

Monotonic uniaxial tension was simulated on the EFM-MCF system according to protocol described in⁴³ and the load-deformation behaviour was evaluated. Prior to the main simulation, a short energy minimization was conducted to remove any possible bead overlap followed by an energy equilibration of 20 ns to generate the correct atomic position and velocity distributions. The equilibration stage was carried out in a constant Number of particles, constant Pressure and constant Temperature (NPT) ensemble, with Nose–Hoover thermostat and barostat implemented with the equation of motion of Shinoda et al.⁴⁴ The temperature and pressure of the system were kept fixed in T = 310 K and P = 1 atm, respectively, with the number of beads for each system provided in Table S1.† The use of canonical ensemble assures the anisotropy of the extrafibrillar minerals. In this study, a strain rate of SR = 5 × 10⁵ s⁻¹ was adapted to achieve the quasi-static loading regime. The stress values were calculated through the virial equation.⁴⁵ The virial stress was calculated according to the eqn (8) in which the integration is carried out over N_p, N_a or N_a neighbours of atoms i, its bonded neighbours and the atoms with whom it has angle interactions, respectively. The S_ab, r_1a, r_2a, (r_3a) represent the ab component of the virial stress tensor and the positions of 2 atoms (3 atoms) in pairwise (angle) interactions. Since the virial stress values are stress × volume, in calculating the stress applied to each component of the system it was assumed that the volume was proportional to the number of beads belonging to that component. The toughness was defined as the area under the stress–strain plot.

Parameter studies

Various combinations of DoMs in the form of intra- and extra-fibrillar mineralisation patterns summarised in Table S1† were considered. Specifically, this study investigated the effect of various DoM in the range of 5–83.85% w/w for three iDoM values of 0% w/w, 5% w/w and 35% w/w. Also, several simulations with values of “d” other than the default value of 2 nm (3 nm, 4 nm, and 5 nm) were conducted to study the effect of EFM-MCF arrangement. There were 31 simulation sets, with each simulation repeated on average 5 times and average simulation time of 0.8 μs leading to the total number of 138 simulations with the cumulative simulation time of 124 μs. More information on the details of mineralisation patterns for each system considered in the current study is provided in that Table S1.†

Data availability

All the files necessary to reproduce the results reported here alongside with the processed simulation data are openly available in Figshare at https://dx.doi.org/10.6084/m9.figshare.23936445.

Code availability

All Codes written for different pre and post processing of the simulations are available at GitHub under the addresses of: https://github.com/MahdiTavakol/CollagenCGBuilder, https://github.com/MahdiTavakol/LammpsDataFile4CGCollagen

Author contributions

T. V. conceived and directed the project; M. T. prepared the models, carried out the MD simulations and prepared the figures; M. T. and T. V. analyzed the data, interpreted the results and wrote the manuscript.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

This project has received funding from the European Research Council under the EU's horizon 2020 research and innovation program (Grant agreement No. 804108). This publication reflects only the authors’ view and the REA is not responsible for any use that may made of the information it contains. The authors also wish to acknowledge the Partnership for Advanced Computing in Europe (PRACE) and Irish Center for High-End Computing (ICHEC) for the provision of the computational facilities and support.

References

1. T. Newman, Bones: All you need to know, Medical New Today, 2018, https://www.medicalnewstoday.com/articles/320444#The-structure-of-bones (accessed 2021 06/12/2021).
2. N. Reznikov, R. Shahar and S. Weiner, Bone hierarchical structure in three dimensions, Acta Biomater., 2014, 10(9), 3815–3826,  DOI:10.1016/j.actbio.2014.05.024.
3. J. Parvizi, High yield orthopaedics E-Book, Elsevier Health Sciences, 2010.
4. Y. Liu, D. Luo and T. Wang, Hierarchical structures of bone and bioinspired bone tissue engineering, Small, 2016, 12(34), 4611–4632.
5. W. J. Landis, M. J. Song, A. Leith, L. McEwen and B. F. McEwen, Mineral and Organic Matrix Interaction in Normally Calcifying Tendon Visualized in Three Dimensions by High-Voltage Electron Microscopic Tomography and Graphic Image Reconstruction, J. Struct. Biol., 1993, 110(1), 39–54,  DOI:10.1006/jsbi.1993.1003.
6. Y. Liu, Y.-K. Kim, L. Dai, N. Li, S. O. Khan, D. H. Pashley and F. R. Tay, Hierarchical and non-hierarchical mineralisation of collagen, Biomaterials, 2011, 32(5), 1291–1300.
7. H. S. Gupta, J. Seto, W. Wagermaier, P. Zaslansky, P. Boesecke and P. Fratzl, Cooperative deformation of mineral and collagen in bone at the nanoscale, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(47), 17741–17746.
8. P. Fratzl, H. Gupta, E. Paschalis and P. Roschger, Structure and mechanical quality of the collagen–mineral nano-composite in bone, J. Mater. Chem., 2004, 14(14), 2115–2123.
9. X. Su, K. Sun, F. Cui and W. Landis, Organization of apatite crystals in human woven bone, Bone, 2003, 32(2), 150–162.
10. F. H. Silver and W. J. Landis, Deposition of apatite in mineralizing vertebrate extracellular matrices: A model of possible nucleation sites on type I collagen, Connect. Tissue Res., 2011, 52(3), 242–254.
11. H. P. Schwarcz, E. A. McNally and G. A. Botton, Dark-field transmission electron microscopy of cortical bone reveals details of extrafibrillar crystals, J. Struct. Biol., 2014, 188(3), 240–248.
12. A. Karunaratne, C. R. Esapa, J. Hiller, A. Boyde, R. Head, J. D. Bassett, N. J. Terrill, G. R. Williams, M. A. Brown and P. I. Croucher, Significant deterioration in nanomechanical quality occurs through incomplete extrafibrillar mineralization in rachitic bone: Evidence from in–situ synchrotron X–ray scattering and backscattered electron imaging, J. Bone Miner. Res., 2012, 27(4), 876–890.
13. E. A. McNally, H. P. Schwarcz, G. A. Botton and A. L. Arsenault, A model for the ultrastructure of bone based on electron microscopy of ion-milled sections, PLoS One, 2012, 7(1), e29258.
14. F. Hang and A. H. Barber, Nano-mechanical properties of individual mineralized collagen fibrils from bone tissue, J. R. Soc., Interface, 2011, 8(57), 500–505.
15. S. Nikolov and D. Raabe, Hierarchical modeling of the elastic properties of bone at submicron scales: the role of extrafibrillar mineralization, Biophys. J., 2008, 94(11), 4220–4232.
16. H. Alijani and T. J. Vaughan, A multiscale finite element investigation on the role of intra-and extra-fibrillar mineralisation on the elastic properties of bone tissue, J. Mech. Behav. Biomed. Mater., 2022, 129, 105139.
17. M. Maghsoudi-Ganjeh, X. Wang and X. Zeng, Computational investigation of the effect of water on the nanomechanical behavior of bone, J. Mech. Behav. Biomed. Mater., 2020, 101, 103454.
18. L. Lin, J. Samuel, X. Zeng and X. Wang, Contribution of extrafibrillar matrix to the mechanical behavior of bone using a novel cohesive finite element model, J. Mech. Behav. Biomed. Mater., 2017, 65, 224–235.
19. A. G. Reisinger, D. H. Pahr and P. K. Zysset, Sensitivity analysis and parametric study of elastic properties of an unidirectional mineralized bone fibril-array using mean field methods, Biomech. Model. Mechanobiol., 2010, 9(5), 499–510.
20. J. Liu, D. Das, F. Yang, A. G. Schwartz, G. M. Genin, S. Thomopoulos and I. Chasiotis, Energy dissipation in mammalian collagen fibrils: Cyclic strain-induced damping, toughening, and strengthening, Acta Biomater., 2018, 80, 217–227.
21. B. Depalle, Z. Qin, S. J. Shefelbine and M. J. Buehler, Influence of cross-link structure, density and mechanical properties in the mesoscale deformation mechanisms of collagen fibrils, J. Mech. Behav. Biomed. Mater., 2015, 52, 1–13,  DOI:10.1016/j.jmbbm.2014.07.008.
22. B. Depalle, Z. Qin, S. J. Shefelbine and M. J. Buehler, Large deformation mechanisms, plasticity, and failure of an individual collagen fibril with different mineral content, J. Bone Miner. Res., 2016, 31(2), 380–390.
23. M. Tavakol and T. J. Vaughan, A coarse-grained molecular dynamics investigation of the role of mineral arrangement on the mechanical properties of mineralized collagen fibrils, J. R. Soc., Interface, 2023, 20(198), 20220803.
24. M. J. Buehler, Atomistic and continuum modeling of mechanical properties of collagen: elasticity, fracture, and self-assembly, J. Mater. Res., 2006, 21(8), 1947–1961.
25. M. J. Buehler, Molecular nanomechanics of nascent bone: fibrillar toughening by mineralization, Nanotechnology, 2007, 18(29), 295102.
26. A. K. Nair, A. Gautieri and M. J. Buehler, Role of intrafibrillar collagen mineralization in defining the compressive properties of nascent bone, Biomacromolecules, 2014, 15(7), 2494–2500.
27. A. K. Nair, A. Gautieri, S.-W. Chang and M. J. Buehler, Molecular mechanics of mineralized collagen fibrils in bone, Nat. Commun., 2013, 4(1), 1–9.
28. Y. Wang and A. Ural, Mineralized collagen fibril network spatial arrangement influences cortical bone fracture behavior, J. Biomech., 2018, 66, 70–77.
29. E. Beniash, Biominerals—hierarchical nanocomposites: the example of bone, NanoBiotechnology, 2011, 3(1), 47–69.
30. D. T. Reilly and A. H. Burstein, The elastic and ultimate properties of compact bone tissue, J. Biomech., 1975, 8(6), 393–405.
31. S. Ebrahimi, A. Montazeri and H. Rafii-Tabar, Molecular dynamics study of the interfacial mechanical properties of the graphene–collagen biological nanocomposite, Comput. Mater. Sci., 2013, 69, 29–39.
32. E. Macías-Sánchez, N. V. Tarakina, D. Ivanov, S. Blouin, A. M. Berzlanovich and P. Fratzl, Spherulitic Crystal Growth Drives Mineral Deposition Patterns in Collagen-Based Materials, Adv. Funct. Mater., 2022, 2200504.
33. J. Almer and S. R. Stock, Micromechanical response of mineral and collagen phases in bone, J. Struct. Biol., 2007, 157(2), 365–370.
34. S. K. Burley, C. Bhikadiya, C. Bi, S. Bittrich, L. Chen, G. V. Crichlow, C. H. Christie, K. Dalenberg, L. Di Costanzo and J. M. Duarte, et al., RCSB Protein Data Bank: powerful new tools for exploring 3D structures of biological macromolecules for basic and applied research and education in fundamental biology, biomedicine, biotechnology, bioengineering and energy sciences, Nucleic Acids Res., 2020, 49(D1), D437–D451,  DOI:10.1093/nar/gkaa1038%J , Nucleic Acids Research (acccessed 11/16/2021).
35. J. P. Orgel, T. C. Irving, A. Miller and T. J. Wess, Microfibrillar structure of type I collagen in situ, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(24), 9001–9005,  DOI:10.1073/pnas.0502718103%J.
36. M. Tavakol, A git repository for building coarse grained models of collagen. 2022. https://github.com/MahdiTavakol/CollagenCGBuilder (accessed).
37. M. Tavakol, A git repository for writing LAMMPS data files of coarse grained collagens. 2021. https://github.com/MahdiTavakol/LammpsDataFile4CGCollagen (accessed).
38. W. Humphrey, A. Dalke and K. Schulten, VMD: visual molecular dynamics, J. Mol. Graphics Modell., 1996, 14(1), 33–38.
39. B. Depalle, Z. Qin, S. J. Shefelbine and M. J. Buehler, Large deformation mechanisms, plasticity, and failure of an individual collagen fibril with different mineral content, J. Bone Miner. Res., 2016, 31(2), 380–390.
40. P. Zioupos, Recent developments in the study of failure of solid biomaterials and bone: fracture and pre-fracture toughness, Mater. Sci. Eng., C, 1998, 6(1), 33–40.
41. J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. De Groot, H. Grubmüller and A. D. MacKerell, CHARMM36m: an improved force field for folded and intrinsically disordered proteins, Nat. Methods, 2017, 14(1), 71–73.
42. M. Tavakol and T. J. Vaughan, Energy dissipation of osteopontin at a HAp mineral interface: Implications for bone biomechanics, Biophys. J., 2022, 121(2), 228–236.
43. M. Tavakol, M. Mahnama and R. Naghdabadi, Shock wave sintering of Al/SiC metal matrix nano-composites: A molecular dynamics study, Comput. Mater. Sci., 2016, 125, 255–262.
44. W. Shinoda, M. Shiga and M. Mikami, Rapid estimation of elastic constants by molecular dynamics simulation under constant stress, Physical Review B: Solid State, 2004, 69(13), 134103.
45. A. P. Thompson, S. J. Plimpton and W. Mattson, General formulation of pressure and stress tensor for arbitrary many-body interaction potentials under periodic boundary conditions, J. Chem. Phys., 2009, 131(15), 154107,  DOI:10.1063/1.3245303.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr04660e

‡ Equilibrating the intrafibrillar mineralised collagens and then adding the extrafibrillar minerals would imply the start of mineralisation from the intrafibrillar space.

---