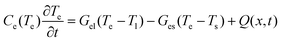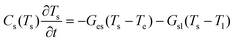Ultrafast switching to zero field topological spin textures in ferrimagnetic TbFeCo films

Abstract

The capability of femtosecond (fs) laser pulses to manipulate topological spin textures on a very short time scale is sparking considerable interest. This article presents the creation of high density zero field topological spin textures by fs laser excitation in ferrimagnetic TbFeCo amorphous films. The topological spin textures are demonstrated to emerge under fs laser pulse excitation through a unique ultrafast nucleation mechanism, rather than thermal effects. Notably, large intrinsic uniaxial anisotropy could substitute the external magnetic field for the creation and stabilization of topological spin textures, which is further verified by the corresponding micromagnetic simulation. The ultrafast switching between topological trivial and nontrivial magnetic states is realized at an optimum magnitude of magnetic field and laser fluence. Our results would broaden the options to generate zero-field topological spin textures from versatile magnetic states and provides a new perspective for ultrafast switching of 0/1 magnetic states in spintronic devices.

---

Introduction

Magnetic chiral skyrmions with spherical spin configuration topology and nanoscale dimensions are usually stabilized by the Dzyaloshinskii–Moriya interaction (DMI),^1–6 which is introduced from asymmetric interfaces^4–6 or non-centrosymmetric magnets.^1–3 In centrosymmetric thin film magnets, similar topological spin structures can be stabilized by the long-range dipolar energy term.^7–10 Assuming an axisymmetric soliton solution θ(r) in a centrosymmetric thin film magnet with the boundary conditions θ(0) = π, θ(∞) = 0,^11,12 we can calculate the contributions to the total energy associated with θ(r) and denote them as ε_e (exchange), ε_d (long-range dipolar), ε_A (anisotropy) and ε_z (Zeeman).¹³ Then we consider a family of functions θ(r) = θ(r/η)¹² obeying the same boundary conditions and a unique soliton solution characterized by η = 1.^14,15 The soliton energy F can be expressed as a function of η (details are provided in ESI Note S1†):

F(η) = ε_e − ε_dη + (ε_A + ε_Z)η² (1)

Therefore, a unique soliton solution characterized by η = ε_d/2(ε_A + ε_Z) = 1 can be stabilized in the low saturation magnetization (M_s) but high perpendicular uniaxial anisotropy (K_u) region even without the Zeeman term.^13,16,17 In order to promote the skyrmion generation in thin film magnets, the quality factor Q = K_u/2πM_s² near 1 is usually required for the canted magnetization ground state.^4–10 In chiral magnetic thin films, the stabilization of zero field skyrmions can coexist with the Q near 1 condition due to the presence of DMI.^6,18–21 However, in centrosymmetric ferromagnetic thin-films, the stabilization of zero field skyrmions requires low-M_s and high-K_u conditions, which contradicts the simultaneous coexistence of the Q near 1 condition. In contrast, the parameters of K_u and M_s in ferrimagnets generally show little correlation and can be independently tuned to achieve the combination of low-M_s and high-K_u by altering the composition of rare earth (RE) -transition metal (TM) alloys,^22,23 which could sustain zero-field skyrmions in centrosymmetric magnetic films.^24,25

Although in low-M_s and high-K_u centrosymmetric ferrimagnetic film magnets there is no stripe domain ground state or DMI required for the regular generation of skyrmions, ultrafast lasers have opened an alternative way. The capabilities of fs laser pulses to create an ultrafast magnetic nonequilibrium state on a very short time scale and to condense the short-range interaction spins into skyrmions via localized spin dynamics have been demonstrated.^26–28 However, an external magnetic field is required for fs laser manipulation of the magnetic states of materials and the stabilization of laser-induced skyrmions.^26,28 Here, we propose that in ferrimagnetic TbFeCo films, intrinsic perpendicular uniaxial anisotropy with high enough magnitude can substitute the external magnetic field to condense the fs laser induced short-range correlation state into topological spin textures and stabilize it under zero field. Moreover, skyrmions in ferrimagnetic films are attracting ever-increasing attention because the deflection motion as a result of the skyrmion Hall effects can be avoided.^29–31 Actually, a previous study has attempted to generate skyrmions by using a fs laser in TbFeCo thin films, but only the magnetization of a local micrometer laser spot region is reversed and considered as an isolated skyrmion.¹³

In this work, multiple topological spin textures are generated from the saturated ground state under zero field by using an ultrafast laser pulse in amorphous ferrimagnetic TbFeCo films, as observed directly via in situ Lorentz transmission electron microscopy (L-TEM). Large intrinsic uniaxial anisotropy could substitute the external field to create and stabilize those topological spin textures, which is further verified by the corresponding micromagnetic simulation. Moreover, it is demonstrated that the condensation nucleation from the fs-laser-induced short-range ordered phase on the picosecond (ps) timescale rather than the thermally activated domain wall motion nucleation is responsible for the generation of topological spin textures. The ultrafast switching between topological trivial and nontrivial magnetic states by changing the value of the magnetic field or laser fluence provides a solid experimental basis for spintronic applications.

Results and discussion

Direct observation of ultrafast topological spin textures generation by fs laser pulses under zero field

Pt (3 nm)/Tb₁₅(Fe₇₅Co₂₅)₈₅(20 nm)/Pt (3 nm) trilayer films were grown on 10 nm-thick Si₃N₄ membrane windows by magnetron sputtering for direct L-TEM observation and simultaneously on Si wafers for magnetic property measurements. The TbFeCo layer structure with a ferrimagnetic arrangement of TM and RE magnetic moments under the irradiation of an electron beam and linear polarization laser is schematically shown in Fig. 1a. It should be noted that the residual magnetic field is approximately 200 Oe in traditional TEM, even after the objective lens is switched off.³² Here, we could successfully obtain an adjustable magnetic field in the range of 0–200 Oe by reversing the current of the objective lens via an external current source meter as shown in Fig. 1b. The residual magnetic domain at zero field could be demonstrated as homogenous saturated ferromagnetic (FM) state without any domain contrast (Fig. 1c), corresponding well with a typical ferromagnetic square hysteresis loop at room temperature in Tb₁₅(Fe₇₅Co₂₅)₈₅.

Fig. 1 Fs laser-induced topological spin textures from the saturated FM ground state under zero field in a Tb₁₅(Fe₇₅Co₂₅)₈₅ film. (a) Schematic illustration of the experimental setup and the layer configuration. (b) Schematic of L-TEM with external fs laser irradiation and a current source meter. (c) Hysteresis loop of the amorphous ferrimagnetic Tb₁₅(Fe₇₅Co₂₅)₈₅ film at room temperature, where the red star indicates the experimental TEM observation point under zero field. (d and e) L-TEM images of magnetic domains at a tilting angle about 20° along the x-axis induced by a fs laser. The scale bar in (d) and (e) is 2 μm.

Repeated experiments demonstrate that versatile domains can be generated from a homogeneous saturated FM state under zero field via 300 fs single laser pulse excitation only when the laser fluence exceeds a critical value. An elliptic region with high density topological spin textures in the middle and low density common magnetic bubbles at the edge is generated (Fig. 1d) at a laser pulse fluence of 12 mJ cm⁻². The distribution of saturated FM, low density bubbles, high density topological spin textures, and reticulation domains along the radius (Fig. 1e) is observed under a higher fluence laser pulse magnitude of 13.5 mJ cm⁻². The sample is tilted by approximately 20° along the x-axis to better characterize the magnetic contrast and laser irradiation for the generation of topological spin textures. Further domain characterization without tilting the sample demonstrates the random dark and bright dot contrast (ESI Fig. S1†), indicating versatile topological spin textures with random chirality, as expected in this nonchiral magnets.⁸ It is clear that the emergence of topological spin textures via fs laser pulse excitation is a totally field-free behavior; however, topological spin textures are not the only domain structures generated by fs laser pulses under zero field. To eliminate other domain structures and obtain a homogeneous topological spin texture, a magnetic field is applied during fs laser excitation.

It is demonstrated that the higher perpendicular magnetic field at the same single laser fluence of 13.5 mJ cm⁻² produces a larger region for topological spin textures and smaller regions for both magnetic bubbles and the reticulation domain (Fig. 2a–c). The optimum magnetic field to generate the complete homogeneous topological spin texture from a saturated FM state is a field of 200 Oe (Fig. 2c). It should be noted that the magnetic field is applied only to assist the homogeneous nucleation of topological spin textures during the laser excitation period and all L-TEM images in Fig. 2 are obtained under zero field; the corresponding mechanism is further discussed.

Fig. 2 The magnetic structure evolution via increased magnetic field and versatile magnetic structures induced by fs laser pulses. (a–c) L-TEM domain images at a tilting angle of 20° induced by fs laser pulses under the perpendicular magnetic field with value of (a) 0 Oe, (b) 130 Oe and (c) 200 Oe. Obviously, the magnetic bubbles and the reticulation domain region get smaller until they disappear, and the topological spin texture region grows larger and pure topological spin textures are obtained under 200 Oe after fs laser pulse excitation. (d) Magnified L-TEM image extracted from the region indicated by the yellow dashed box in (c). (e) The magnified L-TEM images of the topological structure marked in (d) without tilting of the sample, 1, 2 are Bloch-type skyrmions with opposite chirality. 3, 4 are Skyrmion bubbles with reversed helicity. Their in-plane magnetic component distributions (determined by TIE), L-TEM simulation images, and schematics of arrangement of magnetic moments are sequentially arranged after the L-TEM images. (f) Top, line profiles along the direction of the yellow dashed line, showing their contrast differences. The direction of the asymmetry (bright-dark or dark-bright) is indicative of the skyrmion's polarity. Bottom, identification of Néel-type skyrmions performed by tilting the sample at −20°, 0°, and 20°, showing the disappearance of the contrast at zero tilt and the reversal of contrast that occurs for opposite tilt angles. The scale bar in (a–c) is 5 μm and that in (d) is 500 nm.

The extracted and magnified regions indicated by the yellow dashed box in Fig. 2c are classified into different types of topological spin textures in Fig. 2d. The corresponding in-plane magnetization distribution reconstructed from the transport-of-intensity (TIE) equation analysis clearly depicts the individual spin configurations of the magnified textures without tilting of the sample and they are consistent with the simulated L-TEM images (Fig. 2e). The domain structures with opposite chirality in numbers 1 and 2 of Fig. 2e are identified as Bloch-type skyrmions. Skyrmion bubbles with reversed helicity are also observed as shown in numbers 3 and 4 of Fig. 2e.⁷ The alternated half-bright and half-dark magnetic contrast after tilting toward opposite angles verifies the presence of Néel-type skyrmions with a corresponding intensity distribution across the skyrmion (Fig. 2f).³² Despite their different configurations and random chirality, these magnetic structures share the same topological charge of 1.

The generation mechanism for different magnetic domain structures

The uniaxial anisotropy in RE-TM alloys originates from the anisotropy of the nearest neighbor ions around rare earth atoms, which is called single-ion anisotropy.^33,34 Therefore, stabilized uniaxial anisotropy is established after the thermal equilibrium between the electronic and lattice subsystem within 10 ps after ultrafast laser excitation.³⁵ M-H measurement of the ferrimagnetic TbFeCo amorphous film reveals a near consistent saturation magnetization M_s from 300 to 600 K in contrast to the significant decreases of perpendicular uniaxial anisotropy as shown in Fig. 3b. Correspondingly, the increase of the lattice temperature due to the thermal equilibrium between electronic and lattice subsystems after laser excitation would lead to the decrease of K_u. Thus, the gradual decrease of K_u from the edge to the center of the laser spot after the thermal equilibrium is expected according to the Gaussian distribution of the laser pulse intensity (Fig. 3b, inset. Detailed information can be found in ESI Fig. S2†).

Fig. 3 Temperature dependent uniaxial anisotropy and energy simulation of uniaxial anisotropy correlation. (a) Top, magnified L-TEM image of yellow dashed box in Fig. 1e, indicates four different domain structures along the arrow direction. Bottom, corresponding magnetic structures in micromagnetic simulation. (b) Magnetic parameters measured at different temperatures. No significant change in the saturation magnetization, and uniaxial anisotropy decreases with an increase of temperature. Inset: Gaussian intensity distribution of fs laser pulses. (c) Energy of the four different states as a function of the uniaxial anisotropy under zero field and at the magnetic field with the direction perpendicular to the film: skyrmion bubbles (dotted green line), common magnetic bubbles (dotted red line), reticulation domain (dotted blue line) and FM state (dotted black line). The colored areas mark the different ground state areas, B stands for common magnetic bubbles, Skb stands for skyrmion bubbles and Ret stands for reticulation domain. With the increase of the magnetic field, the bubble domain transforms to the FM state and the reticulation domain transforms to skyrmion bubbles.

The micromagnetic simulation of the minimum energy domain states at different K_u suitably explains the different domains induced by the decreased K_u from the edge to center due to the Gaussian intensity distribution of the laser spot (Fig. 3a). The saturated FM state prefers to be the lowest energy state when K_u is large, which explains that fs laser must exceed a critical value to reduce K_u to stabilize versatile domains as lower energy states (Fig. 3c). Under zero field, after a single laser pulse excitation, the saturated FM state is the lowest energy state at the edge of the laser spot, and as K_u gets smaller along the radius of the laser spot, the thermally activated domain wall motion enables the generation of low-density magnetic bubbles as the lowest energy state.³⁶ And then the uniform spin subsystem enters the fluctuation-disordered state with a short-range correlation, where the uniaxial anisotropy helps to align, order, and condense short-range ordered spins into high-density skyrmion bubbles and serve as the lowest energy state. As K_u continues to decrease along the radius, intrinsic uniaxial anisotropy is not sufficient to support the nucleation of skyrmion bubbles and the disorganized, continuous reticulation domains generated at zero field is the lowest energy state (Fig. 3c).²⁸ The versatile domains generated by fs laser pulses is preserved after cooling to room temperature because of the increased energy barrier during cooling. We also find that the inhomogeneity of the material or enhanced laser intensity can lead to the enlarged skyrmion region through manipulating the K_u value under zero field (ESI Fig. S3†).

Furthermore, the contribution of a higher perpendicular magnetic field during fs laser excitation is emphasized by micromagnetic simulations with the increased skyrmion bubble region and decreased domain regions for the magnetic bubbles and reticulation domain (Fig. 3c) due to the relative energy change between the different magnetic states, which suitably explains the experimental results (Fig. 2a–c). It should be noted that the generation and stabilization of topological spin textures essentially does not require any magnetic field, and the magnetic field is only applied during the laser excitation period to increase the proportion of the topological spin textures.

Here, we propose the creation of topological spin textures based on the highly localized spin dynamics in the fs laser induced short-range correlation state. In RE-TM alloys, a fs laser within tens of fs couples to the valence electronic system and leads to a transient temperature increase of valence electrons, and the crystal lattice is immediately excited by the scattering of the hot valence electrons with phonons.³⁷ The 3d4s spins from transition metals can be easily excited directly by coupling to the hot valence electrons, while the localized 4f electrons of the rare-earth metals are mainly excited by hot phonons via spin–lattice coupling ∼ξL·S.^37,38 The lattice system dissipates the angular momentum of the electrons and leads to a short-range correlation in the spin system.^38–40 For Gd with zero orbital momentum L in the GdFeCo alloy, the weak lattice coupling to the 4f spin leads to a much slower disorder time of Gd 4f spin (14 ps)³⁷ in comparison with that of FeCo 3d4s spin (0.2–0.4 ps)^41,42 and prevents the formation of uniform topological skyrmions.²⁷ But for Tb (L = 3) in the TbFeCo alloy, the strong lattice coupling to the 4f spin drives the disorder time of Tb 4f spin (0.4 ps)³⁷ comparable to that of the FeCo 3d4s spin (0.2–0.4 ps),^41,42 which enables the synchronous ultrafast dynamics of Tb 4f and FeCo 3d4s spins after optical excitation and provides a platform for ultrafast nucleation of the ferrimagnetic topological texture. The formation of a synchronous short-range correlation state in the spin system after laser excitation²⁷ is consistent with the short-range fluctuation-disordered state that occurs above the long-range magnetic order but below the completely disordered paramagnetic phase in magnetic materials,^28,43–45 which allows highly localized spin dynamics to generate topological spin textures. A magnetic field is required to condense skyrmions with preferred polarities.²⁸ Here, we emphasize that the stabilized uniaxial anisotropy with high enough magnitude established within 10 ps after laser excitation can substitute the applied field to condense the short range ordered spins into topological spin textures with preferred polarities.

Verification of ultrafast nucleation mechanism of topological spin textures

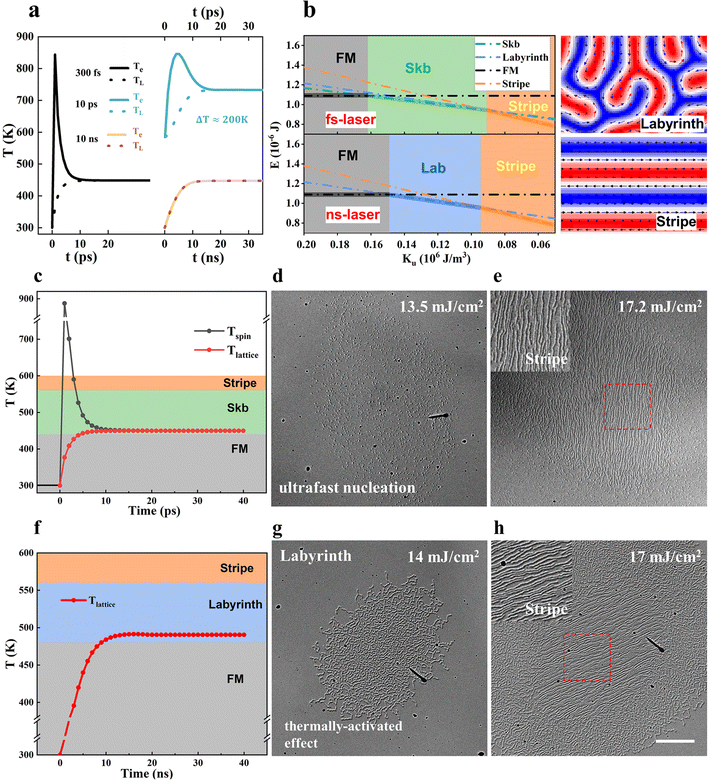
The temperature for the electronic and lattice subsystems follows a different dynamic evolution on a different timescale after fs laser pulse excitation. We introduce a three-temperature model (3TM) to describe the dynamic evolution of the electronic and lattice temperature as a function of time (see the Experimental section).⁴⁶ Interplay between the fs laser pulse and electrons leads to a transient temperature increase of electrons and is responsible for the ultrafast spin behavior on the ps timescale. The thermally activated effect occurs on a nanosecond (ns) timescale after the electronic and lattice subsystems have established a thermal equilibrium.⁴⁷ Typically, the longer the laser pulses are, the lower the electronic temperature will be, resulting in smaller differences between the lattice temperature and electronic temperature at the early stage of the dynamics, as depicted in Fig. 4a. No ultrafast spin behavior but only thermal activated effect is introduced beyond 10 ns duration of the pulse owing to a consistent temperature between the electronic and lattice subsystems.

Fig. 4 Magnetization structure evolution in amorphous ferrimagnetic TbFeCo films via fs and ns laser manipulation. (a) Three temperature model calculations for three pulse durations, 300 fs,10 ps, and 10 ns at the films (solid and dashed lines for electronic and lattice temperatures, respectively. The spin temperature is not displayed), the laser fluence used for the simulation is 13 mJ cm⁻². (b) Left: Energy of the four different states as a function of the uniaxial anisotropy: skyrmion bubbles (dotted green line), stripe domain (dotted orange line), labyrinth domain (dotted blue line) and FM state (dotted black line). The colored areas mark the different ground state areas. Lab stands for labyrinth domain and Skb stands for skyrmion bubbles, respectively. Right: Labyrinth and stripe domains in micromagnetic simulation. (c) Simulated behavior of the fs laser pulse action, with equilibrium temperature stabilized in the skyrmion state, the laser fluence used for the simulation is 13 mJ cm⁻². (d and e) L-TEM images of the skyrmions and the stripe domains induced by a single 300 fs laser pulse. (f) Simulated behavior of the ns laser pulse action, where the final temperature is stabilized in the labyrinth domain. The solid dots represent the simulation points, the laser fluence used for the simulation is 14 mJ cm⁻². (g and h) L-TEM images of the labyrinth and stripe domains induced by a single 10 ns laser pulse. The scale bar in (d and e), (g and h) is 5 μm.

When the single fs laser pulse with the fluence of 13.5 mJ cm⁻² is applied on the Tb₁₅(Fe₇₅Co₂₅)₈₅ sample, the uniform spin subsystem enters the fluctuation-disordered state in the initial few ps, where the short-range spin correlation generates and contributes to subsequent topological spin texture condensation. Labyrinth domain formation cannot be generated upon fs laser exaction due to its higher energy than the skyrmion bubble state (Fig. 4b). When the thermal equilibrium temperature is reached after the single fs laser pulse with the fluence of 17.2 mJ cm⁻², K_u gets small enough in the center of the spot, and the stripe domain is generated via the thermally activated domain wall motion (Fig. 4e) and preserved due to the lower energy than that of the skyrmion bubbles (Fig. 4b). The criterion for the formation of the labyrinth and stripe domains can be found in ESI Fig. S5.†

As for the ferromagnetic thin films with DMI, DMI promotes the formation and stabilization of skyrmions. Under the assistance of a magnetic field, skyrmions can be obtained via the thermally activated motion of the domain walls on a ns timescale after laser excittion.^48–50 The Pt/Co/Ta multilayer with interfacial DMI is prepared to demonstrate the thermally activated nucleation mechanism of skyrmions. For the Pt/Co/Ta multilayer with a saturated FM state at a perpendicular magnetic field of 600 Oe, the dominant contribution of the thermally activated effects is emphasized. The laser-accessible skyrmions via the thermally activated domain wall motion can be obtained by both 300 fs and 10 ns lasers when a single linear polarization fs or ns laser pulse is applied to a Pt/Co/Ta multilayer sample, as long as the lattice temperature is above the critical value T_sky (ESI Fig. S4†).

But in the centrosymmetric TbFeCo film without DMI, the labyrinth domain is generated via the thermally activated domain wall motion upon ns laser excitation, where the ns laser fluence of about 14 mJ cm⁻² decreases K_u to the region suitable for the labyrinth domain state (Fig. 4g). No topological magnetic state forms even if its energy is lower than that of the labyrinth domain state, because the ns laser does not have the ability to separate the electronic and lattice subsystems and excite short-range interaction spins, which is confirmed to be necessary for the ultrafast topological spin texture nucleation. Then, the laser fluence is increased further to approximately 17 mJ cm⁻² with K_u decreased suitably for stripe domain generation via the thermally activated domain wall motion in the central area of the laser spot (Fig. 4h). No topological magnetic state is obtained under different ns laser excitation fluences, thus signifying the different mechanisms of the unique fs laser process. The in situ pure temperature-dependent domain evolution demonstrates a labyrinth domain formation at 500 K, and as the temperature increases the labyrinth domain becomes denser. Typical spin reorientation occurs near 580 K and a complete in-plane domain structure is formed above 600 K. No topological magnetic structure appears during the whole warming process (ESI Fig. S5†). Both ns laser excitation and pure thermal excitation do not result in an observable topological magnetic state, and together with micromagnetic simulation imply that the mechanism for creating topological spin textures in TbFeCo film is a fast process.

Ultrafast switching behavior induced by fs laser pulses

Skyrmions are generated at random positions under fs laser excitation in TbFeCo amorphous films. We have measured the evolution of skyrmion positions perturbed by fs laser pulses. Fig. 5a–d shows the sequence of images after every single laser pulse at a laser fluence of 14 mJ cm⁻². The high probability of reproducing the skyrmions with fixed chirality at the same position after each laser pulse (red and green circles in Fig. 5a–d) is probably caused by the strong pinning sites although the shapes are slightly different. Skyrmions are periodically created and annihilated (yellow circles) or their chirality is altered (blue circles) after each laser pulse, which is also observed at some pinning sites. The pinning strength can be adjusted by ion irradiation^51,52 or geometric restrictions,⁶ and the tunability of the pinning strength means the tunability of optical writing and deleting of skyrmions, which anticipates a pathway for information recording.

Fig. 5 Topological spin texture distribution after each single laser pulse and the ultrafast switching between topological trivial and nontrivial magnetic states. (a–d) LTEM images taken after successive single laser pulses with the same fluence of 14 mJ cm⁻² under 200 Oe field demonstrating the skyrmions with unchanged chirality and position after several pulses (marked with red and green circles) and periodically created and annihilated skyrmions (marked with yellow circles) and sometimes chirality of skyrmion can be altered by one laser pulse (blue circles). (e–h) LTEM images taken after every single laser pulse with the same fluence of 14 mJ cm⁻² but alternated magnetic field between 200 Oe and 400 Oe, corresponding to the generation of skyrmions and saturated FM, respectively. (i–l) LTEM images taken after every single laser pulse with alternated fluence between 14 mJ cm⁻² and 17 mJ cm⁻² under 200 Oe field, corresponding to the generation of skyrmions and stripe domains, respectively. The laser pulse has the same pulse width of 300 fs. The scale bar of 500 nm in (a–d) and 2 μm in (e–h), (i–l).

The energy of saturated FM state decreases with the increase of the perpendicular magnetic field; under a single laser pulse fluence of 14 mJ cm⁻² and a field of 400 Oe field, the energy of the saturated FM state is lower than the topological magnetic state in the entire laser spot area. Therefore, the saturated FM state is generated under a single laser pulse fluence of 14 mJ cm⁻² and a field of 400 Oe in contrast to the topological magnetic state generated under the same fluence laser pulse but a field of 200 Oe. Based on this, the switching between the saturated FM state and the topological magnetic state is realized in Fig. 5e–h. The stripe domain is generated under the higher laser fluence of 17 mJ cm⁻² and a field of 200 Oe due to the thermally activated motion of the domain walls, and it should be noted that the initial state will not affect the final state generated by laser excitation; therefore, we can realize the pure optical switching between the stripe domain and topological magnetic state as displayed in Fig. 5i–l. The magnetic field is applied only during the laser excitation period and none of the above domains requires a magnetic field to be maintained. The saturated FM state and stripe domain state are distinguished from the topological magnetic state as a topologically trivial state, and the two kinds of switching, in fact, realize an ultrafast switching between topologically trivial and nontrivial magnetic states.

Conclusions

In summary, we have successfully generated high density zero field topological spin textures from a saturated FM state by using fs laser pulses in amorphous ferrimagnetic TbFeCo films. The intrinsic uniaxial anisotropy contributes to producing and stabilizing those topological spin textures. The interplay between the fs laser pulses and the spin/electrons stimulates the system to different domain thresholds and results in visible ultrafast evolution into a variety of topological structures on a ps timescale. From an application viewpoint, the fs laser induced ultrafast nucleation of skyrmions undoubtedly represents one of the fastest ways to switch magnetic information between the magnetic states of 0 and 1. Furthermore, the field free room temperature skyrmions and their unique ferrimagnetic feature to overcome the Hall effect in the skyrmions have demonstrated perspectives for low-energy-consumption spintronic applications, which will enable advanced applications in magnetic devices.

Experimental

Sample preparation and characterization

Pt (3 nm)/Tb₁₅ (Fe₇₅Co₂₅)₈₅ (20 nm)/Pt trilayer films were grown on 10 nm-thick Si₃N₄ membrane windows by magnetron sputtering for direct TEM observation and on thermally oxidized Si wafers to perform physical property measurements, where the base vacuum pressure of the system was 1 × 10⁻⁶ Pa and the working pressure of the Ar (5N) gas was 0.5 Pa. The amorphous TbFeCo alloy layers were deposited via a co-sputtering method with Fe₇₅Co₂₅ and Tb targets, with the alloy composition being varied by adjusting the sputtering power for CoFe at a fixed power for Tb. The labeled thicknesses of the Pt and TbFeCo layers were calibrated via X-ray reflectivity measurements. The magnetic hysteresis (M-H) loops of the Si-based samples were measured at various temperatures using a vibrational sample magnetometer (VSM).

L-TEM observation and laser excitation

The magnetic domain structures were studied using a JEOL Lorentz TEM (JEOL2100F). The magnetic domain wall contrast was imaged using a convergent or divergent electron beam because of the interactions of the electron beam with the in-plane magnetization. The under- and over-focal images were recorded using a CCD camera to extract the phase images and the quantitative in-plane magnetization component was then extracted on the basis of the TIE equation using QPt commercial software.⁵³ The colors and the arrows depict the magnitudes and orientations of the in-plane magnetization according to the color wheel. Linearly polarized fs laser pulses at a wavelength of 515 nm and with a pulse duration of 300 fs were generated using a Spirit solid-state laser, and the ns laser pulses at a wavelength of 532 nm and with a pulse duration of 10 ns were generated using an EXPL-532-2W-E solid-state laser with software-controlled power and single pulse emission.

TIE analysis

The TIE equation is composed of the following two equations:⁵³

The first equation represents the relationship between the intensity I(x,y,z) and the phase ϕ(x,y,z). λ is the spectrally weighted mean wavelength of the illumination. In our experiment, we processed the under-focused and over-focused images using QPt software to determine the value of ∂I(x,y,z)/∂Z and obtain the phase information. Then, the in-plane magnetization components 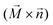could be found using the second equation. is the unit vector acting along the beam direction, is the magnetization vector, and t is the local sample thickness. The L-TEM image simulation was carried out using the software called micromagnetic analysis to Lorentz TEM simulation (MALTS).⁵⁴

Micromagnetic simulation

Micromagnetic simulations were carried out using a three-dimensional object-oriented micromagnetic framework (OOMMF) code based on the LLG function.⁵⁵ The size of the thin plate TbFeCo film for simulation is about 312 × 416 × 6 nm³ with periodic boundary conditions in the x-direction and open boundary conditions in the y-direction. The mesh size is 2 × 2 × 2 nm³, which is much smaller than the typical exchange length and the skyrmion size. The material parameters were chosen according to the experimental values of TbFeCo, with a fixed saturation magnetization M_s = 5 × 10⁵ A m⁻¹ and a perpendicular magnetic anisotropy (PMA) constant K_u varying from 0.05 × 10⁶ J m⁻³ to 0.25 × 10⁶ J m⁻³. The value of the exchange constant A we used was 1 × 10⁻¹² J m⁻¹. To simulate the minimum energy state under different uniaxial anisotropy, we set a series of states that corresponded to the experiment. The energy of different states is obtained by plugging in the set parameters, and the minimum energy state remain unchanged after relaxation to the equilibrium state. We then changed the PMA, and the minimum energy states were different for different K_u. The evolution of the magnetic field from the domains was achieved by increasing the field upon the previously converged magnetization structure.

Fs and ns laser simulation

To perform a theoretical analysis of the dynamic evolution of the magnetic structure induced by fs laser pulses that we observed in our experiments, we used the three-temperature model (3TM) for sub-100 ps dynamics as described by Beaurepaire,⁴⁶ and calculated the laser-induced electron system temperature T_e, the spin system temperature T_s, and the lattice system temperature T_l using COMSOL Multiphysics™ software. In addition, the longitudinal temperature gradients (normal to the surface) and the exponential decay of the source within the material were taken into account to provide a more accurate simulation. The 3TM equations read as follows:



where C_l, C_e, and C_s are the specific heats for the lattice, electron, and spin subsystems, respectively, and the electronic specific heat C_e = γT_e, which is approximated linearly using the electron temperature T_e. In this simulation, we assumed that C_e = 0.6^a). G_el, G_es, and G_sl are the interaction constants for the electron–lattice, electron–spin, and spin–lattice interactions, respectively. x represents the direction normal to the surface, Q(x,t) is the laser source term that includes an exponential decay in space to consider the absorption in a nontransparent medium and was calculated based on our pump laser characteristics with set parameters for the reflectivity R = 0.3, the penetration depth d = 50 nm, and the pulse duration δt = 300 fs. F is the fs laser fluence. The thermal constants and the interaction constants were estimated from ref. 56–58. The realistic optical and thermal parameters for the simulations were set as follows: C_s = 1.0^(a), C_l = 8.8^(a), G_el = 0.8^(b), G_es = 1.8^(b), and G_sl = 0.08^(b), where ^(a) represents 10⁶ J m⁻³ K⁻¹ and ^(b) represents 10¹⁸ W m⁻³ K⁻¹. The ns laser excitation was simulated using the one-dimensional thermal diffusion model 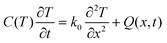. As per the analysis of the fs laser excitation, the system temperature is the result of the integration of the penetration depth; the system's specific heat C = 8.8^(a) here, and k₀ = 76.2, which is the thermal conductivity of the system. Q(x,t) is the same laser source term that was used for the fs laser excitation.

Author contributions

J. Q. L. designed and supervised the project. K. X. Z., L. Z. B., and J. W. C. fabricated the TbFeCo films by magnetron sputtering and performed the transport and magnetization measurements. K. X. Z. and Y. Z. performed the Lorentz TEM observations. K. X. Z. performed the micromagnetic simulation. K. X. Z., Y. Z. Z., and D. G. Z. performed the fs and ns laser experiments. K. X. Z. and H. F. T. performed the in situ temperature experiment. K. X. Z., L. Z. B., Y. Z. Z., Y. Z., and J. Q. L. analyzed the experimental data and plotted the figures. K. X. Z., Y. Z., and J. Q. L. wrote the manuscript after discussing the data with J. L., H. X. Y. and all the authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. U22A6005, 12074408, 52271195 and 52130103), the National Key Research and Development Program of China (Grant No. 2021YFA13011502), the Strategic Priority Research Program (B) of the Chinese Academy of Sciences (Grant No. XDB25000000, XDB33000000, and XDB33030100), the CAS Project for Young Scientists in Basic Research (Grant No. YSBR-084 and YSBR-059), the Scientific Instrument Developing Project of the Chinese Academy of Sciences (Grant No. YJKYYQ20200055, ZDKYYQ2017002, and 22017BA10), the Synergetic Extreme Condition User Facility (SECUF), the Youth Innovation Promotion Association of CAS (Grant No. 2022004), Beijing Municipal Science and Technology major project (Z201100001820006) and IOP Hundred Talents Program (Y9K5051).

References

1. P. Milde, D. Kohler, J. Seidel, L. M. Eng, A. Bauer, A. Chacon, J. Kindervater, S. Muhlbauer, C. Pfleiderer, S. Buhrandt, C. Schutte and A. Rosch, Science, 2013, 340, 1076–1080.
2. X. Z. Yu, Y. Onose, N. Kanazawa, J. H. Park, J. H. Han, Y. Matsui, N. Nagaosa and Y. Tokura, Nature, 2010, 465, 901–904.
3. N. Nagaosa and Y. Tokura, Nat. Nanotechnol., 2013, 8, 899–911.
4. C. Moreau-Luchaire, S. C. Mouta, N. Reyren, J. Sampaio, C. A. Vaz, N. Van Horne, K. Bouzehouane, K. Garcia, C. Deranlot, P. Warnicke, P. Wohlhuter, J. M. George, M. Weigand, J. Raabe, V. Cros and A. Fert, Nat. Nanotechnol., 2016, 11, 444–448.
5. A. Soumyanarayanan, M. Raju, A. L. G. Oyarce, A. K. C. Tan, M. Y. Im, A. P. Petrovic, P. Ho, K. H. Khoo, M. Tran, C. K. Gan, F. Ernult and C. Panagopoulos, Nat. Mater., 2017, 16, 898–904.
6. O. Boulle, J. Vogel, H. Yang, S. Pizzini, D. de Souza Chaves, A. Locatelli, T. O. Mentes, A. Sala, L. D. Buda-Prejbeanu, O. Klein, M. Belmeguenai, Y. Roussigne, A. Stashkevich, S. M. Cherif, L. Aballe, M. Foerster, M. Chshiev, S. Auffret, I. M. Miron and G. Gaudin, Nat. Nanotechnol., 2016, 11, 449–454.
7. X. Z. Yu, M. Mostovoy, Y. Tokunaga, W. Z. Zhang, K. Kimoto, Y. Matsui, Y. Kaneko, N. Nagaosa and Y. Tokura, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 8856–8860.
8. S. A. Montoya, S. Couture, J. J. Chess, J. C. T. Lee, N. Kent, D. Henze, S. K. Sinha, M. Y. Im, S. D. Kevan, P. Fischer, B. J. McMorran, V. Lomakin, S. Roy and E. E. Fullerton, Phys. Rev. B, 2017, 95, 024415.
9. W. Wang, Y. Zhang, G. Xu, L. Peng, B. Ding, Y. Wang, Z. Hou, X. Zhang, X. Li, E. Liu, S. Wang, J. Cai, F. Wang, J. Li, F. Hu, G. Wu, B. Shen and X. X. Zhang, Adv. Mater., 2016, 28, 6887–6893.
10. X. Yu, Y. Tokunaga, Y. Taguchi and Y. Tokura, Adv. Mater., 2017, 29, 1603958.
11. N. S. Kiselev, A. N. Bogdanov, R. Schäfer and U. K. Rößler, J. Phys. D: Appl. Phys., 2011, 44, 392001.
12. A. O. Leonov, T. L. Monchesky, N. Romming, A. Kubetzka, A. N. Bogdanov and R. Wiesendanger, New J. Phys., 2016, 18, 065003.
13. M. Finazzi, M. Savoini, A. R. Khorsand, A. Tsukamoto, A. Itoh, L. Duo, A. Kirilyuk, T. Rasing and M. Ezawa, Phys. Rev. Lett., 2013, 110, 177205.
14. G. H. Derrick, J. Math. Phys., 1964, 5, 1252.
15. R. H. Hobart, Proc. Phys. Soc., 1963, 82, 201.
16. D. Clarke, O. A. Tretiakov and O. Tchernyshyov, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 174433.
17. M. N. Wilson, A. B. Butenko, A. N. Bogdanov and T. L. Monchesky, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 094411.
18. N. K. Duong, M. Raju, A. P. Petrović, R. Tomasello, G. Finocchio and C. Panagopoulos, Appl. Phys. Lett., 2019, 114, 072401.
19. M. Li, A. Rai, A. Pokhrel, A. Sapkota, C. Mewes, T. Mewes, M. D. Graef and V. Sokalski, Appl. Phys. Lett., 2020, 117, 112403.
20. S. Mallick, S. Panigrahy, G. Pradhan and S. Rohart, Phys. Rev. Appl., 2022, 18, 064072.
21. J. C. Gallagher, K. Y. Meng, J. T. Brangham, H. L. Wang, B. D. Esser, D. W. McComb and F. Y. Yang, Phys. Rev. Lett., 2017, 118, 027201.
22. P. Hansen, C. Clausen, G. Much, M. Rosenkranz and K. Witter, J. Appl. Phys., 1989, 66, 756–767.
23. T. A. Ostler, R. F. L. Evans, R. W. Chantrell, U. Atxitia, O. Chubykalo-Fesenko, I. Radu, R. Abrudan, F. Radu, A. Tsukamoto, A. Itoh, A. Kirilyuk, T. Rasing and A. Kimel, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 024407.
24. J. Brandao, D. A. Dugato, M. V. P. dos Santos and J. C. Cezar, ACS Appl. Nano Mater., 2019, 2, 7532–7539.
25. J. Brandao, D. A. Dugato, M. V. P. dos Santos, F. Beron and J. C. Cezar, Appl. Surf. Sci., 2022, 585, 152598.
26. E. V. Boström, A. Rubio and C. Verdozzi, npj Comput. Mater., 2022, 8, 62.
27. E. Iacocca, T. M. Liu, A. H. Reid, Z. Fu, S. Ruta, P. W. Granitzka, E. Jal, S. Bonetti, A. X. Gray, C. E. Graves, R. Kukreja, Z. Chen, D. J. Higley, T. Chase, L. Le Guyader, K. Hirsch, H. Ohldag, W. F. Schlotter, G. L. Dakovski, G. Coslovich, M. C. Hoffmann, S. Carron, A. Tsukamoto, A. Kirilyuk, A. V. Kimel, T. Rasing, J. Stohr, R. F. L. Evans, T. Ostler, R. W. Chantrell, M. A. Hoefer, T. J. Silva and H. A. Durr, Nat. Commun., 2019, 10, 1756.
28. F. Buttner, B. Pfau, M. Bottcher, M. Schneider, G. Mercurio, C. M. Gunther, P. Hessing, C. Klose, A. Wittmann, K. Gerlinger, L. M. Kern, C. Struber, C. von Korff Schmising, J. Fuchs, D. Engel, A. Churikova, S. Huang, D. Suzuki, I. Lemesh, M. Huang, L. Caretta, D. Weder, J. H. Gaida, M. Moller, T. R. Harvey, S. Zayko, K. Bagschik, R. Carley, L. Mercadier, J. Schlappa, A. Yaroslavtsev, L. Le Guyarder, N. Gerasimova, A. Scherz, C. Deiter, R. Gort, D. Hickin, J. Zhu, M. Turcato, D. Lomidze, F. Erdinger, A. Castoldi, S. Maffessanti, M. Porro, A. Samartsev, J. Sinova, C. Ropers, J. H. Mentink, B. Dupe, G. S. D. Beach and S. Eisebitt, Nat. Mater., 2021, 20, 30–37.
29. Y. Hirata, D. H. Kim, S. K. Kim, D. K. Lee, S. H. Oh, D. Y. Kim, T. Nishimura, T. Okuno, Y. Futakawa, H. Yoshikawa, A. Tsukamoto, Y. Tserkovnyak, Y. Shiota, T. Moriyama, S. B. Choe, K. J. Lee and T. Ono, Nat. Nanotechnol., 2019, 14, 232–236.
30. S. K. Kim, G. S. D. Beach, K. J. Lee, T. Ono, T. Rasing and H. Yang, Nat. Mater., 2022, 21, 24–34.
31. S. Woo, K. M. Song, X. Zhang, Y. Zhou, M. Ezawa, X. Liu, S. Finizio, J. Raabe, N. J. Lee, S. I. Kim, S. Y. Park, Y. Kim, J. Y. Kim, D. Lee, O. Lee, J. W. Choi, B. C. Min, H. C. Koo and J. Chang, Nat. Commun., 2018, 9, 959.
32. S. D. Pollard, J. A. Garlow, J. Yu, Z. Wang, Y. Zhu and H. Yang, Nat. Commun., 2017, 8, 14761.
33. R. Sato, N. Saito and Y. Togami, Jpn. J. Appl. Phys., 1985, 24, L266.
34. Y. Suzuki, S. Takayama, F. Kirino and N. Ohta, IEEE Trans. Magn., 1987, 23, 2275–2277.
35. S. K. Sundaram and E. Mazur, Nat. Mater., 2002, 1, 217–224.
36. J. Choi, J. Wu, C. Won, Y. Z. Wu, A. Scholl, A. Doran, T. Owens and Z. Q. Qiu, Phys. Rev. Lett., 2007, 98, 207205.
37. B. Frietsch, A. Donges, R. Carley, M. Teichmann, J. Bowlan, K. Dobrich, K. Carva, D. Legut, P. M. Oppeneer, U. Nowak and M. Weinelt, Sci. Adv., 2020, 6, eabb1601.
38. B. Koopmans, G. Malinowski, F. D. Longa, D. Steiauf, M. Fahnle, T. Roth, M. Cinchetti and M. Aeschlimann, Nat. Mater., 2010, 9, 259–265.
39. C. Dornes, Y. Acremann, M. Savoini, M. Kubli, M. J. Neugebauer, E. Abreu, L. Huber, G. Lantz, C. A. F. Vaz, H. Lemke, E. M. Bothschafter, M. Porer, V. Esposito, L. Rettig, M. Buzzi, A. Alberca, Y. W. Windsor, P. Beaud, U. Staub, D. L. Zhu, S. Song, J. M. Glownia and S. L. Johnson, Nature, 2019, 565, 209–212.
40. S. R. Tauchert, M. Volkov, D. Ehberger, D. Kazenwadel, M. Evers, H. Lange, A. Donges, A. Book, W. Kreuzpaintner, U. Nowak and P. Baum, Nature, 2022, 602, 73–77.
41. M. Hofherr, S. Moretti, J. Shim, S. Häuser, N. Y. Safonova, M. Stiehl, A. Ali, S. Sakshath, J. W. Kim, D. H. Kim, H. J. Kim, J. I. Hong, H. C. Kapteyn, M. M. Murnane, M. Cinchetti, D. Steil, S. Mathias, B. Stadtmüller, M. Albrecht, D. E. Kim, U. Nowak and M. Aeschlimann, Phys. Rev. B, 2018, 98, 174419.
42. M. Shalaby, A. Donges, K. Carva, R. Allenspach, P. M. Oppeneer, U. Nowak and C. P. Hauri, Phys. Rev. B, 2018, 98, 014405.
43. A. Bauer, M. Garst and C. Pfleiderer, Phys. Rev. Lett., 2013, 110, 177207.
44. M. Böttcher, S. Heinze, S. Egorov, J. Sinova and B. Dupé, New J. Phys., 2018, 20, 103014.
45. L. Rózsa, E. Simon, K. Palotás, L. Udvardi and L. Szunyogh, Phys. Rev. B, 2016, 93, 024417.
46. E. Beaurepaire, J. C. Merle, A. Daunois and J. Y. Bigot, Phys. Rev. Lett., 1996, 76, 4250–4253.
47. T. R. Harvey, N. R. da Silva, J. H. Gaida, M. Moller, A. Feist, S. Schafer and C. Ropers, MRS Bull., 2021, 46, 711–719.
48. W. Zhang, T. X. Huang, M. Hehn, G. Malinowski, M. Verges, J. Hohlfeld, Q. Remy, D. Lacour, X. R. Wang, G. P. Zhao, P. Vallobra, Y. Xu, S. Mangin and W. S. Zhao, ACS Appl. Mater. Interfaces, 2023, 15, 5608–5619.
49. G. Berruto, I. Madan, Y. Murooka, G. M. Vanacore, E. Pomarico, J. Rajeswari, R. Lamb, P. Huang, A. J. Kruchkov, Y. Togawa, T. LaGrange, D. McGrouther, H. M. Ronnow and F. Carbone, Phys. Rev. Lett., 2018, 120, 117201.
50. S. G. Je, P. Vallobra, T. Srivastava, J. C. Rojas-Sanchez, T. H. Pham, M. Hehn, G. Malinowski, C. Baraduc, S. Auffret, G. Gaudin, S. Mangin, H. Bea and O. Boulle, Nano Lett., 2018, 18, 7362–7371.
51. R. Juge, K. Bairagi, K. G. Rana, J. Vogel, M. Sall, D. Mailly, V. T. Pham, Q. Zhang, N. Sisodia, M. Foerster, L. Aballe, M. Belmeguenai, Y. Roussigne, S. Auffret, L. D. Buda-Prejbeanu, G. Gaudin, D. Ravelosona and O. Boulle, Nano Lett., 2021, 21, 2989–2996.
52. L. M. Kern, B. Pfau, V. Deinhart, M. Schneider, C. Klose, K. Gerlinger, S. Wittrock, D. Engel, I. Will, C. M. Günther, R. Liefferink, J. H. Mentink, S. Wintz, M. Weigand, M. J. Huang, R. Battistelli, D. Metternich, F. Büttner, K. Höflich and S. Eisebitt, Nano Lett., 2022, 22, 4028–4035.
53. M. De Graef and Y. Zhu, J. Appl. Phys., 2001, 89, 7177–7179.
54. S. K. Walton, K. Zeissler, W. R. Branford and S. Felton, IEEE Trans. Magn., 2013, 49, 4795–4800.
55. M. J. Donahue and D. G. Porter, OOMMF User's Guide, Interagency Report NISTIR Report No. NISTIR 6376 (NISTIR, 1999).
56. F. Hellman, E. N. Abarra, A. L. Shapiro and R. B. van Dover, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 5672–5683.
57. X. Jiao, Y. Ren, Z. Zhang, Q. Jin and Y. Liu, IEEE Trans. Magn., 2013, 49, 3191–3194.
58. J.-W. Kim, K.-D. Lee, J.-W. Jeong and S.-C. Shin, Appl. Phys. Lett., 2009, 94, 192506.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr04529c

‡ These authors contributed equally to this work.

---