Effect of hydrophilicity-imparting substituents on exciton delocalization in squaraine dye aggregates covalently templated to DNA Holliday junctions†
Abstract
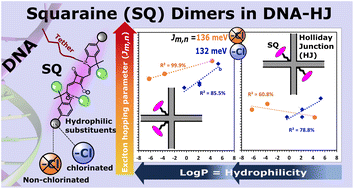
Molecular aggregates exhibit emergent properties, including the collective sharing of electronic excitation energy known as exciton delocalization, that can be leveraged in applications such as quantum computing, optical information processing, and light harvesting. In a previous study, we found unexpectedly large excitonic interactions (quantified by the excitonic hopping parameter Jm,n) in DNA-templated aggregates of squaraine (SQ) dyes with hydrophilic-imparting sulfo and butylsulfo substituents. Here, we characterize DNA Holliday junction (DNA-HJ) templated aggregates of an expanded set of SQs and evaluate their optical properties in the context of structural heterogeneity. Specifically, we characterized the orientation of and Jm,n between dyes in dimer aggregates of non-chlorinated and chlorinated SQs. Three new chlorinated SQs that feature a varying number of butylsulfo substituents were synthesized and attached to a DNA-HJ via a covalent linker to form adjacent and transverse dimers. Various characteristics of the dye, including its hydrophilicity (in terms of log Po/w) and surface area, and of the substituents, including their local bulkiness and electron withdrawing capacity, were quantified computationally. The orientation of and Jm,n between the dyes were estimated using a model based on Kühn–Renger–May theory to fit the absorption and circular dichroism spectra. The results suggested that adjacent dimer aggregates of all the non-chlorinated and of the most hydrophilic chlorinated SQ dyes exhibit heterogeneity; that is, they form a mixture of dimers subpopulations. A key finding of this work is that dyes with a higher hydrophilicity (lower log Po/w) formed dimers with smaller Jm,n and large center-to-center dye distance (Rm,n). Also, the results revealed that the position of the dye in the DNA-HJ template, that is, adjacent or transverse, impacted Jm,n. Lastly, we found that Jm,n between symmetrically substituted dyes was reduced by increasing the local bulkiness of the substituent. This work provides insights into how to maintain strong excitonic coupling and identifies challenges associated with heterogeneity, which will help to improve control of these dye aggregates and move forward their potential application as quantum information systems.
- This article is part of the themed collections: Fundamental Processes in Optical Nanomaterials and Celebrating International Women’s day 2024: Women in Nanoscience

 Please wait while we load your content...
Please wait while we load your content...
