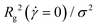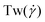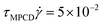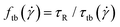Open Access Article
Open Access ArticleSupercoiled ring polymers under shear flow
Christoph
Schneck
 ab,
Jan
Smrek†
ab,
Jan
Smrek†
 a,
Christos N.
Likos
a,
Christos N.
Likos
 *a and
Andreas
Zöttl†
*a and
Andreas
Zöttl†
 a
a
aFaculty of Physics, University of Vienna, Boltzmanngasse 5, 1090 Vienna, Austria. E-mail: christoph.schneck@ehu.eus; jan.smrek@univie.ac.at; christos.likos@univie.ac.at; andreas.zoettl@univie.ac.at
bCentro de Física de Materiales (CSIC, UPV/EHU) and Materials Physics Center MPC, Paseo Manuel de Lardizabal 5, 20018 San Sebastián, Spain
First published on 28th March 2024
Abstract
We apply monomer-resolved computer simulations of supercoiled ring polymers under shear, taking full account of the hydrodynamic interactions, accompanied, in parallel, by simulations in which these are switched off. The combination of bending and torsional rigidities inherent in these polymers, in conjunction with hydrodynamics, has a profound impact on their flow properties. In contrast to their flexible counterparts, which dramatically deform and inflate under shear [Liebetreu et al., Commun. Mater. 2020, 1, 4], supercoiled rings undergo only weak changes in their overall shape and they display both a reduced propensity to tumbling (at fixed Weissenberg number) and a much stronger orientational resistance with respect to their flexible counterparts. In the presence of hydrodynamic interactions, the coupling of the polymer to solvent flow is capable of bringing about a topological transformation of writhe to twist at strong shear upon conservation of the overall linking number.
1. Introduction
DNA molecules have been largely adopted in nanotechnology thanks to the designability and specificity of the complementary sequences, allowing for construction of highly complex meso-structures from DNA nano-components.1 It is being progressively recognized that also topology2,3 and geometry of DNA molecules are highly versatile control parameters for future material applications.4,5 While it is well known that any particular chain topology (linear, branched, circular…) affects the effective interactions with other chains and the solvent,6,7 the DNA with ring topology provides extra tuning parameters. Besides the knottedness,8 joining of the ends of a linear double-stranded DNA into the circular unknotted form allows to couple the topological and the geometrical features of the molecule by locking in any pre-existing excess linking between the two strands. Such ring molecules can then exhibit supercoiled conformations as a result of the competition between the bending and the torsional stiffness. While much of the interest has been initially devoted to equilibrium structures,5,9 many of the challenges for technological applications of DNA materials lie out of equilibrium. The material response functions, crucial in material characterization and processing, are strongly impacted out of the linear regime as the polymeric degrees of freedom have to adapt to the external stresses in the presence of hydrodynamic interactions and other chains.Besides the materials perspective, the properties of non-equilibrium supercoiled DNA polymers touch upon two other highly active research areas. First, the circular DNA is found naturally in the form of (typically supercoiled) bacterial plasmids,10 extrachromosomal DNA of eukaryotes,11 kinetoplast DNA12,13 of trypanosoma and supercoiled segments have been suspected to form distinct architectural and functional domains also on chromosomal DNA.14 Supercoiling itself can affect gene expression15 or DNA metabolism16 by modulating access to distinct regions. In the biological context the DNA molecules are also typically out of equilibrium, subject to flows and stresses arising through the action of molecular motors and inducing non-equilibrium conformations17 and dynamics18 that in turn can impact the biological function.19
Second, the properties of unknotted ring polymers under various conditions are one of the largest unsolved problems in polymer physics. The crux lies in the difficulty of capturing the restrictions that the fixed ring topology imposes on the phase space in the presence of other interactions. This general principle is present across different concentration regimes. In dense many-chain systems the chain topology prevents mutual ring linking, resulting in compact, fractal tree-like, conformations,20,21 power-law stress relaxation,22 distinct shear-thinning exponents,23 extensional viscosity thickening,24,25 viscosity of ring-linear blend exceeding that of the two components26,27 or vitrification upon heterogeneous activation.28 Some of these effects are due to ring interpenetration (threading) by other chains, although their general impact on the viscoelastic properties is still an open question.29–32 However, the impact of threadings is apparent in simulations and experiments on supercoiled plasmids. There, the supercoiling induces tighter branched ring conformations, reduces mutual ring interpenetration and speeds up the dynamics.5 Therefore, investigating the systems with torsional degrees of freedom can help to understand dynamical effects also in torsionally relaxed rings, by giving a control on the degrees of the branching and the threading. In semi-dilute and dilute conditions, both, the interchain interactions and the hydrodynamics coupled with the ring topology of the chains affect the chain relaxation dynamics and fluctuations of the metric properties.33–35 For dilute solutions under non-equilibrium flow conditions, the combination of topology with hydrodynamic interactions has dramatic effects on the conformations and dynamics of the solutes. Vorticity swelling in shear,36 extensional or mixed flows37,38 has been predicted in simulations and recently confirmed experimentally,39 whereas hydrodynamic inflation under steady shear40 results into a strong suppression of tumbling and of the Brownian nature of the polymer dynamics for certain domains of shear rate for flexible polymers. To summarize, the supercoiling reduces penetrable area of rings which is relevant for viscoelasticity, but hydrodynamic swelling acts in the opposite way. Therefore here we aim to study systematically in simulation how does the hydrodynamic interaction couple with the supercoiled ring structure in dilute (single chain) conditions in shear. To do so, we employ the multiparticle collision dynamics to account for the hydrodynamic interaction in combination with molecular dynamics for the time evolution of the polymer.
Under non-equilibrium conditions such as shear flow that we focus on in here,40,41 non-local hydrodynamic effects play an essential role for the transport and dynamical properties of polymers. Considering the molecular dynamics of all of the fluid particles interacting with the polymers would be too time-consuming on the typical experimental time-scales (seconds). Hence, several coarse-grained simulation techniques had been developed which capture hydrodynamic interactions in polymers, such as dissipative particle dynamics (DPD),42 the lattice Boltzmann method (LBM)43 and multiparticle collision dynamics (MPCD).44 In particular MPCD had been heavily used in the last two decades to study polymer dynamics under equilibrium and under shear flow conditions. In MPCD the Newtonian background solvent is modeled by effective point-like fluid particles which perform alternating streaming and collision steps.44,45 While intramolecular forces are advanced through molecular dynamics (MD) purely between monomers, the hydrodynamic effects on the monomers stem from monomer-fluid particle interactions. In the simplest and most popular approach of such a hybrid MPCD-MD scheme the monomers are assumed to be pointlike but heavier than the fluid particles and exchange momentum with the local fluid particles in the collision step.46 This allows simulations of single/dilute47–49 and semidilute/dense50,51 polymer solutions in the presence of an explicit solvent. Simple unidirectional shear flow is usually realized by applying Lees–Edwards boundary conditions,47,48,52,53 and the flow can be disturbed by the presence of polymers and their coupling to the fluid motion.
MPCD had been used to quantify the shear-thinning behavior of linear flexible,48,51 semiflexible54 and stiff47,50 polymer solutions, as well as the dynamics of single crosslinked polymer chains.55,56 Furthermore, the MPCD method can easily be adapted to simulate pressure-driven Poiseuille flow bounded by no-slip channel walls.57–59 Consequently the dynamics of single linear flexible60 and semiflexible61 polymers, as well as the shape transitions of a tethered linear polymer62 had been investigated. The properties of polymers with other architectures under shear flow had also been studied in detail, such as star polymers and dendrimers,41,49,63–68 as well as ring polymers.36,40,69,70 Noteworthy, in MPCD hydrodynamic interactions can be turned off easily without modifying other physical properties of the fluid.40,41 This allows to directly determine the influence of hydrodynamic interactions in polymer simulations, of particular importance in out-of-equilibrium conditions.71–73
The article is organized as follows: in section 2 we introduce the model and in section 3 the quantities that characterize the topology and the shapes of the supercoiled polymers in equilibrium and under shear. In sections 4 and 5 we present the extracted equilibrium properties and the behavior under shear flow of supercoiled ring polymers, respectively. We conclude our work in section 6, whereas certain technical details of our work are delegated to the Appendix.
2. Model
2.1. Multiparticle collision dynamics
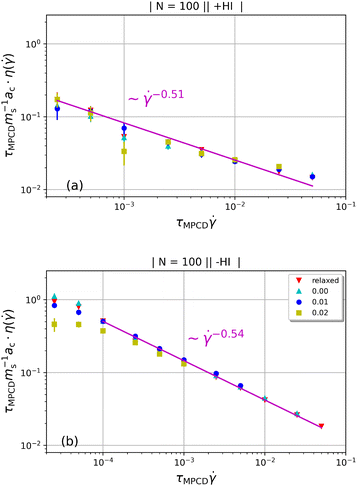
Multiparticle collision dynamics (MPCD) is a method of simulating a particle-based solvent put forward by Malevanets and Kapral74 that is used to generate hydrodynamic interactions (HI) and mimic thermal fluctuations in molecular dynamics (MD) simulations of embedded objects such as colloids and polymers. It models the solvent fluid as Ns individual point particles with mass ms within a rectangular simulation box with side lengths Lx, Ly, Lz. Positions and velocities are described by continuous variables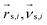 , i ∈ {1,…, Ns}. The algorithm consists of two alternating steps. During the streaming step the particles are allowed to move ballistically for a time period h according to their current velocities:
, i ∈ {1,…, Ns}. The algorithm consists of two alternating steps. During the streaming step the particles are allowed to move ballistically for a time period h according to their current velocities: | (1) |
Periodic boundary conditions are applied for particles crossing the dimensions of the simulation box. In the subsequent collision step the entire simulation box is coarse-grained into cubic cells of a grid with lattice constant ac and the solvent particles are sorted according to their current positions. The velocities of all Nc particles in one particular cell are summed up to a center-of-mass velocity, 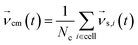 , and a rotation matrix R[α] is generated and assigned to the cell. The orientation of the rotation axis is picked randomly at each step and varies from cell to cell, whereas the rotation angle α is fixed. This randomness is the ingredient endowing MPCD with thermal fluctuations. The velocities of all particles within the cell are then rotated relative to the center-of-mass velocity of the cell,
, and a rotation matrix R[α] is generated and assigned to the cell. The orientation of the rotation axis is picked randomly at each step and varies from cell to cell, whereas the rotation angle α is fixed. This randomness is the ingredient endowing MPCD with thermal fluctuations. The velocities of all particles within the cell are then rotated relative to the center-of-mass velocity of the cell,
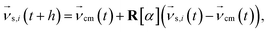 | (2) |
 . The internal interaction of the simulated fluid is coarse-grained both in space (the division into cells) and time (collision at discrete time steps). Because of the lack of systematic forces, MPCD solvent particles obey an ideal gas equation of state44 and one can show that the algorithm conserves mass, momentum, and energy locally at cell level.74 MPCD is an effective way of solving the Navier–Stokes equations and reproducing hydrodynamic interactions and thermal fluctuations down to the size of a collision cell.
. The internal interaction of the simulated fluid is coarse-grained both in space (the division into cells) and time (collision at discrete time steps). Because of the lack of systematic forces, MPCD solvent particles obey an ideal gas equation of state44 and one can show that the algorithm conserves mass, momentum, and energy locally at cell level.74 MPCD is an effective way of solving the Navier–Stokes equations and reproducing hydrodynamic interactions and thermal fluctuations down to the size of a collision cell.
There are three basic units all set to unity: the mass ms of the fluid particles, the length of the cubic collision cells ac, and the energy kBT specifying the average kinetic energy of a solvent particle by  . This corresponds to expressing length, energy, and mass in units of ac, kBT, and ms. A reference unit for time can then be derived as
. This corresponds to expressing length, energy, and mass in units of ac, kBT, and ms. A reference unit for time can then be derived as 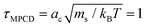 . The box dimensions are set to Lx = 80ac, Ly = 50ac, Lz = 50ac, which has been shown to be large enough to avoid flow interference through periodic boundary conditions or polymer self-interactions for similar simulations.40 The box is rectangular with its long side in the shear flow direction – see later below the description of the system. The time between collisions is set to h = 0.1τMPCD, the collision angle α = 130° and the solvent particle number density
. The box dimensions are set to Lx = 80ac, Ly = 50ac, Lz = 50ac, which has been shown to be large enough to avoid flow interference through periodic boundary conditions or polymer self-interactions for similar simulations.40 The box is rectangular with its long side in the shear flow direction – see later below the description of the system. The time between collisions is set to h = 0.1τMPCD, the collision angle α = 130° and the solvent particle number density  , where 〈Nc〉 = 10 is the average number of solvent particles in each collision cell. This choice of parameters corresponds to a dynamic viscosity75 of η = 8.7τMPCD−1msac−1.
, where 〈Nc〉 = 10 is the average number of solvent particles in each collision cell. This choice of parameters corresponds to a dynamic viscosity75 of η = 8.7τMPCD−1msac−1.
For short time steps h the mean free path  between consecutive collisions is small compared to the cell size. The discrete nature of the grid causes particles to stay in the same cell for several collisions before particle exchange with neighbouring cells occurs. This causes particles within one collision cell to build up correlations and breaks the translational symmetry of the system. Galilei invariance can be recovered by performing a random shift of the sorting grid by the shift vector
between consecutive collisions is small compared to the cell size. The discrete nature of the grid causes particles to stay in the same cell for several collisions before particle exchange with neighbouring cells occurs. This causes particles within one collision cell to build up correlations and breaks the translational symmetry of the system. Galilei invariance can be recovered by performing a random shift of the sorting grid by the shift vector 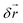 with the components that are sampled uniformly from
with the components that are sampled uniformly from  . Additionally, the shifting procedure accelerates momentum transfer between particles.76
. Additionally, the shifting procedure accelerates momentum transfer between particles.76
To generate shear flow with a tunable shear rate  the periodic boundaries are modified to Lees–Edwards boundary conditions.52 This defines three distinct space directions: the shear motion is along the flow direction (x-axis), the magnitude of shear flow varies along the gradient direction (y-axis), and the remaining one is called the vorticity direction (z-axis). Thereby, energy is constantly pumped into the system, and then is converted into heat due to the MPCD-fluid viscosity, which, if left unattended, would result into constant viscous heating of the system. A thermostat is thus necessary in such a non-equilibrium system to maintain the temperature at its prescribed value. We employ here a cell-level thermostat,44,77 which further ensures that the particle velocities follow a Maxwell–Boltzmann distribution and it restricts the fluctuations of the total energy of the system to those leading to the desired value kBT.
the periodic boundaries are modified to Lees–Edwards boundary conditions.52 This defines three distinct space directions: the shear motion is along the flow direction (x-axis), the magnitude of shear flow varies along the gradient direction (y-axis), and the remaining one is called the vorticity direction (z-axis). Thereby, energy is constantly pumped into the system, and then is converted into heat due to the MPCD-fluid viscosity, which, if left unattended, would result into constant viscous heating of the system. A thermostat is thus necessary in such a non-equilibrium system to maintain the temperature at its prescribed value. We employ here a cell-level thermostat,44,77 which further ensures that the particle velocities follow a Maxwell–Boltzmann distribution and it restricts the fluctuations of the total energy of the system to those leading to the desired value kBT.
To create coupling with the fluid and thereby enable HI, we include the monomers in the MPCD collision, step46 but other approaches also exist.78 An embedded monomer i with mass mm and velocity  contributes to the center-of-mass velocity of the collision cell. If Nm is the number of monomers in a particular cell, the center-of-mass velocity is
contributes to the center-of-mass velocity of the collision cell. If Nm is the number of monomers in a particular cell, the center-of-mass velocity is
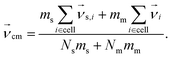 | (3) |
A stochastic rotation as in eqn (2) is then performed on the relative velocities of both the solvent particles and the embedded monomers. This results in an exchange of momentum and energy between all particles within a collision cell. The updated monomer velocities are then used as initial conditions for the subsequent MD time step. 100 MD time steps are performed between consecutive MPCD collisions.
Gompper et al.44 have noted that the average number of monomers per collision cell should be smaller than unity in order to properly resolve HI between them. The bond length of polymer chains should be of order of the cell size ac so that monomers are close enough to display effects due to HI but far enough apart to avoid multiple monomers within a cell. Furthermore, Ripoll et al.79 have demonstrated that the mass ratio mm/ms should equal the average number of solvent particles per cell 〈Nc〉 (assuming there is only one monomer per cell). Under this condition the monomer collides with a piece of solvent with equal mass so that the mutual momentum exchange is balanced. For mm ≫ 〈Nc〉ms the polymer is barely affected by the solvent, whereas for mm ≪ 〈Nc〉ms the monomers are kicked around too violently. Hence we chose mm = 〈Nc〉ms = 10ms.
In order to study the specific effects of the hydrodynamic interactions on the dynamics of the system the same simulations have to be performed with and without HI. An alternative concept of simulating the solvent and the interaction with the monomer has to be found, that differs as little as possible from the original conditions except for the presence of HI. Ripoll et al. invented an efficient method to switch off HI in a MPCD algorithm.80 They suggest that the positions of the solvent particles do not contribute in the collision step and therefore, no explicit particles have to be considered at all. Instead, every monomer is coupled with an effective solvent momentum  that is chosen randomly from a Maxwell–Boltzmann distribution of variance ms〈Nc〉kBT and zero mean. A center-of-mass velocity is assigned to every monomer velocity
that is chosen randomly from a Maxwell–Boltzmann distribution of variance ms〈Nc〉kBT and zero mean. A center-of-mass velocity is assigned to every monomer velocity 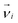 given by:
given by:
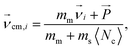 | (4) |
 is added to the random solvent by setting the mean of
is added to the random solvent by setting the mean of  from zero to
from zero to 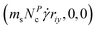 , where the monomer's position in gradient direction riy determines the local shear velocity in flow direction. The number of collision partners NPc is picked randomly from a Poisson distribution with expectation value 〈Nc〉 which corresponds to the distribution of the number density in a particle-based MPCD cell. In the following this heat bath will be referred to as random MPCD solvent or ‘−HI’, meaning there are no hydrodynamic interactions, whereas the conventional particle-based procedure, with hydrodynamic interactions, will be referenced to as ‘+HI’.
, where the monomer's position in gradient direction riy determines the local shear velocity in flow direction. The number of collision partners NPc is picked randomly from a Poisson distribution with expectation value 〈Nc〉 which corresponds to the distribution of the number density in a particle-based MPCD cell. In the following this heat bath will be referred to as random MPCD solvent or ‘−HI’, meaning there are no hydrodynamic interactions, whereas the conventional particle-based procedure, with hydrodynamic interactions, will be referenced to as ‘+HI’.
2.2. Polymer model
We use a coarse-grained polymer model used previously5 with parameters tuned to represent typical properties of double-stranded DNA (see below). The polymer rings consist of N = 100 beads with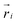 ,
, 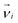 representing their positions and velocities respectively. Their time evolution is governed by a velocity Verlet algorithm with time step length δt = 10–2h. The beads are subject to a pair-wise Weeks–Chandler–Andersen (WCA) potential5,40 with a cutoff distance at
representing their positions and velocities respectively. Their time evolution is governed by a velocity Verlet algorithm with time step length δt = 10–2h. The beads are subject to a pair-wise Weeks–Chandler–Andersen (WCA) potential5,40 with a cutoff distance at  ,
, | (5) |
 . The parameters ε and σ define energy and length scales of the polymer and are set to ε = kBT = 1 and σ = ac = 1.
. The parameters ε and σ define energy and length scales of the polymer and are set to ε = kBT = 1 and σ = ac = 1.
Neighbouring beads are attached to each other along the backbone by applying a pair-wise attractive FENE (finitely extensible nonlinear elastic) potential given by
 | (6) |
We further include bending and torsional stiffness as in Smrek et al.,5 to mimic the coarse-grained properties of the DNA. We show a sketch of the polymer in Fig. 1(a), and we describe the model in more detail in what follows. The bending energy is introduced between every consecutive triplets of chain neighbours  ,
,  , and
, and  (again respecting the ring topology):
(again respecting the ring topology):
Ubend(θb) = kbend(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θb), θb), | (7) |
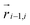 and
and  , see Fig. 1(b), so that
, see Fig. 1(b), so that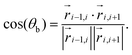 | (8) |
The bending constant is chosen to be kbend = 20kBT leading to a persistence length lp = 20σ. The scale of the monomer diameter should be mapped5 to DNA's thickness in real units of σ = 2.5 nm, i.e., 2.5/0.34 = 7.35 bp per bead and lp = 150 bp = 50 nm.
To model the torsional degrees of freedom, every bead is equipped with three patches which remain at a fixed distance 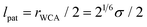 . The vectors
. The vectors  are defined as the vectors going from the position of bead i to its k-th patch where k = 1, 2, 3 so that each triplet
are defined as the vectors going from the position of bead i to its k-th patch where k = 1, 2, 3 so that each triplet  forms an orthogonal basis with the respective bead position
forms an orthogonal basis with the respective bead position  as the origin. In Fig. 1(a), we show a short segment of a polymer chain with patches where colours blue, red, and green correspond to the numeration k = 1, 2, 3, respectively. The blue and red patches are used to introduce two dihedral springs that constrain the torsional angle ψb/r between consecutive beads close to a fixed equilibrium value ψ0. Here, ψb/r is defined as the angle between the planes with normal vectors
as the origin. In Fig. 1(a), we show a short segment of a polymer chain with patches where colours blue, red, and green correspond to the numeration k = 1, 2, 3, respectively. The blue and red patches are used to introduce two dihedral springs that constrain the torsional angle ψb/r between consecutive beads close to a fixed equilibrium value ψ0. Here, ψb/r is defined as the angle between the planes with normal vectors  and
and  , see Fig. 1(c), and it is evaluated for the blue and red patches, respectively. The corresponding potential is given by the expression:
, see Fig. 1(c), and it is evaluated for the blue and red patches, respectively. The corresponding potential is given by the expression:
 | (9) |
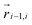 and
and  . The green patch
. The green patch  is forced onto the segment line
is forced onto the segment line  by the alignment potential:
by the alignment potential:Ualign(θa) = kalign(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θa), θa), | (10) |
 | (11) |
In this way, blue and red patches are aligned orthogonal to the polymer backbone consisting of the beads so that dihedral angles between consecutive beads can be formed properly, see Fig. 1(d). The constant is chosen to be as high as kalign = 200kBT to minimize the fluctuations of the alignment.
Forces derived from all potentials presented act on the beads i whereas torsion, eqn (9), and alignment, eqn (10), also yield forces upon the respective patches k denoted by 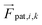 . Forces acting on the beads are calculated as
. Forces acting on the beads are calculated as
 | (12) |
 | (13) |
 | (14) |
Adding patches to the beads effectively transforms the previous point particles i to rigid bodies with a rotational degree of freedom χi, angular velocity  , and inertia tensor Iiαβ. The set of three angles χi defines the orientation of the monomer i with respect to the lab frame, and hence define the positions of the patches
, and inertia tensor Iiαβ. The set of three angles χi defines the orientation of the monomer i with respect to the lab frame, and hence define the positions of the patches  on the monomer i. Their explicit representation with quaternions is discussed in the Appendix. The monomers are modeled as extended spheres with radius lpat and continuous mass density ρm = 3mm/(4πlpat3), which corresponds to a trivial inertia tensor Iiαβ = Isphereδα,β with the moment of inertia
on the monomer i. Their explicit representation with quaternions is discussed in the Appendix. The monomers are modeled as extended spheres with radius lpat and continuous mass density ρm = 3mm/(4πlpat3), which corresponds to a trivial inertia tensor Iiαβ = Isphereδα,β with the moment of inertia  . The position of the bead
. The position of the bead  is the central point of the rigid body and coincides with the center-of-mass of the monomer, whereas the patches reside on the sphere's surface. Therefore, only the forces
is the central point of the rigid body and coincides with the center-of-mass of the monomer, whereas the patches reside on the sphere's surface. Therefore, only the forces 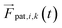 contribute to the total torque
contribute to the total torque 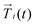 on monomer i, expressed as
on monomer i, expressed as
 | (15) |
 of bead i. Rotations around the center-of-mass only affect the orientations χi but not the bead positions. The rotational dynamics are added to the velocity Verlet algorithm, see Appendix for details. When the polymer is suspended in the MPCD solvent, the collisions only rotate the monomer velocities
of bead i. Rotations around the center-of-mass only affect the orientations χi but not the bead positions. The rotational dynamics are added to the velocity Verlet algorithm, see Appendix for details. When the polymer is suspended in the MPCD solvent, the collisions only rotate the monomer velocities  but not the angular velocities
but not the angular velocities  and so the solvent-solute interaction does not affect the rotational degrees directly. This is an approximation originating in our choice of the coarse-grained model. More details on the force calculations as well as on the integration of the equations of motion for the translations and the rotations of the beads are given in the Appendix.
and so the solvent-solute interaction does not affect the rotational degrees directly. This is an approximation originating in our choice of the coarse-grained model. More details on the force calculations as well as on the integration of the equations of motion for the translations and the rotations of the beads are given in the Appendix.
3. Polymer topology and shapes
3.1. Writhe and twist
The conformations of the supercoiled ring polymers are influenced by an interplay of the applied bending and torsional constraints. Their geometry is analyzed by measuring the topological parameters writhe and twist
and twist 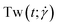 , where we explicitly denote the time-dependence of these quantities as well as their parametric dependence on the applied shear rate
, where we explicitly denote the time-dependence of these quantities as well as their parametric dependence on the applied shear rate  . The former is defined for any instantaneous configuration Ct of a closed curve in three-dimensional space as:
. The former is defined for any instantaneous configuration Ct of a closed curve in three-dimensional space as: | (16) |
where 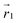 and
and  are points on the curve Ct and
are points on the curve Ct and 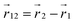 at a given time t. The writhe gives an intuitive measure of how many crossings an average 2D projection of the molecular backbone forms with itself. For the actual computation we use a version of eqn (16) detailed in Klenin and Langowski,81 where the bead positions serve as the reference points of the discretized curve Ct.
at a given time t. The writhe gives an intuitive measure of how many crossings an average 2D projection of the molecular backbone forms with itself. For the actual computation we use a version of eqn (16) detailed in Klenin and Langowski,81 where the bead positions serve as the reference points of the discretized curve Ct.
The twist is computed for the torsionally constrained polymer rings by summing over the difference of all dihedral angles from the respective equilibrium value ψ0:
 | (17) |
The blue and red patches each form an individual set of dihedral angles 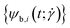 , respectively
, respectively 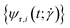 which is why an arithmetic mean over the two is taken in the evaluation of
which is why an arithmetic mean over the two is taken in the evaluation of  in eqn (17). The alignment potential forces the green patches to be orientated nearly perfectly with the polymer backbone so that the blue and red patches are kept in a perpendicular orientation to it. A high value is picked for the constant kalign = 200kBT which limits the fluctuations from this structure. For this reason, the vectors
in eqn (17). The alignment potential forces the green patches to be orientated nearly perfectly with the polymer backbone so that the blue and red patches are kept in a perpendicular orientation to it. A high value is picked for the constant kalign = 200kBT which limits the fluctuations from this structure. For this reason, the vectors  serve as (unnormalized) normal vectors to the space curve approximated by the bead positions
serve as (unnormalized) normal vectors to the space curve approximated by the bead positions  . With the brackets 〈…〉t denoting averaging over time, we also define the quantities:
. With the brackets 〈…〉t denoting averaging over time, we also define the quantities:
 | (18) |
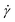 .
.
The patches endow the simulated ring polymer with the structure of a closed ribbon, which therefore obeys Călugăreanu's theorem, stating that the sum over its writhe and twist, i.e., its linking number Lk is a conserved quantity:82
 | (19) |
The linking number is thus a topological invariant of the ribbon, independently of time or applied shear rate, akin to the knotedness of single rings or the catenation connectivities of several ones in composite macromolecular entities, such as catenanes. Note that the model is torsionally symmetric, i.e., it does not distinguish between left-handed and right-handed torsion and therefore we have chosen one of them and we do not specify the sign of the supercoiling or the linking number.
Supercoiled rings must be initialized in a state with minimal torsional energy to avoid large initial torsional forces that could cause a simulation crash. The initial conformations of rings with σsc > 0 are generated by starting from a flat open ribbon with a linking number of zero and performing MD steps while gradually ramping up the offset of the torsional potential ψ0 from zero to the desired angle 2πσsc in small steps. During this procedure monomers are coupled to the random MPCD solvent. The offset is increased in steps of 10–3 × 2πσsc after every 2000th collision with the solvent until the final angle is reached. The resulting conformations are supercoiled rings for which  is indeed conserved up to fluctuations around the mean. The initialization process is performed for the supercoiling values σsc = 0.01 and σsc = 0.02. In Fig. 2, we show snapshots of all four types of ring polymers investigated.
is indeed conserved up to fluctuations around the mean. The initialization process is performed for the supercoiling values σsc = 0.01 and σsc = 0.02. In Fig. 2, we show snapshots of all four types of ring polymers investigated.
 | ||
Fig. 2 Snapshots of the supercoiled polymers at equilibrium  . (a) Relaxed ring with ktorsion = 0, (b) σsc = 0.00, (c) σsc = 0.01, (d) σsc = 0.02. . (a) Relaxed ring with ktorsion = 0, (b) σsc = 0.00, (c) σsc = 0.01, (d) σsc = 0.02. | ||
3.2. The gyration tensor and its rotational invariants
The conformations of polymers are investigated and quantified by measuring the ring's gyration tensor:83 | (20) |
and additional quantities derived from it, to be specified in what follows. Here, 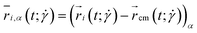 is the α-coordinate of i-th monomer's position relative to the center-of-mass
is the α-coordinate of i-th monomer's position relative to the center-of-mass  of the polymer at a given time t and shear rate
of the polymer at a given time t and shear rate 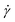 . The diagonal element
. The diagonal element  reflects the elongation of the polymer along the α-coordinate. Of particular importance are the instantaneous eigenvalues
reflects the elongation of the polymer along the α-coordinate. Of particular importance are the instantaneous eigenvalues  , out of which several useful rotational invariants can be constructed. The instantaneous radius of gyration squared,
, out of which several useful rotational invariants can be constructed. The instantaneous radius of gyration squared,  , is defined as the trace of the gyration tensor:
, is defined as the trace of the gyration tensor:
 | (21) |
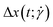 defined as:
defined as: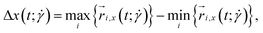 | (22) |
 is the x-component of the position vector
is the x-component of the position vector 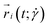 of the i-th monomer.
of the i-th monomer.
The shape of the conformation can be characterized by the prolateness 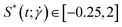 , defined as:40
, defined as:40
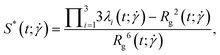 | (23) |
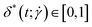 , which is defined as:40
, which is defined as:40 | (24) |
where  . For this quantity,
. For this quantity,  occurs if all eigenvalues are identical (e.g. spherical or polyhedral group symmetry) while
occurs if all eigenvalues are identical (e.g. spherical or polyhedral group symmetry) while 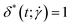 indicates that two eigenvalues are zero (e.g. all monomers on a line). The (squared) gyration radius, the prolateness and the relative shape anisotropy are all independent of the orientation of the polymer in space. Similar to the writhe and twist, eqn (18), we define time-averages as
indicates that two eigenvalues are zero (e.g. all monomers on a line). The (squared) gyration radius, the prolateness and the relative shape anisotropy are all independent of the orientation of the polymer in space. Similar to the writhe and twist, eqn (18), we define time-averages as
 | (25) |
where ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) = Gαβ, Rg2, Δx, S*, or δ*, and we report on their values in what follows.
= Gαβ, Rg2, Δx, S*, or δ*, and we report on their values in what follows.
4. Equilibrium properties
Supercoiled rings with σsc = 0.00, 0.01, 0.02 as well as torsionally relaxed ones with N = 100 monomers were allowed to evolve freely in time under equilibrium conditions while we monitor the quantities of interest to establish when the equilibrium was reached. In that process, the monomers were coupled to the MPCD solvent both with and without HI in separate runs to confirm the independence of the equilibrium state on the HI. After the equilibration run of 2 × 107 MD steps for + HI and 5 × 108 steps for −HI followed a production run of 6 × 107 and 1.5 × 109 steps, respectively for ±HI. All quantities were sampled at least every 100τMPCD for +HI and 1000τMPCD for −HI, while quickly fluctuating quantities, the intrinsic viscosity and the tumbling cross correlation function, were sampled every 10τMPCD. All the quantities measured contributed to their equilibrium averages and distributions. To get more precise results, 38 independent simulation runs were conducted for
while we monitor the quantities of interest to establish when the equilibrium was reached. In that process, the monomers were coupled to the MPCD solvent both with and without HI in separate runs to confirm the independence of the equilibrium state on the HI. After the equilibration run of 2 × 107 MD steps for + HI and 5 × 108 steps for −HI followed a production run of 6 × 107 and 1.5 × 109 steps, respectively for ±HI. All quantities were sampled at least every 100τMPCD for +HI and 1000τMPCD for −HI, while quickly fluctuating quantities, the intrinsic viscosity and the tumbling cross correlation function, were sampled every 10τMPCD. All the quantities measured contributed to their equilibrium averages and distributions. To get more precise results, 38 independent simulation runs were conducted for  and observed quantities were averaged among them. The error bars were computed as the error of the mean from the 38 independent runs. We simulate longer than the characteristic time as estimated in the sheared case, see section 5.
and observed quantities were averaged among them. The error bars were computed as the error of the mean from the 38 independent runs. We simulate longer than the characteristic time as estimated in the sheared case, see section 5.
For the supercoiled rings with nonzero Linking number, σsc > 0, the simulation occasionally crashed, due to the relatively large timestep and the buildup of numerical instabilities leading to unphysically large forces. In such cases, we discarded the data. Higher degrees of writhe constrain the rings to take on more contracted conformations and the resulting contorted macrostructure of the polymer forces some beads to be pressed together increasing the risk of building up large repulsive forces. High shear rates amplify this behaviour as the solvent flow stretches out the polymer rings. More specifically, two different kinds of undesired behaviour have been observed. The first is rupture of the polymer, where a small part (usually up to 5 monomers) leaves its place within the chain. The second type of undesired behaviour amounts to Lk spontaneously being changed by an integer value ±1, violating the topological constraints that force the ring to have a constant linking number (apart from small deviations due to the fact that the patches are not necessarily aligned in a perfect right angle relative to the backbone). These crashes happened mostly when using the −HI-solvent at high shear rates, since the total number of MD steps was much higher compared to the costly particle-based solvent with +HI and the chances of a crashing situation increased with the length of the simulation runs which could not be decreased significantly. Both types of crashes can presumably be avoided by using a smaller ΔtMD.
In Fig. 3(a)–(d), we show time series of the topological quantities, writhe and twist, for all systems simulated, whereby the curves of the single runs are averaged to a single curve. Whereas both the relaxed rings and the rings without supercoiling assume conformations that are essentially writhe-free, the rings with σsc = 0.01 and σsc = 0.02 display conformations that carry finite writhe. Connected to this, and rather insensitively of the degree of supercoiling, the twist fluctuates closely around zero in case of σsc = 0.00 whereas for σsc > 0,  takes on small but nonzero values. Up to this value, the writhe equals the linking number for the entire duration of the simulation and Călugăreanu's theorem (19) is indeed fulfilled for all systems. The relaxed chains remain in a state with only low writhe because of the high bending stiffness-cost that a high writhe would incur, and the twist fluctuates arbitrarily for the same chains because of the absence of torsional springs. The overall behaviour of the topological parameters does not depend on the presence of HI, as it should be the case for polymers in equilibrium.
takes on small but nonzero values. Up to this value, the writhe equals the linking number for the entire duration of the simulation and Călugăreanu's theorem (19) is indeed fulfilled for all systems. The relaxed chains remain in a state with only low writhe because of the high bending stiffness-cost that a high writhe would incur, and the twist fluctuates arbitrarily for the same chains because of the absence of torsional springs. The overall behaviour of the topological parameters does not depend on the presence of HI, as it should be the case for polymers in equilibrium.
The equilibrium distributions of the squared radius of gyration are presented in Fig. 3(e) and the expectation values of this quantity are summarized in Table 1, which also provides a comparison with the gyration radius of a fully flexible ring. As a first remark, we note that the presence of the bending stiffness, independently of the supercoiling, causes the rings to swell with respect to their flexible counterparts, as expected. For σsc = 0.00 both the bending and the torsional stiffness force the ring to remain in an open circular shape which leads to a sharp peak in the Rg2(t;0)-distributions. The absence of torsional stiffness softens considerably the relaxed rings, leading to slightly smaller sizes as well as a broader distribution of the gyration radius values. The σsc = 0.00 rings are locked in a rather open and flat conformation and Rg2(t;0) fluctuates more weakly around a larger mean compared to the relaxed counterparts. The values of the gyration radius agree with Smrek et al.,5 which confirming the correct implementation of the model. Moreover the Rg-distribution of the relaxed case shows a long tail at low values, indicating a weakly bimodal character of the distribution in agreement with the findings of Smrek et al.5 Nonzero supercoiling forces the polymers to take on more complex supercoiled shapes, characterized by a smaller Rg2(t;0) for σsc > 0, as can be also confirmed by the prolateness data below. The values of Rg2(t;0) coincide for the solvents with and without HI, again as expected, and confirming that equilibrium has indeed been achieved for both simulation variants.
 , for the various types of ring polymers with N = 100 monomers considered in this work, along with the value of the same quantity for a fully flexible polymer (last row). The error values indicated are computed as the standard deviation of the equilibrium distribution
, for the various types of ring polymers with N = 100 monomers considered in this work, along with the value of the same quantity for a fully flexible polymer (last row). The error values indicated are computed as the standard deviation of the equilibrium distribution
The equilibrium distributions of the prolateness parameter S* are depicted in Fig. 3(f). As intuitively expected, the σsc = 0.00-ring and the relaxed one are mainly found in oblate shapes as they tend to be open rings, a property manifested in the fact that their S*(t;0)-distributions peak at values below zero. Nevertheless, even for these rings the probability distributions have sufficiently long tails into the prolate domain, resulting into expectation values S*(0) ≅ 0 overall, see Fig. 7(d) (at  ): to obtain rings that are oblate on average, one would need a higher value of kbend and/or a smaller value of N, so as to obtain a larger ratio of persistence to contour lengths. On the other hand, supercoiling increases the prolateness markedly, as it constrains the rings in a more elongated conformation, consistent with the increasingly writhed conformations they assume. Accordingly, the prolateness distribution of the σsc = 0.01-supercoiled ring has a peak at S*(t, 0) ≅ 0.5 and that of the σsc = 0.02-ring at S*(t,0) ≅ 1.25. Despite the increase in prolateness, the gyration radius of the σsc = 0.02-ring remains unchanged with respect to that of its σsc = 0.01-counterpart, as the elongation in one direction is compensated by shrinking in the two orthogonal ones.
): to obtain rings that are oblate on average, one would need a higher value of kbend and/or a smaller value of N, so as to obtain a larger ratio of persistence to contour lengths. On the other hand, supercoiling increases the prolateness markedly, as it constrains the rings in a more elongated conformation, consistent with the increasingly writhed conformations they assume. Accordingly, the prolateness distribution of the σsc = 0.01-supercoiled ring has a peak at S*(t, 0) ≅ 0.5 and that of the σsc = 0.02-ring at S*(t,0) ≅ 1.25. Despite the increase in prolateness, the gyration radius of the σsc = 0.02-ring remains unchanged with respect to that of its σsc = 0.01-counterpart, as the elongation in one direction is compensated by shrinking in the two orthogonal ones.
5. Properties under shear flow
The supercoiled and relaxed ring polymers discussed so far are simulated under shear flow for a wide range of shear rates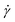 spanning multiple orders of magnitude. They are coupled both to the particle-based MPCD solvent (+HI) and to the random MPCD solvent (−HI) in 10 separate runs to determine any effects of HI on the supercoiled ring conformations. The systems without HI are run for longer times (5 × 108 MD steps compared to 2 × 107 for +HI) since the particle-based MPCD took up most of the numerical effort when HI is present. On the flip side the polymers with σsc > 0 are more prone to crashes (as explained in section 4) for −HI so it is not possible to measure their properties for very high shear rates. After the “equilibration” time of 20% of the respective simulation run time we considered the systems to be in a stationary state since all key observed quantities had reached stationary values.
spanning multiple orders of magnitude. They are coupled both to the particle-based MPCD solvent (+HI) and to the random MPCD solvent (−HI) in 10 separate runs to determine any effects of HI on the supercoiled ring conformations. The systems without HI are run for longer times (5 × 108 MD steps compared to 2 × 107 for +HI) since the particle-based MPCD took up most of the numerical effort when HI is present. On the flip side the polymers with σsc > 0 are more prone to crashes (as explained in section 4) for −HI so it is not possible to measure their properties for very high shear rates. After the “equilibration” time of 20% of the respective simulation run time we considered the systems to be in a stationary state since all key observed quantities had reached stationary values.
We begin our analysis by looking at the topological characteristics of the supercoiled rings, and in particular at the writhe  and the twist
and the twist  , reported in Fig. 4(a)–(d). The linking number is also depicted as their sum, which is constant for all
, reported in Fig. 4(a)–(d). The linking number is also depicted as their sum, which is constant for all 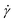 , serving as a test of the validity of the simulations. In all cases and for most shear rates considered, writhe and twist remain constant at their preferred values as in equilibrium according to their degree of supercoiling σsc; hydrodynamic forces are not capable of “unwrithing” the molecules for most of the range of shear rates considered. However, for the highest values of
, serving as a test of the validity of the simulations. In all cases and for most shear rates considered, writhe and twist remain constant at their preferred values as in equilibrium according to their degree of supercoiling σsc; hydrodynamic forces are not capable of “unwrithing” the molecules for most of the range of shear rates considered. However, for the highest values of  tested and in the +HI-variant, where simulations at these shear rates could be performed without crashes, considerable transformation of
tested and in the +HI-variant, where simulations at these shear rates could be performed without crashes, considerable transformation of  into
into 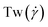 takes place (see Fig. 4(a) and (c) at
takes place (see Fig. 4(a) and (c) at  ). This is interpreted as a forced opening of the writhed structure since the process is connected with a high torsional energy penalty. The snapshots of supercoiled rings with σsc = 0.02 and σsc = 0.01 in Fig. 4(e) and (f), respectively (both +HI), are representatives of the polymers’ behaviour under shear flow in comparison to their shapes in equilibrium
). This is interpreted as a forced opening of the writhed structure since the process is connected with a high torsional energy penalty. The snapshots of supercoiled rings with σsc = 0.02 and σsc = 0.01 in Fig. 4(e) and (f), respectively (both +HI), are representatives of the polymers’ behaviour under shear flow in comparison to their shapes in equilibrium  . At zero shear rate the σsc = 0.02-ring rotates freely in space and takes on more compact, prolate shapes. Although bending and torsion constrains it to have a writhe of nearly
. At zero shear rate the σsc = 0.02-ring rotates freely in space and takes on more compact, prolate shapes. Although bending and torsion constrains it to have a writhe of nearly  it is not elongated in any direction. In contrast, the polymer is almost completely stretched out and aligned along flow direction at high shear rate of
it is not elongated in any direction. In contrast, the polymer is almost completely stretched out and aligned along flow direction at high shear rate of  . Above
. Above  the shear flow is even able to counteract the torsional forces so that writhe and twist experience large fluctuations and the conformation unwrithes, see Fig. 4(e) and (f).
the shear flow is even able to counteract the torsional forces so that writhe and twist experience large fluctuations and the conformation unwrithes, see Fig. 4(e) and (f).
In Fig. 5 we show the diagonal elements of  for both cases when hydrodynamic interactions are active (+HI) as well as the situation when the polymer is coupled to the random MPCD solvent (−HI). All ring polymers considered in this work are not affected by the shear flow up to a certain threshold shear rate of
for both cases when hydrodynamic interactions are active (+HI) as well as the situation when the polymer is coupled to the random MPCD solvent (−HI). All ring polymers considered in this work are not affected by the shear flow up to a certain threshold shear rate of  for + HI and
for + HI and  for −HI. As of the behaviour of polymers under shear flow starts deviating from its equilibrium pattern at Weissenberg number Wi× ≅ 1, this suggests that the longest relaxation times should be of the order τR ≅ 104 for +HI and τR ≅ 105 for −HI, in agreement with previous findings for flexible ring polymers36 or star polymers,66 where the two relaxation times were indeed found to differ by about one order of magnitude for polymers of N ≅ 100.‡
for −HI. As of the behaviour of polymers under shear flow starts deviating from its equilibrium pattern at Weissenberg number Wi× ≅ 1, this suggests that the longest relaxation times should be of the order τR ≅ 104 for +HI and τR ≅ 105 for −HI, in agreement with previous findings for flexible ring polymers36 or star polymers,66 where the two relaxation times were indeed found to differ by about one order of magnitude for polymers of N ≅ 100.‡
For all degrees of supercoiling as well as for the relaxed rings the component of the gyration tensor in the flow direction grows with increasing shear rates while the components in vorticity and gradient directions both get smaller. As the curves do not differ between relaxed and supercoiled rings, we can attribute the trends as well as their deviations from those of flexible rings to the non-vanishing bending rigidity of the polymers. Interestingly, the growth of  (i.e. size extension in the flow direction) with shear rate, shown in Fig. 5(a), is moderate limited to a factor of ≈2–3 with respect to its equilibrium value for all shear rates covered, which is small compared to the growth factor of the fully flexible rings,36,40 which reach values up to ≈15–20. The rings at hand do not stretch as much in the flow direction as the flexible ones, due to the stiffness of the bonds that prevents elongated conformations, which would necessarily result into sharp turns and thus very high bending penalties at the tips of the rings. For the −HI case, Fig. 5(b) there is even a saturation of
(i.e. size extension in the flow direction) with shear rate, shown in Fig. 5(a), is moderate limited to a factor of ≈2–3 with respect to its equilibrium value for all shear rates covered, which is small compared to the growth factor of the fully flexible rings,36,40 which reach values up to ≈15–20. The rings at hand do not stretch as much in the flow direction as the flexible ones, due to the stiffness of the bonds that prevents elongated conformations, which would necessarily result into sharp turns and thus very high bending penalties at the tips of the rings. For the −HI case, Fig. 5(b) there is even a saturation of  at the highest shear rates, corresponding to 102 ≲ Wi ≲ 103. In Fig. 6, we show a quantity closely related to
at the highest shear rates, corresponding to 102 ≲ Wi ≲ 103. In Fig. 6, we show a quantity closely related to  , namely the extent
, namely the extent  . The growth of the extent over its equilibrium value is by about a factor 2 for the whole range of shear rates applied, much less than values experimentally measured for fully flexible rings under similar conditions in, e.g., extensional flow.84
. The growth of the extent over its equilibrium value is by about a factor 2 for the whole range of shear rates applied, much less than values experimentally measured for fully flexible rings under similar conditions in, e.g., extensional flow.84
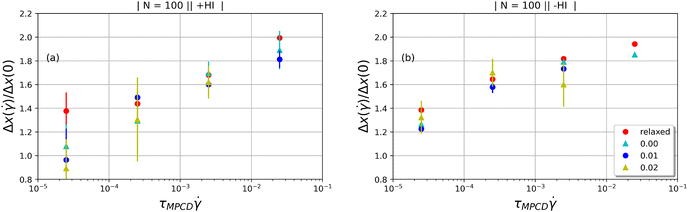 | ||
Fig. 6 The extent  of the polymer along the flow direction normalized over its equilibrium value, Δx(0), as a function of the shear rate of the polymer along the flow direction normalized over its equilibrium value, Δx(0), as a function of the shear rate  . (a) +HI-case; (b) −HI-case. . (a) +HI-case; (b) −HI-case. | ||
In the gradient and vorticity directions (y and z directions respectively), the diagonal elements of the gyration tensor decrease with shear rate but again in ways that differ from those of the flexible cyclic polymers. The contraction in gradient direction is more pronounced than in vorticity direction, as is also the case for flexible rings, but here it decreases with a stronger power-law,  as opposed to the power-law
as opposed to the power-law  , valid for flexible rings,36 independently of the inclusion or exclusion of HI, see Fig. 5(c) and (d). One would naively expect that this is due to a stronger alignment of the rigid rings with the flow direction but, as we will establish in what follows, this is not the case. The rigid and supercoiled rings at hand align, in fact, much less with the flow direction than flexible ones but at the same time they also tumble much less. Accordingly, time intervals of tumbling, in which the (flexible) rings extend stronger into the gradient direction contribute much less to the time-averages and the contraction of the gradient-direction extent with the shear rate is less strong for the flexible rings, resulting into new exponents of the semiflexible ones.
, valid for flexible rings,36 independently of the inclusion or exclusion of HI, see Fig. 5(c) and (d). One would naively expect that this is due to a stronger alignment of the rigid rings with the flow direction but, as we will establish in what follows, this is not the case. The rigid and supercoiled rings at hand align, in fact, much less with the flow direction than flexible ones but at the same time they also tumble much less. Accordingly, time intervals of tumbling, in which the (flexible) rings extend stronger into the gradient direction contribute much less to the time-averages and the contraction of the gradient-direction extent with the shear rate is less strong for the flexible rings, resulting into new exponents of the semiflexible ones.
The vorticity-direction dependence of the gyration tensor, shown in Fig. 5(e) and (f), is also quite unique for the rigid rings. The phenomenon of vorticity swelling of the flexible rings36,40 is absent here, because the solvent back-flow is not strong enough to stretch the stiff bonds of these rings. One sees, nevertheless, the solvent backflow effect in comparing the +HI-case, Fig. 5(e), in which it is present, with the −HI-case, Fig. 5(f), in which it is absent. Indeed, in the latter the ring contracts much more in the vorticity direction than in the former, where solvent backflow creates additional swelling pressure in the ring's interior.36 In this respect, it is important to notice that the conversion of writhe to twist and the reduction in vorticity contraction are both effects that take place solely in the presence of HI. Accordingly, we claim that the solvent backflow is crucial for both, i.e., only solvent backflow generates the necessary local stresses along the polymer backbone to bring about the topological conversion while at the same time keeping the ring sufficiently open in the vorticity direction, consistently with the unwrithed conformation seen, e.g., in Fig. 4(f).
The dependence of the shape parameters on the shear rate is summarized in Fig. 7. The decrease of  and
and  is compensated by the increase in the flow direction, so that
is compensated by the increase in the flow direction, so that  is more or less constant over most of the range of
is more or less constant over most of the range of  , see Fig. 7(a) and (b). This is again in stark contrast with flexible rings, for which
, see Fig. 7(a) and (b). This is again in stark contrast with flexible rings, for which  is dominated by
is dominated by  and it grows rapidly with shear rate.36,40 Here, in fact, the radius of gyration of all ring types decreases by a small amount before experiencing growth again for very high shear rates. The effect is observed more clearly in the case of −HI because the sample size covers longer time periods.
and it grows rapidly with shear rate.36,40 Here, in fact, the radius of gyration of all ring types decreases by a small amount before experiencing growth again for very high shear rates. The effect is observed more clearly in the case of −HI because the sample size covers longer time periods.
For the overall polymer size, as expressed by the gyration radius, neither the degree of supercoiling nor the hydrodynamics seem to significantly affect its dependence on shear rate. This changes if one looks at more detailed shape characteristics, such as the prolateness, Fig. 7(c) and (d), and anisotropy, Fig. 7(e) and (f). As they share common characteristics, we discuss  and
and  together. First of all, for the lower shear rates, there is now a clear splitting of the curves depending on the degree of supercoiling. Whereas the relaxed ring as well as the σsc = 0.00 start with
together. First of all, for the lower shear rates, there is now a clear splitting of the curves depending on the degree of supercoiling. Whereas the relaxed ring as well as the σsc = 0.00 start with  and low
and low  values at low shear rates, which grow as
values at low shear rates, which grow as  increases, the supercoiled rings are already prolate and very anisotropic at equilibrium, due to the writhed conformations they assume, see Fig. 3. Accordingly, the prolateness and shape anisotropy are affected very weakly by shear for the rings with high supercoiling degree, especially for the +HI-case, whereas in the −HI case prolateness and anisotropy become monotonically increasing at high
increases, the supercoiled rings are already prolate and very anisotropic at equilibrium, due to the writhed conformations they assume, see Fig. 3. Accordingly, the prolateness and shape anisotropy are affected very weakly by shear for the rings with high supercoiling degree, especially for the +HI-case, whereas in the −HI case prolateness and anisotropy become monotonically increasing at high  and all rings follow the same curves there. As mentioned above, solvent backflow for the +HI-case reduces prolateness and anisotropy by temporarily stabilizing more open, oblate conformations of the rings and by converting writhe into twist for the supercoiled ones.
and all rings follow the same curves there. As mentioned above, solvent backflow for the +HI-case reduces prolateness and anisotropy by temporarily stabilizing more open, oblate conformations of the rings and by converting writhe into twist for the supercoiled ones.
The average alignment of a polymer with the shear flow direction and its dependence on shear rate can be quantified by the orientational resistance  , a dimensionless quantity that can be constructed from the gyration tensor elements as:85
, a dimensionless quantity that can be constructed from the gyration tensor elements as:85
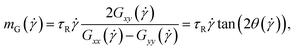 | (26) |
 is subtended between the flow direction and the axis of largest extension, i.e., the eigenvector corresponding to the largest eigenvalue,
is subtended between the flow direction and the axis of largest extension, i.e., the eigenvector corresponding to the largest eigenvalue,  , of the gyration tensor. We show in Fig. 8 the dependence of
, of the gyration tensor. We show in Fig. 8 the dependence of  on the shear rate for both the +HI-case, Fig. 8(a) and the −HI-case, Fig. 8(b). Here, the effect of hydrodynamics is quite pronounced, as we obtain quite different power-law dependencies for each case. As expected, the long axis of the rings tends to align with flow direction as
on the shear rate for both the +HI-case, Fig. 8(a) and the −HI-case, Fig. 8(b). Here, the effect of hydrodynamics is quite pronounced, as we obtain quite different power-law dependencies for each case. As expected, the long axis of the rings tends to align with flow direction as  grows but much weaker in the +HI-case than in the −HI-case. Indeed, the orientational resistance
grows but much weaker in the +HI-case than in the −HI-case. Indeed, the orientational resistance  is very strong for the +HI-case, scaling as
is very strong for the +HI-case, scaling as  , to be compared with the scaling
, to be compared with the scaling  for flexible rings,40 whereas
for flexible rings,40 whereas 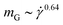 in the −HI-case. Rigid and supercoiled rings are therefore orientationally stiff under shear, since the solvent backflow hinders strong alignment with the flow axis. The forces of the solvent on the rings are ‘used up’ in bringing about occasional opening of the ring as well as the associated conversion of writhe into twist for the supercoiled ones, and not for aligning the rings with the flow, whereas in the −HI-case, the absence of coupling with the solvent allows the undisturbed velocity profile of the latter to align the polymer more strongly with the x-axis.
in the −HI-case. Rigid and supercoiled rings are therefore orientationally stiff under shear, since the solvent backflow hinders strong alignment with the flow axis. The forces of the solvent on the rings are ‘used up’ in bringing about occasional opening of the ring as well as the associated conversion of writhe into twist for the supercoiled ones, and not for aligning the rings with the flow, whereas in the −HI-case, the absence of coupling with the solvent allows the undisturbed velocity profile of the latter to align the polymer more strongly with the x-axis.
The strong orientational resistance of the supercoiled polymers, in conjunction with the previous results on the dependence of  on the shear rate, shown in Fig. 5, creates an apparent contradiction. Indeed, if we visualize the polymer as an object oriented on a stable configuration that forms an angle
on the shear rate, shown in Fig. 5, creates an apparent contradiction. Indeed, if we visualize the polymer as an object oriented on a stable configuration that forms an angle 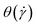 with the x-axis, and making the small-angle approximation
with the x-axis, and making the small-angle approximation  , valid only for the −HI-case, we can write:
, valid only for the −HI-case, we can write:
 | (27) |
Ignoring the weak dependence of  on the shear rate [Fig. 5(b)] (fitted exponent 0.03, for
on the shear rate [Fig. 5(b)] (fitted exponent 0.03, for  , not shown) and writing
, not shown) and writing 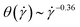 , eqn (27) yields the power-law
, eqn (27) yields the power-law  , stronger than the measured power-law
, stronger than the measured power-law 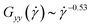 in Fig. 5(c). Moreover, the corresponding power-laws for flexible polymers read
in Fig. 5(c). Moreover, the corresponding power-laws for flexible polymers read 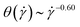 and
and  , i.e., in that case the gradient-direction contraction is weaker than that of the rigid rings although their alignment with the flow direction is stronger. This can be partially explained by the fact that for the flexible ring case,
, i.e., in that case the gradient-direction contraction is weaker than that of the rigid rings although their alignment with the flow direction is stronger. This can be partially explained by the fact that for the flexible ring case, 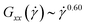 ; even so, it is evident that the picture of an effective ellipsoid orienting itself at a stable angle
; even so, it is evident that the picture of an effective ellipsoid orienting itself at a stable angle  with the x-axis during shear flow is too simplistic, as the polymer dynamics is richer in patterns developed by the combination of thermal and hydrodynamic forces on the monomers.
with the x-axis during shear flow is too simplistic, as the polymer dynamics is richer in patterns developed by the combination of thermal and hydrodynamic forces on the monomers.
Polymers have been shown to undergo tumbling motion under shear flow both in experiment86,87 and simulations.36,69 The tumbling dynamics are characterized by a rapid collapse in one direction (x-axis) followed by the expansion in another direction (y-axis). Such events are cyclical yet not periodic, as the molecule undergoes intermittent phases between stable orientations and vivid tumbling motions. During the latter, a tumbling frequency  can be deducted from the cross-correlation function between fluctuations of
can be deducted from the cross-correlation function between fluctuations of  and
and 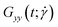 around their mean values separated by a time difference τ:36,86,87
around their mean values separated by a time difference τ:36,86,87
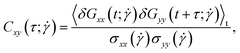 | (28) |
 and
and 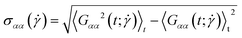 . If the polymer undergoes tumbling motions, the cross-correlation function will have a damped oscillatory behaviour with a pronounced maximum at a time
. If the polymer undergoes tumbling motions, the cross-correlation function will have a damped oscillatory behaviour with a pronounced maximum at a time  and a pronounced minimum at
and a pronounced minimum at 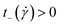 . Similar to their flexible counterparts, supercoiled rings feature tumbling dynamics at high shear rates, see Fig. 9, with clear minimum and maximum peaks. The oscillation period
. Similar to their flexible counterparts, supercoiled rings feature tumbling dynamics at high shear rates, see Fig. 9, with clear minimum and maximum peaks. The oscillation period  of this motion can be extracted from the correlation function
of this motion can be extracted from the correlation function  as:
as: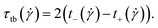 | (29) |
The resulting tumbling frequencies  , normalized with the inverse of the relaxation time, are shown in Fig. 10. As expected, the tumbling frequency grows with the shear rate; however, the resulting growth
, normalized with the inverse of the relaxation time, are shown in Fig. 10. As expected, the tumbling frequency grows with the shear rate; however, the resulting growth  is much weaker than the
is much weaker than the 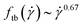 dependence of the flexible rings.36 Rigidity slows down the rotational motion of the rings under shear, so that a rigid ring at a specific Weissenberg number tumbles and orients to the flow in a way akin to a flexible ring at some lower Weissenberg number, where tumbling is less frequent. In this way, for the same Weissenberg number, the rigid rings have fewer phases than their flexible counterparts in which they undergo tumbling motions that cause
dependence of the flexible rings.36 Rigidity slows down the rotational motion of the rings under shear, so that a rigid ring at a specific Weissenberg number tumbles and orients to the flow in a way akin to a flexible ring at some lower Weissenberg number, where tumbling is less frequent. In this way, for the same Weissenberg number, the rigid rings have fewer phases than their flexible counterparts in which they undergo tumbling motions that cause  to grow, resulting thereby in a stronger gradient-direction contraction than for flexible cyclic macromolecules.
to grow, resulting thereby in a stronger gradient-direction contraction than for flexible cyclic macromolecules.
We finally discuss the effect of the polymers’ presence on the solvent's viscosity, by extracting their intrinsic viscosity  , defined as:
, defined as:
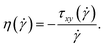 | (30) |
In eqn (30) above, the polymer stress tensor  is calculated in the simulation as a time average:48
is calculated in the simulation as a time average:48
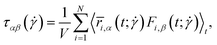 | (31) |
 has been defined after eqn (20) and
has been defined after eqn (20) and  is the β-component of the total force from other beads acting on monomer i at time t. Results are shown in Fig. 11. As with other polymer architectures, upon a certain threshold value of
is the β-component of the total force from other beads acting on monomer i at time t. Results are shown in Fig. 11. As with other polymer architectures, upon a certain threshold value of  , shear thinning takes place and the shear-rate-dependent viscosity has a power-law dependence on
, shear thinning takes place and the shear-rate-dependent viscosity has a power-law dependence on 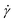 with an exponent matching that of the scaling of
with an exponent matching that of the scaling of  . This is in agreement with predictions of the Giesekus approximation for the stress tensor,51,88,89 according to which
. This is in agreement with predictions of the Giesekus approximation for the stress tensor,51,88,89 according to which  . As the latter is based on a free-draining approximation (no HI) but the scaling holds here also for the +HI-case, we surmise that the intrinsic viscosity is not affected by the presence of hydrodynamic interactions, despite the significant effects these have on the molecular orientation in the shear cell.
. As the latter is based on a free-draining approximation (no HI) but the scaling holds here also for the +HI-case, we surmise that the intrinsic viscosity is not affected by the presence of hydrodynamic interactions, despite the significant effects these have on the molecular orientation in the shear cell.
6. Conclusions
By means of computer simulations that take into account hydrodynamic interactions, we have examined in detail the behavior of supercoiled ring polymers in steady shear, comparing the results to those obtained for flexible polymers and therefore identifying the key factors that influence the conformation and dynamics under steady flow. We found that the combination of bending rigidity and supercoiling renders such rings much more robust in their sizes, shapes and orientations than their flexible counterparts and that it also reduces the frequency of their tumbling motions. Despite the fact that they display a much higher orientational resistance to flow than flexible rings, supercoiled rings are indeed affected by shear in nontrivial ways, and mostly when hydrodynamic interactions are taken into account. Particularly relevant are the effects of the solvent on the vorticity extension of the ring, where back-flow significantly reduces the vorticity contraction seen in simulations in the absence of hydrodynamics. The topological properties of the rings, namely their writhe and twist, are quite robust for a wide range of shear rates, with the polymers maintaining mostly writhed configurations with very little twist. However, at sufficiently strong shear rates, writhe is rapidly reduced in favour of the twist in the case in which hydrodynamics is active. We have not been able to test whether the same topological transformation of writhe to twist would also take place in the absence of hydrodynamic interactions due to current simulation limitations outlined before.Our results highlight the interplay between topology, hydrodynamics and thermal fluctuations in dilute polymer solutions. Experimentally, they can in principle be tested in suitably constructed microfluidic devices with single-molecule techniques.39,90,91 Indeed, properties of ring polymers in flows are being elucidated with these techniques33,84,91–93 and even viscoelasticity of supercoiled plasmids has been considered, however only in higher concentration blends so far.5,94 Our results include experimentally accessible chain extent and other characteristics, but to be measured in experiment the DNA plasmids would have to be first sorted according to their supercoiling degree. As our simulations concerned only relatively short rings, the gyration radius depends only weakly on the supercoiling, hence a method other than gel electrophoresis would have to be used. Future directions include the study of the dynamical behaviour in higher concentrations or for topologically linked rigid rings, such as catenanes and the kinetoplast. As a further highly interesting avenue of exploration, particularly in connection to experiments, we see the investigation of longer and/or more flexible rings with torsional stiffness in shear flow. Such rings with high supercoiling degrees display branched structure in equilibrium. The orientation of the branches as well as their restructuring and hydrodynamic swelling connected to the conversion of writhe to twist in shear flow is highly desired, not only due to the biological context, but also as a future perspective tool to tune mechanical properties of polymer solutions using topology in nonequilibrium conditions. The work at hand presents the first step on the way to achieve these goals.
Author contributions
CS wrote the simulation code, performed the calculations, analysed the results and wrote the paper. JS and AZ designed research, advised on the calculations, analysed the results and wrote the paper. CNL designed research, analysed the results and wrote the paper.Conflicts of interest
There are no conflicts to declare.Appendix
Software details
The code for the simulations is written in Fortran 90, visualisations of polymers are created with VMD.95Velocity Verlet algorithm with rotational degrees of freedom
The rotational degrees of freedom have to be considered within the velocity Verlet algorithm which is extended by the rotational dynamics consisting of the following three steps: | (32) |
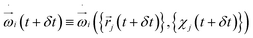 , i.e. the angular acceleration at time t + δt is computed from the positions
, i.e. the angular acceleration at time t + δt is computed from the positions  and orientations χj at time t + δt. The steps are performed simultaneously to the translational counterparts where the monomer is moved as a whole according to the bead velocity
and orientations χj at time t + δt. The steps are performed simultaneously to the translational counterparts where the monomer is moved as a whole according to the bead velocity  . In the rotational part, first, the angular velocity is boosted by a half-kick of the current angular acceleration. A rotation
. In the rotational part, first, the angular velocity is boosted by a half-kick of the current angular acceleration. A rotation  of the monomer orientation χi(t) by an angle
of the monomer orientation χi(t) by an angle  around rotation axis
around rotation axis  follows. Next,
follows. Next,  is calculated as
is calculated as  . The torque and hence also the angular acceleration depend on both, the location (all potentials) and the orientation (torsion and alignment) of the monomers.
. The torque and hence also the angular acceleration depend on both, the location (all potentials) and the orientation (torsion and alignment) of the monomers.  and
and  are always related by the linear equation
are always related by the linear equation  . The forces are calculated as a sum over the gradients of the potentials (5), (6), (7), (9), and (10). Finally, in step 4 a second half-kick updates the angular velocity with the new
. The forces are calculated as a sum over the gradients of the potentials (5), (6), (7), (9), and (10). Finally, in step 4 a second half-kick updates the angular velocity with the new 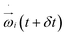 .
.  is computed during the calculation of the torque in step 3 of (32) at time t and is therefore stored for the next rotation at t + δt.
is computed during the calculation of the torque in step 3 of (32) at time t and is therefore stored for the next rotation at t + δt.
Computation of forces on patches
The potentials for bending (7) and alignment (10) depend on angles formed by two segments connecting three positions, respectively, so that their gradients are the same function with different arguments. In contrast, the torsion potential (9) involves angles formed by three segments connecting four positions and has an offset ψ0 in the argument of the cosine cos(ψb/r − ψ0). The cosine and sine in (9) are computed as | (33) |
 | (34) |
The forces on beads and patches are derived from their gradients with respect to the position  where a stands for either a bead or a patch. The force on particle a resulting from the three potentials amounts to:
where a stands for either a bead or a patch. The force on particle a resulting from the three potentials amounts to:
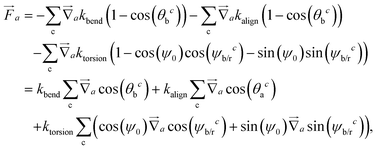 | (35) |
 ,
, 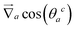 , and
, and  is performed following the calculations of Allen and Tildesley96 (App. C.2, p. 491–494). The authors omit the gradient terms of the sine appearing in (35). The missing derivations are performed in an analogous way by rewriting the sine of the torsional angle (34) formed by beads
is performed following the calculations of Allen and Tildesley96 (App. C.2, p. 491–494). The authors omit the gradient terms of the sine appearing in (35). The missing derivations are performed in an analogous way by rewriting the sine of the torsional angle (34) formed by beads  ,
,  and patches
and patches  ,
,  :
: | (36) |
 and
and  and
and  are defined for convenience. The gradients with respect to bead position i and i + 1 are computed by the following derivatives with
are defined for convenience. The gradients with respect to bead position i and i + 1 are computed by the following derivatives with  and
and  :
: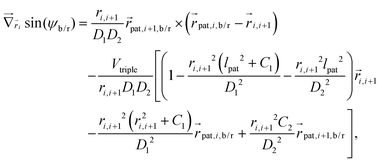 | (37) |
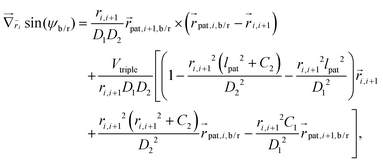 | (38) |
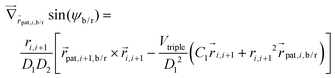 | (39) |
 | (40) |
Quaternion formalism
Quaternions are used to quantify the monomer orientation and the corresponding rotational dynamics for the implementation of the χi into the simulations. This reduces the rotational dynamics to quaternion multiplications and offers a way of regaining the patch positions relative to their beads if they are needed for calculations. A quaternion can be written as the 4-tuple where q0 ∈
where q0 ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) is called the scalar part and
is called the scalar part and  the vector part.
the vector part.  with zero scalar part is called a vector quaternion.
with zero scalar part is called a vector quaternion.  is called a scalar quaternion for
is called a scalar quaternion for  in which case it is equivalent to a scalar q0. The multiplication of two quaternions qa and qb is defined in the following way:
in which case it is equivalent to a scalar q0. The multiplication of two quaternions qa and qb is defined in the following way: | (41) |
The quaternions form a non-abelian group with respect to their multiplication which is associative. The conjugate of a quaternion  is defined as
is defined as  which brings about the quaternion norm
which brings about the quaternion norm  and the inverse quaternion q−1 = q*/|q|2, qq−1 = q−1q = 1. A rotation
and the inverse quaternion q−1 = q*/|q|2, qq−1 = q−1q = 1. A rotation ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3 →
3 → ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3,
3,  by an angle α around axis
by an angle α around axis 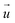 can be expressed by quaternion multiplication. A 3D vector
can be expressed by quaternion multiplication. A 3D vector  is projected onto the vector quaternion
is projected onto the vector quaternion  and the rotation is performed with a unit quaternion
and the rotation is performed with a unit quaternion 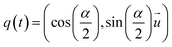 with
with  , so that97q* = q−1:
, so that97q* = q−1:
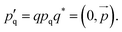 | (42) |
The rotated vector  is read off the resulting vector quaternion
is read off the resulting vector quaternion  . The monomer orientations χi(t) are represented by unit quaternions
. The monomer orientations χi(t) are represented by unit quaternions  with
with  . The qi(t) carry the information about a rotation axis
. The qi(t) carry the information about a rotation axis  and an angle αi corresponding to the orientation of monomer i at time t. The patch positions k = 1, 2, 3 ≡ blue, red, green are recovered by scaling the standard basis vectors to
and an angle αi corresponding to the orientation of monomer i at time t. The patch positions k = 1, 2, 3 ≡ blue, red, green are recovered by scaling the standard basis vectors to  and rotating them with qi(t):
and rotating them with qi(t):
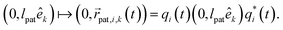 | (43) |
In this way, the patch vectors are always guaranteed to both have the correct distance to the bead and be orthogonal to each other so that they span an orthogonal reference system. At the beginning of a simulation run the monomers are given a starting orientation qi(0) that sets the initial patch positions 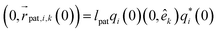 . The second step of the rotational velocity Verlet algorithm (32) comprises a rotation of the orientation qi(t) around axis
. The second step of the rotational velocity Verlet algorithm (32) comprises a rotation of the orientation qi(t) around axis  and by an angle
and by an angle  to qi(t + δt). In terms of quaternions it is computed in the following way with
to qi(t + δt). In terms of quaternions it is computed in the following way with  :
:
 | (44) |
Because of associativity the updated qi(t+δt) imparts the same 3D rotation of a vector  to
to  as qi(t) followed by a rotation according to
as qi(t) followed by a rotation according to  :
:
 | (45) |
At time t, the orientation is given by the time-ordered product of all rotations to the left of qi(0):
 | (46) |
and the step (45) can be repeated t/δt + 1 many times:
 | (47) |
Inserting  and
and 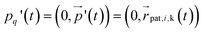 into (45) and (47) makes evident that (43) and (44) reproduce the monomer orientations at all time steps. The quaternions must always have unity norm, i.e., |qi(t)| = 1 so that they represent proper rotations. It holds that
into (45) and (47) makes evident that (43) and (44) reproduce the monomer orientations at all time steps. The quaternions must always have unity norm, i.e., |qi(t)| = 1 so that they represent proper rotations. It holds that  , i.e., normalization to unity is guaranteed for all time steps t, if the initial qi(0) have unity norm. The quaternions are normalized
, i.e., normalization to unity is guaranteed for all time steps t, if the initial qi(0) have unity norm. The quaternions are normalized  every 100th MD step to counteract numerical errors that can possibly occur along the way.
every 100th MD step to counteract numerical errors that can possibly occur along the way.
Relaxation time of supercoiled rings
The relaxation times of supercoiled rings can be extracted by means of the “end-to-end” correlation function,40,98 | (48) |
 defines a vector joining two monomers of the chain that are separated by N/2 monomers and 〈…〉m represents an average over the N/2 end-to-end connections; results are shown in Fig. 12. For the +HI-case, shown in Fig. 12(a), we extended the simulation up to times t ≅ 4 × 104τMPCD, whereas for the −HI-case, shown in Fig. 12(b), which is computationally cheaper, we were able to reach times t ≅ 106τMPCD. The latter case clearly shows the characteristic exponential decay of the correlation functions, establishing a relaxation time τR ≅ 3 × 105τMPCD, in very good agreement with the estimate presented in the main text. On the other hand, the curves in Fig. 12(a) demonstrate that the correlation functions for the +HI-case decay much faster (by about one order of magnitude), again confirming the estimate of τR in the main text.
defines a vector joining two monomers of the chain that are separated by N/2 monomers and 〈…〉m represents an average over the N/2 end-to-end connections; results are shown in Fig. 12. For the +HI-case, shown in Fig. 12(a), we extended the simulation up to times t ≅ 4 × 104τMPCD, whereas for the −HI-case, shown in Fig. 12(b), which is computationally cheaper, we were able to reach times t ≅ 106τMPCD. The latter case clearly shows the characteristic exponential decay of the correlation functions, establishing a relaxation time τR ≅ 3 × 105τMPCD, in very good agreement with the estimate presented in the main text. On the other hand, the curves in Fig. 12(a) demonstrate that the correlation functions for the +HI-case decay much faster (by about one order of magnitude), again confirming the estimate of τR in the main text.
 | ||
| Fig. 12 The equilibrium end-to-end correlation function of supercoiled rings of length N = 100 as a function of time starting from the initialization states for + HI, panel (a), and −HI, panel (b). | ||
Acknowledgements
We acknowledge support from the European Union (Horizon-MSCA-Doctoral Networks) through the project QLUSTER (HORIZON-MSCA-2021-DN-01-GA101072964). The computations leading to the results of this work have been carried out in part at the Vienna Scientific Cluster (VSC).References
- A. V. Pinheiro, D. Han, W. M. Shih and H. Yan, Nat. Nanotechnol., 2011, 6, 763–772 CrossRef CAS PubMed
.
- N. Seeman, J. Chen, S. Du, J. Mueller, Y. Zhang, T.-J. Fu, H. Wang, Y. Wang and S. Zhang, New J. Chem., 1993, 17, 739–755 CAS
.
- J. Chen and N. C. Seeman, Nature, 1991, 350, 631–633 CrossRef CAS PubMed
.
- E. Stiakakis, N. Jung, N. Adžić, T. Balandin, E. Kentzinger, U. Rücker, R. Biehl, J. K. G. Dhont, U. Jonas and C. N. Likos, Nat. Commun., 2021, 12, 7167 CrossRef CAS PubMed
.
- J. Smrek, J. Garamella, R. Robertson-Anderson and D. Michieletto, Sci. Adv., 2021, 7, eabf9260 CrossRef CAS PubMed
.
- C. N. Likos, Phys. Rep., 2001, 348, 267–439 CrossRef CAS
.
- R. Staňo, C. N. Likos and J. Smrek, Soft Matter, 2023, 19, 17–30 RSC
.
- A. Narros, A. J. Moreno and C. N. Likos, Soft Matter, 2010, 6, 2435–2441 RSC
.
- A. V. Vologodskii, V. V. Anshelevich, A. V. Lukashin and M. D. Frank-Kamenetskii, Nature, 1979, 280, 294–298 CrossRef CAS PubMed
.
-
Plasmid Biology, ed. B. E. Funnell and G. J. Phillips, John Wiley & Sons, Ltd, 2004 Search PubMed
.
- R. P. Koche, E. Rodriguez-Fos, K. Helmsauer, M. Burkert, I. C. MacArthur, J. Maag, R. Chamorro, N. Munoz-Perez, M. Puiggròs, H. Dorado Garcia, Y. Bei, C. Röefzaad, V. Bardinet, A. Szymansky, A. Winkler, T. Thole, N. Timme, K. Kasack, S. Fuchs, F. Klironomos, N. Thiessen, E. Blanc, K. Schmelz, A. Künkele, P. Hundsdörfer, C. Rosswog, J. Theissen, D. Beule, H. Deubzer, S. Sauer, J. Toedling, M. Fischer, F. Hertwig, R. F. Schwarz, A. Eggert, D. Torrents, J. H. Schulte and A. G. Henssen, Nat. Genet., 2020, 52, 29–34 CrossRef CAS PubMed
.
- A. R. Klotz, B. W. Soh and P. S. Doyle, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 121–127 CrossRef CAS PubMed
.
- J. Chen, P. T. Englund and N. R. Cozzarelli, EMBO J., 1995, 14, 6339–6347 CrossRef CAS PubMed
.
- D. Racko, F. Benedetti, J. Dorier and A. Stasiak, Nucleic Acids Res., 2018, 47, 521–532 CrossRef PubMed
.
- Y. Ding, C. Manzo, G. Fulcrand, F. Leng, D. Dunlap and L. Finzi, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15402–15407 CrossRef CAS PubMed
.
- R. N. Irobalieva, J. M. Fogg, D. J. Catanese, T. Sutthibutpong, M. Chen, A. K. Barker, S. J. Ludtke, S. A. Harris, M. F. Schmid, W. Chiu and L. Zechiedrich, Nat. Commun., 2015, 6, 8440 CrossRef CAS PubMed
.
- G. Fudenberg, M. Imakaev, C. Lu, A. Goloborodko, N. Abdennur and L. A. Mirny, Cell Rep., 2016, 15, 2038–2049 CrossRef CAS PubMed
.
- A. Zidovska, D. A. Weitz and T. J. Mitchison, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15555–15560 CrossRef CAS PubMed
.
- C. Arnould, V. Rocher, A.-L. Finoux, T. Clouaire, K. Li, F. Zhou, P. Caron, P. E. Mangeot, E. P. Ricci, R. Mourad, J. E. Haber, D. Noordermeer and G. Legube, Nature, 2021, 590, 660–665 CrossRef CAS PubMed
.
- J. D. Halverson, W. B. Lee, G. S. Grest, A. Y. Grosberg and K. Kremer, J. Chem. Phys., 2011, 134, 204904 CrossRef PubMed
.
- A. Rosa and R. Everaers, Phys. Rev. Lett., 2014, 112, 118302 CrossRef PubMed
.
- M. Kapnistos, M. Lang, D. Vlassopoulos, W. Pyckhout-Hintzen, D. Richter, D. Cho, T. Chang and M. Rubinstein, Nat. Mater., 2008, 7, 997–1002 CrossRef CAS PubMed
.
- D. Parisi, S. Costanzo, Y. Jeong, J. Ahn, T. Chang, D. Vlassopoulos, J. D. Halverson, K. Kremer, T. Ge, M. Rubinstein, G. S. Grest, W. Srinin and A. Y. Grosberg, Macromolecules, 2021, 54, 2811–2827 CrossRef CAS
.
- Q. Huang, J. Ahn, D. Parisi, T. Chang, O. Hassager, S. Panyukov, M. Rubinstein and D. Vlassopoulos, Phys. Rev. Lett., 2019, 122, 208001 CrossRef CAS PubMed
.
- T. C. O'Connor, T. Ge, M. Rubinstein and G. S. Grest, Phys. Rev. Lett., 2020, 124, 027801 CrossRef PubMed
.
- J. D. Halverson, G. S. Grest, A. Y. Grosberg and K. Kremer, Phys. Rev. Lett., 2012, 108, 038301 CrossRef PubMed
.
- T. C. O'Connor, T. Ge and G. S. Grest, J. Rheol., 2022, 66, 49–65 CrossRef
.
- J. Smrek, I. Chubak, C. N. Likos and K. Kremer, Nat. Commun., 2020, 11, 26 CrossRef CAS PubMed
.
- T. Ge, S. Panyukov and M. Rubinstein, Macromolecules, 2016, 49, 708–722 CrossRef CAS PubMed
.
- J. Smrek and A. Y. Grosberg, J. Phys.: Condens. Matter, 2015, 27, 064117 CrossRef CAS PubMed
.
- A. Rosa and R. Everaers, Eur. Phys. J. E, 2019, 42, 7 CrossRef PubMed
.
- E. Ghobadpour, M. Kolb, M. R. Ejtehadi and R. Everaers, Phys. Rev. E, 2021, 104, 014501 CrossRef CAS PubMed
.
- Y. Zhou, K.-W. Hsiao, K. E. Regan, D. Kong, G. B. McKenna, R. M. Robertson-Anderson and C. M. Schroeder, Nat. Commun., 2019, 10, 1753 CrossRef PubMed
.
- Y. Zhou, C. D. Young, M. Lee, S. Banik, D. Kong, G. B. McKenna, R. M. Robertson-Anderson, C. E. Sing and C. M. Schroeder, J. Rheol., 2021, 65, 729–744 CrossRef CAS
.
- C. D. Young, Y. Zhou, C. M. Schroeder and C. E. Sing, J. Rheol., 2021, 65, 757–777 CrossRef CAS
.
- M. Liebetreu, M. Ripoll and C. N. Likos, ACS Macro Lett., 2018, 7, 447–452 CrossRef CAS PubMed
.
- K. W. Hsiao, C. M. Schroeder and C. E. Sing, Macromolecules, 2016, 49, 1961–1971 CrossRef CAS
.
- C. D. Young, J. R. Qian, M. Marvin and C. E. Sing, Phys. Rev. E, 2019, 99, 062502 CrossRef CAS PubMed
.
- M. Q. Tu, M. Lee, R. M. Robertson-Anderson and C. M. Schroeder, Macromolecules, 2020, 53, 9406–9419 CrossRef CAS
.
- M. Liebetreu and C. N. Likos, Commun. Mater., 2020, 1, 4 CrossRef
.
- M. Ripoll, R. Winkler and G. Gompper, Eur. Phys. J. E, 2007, 23, 349–354 CrossRef CAS PubMed
.
- C. Pastorino, T. Kreer, M. Müller and K. Binder, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 026706 CrossRef CAS PubMed
.
-
B. Dünweg and A. J. Ladd, Advanced computer simulation approaches for soft matter sciences III, 2009, pp. 89–166 Search PubMed
.
-
G. Gompper, T. Ihle, D. M. Kroll and R. G. Winkler, in Multi-Particle Collision Dynamics: A Particle-Based Mesoscale Simulation Approach to the Hydrodynamics of Complex Fluids, ed. C. Holm and K. Kremer, Springer Berlin Heidelberg, Berlin, Heidelberg, 2009, pp. 1–87 Search PubMed
.
- R. Kapral, Adv. Chem. Phys., 2008, 140, 89 CrossRef CAS
.
- A. Malevanets and J. M. Yeomans, EPL, 2000, 52, 231 CrossRef CAS
.
- R. G. Winkler, K. Mussawisade, M. Ripoll and G. Gompper, J. Phys.: Condens. Matter, 2004, 16, S3941–S3954 CrossRef CAS
.
- J. F. Ryder and J. M. Yeomans, J. Chem. Phys., 2006, 125, 194906 CrossRef CAS PubMed
.
- M. Ripoll, R. G. Winkler and G. Gompper, Phys. Rev. Lett., 2006, 96, 188302 CrossRef CAS PubMed
.
- M. Ripoll, P. Holmqvist, R. G. Winkler, G. Gompper, J. K. Dhont and M. P. Lettinga, Phys. Rev. Lett., 2008, 101, 168302 CrossRef CAS PubMed
.
- C. C. Huang, R. G. Winkler, G. Sutmann and G. Gompper, Macromolecules, 2010, 43, 10107–10116 CrossRef CAS
.
- A. W. Lees and S. F. Edwards, J. Phys. C: Solid State Phys., 1972, 5, 1921 CrossRef
.
- N. Kikuchi, C. M. Pooley, J. F. Ryder and J. M. Yeomans, J. Chem. Phys., 2003, 119, 6388–6395 CrossRef CAS
.
- A. Nikoubashman and M. P. Howard, Macromolecules, 2017, 50, 8279–8289 CrossRef CAS
.
- M. Formanek and A. J. Moreno, Macromolecules, 2019, 52, 1821–1831 CrossRef CAS
.
- J. K. Novev, A. Doostmohammadi, A. Zöttl and J. M. Yeomans, Curr. Res. Food Sci., 2020, 3, 122–133 CrossRef CAS PubMed
.
- E. Allahyarov and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 036702 CrossRef CAS PubMed
.
- D. S. Bolintineanu, J. B. Lechman, S. J. Plimpton and G. S. Grest, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 066703 CrossRef PubMed
.
- L. B. Weiss, A. Nikoubashman and C. N. Likos, ACS Macro Lett., 2017, 6, 1426–1431 CrossRef CAS PubMed
.
- L. Cannavacciuolo, R. Winkler and G. Gompper, EPL, 2008, 83, 34007 CrossRef
.
- R. Chelakkot, R. G. Winkler and G. Gompper, EPL, 2010, 91, 14001 CrossRef
.
- M. Webster and J. Yeomans, J. Chem. Phys., 2005, 122, 164903 CrossRef CAS PubMed
.
- A. Nikoubashman and C. N. Likos, Macromolecules, 2010, 43, 1610–1620 CrossRef CAS
.
- D. A. Fedosov, S. P. Singh, A. Chatterji, R. G. Winkler and G. Gompper, Soft Matter, 2012, 8, 4109–4120 RSC
.
- S. P. Singh, A. Chatterji, G. Gompper and R. G. Winkler, Macromolecules, 2013, 46, 8026–8036 CrossRef CAS
.
- D. Jaramillo-Cano, M. Formanek, C. N. Likos and M. Camargo, J. Phys. Chem. B, 2018, 122, 4149–4158 CrossRef CAS PubMed
.
- D. Toneian, C. N. Likos and G. Kahl, J. Phys.: Condens. Matter, 2019, 31, 24LT02 CrossRef CAS PubMed
.
- D. Jaramillo-Cano, M. Camargo, C. N. Likos and I. C. Gârlea, Macromolecules, 2020, 53, 10015–10027 CrossRef CAS PubMed
.
- W. Chen, J. Chen and L. An, Soft Matter, 2013, 9, 4312–4318 RSC
.
- W. Chen, J. Chen, L. Liu, X. Xu and L. An, Macromolecules, 2013, 46, 7542–7549 CrossRef CAS
.
- A. Zöttl and J. M. Yeomans, Nat. Phys., 2019, 15, 554–558 Search PubMed
.
- K. Qi, E. Westphal, G. Gompper and R. G. Winkler, Phys. Rev. Lett., 2020, 124, 068001 CrossRef CAS PubMed
.
- A. Zöttl, EPL, 2023, 143, 17003 Search PubMed
.
- A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605–8613 CrossRef CAS
.
- T. Ihle, E. Tüzel and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 035701 CrossRef CAS PubMed
.
- T. Ihle and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 066705 CrossRef CAS PubMed
.
- C.-C. Huang, A. Varghese, G. Gompper and R. G. Winkler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 013310 CrossRef PubMed
.
- S. H. Lee and R. Kapral, J. Chem. Phys., 2006, 124, 214901 CrossRef PubMed
.
- M. Ripoll, K. Mussawisade, R. G. Winkler and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 016701 CrossRef CAS PubMed
.
- M. Ripoll, R. Winkler and G. Gompper, Eur. Phys. J. E, 2007, 23, 349–354 CrossRef CAS PubMed
.
- K. Klenin and J. Langowski, Biopolymers, 2000, 54, 307–317 CrossRef CAS PubMed
.
- G. Călugăreanu, Czechoslov. Math. J., 1961, 11, 588–625 Search PubMed
.
- J. Rudnick and G. Gaspari, J. Phys. A: Math. Gen., 1986, 19, L191 CrossRef
.
- K. W. Hsiao, C. M. Schroeder and C. E. Sing, Macromolecules, 2016, 49, 1961–1971 CrossRef CAS
.
- C. Aust, M. Kröger and S. Hess, Macromolecules, 1999, 32, 5660–5672 CrossRef CAS
.
- R. E. Teixeira, H. P. Babcock, E. S. G. Shaqfeh and S. Chu, Macromolecules, 2005, 38, 581–592 CrossRef CAS
.
- C. M. Schroeder, R. E. Teixeira, E. S. G. Shaqfeh and S. Chu, Phys. Rev. Lett., 2005, 95, 018301 CrossRef PubMed
.
- P. S. Doyle, E. S. G. Shaqfeh and A. P. Gast, J. Fluid Mech., 1997, 334, 251–291 CrossRef CAS
.
- C. M. Schroeder, R. E. Teixeira, E. S. G. Shaqfeh and S. Chu, Macromolecules, 2005, 38, 1967–1978 CrossRef CAS
.
- M. Tanyeri and C. M. Schroeder, Nano Lett., 2013, 13, 2357–2364 CrossRef CAS PubMed
.
- C. M. Schroeder, J. Rheol., 2018, 62, 371–403 CrossRef CAS
.
- C. M. Schroeder, H. P. Babcock, E. S. G. Shaqfeh and S. Chu, Science, 2003, 301, 1515–1519 CrossRef CAS PubMed
.
- B. W. Soh, A. R. Klotz, R. M. Robertson-Anderson and P. S. Doyle, Phys. Rev. Lett., 2019, 123, 048002 CrossRef PubMed
.
- K. R. Peddireddy, M. Lee, Y. Zhou, S. Adalbert, S. Anderson, C. M. Schroeder and R. M. Robertson-Anderson, Soft Matter, 2020, 16, 152–161 RSC
.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed
.
-
M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, 2017, vol. 2, pp. 491–494 Search PubMed
.
- D. J. Evans and S. Murad, Mol. Phys., 1977, 34, 327–331 CrossRef CAS
.
- L. Tubiana, A. Rosa, F. Fragiacomo and C. Micheletti, Macromolecules, 2013, 46, 3669–3678 CrossRef CAS
.
Footnotes |
| † These authors contributed equally to this work. |
| ‡ We show in the Appendix that these estimates agree well with the characteristic decay times of the orientational correlation functions of the rings at equilibrium. |
| This journal is © The Royal Society of Chemistry 2024 |