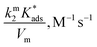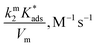Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quinolin-2(1H-)-one-isoxazole dye as an acceptor for mild addition of bisulfite in cationic or zwitterionic aqueous micellar solutions†
Guillermo E.
Quintero
 a,
Catalina
Espinoza
a,
Jhesua
Valencia
b,
Daniel
Insuasty
b,
William
Tiznado
a,
Catalina
Espinoza
a,
Jhesua
Valencia
b,
Daniel
Insuasty
b,
William
Tiznado
 c,
Luis
Leiva-Parra
c,
Luis
Leiva-Parra
 d,
José G.
Santos
a,
Edwin G.
Pérez
d,
José G.
Santos
a,
Edwin G.
Pérez
 a and
Margarita E.
Aliaga
a and
Margarita E.
Aliaga
 *a
*a
aFacultad de Química y de Farmacia, Escuela de Química, Pontificia Universidad Católica de Chile, Casilla 306, Santiago 6094411, Chile. E-mail: mealiaga@uc.cl
bDepartamento de Química y Biología, División de Ciencias Básicas, Universidad del Norte, Km 5 vía Puerto Colombia, Barranquilla 081007, Colombia
cCentro de Química Teórica & Computacional (CQT&C), Departamento de Ciencias Químicas, Facultad de Ciencias Exactas, Universidad Andres Bello, República 275, 8370146, Santiago, Chile
dFacultad de Ingeniería y Arquitectura, Universidad Central de Chile (UCEN), Santa Isabel 1186, 8370146, Santiago, Chile
First published on 2nd October 2024
Abstract
(E)-6-Methoxy-1-methyl-3-(2-(3-methyl-4-nitroisoxazol-5-yl)vinyl)quinolin-2(1H)-one dye (MQI) has been synthesized, and its structural and electronic properties have been characterized by employing UV-vis spectroscopy in combination with computational methods. The MQI dye has been assessed as an activated Michael acceptor-type probe toward bisulfite ions. This reaction was kinetically tested in different mild, cationic (cetyltrimethylammonium bromide, cetyltrimethylammonium chloride, and cetylpyridinium bromide), and zwitterionic (N-decyl-N,N-dimethyl-3-ammonio-1-propanesulfonate, N-tetradecyl-N,N-dimethyl-3-ammonio-1-propanesulfonate, and N-hexacyl-N,N-dimethyl-3-ammonio-1-propanesulfonate) micellar solutions at pH ∼ 5.5. Both micellar media remarkably allow the addition reactions, increasing the reactivity of MQI towards bisulfite ions, the biggest effects were found in the presence of cationic micelles. The binding constants of MQI with the micelles and the rate constants were determined from kinetic data, which were interpreted on the basis of the pseudophase kinetic model. The kinetic study and the product analysis allow us to highlight the relevant role of the association between MQI dye and the micellized surfactant, allowing efficient nucleophilic addition of bisulfite ions. The findings of this work will be valuable for the use of micellar solutions as an alternative medium to replace the use of toxic solvents to carry out organic reactions to perform nucleophilic addition reactions of bisulfite.
1. Introduction
Micelles are nanosized structures of amphiphilic nature that self-assemble in aqueous solutions into core–shell structures composed of hydrophobic cores stabilized by the hydrophilic heads and can solubilize molecules with poor solubility in water.1 In this context, the use of micellar solutions is particularly interesting in a variety of chemical transformations, ranging from C–C cross-couplings,2 to oxidation reactions,3 acyl transfer,4 click reactions,5etc., as it provides a sustainable alternative to some of the undesirable solvents classically used.Cationic cetyltrimethylammonium bromide (CTABr) and tetradecyltrimethylammonium bromide (TTABr) micelles have been used to modulate the photophysical properties of 7-(diethylamino)coumarin derivatives and their reactivity towards nucleophilic agents.6–9
In this sense, zwitterionic surfactants, such as sulfobetaine, can also modulate the physicochemical properties and reactivity of organic compounds toward anionic nucleophiles in a similar way as cationic surfactants do,10–12 because of the specific interactions between nucleophilic anions and the zwitterionic interface.13
On the other hand, organic dyes such as quinolin-2(1H)-ones have been a fashionable class of compound because of their similarity to the very popular coumarins; in fact, quinolin-2(1H)-ones are the aza-analogs of coumarins. Like coumarins, quinolinones can be functionalized by adding molecular moieties to broaden their applicability range, taking advantage of the photophysical properties of these derivatives.14 In this context, the presence of a carbon–carbon double bond results in a new reactive site within the molecule towards nucleophilic analytes via Michael additions, as it has already been reported in other studies.15–17
Particular attention has been focused on developing probes for detecting bisulfite (HSO3−) based on Michael addition.18 The reactivity towards HSO3− may also be affected when micelles are present in the medium. In fact, it has been reported that a coumarin derivative can detect bisulfite by Michael addition18,19 in aqueous matrices in the presence of a cationic micellar medium such as CTABr by increasing the reactivity towards this analyte through the use of micelles.19,20 Zwitterionic micelles of sulfobetaine have also been considered as a strategy for optimizing the detection of sulfite via its addition reaction to activated olefins containing, for example, an isoxazole moiety.16
Thus, bearing in mind the catalytic effect that cationic and zwitterionic micelles would have on different organic reactions21 and expanding the current knowledge on bisulfite addition reactions, we undertook a kinetic and theoretical study with the aim of understanding the kinetics and mechanism of this relevant reaction in the presence of micelles. In the present work, we investigated, for the first time, the effects of a micellar medium on the reactivity of a new acceptor (E)-6-methoxy-1-methyl-3-(2-(3-methyl-4-nitroisoxazol-5-yl)vinyl)quinolin-2(1H)-one (MQI) (see structure Scheme 1) toward bisulfite in the presence of cationic and zwitterionic surfactants. Our aim is to contribute to developing new strategies for the addition reaction of HSO3−, taking advantage of the micellar effects on chemical reactivity. We also aim to promote the use of micellar solutions as an alternative reaction medium to carry out this reaction under mild conditions, replacing the use of potentially toxic solvents.
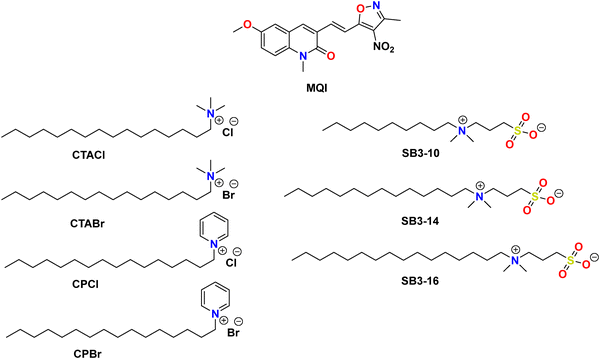 | ||
| Scheme 1 Chemical structures of dye (E)-6-methoxy-1-methyl-3-(2-(3-methyl-4-nitroisoxazol-5-yl)vinyl)quinolin-2(1H)-one (MQI) and the cationic and zwitterionic surfactants employed in this work. | ||
2. Materials and methods
2.1. Materials
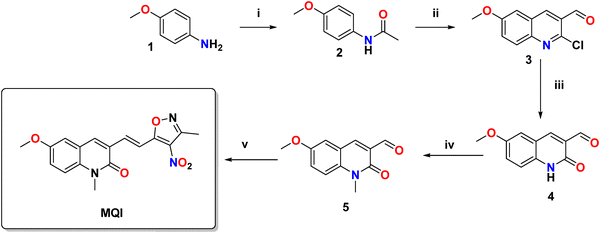
All reagents were purchased from Sigma-Aldrich and employed as received. The preparation of the intermediate 3-formyl-6-methoxy-2-quinolone (4) was carried out according to the methodology reported by Meth-Cohn et al.22 (Scheme 2). In the first step, commercial 4-methoxyaniline (1) was acetylated with acetic anhydride to give the respective acetanilide (2). Cyclization and hydroformylation (in situ) were performed using the Vilsmeier–Haack reagent to give 2-chloro-3-formyl-6-methoxyquinoline (3). Subsequently, acid hydrolysis with 70% acetic acid leads to the formation of methoxy quinolone 4. Compound 4 was methylated using NaH as the base and CH3–I in DMF, furnishing the N-methylated derivative (5). In the final step to obtain the desired MQI, intermediate 5 was coupled with 4-nitro-3,5-dimethylisoxazole in ethanol and using catalytic quantities of piperidine.The structure of MQI was confirmed by 1H- and 13C-NMR spectroscopy (Fig. S1 and S2, ESI†).
2.2. High resolution (HR) QTOF-MS studies
Mass spectrometry (HR-MS) experiments were carried out using a compact QTOF instrument (Bruker), ionization voltage of 6 kV, and negative polarity. Scan parameters: mass range: 50–3000 m/z, spectra rate: 2 Hz, capillary voltage: 6000 V, nebulizer: 0.6 bar, dry gas: 5 L min−1, dry temp: 200 °C.2.3. Kinetic measurements
Stock solutions of MQI in dimethyl sulfoxide and surfactants in aqueous solutions were prepared daily. The percentage of organic solvent in the working solution was 1% by volume. The absorption spectra were recorded on a Cary 60 UV-visible spectrophotometer. The kinetics of the addition reactions of MQI were monitored by an HP8453 UV-vis spectrophotometer with the aid of a 1 cm quartz cuvette at T = 25.0 ± 0.1 °C. The reactions were followed in the 300 to 800 nm wavelength range, with the initial concentration of the substrate ranging from 3–8 × 10−5 M. Reactions were carried out under pseudo-first-order conditions ([MQI] ≪ [Bisulfite]), and the pseudo-first-order rate coefficients (kobsd) were obtained by fitting the experimental (absorbance, time) data with the aid of the pre-loaded spectrophotometer kinetic software.Quantitative treatment of the kinetics of the reaction in micellar systems was carried out in terms of the pseudophase kinetic model according to eqn (1):23
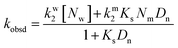 | (1) |
| Dn = DT − CMC | (2) |
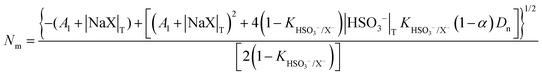 | (3) |
| A1 = αDn + CMC + KHSO3−/X−|HSO3−|T + (1 − α)DnKHSO3−/X− | (4) |
On the other hand, zwitterionic sulfobetaine micelles are formally uncharged, with the quaternary ammonium groups covalently bonded to sulfonate groups. Therefore, there is no presence of counterion in the Stern layer. Consequently, there are no ion exchanges of a reactive nucleophile with the counterion of the surfactants, as in the case of cationic surfactants. In the case of sulfobetaine, the interaction of the ions with micelles is rather a kind of ion absorption that is an ion exchange on the micellar surface. So, the equilibrium constant  for ion absorption is defined employing eqn (5):25
for ion absorption is defined employing eqn (5):25
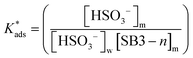 | (5) |
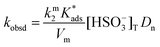 | (6) |
2.4. DFT calculations
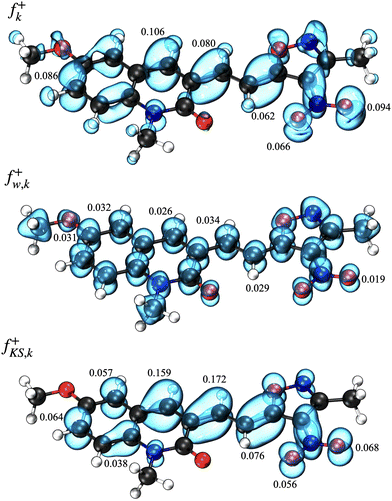
The molecular geometry of the MQI molecule in its ground state was optimized using density functional theory (DFT), utilizing the PBE026 functional and the 6-311G(d,p)27 basis set. This methodology was selected based on evidence from previous studies demonstrating the accuracy of the PBE0 functional in predicting the ground state geometry of organic molecules.28 The UV-visible spectra of MQI were subsequently analyzed employing time-dependent density functional theory (TD-DFT)29 at the same level of theory, specifically targeting the first twenty electronic excitations (td = (nstates = 20)). The polarizable continuum model (PCM)30 was incorporated into the calculations to model solvent effects accurately. Electrostatic potential (ESP) surface maps of the optimized geometries were generated and visualized with Multiwfn31 and VMD32 software, at an isovalue of 0.05, enabling detailed insights into the distribution of molecular electrostatic potential. All other computations were performed using the Gaussian 16/B.01 program suite.33 Additionally, the Fukui function, a key descriptor in understanding the reactivity of molecules, was evaluated. This was done by analyzing atom condensed values of the Fukui funtion computed using three different approximations, finite difference, f+k, as the square of the HOMO (highest molecular orbital), f+KS,k,34,35 and utilizing an orbital-weighted approximation, f+w,k,36,37 within the Multiwfn software. This approach provides insight into the reactive sites of the molecule, highlighting areas prone to nucleophilic and electrophilic attacks, thereby offering a deeper understanding of the molecule's chemical reactivity and stability under various conditions. We calculated local and total dipole moments using the Multiwfn software (at the PBE0/6-311G** level). The wavefunction was analyzed in Multiwfn to obtain the local and total dipole moments.This integration of advanced computational methodologies underscores the detailed analysis of both the structural and electronic properties of the MQI molecule, ensuring a comprehensive investigation of its physicochemical characteristics.
3. Results and discussion
3.1. Synthesis and characterization
Different 2-quinolones and 3,5-dimethyl-4-nitroisooxazoles have been used as sensors for diverse metabolites, but this is the first time that the combination of these two molecules is reported for kinetics purposes with potential for chemical sensing.The synthesis of 2-quinolone was carried out by following the method reported by Meth-Cohn et al.,22 while 3,5-dimethyl-4-nitroisooxazole was synthesized by employing the method reported by Wang et al.38 The synthesis of the novel MQI, was achieved through the coupling of the methoxyquinolone 5 and 3,5-dimethyl-4-nitroisooxazole, with a yield of 83% (see Scheme 2).
MQI was successfully characterized by 1H and 13C NMR spectroscopy (see Fig. S1 and S2, ESI†). The UV-vis spectra of MQI in various solvents, including tetrahydrofuran (THF), ethyl acetate (AcOEt), dichloromethane (DCM), ethanol (EtOH), dimethyl sulfoxide (DMSO), acetonitrile (ACN), acetone, water and CTABr micellar solution are shown in Fig. 1. The spectra depict a similar wavelength, showing a slight bathochromic movement of 10 nm when varying the polarity of the solvent from tetrahydrofuran (THF) to water, being the latter solvent where MQI presented a maximum wavelength of 376 nm. Similar wavelengths are reported in the literature for coumarinic systems.39–41 On the other hand, fluorescence studies showed that the compound MQI presented low fluorescence in the various solvents employed; emission bands and fluorescence quantum yields could not be obtained due to the presence of a nitro group within the molecule. The presence of this group favors cross-system crossover from an excited singlet state to a triplet, preventing deactivation by fluorescence.42–44 Therefore, subsequent kinetic studies were carried out using UV-vis spectroscopy.
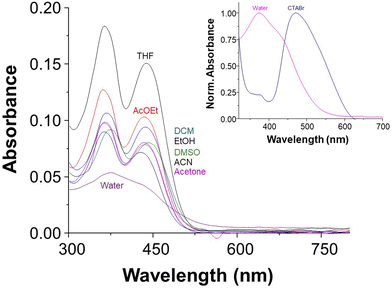 | ||
| Fig. 1 UV-vis spectra of MQI (5 μM), 1% DMSO, in different representative solvents, at 25 °C. Inset shows the UV-vis of MQI in CTABr (0.01 M) micellar solution. | ||
The UV-visible absorption spectrum of MQI in the presence of CTABr micelles (inset Fig. 1) displayed bathochromic shift with maximum absorbance at 480 nm compared to that in the absence of CTABr in keeping with literature reports demonstrating the effects of CTABr micelles on UV-vis spectra of other dyes.7,45,46
3.2. DFT calculations
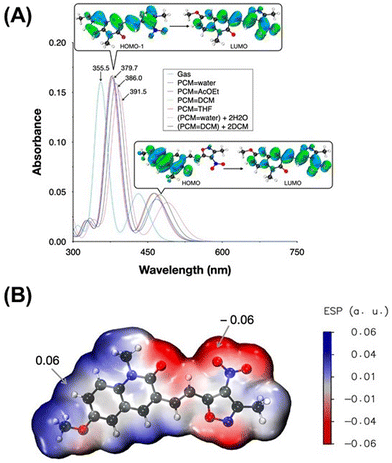
The time-dependent density functional theory (TD-DFT) methodology is an excellent tool for predicting the UV-Vis spectra.47–49Fig. 2a shows the results of the TD-DFT calculations, confirming that both the dominant and the minor bands come from π → π* transitions. This finding is significant as it underscores the electronic nature of the transitions observed in the UV-vis spectra of MQI. Furthermore, Fig. 2A demonstrates a bathochromic shift attributed to the solvent effect.The solvent effect was modeled using the implicit solvent approach provided by the polarizable continuum model (PCM). In addition, we evaluated the effect of explicitly including solvent molecules alongside PCM. We added 1–6 molecules of water at the locations most prone to electrostatic interactions (Fig. 2B and Fig. S3, ESI†). As shown in Fig. S4 (ESI†), a small bathochromic shift is observed; however, the property remained unchanged after adding three water molecules, indicating that further additions had no significant impact. PCM qualitatively captures the bathochromic shifts observed experimentally due to the solvent's nature; for this reason, we consider PCM sufficient to explain the solvent effects observed experimentally. Although some discrepancy exists between the computational and experimental values, these theoretical results nonetheless validate the influence of solvent interactions on the spectral shift observed in MQI. Moreover, the explicit inclusion of solvent molecules in the computational model provides a deeper understanding of how solvent polarity and specific solvent-molecule interactions can influence the electronic absorption spectrum of MQI, offering a more comprehensive view of the solvent's impact on the molecule's spectral behavior. The differences between the experimental and computed UV-vis band values may also be attributed to the absence of surfactant molecules in our model. These surfactants likely engage in important intermolecular interactions with the MQI molecule, which could further affect the UV-vis signals and lead to deviations from the experimentally observed values.
However, it is important to note that despite the Fukui function highlighting the oxygens of the nitro group as reactive centres, their reactivity is predominantly aligned with electrostatic interactions rather than direct engagement in bond-forming processes.
3.3. Evidence of Michael's adduct formation by mass spectrometry
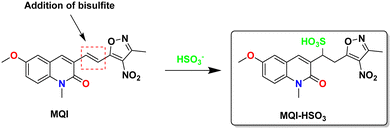
The product of the reaction obtained after the Michael-type reaction between MQI and NaSO3 was confirmed by mass spectrometry. In the first instance, the mass of MQI ([M + H]+) corresponding to 342.106 m/z (calculated to be 342.108 m/z) was obtained (Fig. 4A), corroborating the formation of MQI after the synthesis. In the presence of bisulfite in the medium, the carbon–carbon double bond would act as an electrophile, adding bisulfite into the MQI structure. This was confirmed by mass spectrometry, which is shown in Fig. 4B. The calculated theoretical m/z ratio value for [M-SO3H + H]+ is 424.080, which resembles the one obtained experimentally after the Michael reaction of 424.005 m/z. This shows that MQI is suitable to generate the desired product in the presence of bisulfite (see Scheme 3), which is the starting point for the kinetic studies of this reaction in different cationic and zwitterionic micellar systems.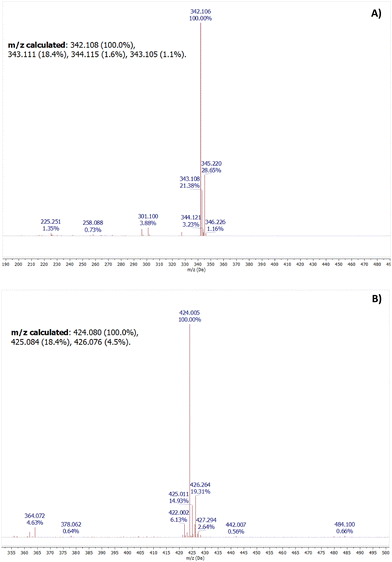 | ||
Fig. 4 HR-MS of MQI dye in the absence (A) and presence (B) of Na2SO3 (10 eq.) in DMSO/CTABr (0.01 M) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. 1. | ||
3.4. Kinetic studies
We investigated kinetically if the tested MQI dye is more reactive towards the nucleophilic attack of bisulfite in the presence of cationic and zwitterionic micelles (see structures in Scheme 1), hence increasing their effective concentration in the Stern layer.52The kobsd values with the added surfactant variation were adjusted assuming the kinetic pseudophase model and eqn (1)–(4), and assuming equilibrium ion exchange constant in the 0.064–0.086 range are summarized in Table 1.
| Surfactants | k m2, M−1 s−1 | K s, M−1 | Slopea | CMC, mM | |
|---|---|---|---|---|---|
| a Values from Fig. 6 plots. b Values from the Sigma-Aldrich catalog. | |||||
| CTACl | 0.0096 | 6434 | — | — | 1.2554 |
| CTABr | 0.0121 | 1492 | — | — | 0.9655 |
| CPBr | 0.0189 | 7300 | — | — | 0.7156 |
| SB3-10 | — | — | 0.0117 ± 2.6 × 10−4 | 39.0 | 25–40b |
| SB3-14 | — | — | 1.2341 ± 3.3 × 10−2 | 4114 | 2.025 |
| SB3-16 | — | — | 1.4348 ± 6.0 × 10−2 | 4783 | 0.225 |
In Table 1, it is possible to observe that there are no significant differences between the values of km2, a factor of two between the highest and the lowest of the cationic micelles studied. Regarding the association constant of the substrate with the two micelles, it is possible to observe that the value of Ks is 4 times higher for CTACl than for CTABr and that CPBr is 5 times higher for CPBr than for CTABr.
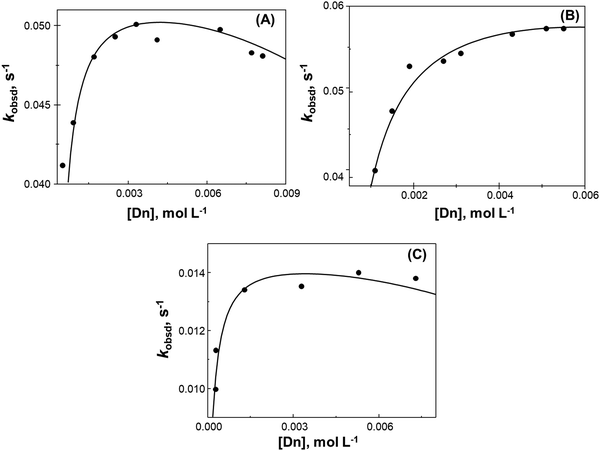
Fig. 6 shows the behavior of the zwitterionic micelles as a reaction medium. The plots of kobsd against micelle concentration, at constant [HSO3−] = 3 × 10−4 M, were found to be linear. Table 1 summarizes the kinetic parameters obtained from the slopes of these plots.
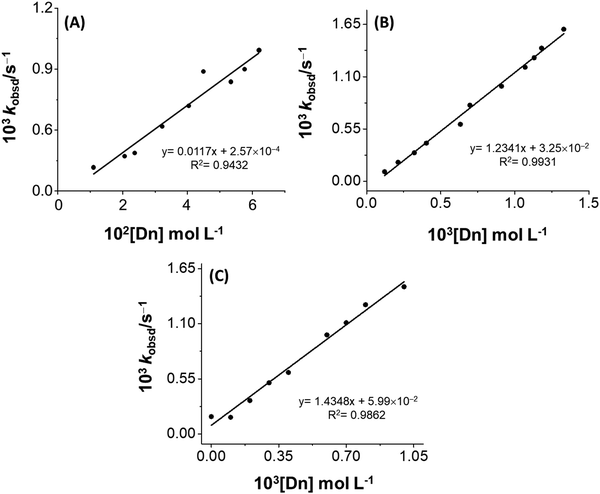 | ||
| Fig. 6 Dependence of the observed rate constant for the reaction MQI (25 μM) and bisulfite (3 × 10−4 M) on the zwitterionic micellar concentration (Dn): (A) SB3-10, (B) SB3-14, and (C) SB3-16. The fitting parameters, slope, intercept, and correlation coefficient (R2) are also given in the figures for each micelle. The model used was according to eqn (6). | ||
According to eqn (6), the slope of these graphs, along with the bisulfite concentration,  was obtained for each zwitterionic micellar solution.
was obtained for each zwitterionic micellar solution.
A similar effect has been reported for the bimolecular reaction between the iodide ion and methyl naphthalene-2-sulfonate. The authors demonstrated that the reaction is accelerated by the micellized sulfobetaine surfactants.25 This kinetic behavior observed was an initial steep increase in kobsd due to the incorporation of the substrate and ion, followed by an approximately linear increase at higher concentrations corresponding to saturation on the Stern layer.25
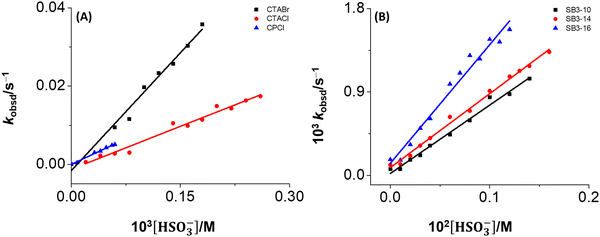
The linear behavior of the kobsd against [HSO3−]T in the reactions in the cationic micelles (Fig. 7A) are in accordance with the predicted eqn (1). Bearing in mind that the reaction in water is negligible due to the poor solubility of MQI in water, the dye should be exclusively micellar-bound in our experimental conditions, KsDn ≫ 1, Dn = 1 × 10−2 – 1 × 10−1 M and the Ks are greater than 1000 M−1 (see Table 1), so the plot kobsd against [HSO3−]T must be linear.
On the other hand, the linearity of the kobsd against [HSO3−]T obtained for the reactions in the zwitterionic micelles (Fig. 7B) can be explained considering the linear eqn (6). As discussed above, for the condition KsDn ≫ 1, Dn = 1 × 10−2 M, Ks somewhat larger than 100 M−1 would suffice, and assuming that [HSO3−]w is equal to [HSO3−]T, the plot kobsdversus [HSO3−]T is a straight line with  . The values of
. The values of  are summarized in Table 2. Values of
are summarized in Table 2. Values of  are somewhat higher in the experiments performed at a constant Dn (Table 2) than those performed at constant bisulfite (Table 1). These differences are between 3 to 6 times attributable to different approaches.
are somewhat higher in the experiments performed at a constant Dn (Table 2) than those performed at constant bisulfite (Table 1). These differences are between 3 to 6 times attributable to different approaches.
| Surfactantb | k 2obsd , M−1 s−1 | |
|---|---|---|
| a 25 μM of probe in 1% DMSO in the cell. b All surfactant concentrations in the cell are 0.01 M except for SB3-10 with 0.1 M. c Second order rate constant obtained from the slope of the kobsd plots versus bisulfite concentration. | ||
| CTACl | 73.1 ± 3.71 | — |
| CTABr | 204.9 ± 12.5 | — |
| CPCl | 87.2 ± 3.30 | — |
| SB3-10 | 0.74 ± 0.03 | 7.4 |
| SB3-14 | 0.80 ± 0.02 | 80 |
| SB3-16 | 1.28 ± 0.06 | 128 |
The slope, in the case of sulfobetaine also involves a product of constants, and the difference between the two types of micelles is 73-fold. In fact, an approximately 200-fold difference in CTABr was observed. From a kinetic point of view, the reaction between MQI and bisulfite is faster in the presence of cationic micelles than in the presence of the zwitterionic micelles due to the presence of the cationic head, which generates an electrostatic effect promoting the negatively charged bisulfite molecules to be attracted to the positive head of the surfactant, promoting Michael-type reaction.16,57–61 This effect is anion exchange between the surfactant counterion and bisulfite, a phenomenon commonly observed in cationic micelles when reactive counterions are present.62–66 The results depicted in Table 2 also align with early reports, which indicate that overall reactions are generally faster in cationic than in zwitterionic micelles.67 In fact, Bunton et al.67 reported that the reactivity could be higher in cationic than in zwitterionic micelles due to some factors: (i) anionic reagents are bound more strongly by cationic than zwitterionic micelles.68 (ii) For some nucleophiles, deprotonation may be incomplete in zwitterionic micelles. In our case, (i) and (ii) would be associated with the observed kinetic effect.
However, sulfobetaines have sulfonate groups in the structure, generating electrostatic repulsions with the bisulfite molecules, promoting decreased rate constants, and thus slowing down the Michael reaction.69–71 The way the micelle increases the reaction rate is clearly due to the interaction of the micelles with the MQI. The molecule partially enters the micelle by lodging itself mostly in the Stern layer, leaving the double bond exposed outside the Stern layer, promoting the cationic head of the surfactant, which is bisulfite anionic, to interact with the carbon–carbon double bond. In fact, only a part of the molecule enters the micelle, and the other part would be lodged in the micellar interface. Based on the above, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond should be located outside the interface, more specifically in the Stern layer, facilitating, through electrostatic interactions, the approach of the bisulfite anions from the bulk solution to the Stern layer, promoting the Michael-type reaction.
C double bond should be located outside the interface, more specifically in the Stern layer, facilitating, through electrostatic interactions, the approach of the bisulfite anions from the bulk solution to the Stern layer, promoting the Michael-type reaction.
The hypothesis has been proven by computational studies with another molecule that is poorly soluble in water69–71 and does not enter completely into the micelle core but rather lodges in the interfacial zone of the micelle. Interestingly, our theoretical calculations of local dipole moments indicate that the quinoline fragment of MQI has the highest local dipole moment (6.8 Debye) compared to the total dipole moment of the molecule (8.6 Debye), as shown in Fig. S5 (ESI†). This suggests that the MQI molecule orients itself with the quinoline fragment interacting with the high polar outer layer of the micelle. Consequently, it is expected that, due to molecular movement, this fragment will preferentially position itself inside the micelle, favoring the interaction of bisulfite with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond in the Stern layer.
C double bond in the Stern layer.
4. Conclusions
Micellar cationic and zwitterionic media have been demonstrated to enable nucleophilic addition reactions of bisulfite to an activated Michael acceptor-type probe to be performed in water under mild conditions. Considering that the chemical reaction does not take place in only water, cationic micelles, such as CTABr, in water serve as nanoreactors that can be viewed as a “green” replacement for organic solvents in addition to Michael reaction type on the novel quinoline-2 (1H)-one derivative MQI.The MQI dye is experimental and theoretically (DFT) proposed as an efficient acceptor toward bisulfite addition. It displays up to 200-fold rate acceleration in CTABr micellar media compared with zwitterionic media. TD-DFT and DFT-reactivity simulations were able to predict batochromic shift by the solvent effects and the regioselectivity predicted for the formation of the Michael adduct. Thus, we believe that the strategy of reactivity modulation (using a micellar media as an assistant reagent) for quinolin-2(1H)-one dyes can be further developed and has extensive potential applications in synthesis and chemical sensing.
Author contributions
GQ: investigation, formal analysis, data curation, writing – original draft. CE: experimental investigation, formal analysis, data curation. EGP, JV, DI: experimental investigation (synthesis and structural characterization). WT and EL: theoretical conceptualization, methodology, validation; JGS and MEA: conceptualization, methodology, validation, writing – original draft. MEA: resources, supervision, project administration, funding acquisition.Data availability
The kinetic data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This work was supported by Fondecyt grant no. 1210751, ANID no. 21210698. This project also received funding from the DIPOG grant and the Vicerrectoria de Investigación de la Pontificia Universidad Católica de Chile, Concurso Pasantías Breves en el Extranjero y Visitas de Investigación de Profesores Extranjeros, Convocatoria 2023. We would like particularly to thank Professor Carlos Bravo-Diaz for his advice and support in this work.References
- S. Mattiello, E. Ghiglietti, A. Zucchi and L. Beverina, Curr. Opin. Colloid Interface Sci., 2023, 64, 101681 CrossRef CAS.
- F. Gallou, P. Guo, M. Parmentier and J. Zhou, Org. Process Res. Dev., 2016, 20, 1388–1391 CrossRef CAS.
- A. Cavarzan, A. Scarso, P. Sgarbossa, R. A. Michelin and G. Strukul, ChemCatChem, 2010, 2, 1296–1302 CrossRef CAS.
- M. K. Turovskaya, I. A. Belousova, N. G. Razumova, T. S. Gaidash, T. M. Prokop’eva, A. A. Kotenko and V. A. Mikhailov, Russ. J. Org. Chem., 2024, 60, 252–258 CrossRef CAS.
- A. Garg and D. Sarma, Green Sustainable Process for Chemical and Environmental Engineering and Science, Elsevier, 2023, pp. 85–112 Search PubMed.
- E. Iglesias, J. Phys. Chem., 1996, 100, 12592–12599 CrossRef CAS.
- A. Chatterjee, B. Maity and D. Seth, RSC Adv., 2014, 4, 34026–34036 RSC.
- M. Sayed, D. K. Maity and H. Pal, J. Photochem. Photobiol., A, 2023, 434, 114265 CrossRef CAS.
- F. Ali, P. E. Hande, D. Kumar Sahoo, R. Roy, S. J. Gharpure and A. Datta, J. Photochem. Photobiol., A, 2023, 434, 114209 CrossRef CAS.
- J. Oakes and P. Gratton, Color. Technol., 2003, 119, 100–107 CAS.
- C. Banerjee, S. Ghosh, S. Mandal, J. Kuchlyan, N. Kundu and N. Sarkar, J. Phys. Chem. B, 2014, 118, 3669–3681 CrossRef CAS PubMed.
- J. Kriwanek, D. Lötzsch, R. Vetter and A. Seeboth, Polym. Adv. Technol., 2003, 14, 79–82 CrossRef CAS.
- G. T. M. Silva and F. H. Quina, Curr. Opin. Colloid Interface Sci., 2019, 44, 168–176 CrossRef CAS.
- M. Cigáň, J. Donovalová, V. Szöcs, J. Gašpar, K. Jakusová and A. Gáplovský, J. Phys. Chem. A, 2013, 117, 4870–4883 CrossRef PubMed.
- M. Liu, Q. Jiang, Z. Lu, Y. Huang, Y. Tan and Q. Jiang, Luminescence, 2015, 30, 1395–1402 CrossRef CAS PubMed.
- M. Gómez, E. G. Perez, V. Arancibia, C. Iribarren, C. Bravo-Díaz, O. García-Beltrán and M. E. Aliaga, Sens. Actuators, B, 2017, 238, 578–587 CrossRef.
- F. Li, L. Zou, J. Xu, F. Liu, X. Zhang, H. Li, G. Zhang and X. Duan, J. Photochem. Photobiol., A, 2021, 411, 113201 CrossRef CAS.
- C. Duan, J.-F. Zhang, Y. Hu, L. Zeng, D. Su and G.-M. Bao, Dyes Pigm., 2019, 162, 459–465 CrossRef CAS.
- H. Tian, J. Qian, Q. Sun, H. Bai and W. Zhang, Anal. Chim. Acta, 2013, 788, 165–170 CrossRef CAS PubMed.
- S. P, S. Prakash and A. Joseph, RSC Adv., 2023, 13, 2552–2560 RSC.
- N. A. Isley, R. T. H. Linstadt, S. M. Kelly, F. Gallou and B. H. Lipshutz, Org. Lett., 2015, 17, 4734–4737 CrossRef CAS PubMed.
- O. Meth-Cohn, B. Narine and B. Tarnowski, J. Chem. Soc., Perkin Trans. 1, 1981, 1520 RSC.
- C. A. Bunton, F. Nome, F. H. Quina and L. S. Romsted, Acc. Chem. Res., 1991, 24, 357–364 CrossRef CAS.
- F. H. Quina and H. Chaimovich, J. Phys. Chem., 1979, 83, 1844–1850 CrossRef CAS.
- M. A. Farrukh, R. C. Beber, J. P. Priebe, M. Lal Satnami, G. A. Micke, A. C. O. Costa, H. D. Fiedler, C. A. Bunton and F. Nome, Langmuir, 2008, 24, 12995–13000 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- A. D. Laurent and D. Jacquemin, Int. J. Quantum Chem., 2013, 113, 2019–2039 CrossRef CAS.
- S. Marković and J. Tošović, J. Phys. Chem. A, 2015, 119, 9352–9362 CrossRef PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- W. Tiznado, E. Chamorro, R. Contreras and P. Fuentealba, J. Phys. Chem. A, 2005, 109, 3220–3224 CrossRef CAS PubMed.
- P. Fuentealba, E. Florez and W. Tiznado, J. Chem. Theory Comput., 2010, 6, 1470–1478 CrossRef CAS PubMed.
- R. Pino-Rios, O. Yañez, D. Inostroza, L. Ruiz, C. Cardenas, P. Fuentealba and W. Tiznado, J. Comput. Chem., 2017, 38, 481–488 CrossRef CAS PubMed.
- R. Pino-Rios, D. Inostroza, G. Cárdenas-Jirón and W. Tiznado, J. Phys. Chem. A, 2019, 123, 10556–10562 CrossRef CAS PubMed.
- J. Zhang, X. Liu, X. Ma and R. Wang, Chem. Commun., 2013, 49, 9329 RSC.
- G. Jones, W. R. Jackson, S. Kanoktanaporn and W. R. Bergmark, Photochem. Photobiol., 1985, 42, 477–483 CrossRef CAS.
- S. Bairu and G. Ramakrishna, J. Phys. Chem. B, 2013, 117, 10484–10491 CrossRef CAS PubMed.
- J. Li, L. Zeng, K. Xiong, T. W. Rees, C. Jin, W. Wu, Y. Chen, L. Ji and H. Chao, Chem. Commun., 2019, 55, 10972–10975 RSC.
- Y. M. Poronik, G. V. Baryshnikov, I. Deperasińska, E. M. Espinoza, J. A. Clark, H. Ågren, D. T. Gryko and V. I. Vullev, Commun. Chem., 2020, 3, 190 CrossRef CAS PubMed.
- D. Pinheiro, M. Pineiro and J. S. Seixas de Melo, Photochem. Photobiol. Sci., 2022, 21, 645–658 CrossRef CAS PubMed.
- M. Chen, D. Chen and P. Chou, ChemPlusChem, 2021, 86, 11–27 CrossRef CAS PubMed.
- A. Delledonne, J. Morla-Folch, M. Anzola, F. Bertocchi, G. Vargas-Nadal, M. Köber, C. Sissa, N. Ventosa and A. Painelli, J. Mater. Chem. C, 2021, 9, 10952–10964 RSC.
- S. S. Shah, G. M. Laghari and K. Naeem, Thin Solid Films, 1999, 346, 145–149 CrossRef CAS.
- A. G. Martynov, J. Mack, A. K. May, T. Nyokong, Y. G. Gorbunova and A. Y. Tsivadze, ACS Omega, 2019, 4, 7265–7284 CrossRef CAS PubMed.
- M. Hédouin, E. Luppi, O. Ward, D. Harrowven, C. Fressigné and I. Chataigner, ChemistrySelect, 2023, 8(29), e202301943 CrossRef.
- N. K. Hien, M. Van Bay, Q. V. Vo, N. D. Y, D. T. Quang and P. C. Nam, New J. Chem., 2024, 48, 1307–1319 RSC.
- P. Fuentealba, E. Florez and W. Tiznado, J. Chem. Theory Comput., 2010, 6, 1470–1478 CrossRef CAS PubMed.
- W. Tiznado, E. Chamorro, R. Contreras and P. Fuentealba, J. Phys. Chem. A, 2005, 109, 3220–3224 CrossRef CAS PubMed.
- F. Fini, M. Nagabelli and M. F. A. Adamo, Adv. Synth. Catal., 2010, 352, 3163–3168 CrossRef CAS.
- A. Rakshit, S. Chowdhury, A. Acharjee, I. Datta, K. Dome, S. Biswas, S. S. Bhattacharyya and B. Saha, Res. Chem. Intermed., 2020, 46, 2559–2578 CrossRef CAS.
- X. Li, B. Hui, Q. Jin, H. Shi, X. Lu, L. Jing and D. Jing, Ind. Eng. Chem. Res., 2023, 62, 16481–16494 CrossRef CAS.
- C. Vautier-Giongo and H. O. Pastore, J. Colloid Interface Sci., 2006, 299, 874–882 CrossRef CAS PubMed.
- Y. G. Devi, J. Gurung and A. K. Pulikkal, J. Chem. Eng. Data, 2021, 66, 368–378 CrossRef CAS.
- C. A. Bunton, L. Baylor Robinson and G. L. Sepulveda, J. Org. Chem., 1970, 35, 108–114 CrossRef CAS.
- C. Wang, H. Hong, M. Chen, Z. Ding, Y. Rui, J. Qi, Z. Li and Z. Liu, Angew. Chem., Int. Ed., 2021, 60, 19750–19758 CrossRef CAS PubMed.
- U. Tonellato, J. Chem. Soc., Perkin Trans. 2, 1976, 771 RSC.
- K. Ruan, Z. Zhao and J. Ma, Colloid Polym. Sci., 2001, 279, 813–818 CrossRef CAS.
- R. A. Sheikh, F. M. Al-Nowaiser, M. A. Malik, A. O. Al-Youbi and Z. Khan, Colloids Surf., A, 2010, 366, 129–134 CrossRef CAS.
- D. Bartet, C. Gamboa and L. Sepulveda, J. Phys. Chem., 1980, 84, 272–275 CrossRef CAS.
- I. B. Blagoeva, N. Ouarti, O. A. El Seoud and M. Ruasse, J. Phys. Org. Chem., 2005, 18, 850–855 CrossRef CAS.
- M. Chen and C. T. Jafvert, Langmuir, 2017, 33, 6540–6549 CrossRef CAS PubMed.
- M. Chen and C. T. Jafvert, Environ. Sci.: Nano, 2018, 5, 1350–1360 RSC.
- N. S. Mohd Yusof, Ultrason. Sonochem., 2021, 71, 105360 CrossRef CAS PubMed.
- C. A. Bunton, M. M. Mhala and J. R. Moffatt, J. Phys. Chem., 1989, 93, 854–858 CrossRef CAS.
- C. A. Bunton, ARKIVOC, 2011, 2011, 490–504 Search PubMed.
- C. A. Bunton, M. M. Mhala and J. R. Moffatt, J. Org. Chem., 1987, 52, 3832–3835 CrossRef CAS.
- K. A. Berberich, V. C. Reinsborough and C. N. Shaw, J. Solution Chem., 2000, 29, 1017–1026 CrossRef CAS.
- M. del Mar Graciani, A. Rodríguez, M. Múñoz and M. L. Moyá, Langmuir, 2002, 18, 3476–3481 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nj03295k |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2024 |