Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fast estimation of intersystem crossing rate constants of radical pairs†
Rashid R.
Valiev
 *,
Rinat T.
Nasibullin
,
Severi
Juttula
and
Theo
Kurten
*,
Rinat T.
Nasibullin
,
Severi
Juttula
and
Theo
Kurten
University of Helsinki, Department of Chemistry, University of Helsinki, P.O. Box 55 (A.I. Virtanens plats 1), FIN-00014, Finland. E-mail: valievrashid@gmail.com
First published on 24th September 2024
Abstract
The spin–flip or intersystem crossing (ISC) process plays a main role in photophysics and photochemistry. ISC is the radiationless electronic transition between singlet and triplet states. ISC is responsible for phosphorescence and the chemical reaction which happens only in the electronic state with the specific spin. One specific and challenging case is the formation of accretion products in peroxy radical cross-reactions, recently demonstrated to be important in atmospheric chemistry. Here, the ISC or spin–flip occurs between triplet and singlet states of a complex of two alkoxy radicals (RO˙⋯R′O˙). The complex is initially formed in a triplet state, while the formation of the ROOR′ accretion product can only happen on the singlet surface. Therefore, the ISC rate dictates the rate of this reaction. We developed a fast algorithm to calculate ISC rate constants (kISC) between the lowest electronic states of alkoxy radical pairs. The kISC calculation requires the spin-orbital coupled interaction matrix elements (SOCME) and the excitation energies (E) of the involved electronic states. The E and SOCME are calculated quickly using the CASSCF level of theory, and a novel analytical expression, respectively. Finally, the kISC calculation is performed efficiently; within 5–60 seconds even for radical pairs with the large substituents such as CH3(CO)CH2O˙ and HOCH2CH(O˙)CH2CH3. This algorithm is applied to a large number of radical pairs with different substituents, and the kISC is calculated for 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 875 radical pair conformers using this algorithm. It provides an opportunity to generate large amounts of data (input and output values, e.g. geometries and associated ISC rates) quickly. Therefore, we believe that the fast algorithm can be useful not only for photophysical calculations, but also for Big Data creation to implement machine learning methods.
875 radical pair conformers using this algorithm. It provides an opportunity to generate large amounts of data (input and output values, e.g. geometries and associated ISC rates) quickly. Therefore, we believe that the fast algorithm can be useful not only for photophysical calculations, but also for Big Data creation to implement machine learning methods.
1. Introduction
Reactions between peroxyl radicals (ROO˙) play an important role in atmospheric chemistry.1 They can, among other things, lead to the formation of secondary organic aerosol (SOA) particles, which are able to penetrate into the lungs of humans and animals.1,2 Aerosol pollution in turn leads to over 3 million deaths per year.3 One potential major source of SOA is the radical recombination reaction R′O2 + RO2, which can, in competition with other channels, lead to low-volatility accretion products (for example, R′OOR peroxides),4 Thus, the investigation of the R′OOR formation mechanism is important.5–8The R′OOR production can be explained on a molecular level though the formation and decomposition of a R′OOOOR tetrooxide intermediate.8–13,14 Radicals, such as peroxyl radicals (ROO˙) and alkoxy radicals (RO˙) have a non-zero spin (S = 1/2), and a doublet ground state (D0).15,16 A system of two such radicals, which is called a radical pair (RP), can have either triplet (S = 1) or singlet (S = 0) spins. Usually, the triplet state is repulsive, and the formation of R′OOOOR tetroxides can happen only on the singlet surface. After that, the decomposition of R′OOOOR leads to an RO˙⋯R′O˙ complex and ground-state (triplet) O2. Due to the spin conservation law, the (RO˙⋯R′O˙) complex must also be formed in the triplet state, so that the overall system can remain on the singlet surface. The O2 molecule is then assumed to rapidly dissociate from the system, and the remaining RO˙ and R′O˙ can react. The reaction between them can lead to different products: (1) dissociation to free alkoxy radicals; (2) H-shift to carbonyl and alcohol products R-HO and R′OH; (3) recombination to R′OOR accretion products; (4) scission of one or both of the alkoxy radicals, and subsequent reaction or recombination, possibly leading to ROR′ or RR′ – type accretion products.17–21 The first two channels can occur on both the triplet and singlet surfaces, but R′OOR formation (as well as post-scission recombination) can only take place on the singlet surface because the triplet is repulsive. Thus, accretion products can only form after a spin–flip or intersystem crossing process ISC(T1 → S1). Thus, the rate constant of kISC(T1 → S1) determines the rate of accretion product formation. Moreover, the kISC(T1 → S1) can determine the H-shift channel in the S1 state. Thus, the knowledge of kISC(T1 → S1) or the probability of the spin–flip process is important for atmospheric chemistry.
Recently, we showed that the ISC process of a RP of RO˙ and R′O˙ is determined not only by the kISC(T1 → S1), but also by the electronic transitions from T1 to the higher three singlet states (S2, S3, and S4).22 This can be explained by the existence of a low-energy first excited doublet state (D1) with the energy ∼1.0 eV of a single RO radical.22,23 The other doublet states are located much higher in energy (>2.5 eV).22,23 The RP thus has four low-energy singlet and four low-energy triplet states, which are formed by combinations of these D0 and D1 states. The energies of the S2, S3, and S4 states with respect to the T1 state of the RP are relatively high, and close to the D1 energy of a single radical, at large distances. Thus, the kISC(T1 → Sn) (n = 2–4) (formally, a reverse ISC) is negligible because of a very small Boltzmann factor.22 However, at short distances, the corresponding S2–S4 energies become smaller (∼0.1–0.3 eV), and the (T1 → Sn) (n = 2–4) ISC is possible.22 From S2, S3, and S4 states, the RP decays to the S1 state by a fast internal conversion (IC) (∼1014 s−1).22,23 Thus, the total rate constant, which is the sum of kISC(T1 → Sn) (n = 1–4), determines the overall rate of the spin–flip process.
In 2019, it was shown that the kISC(T1 → Sn) (n = 1–4) of the RP depends on the distance and angle orientation of RO˙ and R′O˙, and the kind of substituents (R and R′).22 It is well known that kISC(T1 → S1) in general depends on two parameters: the spin-orbital coupling matrix element (SOCME) and the energy gap (E) between T1 and Sn states.24 Previously, we showed that relative energies of S1 and T1 states depend on the both conformational and other types of isomerism, and S1 can be either slightly lower or slightly higher in energy than T1.22–27 The lowest-energy S1 state is an open-shell singlet, and it is thus not a single-reference state.22 At the same time, the Boltzmann factor for the reversed ISC(T1 → Sn) strongly depends on the energy, gap and can’t be reproduced with high accuracy by single-reference methods such as (time-dependent) density functional theory ((TD)DFT).28 Therefore, the calculation of kISC(T1 → Sn) (n = 1–4) requires a high level of theory involving multireference methods for both the E and SOCME. This is particularly true for RP with large substituents (such as monoterpene-derived C10 systems that are highly relevant for SOA formation) due to the computational cost. Therefore, cheaper but still accurate theoretical models for the calculation of SOCME, E and kISC(T1 → Sn) are needed. Here, we develop and present a fast algorithm for the calculation of SOCME, E and kISC(T1 → Sn). We show that the SOCME can be calculated quickly using a quite complicated analytical expression, based on configuration interaction (CI) coefficients and basis function (BF) coefficients of only four molecular orbitals (MOs). The calculation takes only seconds even with an office laptop. The CI and BF coefficients can in turn be obtained using only the complete active space self consistent field (CASSCF) method, with a small active space size. The CASSCF energies are also sufficiently accurate for estimating the E for our RP systems. Finally, the kISC(T1 → Sn) rate is calculated quickly using a simple expression. In the present work, we calculated these values for 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 875 RP with different substitutes using this algorithm.
875 RP with different substitutes using this algorithm.
2. Theory and computation
Our algorithm is based on following statements/hypotheses:1. Only the electronic transitions between 4 MOs form the S1–S4 and T1–T4 electronic states. Therefore, it is enough to include them into CASSCF calculation. Thus, CASSCF(6,4) is enough to describe these electronic states correctly.
2. The CASSCF convergence is obtained quickly starting from Hückel orbitals, avoiding the Hartree–Fock (HF) generation.
3. The computed E by the CASSCF method and the extended multi-configuration quasi-degenerate perturbation theory of second order (XMCQDPT2)29 agree with high accuracy (0.005 eV) for the S1–S4 and T1–T4 electronic states, and therefore the CASSCF can be applied to calculate them.
4. The one-center approximation and the one-electron Pauli-Breit operator30 is enough to calculate SOCME for RP. This statement is based on the fact that the multicenter integrals give negligible contribution to SOCME. The first clear evidence of this fact was presented by B. F. Minaev.31–34 Moreover, Minaev showed that the SOCME dependence on angles and distance between RP is caused by the one-center integrals, not by the multicenter ones, which was mistakenly assumed in the theory proposed by Prof. Dr Lionel Salem and Dr Colin Rowland.35
The one-center approximation and the use of only CASSCF(6,4) wavefunctions give us an opportunity to obtain an analytical solution. Indeed, the 4 MOs are formed mainly by 2px, 2py and 2pz atomic orbitals (AO) of oxygen atoms with the spin localization of RP, as shown in Fig. 1.
Therefore, the SOCME calculation can be simplified into the calculation of matrix elements of the angular momentum operator (![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) ) between the 2px, 2py and 2pz -AOs of oxygen atoms as
) between the 2px, 2py and 2pz -AOs of oxygen atoms as
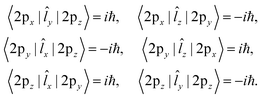 | (1) |
 , where ζA is an effective charge of the oxygen atom, was assumed as 150 cm−1.31–33 The
, where ζA is an effective charge of the oxygen atom, was assumed as 150 cm−1.31–33 The ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) iA and ŝi are the electronic angular momentum and spin operators, respectively, of the i-th electron. Within this approximation, the SOCME between the T1 and Sn states is expressed as a linear combination of matrix elements (1), with the BF and CI coefficients as the linear combination coefficients.
iA and ŝi are the electronic angular momentum and spin operators, respectively, of the i-th electron. Within this approximation, the SOCME between the T1 and Sn states is expressed as a linear combination of matrix elements (1), with the BF and CI coefficients as the linear combination coefficients.
Thus, the CI coefficients of S1–S4 states and BF coefficients of 4 MOs are needed to calculate SOCME analytically. Note that, Minaev considered a similar way for the simplest case – molecular oxygen with only two MOs and 2 electrons for two electronic states.31–34 He obtained a simple expression with two terms.31 However, the RP is a more complicated case because the distance between oxygen atoms is varied, and the orientation of the radical-center part of the RP is different for different conformers. Moreover, the state-average (SA) procedure of CASSCF should be done for S1–S4 and T1–T4 electronic states simultaneously with 4 MOs, not only two. All these conditions lead to a quite complicated analytical expression of SOCME dependence on BF and CI coefficients with thousand terms. However, without additional numerical calculation, the SOCME can be calculated quickly using this expression within several seconds even for large RP. Note that the amount of terms in the analytical expression depends on the basis set size. Previously, Minaev reported that only small basis set such as 6-31G** or even STO-3G are enough to reproduce the SOCME within one order of magnitude.31–33
Previously we showed that the kISC(T1 → Sn) can be calculated quickly as21
| kISC = 1.6 × 109〈i|ĤSO|f〉2FC | (2) |
| kISC = kISC·exp(−Eif/kT) | (3) |
The calculations were done using the Firefly software,38 where the implementation of CASSCF calculation was done efficiently involving the state-specific gradients for state-averaged CASSCF.39 The CASSCF wave function and energies were calculated with 6 electrons in 4 MOs with the SA-procedure for both S1–S4 and T1–T4 electronic states, and 6-311++G(d,p) and 4-31G basis sets. As found in the study by Minaev,31–33 we found that the 4-31G and 6-311++G(d,p) provide the SOCME, which are in agreement with each other within one order of magnitude Therefore, the 4-31G basis set was used to generate the full set of RP.
As objects of investigation we consider following alkoxy radicals: CH3O˙, CH3 CH2O˙, CH3(CO)CH2O˙ and HOCH2CH(O˙)CH2CH3. To simplify notations, we use MeO, ButO, AcO and HOBuO for them, respectively. Finally, we consider 10 clusters: 3(MeO)2, 3(ButO)2, 3(AcO)2, 3(HOBuO)2, 3(MeO⋯ButO), 3(MeO⋯AcO), 3(MeO⋯HOBuO), 3(ButO⋯AcO), 3(BuO⋯HOBuO), and 3(AcO⋯HOBuO). Note that this set was chosen because the kISC(T1 → Sn) was previously calculated for their lowest-energy conformers.22–27
Generation and geometrical optimization of clusters were done using the semi-empirical GNF-xTB level of theory40 in the ABCluster program.41,42 Finally, we generated 95875 conformers and applied our algorithm to obtain SOCME and kISC(T1 → Sn).
We note that the analytical solution was implemented as an external module for FIREFLY. It is available to any user upon request. Currently, it functions only with the 4-31G basis set, but we plan to extend its compatibility to include any basis set.
3. Results and discussion
3.1. The CASSCF and XMCQDPT2 energies
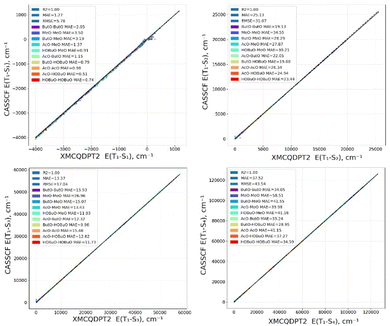
The calculated results are given in this chapter and in Table S1–S4 of the ESI.† Computed energies of S1–S4 states for RP are presented in Fig. 2 using the CASSCF and XMC-QPDT2 level of theory. There is excellent agreement between them, as R2 is 1.00. This result can be explained by the fact that the S1–S4 states are formed by electronic transitions between the MOs which are included into the active space. Therefore, the important electronic correlation covering both static and dynamic effects is already included in the active space, and thus in the CASSCF calculation.As seen from Fig. 2, large energies (∼5000–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) are often observed for the S2, S3 and S4 states. This happens for large distance between the radical O atoms, because in these cases their energies correspond to D1 states of single radicals.
000 cm−1) are often observed for the S2, S3 and S4 states. This happens for large distance between the radical O atoms, because in these cases their energies correspond to D1 states of single radicals.
3.2. SOCME
The calculated SOCME are presented in Fig. 3 using the analytical solution within a one-center approximation based on the CASSCF energies and the full numerical XMCQPDT2 level of theory calculation. | ||
| Fig. 3 The computed SOCME using the analytical solution and the quantum chemical calculation by the XMC-QDPT2 level of theory. | ||
As can be seen from Fig. 3, there is good correlation between the analytical solution and the XMCQDPT2 calculation for SOCME of RP (R2 = 0.57–0.94). The excellent agreement (R2 = 0.94–0.99) is for SOCME(T1 → S1) and SOCME(T1 → S4), where there a lot of conformers for which the SOCME is zero. The deviation is little bit larger for SOCME(T1 → S2) and SOCME(T1 → S3), where a large amount of conformers have large SOCME values. In any case, the accuracy of SOCME(T1 → S2) and SOCME(T1 → S3) is also within an order of magnitude (MAE), and it is enough to estimate the kISC(T1 → Sn), n = 2, 3 correctly, as these ISC rate constants depend more on the E (through Boltzmann factor) than on the SOCME.22
3.3. The kISC(T1 → Sn) calculation
The result of the analytical solution and a XMCQDPT2 calculation is presented in Fig. 4. As can be seen from Fig. 4, The R2 coefficient is 0.98–1.0 for all sub-steps of ISC rate constants as well as for the total rate constant. Thus, the analytical solution can be used for the calculation of all considered ISC rate constants for RP with the different substituents. | ||
| Fig. 4 The computed order of magnitude of kISC(T1 → Sn), n = 1–4 using the analytical solution and the quantum chemical calculation by the XMCQDPT2 level of theory. | ||
Summary and conclusions
We present a fast algorithm for calculating the kISC(T1 → Sn), n = 1–4 between four lowest-energy electronic states of a radical pair (RP) consisting of two alkoxy radicals. This algorithm involves a combination of CASSCF-level excitation energies (E), and an analytical solution for calculating SOCME. The CASSCF wavefunctions were generated quickly from Hückel orbitals. The calculation of E, SOCME and finally kISC(T1 → Sn), n = 1–4, take only 5–60 seconds even for the largest considered RP. This gives us the opportunity for Big Data creation, a necessary precondition for example for machine learning.Although the presented algorithm has been applied only to RP formed by alkoxy radicals, it can potentially be applied to other RP. Indeed, the one-center approximation provides a good approximation for calculating SOCME for RP formed by one-center radicals of almost any nature,31–33 and most radicals have a low-lying first excited doublet state,23,43 which fully satisfies our model. We can only note that calculating energies using the CASSCF method may be insufficient for π-radicals43 and the XMCQDPT2 method might be necessary.
Although the main focus of this work is the RP of alkoxy radicals, we performed a test calculation for one RP of CH3OO⋯OOCH3 and one RP of an alkoxy radical with a phenyl ring to validate this statement. The results are provided in Table S4 of the ESI.† These results clearly demonstrate that the fast algorithm and the explicit XMCQDPT2 calculation yield nearly similar values for kISC(T1 → S1) within one order of magnitude for both systems. However, the kISC(T1 → S2), kISC(T1 → S3), and kISC(T1 → S4) values differ by 1–2 orders of magnitude for the RP with the alkoxy radical with a phenyl ring because the energies of the XMCQDPT2 and CASSCF methods differ for the S2, S3, and S4 states. This is a small discrepancy. However, for the RP of CH3OO⋯OOCH3, the difference for kISC(T1 → S2), kISC(T1 → S3), and kISC(T1 → S4) is 3–10 orders of magnitude because CASSCF underestimates these energies significantly. Nevertheless, the total kISC(T1 → Sn) agrees within one order of magnitude between our fast method and the explicit ab initio calculations, as kISC(T1 → S1) contributes the most. Finally, according to Table S4 (ESI†), the SOCME shows excellent agreement, and the one-center approximation works well. However, CASSCF significantly underestimates the energies of the S2, S3, and S4 states for other systems, such as peroxide radical systems. Therefore, the XMCQDPT2 level of theory is necessary here. Naturally, this algorithm cannot be applied to RP systems where the spin is delocalized and the one-center approximation fails. The RPs of alkoxy radicals are very important in the atmospheric phenomena43,44 and this algorithm works well for them.45
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Academy of Finland through projects 340582 (RRV) and 346369 (TK). We thank CSC – IT Center for Science, Finland for computer time.Notes and references
- R. A. Silva, J. West, Y. Zhang, S. Anenberg, J.-F. Lamarque, D. T. Shindell, W. J. Collins, S. Dalsoren, G. Faluvegi and G. Folberth, Environ. Res. Lett., 2013, 8, 034005 CrossRef CAS.
- M. Brauer, G. Freedman, J. Frostad, A. van Donkelaar, R. V. Martin, F. Dentener, R. van Dingenen, K. Estep, H. Amini, J. S. Apte, K. Balakrishnan, L. Barregard, D. Broday, V. Feigin, S. Ghosh, P. K. Hopke, L. D. Knibbs, Y. Kokubo, Y. Liu, S. Ma, L. Morawska, J. S. Texcalac Sangrador, G. Shaddick, H. R. Anderson, T. Vos, M. H. Forouzanfar, R. T. Burnett and A. Cohen, Environ. Sci. Technol., 2016, 50, 79–88 CrossRef CAS.
- J. H. Seinfeld, C. Bretherton, K. S. Carslaw, H. Coe, P. J. DeMott, E. J. Dunlea, G. Feingold, S. Ghan, A. B. Guenther, R. Kahn, I. Kraucunas, S. M. Kreidenweis, M. J. Molina, A. Nenes, J. E. Penner, K. A. Prather, V. Ramanathan, V. Ramaswamy, P. J. Rasch, A. R. Ravishankara, D. Rosenfeld, G. Stephens and R. Wood, PNAS, 2016, 113, 5781–5790 CrossRef CAS.
- M. Ehn, J. A. Thornton, E. Kleist, M. Sipilä, H. Junninen, I. Pullinen, M. Springer, F. Rubach, R. Tillmann, B. Lee, F. Lopez-Hilfiker, S. Andres, I. H. Acir, M. Rissanen, T. Jokinen, S. Schobesberger, J. Kangasluoma, J. Kontkanen, T. Nieminen, T. Kurtén, L. B. Nielsen, S. Jørgensen, H. G. Kjaergaard, M. Canagaratna, M. D. Maso, T. Berndt, T. Petäjä, A. Wahner, V. M. Kerminen, M. Kulmala, D. R. Worsnop, J. Wildt and T. F. Mentel, Nature, 2014, 506, 476–479 CrossRef CAS.
- J. Tröstl, W. K. Chuang, H. Gordon, M. Heinritzi, C. Yan, U. Molteni, L. Ahlm, C. Frege, F. Bianchi, R. Wagner, M. Simon, K. Lehtipalo, C. Williamson, J. S. Craven, J. Duplissy, A. Adamov, J. Almeida, A. K. Bernhammer, M. Breitenlechner, S. Brilke, A. Dias, S. Ehrhart, R. C. Flagan, A. Franchin, C. Fuchs, R. Guida, M. Gysel, A. Hansel, C. R. Hoyle, T. Jokinen, H. Junninen, J. Kangasluoma, H. Keskinen, J. Kim, M. Krapf, A. Kürten, A. Laaksonen, M. Lawler, M. Leiminger, S. Mathot, O. Möhler, T. Nieminen, A. Onnela, T. Petäjä, F. M. Piel, P. Miettinen, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, K. Sengupta, M. Sipilä, J. N. Smith, G. Steiner, A. Tomè, A. Virtanen, A. C. Wagner, E. Weingartner, D. Wimmer, P. M. Winkler, P. Ye, K. S. Carslaw, J. Curtius, J. Dommen, J. Kirkby, M. Kulmala, I. Riipinen, D. R. Worsnop, N. M. Donahue and U. Baltensperger, Nature, 2016, 533, 527–531 CrossRef.
- M. Mohr, F. D. Lopez-Hilfiker, T. Yli-Juuti, A. Heitto, A. Lutz, M. Hallquist, E. L. D'Ambro, M. P. Rissanen, L. Hao, S. Schobesberger, M. Kulmala, R. L. Mauldin, U. Makkonen, M. Sipilä, T. Petäjä and J. A. Thornton, Geophys. Res. Lett., 2017, 44, 2598–2966 CrossRef.
- Y. Zhao, J. A. Thornton and H. O. T. Pyem, PNAS, 2018, 115, 12142–12147 CrossRef CAS.
- F. Bianchi, T. Kurtén, M. Riva, C. Mohr, M. P. Rissanen, P. Roldin, T. Berndt, J. D. Crounse, P. O. Wennberg, T. F. Mentel, J. Wildt, H. Junninen, T. Jokinen, M. Kulmala, D. R. Worsnop, J. A. Thornton, N. Donahue, H. G. Kjaergaard and M. Ehn, Chem. Rev., 2019, 119, 3472–3509 CrossRef CAS.
- M. Ehn, T. Berndt, J. Wildt and T. Mentel, Int. J. Chem. Kinet., 2017, 49, 821–831 CrossRef CAS.
- M. Kalberer, D. Paulsen, M. Sax, M. Steinbacher, J. Dommen, A. S. H. Prevot, R. Fisseha, E. Weingartner, V. Frankevich, R. Zenobi and U. Baltensperger, Science, 2004, 303, 1659–1662 CrossRef CAS.
- T. Berndt, W. Scholz, B. Mentler, L. Fischer, H. Herrmann, M. Kulmala and A. Hansel, Angew. Chem., Int. Ed., 2018, 57, 3820–3824 CrossRef CAS.
- A. C. Noell, L. S. Alconcel, D. J. Robichaud, M. Okumura and S. P. Sander, J. Phys. Chem. A, 2010, 114, 6983–6995 CrossRef CAS.
- J. J. Orlando and G. S. Tyndall, Chem. Soc. Rev., 2012, 41, 6294–6317 RSC.
- A. C. Noell, L. S. Alconcel, D. J. Robichaud, M. Okumura and S. P. Sander, J. Phys. Chem. A, 2010, 114, 6983–6995 CrossRef CAS.
- Y.-N. Liang, J. Li, Q.-D. Wang, F. Wang and X.-Y. Li, J. Phys. Chem. A, 2011, 115, 13534–13541 CrossRef CAS.
- G. A. Russell, J. Am. Chem. Soc., 1957, 79, 3871–3877 CrossRef CAS.
- P. Zhang, W. Wang, T. Zhang, L. Chen, Y. Du, C. Li and L. Lü, J. Phys. Chem. A, 2012, 116, 4610–4620 CrossRef CAS.
- R. Lee, G. Gryn'ova, K. U. Ingold and M. L. Coote, Phys. Chem. Chem. Phys., 2016, 18, 23673–23679 RSC.
- G. Ghigo, A. Maranzana and G. Tonachini, J. Chem. Phys., 2003, 118, 10575–10583 CrossRef CAS.
- L. Vereecken, D. R. Glowacki and M. J. Pilling, Chem. Rev., 2015, 115, 4063–4114 CrossRef CAS.
- O. Peräkylä, T. Berndt, L. Franzon, G. Hasan, M. Meder, R. R. Valiev, C. D. Daub, J. G. Varelas, F. M. Geiger, R. J. Thomson, M. Rissanen, T. Kurtén and M. Ehn, J. Am. Chem. Soc., 2023, 145, 7780–7790 CrossRef.
- R. R. Valiev, G. Hasan, V.-T. Salo, J. Kubečka and T. Kurten, J. Phys. Chem. A, 2019, 123, 6596–6604 CrossRef CAS.
- R. R. Valiev and T. Kurten, R. Soc. Open Sci, 2020, 7, 200521 CrossRef CAS.
- E. S. Medvedev and V. I. Osherov, Radiationless transitions in polyatomic molecules, Springer, 1995, vol. 57 Search PubMed.
- G. Hasan, V.-T. Salo, T. G. Almeida, R. R. Valiev and T. Kurtén, J. Phys. Chem. A, 2023, 127, 1686–1696 CrossRef CAS.
- G. Hasan, R. R. Valiev, V.-T. Salo and T. Kurtén, J. Phys. Chem. A, 2021, 125, 10632–10639 CrossRef CAS.
- G. Hasan, V.-T. Salo, R. R. Valiev, J. Kubečka and T. Kurtén, J. Phys. Chem. A, 2020, 124, 8305–8320 CrossRef CAS.
- M. E. Casida, Recent advances in density functional methods: (Part I), World Scientific, 1995, pp. 155–192 Search PubMed.
- A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113 CrossRef.
- D. G. Fedorov, S. Koseki, M. W. Schmidt and M. S. Gordon, Int. Rev. Phys. Chem., 2003, 22, 551–592 Search PubMed.
- B. F. Minaev and S. Lunell, Z. Phys. Chem., 1993, 182, 263–284 CrossRef CAS.
- B. F. Minaev, Theoretical analysis and prognostication of spin–orbit coupling effects in molecular spectroscopy and chemical kinetics, Dissert, of Dr Sc., Chem. Phys. Institute, Moscow, 1983.
- B. F. Minaev, Dissert, of Cand. Sc. TGU, Tomsk, 1973.
- B. F. Minaev and H. Ågren, Chem. Inf., 2010 DOI:10.1002/chin.199926316.
- L. Salem and C. Rowland, Angew. Chem., Int. Ed. Engl., 1972, 11, 197 CrossRef.
- R. R. Valiev, V. N. Cherepanov, G. V. Baryshnikov and D. Sundholm, Phys. Chem. Chem. Phys., 2018, 20, 6121–6133 RSC.
- B. F. Minaev, R. R. Valiev, E. N. Nikonova, R. M. Gadirov, T. A. Solodova and T. N. Kopylova, J. Phys. Chem. A, 2015, 119, 1948–1956 CrossRef CAS.
- A. A. Granovsky, Firefly version 8.0.0, https://classic.chem.msu.su/gran/firefly/index.html.
- A. A. Granovsky, J. Chem. Phys., 2015, 143, 231101 CrossRef.
- S. Grimme, C. Bannwarth and P. Shuskov, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS.
- J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2016, 18, 3003–3010 RSC.
- J. Zhang and M. Dolg, Chem. Phys., 2015, 17, 24173–24181 CAS.
- I. Sahalianov, R. Valiev, R. Ramazanov and G. Baryshnikov, J. Phys. Chem. A, 2024, 26, 5138–5145 CrossRef.
- P. D. Lightfoot, R. Lesclaux and B. Veyret, J. Phys. Chem., 1990, 94(2), 700–707 CrossRef CAS.
- Y. Hori, T. Abe, Y. Shiota and K. Yoshizawa, Bull. Chem. Soc. Jpn., 2019, 92(11), 1840–1846 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nj03110e |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2024 |