Open Access Article
Open Access ArticleUnderstanding the second and third order nonlinear optical responses of M@b66/64Al12N12: a comprehensive DFT and TD-DFT study†
Meriem
Zaidi
 ab,
Douniazed
Hannachi
ab,
Douniazed
Hannachi
 *cd,
Nahla
Chaoui
a and
Henry
Chermette
*cd,
Nahla
Chaoui
a and
Henry
Chermette
 *e
*e
aDépartement de chimie, Faculté des Sciences, Université Ferhat Abbas, Setif-1, Algérie, Algeria
bLaboratoire de Chimie, Ingénierie Moléculaire et Nanostructures (LCIMN), Université Ferhat Abbas, Sétif 1, Sétif 19000, Algeria
cLaboratoire d'Électrochimie, d'Ingénierie Moléculaire et de Catalyse Redox (LEIMCR), Département d’Enseignement de Base en Technologie, Faculté de Technologie, Université Ferhat Abbas, Sétif-1, Algeria. E-mail: h_douniazed@yahoo.fr
dDépartement de Chimie, Faculté des Sciences de la Matière, Université de Batna-1, Algeria
eUniversité de Lyon, Université Claude Bernard Lyon 1, Institut des Sciences Analytiques, UMR CNRS 5280, 69622 Villeurbanne Cedex, France. E-mail: Henry.chermette@univ-lyon1.fr
First published on 29th May 2024
Abstract
Materials with significant first hyperpolarizability values are essential for application in second harmonic generation to achieve frequency doubling. Therefore, ideal NLO materials must not only exhibit a substantial NLO response but also maintain transparency when exposed to laser light. In this study, we investigate two series of nanoparticles, namely M@b64Al12N12 and M@b66Al12N12 (M ranges from Sc to Zn). The aim is to evaluate the second and third NLO responses through DFT and TD-DFT calculations. These evaluations are performed using the CAM-B3LYP/6-311+G(d) level of theory and the sum-over-states method in the static and dynamic regime (λ = ∞, 1906, 1341, and 1064 nm). These properties are further explained by considering factors such as molecular topology, delocalization indices, Waber–Cromer radius, excitation energy, oscillator strengths, variations of dipole moment of the excited state, and one/two-photon resonance effects. The results indicate that incorporating transition metals into Al12N12 substantially increases both the first and second hyperpolarizability. The delocalization index values reveal a higher degree of electron delocalization between the transition metal and nitrogen compared to that between the transition metal and aluminum. The QTAIM analysis displays that the presence of a closed quasi-ring structure between the metal and the nanocage, combined with electron delocalization, significantly enhances the first hyperpolarizability. TD-DFT calculations suggest potential application of these compounds in deep ultraviolet laser devices due to their transparency below 200 nm. The SOS approach reveals that the most critical excited states are local excitations, characterized by high Sr, small D, and negative t values. On the other hand, in the dynamic regime, our results indicated that the values of βHRS, βSHG(−2ω; ω, ω) and γESHG(−2ω; ω, ω, 0) are larger than their static counterparts. Additionally, one/two photon resonance energy, along with substantial oscillator strength, plays a pivotal role in enhancing the dynamic hyperpolarizability of the investigated nanoparticles. Our findings suggest that the increase in βλ is primarily linked to two-photon resonance rather than one-photon resonance. Based on our current understanding, this study provides novel evidence that, at λ = ∞, the first hyperpolarizability of M@b64/66Al12N12 is correlated with the Waber–Cromer radius of the transition metal. Additionally, in the dynamic regime, the first hyperpolarizability is correlated with the second hyperpolarizability.
Introduction
Nonlinear optics (NLO) is a branch of science that deals with the interaction of materials with strong oscillating electromagnetic fields, resulting in the generation of new electromagnetic fields with different phase, amplitude, frequency, and other optical properties from the incident ones.1,2When light propagates through a molecule, the valence electrons create a charge transfer relative to the atoms in the compound under the action of the induced electric field, resulting in the polarization of matter (P). The integration of first-principles methodologies with the finite-field (FF) approach is extensively utilized in the exploration of nonlinear optical responses due to its compatibility with diverse electronic structure techniques for the calculation of NLO coefficients.3 In the FF approach, the energy of a system subjected to a weak and static electric field can be expressed as
 | (1) |
The field of nonlinear optics gained significant attention in scientific research after the discovery of second harmonic generation (SHG) by Franken et al. in 1961.4 The following decades have evidenced various developments in the domain of nonlinear optics including new NLO phenomena and different new applications. These developments include for example the discovery of third harmonic generation (THG), sum or difference frequency generation, optical parametric amplification and optical parametric oscillation. These phenomena have led to the evolution of new technologies such as ultrafast lasers,5,6 nonlinear microscopy,7 and nonlinear optical switching.5,6,8 Furthermore, nonlinear optical materials have great potential applications in different fields such as optoelectronics,9,10 photonics,11 optical computing, optical communications,12,13 holographic imaging, dynamic image processing, etc.14,15 In this regard, several strategies for tuning the NLO response of materials have been suggested: for example, reinforcing push–pull effects,16–19 designing octupolar compounds20,21 and asymmetric coordination complexes22–24 introducing diffuse excess electrons,25–28 using multi-decker sandwich clusters,29,30 designing metal organic frameworks,31 and so forth.
Among the many strategies reported in the literature, recent theoretical investigations have revealed that introducing excess electrons into different structures can result in a considerably large first hyperpolarizability. This effect is often observed when a metal atom (such as alkali metals, transition metals, alkaline earth metals and superalkalis) is doped into various structures (mostly the nanocages).32–34 In recent years, significant efforts have been devoted to the study of hybrid or heterofullerene structures of group II–VI and III–V (Al12N12, Al12P12, Al12N12, B12N12, etc.) due to their extraordinary physicochemical properties, which include chemical stability, high thermal conductivity, wide energy gap and resistance to oxidation.35,36 Niu et al. observed that alkali metal doping at various positions (b64 and r6) of Al12N12 nanocages lowered the energy gap, leading to an enhancement in the nonlinear optical response of Al12N12. Let us remember that b64 nomenclature means above the bond between a 6 atom ring and a 4 atom ring, and r6 means above the center of a 6 atom ring. The highest first hyperpolarizability was observed for Li@r6Al12N12.37 The results of Shakerzadeh et al. demonstrate that the structural and optoelectronic properties of Be12O12 and Mg12O12 are strongly influenced by their interaction with alkali metals. Additionally, exohedral doping resulted in larger nonlinear optical (NLO) responses than encapsulated doping for these metal oxide nanoclusters.38 Furthermore, the same group observed that the optoelectronic nitride nanoclusters exhibit a remarkable NLO response compared to their corresponding carbides.39,40
On the other hand, Gilani et al. conducted exohedral and endohedral doping of copper on Al12N12 nanocages and concluded that Cu@r6Al12N12 exhibited higher nonlinear optical responses compared to Cu@b66, Cu@b64 and Cu@endo41 (r4 means above the center of a 4-atom ring). According to Arshad et al.,34,42 the exohedral doping of first-row transition metals at various sites (@: b64, b66, r6, and r4) on the Al12N12 and B12N12 nanocage resulted in the highest NLO response, with Cu@r6Al12N12 showing the most significant first hyperpolarizability (b66 signifies a bond shared between two hexagonal rings). Additionally, it was shown that the r4Al12N12 structure is thermodynamically less stable than b64Al12N12.42 Similarly, Irshad et al. performed theoretical studies on transition metal-doped B12P12 nanoclusters and observed that the first hyperpolarizability of Sc@r4B12P12 was remarkably enhanced up to 4.4 × 104 a.u. Furthermore, Sc@r4B12P12 and Sc@r6B12P12 exhibited the highest values for the electro-optical Pockels effect (EOPE) and second harmonic generation (SHG), respectively.43
In this paper, with the objective of achieving a more comprehensive understanding of the second- and third-order nonlinear optical characteristics present in M@Al12N12 (where M spans from Sc to Zn), we conduct QTAIM, DFT, and TD-DFT calculations. These calculations are employed to investigate the electronic geometries, excited state properties, and NLO responses of two series of nanocages: M@b64Al12N12 and M@b66Al12N12. Key focal points encompass (i) scrutinizing the evolution of both linear and nonlinear optical properties as they relate to frequency intensity (ω = 0, 0.0239, 0.0340 and 0.0428 a.u.), (ii) evaluating the implications of transition metal atoms for these properties, and (iii) drawing insightful comparisons between M@b64Al12N12 and M@b66Al12N12 (we will use M@b64 and M@b66 in the following to shorten the typing).
The present paper is organized as follows: First, some computational details and definitions are given; next, the quantum theory of atoms in molecules (QTAIM) is analysed and delocalization indices (DI) are calculated; then, absorption spectra are discussed; in the following part, the static and dynamic NLO parameters of the doped nanocage are calculated; finally the sum-over-states method (SOS) is studied; the paper ends with some concluding remarks.
Computational methodology
The density functional theory (DFT) and time-dependent DFT (TD-DFT) calculations are performed by means of Gaussian 16 software.44 The starting point for this computational study was the optimized structures of two nanoparticle series, specifically M@b64Al12N12 and M@b66Al12N12, where M ranges from Sc to Zn, previously achieved by Arshad and co-workers.42The NLO response and the absorption spectra of all the studied nanoparticles were calculated at CAM-B3LYP45 with the 6-311+G(d) basis set. CAM-B3LYP is a long-range corrected functional developed to handle the inaccuracies of the non-Coulomb part of the exchange functional at long distances. On the other hand, the Amsterdam density functional (ADF2017) software was used to perform topological analysis of the electron density at bond critical points, utilizing the concept of Bader's atoms in molecules (AIM) theory.46–49
The first hyperpolarizability is given as follows:
 | (2) |
| βx = βxxx + βxyy + βxzz | (3) |
| βy = βyyy + βxxy + βyzz | (4) |
| βz = βzzz + βzyy + βxxz | (5) |
The total magnitude of γ is estimated as3,50,51
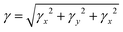 | (6) |
 | (7) |
The i components of the second hyperpolarizabilities are defined as
 | (8) |
 | (9) |
Furthermore, the depolarization ratios (DR) provide information about the geometry of the chromophore, which is the part of the compound responsible for the nonlinear optical (NLO) response. An ideal one-dimensional system has a DR of 5, while an octupolar molecule has a DR of 1.5.
 | (10) |
The electron density difference maps (EDDM) for the crucial excited states can be precisely evaluated as follows:
| Δρ(r) = ρex(r) − ρGS(r) | (11) |
On the other hand, to investigate the nature of electronic excitation in compounds, an analysis of the hole–electron distribution was performed. The distributions of holes and electrons are defined as follows:62,63
 | (12) |
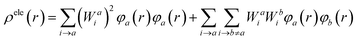 | (13) |
The overlap distribution between the hole and the electron can be expressed as
 | (14) |
 | (15) |
| Dindex = [(Dx)2 + (Dy)2 + (Dz)2]1/2 | (16) |
| HCT = |H·uCT| | (17) |
t index is used to measure the separation degree between the hole and the electron in the CT direction:
| tindex = Dindex − HCT | (18) |
 | (19) |
and
In our work, the crucial excited state wavefunctions have been obtained by natural transition orbitals (NTOs) in terms of “excited particle” to “empty hole” of the electronic transition density matrix. The CT indices have been determined with the MULTIWFN program.62
Results and discussion
QTAIM
In order to understand the nature of the bonding interaction between the transition metal (M) and the Al12N12 nanocage (Scheme S1, ESI†), we have carried out topological analysis of electron density on all doped geometries M@Al12N12 according to quantum theory of atoms in molecules (QTAIM) introduced by Bader46–49,64 using the Amsterdam density functional (ADF17) program developed by Baerends et al.65,66 In QTAIM, the critical points (in ring (RCP) or bond (BCP)) are the positions where the gradient is null and which can be classified according to the electron density (ρ) and its Laplacian (∇2(ρ)), total electron energy density (H), kinetic electron energy density (G) and potential electron energy density (V).49,67 The results of the calculation are listed in Table 1. Fig. 1 and Fig. S1 (ESI†) depict the molecular graphs corresponding to the M@b66Al12N12 and M@b64Al12N12 nanocage where the red circle indicates the ring critical point (RCP) and the green circle indicates the bond critical point (BCP).| M | ρ | ∇ | G | V | H | |
|---|---|---|---|---|---|---|
| M@b64Al12N12 | ||||||
| Sc | BCP Sc–Al | 0.039 | −0.020 | 0.009 | −0.024 | −0.014 |
| BCP Sc–N | 0.123 | 0.375 | 0.150 | −0.208 | −0.057 | |
| Ti | BCP Ti–Al | −5.361 | −3.505 | 1.855 | 4.433 | 5.296 |
| BCP Ti–N | 0.043 | −0.025 | 0.011 | −0.029 | −0.017 | |
| V | BCP V–Al | 0.139 | 0.413 | 0.177 | −0.251 | −0.073 |
| BCP V–N | −5.388 | −2.708 | 2.680 | 4.048 | 3.057 | |
| Cr | RCP | 0.048 | −0.037 | 0.011 | −0.033 | −0.021 |
| BCP Cr–N | 0.135 | 0.436 | 0.175 | −0.242 | −0.066 | |
| BCP Cr–Al | −5.710 | −2.914 | 2.795 | 4.312 | 3.326 | |
| Mn | BCP Mn–N | 0.041 | 0.009 | 0.015 | −0.029 | −0.013 |
| Fe | RCP | 0.115 | 0.409 | 0.147 | −0.192 | −0.045 |
| BCP Fe–Al | 0.041 | −0.016 | 0.011 | −0.027 | −0.015 | |
| BCP Fe–N | 0.091 | 0.326 | 0.107 | −0.134 | −0.026 | |
| Co | RCP | 0.043 | 0.012 | 0.017 | −0.031 | −0.014 |
| BCP Co–Al | 0.043 | 0.004 | 0.016 | −0.031 | −0.015 | |
| BCP Co–N | 0.110 | 0.387 | 0.137 | −0.179 | −0.041 | |
| Ni | RCP | 0.045 | 0.024 | 0.020 | −0.035 | −0.014 |
| BCP Ni–Al | 0.045 | 0.018 | 0.019 | −0.035 | −0.015 | |
| BCP Ni–N | 0.111 | 0.406 | 0.141 | −0.182 | −0.040 | |
| Cu | RCP | 0.048 | 0.058 | 0.028 | −0.042 | −0.013 |
| BCP Cu–Al | 0.049 | 0.047 | 0.026 | −0.041 | −0.015 | |
| BCP Cu–N | 0.113 | 0.429 | 0.147 | −0.188 | −0.040 | |
| Zn | BCP Zn–N | 0.050 | 0.069 | 0.031 | −0.044 | −0.013 |
| M@b66Al12N12 | ||||||
| Sc | RCP | 0.036 | 0.029 | 0.016 | −0.025 | −0.009 |
| BCP Sc–N | 0.113 | 0.336 | 0.132 | −0.181 | −0.048 | |
| BCP Sc–Al | 0.037 | −0.009 | 0.010 | −0.022 | −0.012 | |
| Ti | RCP | 0.035 | 0.046 | 0.018 | −0.025 | −0.007 |
| BCP Ti–Al | 0.035 | −0.0005 | 0.011 | −0.022 | −0.011 | |
| BCP Ti–N | 0.110 | 0.329 | 0.127 | −0.173 | −0.045 | |
| V | RCP | 0.042 | 0.016 | 0.017 | −0.031 | −0.013 |
| BCP V–Al | 0.042 | −0.012 | 0.012 | −0.029 | −0.016 | |
| BCP V–N | 0.115 | 0.370 | 0.140 | −0.188 | −0.047 | |
| Cr | BCP Cr–N | 0.118 | 0.410 | 0.150 | −0.197 | −0.047 |
| Mn | BCP Mn–N | 0.093 | 0.332 | 0.111 | −0.138 | −0.027 |
| Fe | BCP Fe–N | 0.111 | 0.391 | 0.139 | −0.181 | −0.041 |
| Co | BCP Co–N | 0.112 | 0.410 | 0.143 | −0.183 | −0.040 |
| Ni | BCP Ni–N | 0.114 | 0.439 | 0.151 | −0.192 | −0.041 |
| Cu | BCP Cu–N | 0.126 | 0.490 | 0.173 | −0.224 | −0.050 |
| Zn | BCP Zn–N | 0.066 | 0.244 | 0.071 | −0.082 | −0.010 |
According to our calculations, Cr@b66, Mn@b66, Mn@b64, Fe@b66, Co@b66, Ni@b66, Zn@b66 and Zn@b64 have one BCP that is connected to the metal. This BCP found between the transition metal (M) atom and the nitrogen atom suggests the presence of M–N bonding interactions. As shown in Table 1 and Fig. 1 and Fig. S1 (ESI†), HBCP values are negative and ∇2(ρ) are high positive values, indicating that the M–N interaction is partly covalent and partly electrostatic (the average value of  is 1.293). Exceptions are Mn and Zn aluminium nitride nanocages, in which we can observe that the BCP (M–N) bond exhibits closed-shell interaction (ionic) due to their small values of ρBCP (less than 0.1) and large positive value of ∇2ρBCP.
is 1.293). Exceptions are Mn and Zn aluminium nitride nanocages, in which we can observe that the BCP (M–N) bond exhibits closed-shell interaction (ionic) due to their small values of ρBCP (less than 0.1) and large positive value of ∇2ρBCP.
On the other hand, Fig. 1 and Fig. S1 (ESI†) clearly show that M@b64Al12N12 (M: Cr, Fe, Co, Ni and Cu) and M@b66Al12N12 (M: Sc, Ti and V) have two BCPs (BCP(M–N) and BCP(M–Al)) and RCP. It is found that HBCP(M–N) values are negative and ∇2ρBCP(M–N) is high and positive, meaning that the M–N bonding interactions are characteristic of partially ionic and partially covalent owing to  . The Laplacian of the electron density (∇2ρBCP) and the local total electronic energy density (H) are negative values and ρBCP < 0.1 at BCP(M–Al) indicates that this bonding is mixed covalent–ionic interaction (
. The Laplacian of the electron density (∇2ρBCP) and the local total electronic energy density (H) are negative values and ρBCP < 0.1 at BCP(M–Al) indicates that this bonding is mixed covalent–ionic interaction ( on M–Al is 1.937, 1.842, 1.576 and 1.50, where M = Fe, Co, Ni and Cu, respectively).
on M–Al is 1.937, 1.842, 1.576 and 1.50, where M = Fe, Co, Ni and Cu, respectively).
In the case of Sc@b64Al12N12, Ti@b64Al12N12 and V@b64Al12N12, the existence of two BCPs between M and N can be observed, exhibiting both covalent and electrostatic characteristics (∇2ρBCP > 0 and HBCP < 0). ∇2ρBCP and HBCP at the second BCP between M and Al are negative, which indicates the presence of “open shell” (covalent) character of the coordination bonds. The degree of covalence of a chemical bond can be estimated utilizing the ratio −VBCP/GBCP. The greater its amount, the more covalent character a bond has. Our results display that the covalent character of all M–Al (where M = Sc, Ti and V) bonds is much larger compared to any other bonds  . Furthermore, for M = Sc, Ti, and V, we observe that the HBCP values of the M–N and M–Al bonds for M@b64Al12N12 are more negative compared to those for M@b66Al12N12. This suggests that the Sc@b66, Ti@b66 and V@b66 nanocages have weaker covalent bonds, which can be attributed to the presence of the RCP. The ascending sequence for the covalent character of the M–Al bond is as follows:
. Furthermore, for M = Sc, Ti, and V, we observe that the HBCP values of the M–N and M–Al bonds for M@b64Al12N12 are more negative compared to those for M@b66Al12N12. This suggests that the Sc@b66, Ti@b66 and V@b66 nanocages have weaker covalent bonds, which can be attributed to the presence of the RCP. The ascending sequence for the covalent character of the M–Al bond is as follows:
Cu < Ni < Co < Fe < Cr < Ti < Sc < V.
When examining the range of M elements spanning from Cr to Zn, a noteworthy observation is that the HBCP values for the M–N bond within M@b66 are akin to those found in M@b64. However, it is important to highlight that the Cu–N bond displays a notably enhanced covalent character (HBCP(Cu–N) = −0.046 a.u.) when compared to the covalency of Cr–N, Ni–N, Co–N, Fe–N, Mn–N, and Zn–N bonds, respectively (HBCP(Fe–N) = HBCP(Co–N) = HBCP(Ni–N) = −0.041, HBCP(Zn–N) = −0.010 a.u.).
Delocalization indices
The concept of the “delocalization index” (DI), δ(A, B), was developed by Bader and colleagues as a method to measure electron delocalization within the framework68,69 of the quantum theory of atoms in molecules. This index quantifies the extent of electron sharing between pairs of atoms A and B in a molecule, providing a real space measure of electron delocalization. Table 2 and Table S1 (ESI†) provide the values of δ(M, A) in M@b64Al12N12 and M@b66Al12N12, where A is N or Al and M is a transition metal (Scheme S1, ESI†).| Sc | Ti | V | Cr | Mn | Fe | Co | Ni | Cu | Zn | |
|---|---|---|---|---|---|---|---|---|---|---|
| M@b64Al12N12 | ||||||||||
| δ(M, Al1) | 0.93 | 0.94 | 0.95 | 0.81 | 0.72 | 0.81 | 0.81 | 0.82 | 0.77 | 0.65 |
| δ(M, N3) | 1.74 | 1.74 | 1.65 | 1.29 | 1.14 | 1.17 | 1.12 | 1.08 | 1.20 | 0.80 |
| M@b66Al12N12 | ||||||||||
| δ(M, Al6) | 0.90 | 0.87 | 0.86 | 0.84 | 0.74 | 0.85 | 0.83 | 0.83 | 0.79 | 0.66 |
| δ(M, N19) | 1.58 | 1.46 | 1.41 | 1.28 | 1.14 | 1.18 | 1.12 | 1.10 | 1.19 | 0.80 |
In our analysis of both nanoparticles, it was noted that the delocalization index for δ(M, N) is substantially larger than that for δ(M, Al). This finding indicates a higher degree of electron delocalization between the transition metal and nitrogen in comparison to the electron delocalization between the transition metal and aluminium.
In the series of M@b64 nanoparticles, where M represents Sc, Ti, V, and Cr, the δ(M, N) values range from 1.29 to 1.74. For the M@b66 compounds, these values are observed to be between 1.28 and 1.58. This range in δ(M, N) values implies a partial double-bond character in these complexes. Additionally, it is noted that M@b64 exhibits higher DI values compared to M@b66, with a decreasing trend observed from Sc to Cr. The δ(M, Al) values for M@b64/66 (M from Sc to Zn) fall within the range of 0.65 to 0.95. This range aligns with the expected characteristics of a donor–acceptor interaction in the M–Al bond.70 On the other hand, it is observed that in the M@b64 series (where M ranges from Cr to Zn), the δ(M, N) and δ(M, Al) values closely resemble those reported for the M@b66 series. In the M@b66/64 complexes, where M ranges from Sc to Cr, the δ(M, N) and δ(M, Al) values are observed to be higher than those in nanoparticles where M spans from Mn to Zn. Generally, it is noted that the DI values tend to decrease as the atomic number of the metal increases, with notable exceptions being the compounds of Mn and Cu. Furthermore, in the M@b66/64 complexes, the observed delocalization index values are below 0.1. This low DI value confirms the lack of bonding interactions between the transition metal and the other atoms within the nanocage (Table S1, ESI†).
Electronic spectra: UV-vis spectra and excited states
In order to achieve a more comprehensive understanding of the underlying source of nonlinear optical (NLO) properties, TD-DFT calculations were performed on the studied complexes. Table S1 (ESI†) and Table 3 summarize the spectroscopic parameters of crucial electronic transitions, including absorption wavelengths (λ0→n), oscillator strengths (f0→n), transition dipole moment (Δμ0→n), overlap (Sr(r)), and D and t indices.| M | S0→n | λ 0→n | f 0→n | S r | D | t |
|---|---|---|---|---|---|---|
| M@b64Al12N12 | ||||||
| Sc | S0→5 | 766 | 0.009 | 0.795 | 1.085 | −0.434 |
| S0→13 | 463 | 0.144 | 0.578 | 1.187 | −0.443 | |
| Ti | S0→5 | 996 | 0.005 | 0.597 | 0.628 | −0.455 |
| S0→16 | 428 | 0.055 | 0.662 | 1.044 | −0.749 | |
| V | S0→5 | 822 | 0.001 | 0.596 | 0.442 | −0.588 |
| S0→15 | 407 | 0.116 | 0.757 | 0.896 | −0.773 | |
| Cr | S0→1 | 917 | 0.001 | 0.602 | 0.558 | −0.736 |
| S0→7 | 484 | 0.088 | 0.590 | 1.213 | −0.664 | |
| Mn | S0→1 | 850 | 0.01 | 0.86 | 0.245 | −1.195 |
| S0→9 | 416 | 0.140 | 0.733 | 1.205 | −0.443 | |
| Fe | S0→4 | 952 | 0.023 | 0.872 | 0.164 | −1.171 |
| S0→9 | 512 | 0.057 | 0.486 | 3.156 | 1.111 | |
| Co | S0→8 | 717 | <0.001 | 0.581 | 0.329 | −0.633 |
| S0→9 | 671 | 0.072 | 0.805 | 0.358 | −1.001 | |
| Ni | S0→5 | 676 | 0.037 | 0.845 | 0.163 | −1.305 |
| S0→7 | 480 | 0.055 | 0.469 | 3.107 | 1.098 | |
| Cu | S0→1 | 591 | 0.076 | 0.726 | 0.667 | −0.782 |
| S0→2 | 468 | 0.057 | 0.489 | 2.952 | 0.927 | |
| Zn | S0→3 | 414 | 0.215 | 0.699 | 0.219 | −1.546 |
| S0→5 | 372 | 0.09 | 0.413 | 3.057 | 1.006 | |
| M@b66Al12N12 | ||||||
| Sc | S0→6 | 885 | 0.001 | 0.706 | 0.522 | −0.710 |
| S0→13 | 527 | 0.251 | 0.658 | 1.022 | −0.739 | |
| Ti | S0→8 | 837 | <0.001 | 0.802 | 0.131 | −1.166 |
| S0→13 | 590 | 0.177 | 0.670 | 0.853 | −0.837 | |
| V | S0→7 | 859 | <0.001 | 0.544 | 0.514 | −0.455 |
| S0→12 | 495 | 0.075 | 0.594 | 1.841 | −0.195 | |
| Cr | S0→1 | 861 | <0.001 | 0.601 | 0.536 | −0.723 |
| S0→7 | 495 | 0.097 | 0.579 | 1.409 | −0.411 | |
| Mn | S0→1 | 845 | 0.011 | 0.858 | 0.332 | −1.199 |
| S0→8 | 424 | 0.118 | 0.771 | 1.011 | −0.542 | |
| Fe | S0→4 | 866 | 0.022 | 0.848 | 0.213 | −1.111 |
| S0→9 | 513 | 0.05 | 0.439 | 3.305 | 1.354 | |
| Co | S0→7 | 804 | 0.031 | 0.856 | 0.134 | −1.170 |
| S0→9 | 510 | 0.049 | 0.438 | 3.214 | 1.260 | |
| Ni | S0→5 | 649 | 0.068 | 0.803 | 0.400 | −0.940 |
| S0→7 | 500 | 0.056 | 0.444 | 3.184 | 1.221 | |
| Cu | S0→1 | 622 | 0.077 | 0.711 | 0.689 | −0.701 |
| S0→2 | 491 | 0.053 | 0.424 | 3.085 | 1.128 | |
| Zn | S0→3 | 427 | 0.197 | 0.694 | 0.233 | −1.505 |
| S0→5 | 387 | 0.076 | 0.386 | 2.936 | 0.940 | |
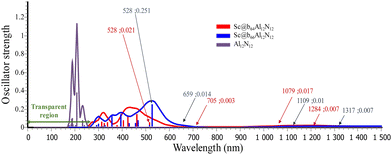
Materials that exhibit large first hyperpolarizability values are primarily employed for second harmonic generation (SHG) to double the frequency (2ω). It should be emphasized that the excellent NLO materials should not only have a large NLO response but also possess transparency under the laser light used.71 For this objective, the ultraviolet-visible-infrared (UV-VIS-NIR) absorption spectrum of the lowest-energy Al12N12 and M@Al12N12 (M = Sc to Zn, b64 and b66) is obtained and shown in Fig. 2 and Fig. S2 (ESI†). Based on the TD-DFT results (we used 120 excited states, which is sufficient for the objectives of this investigation72,73) it is evident that the absorption spectrum of isolated Al12N12 appears in the ultraviolet region between 170 and 300 nm. However, upon interaction with a transition metal, the absorption peaks of M@Al12N12 are red-shifted towards the visible region. It can be seen that Cr@b64/66, Mn@b64/66 and Cu@b64/66 exhibit infrared (IR) transparent regions at a wavelength greater than 950 nm, indicating good transparency to infrared light. All these systems are fully transparent in the deep ultraviolet region (≤200 nm). Therefore, they can be considered as potential candidates for high-performance nonlinear optical (NLO) materials in the deep ultraviolet range.
Our calculations reveal a minor red-shift in the calculated wavelength for M@b66Al12N12 in comparison to M@b64Al12N12 (with the exception of M = Fe). We can observe that the UV-Vis spectrum of Sc@b66 shows two peaks at 528 nm and 356 nm (f = 0.251, 0.121), whereas the spectrum of Sc@b64 displays peaks at 463 and 424 nm (f = 0.144, 0.121) and may be assigned to a mixed contribution of intra-charge transfer in the metal (ICT) and CT from the metal to nanocage (MNCT). For V@b64, the absorption band appearing at 408 nm (f = 0.116) is formed by the αHOMO−1 → αLUMO+1 and βHOMO → βLUMO+2 excitation, which is regarded as a mixed ICT in the metal and MNCT transition (local transition Sr = 0.757). For V@b66, the absorption band at 496 nm is formed by βHOMO → βLUMO+2 transitions which are of the MNCT (Sr = 0.594) character. For Ti@b64 the absorption band located at 394 nm, with a large oscillator strength (f = 0.12), is dominated by αHOMO−2 → αLUMO+3 and βHOMO → βLUMO+3, which are assigned to a mixed contribution from ICT and MNCT. As for Ti@b66 the βHOMO → βLUMO+2 excitation at 590 nm (f = 0.177) is ICT in the metal and of small MNCT character (Fig. S3, ESI†).
The electronic transition S0 → S1 and S0 → S2 of Cu@b66 at 622 and 492 is assigned as ICT in Cu and MNCT (CT from metal to nanocage) [αHOMO → αLUMO+1 and αHOMO → αLUMO, respectively] and the transition at 343 and 328 nm may be attributed to NMCT (CT from nanocage to metal) [βHOMO → βLUMO and βHOMO−1 → βLUMO, respectively]. We found similar results for Cu@b64 at 592, 468, 343 and 331 nm (see Table S2 and Fig. S3, ESI†). The absorption spectrum of Cr@b64/66Al12N12 exhibits a moderate absorption band ranging from 600 to 900 nm, as well as strong absorption peaks at 490, 402, and 350 nm. These four states are traced to the electronic transitions of αHOMO−1 → αLUMO+1, βHOMO → βLUMO, αHOMO → αLUMO+3 and βHOMO → βLUMO+1 (S0 → S1 (ICT), S0 → S7 (MNCT), S0 → S11 (MNCT) and S0 → S16 (mixed contributions of ICT and MNCT), respectively).
It should be noted that the transition of M@b64/66Al12N12, where M = Mn, Fe, Co and Ni, from αHOMO to αLUMO+1 primarily involves an intra-charge transfer within the metal at 850 nm (Ni@Al12N12), 952 nm (Fe@b64), 866 nm (Fe@b66), 671 nm (Co@b64), 804 nm (Co@b66) and 663 nm (for Ni@Al12N12). These absorptions show significantly high overlap index between the hole and the electron (Sr > 0.8), small Dindex (from 0.1 to 0.4 Å), and negative tindex (≥−1), indicating that they display the local excitation feature during electron transition. Furthermore, the electronic transition at ∼500 nm is dominated by αHOMO → αLUMO, which shows the dominant electron transfer trend from metal to nanocage (for Mn@Al12N12, Sr = 0.6 and Sr = 0.4 where M = Fe, Co and Ni, (see Fig. 3, Fig. S3 and Table S2, ESI†). The energy absorption band appearing at ∼400 nm (M = Mn, Fe and Co) is formed by the βHOMO → βLUMO+1, +2 excitation, which is regarded as a mixed ICT and MNCT transition. The absorption region at 320 nm for Ni@Al12N12 is created by the βHOMO → βLUMO transition. The shapes of molecular orbitals indicate that these transitions belong to NMCT, which involves charge transfer from a nanocage to Ni metal (Sr = 0.5) (Fig. S3 in ESI†).
On the other hand, Zn@Al12N12 exhibits electronic transition absorbing at ∼420, ∼378 and ∼300 nm, and the major transitions are from HOMO → LUMO+1, HOMO → LUMO and HOMO−1 → LUMO. The molecular orbitals indicate that these transitions belong to ICT in Zn and MNCT and ICT in the nanoparticle (Fig. S3 and Table S2, ESI†).
Nonlinear optical parameters
The second and third order NLO properties of materials are closely related to various parameters, including electric dipole moment, chemical hardness, and electronic structures of compounds. Quantum chemical calculations can provide useful guidance for further experimental investigations into the second- and third-order NLO behaviour.22–24 However, predicting the NLO properties of large nanoparticle systems using density functional theory remains a major challenge.Nonlinear optical properties, e.g. first hyperpolarizability (βλHRS and βλSHG(−2ω; ω, ω)), second hyperpolarizability (γλ(−2ω; ω, ω, 0)) and depolarization ratios (DRλ) (static (λ = ∞) as well as dynamic), for all M@b64/66Al12N12 are provided in Tables 4, 5, Fig. 4 and Fig. S3 (ESI†). For calculating dynamic characteristics, three frequencies (ω) are employed, including two laser frequencies of 0.0340 a.u. (1341 nm) and 0.0428 a.u. (1064 nm) that are chosen to prevent resonance enhancement effects. Furthermore, a non-resonant frequency of 0.0239 a.u. (1906 nm) is also integrated into these systems.
| M@b64Al12N12 | Sc | Ti | V | Cr | Mn | Fe | Co | Ni | Cu | Zn | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Most stable spin state | Doublet | Triplet | Quartet | Quintet | Sextet | Quintet | Quartet | Triplet | Doublet | Singlet | |
| Magnetic moment | 10.439 | 10.479 | 10.519 | 10.559 | 10.599 | 10.639 | 10.679 | 10.72 | 10.759 | 10.800 | |
| λ = ∞ | β ∞HRS | 6824 | 2844 | 1718 | 2022 | 769 | 813 | 873 | 923 | 1010 | 448 |
| DR∞ | 7.614 | 7.769 | 7.812 | 7.325 | 3.725 | 3.779 | 5.085 | 5.550 | 5.584 | 5.462 | |
| γ(0; 0, 0, 0) | 345![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 236 236 |
253![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 934 934 |
192![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 576 576 |
267![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 954 954 |
306![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 434 434 |
212![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 848 848 |
200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 176 176 |
200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 397 397 |
187![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 169 169 |
152![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 310 310 |
|
| λ = 1064 | β SHG(−2ω; ω, ω) | 391![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 027 027 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472 472 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 078 078 |
9120 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 180 |
47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 175 175 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298 298 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 645 645 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 744 744 |
2609 |
| β λ HRS | 236![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 559 559 |
7129 | 7078 | 3640 | 8985 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 727 727 |
6197 | 5417 | 7316 | 1136 | |
| DRλ | 1.339 | 1.454 | 1.883 | 6.937 | 2.565 | 2.038 | 0.661 | 2.474 | 3.224 | 3.941 | |
| γ(−2ω; ω, ω, 0) | 82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 236 236![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 510 510 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 035 035![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 118 118 |
234![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 015 015 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 338 338![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 979 979 |
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 509 509![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 417 417 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 591 591![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340 340 |
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 147 147![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 931 931 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 749 749![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 344 344 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 107 107![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 949 949 |
360![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 334 334 |
|
| γ(−ω; ω, 0, 0) | 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 314 314![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 110 110 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 063 063![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 860 860 |
272![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 615 615 |
463![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 597 597 |
685![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 365 365 |
323![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 649 649 |
245![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 229 229 |
313![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 902 902 |
290![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504 504 |
186![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 927 927 |
|
| γ DFWM | 125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 611 611![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 201 201 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 657 657![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 588 588 |
286![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 428 428 |
820![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 605 605 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 086 086![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 359 359 |
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 783 783![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 146 146 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 561 561![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 147 147 |
830![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 217 217 |
597![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 430 430 |
256![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 268.333 268.333 |
|
| n 2 (cm2 W−1) | 1.04 × 10−14 | 1.54 × 10−15 | 2.37 × 10−17 | 6.79 × 10−17 | 1.72 × 10−16 | 4.78 × 10−16 | 1.29 × 10−16 | 6.87 × 10−17 | 4.94 × 10−17 | 2.1219 × 10−17 | |
| λ = 1341 | β SHG (−2ω; ω, ω) | 230![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157 157 |
47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 264 264 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 401 401 |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 321 321 |
5938 | 4056 | 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 387 387 |
48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 639 639 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 423 423 |
1786 |
| β λ HRS | 185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 510 510 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 823 823 |
5857 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 974 974 |
2724 | 2225 | 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 858 858 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 495 495 |
5108 | 747 | |
| DRλ | 0.531 | 4.602 | 3.301 | 2.814 | 4.028 | 1.011 | 3.278 | 2.874 | 4.414 | 4.721 | |
| γ(−2ω; ω, ω, 0) | 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 964 964![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 740 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 793 793![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 484 484 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 078 078![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 111 111 |
7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 755 755![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 519 519 |
880![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 009 009 |
986![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 328 328 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 036 036![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 070 070 |
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 279 279![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 438 438 |
777![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 884 884 |
237![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 633 633 |
|
| γ(−ω; ω, 0, 0) | 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 946 946![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 960 960 |
502![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 537 537 |
836![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 282 282 |
360![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 031 031 |
441![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 008 008 |
206![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 335 335 |
255![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 234 234 |
258![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 541 541 |
241![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 221 221 |
171![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 978 978 |
|
| γ DFWM | 83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 486 486![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 794 794 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 349 349![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 053 053 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 464 464![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 793 793 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 855 855![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 886 886 |
632![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 199 199 |
464![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 161 161 |
9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 867 867![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 198 198 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 284 284![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 888 888 |
438![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 126 126 |
200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 419 419 |
|
| n 2 (cm2 W−1) | 6.91 × 10−15 | 1.11 × 10−16 | 1.21 × 10−16 | 2.36 × 10−16 | 5.23 × 10−17 | 3.84 × 10−17 | 8.17 × 10−16 | 1.89 × 10−16 | 3.62 × 10−17 | 1.6595 × 10−17 | |
| λ = 1906 | β SHG(−2ω; ω, ω) | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 663 663 |
716![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 168 168 |
6097 | 8840 | 6701 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 212 212 |
3446 | 3877 | 4214 | 1454 |
| β λ HRS | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 779 779 |
317![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 616 616 |
2370 | 3334 | 2899 | 8476 | 1473 | 1592 | 1709 | 592 | |
| DRλ | 2.541 | 2.588 | 5.721 | 7.856 | 4.271 | 0.885 | 4.800 | 4.595 | 5.161 | 5.299 | |
| γ(−2ω; ω, ω, 0) | 830![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340 340 |
732![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 872 872![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
271![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 797 797 |
468![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 308 308 |
735![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 755 755 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 325![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 355 355 |
285![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 028 028 |
294![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 109 109 |
282![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 428 428 |
184![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 297 297 |
|
| γ(−ω; ω, 0, 0) | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 126 126![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 709 709 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 330 330![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 356 356 |
211![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 553 553 |
305![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 011 011 |
355![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 683 683 |
221![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 614 614 |
221![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 461 461 |
181![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 224 224 |
211![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 312 312 |
160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 842 842 |
|
| γ DFWM | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 288 288![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 410 410 |
245![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536 536![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 545 545 |
237![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 960 960 |
371![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 795 795 |
498![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 790 790 |
925![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 783 783 |
249![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 745 745 |
212![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 461 461 |
243![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 065 065 |
171![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504.333 504.333 |
|
| n 2 (cm2 W−1) | 2.72 × 10−16 | 2.03 × 10−14 | 1.97 × 10−17 | 3.07 × 10−17 | 4.13 × 10−17 | 7.66 × 10−17 | 2.06 × 10−17 | 1.75 × 10−17 | 2.01 × 10−17 | 1.4201 × 10−17 |
| M@b66Al12N12 | Sc | Ti | V | Cr | Mn | Fe | Co | Ni | Cu | Zn | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Most stable spin state | Doublet | Triplet | Quartet | Quintet | Sextet | Quintet | Quartet | Triplet | Doublet | Singlet | |
| Magnetic moment | 10.44 | 10.47 | 10.51 | 10.55 | 10.60 | 10.64 | 10.68 | 10.72 | 10.76 | 10.79 | |
| λ = ∞ | β ∞HRS | 5857 | 4553 | 2701 | 2042 | 752 | 675 | 618 | 767 | 1012 | 428 |
| DR∞ | 7.748 | 7.124 | 7.313 | 7.457 | 4.138 | 4.174 | 4.402 | 5.710 | 5.902 | 6.059 | |
| γ(0; 0, 0, 0) | 334![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 662 662 |
531![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 334 334 |
310![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 923 923 |
278![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 703 703 |
321![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 552 552 |
222![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 456 456 |
199![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 732 732 |
199![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 353 353 |
195![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 136 136 |
152![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 891 891 |
|
| λ = 1064 | β SHG(−2ω; ω, ω) | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 187 187![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 634 634 |
109![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 971 971 |
51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 710 710 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 250 |
149![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 819 819 |
47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 834 834 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 273 273 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 244 244 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 372 372 |
2725 |
| β λ HRS | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 550 550![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 925 925 |
55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 883 883 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 770 770 |
4511 | 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 933 933 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 887 887 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 803 803 |
9860 | 8468 | 1163 | |
| DRλ | 1.746 | 2.885 | 4.882 | 4.064 | 2.806 | 2.340 | 2.393 | 2.653 | 2.886 | 3.982 | |
| γ(−2ω; ω, ω, 0) | 155![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 310 310![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 682 682![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340 340 |
822![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 039 039 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 915 915![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 764 764 |
139![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 672 672![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 137 137![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 033 033![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 410 410 |
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 442 442![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 446 446 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 299 299![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 681 681 |
388![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 926 926 |
|
| γ(−ω; ω, 0, 0) | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 233 233![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 040 040 |
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 526 526![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 496 496 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 608 608![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 486 486 |
502![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 203 203 |
752![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 363 363 |
343![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 558 558 |
267![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 690 690 |
316![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 381 381 |
319![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 047 047 |
189![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 152 152 |
|
| γ DFWM | 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 891 891![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 786 786 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 243 243![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 498 498 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 778 778![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 858 858 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 047 047![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 890 890 |
47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 202 202![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 512 512 |
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 981 981![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 906 906 |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 878 878![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 916 916 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730 730![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 745 745 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020 020![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 562 562 |
267![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 830 830 |
|
| n 2 (cm2 W−1) | 4.37 × 10−15 | 1.17 × 10−15 | 1.47 × 10−16 | 8.67 × 10−17 | 3.91 × 10−15 | 4.95 × 10−16 | 3.21 × 10−16 | 1.43 × 10−16 | 8.45 × 10−17 | 2.21 × 10−17 | |
| λ = 1341 | β SHG(−2ω; ω, ω) | 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 248 248![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 106 106 |
84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 759 759 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 823 823 |
39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 096 096 |
5895 | 4809 | 3275 | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 376 376 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 939 939 |
1764 |
| β λ HRS | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 587 587![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 374.28 374.28 |
49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485.370 485.370 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 263.96 263.96 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938.99 938.99 |
2647.389 | 2435.229 | 1997.405 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 324.284 324.284 |
9025.444 | 718.428 | |
| DRλ | 5.005 | 1.946 | 2.569 | 2.394 | 2.813 | 1.604 | 0.617 | 3.215 | 4.169 | 5.087 | |
| γ(−2ω; ω, ω, 0) | 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 077 077![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140 140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 552 552![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 660 660 |
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 269 269![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 732 732 |
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 872 872![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 853 853 |
942![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 345 345 |
755![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 401 401 |
719![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 943 943 |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 069 069![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 455 455 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 482 482![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664 664 |
244![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 096 096 |
|
| γ(−ω; ω, 0, 0) | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 196 196![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 123 123![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 532 532 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 981 981![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 540 540 |
382![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 725 725 |
475![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 032 032 |
283![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
243![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 691 691 |
260![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 403 403 |
258![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 023 023 |
173![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 415 415 |
|
| γ DFWM | 2.88 × 10−10 | 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 463 463![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 974 974 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 634 634![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 476 476 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 580 580![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 775 775 |
681![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 963 963 |
460![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 748 748 |
417![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 094 094 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 217 217![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 103 103 |
687![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 199 199 |
203![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 816 816 |
|
| n 2 (cm2 W−1) | 2.39 × 10−12 | 6.18 × 10−16 | 1.79 × 10−15 | 2.13 × 10−16 | 5.64 × 10−17 | 3.81 × 10−17 | 3.45 × 10−17 | 1.01 × 10−16 | 5.69 × 10−17 | 1.68 × 10−17 | |
| λ = 1906 | β SHG(−2ω; ω, ω) | 8205 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
4135 | 8983 | 6774 | 108![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 286 286 |
3270 | 3244 | 4650 | 1423 |
| β λ HRS | 4741 | 4247 | 1680 | 3419 | 2898 | 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 318 318 |
1496 | 1328 | 1870 | 564 | |
| DRλ | 1.010 | 6.705 | 3.706 | 6.743 | 4.448 | 5.150 | 3.664 | 4.821 | 5.244 | 5.834 | |
| γ(−2ω; ω, ω, 0) | 892![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 444 444 |
297![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 653 653 |
868![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 389 389 |
488![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 483 483 |
797![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 644 644 |
63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 013 013![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 320 320 |
268![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 039 039 |
308![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134 134 |
309![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 511 511 |
186![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 375 375 |
|
| γ(−ω; ω, 0, 0) | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 154 154![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 396 396 |
204![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 326 326 |
399![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 667 667 |
320![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 182 182 |
377![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 603 603 |
69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 204 204![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
222![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 236 236 |
226![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 894 894 |
222![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 761 761 |
161![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 804 804 |
|
| γ DFWM | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 042 042![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 844 844 |
126![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 432 432 |
585![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 489 489 |
390![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 108 108 |
536![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134 134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 488 488 |
245![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 005 005 |
263![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 154 154 |
260![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 886 886 |
172![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 965 965 |
|
| n 2 (cm2 W−1) | 1.69 × 10−16 | 1.04 × 10−17 | 4.84 × 10−17 | 3.23 × 10−17 | 4.44 × 10−17 | 7.46 × 10−15 | 2.02 × 10−17 | 2.17 × 10−17 | 2.16 × 10−17 | 1.43 × 10−17 |
 | ||
| Fig. 4 Variation of the static and dynamic first hyperpolarizability (βλHRS) and second hyperpolarizability (γλ) of M@b64Al12N12 and M@b66Al12N12 (M from Sc to Zn). | ||
First, the β∞HRS value of Cr@b64, Mn@b64, Cu@b64 and Zn@b64 is 2021, 769, 1010 and 449 a.u., which is close to 2042, 752, 1012 and 428 a.u. for Mn@b66, Cu@b66 and Zn@b66, respectively. However, the β∞HRS value of V@b66 and Ti@b66 is ∼2 times as large as that of V@b64 and Ti@b64, respectively, and the β∞HRS value of M@b64 is slightly larger than that of M@b66, where M = Sc, Fe, Co and Ni. This suggests that the topological structure of M@Al12N12 can enhance the NLO response of materials. It can be observed that the enhancement in the first hyperpolarizability of the system can be attributed to the existence of the closed-quasi-ring (CQR) structure connecting metal and Al12N12, which includes a critical point (RCP) rather than the type of dopants (b64 or b66). This improvement arises from the effective charge transfer between the nanocage and the metal through both the bonds and RCP, which proves to be more efficient compared to a similar charge transfer occurring in an open quasi-ring configuration. As an illustration, the larger first hyperpolarizability values observed in M@b66, compared to M@b64 (for M = Ti and V), can be attributed to the presence of a closed-quasi-ring (CQR) in M@b66, which is absent in M@b64. This trend also holds for M = Fe, Co, Ni, and Cu, wherein a CQR is present within the M@b64 nanocage. Consequently, β∞HRS[M@b64] surpasses β∞HRS[M@b66], see Fig. 1 and Fig. S4 (ESI†) and Tables 1, 4 and 5.
Our conclusion is that the presence of a CQR structure, marked by electron delocalization, offers an explanation for the variations in first hyperpolarizability values. This elucidation effectively accounts for the distinct β∞HRS disparities evident between the M@b64 and M@b66 configurations (Fig. 4 and Fig. S4, ESI†).
On the other hand, the static first hyperpolarizability trends for M@b66Al12N12 are similar to those observed for M@b64Al12N12. Zn@b64/66Al12N12 exhibits the smallest β∞HRS value within this series. Sc@b64Al12N12 presents a large static HRS hyperpolarizability of 6824 a.u. as shown in Tables 4, 5, Fig. 4 and Fig. S4 (ESI†), which is 15 times higher than the value of Zn@b64Al12N12. It is noteworthy that the βλ=∞HRS values of M@b64Al12N12 increase as Zn < Co < Fe < Mn < Ni < Cu < Cr < V < Ti < Sc (similar to the case of the M@b66Al12N12 nanocage in which the trend is Zn < Mn < Fe < Co < Ni < Cu < V < Cr < Ti < Sc).
For a deeper investigation into the underlying factors influencing the first hyperpolarizability of the compounds under study (M@b64/66Al12N12 nanoparticles), we conducted polarization scans of the HRS intensity I2ωΨV. The relationship between I2ωΨV and the polarization angle ψ was computed and graphed (Fig. 5 and Fig. S5, ESI†). The values of βJ=1 and βJ=3 are detailed in Table S3 (ESI†). We can observe that the DR values are sensitive to the transition metal and decrease in the following order: M@b64/66 M: Sc ≈ Ti ≈ V ≈ Cr > Zn ≈ Cu ≈ Ni > Co > Fe > Mn. Moreover, it is worth mentioning that the nanocages M@b64/66Al12N12 (M = Sc to Zn) exhibit a predominant dipolar symmetry within their nonlinear optical (NLO) responses. The DR values for these structures span from 4.1 to 7.7.
Several years ago, Hohm and Thakkar obtained a relation between the polarizability (α) and the second ionization potential (I2) and Waber–Cromer radius (rWC) of 101 elements from helium to nobelium, which can be expressed as74
| α = P1I2−4 + P2rWC3Iy2 | (20) |
In this work, we observe that the static hyperpolarizability (βHRS) for M@b64/66Al12N12 (M = from Sc to Zn) increases with the increase of the Waber–Cromer radius (rWC) of metal (correlation coefficient equal to 0.910; see Fig. 6, Mn@b64/66 excepted).
It is widely recognized that the measured values of the first hyperpolarizability are estimated by dispersion effects on the chromophores. Typically, the wavelength-dependent experiments are generally performed to investigate the optical resonance effects by the use of a 1064 nm (ω = 0.04282 a.u.) near infrared ray (NIR) laser. Here, the wavelengths λ = 1906, 1341 and 1064 nm were applied in calculations to compare the dispersion effect on the first hyperpolarizability of the nanocages. The second harmonic generation (βλSHG(−2ω; ω, ω)) and dynamic hyper-Rayleigh scattering response (βλHRS) and its DRλ of the studied nanoparticles are depicted in Tables 4 and 5. Fig. S6 in the ESI† shows an excellent correlation between βλHRS and βλSHG(−2ω; ω, ω) for the studied nanocage (R2 ≈ 0.980). Furthermore, we can see that the dynamic βλHRS values are significantly higher than the zero-frequency β∞HRS, except for Sc@b66, Ti@b66 and V@b66 at λ = 1906 nm (see Fig. 4). As illustrated in this figure, a clear disparity in trends can be observed between the static and dynamic first hyperpolarizability values for the compounds. In simpler terms, when there is an increase in the static first hyperpolarizability value for a given nanoparticle, the dynamic value does not necessarily exhibit a similar pattern.
A careful analysis of the results obtained shows that βλSHG(−2ω; ω, ω) of M@b66Al12N12 where M = Sc, Ti, V, Mn, Co and Ni is about 8, 10, 4, 7, 4 and 2 times larger than that of M@b64Al12N12, respectively, at λ = 1064 nm. For M = Cr, Fe, Cu and Zn, we note that β1064SHG[M@b64] ≈ β1906SHG[M@b66]. At λ = 1906 nm, the βSHG(−2ω; ω, ω) response values of M@b64Al12N12 decrease in the order Ti > Sc > Fe > Cr > Mn > V > Cu > Ni > Co > Zn (for M@b66Al12N12 the variation of βSHG takes the trend Fe > Ti > Cr > Sc > Mn > V > Co > Ni > Cu > Zn).
Regarding the HRS hyperpolarizability (Fig. 7), the static first hyperpolarizability of each nanoparticle is compared to their dynamic values (βλHRS) at different wavelengths. The graph shows that for M@b64Al12N12 at wavelengths of λ = 1906 and 1341 nm, a good linear relationship is observed, with a slope of 1.111 (R2 = 0.985) and 1.921 (R2 = 0.960), respectively, except for M = Ti, Fe and Mn at 1906 nm and M = Ni and Co at 1341 nm. This suggests that the frequency dispersion consistently affects this type of nanoparticle. Furthermore, the slopes obtained for M@b64Al12N12 provide a correcting factor for the frequency dispersion of these nanoparticles at the corresponding wavelengths. We observed identical findings for M@b66Al12N12 at λ = 1341 nm with a slope of 2.967 (R2 = 0.942) (M = Ti, V and Ni excepted). On the other hand, at λ = 1064 nm, a significant resonance effect was observed, leading to numerical instability that disrupted the linear relationship. We noticed the same results for M@b66Al12N12 at λ = 1906 nm (weak linear relationship βHRS ↔ β1906HRS).
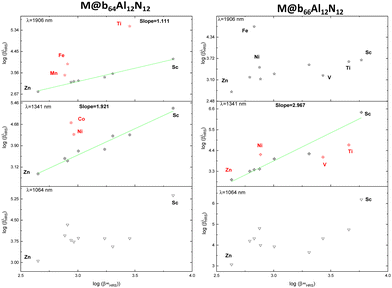 | ||
| Fig. 7 The dynamic first hyperpolarizabilities of M@b64/66Al12N12 (M = Sr–Zn) versus their static value at 1906, 1341 and 1064 nm. | ||
Regarding the dynamic depolarization ratio (DR), we observe that the nanoparticles Co@b64Al12N12, Sc@b64Al12N12 and Ti@b64Al12N12 at a wavelength of 1064 nm, as well as {M@b66 (M = Sc, Ti, Mn, Fe, Co, Ni and Cu) and M@b64 (M = V, Mn, Fe, Ni, Cu)} and {M@b66 (M = Sc, Ti, Mn, Fe, Co, Ni and Cu) and M@b64 (M = V, Mn, Fe, Ni, Cu)} at wavelengths of 1341 nm and 1906 nm, respectively, are anticipated to display a dominant octupolar character. In contrast, the remaining compounds generally display a dipolar nature, with the exception of Sc@b64/66, Ti@b64/66 and Co@b64/66 at λ = 1064 nm, Co@b66, Sc@b64 and Fe@b64 at λ = 1341 and Sc@b66 and Fe@b64 at λ = 1906 nm, which possess a depolarization ratio (DR) less than 1.5 (Tables 3, 4 and Table S3, ESI†).
Frequency dispersion effects
The frequency dispersion factor (FDFλ) between static and dynamic HRS hyperpolarizability74 at a specific wavelength (λ = 1064, 1341 and 1906 nm (1.165, 0.942 and 0.65 eV)) can be expressed as the ratio of βλHRS/β∞HRS, as listed in Table S4 in the ESI.† As seen in this table, when moving from λ = ∞ to 1064 nm (ω = 0 to 1.165 eV), the variation in the FDFλ value is more significant for Sc@b64/66Al12N12, Ti@b64Al12N12, Mn@b66Al12N12, Fe@b66Al12N12, Co@b64Al12N12, and Ni@b64/66Al12N12, while it is negligible for Zn@b64/66Al12N12 and moderate for the other nanoparticles (see Tables 3 and 4).The dispersion of first hyperpolarizability increases significantly due to one-photon (two-photon) resonance when the frequency of the generated light ω (2ω) is close to the strong allowed excitation energy.
From the TD-DFT results (see Fig. S2, ESI†), the excitation energy of Sc@b64: 2.34 eV, Sc@b66: 2.35 eV, Ti@b66: 2.39 eV, V@b64: 2.32 eV and Mn@b66: 2.35 eV is very close to the energy of the incident light 2ω (2.33 eV), whereas it is slightly different at 2.33 eV for Ti@b64: 2.22 eV, Mn@b64: 2.41 eV, Fe@b64: 2.42 eV, Co@b64: 2.48 eV and Cu@b64: 2.09 eV, which is an indication of two-photon resonance. On the other hand, the excitation energy of Sc@b64, Sc@b66, Ti@b66, V@b66 and Co@b64 at 1.15, 1.12, 1.11, 1.10 and 1.13 eV, respectively, indicates that these nanoparticles are close to one-photon resonance (ω = 1.165 eV).
In the case of ω = 0.924 eV, the two-photon resonance value of Sc@b66, Co@b64 and Ni@b64 is 1.88, 1.83 and 1.84 eV and that of Sc@b64, Co@b66 and Ni@b66 is 1.75, 1.68 and 1.91 eV, respectively. We can note that the resonance value of Sc@b66, Co@b64 and Ni@b64 is the closest to the near-resonant energy of 1.847 eV and that of Sc@b64, Co@b66 and Ni@b66 is the most deviated from the near-resonant energy (see Fig. S2, ESI†). On the other hand, the excitation energy values of Sc@b64, Sc@b66 and V@b66 at 0.96, 0.94 and 0.92 eV (f = 0.007, 0.007 and 0.001), respectively, which correspond to one-photon resonance values, are in close proximity to the near-resonant energy of 0.924 eV, which causes resonance.
Based on Table S3 (ESI†), we can observe that the FDF1064 value of Ti@b66 and V@b66 is about 5 and 2 times larger than that of Ti@b64 and V@b64 and the FDF1341 and FDF1906 value of V@b66 and Fe@b66, respectively, is higher than that of V@b64 and Fe@b64, which can be attributed to the presence of one- and two-photon resonance at the same incident wavelengths. Except for Co@b64 and Co@b66 at 1064 nm, where FDF1064[Co@b64] < FDF1064[Co@b66], this can be ascribed to the smallest oscillator strength of Co@b64. Furthermore, we notice that the FDF1064 value of Sc@b66 is ∼9 times larger than that of Sc@b64. This can be attributed to Sc@b66 having the highest oscillator strength at two-photon resonance (f = 0.251, λ = 528 nm).
On the other hand, our results revealed that the FDF1906 of M@b64/66Al12N12 (where M = V–Cr, Ni–Zn), Sc@b66, Ti@b66 and Co@b64 ranges from 0.62 to 1.8, indicating that the systems are far from the resonance region, i.e. off-resonance. A similar finding was obtained for Cr@b64 at 1064 nm and Zn@b64/66Al12N12 at 1341 nm.
Our results indicate that both the resonance energy value and the significant oscillator strength play a pivotal role in augmenting the FDFλ (dynamic first hyperpolarizability) of the investigated nanoparticles. Additionally, we hypothesize that the augmentation of βλ is primarily attributed to two-photon resonance rather than one-photon resonance.
Second hyperpolarizability
The second hyperpolarizability values for Al12N12 and M@b64/66Al12N12 (M = Sc to Zn) at the zero-frequency limit, as well as for frequency-dependent fields, calculated at the same level, are listed in Tables 4 and 5 and Table S5 (ESI†). As evident from the results, the values of γ(0; 0, 0, 0) exhibit sensitivity to the presence of the transition metal attached to Al12N12. There is a significant increase of approximately 8 times for Ti@b66, around 5 times for Sc@b64/66, V@b66 and Mn@b64/66, roughly 4 times for Cr@b64/66, Ti@b64 and Fe@b66, and about 3 times for V@b64, Fe@b64, Co@b64/66, Ni@b64/66, Cu@b64/66 and Zn@b64/66. The ordering of the γ(0; 0, 0, 0) values for M@b66 is Ti > Sc > Mn > V > Cr > Fe > Co ≈ Ni > Cu > Zn, whereas for M@b64 it is Sc > Mn > Cr > Ti > Fe > Co ≈ Ni > V > Cu > Zn (see Fig. S4, ESI†).The estimation of the frequency-dependent third-order non-linear optical (NLO) response is performed using the dynamic second hyperpolarizability γ(ω), and the corresponding values are provided in Tables 4 and 5 and Fig. 4. It is noteworthy that the frequency-dependent second hyperpolarizability values are considerably larger than the values of βλSHG(−2ω; ω, ω) at different dispersion frequencies. The sequence of the γ(−2ω; ω, ω, 0) values was γ (∞ nm) < γ (1906 nm) < γ (1341 nm) < γ (1064 nm) for nanoparticles Sc@b64, Mn@b64/b66, Co@b66, Ni@b66, Cu@b64/b66 and Zn@b64/b66 and for compounds V@b64/b66, Cr@b64/b66, Co@b64 and Ni@b64, the γ(−2ω; ω, ω, 0) values were γ (∞ nm) < γ (1906 nm) < γ (1064 nm) < γ (1341 nm). Taking M@b66Al12N12 (M = Co to Zn) as an example, the γ value at 1064 nm (110 × 105, 44 × 105, 22 × 105 and 4 × 105 a.u., respectively) is evaluated to be the largest and at 1906 nm the smallest value of γ is observed (2.6 × 105, 3.08 × 105, 3.09 × 105 and 1.86 × 105 a.u.). This order indicates that third-order NLO response can be effectively enhanced when the wavelength of incident light is decreased from ∞ to 1064 nm, indicating that dispersion of optical nonlinearity reaches its highest point at 1064 nm. This observation is in agreement with the finding of Chen et al. for the cyclo[18]carbon system.75 An opposite trend can be noticed for Ti@b64Al12N12, where the γ(−2ω; ω, ω, 0) values are 7329 × 105 (λ = 1906) > 28 × 105 (λ = 1341 nm) > 20 × 105 (λ = 1064 nm); a similar enhanced response with increasing wavelength was observed by Naveen et al. in the study of transition metal doped C6O6Li6.76 On the other hand, we observed that Sc@b66 exhibits the highest ESHG value at 1341 and 1064 nm (320![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 771 × 105 and 1553 × 105 a.u., respectively), which is 137
771 × 105 and 1553 × 105 a.u., respectively), which is 137![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 464 times larger than the value in the static regime. This suggests a noteworthy correlation between the resonance energy and the second-third hyperpolarizability. A comparison between the dynamic first and second hyperpolarizability is provided in Fig. 8. The agreement between βλSHG(−2ω; ω, ω) and γλ(−2ω; ω, ω, 0) values is prominently robust, with a correlation coefficient of approximately 0.92. The slope of the linear relationship, as obtained from the least-squares fitting, spans from 1.05 to 1.41 (Fig. 8), which indicates a tendency of second hyperpolarizability to overestimate the values.
000 and 464 times larger than the value in the static regime. This suggests a noteworthy correlation between the resonance energy and the second-third hyperpolarizability. A comparison between the dynamic first and second hyperpolarizability is provided in Fig. 8. The agreement between βλSHG(−2ω; ω, ω) and γλ(−2ω; ω, ω, 0) values is prominently robust, with a correlation coefficient of approximately 0.92. The slope of the linear relationship, as obtained from the least-squares fitting, spans from 1.05 to 1.41 (Fig. 8), which indicates a tendency of second hyperpolarizability to overestimate the values.
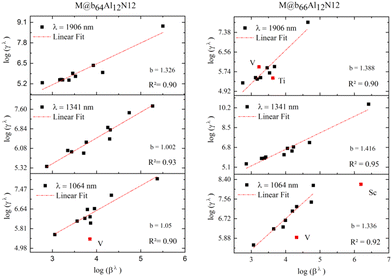 | ||
| Fig. 8 Correlation between the dynamic second and third order NLO responses of M@b66/64Al12N12 (M = Sc to Zn, b = slope). | ||
The computed results for the dc-Kerr effect γ(−ω; ω, 0, 0) are presented in Tables 4 and 5. Generally, for the title compounds, the dc-Kerr effect is more pronounced at a wavelength of 1064 nm compared to 1341 nm and 1906 nm. This suggests that the dc-Kerr effect can be enhanced by using a lower wavelength. However, there are exceptions. For Sc@b66, V@b66, and V@b64, the highest dc-Kerr effect values are observed at 1341 nm, with values of 1.819 × 1010, 1.998 × 107 and 8.362 × 105 a.u., respectively. For Fe@b66, the highest value is at 1906 nm, with a dc-Kerr effect of 6.920 × 108 a.u.
On the other hand, the estimation of the quadratic nonlinear refractive index is derived from the second hyperpolarizability coefficients, utilizing the following equation:77
 | (21) |
 , are calculated using the equation presented below:78
, are calculated using the equation presented below:78 | (22) |
Controlling factors of first hyperpolarizability
A two level model is utilized to comprehend the controlling factors of the first hyperpolarizability. According to the two level model79,80 | (23) |
To investigate the reason why some compounds exhibit large or small β0 values, we conducted a calculation using the equation for the two-level model and compared the results with those obtained from our theoretical simulations.
As is widely recognized, the first hyperpolarizability computed using the SOS method exhibits a strong correlation with the number of excited states. Therefore, we conducted a test to investigate the convergence behaviour between the first hyperpolarizability (βSOS) and the number of excited states. Fig. 9 displays the relationship between the βSOS value and 120 excited states and our findings indicate that 120 excited states are adequate for achieving convergence of the βSOS value.
The results presented in Fig. 10 and Table S6 (ESI†) indicate that the SOS method is capable of providing a qualitative evaluation of the first hyperpolarizability for the majority of compounds. Furthermore, the trend observed in the HRS hyperpolarizability using the SOS method is comparable to that obtained at the CAM-B3LYP/6-311+G(d) level, with only minor deviations due to the limitations of the SOS method. This consistency implies that the crucial excited states identified in Table 6 and Fig. 9 have a substantial impact on the first hyperpolarizability.
| M@b64Al12N12 | ||||||
|---|---|---|---|---|---|---|
| M | Sn | ΔE0→n | f 0→n | Δμ0→n | I | I × Δμ0→n |
| Sc | S13 | 2.676 | 0.144 | 2.201 | 0.007 | 0.016 |
| Ti | S16 | 2.895 | 0.055 | 1.441 | 0.002 | 0.003 |
| V | S15 | 3.041 | 0.116 | 1.675 | 0.004 | 0.007 |
| Cr | S7 | 2.558 | 0.088 | 2.267 | 0.005 | 0.012 |
| Mn | S9 | 2.98 | 0.14 | 2.254 | 0.005 | 0.012 |
| Fe | S9 | 2.42 | 0.057 | 5.929 | 0.004 | 0.024 |
| Co | S9 | 1.848 | 0.072 | 0.672 | 0.011 | 0.008 |
| Ni | S7 | 2.582 | 0.055 | 5.838 | 0.003 | 0.019 |
| Cu | S1 | 2.095 | 0.076 | 1.25 | 0.008 | 0.010 |
| Zn | S3 | 2.994 | 0.215 | 0.412 | 0.008 | 0.003 |
| M@b66Al12N12 | ||||||
| Sc | S13 | 2.35 | 0.251 | 1.888 | 0.020 | 0.036 |
| Ti | S13 | 2.100 | 0.177 | 1.59 | 0.020 | 0.030 |
| V | S12 | 2.503 | 0.075 | 3.033 | 0.005 | 0.014 |
| Cr | S7 | 2.504 | 0.097 | 2.636 | 0.006 | 0.016 |
| Mn | S8 | 2.924 | 0.118 | 1.901 | 0.005 | 0.009 |
| Fe | S9 | 2.416 | 0.05 | 6.208 | 0.003 | 0.022 |
| Co | S9 | 2.428 | 0.049 | 6.04 | 0.003 | 0.020 |
| Ni | S5 | 1.909 | 0.068 | 0.75 | 0.010 | 0.008 |
| Cu | S1 | 1.993 | 0.077 | 1.293 | 0.010 | 0.012 |
| Zn | S3 | 2.901 | 0.197 | 0.439 | 0.008 | 0.003 |
For Fe@b66, Co@b66, Fe@b64 and Ni@b64 the critical states correspond to the S9, S9, S9 and S7 excited states, respectively. These states show a small overlap index between the hole and the electron (Sr ∼ 0.4), a large Dindex (3.1–3.3 Å), and a positive tindex (1 to 1.35), indicating that they display the nonlocal excitation feature during electron transition. From EDDM (Fig. 9 and Fig. S3, ESI†) the crucial transition of these doped systems exhibits apparent charge transfer (CT) character from metal to Al12N12. On the other hand, for the cases of Ti@b64, V@b64, Mn@b64, Co@b64, Cu@b64, Zn@b64, Sc@b66, Ti@b66, Mn@b66, Ni@b66, Cu@b66 and Zn@b66 the dominant contribution to first hyperpolarizability values can be assigned to S16, S15, S9, S9, S1, S3, S13, S13, S8, S5, S1, and S3, respectively. Based on the analysis of the hole–electron distribution, it has been revealed that all these electronic transitions are local excitations characterized by a relatively small Dindex (from 0.2 to 1.2 Å) a large overlap index (Sr > 0.6) and a negative tindex. This indicates that the hole and electron are in close proximity to each other (see Table S1 and Fig. S3, ESI†). For doped systems Sc@b64, Cr@b64, V@b66 and Cr@b66 the excited states S13, S7, S12, and S7, respectively, have large contributions to the β value, and the corresponding overlap index (and tindex) values of the crucial excited state are 0.578 (t = −0.443), 0.59 (t = −0.664), 0.594 (t = −0.195) and 0.579 Å (t = −0.411), respectively.
In general, a larger f/ΔE3 term can lead to larger first hyperpolarizability values, despite the constraint imposed by the Δμ term, which also reflects the charge transfer character of the electronic transitions. Accordingly, the large β values of Sc@b66 and Ti@b66 can be primarily ascribed to the lower electronic absorption energy paired with stronger oscillator strength (large f/ΔE3 term (0.02)). As for Zn@b64/66Al12N12, its smaller β values can be attributed to its larger ΔE (2.9 eV) and smaller Δμ (0.4 a.u.). On the other hand, when the f/ΔE3 terms of two compounds are similar, the Δμ terms will have a greater influence on the resulting β values. A typical example of compounds V@b64 and V@b66 (I = 0.004, Δμ = 1.675 and 3.033 respectively) is illustrated here, where the significant improvement in the first hyperpolarizability value of one doped system, as compared to the other (β[V@b64] < β[V@b66]), is primarily attributed to the larger μ term. The same result can be achieved from Cu@b64 and Zn@b64 (I = 0.008, Δμ = 1.25 and 0.412 respectively). Furthermore, we observed that the β values of Cu@b64 and Cu@b66 are slightly similar to each other (see Tables 4 and 5). This can be explained by the similarities of their corresponding f, ΔE and Δμ terms, which result in similar I × Δμ products that are proportional to the β values. The same outcome can be attained from {Cr@b64 and Cr@b66}, {Mn@b64 and Mn@b66} and {Zn@b64 and Zn@b66}. It is important to note that when the I and Δμ terms of two compounds are similar and comparable, their f and ΔE terms play a more significant role in determining the β values than the I × Δμ products. A typical case is that of Cr@b64 and Mn@b64 (I = 0.005, I × Δμ = 0.012 and β[Cr@b64] > β[Mn@b64]) where the higher first hyperpolarizability is primarily attributed to the smaller E value of Cr@b64.
Conclusions
In the present study, we explored the molecular topology, delocalization index, and first- and second-order hyperpolarizabilities of two nanoparticle series, specifically M@b64Al12N12 and M@b66Al12N12, spanning a range of transition metals from Sc to Zn, to detail their linear and nonlinear optical properties in both static and dynamic regimes.Our results revealed a noteworthy trend: the incorporation of transition metals into the Al12N12 nanocage led to a significant increase in both the first and second hyperpolarizabilities. This enhancement in static first hyperpolarizability was linked to the presence of a ring structure bridging the M and Al12N12 nanocage. This structural pattern facilitates electron delocalization, thereby contributing to the observed increase. For instance, the Ti@b66 nanoparticle exhibits the highest first hyperpolarizability (β∞HRS = 4554 a.u.) compared to Ti@b64 (β∞HRS = 2844 a.u.), attributed to the presence of a closed ring structure in Ti@b66 that was missing in Ti@b64. According to the sum-over-states approach, the majority of crucial excited states displayed a high Sr, small D and negative t, indicating that these electronic excitations are characterized to be local excitations. Detailed UV-Vis analysis suggested that these compounds could find application in deep ultraviolet laser devices due to their transparency below 200 nm. On the other hand, in the dynamic regime, our results indicated that the values of βHRS, βSHG(−2ω; ω, ω) and γESHG(−2ω; ω, ω, 0) were larger than their static counterparts. This observation emphasizes the pivotal role of one/two photon resonance energy and substantial oscillator strength in enhancing the dynamic first hyperpolarizability within the investigated nanoparticles. Moreover, our inquiry has resulted in the proposal that the enhancement of βλ is predominantly motivated by the influence of two-photon resonance, rather than the conventional one-photon resonance.
The interest in new materials' picosecond and femtosecond responses spans various applications and benefits. For instance, femtosecond and picosecond lasers are instrumental in generating superhydrophilic surfaces, illustrating their significant role in material fabrication and alteration.81 Moreover, ultrafast lasers, encompassing both picosecond and femtosecond varieties, have transformed material processing techniques, introducing novel methods for precise cutting, engraving, and drilling.82 Additionally, treatments using picosecond and femtosecond lasers have diminished material corrosion, enhancing their durability.83 Additionally, femtosecond lasers have been employed in direct writing processes, allowing for the precise creation of complex structures ranging from 0D to 3D.84
In light of our current understanding, our investigation introduces a fresh perspective by unveiling a correlation between the static first hyperpolarizability of M@b64/66Al12N12 and the Waber–Cromer radius of the transition metal. Furthermore, in the dynamic regime, a remarkable linear correlation exists between the first hyperpolarizability and the second hyperpolarizability.
Author contributions
Conceptualization and methodology: D. H. and H. C.; investigation: M. Z., D. H., and N. C.; writing – original draft preparation: D. H. and H. C.; writing – review & editing: M. Z., D. H., N. C. and H. C.; data curation: M. Z., D. H., N. C. and H. C. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge GENCI/IDRIS for HPC resources/computer time (Project AD010814942) and the PSMN of the ENS-Lyon for computing resources.References
- F. Tessore, A. O. Biroli, G. Di Carlo and M. Pizzotti, Inorganics, 2018, 6, 1–17 CrossRef.
- R. Bano, M. Asghar, K. Ayub, T. Mahmood and J. Iqbal, Front. Mater., 2021, 8, 1–24 CrossRef.
- H. Li, H. Xu, X. Shen, K. Han, Z. Bi and R. Xu, Sci. Rep., 2016, 6, 28067 CrossRef CAS PubMed.
- P. A. Franken, A. E. Hill, C. W. Peters and G. Weinreich, Phys. Rev. Lett., 1961, 7, 118–119 CrossRef.
- L. T. Cheng, W. Tam, S. R. Marder, A. E. Stiegman, G. Rikken and C. W. Spangler, J. Phys. Chem., 1991, 95, 10643–10652 CrossRef CAS.
- K. A. Green, M. P. Cifuentes, M. Samoc and M. G. Humphrey, Coord. Chem. Rev., 2011, 255, 2530–2541 CrossRef CAS.
- J. A. Delaire and K. Nakatani, Chem. Rev., 2000, 100, 1817–1845 CrossRef CAS PubMed.
- J. Dang, D. Mei, Y. Wu and Z. Lin, Coord. Chem. Rev., 2021, 431, 213692 CrossRef CAS.
- M. S. Kodikara, R. Stranger and M. G. Humphrey, Coord. Chem. Rev., 2018, 375, 389–409 CrossRef CAS.
- Y. Y. Liang, B. Li, X. Xu, F. Long Gu and C. Zhu, J. Comput. Chem., 2019, 40, 971–979 CrossRef CAS PubMed.
- N. Baggi, E. Garoni, A. Colombo, C. Dragonetti, S. Righetto, D. Roberto, J. Boixel, V. Guerchais and S. Fantacci, Polyhedron, 2018, 140, 74–77 CrossRef CAS.
- C. Andraud, F. Cyril, B. Olivier, H. Chermette and P. L. Baldeck, Adv. Polym. Sci., 2008, 214, 149–203 CrossRef CAS.
- Z. R. Khan, M. Shkir, V. Ganesh, S. AlFaify, I. S. Yahia and H. Y. Zahran, J. Electron. Mater., 2018, 47, 5386–5395 CrossRef CAS.
- K. Iliopoulos, O. Krupka, D. Gindre and M. Salle, J. Am. Chem. Soc., 2010, 132, 14343–14345 CrossRef CAS PubMed.
- M. Homocianu, A. Airinei, C. Hamciuc and A. M. Ipate, J. Mol. Liq., 2019, 281, 141–149 CrossRef CAS.
- M. Blanchard-Desce, I. Ledoux, J. M. Lehn, J. Malthête and J. Zyss, J. Chem. Soc., Chem. Commun., 1988, 737–739 RSC.
- D. Hannach, N. Khelfaoui, M. Zaidi, D. Yahiaoui, S. Lakehal, C. Morell and H. Chermette, New J. Chem., 2023, 47, 1234–1246 RSC.
- E. Cariati, C. Dragonetti, E. Lucenti, F. Nisic, S. Righetto and E. Tordin, Chem. Commun., 2014, 50, 1608–1610 RSC.
- F. Ricci, F. Elisei, P. Foggi, A. Marrocchi, A. Spalletti and B. Carlotti, J. Phys. Chem., 2016, 120, 23726–23739 CAS.
- F. Chérioux, H. Maillotte, P. Audebert and J. Zyss, Chem. Commun., 1999, 2083–2084 RSC.
- M. Fontani, A. Colombo, C. Dragonetti, S. Righetto, D. Roberto and D. Marinotto, Inorganics, 2020, 8, 36 CrossRef CAS.
- D. Hannachi, M. F. Haroun, A. Khireddine and H. Chermette, New J. Chem., 2019, 43, 14377 RSC.
- M. Zaidi, D. Hannachi and H. Chermette, Inorg. Chem., 2021, 60, 6616–6632 CrossRef CAS PubMed.
- D. Kamli, D. Hannachi, D. Samsar and H. Chermette, New J. Chem., 2023, 47, 1234–1246 RSC.
- A. Ahsin and K. Ayub, J. Nanostruct. Chem., 2022, 12, 529–545 CrossRef CAS.
- A. Ahsan and K. Ayub, Opt. Laser Technol., 2020, 129, 106298 CrossRef CAS.
- A. Ahsan, S. Sarfaraz, F. Fayyaz, M. Asghar and K. Ayub, J. Mol. Liq., 2022, 350, 118504 CrossRef CAS.
- A. Ahsan and K. Ayub, J. Mol. Liq., 2020, 297, 36–40 CrossRef.
- S. J. Wang, Y. F. Wang and C. Cai, J. Phys. Chem. C, 2015, 119, 16256–16262 CrossRef CAS.
- S. J. Wang, Y. F. Wang and C. Cai, J. Phys. Chem. C, 2015, 119, 5589–5595 CrossRef CAS.
- B. Ni, W. Sun, J. Kang and Y. Zhang, J. Phys. Chem. C, 2020, 124, 11595–11608 CrossRef CAS.
- D. Paul, J. Deb and U. Sarkar, ChemistrySelect, 2020, 5, 6987–6999 CrossRef CAS.
- F. Khaliq, T. Mahmood, K. Ayub, S. Tabassum and M. Amjad, Polyhedron, 2021, 200, 115145 CrossRef CAS.
- Y. Arshad, M. Asghar, M. Yar, T. Bibi and K. Ayub, J. Inorg. Organomet. Polym. Mater., 2023, 33, 943–955 CrossRef CAS.
- K. A. Faizan Ullah, N. Kosar, A. Ali, Maria and T. Mahmood, Opt. - Int. J. Light Electron Opt., 2019, 207, 163792 CrossRef.
- H. Wu, F. Zhang, X. Xu, C. Zhang and H. Jiao, J. Phys. Chem. A, 2003, 107, 204–209 CrossRef CAS.
- M. Niu, G. Yu, G. Yang, W. Chen, X. Zhao and X. Huang, Inorg. Chem., 2014, 53, 349–358 CrossRef CAS PubMed.
- E. Shakerzdeh, E. Tahmasebi and H. R. Shamlouei, Synth. Met., 2015, 204, 17–24 CrossRef CAS.
- E. Shakerzadeh, E. Tahmasebi and Z. Biglari, J. Mol. Liq., 2016, 221, 443–451 CrossRef CAS.
- E. Tahmasebi, E. Shakerzadeh and Z. Biglari, Appl. Surf. Sci., 2016, 363, 197–208 CrossRef CAS.
- M. A. Gilani, S. Tabassum, U. Gul, T. Mahmood, A. I. Alharthi, M. A. Alotaibi, M. Geesi, R. Sheikh and K. Ayub, Appl. Phys. A: Mater. Sci. Process., 2018, 124, 14 CrossRef.
- Y. Arshad, S. Khan, M. A. Hashmi and K. Ayub, New J. Chem., 2018, 42, 6976–6989 RSC.
- S. Irshad, F. Ullah, S. Khan, R. Ludwig and T. Mahmood, Opt. Laser Technol. J., 2021, 134, 106570 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallin, 2016 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- R. F. W. Bader, T. T. Nguyen-Dang and Y. Tal, J. Chem. Phys., 1979, 70, 4316–4329 CrossRef CAS.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- R. F. W. Bader, Acc. Chem., 1985, 18, 9–15 CrossRef CAS.
- P. S. V. Kumar, V. Raghavendra and V. Subramanian, J. Chem. Sci., 2016, 128, 1527–1536 CrossRef CAS.
- H. A. Kurtz, J. J. P. Stewart and K. M. Dieter, J. Comput. Chem., 1990, 11, 82–87 CrossRef CAS.
- D. P. Shelton and J. E. Rice, Chem. Rev., 1994, 94, 3–29 CrossRef CAS.
- A. Plaquet, M. Guillaume, B. Champagne, F. Castet, L. Ducasse, J. L. Pozzo and V. Rodriguez, Phys. Chem. Chem. Phys., 2008, 10, 6223–6232 RSC.
- N. Hou, R. Feng and X. H. Fang, Int. J. Quantum Chem., 2022, 122, 1–14 CrossRef.
- M. Chołuj, M. M. Alam, M. T. P. Beerepoot, S. P. Sitkiewicz, E. Matito, K. Ruud and R. Zaleśny, J. Chem. Theory Comput., 2022, 18, 1046–1060 CrossRef PubMed.
- P. Besalú-Sala, S. P. Sitkiewicz, P. Salvador, E. Matito and J. M. Luis, Phys. Chem. Chem. Phys., 2020, 22, 11871–11880 RSC.
- D. Grabarek and T. Andruniów, J. Chem. Theory Comput., 2019, 15, 490–508 CrossRef CAS PubMed.
- Maria, J. Iqbal and K. Ayub, RSC Adv., 2016, 6, 94228–94235 RSC.
- S. Sarwar, J. Yaqoob, M. U. Khan, R. Hussain, S. Zulfiqar, A. Anwar, M. A. Assiri, M. Imran, M. M. Ibrahim, G. A. M. Mersal and A. Y. Elnaggar, ACS Omega, 2022, 7, 24396–24414 CrossRef CAS PubMed.
- L. M. G. Abegaõ, R. D. Fonseca, F. A. Santos, J. J. Rodrigues, K. Kamada, C. R. Mendonca, S. Piguel and L. De Boni, RSC Adv, 2019, 9, 26476–26482 RSC.
- H. M. He, H. Yang, Y. Li and Z. R. Li, Front. Chem., 2022, 10, 1–10 Search PubMed.
- L. Lescos, S. P. Sitkiewicz, P. Beaujean, M. Blanchard-Desce, B. Champagne, E. Matito and F. Castet, Phys. Chem. Chem. Phys., 2020, 22, 16579–16594 RSC.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- Z. Liu, T. Lu, Q. Chen, T. Lu and Q. Chen, Carbon N. Y., 2020, 165, 461–467 CrossRef CAS.
- D. Hannachi, N. Ouddai, M. Arotçaréna and H. Chermette, Mol. Phys., 2015, 113, 1541–1550 CrossRef CAS.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- E. J. Baerends, T. Ziegler, A. J. Atkins, J. Autschbach, D. Bashford, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerrigter, L. Cavallo, D. P. Chong, D. V. Chul-hai, L. Deng, R. M. Dickson, J. M. Dieterich, D. E. Ellis, M. van Faassen, L. Fan, T. H. Fischer, C. Fonseca Guerra, M. Franchini, A. Ghysels, A. Giammona, S. J. A. van Gisbergen, A. W. Götz, J. A. Groeneveld, O. V. Gritsenko, M. Grüning, S. Gusarov, F. E. Harris, P. van den Hoek, C. R. Jacob, H. Jacobsen, L. Jensen, J. W. Kaminski, G. van Kessel, F. Kootstra, A. Kovalenko, M. V. Krykunov, E. van Lenthe, D. A. McCormack, A. Michalak, M. Mitoraj, S. M. Morton, J. Neugebauer, V. P. Nicu, L. Noodleman, V. P. Osinga, S. Patchkovskii, M. Pavanello, C. A. Peeples, P. H. T. Philipsen, D. Post, C. C. Pye, W. Ravenek, J. I. Rodriguez, P. Ros, R. Rüger, P. R. T. Schipper, H. van Schoot, G. Schreckenbach, J. S. Seldenthuis, M. Seth, J. G. Snijders, M. Solà, M. Swart, D. Swerhone, G. te Velde, P. Vernooijs, L. Ver-sluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. M. van Wezenbeek, G. Wiesenekker, S. K. Wolff, T. K. Woo and A. L. Yakovlev, ADF2016.01, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2016, (http://www.Scm.Com) Search PubMed.
- E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542 CrossRef CAS.
- R. F. W. Bader, A. Streitwieser, A. Neuhaus, K. E. Laidig and P. Speers, J. Am. Chem. Soc., 1996, 118, 4959–4965 CrossRef CAS.
- X. Fradera, M. A. Austen and R. F. W. Bader, J. Phys. Chem. A, 1999, 103, 304–314 CrossRef CAS.
- L. J. Farrugia, C. Evans, H. M. Senn, M. M. Hänninen and R. Sillanpää, Organometallics, 2012, 31, 2559–2570 CrossRef CAS.
- R. Arun Kumar, M. Arivanandhan and Y. Hayakawa, Prog. Cryst. Growth Charact. Mater., 2013, 59, 113–132 CrossRef CAS.
- F. Ullah, N. Kosar, K. Ayub, M. A. Gilani and T. Mahmood, New J. Chem., 2019, 43, 5727–5736 RSC.
- C. C. Yang, L. Li, W. Q. Tian, W. Q. Li and L. Yang, Phys. Chem. Chem. Phys., 2022, 24, 13275–13285 RSC.
- U. Hohm and A. J. Thakkar, J. Phys. Chem. A, 2012, 116, 697–703 CrossRef CAS PubMed.
- Z. Liu, T. Lu and Q. Chen, Carbon, 2020, 165, 461–467 CrossRef CAS.
- N. Kosar, S. Wajid, K. Ayub and A. Mahmood, Optik, 2023, 276, 170660 CrossRef CAS.
- C. Brée, A. Demircan and G. Steinmeyer, IEEE J. Quantum Electron., 2010, 46, 433–437 Search PubMed.
- M. Tarazkar, D. A. Romanov and R. J. Levis, J. Chem. Phys., 2014, 140, 214316 CrossRef PubMed.
- J. L. Oudar and D. S. Chemla, J. Chem. Phys., 1976, 66, 2664–2668 CrossRef.
- J. L. Oudar, J. Chem. Phys., 1977, 67, 446–457 CrossRef CAS.
- R. A. Rajan, C. V. Ngo, J. Yang, Y. Liu, K. S. Rao and C. Guo, Opt. Laser Technol., 2021, 143, 107241 CrossRef CAS.
- K. Sugioka, Nanophotonics, 2017, 6, 393–413 CAS.
- P. Pou-Álvarez, A. Riveiro, X. R. Nóvoa, M. Fernández-Arias, J. del Val, R. Comesaña, M. Boutinguiza, F. Lusquiños and J. Pou, Surf. Coatings Technol., 2021, 427, 127802 CrossRef.
- R. Kurimoto, E. Niiyama and M. Ebara, Fibrous Materials, Elsevier Inc., 2016 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nj01849d |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2024 |