Structural basis for Cu(II) metallocycle hexamer formation

Abstract

NNN bis-aryl amide pincer ligands may be designed to meet the structural requirements for Cu(II) metallocycle hexamer formation, giving supramolecular crystals containing solvent-accesible voids.

---

Introduction

Metal–organic frameworks are known for their applications in nanotechnology^1,2 and these supermolecules may be constructed by design. Cu(II) metallocycles have been synthesized from various ligands and we introduce a few examples here to highlight requirements for metallocycle formation. We then find that the NNN bis-aryl amide pincer ligand meets these requirements and may be easily functionalized for crystal engineering. Metallocycle hexamers have been constructed from tripodal benzimidazole ligands³ where the cyclic coordination follows the pattern Cu(II)–N–C–N–C–C–O–Cu(II) and the bridging group involves a (1-H-benzimidazol-1-yl)acetic acid moiety. The flexibility of the tripod reduces steric clashes in the hexamer and the good π-accepting ability of the ligand allows the anionic acetate moiety to serve as a bridge between metal centres. These electronic requirements for metallocycle formation have been highlighted by contrasting pyrene-appended ligands.^4,5 The pyrene-appended acylhydrazide ligand provides a single anionic donor while an axially coordinated nitrate provides charge balance and increased electron density at the Cu(II) centre. The acylhydrazide contains a carbonyl that is a good π-acceptor and thus serves as a bridge between copper centres allowing the metallocycle to form. However, the pyrene-appended hydrazone contains neither a carbonyl, nor a suitable σ-donor or π-acceptor moiety to serve as a bridge between metal centres, and hence metallocycle formation does not take place. However, well-balanced electronics are revealed in a pyrazolyl urea ligand,⁶ which contains two anionic σ-donors and a π-acceptor amide carbonyl that serves as the bridging moiety across the metallocycle hexamer. This cyclic coordination, Cu(II)–N–C=O_amide–Cu(II), follows the same pattern as the Cu(II) metallocycles studied in this work, and inspired the use of the previously reported NNN bis-aryl carboxamide pincer ligand^7–9 for the construction of metallocycles. Due to facile functionalization of the bis-aryl rings, the carboxamide pincer ligand enables the construction, and engineering, of Cu(II) metallocycle hexamers.

Results and discussion

The copper pincers presented here, Cu1–Cu3, all crystallized in the triclinic space group P1̄ with a single copper metallocycle in the unit cell and the asymmetric unit described by three monomers of the hexamer. The hexanuclear Cu(II) macrocycle coordination patterns are shown in Fig. 1 and the thermal ellipsoids are shown in Fig. S1.1–S1.3 (ESI†). The coordination follows the sequence Cu(II)–N–C=O_amide–Cu(II) where the amide carbonyl of the complex acts a bridging ligand between copper centres, engendering S₂ symmetry for each supermolecule. The mean plane of each metallocycle lies in the plane of the six nitrogens that make up the coordination pattern and three alternating Cu(II) centres lie in a plane above, and below, the mean plane. The plane-to-plane distance between the Cu(II) triads averages 1.35 ± 0.25 Å and the metallocycle mean plane bisects this interplanar distance. The inner coordination sphere of the Cu(II) centres adopts square pyramidal geometry where the tridentate ligand chelates Cu(II) through the pyridine nitrogen (N_pyr) and two amide nitrogens (N_amide) while exogenous ligands coordinate to make up the square plane as well as occupy the axial position. The copper-based atomic 3d_x²−y² orbital lies in the square plane where the Cartesian x-axis is colinear with the N_pyr–Cu bond and the y-axis is colinear with the N_amide–Cu–N_amide bond as shown in Fig. 2a. The bond lengths between Cu(II) and the neutral donor atoms N_pyr and O_carbonyl are 1.91 ± 0.01 and 1.92 ± 0.02 Å, respectively, while the anionic N_amide donors have bond lengths to Cu(II) that average 2.04 ± 0.02 Å. The strong interelectronic repulsions between the metal ion and the four donor atoms within the square plane raise the energy of the 3d_x²−y² orbital and promote electronic delocalization. This is reflected in the bond lengths of the amide carbonyls that make up the chelate ring and serve as bridging ligands between metal centres.

Fig. 1 Ligands were synthesized and complexed with Cu(II) to produce chelate monomers. The bridging carbonyl moiety is highlighted in red. The copper chelates crystallize as hexamers with S₂ symmetry; the asymmetric unit has been shown. There are three Cu(II) centres that lie above, and below, the mean plane of the metallocycle, shown as solid green and dashed green lines, respectively.

Fig. 2 The inner coordination sphere of the Cu(II) pincers highlighting the Cartesian axes. The bridging carbonyl interaction has also been shown as determined by crystal field theory. This bonding analysis was confirmed by DFT as the spin-density plot shows σ-overlap involving the 3d_x²−y² atomic orbital as well as π-overlap involving the 3d_xy atomic orbital.

The amide C=O that forms part of the chelate ring, but is not a bridging group, has an average bond length of 1.24 ± 0.01 Å. However, when the amide C=O acts as bridging group and forms a Cu–O_carbonyl bond, the bond length increases to an average of 1.27 ± 0.01 Å for Cu1–Cu3. This increase in C=O bond length is due to back-donation of electron density from the 3d_x²−y² into a vacant σ* molecular orbital on the carbonyl, thereby decreasing Coulombic repulsion within the metal-based orbital. There is additional overlap between the atomic 3d_xy orbital and π* molecular orbitals of the carbonyl, resulting in further bond length elongation for the bridging moiety. The orbital analysis has been presented in Fig. 2. The inner coordination sphere of Cu1 is shown in Fig. 2a, and the only symmetry element is a vertical mirror plane, σ_V. The mirror plane defines the Cartesian z-axis as the principal z-axis is collinear with the highest symmetry element. As a result, the x-axis is perpendicular to the z-axis and collinear with highest number of identical atoms, i.e., the two N_amide. That leaves the y-axis to pass through N_pyr and O_carbonyl. The bridging carbonyl interaction is then shown in Fig. 2b. The bonding involves predominately σ-overlap of the metal-based 3d_x²−y² atomic orbital and σ* molecular orbital of the carbonyl. There is additional bonding involving π-overlap of the metal-based 3d_xy atomic orbital and the π* molecular orbitals of the carbonyl. This donation of electron density from the metal-based orbitals into antibonding orbitals of the carbonyl causes the bond length to increase for the bridging moiety. This was confirmed with DFT shown in Fig. S2.1–S2.4 (ESI†), as the spin-density plot shows significant 3d_x²−y² character as well as σ-overlap between copper and the carbonyl. The antibonding π-overlap between carbonyl π* molecular orbitals and the atomic 3d_xy orbital was observed for the LUMOs of the asymmetric unit for Cu1–Cu3.

Our DFT calculations show significant 3d_x²−y² character in the square plane of the Cu(II) centre as well as spin density localized on the bridging carbonyl which is crucial to metallocycle formation. The delocalization of the paramagnetic electron density leads to the emergence of exchange interactions over the three bridging atoms between the metal centres. Cu1 shows low temperature antiferromagnetic coupling at T < 9.3 K at a field strength of 0.1 T. Cu2 shows competing antiferromagnetic and paramagnetic phases below the Néel temperature (T < 8 K). Cu3 is diamagnetically ordered under an applied magnetic field at room temperature. At 100 K, Cu3 undergoes a magnetic moment reversal from diamagnetic to paramagnetic with complete paramagnetism at 2 K. These magnetic measurements are presented in Fig. S3.1–S3.6 (ESI†). Exchange interactions and magnetic ordering have been reported to influence coordination-based solid-state architecture.^10–12 Particularly, hexanuclear copper-based exchange coupling has been compared to the bonding in benzene.¹³ The DFT spin-density plot is consistent with magnetic ordering and shows that paramagnetic electron density is delocalized into the aromatic rings of the ligand and reflects the energy lowering of the metal-based orbitals as a result of the nephelauxetic effect. The coordination pattern Cu(II)–C=O_amide–Cu(II) that drives metallocycle formation is dominated by 3d_x²−y² character as shown in S3 (ESI†). The Cu(II) based atomic 3d_x²−y² orbital is instrumental to metallocycle formation and the resulting coordinating forces impart significant tensional integrity to the cyclic assembly.

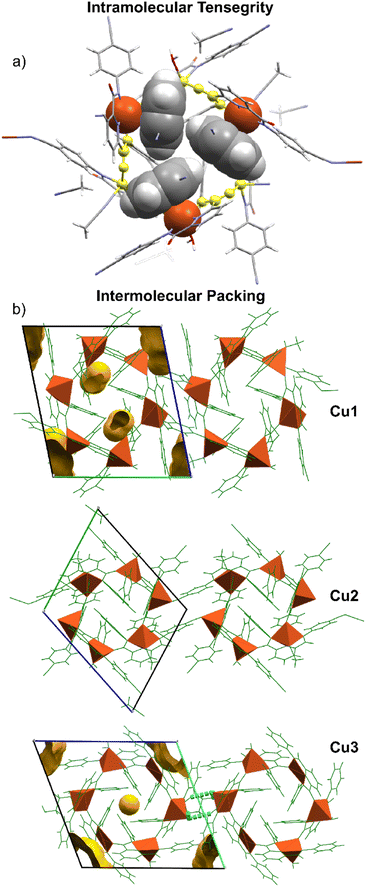
The metallocycle hexamer is held together by a synergistic combination of intramolecular forces that facilitate the tensegrity observed for the supramolecular assembly. The term “tensegrity” was originally coined by the architect, Buckminster Fuller. These forces include coordinative bonding through the cyclic structure, magnetic ordering, van der Waals forces, C–H⋯π¹⁴ and d⋯π¹⁵ interactions. The tensegrity of the copper metallocycles has been highlighted in Fig. 3 as well as the supramolecular packing. The strongest intramolecular forces holding the cyclic structure together are the coordinating bonds that result in the pattern Cu(II)–N–C=O_amide–Cu(II). The short bond lengths Cu–O_carbonyl indicate that the negative charge from the amidate nitrogen has been delocalized into the carbonyl oxygen making it a better σ-donor. Significant C–H⋯π and d⋯π interactions are observed to stabilize the cyclic assembly and impart remarkable tensegrity. This self-recognition and intramolecular stabilisation have been shown in Fig. S4.1–S4.4 (ESI†). The bonding exists between the Cu(II) triad that lies above the mean plane of the metallocycle, and these C–H⋯π and d⋯π interactions are inverted about the centroid of the hexamer and exist between the Cu(II) triad that lies below the mean plane. The aromatic rings that serve as d⋯π acceptors on one face of the aromatic ring, function as C–H⋯π acceptors on the reflected face. Notably, the atom-to-plane distances for the d⋯π interactions average 2.88 ± 0.09 Å which indicates that although the bonding may be weak, it is significant. Also noteworthy is the fact that d⋯π bond angles vary between about 50° and 60°, suggesting that atomic 3d_xz and 3d_yz orbitals are principally involved with d–π overlap. Hence, numerous forces stabilize the supramolecular assembly through intramolecular interactions. There are significantly fewer intermolecular interactions that facilitate packing of the cyclic hexamers in the lattice that result in void space (Fig. S5.1–S5.3, ESI†).

Fig. 3 (a) Intramolecular C–H⋯ π, d⋯ π interactions, and coordinating forces result in tensional integrity for Cu2. (b) Cu1 and Cu2 crystallize as 1D infinite polymers of metallocycles. The hexamers are shown in green and the bridging tetramer that permits polymerization is also shown. Cu1 has the nitrile in the meta position resulting in a void volume of 6.8% whilst Cu2 has the nitrile in the para positing resulting in no voids. Cu3 packs metallocycles through a hydrogen bonding network between an axially coordinated aqua ligand, co-crystalized ethylene glycol, and the carbonyl of neighbouring pincer chelates. The Cu3 crystal is 11% void volume.

The Cu(II) NNN amide pincers presented here all adopt hexameric cyclic coordination in the solid-state. A CSD¹⁶ search of the general amide pincer scaffold yielded 78 unique results, and these have been presented in Table S1 (ESI†). The table shows the search query submitted to the CSD, the coordination number at the metal centre, the charge on the copper ion, and the substitution on the aryl rings. The search filtered out structures with R₁ > 7.5%. The 78 copper NNN amide pincers contain only 5 structures (6.4%) where the aryl ring has been substituted on the 3-position. All 5 of these structures contain dinucleating ligands. Most structures (90%) contain ligands where the aryl ring has been substituted on the 2- and 6-positions or 2-,4-and 6-positions. None of the structures adopt the metallocycle architecture observed for the Cu(II) NNN amide pincers presented in this work. It is suspected that metallocycle formation requires the aryl ring to be substituted in the 3- or 4-position so that the substituents do not sterically block metallocycle formation. The stereoelectronic requirements for hexamer formation are presented in Fig. 4. The metallocycle follows the bonding pattern Cu(II)–N–C=O_amide–Cu(II) and so all 78 CSD structures possess the necessary coordination pattern yet none of them form cyclic supermolecules. It is suggested here that this is because 90% of structures are substituted in the 2-,6-position and the substituents sterically block coordination from one copper pincer to another. When only the 2-position is substituted, the CSD structures do not adopt a hexameric geometry because there is intramolecular self-recognition between the substituent and the Cu(II) centre, or alternatively, the complex is anionic and electrostatic forces dominate the solid-state architecture. The structures that possess no substitution on the aryl rings do not form cyclic supermolecules because they are all anionic. The CSD structures with aryl rings substituted in the 3-position are dinucleating structures and hence the flexibility of these ligands is reduced such that metallocycle formation does not occur.

Fig. 4 The stereoelectronic requirements for metallocycle formation. R-group substitution in the 5- and 6-positions result in steric clashes while structures in the CSD that have been functionalized in the 2-position result in intramolecular self-coordination. The coordination mode for the Cu(II) pincer that results in hexamer formation has also been shown.

The coordination mode of the Cu(II) NNN amide pincer has been presented in Fig. 4 with the general requirements that permit metallocycle hexamer formation. Firstly, the ligand must be suitably functionalized to avoid steric repulsions. The copper complex must also be neutral and have an open face that is available for coordination by a neighbouring monomer. The variable geometry of the copper ion permits supramolecular coordination as bridging groups may adopt favourable conformations around the metal centre. The metallocycles discussed here contain the Cu(II) ion with square pyramidal,^6,17 trigonal bipyramidal³ and octahedral⁴ geometries depending on the ligand's steric requirements and the metal centre's electronic requirements.

The pincers presented here coordinate Cu(II) via anionic amidate donors which increase electron density at the metal centre through σ-donation. The interelectronic repulsion is relieved at the metal centre upon coordination of a σ*- or π*-acceptor that functions as a bridging group. Therefore, electronic requirements of the metal facilitate metallocycle formation as electron density is balanced through a synergistic interplay of σ- and π-effects. Hence, a general coordination pattern for the copper hexamers may be presented as Cu(II)–X_nπ*–Cu(II), where X represents n number of any bridging atoms and the bridging group must be a π-acceptor. This depends on the electronics at the Cu(II) centre, as seen in the structure reported by Fu et al.³ When the ligand coordinates Cu(II) through only one anionic donor, and the ligand is a good π-acceptor, the electron deficient metal centre may coordinate to a bridging σ-donor moiety. Hence, the general coordination pattern may be presented as Cu(II)–X_nσ–Cu(II), where X represents n number of any bridging atoms that contains a good σ-donor. Ultimately, electron density at the metal centre must be appropriately balanced through σ- and π-effects for the general Cu(II)–X_n–Cu(II) cyclic coordination pattern to form. The size of the metallocycle follows the simple arithmetic sequence 6 + 6n, where n is the number of bridging atoms. Hence, an 18-membered metallocycle is formed when two bridging atoms are present, and 24-membered when three bridging atoms are present, and so on.

Experimental

Materials and instrumentation

All chemicals were purchased from Sigma-Aldrich and used without further purification. All solvents were purchased from Merck, and when necessary, freshly distilled. The copper metalation reactions were carried out using inhibitor-free THF. NMR data were acquired on Bruker Avance III 400 spectrometer at a frequency of 400 MHz (¹H) and 100 MHz (¹³C) using a 5 mm BBOZ probe. All proton and carbon chemical shifts are quoted relative to the relevant solvent reference signal. Spectra were analysed with MestReNova (Version 12.0.0-20080). Data were acquired at a temperature of 300 K. Infrared spectra of pure powder or crystalline samples were recorded using a Bruker Alpha FTIR spectrometer using a Bruker Platinum diamond Attenuated Total Reflectance sampling accessory. OPUS software (Version 7.5) was used to analyse spectra. The spectra were acquired over 32 scans at 20 °C with a spectral resolution of 4 cm⁻¹. X-ray intensity data were collected on a Bruker D8 Venture Bio PHOTON III diffractometer with a Mo Kα Iμ DIAMOND source (50 kV, 1.4 mA). The collection method involved ω- and ϕ-scans with 1536 × 1024 bit data frames. The unit cell and full data set were collected using APEX4;¹⁸ SAINT was used to integrate the data, and SADABS was used to make empirical absorption corrections and scale the data. Space group assignments were made using XPREP on all compounds. Using Olex2,¹⁹ the crystal structures were solved with the ShelXT²⁰ structure solution program using Intrinsic Phasing and refined with the ShelXL²¹ refinement package using Least Squares minimization. Non-hydrogen atoms were first refined isotropically followed by anisotropic refinement by full-matrix least-squares calculations based on F².

Synthesis and spectroscopy

H₂L1: N²,N⁶-bis(3-cyanophenyl)pyridine-2,6-dicarboxamide. The reagents, 3-aminobenzonitrile (254 mg, 2.15 mmol) and pyridine-2,6-dicarbonyl dichloride (198 mg, 0.973 mmol), were dissolved in 50 mL of dry acetonitrile (MeCN). The product instantly precipitated as a white powder. The reaction mixture was refluxed at 88 °C open to the atmosphere while being vigorously stirred for 2 hours. The product is soluble in hot MeCN and a clear yellowish solution was obtained during reflux. The reaction mixture was then cooled to 4 °C before filtering off the snow-white H₂L1 (340 mg, 95% yield).

¹H NMR: (400 MHz, DMSO-d₆, 300 K) [δ, ppm] 11.27 (s, 2H), 8.48–8.42 (m, 4H), 8.36 (dd, J = 8.6, 6.9 Hz, 1H), 8.24 (dq, J = 7.8, 2.7 Hz, 2H), 7.75–7.65 (m, 4H). ¹³C NMR: (100 MHz, DMSO-d₆, 300 K) [δ, ppm] 162.53, 148.78, 140.80, 139.35, 130.80, 128.40, 126.32, 126.15, 124.12, 119.15, 112.10. FTIR (cm⁻¹): 3288.66 (m, asymmetric N–H stretch), 3086.81 (w, aromatic C–H stretch), 2230.18 (m, symmetric C≡N stretch), 1667.75 (s, asymmetric C=O stretch; N–H wag), 1534.30 (s, asymmetric N–H wag).

H₂L2: N²,N⁶-bis(4-cyanophenyl)pyridine-2,6-dicarboxamide. The reagents, 4-aminobenzonitrile (110 mg, 0.931 mmol) and pyridine-2,6-dicarbonyl dichloride (85.5 mg, 0.419 mmol), were dissolved in 25 mL of dry MeCN. The product instantly precipitated as a white powder. The reaction mixture was refluxed at 88 °C open to the atmosphere while being vigorously stirred for 2 hours. The product is partially soluble in hot MeCN and hence the reaction mixture was cooled to 4 °C before filtering off the bright white H₂L2 (154 mg, 94% yield).

¹H NMR: (400 MHz, DMSO-d₆, 300 K) [δ, ppm] 11.26 (s, 2H), 8.41 (d, J = 8.0 Hz, 2H), 8.31 (t, J = 7.9 Hz, 1H), 8.17 (d, J = 8.8 Hz, 4H), 7.91 (d, J = 8.7 Hz, 4H). ¹³C NMR: (100 MHz, DMSO-d₆, 300 K) [δ, ppm] 160.40, 146.58, 140.65, 138.56, 131.59, 124.27, 118.98, 117.32, 116.39. FTIR (cm⁻¹): 3340.51 (m, asymmetric N–H stretch), 3099.14 (w, aromatic C–H stretch), 2217.87 (m, symmetric C≡N stretch), 1693.08 (s, asymmetric C=O stretch; N–H wag), 1581.22 (s, asymmetric N–H wag).

H₂L3: N²,N⁶-diphenylpyridine-2,6-dicarboxamide. The solid pyridine-2,6-dicarbonyl dichloride (76.1 mg, 0.373 mmol) was placed in a 50 mL round bottom flask before dispensing 75 μL of liquid aniline (76.4 mg, 0.832 mmol) into the reaction flask. Immediately, a violent reaction took place, releasing white plumes of HCl gas and forming white solid material. This was allowed to subside before adding 20 mL of dry MeCN to the reaction flask which was heated to 88 °C open to the atmosphere for 2 hours. The reaction mixture was then cooled to 4 °C before filtering off the fine white powder H₂L3 (118 mg, 92% yield).

¹H NMR: (400 MHz, DMSO-d₆, 300 K) [δ, ppm] 11.12 (s, 2H), 8.41 (d, J = 8.2 Hz, 2H), 8.31 (t, J = 8.0 Hz, 1H), 7.96 (d, J = 8.0 Hz, 4H), 7.46 (d, J = 7.5 Hz, 4H), 7.20 (t, J = 7.4 Hz, 2H). ¹³C NMR: (100 MHz, DMSO-d₆, 300 K) [δ, ppm] 162.19, 149.40, 140.40, 138.56, 129.22, 125.80, 124.85, 121.64. FTIR (cm⁻¹): 3268.21 (m, asymmetric N–H stretch), 2803.26 (w, aromatic C–H stretch), 1671.83 (s, asymmetric C=O stretch; N–H wag), 1599.41 (s, asymmetric N–H wag).

Cu1: H₂L1 (101 mg, 0.275 mmol) was dissolved in 50 mL of tetrahydrofuran (THF) before adding Cu(OAc)₂·H₂O (186 mg, 0.929 mmol) to the mixture. Instantly, a light-green precipitate began to form. The reaction was refluxed at 50 °C open to the air for 24 hours. The mixture was then allowed to cool to room temperature before filtering under vacuum. The isolated green powder was then washed with 10 mL of THF to yield Cu1·H₂O, (59.8 mg, 49%). The copper chelate may be crystalized by evaporation from a mixture of methanol (MeOH) and ethyl acetate (EtOAc) over 3 weeks at ambient temperatures. Similar crystals can be grown by vapour diffusion of diethyl ether (Et₂O) into a saturated MeOH solution containing Cu1 over 2–4 weeks at ambient temperature, 4 °C and −20 °C.

FTIR (cm⁻¹): 3626.76 (w, O–H stretch), 3066.06 (w, aromatic C–H stretch), 2226.17 (s, nitrile stretch), 1626.57 (s, C=O stretch). Crystal data: C₁₂₈H₇₈Cu₆N₃₀O₁₆, 1.5[CH₃OH] (M = 2721.50 g mol⁻¹): triclinic, space group P1̄ (no. 2), a = 12.8621(7) Å, b = 14.6778(8) Å, c = 17.1404(9) Å, α = 76.085(2)°, β = 70.053(2)°, γ = 81.249(2)°, V = 2943.8(3) ų, Z = 1, T = 173.0 K, μ(MoK_α) = 1.147 mm⁻¹, D_calc = 1.535 g cm⁻³, 343 382 reflections measured (4.23° ≤ 2Θ ≤ 51.992°), 11 552 unique (R_int = 0.1174, R_sigma = 0.0282) which were used in all calculations. The final R₁ was 0.0361 (I > 2σ(I)) and wR₂ was 0.0873 (all data). CCDC 2340637.†

Cu2: H₂L2 (113 mg, 0.308 mmol) was dissolved in 50 mL of THF before adding Cu(OAc)₂·H₂O (154 mg, 0.771 mmol) to the mixture. Instantly, a green precipitate began to form. The reaction was refluxed at 50 °C open to the air for 24 hours. The mixture was then allowed to cool to room temperature before filtering under vacuum. The isolated green powder was then washed with 10 mL of THF to yield Cu2·H₂O, (59.1 mg, 45%). The copper chelate was crystalized by vapour diffusion of Et₂O into a saturated MeCN solution containing Cu2 over 3 weeks at ambient temperature.

FTIR (cm⁻¹): 3396.60 (w, O–H stretch), 3090.05 (w, aromatic C–H stretch), 2223.05 (s, nitrile stretch), 1625.64 (s, C=O stretch). Crystal data: C₁₃₀H₇₆Cu₆N₃₂O₁₄, 4[C₂H₃N] (M = 2855.68 g mol⁻¹): triclinic, space group P1̄ (no. 2), a = 14.4764(11) Å, b = 15.1477(11) Å, c = 16.4380(10) Å, α = 106.667(2)°, β = 95.920(3)°, γ = 110.424(3)°, V = 3152.1(4) ų, Z = 1, T = 173.0 K, μ(MoK_α) = 1.075 mm⁻¹, D_calc = 1.504 g cm⁻³, 162 869 reflections measured (4.062° ≤ 2Θ ≤ 56.86°), 15 772 unique (R_int = 0.1107, R_sigma = 0.0649) which were used in all calculations. The final R₁ was 0.0482 (I > 2σ(I)) and wR₂ was 0.1261 (all data). CCDC 2340638.†

Cu3: H₂L3 (112 mg, 0.353 mmol) was dissolved in 50 mL of THF before adding Cu(OAc)₂·H₂O (176 mg, 0.882 mmol) to the mixture. Instantly, a green precipitate began to form. The reaction was refluxed at 50 °C open to the air for 24 hours. The mixture was then allowed to cool to room temperature before filtering under vacuum. The isolated green powder was then washed with 10 mL of THF to yield Cu3·H₂O, (40.0 mg, 30%). The copper chelate was crystalized by vapour diffusion of Et₂O into a saturated MeOH solution containing Cu3 and a drop of ethylene glycol over 2 weeks at ambient temperature.

FTIR (cm⁻¹): 2854.32 (w, aromatic C–H stretch), 1769.46 (w, aqua O–H wag), 1629.90 (s, C=O stretch). Crystal data: C₁₁₄H₈₆Cu₆N₁₈O₁₆, C₂H₆O₂, 5[CH₃OH] (M = 2567.52 g mol⁻¹): triclinic, space group P1̄ (no. 2), a = 10.8153(11) Å, b = 17.0091(16) Å, c = 17.4196(16) Å, α = 106.568(5)°, β = 100.629(5)°, γ = 107.750(5)°, V = 2793.0(5) ų, Z = 1, T = 173.0 K, μ(MoK_α) = 1.204 mm⁻¹, D_calc = 1.526 g cm⁻³, 94 743 reflections measured (2.554° ≤ 2Θ ≤ 45°), 7314 unique (R_int = 0.3031, R_sigma = 0.1282) which were used in all calculations. The final R₁ was 0.0681 (I > 2σ(I)) and wR₂ was 0.1446 (all data). CCDC 2340639.†

Conclusions

MOFs that contain void space have industrially and globally relevant applications. We have shown that novel NNN bis-aryl Cu(II) pincer chelates may be used as building blocks for the supramolecular construction of porous MOFs. The structural basis for Cu(II) metallocycle formation has been delineated and the facile functionalization of the carboxamide ligand enables the engineering of these solid-state structures.

Author contributions

M. L. B. performed all experimental work, writing, and concept. M. A. F. was crystallographer and editor. D. W. collected and processed magnetic measurements. O. Q. M. conceptualized, directed, and funded the project.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is based on research supported by the South African Research Chairs Initiative of the Department of Science and Innovation (DSI) and National Research Foundation (NRF) of South Africa (Grant No. 64799, OQM). The authors thank WITS University and the NRF for funding to purchase a dual-wavelength Bruker D8 Venture X-ray diffractometer (Grant No. 129920, OQM). We would like to further thank the NRF for funding through the NEP program (grant number UID: 116181). We also thank the Centre for High Performance Computing (Project CHEM1065, CHPC, Cape Town) for access to supercomputing infrastructure.

Notes and references

1. J. Yang, H. Wang, J. Liu, M. Ding, X. Xie, X. Yang, Y. Peng, S. Zhou, R. Ouyang and Y. Miao, RSC Adv., 2021, 11, 3241–3263.
2. N. Hanikel, M. S. Prévot and O. M. Yaghi, Nat. Nanotechnol., 2020, 15, 348–355.
3. L. Fu, Y. Liu, M. Pan, X.-J. Kuang, C. Yan, K. Li, S.-C. Wei and C.-Y. Su, J. Mater. Chem. A, 2013, 1, 8575.
4. S. M. Hossain, V. Prakash, P. Mamidi, S. Chattopadhyay and A. K. Singh, RSC Adv., 2020, 10, 3646–3658.
5. S. M. Hossain, G. K. Dam, S. Mishra and A. K. Singh, New J. Chem., 2020, 44, 15186–15194.
6. G. O. Lloyd and J. W. Steed, Chem. Commun., 2014, 50, 1426–1428.
7. M. Ray, D. Ghosh, Z. Shirin and R. Mukherjee, Inorg. Chem., 1997, 36, 3568–3572.
8. A. K. Patra and R. Mukherjee, Inorg. Chem., 1999, 38, 1388–1393.
9. A. K. Patra, M. Ray and R. Mukherjee, Inorg. Chem., 2000, 39, 652–657.
10. A. S. Lytvynenko, S. V. Kolotilov, O. Cador, S. Golhen, L. Ouahab and V. V. Pavlishchuk, New J. Chem., 2011, 35, 2179.
11. S. Giri, S. Biswas, M. G. B. Drew, A. Ghosh and S. K. Saha, Inorg. Chim. Acta, 2011, 368, 152–156.
12. I.-R. Jeon and R. Clérac, Dalton Trans., 2012, 41, 9569.
13. A. M. Toader, M. C. Buta, F. Cimpoesu, A.-I. Toma, C. M. Zalaru, L. O. Cinteza and M. Ferbinteanu, Chemistry, 2021, 3, 411–439.
14. M. Brandl, M. S. Weiss, A. Jabs, J. Sühnel and R. Hilgenfeld, J. Mol. Biol., 2001, 307, 357–377.
15. D. L. Lichtenberger, S. K. Renshaw and R. M. Bullock, J. Am. Chem. Soc., 1993, 115, 3276–3285.
16. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
17. T. Higa, M. Moriya, Y. Shimazaki, T. Yajima, F. Tani, S. Karasawa, M. Nakano, Y. Naruta and O. Yamauchi, Inorg. Chim. Acta, 2007, 360, 3304–3313.
18. APEX4version 2021.4-1 Data Collection Software Which Includes SAINT Version 8.40B, SADABS-2016/2, and XPREP Version 2014/2. Bruker AXS Inc., Madison, Wisconsin, USA.
19. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. J. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
20. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, A71, 3–8.
21. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, C71, 3–8.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2340637–2340639. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4nj01330a

---