Thickness-dependent characteristics and oxidation of 2D-cadmium

Abstract

In this study, the structural, electronic, and vibrational properties of the thinnest crystal structure that can be obtained by thinning bulk Cd down to a monolayer are investigated by performing first-principles calculations. Total energy optimization and dynamic stability calculations reveal that the single layer crystal structure has a hexagonal unitcell with a two-atomic basis where alternating layers are formed by trigonal arrangements of Cd atoms. Softening occurs with decreasing zone center optical phonon frequencies as a result of structural relaxation when going from a bulk to a single layer (SL) structure. It is also shown that the thinnest structure obtained from bulk Cd crystals maintains its metallic features despite the dimensional crossover. In addition, it is predicted through calculations that the SL Cd crystal strongly interacts with oxygen and that the oxidized regions even undergo chemical transformation to form a CdO crystal. In the double-layer CdO crystal resulting from the oxidation of individual Cd layers, the layers are connected to each other with partially covalent bonds, and this structure is a semiconductor with a band gap of 2.10 eV. On the one hand, the robust metallic structure of the thinnest possible Cd crystal provides flexibility for its use in nanoscale applications, on the other hand, the fact that its electronic properties can be changed by oxidation is important for optoelectronic device applications.

---

1 Introduction

As a member of transition metals, cadmium (Cd) has consistently played a critical role in driving innovation and modern technology, from its use in telecommunications¹ to protective coatings.² Bulk Cd has garnered attention especially due to its ability to resist corrosion.³ Its metallic properties combined with its resistance make it an excellent sacrificial anode⁴ for battery applications.^5,6 In addition, Cd can be alloyed with other metals, to create electrical contacts and connectors.⁷ Moreover, Cd is the base metallic element of II–IV metal chalcogenides: CdX (X = S, Se, and Te) which are used as elements of technological devices such as LEDs,⁸ LCD devices,⁹ photodetectors,¹⁰ photovoltaic cells, photoresistors¹¹ and solar panels.¹² Another one of the most common compounds of cadmium is CdO. In the technology of thin-film transistors (TFTs),¹³ electroplatings^14,15 and transparent conducting films (TCFs),¹⁶ efficient use of CdO has been reported.

In the meantime, there are examples of various low-dimensional forms of Cd crystals that have been used in the advancing field of nanotechnology. Zhao calculated that Cd_n clusters that have closed electronic shells demonstrate magic number behavior for some n, and the size dependence of ionization potentials converges towards the bulk limit.¹⁷ While Alvarez et al. showed that metallicity of Cd_n clusters emerges as a result of sp-hybridization,¹⁸ and a study by Kohaut et al. revealed that such clusters do not show metallic properties up to n = 60.¹⁹ Besides, Oyeniyi et al. developed and used a method to calculate the electronic excitation energies and absorption spectra of zero dimensional Zn, Cd and S clusters.²⁰ Xie et al. demonstrated that nanoribbons of CdTe with their large photoresponse and high gain to visible NIR irradiation are promising candidates for photodetection applications.²¹ As shown by Li et al., CdS nanobelts exhibit high photosensitivity and short decay time making them usable in Schottky junctions.²² In addition, the enhancement of quantum efficiency and electrical conductivity of CdS nanobelts was studied by Zhang et al.²³ As another one-dimensional form, nanowires of Cd-based materials have also been studied widely. It was shown that CdS nanowires have a direct band gap resulting in light emission/absorption in the visible range, while CdTe nanowires exhibit a high absorption coefficient and an optimal band gap for solar cell applications.²⁴ Furthermore, Wang et al. studied the zero-dimensional structures of Cd and predicted that Cd-based clusters generate delocalized π-electron channels, which are used as photoelectrochemical-type photodetectors.²⁵ Moreover, Ganiga et al. reported that quantum dot (QD) CdS is a fluorescence recoverer, therefore it is a promising candidate that can be used in advanced biological sensors.²⁶

Although various low-dimensional forms of Cd crystals have been studied to date, atomically thin possible two-dimensional crystal structures have not been investigated. In this study, we investigate which characteristic properties of Cd crystals change and how they are modulated when going from their known bulk form to their thinnest possible two-dimensional form. In addition, considering the fact that oxidation of Cd crystals is inevitable, the interaction of the surfaces of the single layer (SL) Cd crystals with oxygen is also investigated. It is also predicted here that CdO crystals are formed as a result of the strong Cd–O bonds established by the oxidation of cadmium. The stability and electronic properties of similar ultra-thin CdO crystals were also studied by Hoat et al.²⁷ As a result of such chemical conversion, SL Cd crystals are transformed and have a more stable structure. In this context, it is seen that oxidation acts as a process that strengthens the crystal structure rather than damaging it.

2 Computational methodology

The electronic and vibrational characteristics of bulk Cd, SL Cd, and CdO were investigated by employing Density Functional Theory (DFT) within the framework of the Vienna Ab initio Simulation Package (VASP).²⁸ The choice of the exchange–correlation functional was based on the Generalized Gradient Approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) parameterization²⁹ and corrected with the Heyd–Scuseria–Ernzerhof (HSE) screened-nonlocal-exchange functional.³⁰ Pseudopotential datasets were meticulously constructed utilizing the projector augmented wave (PAW) potentials to ensure an accurate representation of the atomic interactions. This study further investigated the van der Waals (vdW) interactions utilizing the DFT-D3 methodology developed by Grimme.³¹ Atomic charges were analyzed by the Bader technique.³² In order to mitigate undesirable layer-layer interactions along the vacuum direction in the SL Cd configuration, a vacuum spacing of 12.95 Å was judiciously introduced. For precise calculations, a kinetic energy cutoff of 700 eV was implemented, accompanied by a total energy convergence criterion of 10⁻⁵ eV for the total energy calculations. Gaussian smearing with a width of 0.05 eV was employed. To comprehensively explore the Brillouin Zone (BZ), distinct k-point meshes were adopted for structural optimization and density of states calculations. Specifically, a 21 × 21 × 21 k-point mesh was applied for bulk Cd, while a 21 × 21 × 1 is preferred for SL. These choices ensured accurate sampling of the reciprocal space. The relaxation of the unit cell was achieved by reducing pressures along each direction below ±1 kB. Vibrational properties were investigated utilizing the PHON code,³³ which leverages the small displacement method to extract phonon spectra and vibrational modes.

Here, to investigate the Raman activities of the phonon modes, we used the finite-difference method to calculate the polarizability of the crystal lattice by taking the derivative of the polarizability tensor, α_ij, concerning the normal mode describing the whole motion of individual atoms participating in the kth vibrational phonon mode, Q_k.

The total Raman activity is written from the type of Raman invariants given for the backscattering experimental geometry as follows:

where ã represents the isotropic part and β represents the anisotropic part of R. Using these, the Raman activity R_A is given as:

R_A = 45ã² + 7β² (4)

3 Results

3.1 Stability and the electronic properties of single layer cadmium

As shown in Fig. 1, a bulk Cd structure constructed by metallic bonding of atoms to each other forms a hexagonal-close package structure that belongs to the space group of P6₃/mmc and the point group of D_6h.¹⁹ Using total energy calculations, lattice parameters for the bulk structure are found to be a = b = 2.98 Å and c = 5.75 Å. However, as shown in Fig. 1(b), when going from the bulk to single layer, the thinnest possible crystal structure is a hexagonal structure with a two-atomic basis in which Cd atoms are bonded to each other in a highly buckled manner. Additionally, due to the absence of adjacent layers in the out-of-plane direction in the SL crystal structure, stronger Cd–Cd bonds are established in the in-plane direction. Therefore, compared to the bulk structure, the lattice parameters of the SL shrunk to 2.93 Å. The calculated crystal thickness (h) for this structure, defined as the out-of-plane distance between the bottom and top atoms, is 3.09 Å. While the cohesive energy per atom for the bulk crystal is 2.13 eV, it is 1.63 eV for the SL structure. In addition, it should be noted that the single-atom-thick trigonal symmetric crystal structure obtained, which is a thinner alternative to the two-atom primitive cell SL crystal, does not correspond to a possible structure on the Born–Oppenheimer surface.

Fig. 1 (a) and (b) Atomic structures and (c) and (d) phonon dispersions of bulk and SL Cd. Top and side views of the crystal structure are shown in the upper and lower panels, respectively. Phononic eigenmotions are shown as the inset.

Calculation of phonons is important for the investigation of the dynamic stability but not only limited to that, it also allows determination of the characteristic fingerprints of a given material. First of all, it is seen from Fig. 1 that, similar to the bulk crystal, theoretically predicted double-layered SL crystal structure has positive phonon eigenfrequency for all q values. Therefore, the SL structure obtained by total energy calculations corresponds to a dynamically stable structure and its synthesis in the freestanding form can be possible under appropriate experimental conditions. Here, phonon dispersion obtained for the bulk Cd crystal shows that there are two optical phonon branches at the Γ point. While the mode at 54 cm⁻¹ corresponds to in-plane vibrations of neighboring atoms in opposite directions relative to each other, the doubly degenerate mode at 147 cm⁻¹ corresponds to out-of-plane counter-phase movements of neighboring atoms. When switching from the bulk crystal to a SL crystal, it is seen that both in-plane and out-of-plane modes are subjected to dramatic phonon softening, as the inter-atomic distance between neighboring atoms is increased. Apparently, the part of the thermal conductivity mediated by phonons decreases in ultra-thin Cd crystals. In addition, for the SL structure zone center optical phonon eigenfrequencies are 36 and 85 cm⁻¹. Here, the phonon modes are located at lower energies in comparison with other 2D materials such as graphene (∼1600 cm⁻¹) and MoS₂ (∼460 cm⁻¹),^34,35 indicating that SL Cd is a softer material with a lower thermal conductivity.

Determination of the Raman activity spectrum of SL crystals, which allows their characterization and identification at the nanoscale, provides important preliminary information before future experiments. As shown in Table 1, both optical phonon modes of bulk and SL crystals at the Γ point have Raman activity and are expected to appear as distinct peaks in the experimentally measured Raman spectrum. Here, the theoretically obtained prominent R-active phonons are in good agreement with the experimental data.^36,37

Table 1 Calculated quantities for bulk Cd, SL Cd and CdO: optimized lattice parameters (a) and (c), thicknesses (h), bond lengths (d_1(Cd)−2(O), between Cd atoms labeled 1–2 and between Cd–O for CdO), work functions (Φ), cohesive energies (E_c), energy band gaps calculated with GGA (E^GGA_gap) and within HSE06 on top of GGA (E^HSE06_gap), and eigenfrequencies of Raman active vibrational modes

	a (Å)	c (Å)	d 1(Cd)−2(O) (Å)	h (Å)	Φ (eV)	E c (eV per atom)	E ^GGAgap (eV)	E ^HSE06gap (eV)	Raman active modes (cm^−1)
Bulk Cd	2.98	5.75	3.36	—	4.06	2.13	Metal	Metal	54, 147
SL Cd	2.93	—	3.53	3.09	3.95	1.63	Metal	Metal	36, 85
BL CdO	3.76	—	2.17	2.51	4.80	6.90	0.57	2.10	64, 104, 242, 247, 410

---

It is also essential to obtain electronic band dispersion to understand how the dimensional crossover, which occurs by thinning cadmium from the bulk form to two-dimensional SL structure, affects the behavior of charge carriers. As shown in Fig. 2, SL Cd crystals have metallic properties like the bulk material. It is also noteworthy that the number of states crossing the Fermi level decreases due to the absence of atoms surrounding the out-of-plane direction in the SL structure. Linear crossing bands located at the K and H high symmetry points just above the Fermi level arise as a result of the in-plane trigonal symmetry in the crystal structure. Orbital decomposition of the bands crossing the Fermi level shows that the metallicity of both bulk and SL structures mainly originates from the electrons in s and p states.³⁸ It is also seen that, when going from the bulk to SL, the contribution of p state electrons to metallicity is enhanced. As a result, it is theoretically predicted that the Cd material maintains its metallic nature even if it is thinned down to its thinnest possible crystal structure. If it is considered in terms of suitability for use in nanoscale device applications, the Cd material is important because it allows operational errors.

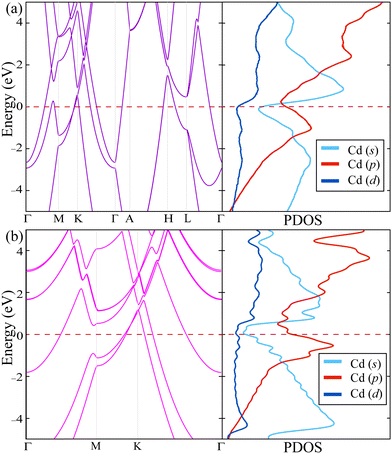Fig. 2 Electronic band dispersions (on the left) and orbital decomposed partial density of states (PDOS) (on the right) of (a) bulk and (b) SL Cd.

3.2 Oxidation characteristics of single layer Cd

Oxidation of materials is an inevitable fact in daily life and under laboratory conditions. Therefore, it is essential to examine the structural stability of the ultra-thin SL Cd crystal against oxidation, which we have examined in detail. Whether a material undergoes structural change when exposed to oxidation depends on how strongly the crystal structure interacts with atomic and molecular oxygen. For the SL Cd crystals, binding energies were calculated on points with high electron density on the surface and points that provide a certain symmetry between them.

As shown in Fig. 3(a), when an oxygen atom approaches the middle of the three Cd atoms at the top and onto another Cd atom at the bottom layer (Top-1 site), it is absorbed with a high binding energy of 4.37 eV. While this strong bond is established, a charge transfer of up to 1.10 e occurs from the Cd atoms to the O atom on the surface. If the O atom is adsorbed on the holey site of the hexagon formed by atoms of two uppermost layers, it forms three strong covalent bonds with three atoms of the uppermost layers. Bonding on the hollow site occurs with a binding energy of 4.34 eV, resulting in a charge transfer of 1.03 e from the neighboring Cd atoms to O.

Fig. 3 Possible adsorption sites, charge density differences, binding energies, and charge transfer for O atoms from the top view: (a) Top-1 site, (b) Hollow site, (c) Nearly Bridge (N-Bridge) site, and (d) Top-2 site. Possible adsorption scenarios from the top view, (e) and (f), for O₂: charge density differences, binding energies, and charge transfers for both situations.

In addition, there are two possible sites for adsorption of the O atom bonded to two Cd atoms; (i) a bridge site between two top layer atoms (Bridge-I) and (ii) a bridge site between Cd atoms, one in the bottom and the other in the top layer (Bridge-II). The total energy calculations performed show that the O atom approaching the Bridge-I site relaxes to the Top-1 shown in Fig. 3(a), and the O atom approaching the Bridge-II relaxes to the N-Bridge site by tilted bonding with only one Cd atom. Absorption on the N-Bridge site occurs at 2.17 eV, with a charge transfer of 0.83 e from the upper one Cd to oxygen. The Top-2 site corresponds to the possible bonding location on the top of an uppermost Cd atom (see Fig. 3(d)). The O atom binds to SL Cd from the Top-2 site with a binding energy of 1.92 eV and a charge transfer of 0.81 e from the surface to the O atom. It seems that when the SL Cd material is exposed to atomic oxygen, the Top-1 and Hollow sites are rapidly oxidized first, followed by the N-Bridge and Top-2 sites.

Moreover, how the SL Cd crystal interacts with the O₂ molecule is also taken into consideration. As shown in Fig. 3(e) and (f), when the O₂ molecule approaches the surface, where its center of mass coincides with the Top-1 or Hollow site, it binds with a binding energy of 170 meV. Ultimately, when the O₂ molecule is bonded, one of the atoms forms two bonds with the Cd atoms, and the other forms a single bond. Here, single-bonded O receives 0.55 e electrons while double-bonded O receives 0.51 e.

3.3 From Cd to CdO through oxidation

It has been revealed that the oxygen atoms of the SL Cd crystal surface interact strongly and therefore chemically converted Cd–O domains are nucleated rapidly. This section is devoted to the investigation of fully oxygenated SL Cd. As shown in Fig. 4, the most intense oxidation of the SL Cd crystal occurs when one O atom is bonded to each Cd atom at the binding points predicted as Top-1 in the previous section. Here the resulting bilayer structure can be called BL CdO. The BL crystal structure has a graphene-like honeycomb symmetry, which can be attributed to the P3m1 space group and the point group of C_3v. From total energy calculations, the lattice constant of BL CdO is found to be 3.76 Å. Bond lengths between Cd and O are 2.17 intralayerly, resulting in charge transfer, and 2.51 Å interlayerly, which is also the thickness (h) of the BL CdO. The cohesive energy per atom for the BL CdO is calculated to be 6.90 eV.

Fig. 4 (a) Crystal structure of CdO from the top (on the left) and side (on the right) views. (b) The corresponding phonon band dispersions (on the left) and normalized Raman spectra in comparison with those of SL Cd. The eigenmotion of each Raman active mode of CdO is shown as the inset.

Calculated phonon dispersion shows that the BL CdO structure, which emerged through the chemical conversion, is also dynamically stable and contains 9 optical phonon branches in its spectrum. Among these, three doubly degenerate modes with in-plane vibrational character lie at 64, 410, and 393 cm⁻¹ and the non-degenerate modes with out-of-plane vibrational character lie at 104, 242, and 247 cm⁻¹.

Raman active vibrational modes are calculated using eqn (4), and then normalized, as shown in Fig. 4(b). CdO crystalline exhibits six characteristic R-active vibrational modes at the Γ point. The highest and lowest R-active modes (410, 64 cm⁻¹) have opposite in-plane vibrational characteristics of inter and intralayer O and Cd atoms, respectively. The remaining R-active modes have out-of-plane characteristics with eigenfrequencies of 104, 242, and 247 cm⁻¹. Specifically, the R-active modes at 104 and 257 cm⁻¹ possess the opposite out-of-plane motion both inter and intralayerly, whereas the interlayered Cd and O atoms follow the same trend for the mode at 242 cm⁻¹. As shown in (b), the R-active modes of SL Cd and CdO show very similar intensities for relatively low frequencies. The reason for this is that the vibrations of Cd atoms dominate the vibrations of oxygen atoms (see insets), reducing them to a regime that can be ignored. This leads to distinguishing the differences of materials by looking at their electronic properties rather than their vibrational characteristics.

Electronically, differing from SL Cd, the BL CdO crystal is a direct gap semiconductor with a bandgap of 2.10 eV (0.57 eV), calculated with GGA + HSE06 (pure GGA) at the Γ point (see Fig. 5). The BL obtained from SL Cd has a smaller band gap compared to the CdO bulk crystals (2.5 eV).^39,40 Here, the VBM is mainly composed of O-p states with a small contribution from Cd-d state electrons, whereas the CBM is formed by the hybridization of O-p and Cd-s states. Moreover, the electron (hole) effective mass of CdO at the vicinity of the Γ point is calculated to be 0.13 m_e (0.56 m_e), where m_e is the electron rest mass. For monolayer MoS₂, electron (hole) effective mass is 0.45 m_e (0.63 m_e).⁴¹ Thereby, charge carriers are expected to move faster in CdO than MoS₂, however, slower than graphene. Compared to the bulk CdO crystals, ultra-thin BL CdO crystals obtained by dimensional reduction hold promise to be used in photodiodes, phototransistors and photovoltaic cell devices that can operate at higher wavelengths.

Fig. 5 Electronic band dispersion of CdO with the corresponding orbital decomposed PDOS of Cd and O atoms.

The fact that ultra-thin Cd crystals can be easily chemically converted into CdO makes possible novel applications of this material. Thanks to the advances in nanotechnology tools, by using masks with nanoscale smoothness, it has become possible to cut materials into desired sizes or functionalize them in patterns suitable for the purpose. As shown in Fig. 6, when a Cd/CdO interface is created, a lateral heterojunction is also obtained. This simple metal–semiconductor interface, obtained by oxidation of a single material, creates a Schottky barrier of 0.58 eV against current carriers. The fact that ultra-thin Cd crystals can be easily obtained with a single material and offer a smaller Schottky barrier height compared to other metals (typically 0.7–0.9 eV)⁴² makes them a promising material for use in nanoscale device applications.

Fig. 6 (a) Top view of the possible lateral SL Cd/CdO heterojunction interface. O atoms are magnified for better visualization. (b) Comparative band alignments of SL Cd and CdO with Schottky barrier height (Φ_b) and energy band gap (E^HSE06_gap) of CdO are given as insets.

4 Conclusions

In this study, the thinnest possible crystal structure of the well-known Cd crystal and its electronic and vibrational properties were investigated using DFT-based calculations. Total energy optimization and dynamical stability analysis showed that in its thinnest stable form, Cd crystallizes in a graphene-like structure consisting of alternating layers formed from trigonal arrangements of Cd atoms. It has also been predicted that this ultra-thin material, called SL Cd, has two characteristic Raman active modes that allow characterization and differentiation from other materials with similar crystal structures. In addition, it has been seen that the Cd crystal retains its metallic properties even if the thinnest possible structure is obtained from the thickest bulk crystal. In the last part, it is shown that SL Cd crystals are transformed into a BL CdO structure, which displays semiconductor behavior, through chemical conversion, and its possible lateral heterojunction applications are discussed. Ultra-thin cadmium with an ultra-thin stable crystal structure, thickness-independent metallic behavior, and chemically controllable electronic properties stands out as a promising material for nanoscale device applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was supported by Scientific and Technological Research Council of Turkey (TUBITAK) under the Grant Number 221N401. HS thanks to TUBITAK for their supports. Computational resources were provided by TUBITAK ULAKBIM, High Performance and Grid Computing Center (TR-Grid e-Infrastructure).

References

1. A. Green, The Characterization of Nickel Cadmium Batteries for Telecommunications Applications-Part 1. Telescon 97 proceedings. 1997.
2. G. Soderberg and L. Westbrook, Cadmium Plating, Trans. Electrochem. Soc., 1941, 80, 429.
3. N. R. Council, et al.Toxicity and related data on selected cadmium compounds, Toxicologic Assessment of the Army's Zinc Cadmium Sulfide Dispersion Tests, 1997.
4. Z. Zhao, G. K. Walia, G. Li and T. Tang, Nano Technology for Battery Recycling, Remanufacturing, and Reusing, Elsevier, 2022, pp. 321–347.
5. F. Putois, Market for nickel-cadmium batteries, J. Power Sources, 1995, 57, 67–70.
6. S. Petrovic and S. Petrovic, Nickel-cadmium batteries, Battery Technology Crash Course: A Concise Introduction, 2021, pp. 73–88.
7. W. Kemp, P. Klemens, A. Sreedhar and G. White, The thermal and electrical conductivity of silver-palladium and silver-cadmium alloys at low temperatures, Proc. R. Soc. London, Ser. A, 1956, 233, 480–493.
8. W. H. Jeong, Z. Yu, L. Gregori, J. Yang, S. R. Ha, J. W. Jang, H. Song, J. H. Park, E. D. Jung and M. H. Song, et al., In situ cadmium surface passivation of perovskite nanocrystals for blue LEDs, J. Mater. Chem. A, 2021, 9, 26750–26757.
9. K. Pal, M. A. Elkodous and M. M. Mohan, CdS nanowires encapsulated liquid crystal in-plane switching of LCD device, J. Mater. Sci.: Mater. Electron., 2018, 29, 10301–10310.
10. K. Deng and L. Li, CdS nanoscale photodetectors, Adv. Mater., 2014, 26, 2619–2635.
11. E. Klugmann and O. Onyeogu, Measurement of insolation using CdS photoresistor, Energy Convers., 1979, 19, 153–157.
12. K. W. Böer, Cadmium sulfide enhances solar cell efficiency, Energy Convers. Manage., 2011, 52, 426–430.
13. S. E. AlGarni and A. Qasrawi, Preparation and characterization of CdO/In 6 Se 7 thin film transistors, Mater. Res., 2020, 23(6), e20200449.
14. C. Karunakaran and R. Dhanalakshmi, Selectivity in photocatalysis by particulate semiconductors, Cent. Eur. J. Chem., 2009, 7, 134.
15. R. A. Lewis, Hawley's condensed chemical dictionary, John Wiley & Sons, 2016.
16. Y. Yang, S. Jin, J. E. Medvedeva, J. R. Ireland, A. W. Metz, J. Ni, M. C. Hersam, A. J. Freeman and T. J. Marks, CdO as the archetypical transparent conducting oxide. Systematics of dopant ionic radius and electronic structure effects on charge transport and band structure, J. Am. Chem. Soc., 2005, 127, 8796–8804.
17. J. Zhao, Density-functional study of structures and electronic properties of Cd clusters, Phys. Rev. A, 2001, 64, 043204.
18. P. Álvarez-Zapatero and A. Aguado, Computational characterisation of structure and metallicity in small neutral and singly-charged cadmium clusters, Phys. Chem. Chem. Phys., 2019, 21, 12321–12334.
19. S. Kohaut and M. Springborg, Growth patterns and structural motifs of cadmium clusters with up to 60 atoms: disordered or not?, Phys. Chem. Chem. Phys., 2016, 18, 28524–28537.
20. E. Oyeniyi, O. Akin-Ojo and O. O. Popoola, oeINDO: Efficient determination of excitation energies and UV-Vis absorption spectra of nano-sized Zn, Cd, S and their complexes, Comput. Theor. Chem., 2023, 1223, 114096.
21. X. Xie, S.-Y. Kwok, Z. Lu, Y. Liu, Y. Cao, L. Luo, J. A. Zapien, I. Bello, C.-S. Lee and S.-T. Lee, et al., Visible-NIR photodetectors based on CdTe nanoribbons, Nanoscale, 2012, 4, 2914–2919.
22. L. Li, S. Yang, F. Han, L. Wang, X. Zhang, Z. Jiang and A. Pan, Optical sensor based on a single CdS nanobelt, Sensors, 2014, 14, 7332–7341.
23. L. Zhang, M. Liu, M. Zhao, Y. Dong, C. Zou, K. Yang, Y. Yang, S. Huang and D.-M. Zhu, Electrical and optoelectrical modification of cadmium sulfide nanobelts by low-energy electron beam irradiation, Nanotechnology, 2016, 27, 395704.
24. L. Huang and J. G. Lu, Synthesis, characterizations and applications of cadmium chalcogenide nanowires: a review, J. Mater. Sci. Technol., 2015, 31, 556–572.
25. H.-R. Wang, X.-K. Tian, J.-R. Zhang, M.-Y. Wen and X.-G. Yang, Acridine based metal-organic framework host-guest featuring efficient photoelectrochemical-type photodetector and white LED, Dalton Trans., 2022, 51, 11231–11235.
26. M. Ganiga and J. Cyriac, An ascorbic acid sensor based on cadmium sulphide quantum dots, Anal. Bioanal. Chem., 2016, 408, 3699–3706.
27. D. Hoat, M. Naseri, T. V. Vu, J. Rivas-Silva, N. N. Hieu and G. H. Cocoletzi, Structural, electronic and optical properties of CdO monolayer and bilayers: Stacking effect investigations, Superlattices Microstruct., 2020, 145, 106644.
28. G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865.
30. J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215.
31. J. Moellmann and S. Grimme, DFT-D3 study of some molecular crystals, J. Phys. Chem. C, 2014, 118, 7615–7621.
32. G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360.
33. D. Alfè, PHON: A program to calculate phonons using the small displacement method, Comput. Phys. Commun., 2009, 180, 2622–2633.
34. L. Falkovsky, Phonon dispersion in graphene, J. Exp. Theor. Phys., 2007, 105, 397–403.
35. J. Su, Z.-t Liu, L.-p Feng and N. Li, Effect of temperature on thermal properties of monolayer MoS2 sheet, J. Alloys Compd., 2015, 622, 777–782.
36. J. Weszka, A. Burian, A. Zwick and M. Renucci, On Raman scattering in Cd-As disordered thin films, Solid State Commun., 1987, 63, 181–182.
37. B. Børresen, G. A. Voyiatzis and G. N. Papatheodorou, The Cd₂²⁺ in molten metal halides and at electrode interfaces, Phys. Chem. Chem. Phys., 1999, 1, 3309–3314.
38. S. Daniuk, T. Jarlborg, G. Kontrym-Sznajd, J. Majsnerowski and H. Stachowiak, Electronic structure of Mg, Zn and Cd, J. Phys.: Condens. Matter, 1989, 1, 8397.
39. A. Adhikari, P. Strak, P. Dluzewski, A. Kaminska and E. Przezdziecka, Pressure-dependent bandgap study of MBE grown CdO/MgO short period SLs using diamond anvil cell, Appl. Phys. Lett., 2022, 121, 242103.
40. K. Manickathai, S. Viswanathan and M. Alagar, Synthesis and characterization of CdO and CdS nanoparticles, Indian J. Pure Appl. Phys., 2008, 46, 561–564.
41. H. V. Phuc, N. N. Hieu, B. D. Hoi, N. V. Hieu, T. V. Thu, N. M. Hung, V. V. Ilyasov, N. A. Poklonski and C. V. Nguyen, Tuning the Electronic Properties, Effective mass and carrier mobility of MoS₂ monolayer by strain engineering: first-principle calculations, J. Electron. Mater., 2018, 47, 730–736.
42. C. Palmstrøm, Contacts for Compound Semiconductors: Ohmic Type, Encycl. Mater.: Sci. Technol., 2001, 1581–1587.

---