Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structural and thermodynamic investigations of Zr(BH4)4 and Hf(BH4)4 between 280 K and their decomposition temperatures†
Konrad
Burkmann
 a,
Franziska
Habermann
a,
Erik
Schumann
a,
Franziska
Habermann
a,
Erik
Schumann
 a,
Jakob
Kraus
a,
Jakob
Kraus
 b,
Bianca
Störr
a,
Horst
Schmidt
cd,
Erica
Brendler
b,
Bianca
Störr
a,
Horst
Schmidt
cd,
Erica
Brendler
 e,
Jürgen
Seidel
a,
Klaus
Bohmhammel
a,
Jens
Kortus
e,
Jürgen
Seidel
a,
Klaus
Bohmhammel
a,
Jens
Kortus
 b and
Florian
Mertens
b and
Florian
Mertens
 *af
*af
aInstitut für Physikalische Chemie, TU Bergakademie Freiberg, Leipziger Straße 29, 09599 Freiberg, Germany. E-mail: florian.mertens@chemie.tu-freiberg.de; Tel: +493731-393737
bInstitut für Theoretische Physik, TU Bergakademie Freiberg, Leipziger Straße 23, 09599 Freiberg, Germany
cInstitut für Anorganische Chemie, TU Bergakademie Freiberg, Leipziger Straße 29, 09599 Freiberg, Germany
dInstitut für Technische Chemie, TU Bergakademie Freiberg, Leipziger Straße 29, 09599 Freiberg, Germany
eInstitut für Analytische Chemie, TU Bergakademie Freiberg, Leipziger Straße 29, 09599 Freiberg, Germany
fZentrum für effiziente Hochtemperatur-Stoffwandlung, TU Bergakademie Freiberg, Winklerstraße 5, 09599 Freiberg, Germany
First published on 12th January 2024
Abstract
The borohydrides of zirconium (Zr(BH4)4) and hafnium (Hf(BH4)4) have been prepared by solid state metatheses. The crystal structures were determined slightly below their melting temperature with in situ cryo crystallisation single crystal XRD. The melting and decomposition process was investigated using differential scanning calorimetry coupled with thermogravimetry and mass spectroscopy. The enthalpies of formation were determined using the decomposition enthalpy, the enthalpy of fusion and the heat capacity measurements in the temperature range from 5 °C to 35 °C. Standard entropy values of both compounds were obtained by DFT calculations. The determined values were optimised using the CalPhaD method.
Introduction
Complex hydrides are still in the focus of current research in the field of hydrogen storage.1,2 The covalent borohydrides Zr(BH4)4 and Hf(BH4)4 possess melting points of about 30 °C3 and therefore have been considered as volatile precursors to produce thin layers of ZrB2 and HfB2via chemical vapor deposition for a long time.4–9 Consequently, a significant number of reports on the decomposition of these borohydrides under relatively harsh conditions (high temperatures from the gas phase) have been published so far. To our knowledge, however, there is only one investigation of the decomposition behaviour of Zr(BH4)4 under atmospheric conditions reported by Gennari et al.10 and none in regard to Hf(BH4)4. Furthermore, neither experimental data in respect to the enthalpy of formation nor the absolute entropy of the two compounds nor to their heat capacity functions can be found. However, the melting and extrapolated boiling points as well as the heat of fusion, vaporisation and sublimation were determined by Hoekstra and Katz.3Besides the application as CVD precursors, these borohydrides are currently also used to functionalise surfaces to generate polymerisation and hydrogenation catalysts.11 In respect to the development of metal hydride systems for hydrogen storage, i.e. to generate systems that allow the uptake and release of hydrogen by acceptable pressure and/or temperature variation, it is important to extend the database of thermodynamic values of complex metal hydrides. A way to arrive at such systems is by creating reactive hydride mixtures (often called reactive hybrids) to implement the concept of thermodynamic tuning.12–15 This concept is based on the idea to achieve reversibility of the hydrogenation by the enthalpic contribution of the reaction of the dehydrogenated hydrides. The option to use Zr and Hf as catalysts for the (re)hydrogenation reactions of complex metal hydrides by adding them as halides,16 adds to the importance of understanding and exploring the decomposition behaviour and the thermodynamics of their complex metal hydrides such as their boranates and alanates.
The synthesis procedures mentioned in the following can be used for the generation of Zr(BH4)4 and Hf(BH4)4. Numerous authors report various liquid phase syntheses of Zr(BH4)4 and Hf(BH4)4. Wayda et al.,5 James and Smith,17 Sayer et al.18 and Smith et al.19 used ZrCl4 and LiBH4 in diethyl ether according to reaction (1) (M = Zr). It was then possible to use fractional distillation for the purification of both compounds because of their low melting points and their high vapour pressures.3 Wayda et al.5 and Broach et al.20 used the same method for the preparation of Hf(BH4)4 (M = Hf). Hoekstra and Katz3 further report reactions of ZrCl4 (or HfCl4, respectively) with Al(BH4)3 (see reaction (2), M = Zr, Hf) or with NaZrF5 (see reaction (3), M = Zr, Hf). The last method mentioned was also applied by Reid et al. using KZrF5.21 Banks et al. used Na2ZrF6 and Al(BH4)3 to produce Zr(BH4)4 in the same manner.22
| 4 LiBH4 + MCl4 → M(BH4)4 + 4 LiCl | (1) |
| 4 Al(BH4)3 + 3 MCl4 → 3 M(BH4)4 + 4 AlCl3 | (2) |
| 2 Al(BH4)3 + NaMF5 → M(BH4)4 + 2 AlF2BH4 + NaF | (3) |
Banks et al. mentioned problems with the purification and metathesis reaction (2), which occurred incomplete and with reaction (3) taking several days to finish.22 Reid et al. reported the synthesis from Zr(OR)4 with gaseous B2H6 (see reaction (4)).21
| 3 Zr(OR)4 + 8 B2H6 → 3 Zr(BH4)4 + 4 B(OR)3 | (4) |
We applied the direct metathesis route according to reaction (1) to prepare Zr(BH4)4 and Hf(BH4)4 because of the simplicity of the implementation and purification of the target compounds using this method. We investigated the melting and decomposition behaviour of both compounds including the resulting decomposition products using thermoanalysis, evolved gas analysis, X-ray diffraction and SEM-EDX. Furthermore, heat capacity measurements were performed and density functional theory was chosen to calculate entropy values resulting in a large set of thermodynamic data for both compounds. Additionally, we report the crystal structures of both compounds measured slightly below their melting temperature.
Experimental section
Materials and methods
All handling and manipulation of the chemicals as well as the sample preparation for the measurements were performed in an argon (Nippon Gases, 5N) filled glove box with a gas circulation purifying system (H2O and O2 < 0.1 ppm) from MBraun or at an argon filled Schlenk line.35,36Lithiumborohydride (LiBH4, Chemetall), zirconium tetrachloride (ZrCl4, Merck, anhydrous for synthesis) and hafnium tetrachloride (HfCl4, Alfa Aesar, 98+%, metals basis excluding Zr, Zr < 2.7%) were used as received. Deuterated benzene (C6D6, DEUTERO, 99%) and benzene (C6H6, CARL ROTH, ≥ 99.5%) were distilled from Na/Al2O3 (SOLVONA, Dr Bilger Umweltconsulting, Germany) and benzophenone (C13H10O, SIGMA-ALDRICH, 99%). Tetrahydrofurane (C4H8O, VWR International GmbH, 99%) and deuterated tetrahydrofurane (C4H8O, DEUTERO, 99.5%) were dried over a 4 Å molecular sieve. Zirconocen dibromide (Cp2ZrBr2) was used as reference material for the 91Zr NMR investigations. Sapphire (aluminium oxide, Al2O3) was used as reference material for the heat capacity measurements.
Characterisation techniques
Measurements of the heat capacity of the solids and melts were performed inspired by the method already described by various authors.39–45 In detail, about 120 mg of the sample were filled into standard stainless steel sample vessels. Using a nickel sealing the vessels were crimped tightly. The nickel sealings and the vessels were brought to an identical mass by hand polishing to avoid variations in the blank effects. A CP-by-step method based on six temperature steps (3.75 K, 3 K min−1) in the temperature range from 6 °C to 36 °C each followed by an isothermal period of 60 min duration was carried out. This temperature programme was applied to the measurements of the sample, the reference (sapphire) and the blank, which was an empty steel vessel. Using the recommended reference heat capacity of sapphire from ref. 46 the heat capacities of both samples were calculated viaeqn (5),
 | (5) |
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) p defines the specific heat capacity of the sample at the mean temperature of the ramp. The start and end time of the heat flow
p defines the specific heat capacity of the sample at the mean temperature of the ramp. The start and end time of the heat flow ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) peaks are denoted by ti and ti+1. The masses of the sample and reference material are labeled msample and mref, respectively. Finally,
peaks are denoted by ti and ti+1. The masses of the sample and reference material are labeled msample and mref, respectively. Finally, ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) p,ref is used as the specific heat capacity of the reference material at the mean temperature of the ramp. Each compound was measured four times.
p,ref is used as the specific heat capacity of the reference material at the mean temperature of the ramp. Each compound was measured four times.
Synthesis procedures
Lithium borohydride and the corresponding transition metal tetrachloride (zirconium tetrachloride or hafnium tetrachloride) were mixed in stoichiometric amounts under protective atmosphere (see reaction (1)) in a Schlenk vessel. The vessel was transferred to a Schlenk line and the two solids were stirred for 2 h to 4 h at about 50 °C to 70 °C (oil bath). After that measure, the product was distilled in vacuum into a cold trap and stored in a glove box (about 60% yield). After a few days large crystals grew on the wall of the storage vials. These crystals were used for the previously mentioned measurements.Density functional theory (DFT) calculations
All density functional theory calculations (DFT47,48) were performed using the Quantum ESPRESSO code,49–51 version 6.7. In these calculations, PAW pseudopotentials52 were employed, which were taken from the PSlibrary,53 version 1.0.0. The PAW pseudopotentials were combined with the PBE54 generalized-gradient exchange–correlation functional.Results and discussion
NMR measurements
The success of the syntheses and the purity of both compounds were verified using NMR spectroscopy. For comparison of the measured chemical shifts with already known values from the literature, those regarding 1H and 11B NMR are listed in Table 1. If necessary, the literature values were adapted to reference compounds we used.The reported chemical shifts of the signals in the 1H NMR spectra exhibit only small differences in respect to our data (see Table 1), which is possible due to differences in solvent and concentration. Besides, the chemical shifts for the 11B nuclei determined by us fit well with the data from literature for both transition metal borohydrides.
For 91Zr we obtained a chemical shift of δ = 44.1 ppm, which is in good agreement with the already published literature value of 40.7 ppm.18 For the Hf nuclei, there are no NMR data available. The two NMR active nuclei of Hf (177Hf and 179Hf) exhibit large quadrupole moments,58 resulting in strong line broadenings. For this reason, no Hf NMR data are presented in this paper.
All measured spectra can be found in the ESI† Fig. S1 to S3. The already known coupling patterns are observable in the 1H (Fig. S1, ESI†) and 11B (Fig. S2, ESI†) NMR spectra. From our measurements, it can be concluded that both compounds were synthesised with sufficient purity.
Structure determination sligthly below the melting temperature and calculation of the cubic thermal expansion coefficient
Both boranates have already been crystallographically characterised, Zr(BH4)4 at 100 K31 and Hf(BH4)4 at 110 K,20 and crystallise in the cubic space group P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m. In order to exclude a possible phase transition in the temperature range up to a temperature close to the starting point of our DSC measurements, both boranates were subjected to an SC-XRD investigation. Table 2 shows the results of the measurements and the structures are additionally displayed in Fig. S4 (ESI†).
3m. In order to exclude a possible phase transition in the temperature range up to a temperature close to the starting point of our DSC measurements, both boranates were subjected to an SC-XRD investigation. Table 2 shows the results of the measurements and the structures are additionally displayed in Fig. S4 (ESI†).
| Zirconium(IV) borohydride | Hafnium(IV) borohydride | |
|---|---|---|
| Empirical formula | Zr(BH4)4 | Hf(BH4)4 |
| Formular weight | 150.595 | 237.861 |
| Crystal system, | Cubic, | Cubic, |
| Space group |
P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m 3m |
P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m 3m |
| Temperature (K) | 273 | 288 |
| a (Å) | 5.955 ± 0.011 | 5.9464 ± 0.0010 |
| V (Å3) | 211.1 ± 1.2 | 210.27 ± 0.62 |
| Z | 1 | 1 |
| Radiation type | Mo-Kα | Mo-Kα |
| μ (mm−1) | 1.19 | 12.45 |
| Data collection | ||
| Diffractometer | STOE IPDS 2 | STOE IPDS 2 |
| Absorption correction | — | Integration59 |
| No. of measured, | 3767 | 2072 |
| Independent and observed | 115 | 135 |
| [I > 2σ(I)] reflections | 115 | 135 |
| R int | 0.133 | 0.081 |
(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ)max (Å−1) θ/λ)max (Å−1) |
0.645 | 0.696 |
| Refinement | ||
| R[F2 > 2σ(F2)], wR(F2), S | 0.011, 0.027, 1.05 | 0.034, 0.095, 1.05 |
| No. of reflections | 115 | 135 |
| No. of parameters | 12 | 12 |
| No. of restraints | 2 | |
| H-atom treatment | All H-atom parameters refined | All H-atom parameters refined |
| Δρmax, Δρmin (e Å−3) | 0.09, −0.07 | 0.91, −0.78 |
| Absolute structure | Refined as an inversion twin. | Refined as an inversion twin. |
From the listed data in this table, a fundamental change of the crystal structure besides the thermal expansion can be excluded. A molecular dynamic simulation by Igoshkin et al. supports this result.60 As can be expected, the displacement parameters are enlarged at these high temperatures, especially for Zr(BH4)4, which can be explained by the proximity to the melting point. For more structure related details the reader is referred to the literature.20,31
Additionally, the cubic thermal expansion coefficient γ has been calculated (eqn (7)61) from the data given in the literature20,31 and our own results.
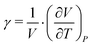 | (6) |
 | (7) |
Thermal investigation of the melting and decomposition events using DSC measurements
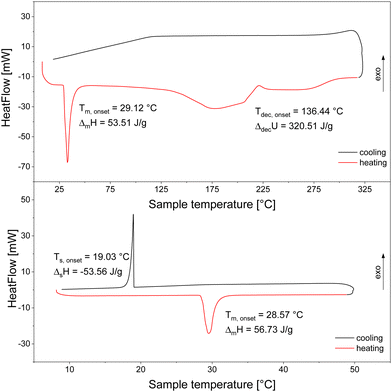
Another measurement with new material at a different heating rate of 5 K min−1 between 8 °C and 325 °C was used for the extrapolation of the heating rate to 0 K min−1 resulting in a melting temperature of 27.94 °C. Furthermore, the decomposition temperature and the released heat during decomposition after the melting was measured. It is noteworthy to mention that the released heat cannot be equated with the decomposition enthalpy since there may have been a pressure built up in the closed crucibles. The value of ΔdecU = 56.94 kJ mol−1 can be taken from Fig. 1. We decided to use a heating rate of 5 K min−1 instead of 1 K min−1 to prevent very broad signals as mentioned by Gennari et al.10 The decomposition does not appear to be reversible since there are no exothermic effects visible during the cooling phase indicating hydrogen uptake. Table 3 serves as a summary of all so far reported melting and decomposition temperatures.
The melting temperature determined by the extrapolation method described above fits well to the corresponding values in the literature. In contrast, the obtained decomposition temperature is about 40 K higher than the one given by Gennari et al.10 and even 50 K higher than that by Nakamori et al.32 An explanation for these discrepancies could be the use of a sealed instead of an open crucible as was used by Gennari et al.10 Utilising open crucibles leads in the investigated systems to a remarkable loss of sample due to evaporation of the molten material before its decomposition. We prevented this problem by using sealed crucibles. The disadvantage, however, of this mode of operation is the shift of the decomposition temperature to higher values due to the rise of the pressure in the gas phase caused by the evaporated material. The decomposition event occurs at an onset temperature of 130.27 °C with broad signals, because it is a decomposition from the liquid state and it is not clear if the decomposition happens as a multi-step process. Further discussion and evaluation of the decomposition is presented in the next section.
Hf(BH4)4
To our knowledge, there are no DSC measurements of Hf(BH4)4 available in the literature. Fig. 2 displays a heating and cooling cycle in the lower part, which exhibits a sharp melting point at 28.57 °C (heating rate of 1 K min−1) with a melting enthalpy of 13.49 kJ mol−1. This value is in good agreement with the value from Hoekstra and Katz of 14.24 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 obtained from vapour pressure measurements. The cooling curve exhibits the solidification peak at somewhat lower temperatures than the liquidification peak which is typical for solidification processes because of supercooling. After having extrapolated the heating rate to 0 K min−1 applying the same procedure as mentioned above we determined the melting temperature to be 28.43 °C.
3 obtained from vapour pressure measurements. The cooling curve exhibits the solidification peak at somewhat lower temperatures than the liquidification peak which is typical for solidification processes because of supercooling. After having extrapolated the heating rate to 0 K min−1 applying the same procedure as mentioned above we determined the melting temperature to be 28.43 °C.
The melting temperature determined also agrees well to what was published by other groups.3,56 Regarding the decomposition temperature, however, there are values obtained from chemical vapour deposition experiments reported (also listed in Table 4) that strongly deviate from each other, but no value from a direct thermal analysis is available. Since the values obtained by CVD are inconsistent and the exact knowledge of the decomposition temperature and decomposition enthalpy are a prerequisite for the investigation of the whole decomposition process, we determined precisely the decomposition temperature as well as the decomposition heat similarly as it was done for Zr(BH4)4 in another measurement (see upper part of Fig. 2) from our DSC measurement. Analogously to Zr(BH4)4, the irreversible decomposition occurred in the liquid phase resulting in a very broad signal (Tdec,onset = 136.44 °C and ΔdecU = 76.24 kJ mol−1). Looking at the shape of the signal, it seems that the decomposition occurs in a multi-step process, presumable just in a two-step one. Further discussion and evaluation is presented in the next section.
Table 4 serves as a summary of all so far reported melting and decomposition temperatures.
Investigation of the decomposition behaviour and the decomposition products using TG-DSC-MS and P-XRD
After the DSC experiment the remaining materials were removed from the crucibles under inert conditions providing a coarse black powder in both cases, the Zr(BH4)4 and the Hf(BH4)4 one. In the following X-ray powder diffraction measurements we did not observe any sharp reflections that could have been clearly assigned to a reference pattern (see Fig. 3).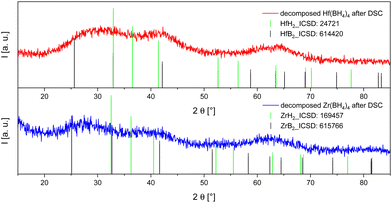 | ||
| Fig. 3 P-XRD results of the decomposed samples of the DSC measurements (Zr: bottom, blue; Hf: top, red). The given reflections (metal borides: black; metal hydrides: green) were taken from the ICSD.63 | ||
SEM-EDX investigations were carried out after combining the sets of all Zr and of all Hf containing samples each to one sample. The joint Zr sample displays a much coarser morphology than the Hf one showing almost spherical particles giving the appearance that the material has undergone a melting process supporting the conclusion from the DSC measurement that the decomposition occurred from the melt. Although the DSC measurement indicates a decomposition from the melt as well, the morphology of the material in the joint Hf sample does not support this interpretation in the same way the joint Zr sample does. The particles or agglomerates in the joint Hf sample are much smaller and are not of spherical or particularly roundish appearance (see ESI† Fig. S5). However, this result does not necessarily contradict the occurrence of the melting process because in contrast to a pure melting and recrystallisation process the material also underwent a decomposition reaction. There is a composition of about (85 ± 3) atom–% boron and (15 ± 3) atom–% Zr and (81 ± 3) atom–% boron and (19 ± 3) atom–% Hf, respectively. By assuming that the EDX analysis measures also a significant portion of the bulk phase (see Fig. S5, ESI†) and taking into account the error of the EDX investigation, the expected ratio of metal to boron of 1:4 can be seen as supported. The postulated decomposition processes of Zr(BH4)4 in the CVD process described by Sung et al.6 and during the DSC measurement in open crucibles described by Gennari et al.10 into ZrB2, B2H6 and H2 probably did not occur in our DSC measurement, because otherwise a metal to boron ratio of 1:2 would have been expected. Given that the pressure built up is the main difference between our DSC measurements and those using open crucibles or the CVD process, which were conducted at atmospheric pressure, we attributed this fact as the main factor for the observed differences. A significant difference between our experimentes and those of Gennari et al.10 is the generation of hydrogen as the sole gaseous product. Therefore, no boron gets lost by diborane emmission during the decomposition and is still available for a later rehydrogenation.
In order to investigate the decomposition product mixtures generated during the DSC measurements further, we performed TG-DSC-MS measurements in the temperature range between RT and 650 °C (see Fig. 4). The heat flow signal does not exhibit large values, which is typical for amorphous compounds. The increase in the TG signals towards the end of the experiments results from the oxidation of the compounds by traces of oxygen in the argon purge gas.
There is a mass loss accompanied by the desorption of hydrogen for both samples of approximately 1.4% and 0.9% for the Zr and Hf containing sample, respectively, but no release of diborane was observed. Furthermore, the powder X-ray diffractograms of the samples after the TG-DSC-MS experiments reveal the reflections of the respective metal diborides (see Fig. 5).
 | ||
| Fig. 5 Powder X-ray diffraction patterns of the decomposed MH2-B mixtures after the hydrogen desorption in the TG-DSC-MS measurements up to 650 °C. The reference patterns were taken from the ICSD.63 | ||
The consideration of the entirety of experimental results leads to the conclusion that the decomposition of the two boranates occurs in the same manner. Firstly, they decompose into hydrogen, the respective metal dihydrides and four equivalents of boron as reflected by reactions (8) and (9). Despite the decomposition into these assumed products no reflections of boron and the metal dihydrides are visible in the corresponding X-ray diffractograms, a phenomenon which is known from other boranates and their respective decomposition products, too.1 Furthermore, it is reported by Paskevicius et al.64 that boron can form stable amorphous B12-clusters that would not be detectable by X-ray diffraction. Secondly, the metal dihydrides react with two equivalents of boron during the TG-DSC-MS measurements releasing hydrogen (see Fig. 4) to produce the metal diborides. Reflections of the diborides have then been seen in the corresponding powder X-ray diffraction patterns (see Fig. 5). The amounts of hydrogen released fit well to the predicted theoretical values of about 1.5% and 0.9% resulting from the reactions (10) and (11), respectively. The remaining boron was not detected by P-XRD presumably because of the reasons given above.
| Zr(BH4)4 → ZrH2 + 4 B + 7 H2 | (8) |
| Hf(BH4)4 → HfH2 + 4 B + 7 H2 | (9) |
| ZrH2 + 4 B → ZrB2 + 2 B + H2 | (10) |
| HfH2 + 4 B → HfB2 + 2 B + H2 | (11) |
Fig. 6 gives a summary of observed and proposed decomposition processes.
 | ||
| Fig. 6 Proposed decomposition reactions of Zr(BH4)4 and Hf(BH4)4 using the mentioned techniques. The literature decomposition route reported by ref. 6 and 10 was not observed during our measurements. | ||
Assuming the reactions (8) and (9), it is possible to determine the decomposition enthalpy ΔdecH. For this purpose eqn (12) was employed using the measured reaction heats accompanying these processes (see Fig. 1 and 2).
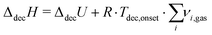 | (12) |
For Zr(BH4)4 and Hf(BH4)4 one obtains ΔdecH(403.42 K) = 80.4 kJ mol−1 and ΔdecH(409.58 K) = 100.1 kJ mol−1, respectively.
Heat capacity measurements
The heat capacity measurements of the two boranates were conducted in the temperature range from approximately 280 K to 310 K allowing to determine values regarding the solid and the liquid phase. At temperatures higher than about 310 K there have been leakage problems with the crucibles used. The compounds exhibit significant pre-melting effects, which can be seen exemplarily for Zr(BH4)4 in Fig. 7.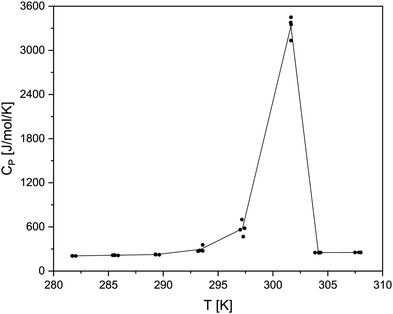 | ||
| Fig. 7 Graph of the measured CP values for Zr(BH4)4 in the temperature range from 280 to 310 K (black dots; black line is drawn to guide the readers eyes). | ||
The occurrence of such a pre-melting effect, i.e. the increase of the heat capacity prior to the actual melting, is a phenomenon also known for other systems.65 In regard to the determination of the heat capacities of the liquid and the solid phase close to the phase transition, this pre-melting effect has the consequence that only rather few data points can be seen as unaffected by the phase transition. Because of this behaviour only three data points for Zr(BH4)4 and four for Hf(BH4)4 are available for the solid phase. For the liquid phase only two data points are available for Zr(BH4)4 and only one for Hf(BH4)4. The obtained heat capacity values for both compounds in the temperature range between app. 280 to 310 K are listed in the ESI† in Table S1. For the fit of the CP values of the solid and the liquid phase, we used a linear function as stated in eqn (13).
| CP = A + B·T | (13) |
| Compound | T range [K] | A [J mol−1 K−1] | B [J mol−1 K−2] | FitStdErr |
|---|---|---|---|---|
| Zr(BH4)4 | 280 to 301 | −4.20· 102 | 2.23· 00 | 2.34·100 |
| 301 to 310 | 9.13· 101 | 5.24·10−1 | 144·100 | |
| Hf(BH4)4 | 280 to 301 | −4.72· 101 | 9.14· 10−1 | 2.14· 100 |
| 301 to 310 | 2.59· 102 | — | 9.03· 10−1 |
To obtain the thermodynamic values of the melting process, we extrapolated the solid and liquid heat capacity functions until the melting point. By integration of the area below the CP/T curve over the measured temperature range we calculated (41.67 ± 0.67) J mol−1 K−1 and (32.84 ± 1.05) J mol−1 K−1 as values of the melting entropies for Zr(BH4) and Hf(BH4)4, respectively. Multiplication of those values with the melting temperature leads to the melting enthalpy of (12.57 ± 0.20) kJ mol−1 for Zr(BH4)4, which is in good agreement with the before mentioned value of 13.25 kJ mol−1 from our DSC measurements. We strongly assume that the given value from Hoekstra and Katz3 of about 18 kJ mol−1 is rather erroneous because of the determination via vapour pressure measurements at low pressures. For Hf(BH4)4 we obtained (9.92 ± 0.30) kJ mol−1 for the melting enthalpy, which is lower than the value from the DSC measurement (13.49 kJ mol−1). The latter fits better to the literature one of 14.24 kJ mol−1 provided by Hoekstra and Katz.3 Probably, the ΔFS value derived from the CP measurements is smaller because of the fact that only one CP value from the liquid phase was useable causing a large uncertainty in the integration of the CP/T curve (see our CP measurement of Hf(BH4)4 in Fig. S7, ESI†).
Enthalpy of formation
Given that the decomposition of the investigated boranates proceeds according to reactions (8) and (9), the calculation of the enthalpy of formation ΔFH(298.15 K) becomes possible. The thermodynamic data needed for the calculations were taken from the HSC 5.1 database (H2, B, ZrB2)66 and FactSage 7.1 (HfB2).67 For the determination of ΔFH(298.15 K) nearly all parameters and quantities measured so far for both compounds (Tm, ΔmH, CP, Tdec, ΔdecH) are needed. Applying Kirchhoff's law to the reactions (8) and (9) one obtains for the enthalpies of formation ΔFH(298.15 K) = −260.6 kJ mol−1 for Zr(BH4)4 and ΔFH(298.15 K) = −228.0 kJ mol−1 for Hf(BH4)4. Nakamori et al.32,33 developed a way to estimate the enthalpy of formation of boranates by exploiting the correlation between the Pauling electronegativity and this quantity. Utilising his correlation function, the value of ΔFH(298.15 K) = −240.1 kJ mol−1 for Zr(BH4)4 and ΔFH(298.15 K) = −270.0 kJ mol−1 for Hf(BH4)4 can be predicted. The values obtained by the same estimation method by Miwa et al.68 and Sato et al.69 are similar, whereas the values from Callini et al.70 deviate with −368.8 kJ mol−1 for Zr(BH4)4 and −398.3 kJ mol−1 for Hf(BH4)4 very strongly from our data and those derived from the work of the other authors. It is important to note that the ΔFH(298.15 K) values for the reference boranates to establish such correlation functions used by Nakamori and the other authors were determined by DFT. In conclusion, there are quite large differences for both compounds between the experimental values and the predicted ones. The large variation of the predictions stresses the need for independently obtained experimental results.Standard entropy via DFT
Regrettably, the entropy of decomposition could not be calculated using the measured decomposition enthalpy at the corresponding decomposition temperature because a scanning measurement is not a suitable method to determine equilibrium values. To compensate for that, DFT was used to obtain the standard entropies of both compounds based on their calculated phonon densities of states using the Quantum ESPRESSO code.49–51For the two systems in question, Zr(BH4)4 and Hf(BH4)4, initial crystal structures were obtained via the previously described in situ single crystal XRD measurements. On these initial structures, convergence tests with respect to the kinetic energy cutoff of the wave function, the kinetic energy cutoff of the density and the integration grid in reciprocal space were conducted and the values for these three parameters were chosen so that any further increase would lead to a total energy difference of less than 1 meV atom−1. Afterwards, the initial structures were relaxed in terms of both the nuclear positions and the cell parameters until the nuclear forces were below 0.1 mRy Bohr−1 and the pressure on the cell was below 0.1 kbar. Then, the optimised unit cells were volume scaled in the range of 95% to 110% of the optimised volume. For each member in this series of volumes, the nuclear positions were relaxed again according to the force convergence tolerance given detailed above, keeping the volume fixed. As a next step, the total energy and the phonon density of states were evaluated for the series of volumes. In this procedure, the vibrational frequencies were determined for a 3 × 3 × 3 grid in reciprocal space; the results for this grid were later Fourier interpolated to a 20 × 20 × 20 grid. For each point in the 3 × 3 × 3 grid, the vibrational frequencies were calculated according to density functional perturbation theory.71–73 With all phonon calculations finished and the phonon density of states available for each of the volumes, the Gibbs energy of Zr(BH4)4 and Hf(BH4)4 and its first temperature derivative were evaluated for a pressure of 1 bar and a temperature of 298.15 K according to the quasi-harmonic approximation. The standard entropy was calculated as the negative of the first temperature derivative, yielding S°(Zr(BH4)4) = 228.4 J mol−1 K−1 and S°(Hf(BH4)4) = 212.7 J mol−1 K−1.
To give more reliability to our DFT calculations, the standard entropy for LiBH4 at 298.15 K in its room temperature polymorph (orthorhombic according to ICSD number 23976374) was calculated under the same conditions, as mentioned for Zr(BH4)4 and Hf(BH4)4. The calculation gives a value of SDFT(298.15 K) = 71.5 J mol−1 K−1, which is in good agreement with the experimental value of Sexp(298.15 K) = 75.8 J mol−1 K−1.66
Optimisation of the values based on the CalPhaD method
All of our obtained data (reaction enthalpies, specific heats, calculated entropies, enthalpies of fusion) and vapour pressure values3 formed the basis for the optimisation via CalPhaD. The optimisation was carried out with the ChemSage 4.375 and FactSage 7.167 software. The optimised thermodynamic data are presented in Table 6.| Zr(BH4)4 | Hf(BH4)4 | |
|---|---|---|
| ΔFHs°(298.15 K) [kJ mol−1] | −260.6 | −228.0 |
| ΔFHl°(298.15 K) [kJ mol−1] | −248.0 | −218.1 |
| ΔFHg°(298.15 K) [kJ mol−1] | −211.6 | −177.8 |
| S S°(298.15 K) [J mol−1 K−1] | 228.4 | 212.7 |
| S l°(298.15 K) [J mol−1 K−1] | 270.1 | 245.4 |
| S g°(298.15 K) [J mol−1 K−1] | 374.8 | 348.7 |
| T m [°C] | 28.8 | 28.9 |
| ΔmH(Tm) [kJ mol−1] | 12.6 | 10.0 |
| ΔmS(Zm) [J mol−1 K−1] | 41.7 | 33.3 |
| T v [°C] | 124.4 | 123.2 |
| ΔvH(Tv) [kJ mol−1] | 35.7 | 36.6 |
| ΔvS(Tv) [J mol−1 K−1] | 89.7 | 92.3 |
| T dec [°C] | 130.4 | 136.4 |
| ΔdecH°(Tdec) [kJ mol−1] | 80.4 | 99.5 |
Furthermore, the values of the entropy of vaporisation at the boiling points (89.7 J mol−1 K for Zr(BH4)4 and 92.3 J mol−1 K−1 for Hf(BH4)4) correspond very well to what would be expected applying Trouton-Pictet's rule (ΔvS(Tv) ≈ 88 J mol−1 K−1 to 90 J mol−1 K−1).76 It can therefore be assumed that the liquid boranates do not form associates.
With these data the vapour pressures of both compounds were calculated using DD in the manner as given in eqn (15).
 | (14) |
 | (15) |
ΔTG°: free Gibbs energy of phase transition
p ν,eq: vapour pressure (vaporisation or sublimation)
p°: standard pressure, 1 bar
For comparison reasons, the vapour pressure data published by Hoekstra and Katz3 and those calculated based on our optimised thermodynamic values are both displayed in Fig. 8 for Zr(BH4)4 and in Fig. S8 in the ESI† for Hf(BH4)4.
 | ||
| Fig. 8 Comparison between the measured vapour pressure values of Hoekstra and Katz3 (dots) and our calculated ones (lines) for Zr(BH4)4 (sublimation: black; vaporisation: red). | ||
The calculated vapour pressure values using our optimised data are in good agreement with the experimental ones from Hoekstra and Katz3 and therefore the optimisation was successful.
Conclusions
We synthesised Zr(BH4)4 and Hf(BH4)4via solid state metathesis and determined their crystal structures slightly below their melting temperatures. With the low temperature structure data it was possible to calculate the cubic expansion coefficient which is in the order of magnitude of polymers. This fact underlines the soft character of these boranates as molecular crystals. Furthermore, their melting and decomposition behaviour from the liquid phase and the related enthalpy values were ascertained applying (TG-) DSC measurements. In combination with the measured heat capacity values of both the solid and liquid phases we determined the enthalpies of formation (ΔFH°(298.15 K) = −260.59 kJ mol−1 for Zr(BH4)4 and ΔFH°(298.15 K) = −227.99 J mol−1 K−1 for Hf(BH4)4). In regard to establish absolute entropy values, however, using a PPMS instrument it was not possible to perform low temperature calorimetry measurements because of the high volatility of the compounds and the high vaccum needed in such experiments. Therefore, no experimental determination of the standard entropy was possible and was therefore replaced by DFT calculations (S°(298.15 K) = 228.4 J mol−1 for Zr(BH4)4 and S°(298.15 K) = 212.7 J mol−1 K−1 for Hf(BH4)4). Furthermore, we shed some light on the decomposition mechanism by correlating results from P-XRD, TG-DSC-MS and SEM-EDX investigations. Our results show the formation of MH2 (M = Zr, Hf) as a first step contrary to other studies in the literature suggesting the decomposition into the diborides. This difference must be due to kinetic barriers for the formation of borides at these low temperatures.Although both boranates cannot be used as hydrogen storage materials because of their high vapour pressure and the high stability of the decomposition products (which is supported by calculations regarding their decomposition behaviour presented in the electronic supplementary information), there is still the possibility of using them as catalyst precursors for reversible hydrogen storage in other complex hydride systems. The availability of additional thermodynamic data will help to estimate those (enthalpy of formation, entropies) of new boranates by the use of correlation functions.
Author contributions
K. Burkmann – investigation, validation, visualisation, writing – original draft. F. Habermann – validation, visualisation, writing – review & editing. E. Schumann – investigation, visualisation, writing – original draft. J. Kraus – formal analysis, writing – original draft. B. Störr – investigation, writing – review & editing. H. Schmidt – investigation, visualisation, resources, writing – original draft. E. Brendler – investigation, resources, writing – review & editing. J. Seidel – validation, writing – review & editing. K. Bohmhammel – formal analysis, validation, writing – review & editing. J. Kortus – resources, writing – review & editing. F. Mertens – conceptualisation, funding acquisition, resources, supervision, writing – review & editingConflicts of interest
There are no conflicts to declare.Acknowledgements
The reported research activities have been financially supported by the Free State of Saxony (K. Burkmann, Landesstipendium zur Graduiertenförderung). We also thank the Deutsche Forschungsgemeinschaft (DFG) for financial support (Project ID 449160425). The authors would like to thank Dr. Lesia Sandig-Predzymirska for translating several Russian-language papers. Furthermore, the authors would like to thank Dr. M. Gerwig for the help with the preparation of the samples for the single crystal XRD measurements, Dr. J. Wagler for the help with the preparation of NMR samples, Dr. I. Paschke for several powder XRD measurements, Prof. Dr. R. Gumeniuk and Dr. M. Schwarz for numerous discussions for manufacturing of sample crucibles and A. Obst for the SEM-EDX measurements. Additionally, the authors would like to thank the URZ in Freiberg for computational time and support. The computations at the URZ were performed on the compute cluster of the Faculty of Mathematics and Computer Science of the Technische Universität Bergakademie Freiberg; this cluster is funded by the DFG - Project ID 397252409.Notes and references
- K. Suárez-Alcántara and J. R. Tena García, Materials, 2021, 14, 2561–2616 CrossRef PubMed.
- F. Habermann, K. Burkmann, B. Hansel, B. Störr, C. Schimpf, J. Seidel, M. Bertau and F. Mertens, Dalton Trans., 2023, 52, 4880–4890 RSC.
- H. R. Hoekstra and J. J. Katz, J. Am. Chem. Soc., 1949, 71, 2488–2492 CrossRef CAS.
- G. W. Rice and R. L. Woodin, J. Am. Chem. Soc., 1988, 71, 181–183 Search PubMed.
- A. L. Wayda, L. F. Schneemeyer and R. L. Opila, Appl. Phys. Lett., 1988, 53, 361–363 CrossRef CAS.
- J. Sung, D. M. Goedde, G. S. Girolami and J. R. Abelson, J. Appl. Phys., 2002, 91, 3904–3911 CrossRef CAS.
- Y. Yang, S. Jayaraman, D. Y. Kim, G. S. Girolami and J. R. Abelson, Chem. Mater., 2006, 18, 5088–5096 CrossRef CAS.
- S. Jayaraman, Y. Yang, D. Y. Kim, G. S. Girolami and J. R. Abelson, J. Vac. Sci. Technol., A, 2005, 23, 1619–1625 CrossRef CAS.
- S. Jayaraman, J. E. Gerbi, Y. Yang, D. Y. Kim, A. Chatterjee, P. Bellon, G. S. Girolami, J. P. Chevalier and J. R. Abelson, Surf. Coat. Technol., 2006, 200, 6629–6633 CrossRef CAS.
- F. C. Gennari, L. Fernández Albanesi and I. J. Rios, Inorg. Chim. Acta, 2009, 362, 3731–3737 CrossRef CAS.
- G. A. Nesterov, V. A. Zakharov, V. V. Volkov and K. G. Myakishev, J. Mol. Catal., 1986, 36, 253–269 CrossRef CAS.
- J. J. Vajo, F. Mertens, C. C. Ahn, R. C. Bowman and B. Fultz, J. Phys. Chem. B, 2004, 108, 13977–13983 CrossRef CAS.
- J. J. Vajo, S. L. Skeith and F. Mertens, J. Phys. Chem. B, 2005, 109, 3719–3722 CrossRef CAS PubMed.
- M. Dornheim, S. Doppiu, G. Barkhordarian, U. Boesenberg, T. Klassen, O. Gutfleisch and R. Bormann, Scr. Mater., 2007, 56, 841–846 CrossRef CAS.
- U. Bösenberg, S. Doppiu, L. Mosegaard, G. Barkhordarian, N. Eigen, A. Borgschulte, T. R. Jensen, Y. Cerenius, O. Gutfleisch, T. Klassen, M. Dornheim and R. Bormann, Acta Mater., 2007, 55, 3951–3958 CrossRef.
- Y. Suttisawat, P. Rangsunvigit, B. Kitiyanan, N. Muangsin and S. Kulprathipanja, Int. J. Hydrogen Energy, 2007, 32, 1277–1285 CrossRef CAS.
- B. D. James and B. E. Smith, Synth. React. Inorg. Met.-Org. Chem., 1974, 4, 461–465 CrossRef CAS.
- B. G. Sayer, J. I. A. Thompson, N. Hao, T. Birchall, D. R. Eaton and M. J. McGlinchey, Inorg. Chem., 1981, 20, 3748–3750 CrossRef CAS.
- B. E. Smith, H. F. Shurvell and B. D. James, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 710 Search PubMed.
- R. W. Broach, I. S. Chuang, T. J. Marks and J. M. Williams, Inorg. Chem., 1983, 22, 1081–1084 CrossRef CAS.
- W. E. Reid, J. M. Bish and A. Brenner, J. Electrochem. Soc., 1957, 104, 21–29 CrossRef CAS.
- R. H. Banks and N. Edelstein, J. Chem. Phys., 1980, 73, 3589–3599 CrossRef CAS.
- B. D. James, R. K. Nanda and M. G. H. Wallbridge, J. Chem. Soc. A, 1966, 182–184 RSC.
- N. Davies, D. Saunders and M. G. H. Wallbridge, J. Chem. Soc. A, 1970, 2915–2917 RSC.
- T. J. Marks and L. A. Shimp, J. Am. Chem. Soc., 1972, 94, 1542–1550 CrossRef CAS.
- E. R. Bernstein and T. A. Keiderling, J. Chem. Phys., 1973, 59, 2105–2122 CrossRef.
- N. Davies, M. G. H. Wallbridge, B. E. Smith and B. D. James, Phys. Rev. B: Solid State, 1973, 162–165 CAS.
- T. A. Keiderling and W. C. Schulz, Chem. Phys. Lett., 1980, 71, 123–126 CrossRef CAS.
- A. Haaland, D. J. Shorokhov, A. V. Tutukin, H. V. Volden, O. Swang, G. S. McGrady, N. Kaltsoyannis, A. J. Downs, C. Y. Tang and J. F. C. Turner, Inorg. Chem., 2002, 41, 6646–6655 CrossRef CAS PubMed.
- J. C. Green, M. de Simone, M. Coreno, A. Jones, H. M. I. Pritchard and G. S. McGrady, Inorg. Chem., 2005, 44, 7781–7793 CrossRef CAS PubMed.
- L. H. Rude, M. Corno, P. Ugliengo, M. Baricco, Y.-S. Lee, Y. W. Cho, F. Besenbacher, J. Overgaard and T. R. Jensen, J. Phys. Chem. C, 2012, 116, 20239–20245 CrossRef CAS.
- Y. Nakamori, K. Miwa, A. Ninomiya, H. Li, N. Ohba, S.-I. Towata, A. Züttel and S.-I. Orimo, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 045126 CrossRef.
- Y. Nakamori, H.-W. Li, M. Matsuo, K. Miwa, S. Towata and S. Orimo, J. Phys. Chem. Solids, 2008, 69, 2292–2296 CrossRef CAS.
- V. V. Volkov and K. G. Myakishev, Inorg. Chim. Acta, 1999, 289, 51–57 CrossRef CAS.
- U. Böhme, Inertgastechnik, De Gruyter, Oldenbourg, 2020 Search PubMed.
- D. F. Shriver and M. A. Drezdzon, The manipulation of air-sensitive compounds, Wiley, New York, NY, 2nd edn, 1986 Search PubMed.
- U. Böhme and K.-H. Thiele, Z. Anorg. Allg. Chem., 1994, 620, 1455–1462 CrossRef.
- M. Gerwig, U. Böhme, M. Friebel, F. Gründler, G. Franze, M. Rosenkranz, H. Schmidt and E. Kroke, ChemistryOpen, 2020, 9, 762–773 CrossRef CAS PubMed.
- D. Thomas, M. Abdel-Hafiez, T. Gruber, R. Hüttl, J. Seidel, A. U. Wolter, B. Büchner, J. Kortus and F. Mertens, J. Chem. Thermodyn., 2013, 64, 205–225 CrossRef CAS.
- D. Thomas, M. Zeilinger, D. Gruner, R. Hüttl, J. Seidel, A. U. Wolter, T. F. Fässler and F. Mertens, J. Chem. Thermodyn., 2015, 85, 178–190 CrossRef CAS.
- S. Loos, D. Gruner, M. Abdel-Hafiez, J. Seidel, R. Hüttl, A. U. Wolter, K. Bohmhammel and F. Mertens, J. Chem. Thermodyn., 2015, 85, 77–85 CrossRef CAS.
- F. Taubert, S. Schwalbe, J. Seidel, R. Hüttl, T. Gruber, R. Janot, M. Bobnar, R. Gumeniuk, F. Mertens and J. Kortus, Int. J. Mater. Res., 2017, 108, 942–958 CAS.
- F. Taubert, J. Seidel, R. Hüttl, M. Bobnar, R. Gumeniuk and F. Mertens, J. Chem. Thermodyn., 2018, 116, 323–329 CrossRef CAS.
- F. Taubert, J. Seidel, R. Hüttl, M. Bobnar, R. Gumeniuk and F. Mertens, J. Chem. Thermodyn., 2019, 130, 119–128 CrossRef CAS.
- K. Burkmann, B. Hansel, F. Habermann, B. Störr, M. Bertau and F. Mertens, Z. Naturforsch. B, 2023, 78, 575–578 CrossRef CAS.
- G. Della Gatta, M. J. Richardson, S. M. Sarge and S. Stølen, Pure Appl. Chem., 2006, 78, 1455–1476 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter., 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Boungiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio Jr, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Kücükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otera-de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter., 2017, 29, 465901 CrossRef CAS PubMed.
- P. Giannozzi, O. Baseggio, P. Bonfà, D. Brunato, R. Car, I. Carnimeo, C. Cavazzoni, S. de Gironcoli, P. Delugas, F. F. Ruffino, A. Ferretti, N. Marzari, I. Timrov, A. Urru and S. Baroni, J. Chem. Phys., 2020, 152, 154105 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- A. D. Corso, Comput. Mater. Sci., 2014, 95, 337–350 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. Nöth and B. Wrackmeyer, Nuclear Magnetic Resonance Spectroscopy of Boron Compounds, Springer, Berlin and Heidelberg, 1978, vol. 14 Search PubMed.
- M. Ehemann and H. Nöth, Z. Anorg. Allg. Chem., 1971, 386, 87–101 CrossRef CAS.
- Z. Odziana, P. Blonski, Y. Yan, D. Rentsch and A. Remhof, J. Phys. Chem. C, 2014, 118, 6594–6603 CrossRef.
- T. Parella, eNMR: NMR Periodic Table, 2003, https://triton.iqfr.csic.es/guide/eNMR/chem/NMRnuclei.html Search PubMed.
- P. Coppens, in Crystallographic computing, ed. F. R. Ahmed, S. R. Hall and C. P. Huber, Munksgaard, Copenhagen, 1970, pp. 255–270 Search PubMed.
- A. M. Igoshkin, I. F. Golovnev, V. V. Krisyuk and I. K. Igumenov, J. Struct. Chem., 2016, 57, 1068–1073 CrossRef CAS.
- G. Grimvall, Thermophysical properties of materials, Elsevier, Amsterdam, 1st edn, 1999 Search PubMed.
- CRC Handbook of chemistry and physics, ed. W. M. Haynes, CRC Press, Boca Raton and London and New York, 97th edn, 2017 Search PubMed.
- G. Bergerhoff and I. D. Brown, in Crystallographic Databases, ed. F. H. Allenet al., International Union of Crystallography, Chester, 1987 Search PubMed.
- M. Paskevicius, L. H. Jepsen, P. Schouwink, R. Cerný, D. B. Ravnsbæk, Y. Filinchuk, M. Dornheim, F. Besenbacher and T. R. Jensen, Chem. Soc. Rev., 2017, 46, 1565–1634 RSC.
- J. Acker, S. Köther, K. M. Lewis and K. Bohmhammel, Silicon Chem., 2003, 2, 195–206 CrossRef CAS.
- A. Roine, HSC Chem., 2002 Search PubMed.
- C. W. Bale, E. Bélisle, P. Chartrand, S. A. Decterov, G. Eriksson, A. E. Gheribi, K. Hack, I. H. Jung, Y. B. Kang, J. Melançon, A. D. Pelton, S. Petersen, C. Robelin, J. Sangster, P. Spencer and M. A. van Ende, Calphad, 2016, 54, 35–53 CrossRef CAS.
- K. Miwa, N. Ohba, S.-I. Towata, Y. Nakamori, A. Züttel and S.-I. Orimo, J. Alloys Compd., 2007, 446–447, 310–314 CrossRef CAS.
- T. Sato, K. Miwa, Y. Nakamori, K. Ohoyama, H.-W. Li, T. Noritake, M. Aoki, S.-I. Towata and S.-I. Orimo, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 1041141 Search PubMed.
- E. Callini, Z. Ö. K. Atakli, B. C. Hauback, S.-I. Orimo, C. Jensen, M. Dornheim, D. Grant, Y. W. Cho, P. Chen, B. Hjörvarsson, P. de Jongh, C. Weidenthaler, M. Baricco, M. Paskevicius, T. R. Jensen, M. E. Bowden, T. S. Autrey and A. Züttel, Appl. Phys. A: Mater. Sci. Process., 2016, 122, 353–375 CrossRef.
- S. Baroni, P. Giannozzi and A. Testa, Phys. Rev. Lett., 1987, 59, 2662–2665 CrossRef PubMed.
- S. Y. Savrasov, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16470–16486 CrossRef CAS PubMed.
- X. Gonze and C. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10355–10368 CrossRef CAS.
- E. Roedern, Y.-S. Lee, M. B. Ley, K. Park, Y. W. Cho, J. Skibsted and T. R. Jensen, J. Mater. Chem. A, 2016, 4, 8793–8802 RSC.
- G. Eriksson, K. Hack, M. Philipps and C. Fullerton-Batten, Chemsage - Gibbs Energy Minimizer and Optimazation Routine, database.
- G. Wedler, Lehrbuch der Physikalischen Chemie, Wiley-VCH, Weinheim, 5th edn, 2004 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2173083 and 2173084. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3nj05601e |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2024 |