Direct observation of split-mode exciton-polaritons in a single MoS₂ nanotube

Abstract

A single nanotube synthesized from a transition metal dichalcogenide (TMDC) exhibits strong exciton resonances and, in addition, can support optical whispering gallery modes. This combination is promising for observing exciton-polaritons without an external cavity. However, traditional energy-momentum-resolved detection methods are unsuitable for this tiny object. Instead, we propose to use split optical modes in a twisted nanotube with the flattened cross-section, where a gradually decreasing gap between the opposite walls leads to a change in mode energy, similar to the effect of the barrier width on the eigenenergies in the double-well potential. Using micro-reflectance spectroscopy, we investigated the rich pattern of polariton branches in single MoS₂ tubes with both variable and constant gaps. Observed Rabi splitting in the 40–60 meV range is comparable to that for a MoS₂ monolayer in a microcavity. Our results, based on the polariton dispersion measurements and polariton dynamics analysis, present a single TMDC nanotube as a perfect polaritonic structure for nanophotonics.

---

New concepts

We present the discovery of exciton-polaritons in flattened nanotubes of transition metal dichalcogenides (TMDC). These structures exhibit strong exciton resonances and can support whispering gallery modes in the nanotube wall. A flattened cross-section with gradually decreasing gap between opposite walls splits doubly degenerate whispering gallery modes into two optical modes of different symmetry and leads to a significant change in their energies. As the split mode approaches the exciton resonance, the formation of an exciton-polariton occurs in the strong coupling mode, which is confirmed by the anticrossing of polariton branches with Rabi splitting. This new approach provides an optical-mechanical method to control the interaction of excitonic resonances with an array of whispering gallery modes within a tube, in contrast to traditional energy-momentum-resolved detection methods. The use of micro-reflection spectroscopy allows demonstration of the rich pattern of polariton branches in a single MoS₂ nanotube with a variable gap between the walls and discovery of the dispersionless polaritons with stable energy in a nanotube with a constant gap in an unchanged but flattened cross-section. Obtained results and agreement with theoretical and numerical calculations confirm the possibility of producing polaritons in the strong coupling regime in flattened nanotubes, making them promising candidates for nanophotonics.

1 Introduction

Transition metal dichalcogenides (TMDCs), such as MoX₂ and WX₂ (X = S, Se), have high binding energy and giant oscillator strength of direct A and B excitons in both atomically thin and multilayer structures.^1,2 This leads to a strong interaction between light and matter, resulting in the formation of an exciton-polariton (or polariton for short). The polariton, that is, a quantum superposition of an exciton and a photon mode, was observed in many semiconductor systems, being of practical importance for nanophotonics (threshold-less lasers³) and for quantum technologies (computing and simulators^4,5). Of greatest interest are polaritons in microcavities, where excitons interact with the strongly confined electromagnetic field,^6–8 which increases the interaction energy and makes it greater than the broadening of the bare modes. This situation, called the strong coupling regime, manifests itself as an anticrossing of the upper and lower polariton branches (UPB and LPB, respectively) in the dependence of the eigenenergies on the detuning between the exciton and cavity modes.⁹ The Rabi splitting ħΩ_R = 2g characterizes the frequency of oscillation between the photon and exciton states, where g is a coupling strength.

A quasi-two-dimensional (2D) polariton is characteristic of a quantum well in a microcavity.¹⁰ Its extreme case is the polariton formed when a TMDC monolayer is placed into an external resonator.^11–16 All studies of 2D polaritons have exploited the ability to tune the cavity mode energy either by varying the cavity length or by changing its in-plane wave vector k ≈ (ω/c)sin(θ), that is controlled by detection angle θ.^17,18 For example, angle-resolved reflectivity spectroscopy revealed the strong coupling with the Rabi splitting of ∼46 meV in MoS₂ monolayer inside the Bragg microcavity.¹¹ Similar research of both reflection and photoluminescence (PL) demonstrated a strong coupling in WSe₂ and WS₂ monolayers in photonic crystals.¹⁴ Changing the cavity length in the open microcavity made it possible to observe polaritons with the Rabi splitting ∼20 meV in MoSe₂ monolayers¹² and ∼70 meV in WS₂ monolayers.¹³

TMDC nanotubes (NTs) were synthesized shortly after carbon NTs¹⁹ in the early 1990s.²⁰ They are usually multi-walled, have a length from hundreds of nanometers to several millimeters and a characteristic diameter from tens of nanometers to several micrometers.^21,22 We will use the same designation “NT” for both micro- and nanotubes. Tube shapes can vary from perfectly cylindrical to almost ribbon-like, depending on the internal tensile stresses.^23,24 In twisted tubes, in addition, the flattened cross-section rotates along the tube axis.²⁵ Multi-walled NTs have an indirect band structure; however, resonances of direct excitons are observed up to room temperatures due to their giant oscillator strength and high recombination rate.^26,27 While individual monolayers are unstable under ambient conditions and must be protected by hBN,²⁸ monolayers scrolled in NT are naturally protected by outer layers.

Recently, many interesting phenomena have been discovered in NTs that are promising for wide application.^25,29 Among them is the specific confinement of electromagnetic fields in NTs, leading to the appearance of whispering gallery modes (WGMs), the peaks of which modulate the emission spectra.³⁰ The coexistence of strong direct excitons and pronounced optical modes is very promising for the creation of polaritons in the strong coupling regime without an external cavity. However, the application of the described above detection methods with energy-momentum resolution to NTs seems to be very problematic. Providing a non-zero wave vector k along the NT axis by changing the angle of incidence can hardly be combined with precise focusing on a single NT, especially in cryogenic measurements. It is also impossible to tune the optical mode energy by gradually reducing the diameter of the tube, as it is done for nanowires,³¹ since in conventional synthesized cylindrical NTs the cross-section is constant over a length of more than 50 μm.³²

A reasonable solution seemed to be to observe the dispersion of polaritons by an indirect method from extinction spectra measured in ensembles of NTs of different diameters in the range 36–110 nm, separated by centrifugation.³³ However, the fact that strong coupling can only be realized when the NT diameter exceeds 80 nm³⁴ limits the capabilities of this method. Indisputable proof of the existence of exciton-polaritons would be their direct observation by reflectivity in a single NT, which is still missing.

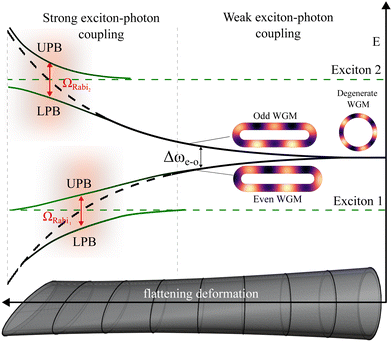
To carry out such an experiment, we propose a new concept that exploits a recently discovered phenomenon, namely, the splitting of optical modes in a NT with a flattened cross-section that features a gradual decrease in the gap between opposite walls along the NT.³⁵Fig. 1 illustrates the principle of split-mode polariton formation. In a cylindrical NT, the WGM is doubly degenerate and has energy of ħω₀. As the minor axis b of the NT cross-section decreases, the gap between the walls also decreases and the evanescent tails of the electric fields begin to overlap. By analogy with the electron states in the double-well potential,³⁶ this leads to the splitting of the WGM into two non-degenerate even and odd modes, which are symmetric and antisymmetric with respect to the major axis. Their energies read ħω_e,o = ħω₀(1 ± t_WGM), where the odd mode has higher energy. Note that the splitting increases exponentially as t_WGM ∝ e^−κ_rb, where κ_r is the decay constant of the evanescent tails (see ESI† for details). When an odd or even mode approaches the exciton resonance, in the case of strong coupling, an exciton-polariton is formed and Rabi splitting of UPB and LPB is observed.

Fig. 1 Split-mode exciton-polaritons. A doubly degenerate WGM in a cylindrical tube, as the gap between the tube walls decreases, splits into even and odd modes. When the mode reaches exciton resonance, UPB and LPB are formed, exhibiting anticrossing with Rabi splitting. Black dashed lines show optical modes without interaction with excitons.

This work presents studies of split-mode polaritons in a single MoS₂ NT using micro-reflectance and micro-PL spectroscopy. It is shown that the energy of the split mode can vary over a wide range in a tube with a variable gap between the walls, which makes it possible to observe the transformation of purely optical modes into polariton branches demonstrating distinct anticrossing. On the contrary, dispersionless polaritons with stable energies are observed in NTs with a constant gap. In both cases, we register close Rabi splitting values of ∼40 meV for A-exciton-polariton and ∼60 meV for B-exciton-polariton. The observed PL dynamics is consistent with the formation of polaritons.

2 Results

2.1 Variable wall-gap nanotube

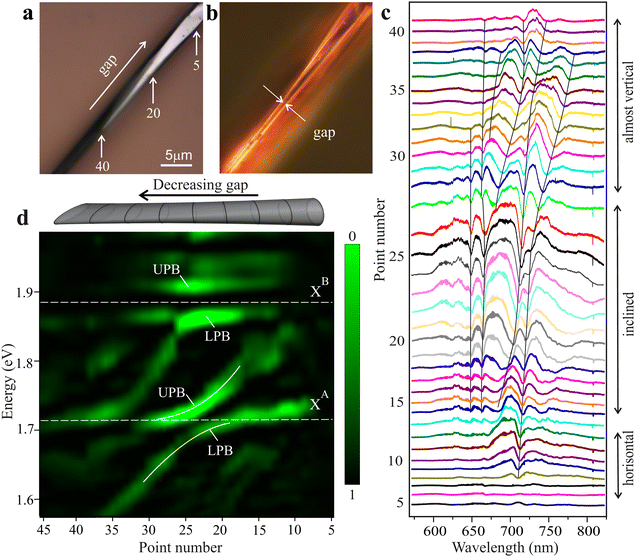
For the experimental study, we selected a twisted MoS₂ NT with a total length of about one hundred microns, synthesized by a chemical vapor transfer reaction using iodine as a transport agent.²⁵ A common property of multi-walled NTs is internal tensile strain, which arises due to the fact that each subsequent layer must be stretched relative to the previous one in order to maintain the crystalline structure. The tensile strain promotes flattening of the cross-section and, in addition, reduces the band gap due to the modification of the band structure,³⁷ as occurs in atomically-thin layers when the conduction band minimum shifts downward.^38–41 Using Raman studies (see the ESI†), we estimated the tensile strain values in the NT to be ≥1%, resulting in a red shift of A exciton towards 1.72–1.75 eV with B exciton being ∼140 meV higher in energy. New strain-induced positions of excitons in NTs are about 100 meV lower than in unstrained flakes obtained in the same synthesis process.²⁷ In different regions, the NT has a different degree of strain which leads to different flattening and rotation of the cross-section, as well as to some change in the exciton energy. The cross-section circumference remains constant along the NT.

Optical images of a part of the NT with a variable gap between the walls, shown in Fig. 2(a and b), were obtained in different registration modes: (a) bright-field, when light scattered perpendicularly from the surface is recorded; (b) dark-field with cross-polarization, when light scattered by inclined surfaces is recorded. The bright-field image shows the rotation of the cross-section along the NT, whereas the dark-field image shows a gradual decrease in the gap between the opposite walls of the NT. It takes place as the detection point number increases. At the narrowest point, the gap is comparable to the thickness of the tube walls of 50–100 nm.

Fig. 2 Bright-field (a) and cross-polarized dark-field (b) images of the NT with the variable gap between walls. Below them is a schematic image of a NT with the direction of gap reduction marked. (c) Raw reflectance spectra taken in different points along the NT (shifted vertically for clearness). (d) Map of the processed reflection spectra, where the bright green stripes represent the main dips in reflection. The dashed lines indicate an average energy of excitons A and B. The LPB and UPB are marked for both exciton-polariton. The numbering of the measurement points in (c) and (d) is the same as in (a).

Fig. 2 shows selected original (c) and processed (d) reflectance spectra measured along the NT axis as described in the Methods section, with a distance between the adjacent points of 1–1.5 μm. In Fig. 2(c), thin lines trace the main dips in the reflectance spectra. Based on the width of isolated peaks of optical modes, the quality factor of the NT cavity is estimated at approximately 500. Far from the exciton resonances, the dips are associated with the pure optical modes excited inside the NT walls. In the points no. 30–40, the modes (even, presumably) are observed up to the region of relative transparency (1.55 eV). The mode splitting is maximal here due to the narrowest gap. When the split modes are close to excitons in energy, which occurs in the inclined region (points no. 15–27), exciton-polaritons are formed. The reflectance in this region is approximately four times higher than in others. This is partly the result of strong exciton-photon coupling, and partly due to the dependence of the WGM mode brightness on the rotation angle of the NT cross-section.³⁵

To get a clearer picture of the mode transformation, we removed hardware interference and background noise from the reflection spectra. In the demo display shown in Fig. 2(d), green areas correspond to dips down to zero in the original reflectance spectra. A clear anticrossing of LPB and UPB is observed when one of the split modes approaches exciton A. The other mode creates anticrossing branches at exciton B. The UPB at exciton B is less pronounced due to high absorption in the spectral region above exciton B.

In the region where the gap between the walls increases (points no. 5–15) and respectively the strain value becomes smaller, a blue shift of the A exciton resonance is observed, which affects the dispersion of polariton branches, bending them towards higher energy compared to the average. The experimentally recorded ħΩ_R = 2g between the LPB and UPB are found to be about 40 meV for exciton A (1.74 eV) and 60 meV for exciton B (1.88 eV), which has higher oscillator strength. These values indicate a strong coupling regime and provide a sufficient ratio of ≳3 to the width of the reflection dip to observe the full picture of polaritons using reflectance spectroscopy. In addition, the value of coupling strength g ensures that the LPB will be located below a dark exciton, which promotes the emission brightening.^42,43

To analyze the evolution of optical modes leading to the formation of polariton, we consider a simplified theoretical model. In the weakly deformed NT, the electric field of WGMs polarized along the NT axis is described by E^(e)_m ∝ cos(mφ) and E^(o)_m ∝ sin(mφ), where e and o denote even and odd modes, m is the angular number, and the angle ϕ is measured from the major axis of the flattened cross-section. If the light falls normally on the NT axis, the back-scattering intensity near the resonance of the even mode ω^(m)_e has the form

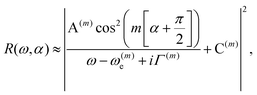where α is the angle between the minor axis of cross-section and light propagation direction, Γ^(m) is the decay rate of the mode, which comprises both the radiative and non-radiative contributions, A^(m) characterizes the strength of the resonance, and C^(m) describes the contribution of all other modes. For an odd WGM, in eqn (1) cos should be replaced by sin. The trigonometric function in the numerator originates from the convolution of the incident field with the field distribution of the mode. This leads to a change in the visibility of modes in the spectra when the cross-section rotates. (The details on the derivation are given in the ESI.†)

We performed numerical calculations to elucidate the evolution of modes taking into account exciton resonances in the strong coupling regime using Comsol Multiphysics as described in the Method section. The dielectric response of NT wall was taken in Drude–Lorentz form with two resonances of A and B excitons:

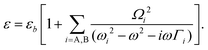here, i denotes excitons A and B, Ω_i is the Rabi splitting in the bulk material, Γ_i is the non-radiative broadening of exciton resonances, ε_b (∼12.3) is the background dielectric constant of MoS₂. We assume that the NT cross-section has a racetrack shape with a constant circumference (∼5.5 μm). The NT wall thickness (50 nm) and rotation angle (65°) are also fixed in the calculations.

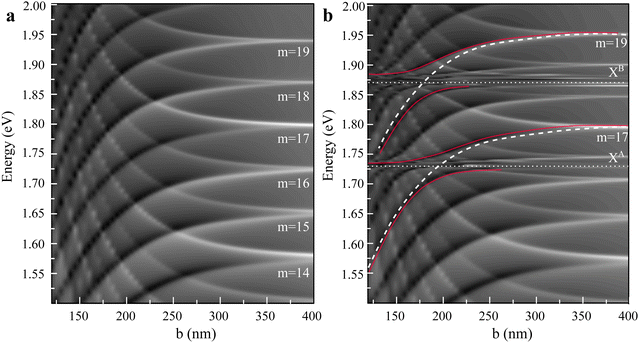
Fig. 3(a) shows the behavior of WGMs without interaction with exciton resonances. As the cross-section flattens, all even modes, curved downward, decrease their energy, and all odd modes, curved upward, increase energy. When the minor axis b of the cross-section becomes less than half the wavelength of the exciting light, the odd-mode resonances begin to quench. At a double-well potential,³⁶ these antisymmetric modes have electric field in antiphase on opposite sides of the cross-section. Therefore, their coupling to the free waves is decreased as the gap between the walls narrows. In contrast, for even modes, which have electric field of the same phase on the opposite sides, the coupling to the free waves increases. This explains why only even, downward-curved modes are retained in the experimental spectra of highly flattened NTs.

Fig. 3 Splitting and evolution of even and odd optical WGMs in reflection with NT flattening described by the minor axis b of cross-section. (a) Bare WGMs without interaction with the resonances of A and B excitons. A change in the color of a curve from light to dark shows the depth of the reflection dip. (b) WGMs and exciton resonances, depicted by white dotted lines, in the strong coupling regime generating polaritons. The red lines indicate the LPB and UPB with Rabi splitting, which arise from the even modes near excitons A and B. The dashed white lines show the same modes without interaction.

The case of strong coupling between the optical modes and the excitons is shown in Fig. 3(b). In the absence of the cross-section deformation, WGMs shift their energies slightly near the exciton resonances due to the changes in the dielectric background. As the axis b decreases to 200–250 nm, stronger even modes reach exciton resonances from above and form exciton-polaritons. For clarity, we have highlighted with red lines the UPB and LPB originating from the WGMs with angular numbers m = 17 and m = 19. The anticrossing with Ω_Rabi of ∼35 meV and ∼55 meV for excitons A and B is quite close to the experimental results. The general picture of the calculated modes and their slopes also satisfactorily reproduce the experimental spectra.

2.2 Constant wall-gap nanotube

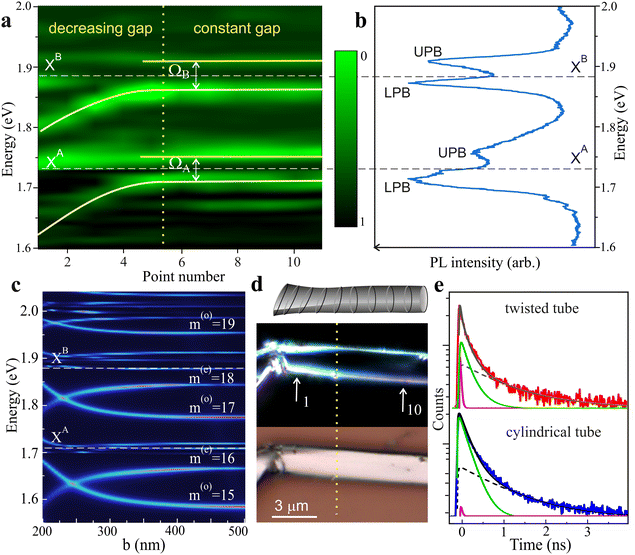
Now let us focus on another NT, which has an extended flat region with a small rotation angle and a constant gap between the walls (see Fig. 4). The map of the reflection spectra presented in Fig. 4(a) shows optical modes of constant energies along the flat region. They are grouped into pairs, with mode spacing in each pair very close to the Rabi splitting for A and B exciton-polaritons. PL spectra measured in this region exhibit four peaks that perfectly correspond to the modes in reflection (Fig. 4(c)). This picture corresponds to the dispersionless polaritons with constant energy, which were previously theoretically considered for TMDC monolayers.⁴⁴ The parameters of these polaritons are stable along the large segment of the NT, where its geometry does not change.

Fig. 4 (a) Map of processed reflectance spectra measured in a NT with a constant gap. Green lines correspond to the main reflection dips, white dotted lines correspond to the energies of A and B excitons, and solid yellow lines highlight the polariton modes. Vertical yellow lines separate the constant and decreasing gap regions. (b) The PL spectrum measured in the constant-gap region, showing four peaks associated with stable polariton branches. (c) Simulation of modes at the rotation angle of 10° as a function of the minor axis b; m^(e,o) denotes the angular number of even or odd modes. (d) Dark-field (top) and bright-field (bottom) optical images of this NT. A schematic image of a NT is shown above. Vertical yellow dotted lines in (a) and (d) separate the constant and decreasing gap regions. (e) PL decay curves measured in A exciton LPB peak in (b) (red) and in a cylindrical tube (blue) shown together with their fitting by three decaying exponents with characteristic decay time about 20 ps (magenta), 200 ps (green) and 1 ns (black, dashed).

Calculations of optical modes for this case were carried out using almost the same model as described above, but assuming a close to zero cross-section rotation angle. We did not divide the NT into two regions, but gradually changed the value of b from 500 nm to 200 nm (Fig. 4). For the same circumference of ∼5.5 μm, the found optical modes have the angular numbers m as in Fig. 3(a). However, there is a remarkable difference due to the small rotation angle. At degrees less than 10°, only one of the two modes (even or odd) is excited, and this occurs in antiphase to each adjacent WGM pair.

Comparison of experimental and calculated pictures in Fig. 4(a and c) shows that the observed stability of mode energies and their separation can be realized only if the axis b exceeds 350 nm. Although the change in mode energies above this value is weak, it can certainly be resolved experimentally. Thus, the gap value is most likely constant and equals to approximately 400 nm. In another part of the NT, close to its kink, when the deformation increases and the gap is narrowed, the even modes begin to shift towards lower energies in both experimental and calculated spectra, as it occurs in the NT with the variable gap (Fig. 2). In the case of completely flattened NT with the shape of a ribbon, it is possible to form the polaritons on Fabry–Pérot modes, as it has been observed in thin WS₂ flakes.⁴⁵

In addition, we performed time-resolved photoluminescence (TRPL) measurements in the time domain of 10 ns as described in the Methods section. Extended PL decay curves for all peaks in Fig. 4(b) and the fitting procedure are given in the ESI.†Fig. 4(e) shows a part of the decay curve for the A-exciton LPB together with a curve measured at the same energy in a reference cylindrical NT with conventional WGMs. Both curves contain two components with characteristic decay times of less than 20 ps and about 200 ps, which are close, respectively, to the published lifetimes of the photon and exciton components of exciton-polariton radiative decay in a monolayer.⁴⁶ In the tube under study, compared to the reference tube, a clear redistribution of intensity is observed in favor of the photonic component associated with the polariton formation.⁴⁷ In particular, its contribution to the integral PL is at least 30 times higher than in the reference tube (see the ESI†). The reason is that as the cross-section of the tube gradually flattens, the resonance of the split WGM is adjusted to the exciton resonance, which leads to a strong coupling with the acceleration of radiative decay, akin to the Purcell effect.⁴⁸ Such adjustment is impossible in a cylindrical tube with stable mode energies. The calculated dependence of the lifetime of optical modes on the degree of flattening is presented in the ESI.† Note that the third component with a decay time of about 1 ns is associated with emission of indirect excitons of close energy, which arise due to the band structure modification during tensile deformation.^41,49,50 In the strong coupling regime, the presence of such excitons does not affect polaritons, since the LPB energy is lower than their energy.^42,43

3 Conclusions

The discovery of anticrossing of polariton branches is usually considered as indisputable evidence of the existence of polaritons in the strong coupling regime. We were able to obtain this result using the change in the energy of split modes in NT with a variable gap between the walls in a flattened cross-section. This approach represents an optical-mechanical method for controlling the interaction of exciton resonances with a set of optical modes excited in NT.

Another important discovery was the observation of polaritons with stable energy in a NT with a constant gap in an unchanged cross-section. The general characteristics of such dispersionless polaritons are in a good agreement with those found for exciton-polaritons in the NT with the variable gap, which excludes another explanation. Note that polaritons of this type were realized at a relatively large gap between NT walls (∼400 nm), which indicates the possibility of their excitation in almost cylindrical MoS₂ NTs.

In both cases, the experimentally observed pattern of optical modes and their transformation into polariton branches are consistent with the proposed theoretical description. The simulation performed reproduces polaritons with Rabi splitting values close to experimental ones and makes it possible to reconstruct the geometric parameters of the NTs under study. Taken together, our experimental and theoretical results confirm the possibility of producing polaritons in the strong coupling regime in individual TMDC NTs, making them promising candidates for nanophotonics. The ability to tune the optical mode energy to exciton resonance and eliminate the negative influence of dark excitons will expand the scope of applications of TMDC NTs for sensoring and creating polariton lasers.

4 Methods

4.1 Optical studies

Optical measurements of MoS₂ NTs were done at 8 K. The Si/SiO₂ substrate with the NTs on its surface was mounted in the ST-500-Attocube (Janis) cryostat, containing the three-coordinate piezo-driver with an accuracy in positioning of ∼20 nm, located in the cold zone of the cryostat. This provides high mechanical stability and vibration isolation necessary for studying such tiny objects. For PL excitation, we used a semiconductor laser PILAS 405 nm (Advanced Laser Systems) with a 40 ps pulse duration and 100 MHz repetition rate. Focusing the laser light using a 100x apochromatic objective (Mitutoyo plan apochromat, NA = 0.7) provided spot size less than 1 μm, which corresponds to ∼6 W cm⁻² (10 nW μm⁻²) power density on the sample surface. The PL signal was collected by the same objective in a confocal setup and directed onto the entrance slit of an SP-2500 spectrometer with cooled PyLoN CCD detector (Princeton Instruments). To measure the time resolved histogram of PL, a single-photon avalanche photodiode PDM 100 (Micro Photon Devices) with time resolution ∼40 ps was used. The time period between exciting pulses was 10 ns. For blocking the scattered laser radiation, a band pass interference filter was used.

The reflection spectra along the NTs were measured on the same optical setup using a halogen lamp coupled to a single-mode optical fiber with subsequent collimation. In this mode, it was possible to achieve high spatial resolution when scanning the NTs. To highlight features, the reflection spectra were subjected to additional processing. First, the reflection spectrum was smoothed using a low-pass Fourier filter to get rid of unwanted noise. Secondly, the moving-average background was subtracted from the reflection spectrum, which made it possible to enhance the visibility of exciton and polariton reflection dips against the background of other effects.

Raman spectra were obtained in backscattering geometry at room temperature. For these investigations, we used a Horiba LabRAM HR Evo UV-VIS-NIR-Open spectrometer (Horiba, Lille, France) with confocal optics. Olympus MPLN100x (Olympus, Tokyo, Japan) objective lens (NA = 0.9) focused the laser beam into a spot ∼1 μm in diameter. As an excitation source, a Nd:YAG laser (Torus Laser Quantum, Stockport, UK) with λ = 532 nm was used. To avoid damage and heating of the NTs, the laser power on its surface was limited to 200 μW.

Optical images of the NTs in different polarizations were obtained using a Nikon ECLIPSE LV150 (Nikon Europe, Amsterdam, Netherlands) industrial microscope operating in bright-field and dark-field modes. The sample under study was illuminated using an LED source passed through a linear polarizer, while long-exposure detection was carried out in orthogonal polarization. This method made it possible to see features of NTs that were inaccessible with the conventional bright-field method.

4.2 Comsol multiphysics calculations

To simulate the reflection and PL map, we divided the computational domain into two parts, outside part with conventional refractive index of air, and inside NT domain with refractive index using Drude–Lorentz dispersion model with A and B exciton resonances. The exciton line broadening was chosen to be 5 meV to resolve the rich pattern of optical modes in the TMDC NT. We assumed a wave vector along the NT axis k_z = 0, because k_z ≠ 0 shifts the energies of optical modes in the NT much less than the flattening effects. To neglect reflection from computational domain boundaries, we added a boundary box with perfectly matched layer. To excite optical modes, we put a plane-wave source incident on the NT with polarization along its axis. To find the back scattered signal, we summed the reflected electric field far away from the NT along a line, while to find the PL signal we calculated the integral of the squared electromagnetic field inside the NT walls.

Author contributions

All authors contributed to this article. A. I. G., M. V. R., I. A. E. and A. A. T. carried out optical measurements and analyzed data; D. R. K. and A. V. P. performed theoretical calculations; M. R. carried out the growth of nanotubes; T. V. S. proposed the physical model, wrote the final version, and supervised this research. All authors gave approval for the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported in part by the Russian Science Foundation project no. 23-12-00300 (A. I. G. - reflection study, T. V. S. - physical model). M. R. thanks the Slovenian Research and Innovation Agency (P1-0099) for funding. D. R. K. acknowledges the grant #SP5068.2022.5. We thank B. Borodin for transferring and positioning the nanotubes on the substrate and A. Veretennikov for his assistance in data processing.

Notes and references

1. B. L. Evans and P. A. Young, Proc. R. Soc. London, Ser. A, 1965, 284, 402–422.
2. G. Wang, A. Chernikov, M. M. Glazov, T. F. Heinz, X. Marie, T. Amand and B. Urbaszek, Rev. Mod. Phys., 2018, 90, 021001.
3. A. Imamoglu, R. J. Ram, S. Pau and Y. Yamamoto, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 53, 4250–4253.
4. S. Ghosh and T. C. H. Liew, npj Quantum Inf., 2020, 6, 16.
5. N. Y. Kim and Y. Yamamoto, Exciton-Polariton Quantum Simulators, Springer International Publishing, Cham, 2017, pp. 91–121.
6. A. V. Kavokin, J. J. Baumberg, G. Malpeuch and F. P. Laussy, Microcavities, Oxford University Press, UK, 2008.
7. S. Luo, H. Zhou, L. Zhang and Z. Chen, Appl. Phys. Rev., 2023, 10, 011316.
8. K. Wei, Q. Liu, Y. Tang, Y. Ye, Z. Xu and T. Jiang, Nat. Commun., 2023, 14, 5310.
9. C. Weisbuch, M. Nishioka, A. Ishikawa and Y. Arakawa, Phys. Rev. Lett., 1992, 69, 3314–3317.
10. V. D. Kulakovskii, A. I. Tartakovskii, D. N. Krizhanovskii, A. Armitage, J. S. Roberts and M. S. Skolnick, Phys.-Usp., 2000, 43, 853.
11. X. Liu, T. Galfsky, Z. Sun, F. Xia, E.-C. Lin, Y.-H. Lee, S. Kéna-Cohen and V. M. Menon, Nat. Photonics, 2015, 9, 30–34.
12. S. Dufferwiel, S. Schwarz, F. Withers, A. A. P. Trichet, F. Li, M. Sich, O. Del Pozo-Zamudio, C. Clark, A. Nalitov, D. D. Solnyshkov, G. Malpuech, K. S. Novoselov, J. M. Smith, M. S. Skolnick, D. N. Krizhanovskii and A. I. Tartakovskii, Nat. Commun., 2015, 6, 8579.
13. L. C. Flatten, Z. He, D. M. Coles, A. A. P. Trichet, A. W. Powell, R. A. Taylor, J. H. Warner and J. M. Smith, Sci. Rep., 2016, 6, 33134.
14. L. Zhang, R. Gogna, W. Burg, E. Tutuc and H. Deng, Nat. Commun., 2018, 9, 713.
15. C. Schneider, M. M. Glazov, T. Korn, S. Höfling and B. Urbaszek, Nat. Commun., 2018, 9, 2695.
16. L. Lackner, M. Dusel, O. A. Egorov, B. Han, H. Knopf, F. Filenberger, S. Schröder, K. Watanabe, T. Taniguchi, S. Tongay, C. Anton-Solanas, S. Höfling and C. Schneider, Nat. Commun., 2021, 12, 4933.
17. R. Houdré, C. Weisbuch, R. P. Stanley, U. Oesterle, P. Pellandini and M. Ilegems, Phys. Rev. Lett., 1994, 73, 2043–2046.
18. D. S. Dovzhenko, S. V. Ryabchuk, Y. P. Rakovich and I. R. Nabiev, Nanoscale, 2018, 10, 3589–3605.
19. S. Iijima, Nature, 1991, 354, 56–58.
20. R. Tenne, L. Margulis, M. Genut and G. Hodes, Nature, 1992, 360, 444–446.
21. M. Remškar, Z. Skraba, F. Cléton, R. Sanjinés and F. Lévy, Appl. Phys. Lett., 1996, 69, 351–353.
22. M. Remškar, Adv. Mater., 2004, 16, 1497–1504.
23. V. Kralj-Iglič, M. Remškar, G. Vidmar, M. Fošnarič and A. Iglič, Phys. Lett. A, 2002, 296, 151–155.
24. A. Enyashin, S. Gemming and G. Seifert, Eur. Phys. J.: Spec. Top., 2007, 149, 103–125.
25. M. Rems̆kar, A. K. Hüttel, T. V. Shubina, A. Seabaugh, S. Fathipour, R. Lawrowski and R. Schreiner, Isr. J. Chem., 2022, 62, e202100100.
26. M. Selig, G. Berghäuser, A. Raja, P. Nagler, C. Schüller, T. F. Heinz, T. Korn, A. Chernikov, E. Malic and A. Knorr, Nat. Commun., 2016, 7, 13279.
27. T. V. Shubina, M. Remškar, V. Y. Davydov, K. G. Belyaev, A. A. Toropov and B. Gil, Ann. Phys., 2019, 531, 1800415.
28. F. Cadiz, E. Courtade, C. Robert, G. Wang, Y. Shen, H. Cai, T. Taniguchi, K. Watanabe, H. Carrere, D. Lagarde, M. Manca, T. Amand, P. Renucci, S. Tongay, X. Marie and B. Urbaszek, Phys. Rev. X, 2017, 7, 021026.
29. J. L. Musfeldt, Y. Iwasa and R. Tenne, Phys. Today, 2020, 73, 42–48.
30. D. R. Kazanov, A. V. Poshakinskiy, V. Y. Davydov, A. N. Smirnov, I. A. Eliseyev, D. A. Kirilenko, M. Remškar, S. Fathipour, A. Mintairov, A. Seabaugh, B. Gil and T. V. Shubina, Appl. Phys. Lett., 2018, 113, 101106.
31. L. Sun, Z. Chen, Q. Ren, K. Yu, L. Bai, W. Zhou, H. Xiong, Z. Q. Zhu and X. Shen, Phys. Rev. Lett., 2008, 100, 156403.
32. D. Kazanov, M. Rakhlin, A. Poshakinskiy and T. Shubina, Nanomaterials, 2020, 10, 373.
33. L. Yadgarov, B. Višić, T. Abir, R. Tenne, A. Y. Polyakov, R. Levi, T. V. Dolgova, V. V. Zubyuk, A. A. Fedyanin, E. A. Goodilin, T. Ellenbogen, R. Tenne and D. Oron, Phys. Chem. Chem. Phys., 2018, 20, 20812–20820.
34. S. S. Sinha, A. Zak, R. Rosentsveig, I. Pinkas, R. Tenne and L. Yadgarov, Small, 2020, 16, 1904390.
35. I. A. Eliseyev, B. R. Borodin, D. R. Kazanov, A. V. Poshakinskiy, M. Remškar, S. I. Pavlov, L. V. Kotova, P. A. Alekseev, A. V. Platonov, V. Y. Davydov and T. V. Shubina, Adv. Opt. Mater., 2023, 11, 2202782.
36. L. Landau and E. Lifshits, Quantum Mechanics: Non-Relativistic Theory, Elsevier Science, 1991, vol. 3.
37. M. Ghorbani-Asl, N. Zibouche, M. Wahiduzzaman, A. F. Oliveira, A. Kuc and T. Heine, Sci. Rep., 2013, 3, 2961.
38. H. Peelaers and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 241401.
39. H. J. Conley, B. Wang, J. I. Ziegler, R. F. Haglund Jr., S. T. Pantelides and K. I. Bolotin, Nano Lett., 2013, 13, 3626–3630.
40. D. Lloyd, X. Liu, J. W. Christopher, L. Cantley, A. Wadehra, B. L. Kim, B. B. Goldberg, A. K. Swan and J. S. Bunch, Nano Lett., 2016, 16, 5836–5841.
41. X. Han, J. Lin, J. Liu, N. Wang and D. Pan, J. Phys. Chem. C, 2019, 123, 14797–14802.
42. V. Shahnazaryan, V. Saroka, I. Shelykh, W. Barnes and M. Portnoi, ACS Photonics, 2019, 6, 904–914.
43. H. Shan, I. Iorsh, B. Han, C. Rupprecht, H. Knopf, F. Eilenberger, M. Esmann, K. Yumigeta, K. Watanabe, T. Taniguchi, S. Klembt, S. Höfling, S. Tongay, C. Antón-Solanas, I. A. Shelykh and C. Schneider, Nat. Commun., 2022, 13, 3001.
44. F. Alpeggiani, S.-H. Gong and L. Kuipers, Phys. Rev. B, 2018, 97, 205436.
45. Q. Wang, L. Sun, B. Zhang, C. Chen, X. Shen and W. Lu, Opt. Express, 2016, 24, 7151.
46. X. Liu, W. Bao, Q. Li, C. Ropp, Y. Wang and X. Zhang, Phys. Rev. Lett., 2017, 119, 027403.
47. N. Lundt, N. S. Stoll, P. Nagler, A. Nalitov, S. Klembt, S. Betzold, J. Goddard, E. Frieling, A. V. Kavokin, C. Schüller, T. Korn, S. Höfling and C. Schneider, Phys. Rev. B, 2017, 96, 241403.
48. E. Purcell, Phys. Rev., 1946, 69, 681.
49. Y. Uchiyama, A. Kutana, K. Watanabe, T. Taniguchi, K. Kojima, T. Endo, Y. Miyata, H. Shinohara and R. Kitaura, npj 2D Mater. Appl., 2019, 3, 26.
50. I. A. Eliseyev, A. I. Galimov, M. V. Rakhlin, E. A. Evropeitsev, A. A. Toropov, V. Y. Davydov, S. Thiele, J. Pezoldt and T. V. Shubina, Phys. Status Solidi RRL, 2021, 15, 2100263.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nh00052h

---