Colloidal spherical stibnite particles via high-temperature metallo-organic synthesis

Abstract

Antimony trisulfide (Sb₂S₃) is an emerging semiconductor with a high absorption coefficient and a bandgap in the visible range. This makes it a promising material for various electronic and optoelectronic applications. However, one of the main challenges is still the synthesis of the material, as it is usually obtained either as a nanomaterial in its amorphous form with inferior optical properties or in crystalline rod-like structures in the micrometer or sub-micrometer range, which leads to application-related difficulties such as clogging in inkjet printing or spraying processes or highly porous layers in film applications. In this study, a one-pot synthesis of highly crystalline, spherical Sb₂S₃ sub-micron particles is presented. The particles are growing encapsulated in a removable, wax-like matrix that is formed together with an intermediate from the precursors SbCl₃ and L-cysteine. Both substances are insoluble in the reaction mixture but well-dispersable in the solvent 1-octadecene (ODE). The intermediate forms a complex crosslinked architecture whose basic building block consists of an Sb atom attached to three cysteine molecules via Sb–S bonds. Embedded in the matrix consisting of excess cysteine, ODE, and chlorine, the intermediate decomposes into amorphous Sb₂S₃ particles that crystallize as the reaction proceeds at 240 °C. The final particles are highly crystalline, spherical, and in the sub-micron range (420 ± 100 nm), making them ideal for further processing. The encapsulation method could not only provide a way to extend the size range of colloidal particles, but in the case of Sb₂S₃, this method circumvents the risk of carbonization of ligands or insufficient crystallization during the annealing of amorphous material.

---

Introduction

Semiconducting materials play an important role in modern society. They are used as memory chips,¹ electronic components,² sensors,³ for photocatalysis,⁴ in bioimaging,⁵ and many other applications. The demands on the properties of these materials are high: the ideal semiconductor has, in addition to its application-related properties, a high abundance, low toxicity, and is environmentally friendly.⁶ The interest in semiconducting Sb₂S₃ is growing for several electronic and optoelectronic applications, such as energy storage⁷ and optical data storage.⁸ However, the application most researchers are focusing on is the photovoltaic use of this material.^9–11 This is due to the high absorption coefficient (1.8 × 10⁵ cm⁻¹ at 450 nm) and direct bandgap energy around 1.7 eV of the crystalline phase.¹²

Electronic and optoelectronic examinations on Sb₂S₃ particles and Sb₂S₃ composite nanomaterials have shown promising results. For example, with voltammetry and impedance measurements, researchers have shown a high rate performance, cycle stability, and capacitance values for Sb₂S₃-carbon nanocompound electrodes.^13,14 Other authors report photoelectric conversion efficiencies of up to 7.12% in performance tests of Sb₂S₃-based solar cells.^15,16

Sb₂S₃ exists in two forms: an amorphous phase that appears orange-red and a crystalline, grayish-black phase (stibnite).¹⁷ However, the crystalline phase of semiconductors is usually preferred in application as the electronic properties are superior to the ones of the amorphous phase.¹⁸ Due to disorder effects and charge trapping, charge transport in amorphous materials is less efficient than in crystalline ones.¹⁹

So far, there are several strategies for synthesizing colloidal Sb₂S₃ particles: solvothermal,²⁰ hydrothermal,²¹ and sonochemical methods,²² chemical bath deposition,²³ and vapor deposition.²⁴

Although similar chalcogenide nanoparticles, e.g., Bi₂S₃, could be obtained in various sizes between 10 and 500 nm with a high crystallinity following comparable strategies,^25–27 the results for Sb₂S₃ particles are different. While amorphous Sb₂S₃ nanoparticles are usually synthesized as spheres ranging from 20–30 nm in diameter to micron size with size deviations of about 15%,^28–30 stibnite particles are usually received as elongated structures, e.g., rods or urchin-like structures, with sizes in the micron or sub-micron range.^{28,29,31–34} This is the case because the particle formation starts with the amorphous phase and undergoes self-assembly and coalescence to larger particle sizes (>200 nm) until the crystallization begins.²⁹

However, spherical particles have an advantage over rod-shaped ones regarding processing and applications. For example, they show favorable performance in inkjet printing due to an enhanced flowability³⁵ and form more densely packed films after spin coating increasing conductivity.³⁶ Though the preferred particle size is strongly dependent on the application, sub-micron- and nano-sized particles are demanded for, e.g., inkjet printing or solar cells. Still, medium-sized crystals in the sub-micron range may lead to enhanced performance.^37–39

To control particle aggregation, size, or shape, researchers developed several strategies. Most commonly, aggregation and size are controlled by electrostatic or steric stabilization, which can be achieved by adjusting the surface charge, adding ligands, or using coordinating solvents.^40–44 In addition, ligands can affect the shape of the final particles.⁴⁵ There are also a few reports in which researchers embedded precursors, which decompose upon heating or irradiation, in a polymer matrix to form a particle-polymer composite. The matrix also prevents aggregation and segregation of the particles.^46–48 However, transferring these methods to the synthesis of crystalline Sb₂S₃ particles appears to be challenging.

Spherical stibnite particles are rarely reported in the literature because stibnite belongs to the orthorhombic crystal system and therefore prefers to grow in the direction of the c-axis into elongated, rod-like shapes.⁴⁹ One approach was made by Zhu et al. using ZnS hollow spheres as a template for several metal sulfide hollow particles in a hydrothermal synthesis.⁵⁰ The Sb₂S₃ spheres were about 1–2 μm in diameter. However, they reported annealing some of the metal sulfides after the synthesis. Thus, although the XRD revealed the stibnite structure for these particles, it remains unclear whether the initially formed particles were obtained in the amorphous or crystalline phase. Another approach was performed by Pan et al. via a hydrothermal synthesis using SbCl₃, tartaric acid, and L-cysteine with a ratio of 2 : 12 : 3.⁵¹ After the reaction at 180 °C for 12 h in an autoclave, they received amorphous alveolate spheres of 2–3 μm in diameter which crystallized after annealing. Doing the same synthesis with a different ratio of the reactants (3 : 20 : 6), at a shorter time scale (8 h) and without annealing, Cao et al. claim to have obtained 2–3 μm sized crystalline Sb₂S₃ spheres with the same appearance as those obtained by Pan et al.⁷via an Sb-thioacetamide complex in a polystyrene solution, Sahoo et al. synthesized Sb₂S₃-carbon composite materials.¹³ By either stirring the solution for 2 h or using microwave irradiation for 10 min and post-annealing the intermediate products, they received Sb₂S₃ nanoparticles anchored on carbon sheets and carbon encapsulated Sb₂S₃ spheres, respectively. The spheres have a diameter of 600 ± 200 nm with a fully crystalline Sb₂S₃ core and a carbon shell. The nanoparticles on the carbon sheet are much smaller, about 5–10 nm, and mainly crystalline. However, some amorphous parts and some Sb₂S₂O are also present. Both materials show a good performance as electrode material.

In the following, a high-temperature synthesis that yields spherical stibnite particles with sub-micron size will be described. To achieve this result, L-cysteine and SbCl₃ were dispersed in 1-octadecene (ODE). The cysteine acts not only as sulfur source but also forms a wax-like substance during the synthesis, which is insoluble in ODE due to the polar character of cysteine. The initially formed amorphous Sb₂S₃ particles are immobilized in this substance and, thus, prevented from growing into large, micron-sized rod-like structures upon crystallization. After the synthesis, the matrix can be removed and single stable particles are obtained. Furthermore, it will be shown that a stable intermediate substance consisting of antimony and cysteine is formed. This substance is crystalline, likely a highly crosslinked compound, and decomposes into Sb₂S₃ particles upon heating. The matrix is formed around this intermediate from excess cysteine, the solvent ODE, and the chlorine from SbCl₃.

Experimental section

Standard glassware was used for all experiments. Prior to the syntheses, all reaction vessels were cleaned with peroxymonosulfuric acid (Piranha solution), which was prepared by mixing sulfuric acid (95–97%, CHEMSOLUTE) with peroxide (30%, VWR chemicals) at a ratio of 7 : 1 (Caution!Piranha solution must be handled with extreme care as it is explosive and reacts violently with organic matter). Subsequently, the glass vessels were rinsed with deionized (DI) water. The heating rate and reaction temperature were controlled using a temperature controller (LTR 3500; Juchheim Solingen).

Materials

Antimony(III) chloride (SbCl₃, >99.95%) and isopropyl alcohol (IPA, 99.5%) were obtained from Sigma-Aldrich and ODE (90%, tech.) from Thermo Scientific. L-Cysteine (98%) was purchased from Carl Roth and N,N-dimethylformamide (DMF, for gas chromatography) from Supelco-Merck. All chemicals were used without further purification. The cysteine was thoroughly ground with a mortar before use.

Synthesis

An argon atmosphere was maintained during all reaction steps.

First, 0.5 mmol SbCl₃, 2.5 mmol L-cysteine, and 25 mL ODE were introduced into a 50 mL three-neck round-bottomed flask. To disperse the SbCl₃ and the L-cysteine, the mixture was sonicated for approximately 15 min (Sonorex RK512H; 860 W; 35 kHz; Bandelin) until a homogenous, turbid dispersion was obtained. The reaction mixture was then magnetically stirred (800 rpm) at ambient temperature, and a vacuum (∼0.01 mbar) was applied for 30 min. The mixture was again set under argon and, subsequently, heated to 240 °C with a heating ramp of 10 K min⁻¹. After holding the reaction temperature for 30 min, the reaction was stopped by removing the heating mantle.

Particle purification

The nanoparticles were thoroughly purified by subsequent centrifugation and redispersing, and the matrix was removed during this process. Details of the procedure can be found in the ESI.†

Characterization

Elemental analysis (CHNS/O analysis). The samples were analyzed using a FlashEA 1112 CHNS/O Automatic Elemental Analyser from Thermo Scientific. For the CHNS analysis, approximately 2 mg of the sample was burned in a pure oxygen atmosphere over tungsten oxide at 1020 °C, and the evolving NO_x and SO₃ were reduced over copper to N₂ and SO₂. The four components obtained, H₂O, N₂, SO₂, and CO₂, were chromatographically separated and detected via thermal conductivity detection.

The oxygen content was determined by immediately pyrolyzing approximately 2 mg of the sample in a helium atmosphere at 1060 °C. Organic oxygen is quantitatively converted to CO over nickel-containing carbon, chromatographically separated from other gases, and detected via thermal conductivity detection.

Energy-dispersive X-ray analysis (EDX). To perform EDX analysis, the SEM was equipped with an EDAX X-ray detector (Octane Elect Plus). During the measurements, the SEM was operated with an acceleration voltage of 15 kV and a spot intensity of 50, while the working distance was set to 10 mm. The resolution of the detector was 126.2 eV.

The samples were deposited on copper grids in a layer several micrometers thick and measured on a STEM holder. Areas of 2 × 2 mm² were measured at three different locations of the sample with 200 s accumulation time.

Atomic absorption spectroscopy (AAS). An iCE 3000 spectrometer from Thermo Fisher Scientific was used for AAS. The samples were prepared by dissolving 10–15 mg substance in 0.5 mL conc. H₂SO₄ at 170 °C. A 0.1 mL aliquot was subsequently diluted with DI water to a total volume of 10 mL. The sample was vaporized in an acetylene flame.

Infrared spectroscopy (IR). IR spectra were recorded with a JASCO FT/IR-4100. The measurement range was 4000–600 cm⁻¹ with a step size of 4 cm⁻¹. The samples were applied as slurry with IPA and left until dried or as a powder on the attenuated total reflectance (ATR) crystal.

Raman spectroscopy. Raman measurements were performed on a transmission spectrometer from Kaiser Optical (HL5R) equipped with a 514 nm argon laser and a CCD camera. Additionally, a Notch filter (514 nm) was used. The samples were measured for 200–240 s with 2–3 accumulations. A laser power of 1.1 mW was applied. The spectral resolution of the measurements is 5 cm⁻¹. Due to grating changes, measurement artifacts occur at the wavelengths 2265 and 2324 nm.

Reflectance measurements. Since the particle dispersions were turbid, the UV/vis spectroscopy measurements were performed in reflectance mode. The instrument used was a Cary 5000 UV-Vis-NIR spectrometer (Agilent Technologies) equipped with an integrating sphere (internal DRA 2500). Dispersions consisting of IPA and 2–2.5 g particles per liter were measured in special quartz cuvettes (type 26.715/Q/10/Z20; Starna) in the range of 400 to 900 nm.

An artifact occurs at a wavelength of 800 nm due to a detector change of the spectrometer. The accuracy of the Tauc method was estimated on the basis of a study by Viezbicke et al., who exemplarily evaluated 120 individual analyses of polycrystalline ZnO and found a deviation of about 0.03 eV.⁵²

Mass spectrometry (MS). To examine the samples, matrix-assisted laser desorption/ionization (MALDI; Autoflex speed TOF/TOF, Bruker Daltonik) and electron ionization (EI; Finnigan MAT 95, Thermo Fisher Scientific) techniques were used. For MALDI, the samples were ground with α-cyano-4-hydroxycinnamic acid (HCCA) at a ratio of 1 : 100. The instrument was equipped with a solid-state laser (2 kHz) and a time-of-flight (TOF) MS. Measurements are limited to a molecule size of ∼100 kDa. For EI, the samples were vacuum evaporated, ionized, and analyzed with a double-focusing sector field device with inverted Nier-Johnson geometry.

Scanning electron microscopy (SEM). A Hitachi SU 5000 scanning electron microscope was used to record SEM images in the secondary electron (SE) mode with an electron acceleration voltage of 15 kV and a spot intensity of 30. The working distance was 3 mm. The particle dispersion (c = 1.5–2 g L⁻¹) in water was dropped on a carbon-coated copper grid (carbon-coating type A, 6–10 nm thickness, Cu 400 mesh, Plano GmbH) and dried before the measurement. The software FIJI was used to evaluate the particle size for 200–300 particles per synthesis on multiple images.⁵³

Transmission electron microscopy (TEM). TEM investigations were conducted on a conventional Tecnai G²20 S-TWIN (FEI/TFS Company, USA) with LaB6 emitter, operated at 200 kV. For image acquisition, a US1000 CCD camera and DigitalMicrograph software (both: Gatan Inc., USA) were used. The sample preparation was identical to the preparation for SEM.

Thermogravimetric analysis (TGA). The determination of organic residues in the final particle samples was performed using a Netzsch TG209 F1 libra with the external cooling system Julabo F32-MA. After a 10 min equilibration period, 4–8 mg dried sample was heated up to 300 °C at a rate of 10 K min⁻¹ and held at this temperature for 50 min. A nitrogen gas flow of 20 mL min⁻¹ was used during the measurement.

X-ray diffraction spectrometry (XRD). The samples for XRD measurements were prepared as follows: the sample dispersions were drop-casted onto a glass slide (76 × 26 mm, Elka) at approx. 110 °C under constant argon flow until approx. 10 mg of the sample had dried on the glass slide. The samples were measured in Bragg–Brentano geometry with a fixed sample stage and movable X-ray source and detector arm. The instrument used was a Bruker D8 Eco equipped with a LYNXEYE XE-T detector and a Cu Kα1 radiation source (25 kV, 40 mA) with a radiation wavelength of 0.15405 nm. The angular range of the measurements was 20–80° 2θ with a step size of 0.025°.

X-ray photoelectron spectroscopy (XPS). The spectrometer used for XPS measurements was from SPECS Surface Nano Analysis GmbH equipped with an Al/Mg X-ray source and a PHOIBOS 100 MCD energy analyzer. The powdered sample was pressed in indium foil before the analysis.

Results and discussion

For this study, Sb₂S₃ particles were synthesized using the heat-up method. The precursors SbCl₃ and L cysteine were used for this purpose. After SbCl₃ and L-cysteine were dispersed in ODE, the heat-up process was started, and the reaction progress could be followed visually. Color changes in the reaction mixture at specific temperatures were associated with distinct reaction stages. Photographs of these stages can be found in Fig. S1 in the ESI.†

The first critical point in the synthesis was reaching a reaction temperature of 140 °C. The precursors, initially dispersed in the solvent, no longer form a milky white mixture (phase P0, Fig. S1(a)†) at this temperature. Instead, they aggregated, forming 1–3 large white flocs, which were slowly changing their color to pale yellow (PI, Fig. S1(b)†). As the reaction progressed, the flocs turned orange and began to break into smaller pieces at about 170 °C (PII, Fig. S1(c)†). They changed their color to dark red and sedimented at 200 °C (PIII, Fig. S1(d)†), where they finally turned black at 240 °C (PIV, Fig. S1(e)†). No further change was visible to the naked eye when the reaction continued at this temperature for 30 min. After the reaction mixture was cooled down at the end of the synthesis, a brownish-black product adhered to the walls of the reaction vessel.

The characterization of this brownish-black product is discussed first, and the individual reaction steps are examined in more detail in the following sections.

Characterization of the reaction product

The brownish-black synthesis product was examined by SEM after removing only the solvent ODE by washing once with hexane (Fig. 1(a)) and after washing several times with water/IPA and DMF (Fig. 1(b)). Both SEM images show spherical particles with an average diameter of 420 ± 100 nm. In the unpurified sample, the particles are immobilized in large lumps of a waxy matrix (Fig. 1(a)). The matrix can be removed in the purification process, yielding the bare particles, see Fig. 1(b). This finding is confirmed by performing a TGA (Fig. S2, ESI†). While the sample with the matrix around the particles showed a mass loss of about 1/3 of the initial mass, no mass loss was detected for the purified sample. However, an XPS measurement (Fig. S3 and S4, ESI†) suggests that ligands are still present on the particle surface. These data show that some ligands containing N and C. S and O are found as well. However, S is also present in the particles themselves, and O 1s overlaps with the Sb 3d_5/2 peak. These findings suggest that the ligands are either cysteine or one of its decomposition products, considering the origin of the ligands. Based on several measurements, the overall accuracy of the TGA can be estimated at around 0.5–1%. Hence, the maximum content of organics in the sample is about 1 wt% corresponding to about 15 cysteine molecules per nm². The particles are stable in aqueous dispersion, which was supported by the agreement of the calculated and observed sedimentation rates (2 cm d⁻¹ for the lower size fraction).

Fig. 1 SEM images of the spherical Sb₂S₃ particles: (a) as received without cleaning and (b) after washing off the matrix.

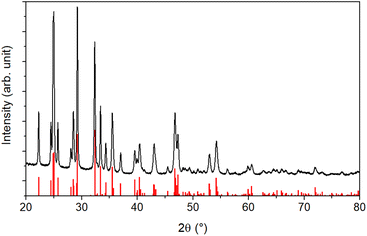
An XRD analysis was performed to determine the crystallinity of the sample. The results shown in Fig. 2 reveal a highly crystalline material corresponding to the orthorhombic stibnite structure (COD 9003460). All diffraction peaks can be assigned to this pattern, indicating no impurities from, e.g., antimony oxides.

Fig. 2 XRD of the purified particles. The pattern for stibnite (COD 9003460) is displayed in red.

Additionally, the crystallite size was estimated via the Debye–Scherrer equation (eqn (1)).⁵⁴ The crystallite size D_hkl is calculated by dividing the product of the crystallite shape factor K and the wavelength λ by the width (full width at half maximum) of the diffraction peak B_hkl and the cosine of the corresponding Bragg angle θ.

For different Laue indices, crystallite sizes between 40 and 55 nm were calculated. Thus, there is a clear discrepancy between the diameter estimated with the SEM, which provides no information about the crystalline composition of the particles, and the crystallite size estimated with the Debye–Scherrer equation, which only gives an average value.

In order to unambiguously characterize the crystalline structure of the particles, measurements with different TEM techniques were performed, which are shown in Fig. 3 and S5 in the ESI.† The SAED analysis of a single particle (Fig. 3(a) and (b)) clearly shows a lattice structure, as would be expected from a single crystalline structure. However, some circular smearing effects can be seen in the diffraction images, which can only occur in samples containing crystalline areas with slightly different orientations or defects. Additionally, the SAED image of a different particle (Fig. S6(a) and (b), ESI†) was analyzed and the interplanar spacing was calculated. The values were compared with reference data (JCPDS card 42-1393) and the corresponding hkl indices were given (Table S2, ESI†). The calculated values match the reference data well.

Fig. 3 TEM analysis of the crystalline structure of the Sb₂S₃ particles: (a) TEM image of a particle with (b) the corresponding SAED pattern, (c) and (d) dark-field images of several particles showing different crystal planes in two different observation planes, and (e) and (f) HRTEM images of two crystallites in a particle. Image (f) is an enlarged view of the area in the red square in image (e). The insets in (f) show the FFT analyses of the three marked spots.

In the dark-field images (Fig. 3(c) and (d)), different crystal planes appear bright depending on the observation plane/angle. The micrographs show that for certain diffraction spots, most areas of various particles appear in the same contrast, i.e., have the same crystalline orientation. However, some smaller parts (approx. 50 nm), especially in the peripheral areas of the particles, show different crystal orientations. Based on these results, it can be concluded that the particles are mainly single crystalline but often contain some smaller, differently oriented crystallites in peripherical areas. Additional SAED and dark-field images of the same series can be found in Fig. S5 in the ESI.† As indicated by HRTEM micrographs in Fig. 3(e) and (f), the smaller crystallites are not aggregated to the large particles but rather intergrown with them. The images show two different crystallites in the same particle. The different crystal orientations are confirmed by Fast Fourier Transform (FFT) analysis (insets in Fig. 3(f)). Since the small crystallites are mainly found on the edges of the particles, it is likely that the crystal could not grow into its orthorhombic structure due to the surrounding matrix and, thus, crystal defects were formed or that other particles coalesced with already existing larger crystalline ones.

The optical properties of the particles were also investigated. The reflectance of the samples was measured, and subsequently, the Tauc plot was applied to determine the bandgap value. Before applying the plot, the reflectance data needs to be transformed into absorption data using the Kubelka–Munk equation (eqn (2)).⁵⁵ The Kubelka–Munk function F(R_∞) corresponds to the ratio of the absorption coefficient k and the scattering coefficient s. These coefficients, in turn, are correlated to the reflection of an infinitely thick specimen R_∞.

F(R_∞) replaces the absorption coefficient α in the Tauc equation, which is displayed in eqn (3).^56,57α is expressed by the Planck constant h, the photon frequency ν, the transition factor γ, the bandgap energy E_g, and a constant B described by Davis and Mott as magnitude of the optical absorption constant.

αhν^1/γ =B(hν − E_g) (3)

γ describes the type of the bandgap transition. It equals 1/2 for a direct allowed transition and 2 for an indirect allowed transition.

There are different opinions in the literature on whether the bandgap of crystalline Sb₂S₃ is direct^58–60 or indirect.^61–63 Still, the bandgap is mainly located between 1.6 and 1.8 eV, with the indirect bandgap about 0.1 eV lower than the direct one. Theoretical calculations have shown that the indirect transition is energetically more favorable.^64,65 Since the difference to the direct transition is small, the authors conclude that the direct transition is most likely dominant.

Fig. 4(a) shows the measured reflectance data, while Fig. 4(b) and (c) show the data transformed according to the Tauc equation for an indirect and a direct bandgap transition, respectively. The reflectance curve shows one steep slope, as is usual for a phase-pure semiconductor, around 720 nm. To estimate the bandgap of the material, a tangent is drawn to the slopes of the Tauc plots, and the x-value is taken where the tangent intersects the extended baseline of the plot. The results correspond to 1.65 eV for the indirect bandgap and 1.75 eV for the direct bandgap.

Fig. 4 UV/vis data of the final particles showing (a) the measured reflectance data, (b) the Tauc plot for estimating the indirect bandgap, and (c) the Tauc plot for estimating the direct bandgap.

Formation and growth of the Sb₂S₃ particles

The results shown in the last section strongly suggest that the matrix is the critical component in the formation of colloidal spherical stibnite particles. Hence, the reaction process was thoroughly studied, and samples were taken at different reaction stages. These samples, taken at the temperatures 140 °C (PI), 170 °C (PII), 200 °C (PIII), and 240 °C (PIV), were further characterized by SEM, XRD, EDX and CHNS/O analysis, UV-vis, and IR spectroscopy.

The samples were purified by the same procedure as the final product prior to characterization (see Experimental part for details). Fig. 5 shows SEM images of the different samples. The samples PI (Fig. 5(a)) and PII (Fig. 5(b)) contain rod-shaped particles with a length of a few micrometers. However, in sample PII, small spherical particles with a diameter of 220 ± 60 nm are also found. In sample PIII, these particles are still present but have grown larger (diameter of 280 ± 110 nm), while the rod-shaped particles are no longer found (Fig. 5(c)). In sample PIV (Fig. 5(d)), the spherical particles have become even larger with a diameter of 430 ± 110 nm and do not differ significantly in size or appearance from the final product. Statistical size distributions of these samples can be found in the ESI in Fig. S7.†

Fig. 5 SEM images of the different reaction stages of the synthesis: (a) after 140 °C (PI), (b) after 170 °C (PII), (c) after 200 °C (PIII), and (d) after 240 °C (PIV). The samples were purified with the same procedure as the final particles.

In addition, the growth process of the particles was characterized crystallographically and optically. The results of the XRD analysis and the UV/Vis spectroscopy are shown in Fig. 6. XRD (Fig. 6(a)) revealed a highly crystalline structure for the samples PI and PII, which was neither be found in the COD database nor corresponded to L-cysteine or SbCl₃ (reference diffractograms in Fig. S8, ESI†). This suggests that a new substance was formed at 140 °C. Since no other phases are detected in sample PII, the small spherical particles likely correspond to the amorphous phase of Sb₂S₃. The reflectance measurement (Fig. 6(b)) shows that no semiconducting substance was formed in PI, and the Tauc plot (Fig. 6(c)) gives further indication that the particles in PII consist of amorphous Sb₂S₃, which has a bandgap value between 2.0 and 2.2 eV.²⁹ For the particles of sample PII, a band gap value of 2.02 eV was determined. To obtain further information about the materials formed during the reaction process, the purified solids were characterized by CHNS/O analysis and EDX. Table 1 provides additional information on the elemental (atomic) composition of the samples and the sizes of the spherical particles.

Fig. 6 Phase and optical characterization of reaction intermediates at different reaction stages of the synthesis. XRD analysis (a) and reflectance measurements (b) were performed using samples taken at 140 °C, 170 °C, 200 °C, and 240 °C (without 30 min additional reaction time). The Tauc plot (c) was applied to all reflection data except that of the sample taken at 140 °C, since no band gap transition can be seen.

Table 1 Elemental (atomic) composition of the purified solids of the different reaction stages, the diameter of the Sb₂S₃ particles, and their bandgap values

Sample	PI	PII	PIII	PIV	Final
Temp. (°C)	140	170	200	240	240 (30 min)
Sb	1.0	1.6	2.0	2.0	2.0
S	2.9	3.9	3.0	3.0	3.0
C	9.0	9.0	—	—	—
H	19.5	19.5	—	—	—
N	2.8	2.9	—	—	—
O	6.6	6.6	—	—	—
Diameter (nm)	—	220 ± 60	280 ± 110	430 ± 110	420 ± 100
Bandgap (eV)	—	2.02	1.99	2.01/1.75	1.75

---

The white crystals in PI are composed of antimony and elements normally found in organic molecules, almost corresponding to the stoichiometry of cysteine (C₃H₇N_SO₂). Chlorine, however, was not found. The results for this substance are discussed in more detail in the following section. Since the particles in PII are Sb₂S₃, their composition results from a mixture of the substance from PI and Sb₂S₃ in an atomic ratio of 3 : 2 for the element antimony. Along with the white rod-like particles, the crystalline XRD pattern disappeared in sample PIII. Also, only the elements antimony and sulfur remain in a 2 : 3 ratio. These results, along with a band gap value of 1.99 eV for this substance, indicate that the white substance is likely an intermediate in the formation of Sb₂S₃ particles, which are in an amorphous state up to this point. Compared to PII, the particles slightly increased in diameter.

For sample PIV, the X-ray diffractogram and optical data are changed compared to those of the samples of earlier reaction stages. A crystalline pattern corresponding to the stibnite structure (COD 9003460) can be seen in the diffractogram, and the absorption edge is shifted to higher wavelengths in the UV/vis spectrum. However, a second absorption edge similar to that of the amorphous material is present. After applying the Tauc plot, this sample fraction becomes more visible. Thus, two band gap values of 2.01 and 1.75 eV could be determined corresponding to the bandgaps of amorphous and crystalline Sb₂S₃, respectively. Apparently, the particles are not yet fully crystallized at 240 °C, so the temperature must be held at this level for several minutes to allow a complete conversion. The crystallite sizes, derived from the Debye–Scherrer equation for different Laue indices, were about 35–50 nm, which is about 5 nm smaller than those of the final particles after 30 min reaction time at 240 °C. The particle diameter obtained from SEM, however, is identical to that at the end of the reaction, but with a diameter of more than 400 nm, they are significantly larger than the amorphous particles.

Characterization of the reaction intermediate

The results discussed in the last section suggest that there is an intermediate in the formation of the colloidal Sb₂S₃ particles. This intermediate is a white, crystalline substance with an atomic ratio of elements that almost corresponds to a composition of antimony and cysteine in a ratio of 1 : 3. The main difference to the atomic ratio of the elements in cysteine is that the value for hydrogen is decreased (∼0.5 atoms per theoretical cysteine molecule) and the value for oxygen is increased (∼0.2 atoms per theoretical cysteine molecule). Assuming that the sample contains some water, e.g., from the purification process or from handling in an ambient atmosphere, the basic building block of the intermediate could be Sb(C₃H₆NSO₂)₃·0.75H₂O.

To investigate the chemical structure of this substance further, Raman and IR spectroscopy, as well as an MS analysis, were performed. The results are shown in the ESI Fig. S9 and S10.† Comparing the IR and Raman spectra of sample PI (Fig. S9, ESI†) with the reference spectra of L-cysteine and L-cystine, the similarity is low for the spectra of cysteine but high for the spectra of cystine. In particular, the absence of the –SH vibration in the measured Raman spectrum should be noted. However, there is also a clear difference in the Raman spectrum between the measured spectrum and that of cystine. The strong signal at ∼500 cm⁻¹ assigned to the vibrational mode of the disulfide bond in cystine,⁶⁶ is not present. Instead, an intense mode at ∼355 cm⁻¹ is found. According to several reports, Sb–S stretching vibrations are found around these wavenumbers.^67,68

For the MS analysis, MALDI and EI were used to ionize the sample as the substance is not soluble in common solvents such as water or isopropanol. With MALDI, two molecular patterns are visible in the spectrum, around 496.9 u and 707.9 u. However, these patterns suggest molecules consisting of one antimony atom, at most one sulfur atom, and mainly cysteine residues with no sulfur but an increased amount of oxygen. Since this is inconsistent with the elemental analysis, the molecule is assumed to be a highly crosslinked polymer with a molecular weight greater than 100 kDa, which is above the mass limit of MALDI for polymeric species.⁶⁹ The molecular patterns found could be due to a slight degradation by oxygen.

With EI, in addition to several Sb_x and Sb_xO_y fragments, the fragmentation pattern shown in Fig. S10(a)† was obtained. The pattern has similarities to both the cysteine and cystine patterns (Fig. S10(b) and (c),† respectively), indicating that the structure is probably intermediate between the two.

In summary, the intermediate substance is assumed to have the following properties:

1. General composition of Sb(C₃H₆NSO₂)₃.

2. Structure of the organic part in between cysteine and cystine.

3. –C–S and –Sb–S bonds but no –S–H or –S–S bonds.

4. Large, crosslinked molecule with M_w > 100 kDa.

5. No absorption in the visible spectrum.

There are also several reports of Sb(III) covalently bound to organic molecules and, additionally, complexed by other molecules, resulting in a 4- or 5-fold coordinated structure.^70–72 Thus, a molecule would be conceivable in which Sb(III) is covalently bound to the S atom of three cysteine molecules and coordinated to the carboxyl group and/or to the amino group of one or two other cysteine molecules. The coordinative bonds would also lead to crosslinking. However, further analysis is needed to determine the exact structure of this molecule.

Matrix analysis

The matrix appears to prevent the amorphous particles from growing into large (micron-sized) rods during crystallization, so they tend to crystallize into a spherical shape. For this reason, the composition of the matrix was studied in more detail. Table 2 shows the results of the CHNS/O analysis, AAS, and EDX of non-purified samples at 140 °C (MI), 170 °C (MII), and at the end of the synthesis (Mfinal). Non-purified means that the samples were only washed with hexane to remove the ODE but not the matrix.

Table 2 Elemental (atomic) composition of three samples at different reaction stages, including the matrix

Sample	MI	MII	Mfinal
Temp. (°C)	140	170	240, 30 min
Sb	1.0	1.0	1.0
S	7.4	6.6	2.0
C	33.7	35.0	8.1
H	73.8	77.5	15.4
N	7.4	7.5	3.3
O	14.2	13.4	1.1
Cl	2.3	2.8	2.9

---

It can easily be seen that the Sb content of MI with respect to the organic moieties is less than half of that of PI. In addition, chlorine is present in the sample, and the stoichiometry of the organic moiety does not resemble cysteine. However, the ratio of S : N : O in the matrix is almost the same as that of cysteine. This result indicates that the increased C and H content originates from the ODE. This finding can also be correlated with the ratio of the excess amount of these two elements, which is 1 : 2; the same ratio as for ODE. It is assumed that the ODE molecules are embedded in the forming matrix, but a further reaction of them cannot be excluded.

It can also be seen that, in contrast to the sample PI, no excess oxygen can be found with respect to sulfur/nitrogen to match the ratio in cysteine. Furthermore, the Sb : S ratio (7.4 : 1) is lower than the ratio at the beginning of the synthesis (1 : 5). This is another indication that the excess H and O atoms of PI originate from washing with water. It can be further concluded that some antimony is lost during the purification process.

As the reaction progresses, the amounts of S and O decrease, while the amounts of C, H, and Cl increase slightly relative to Sb. The decrease in S and O indicates the beginning of cysteine decomposition. However, the amino group seems to belong to a solid rather than a gaseous decomposition product because the amount of N increases relatively to C, H, S, and O. Variations in C and H could be explained by slight differences in the embedding of the ODE into the matrix or an ongoing reaction with it.

The ratio of Sb and Cl is close to their ratio in SbCl₃. It is assumed that not all SbCl₃ has reacted at 140 °C. Since SbCl₃ is thermally unstable, it is likely that unreacted material decomposed under electron beam exposure in the SEM, resulting in Sb residues as the chlorine components evaporated.

At the end of the reaction, the amounts of C, H, N, S, and O decreased due to the decomposition of cysteine starting around 200 °C.⁷³ The main compartments of the residues are N, C, and H. The amount of Cl did not change. It seems to form a stable compound part of the matrix.

Thus, the matrix appears to be a compound derived from cysteine, ODE, and chlorine that decomposes to a different composition upon heating.

Conclusions

In summary, a one-pot synthesis for the preparation of spherical crystalline sub-micron Sb₂S₃ particles has been established. In ODE, the insoluble precursors, SbCl₃ and cysteine, form an intermediate upon heating. In addition, excess cysteine, ODE, and chloride from SbCl₃ form a matrix that encapsulates this intermediate and prevents the initially resulting amorphous particles from aggregating and restructuring into large rod-like shapes upon crystallization. The matrix is removable and the purified particles are stable in dispersion.

It was shown that the intermediate of the particles is likely to consist of a complex architecture with a high degree of crosslinking. The basic building block of the intermediate is assumed to be an Sb atom bound to three cysteine molecules via a covalent Sb–S bond. These units are connected by coordinative bonds between Sb and the other functional groups of the cysteine molecules.

The matrix is formed from cysteine, the solvent ODE, and chlorine from the SbCl₃. Due to partial decomposition, the composition of the matrix changes during the heat-up process. It may be worthwhile to try mixing in another amino acid, such as glycine, and examine the effect on the particle size and shape.

The concept of encapsulation for size and/or shape control of colloid particles could be transferrable to other materials. Depending on the particle system, it may allow an extension of the size range to smaller particles and force nearly isotropic growth for anisotropic materials. In such approaches, the use of cysteine or cysteine–amino acid mixtures may be applicable to various other sulfide materials.⁷⁴

Author contributions

M. Joschko: design and development of the synthesis, characterization of the samples, and preparation of the original draft. C. Malsi: design and development of the synthesis. P. Scharmann and J. Rapier: optimization of the synthesis. S. Selve: TEM measurements. C. Graf: acquisition of funding, supervision, project management, review, and editing of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We greatly acknowledge the support of W. Mosch (Darmstadt University of Applied Sciences, AAS measurements), the research group of C. Hess (Technische Universität Darmstadt, Raman measurements), A. Schieβer and the mass spectrometry core facility team of the Chemistry Department (Technische Universität Darmstadt, EI and MALDI measurements) as well as the German Research Foundation (DFG) through grant no INST 163/445-1 FUGG, and T. Reich (Johannes-Gutenberg-Universität Mainz, XPS measurements). This work was financially supported by a fellowship of the platform for PhD students of Technische Universität Darmstadt and Darmstadt University of Applied Sciences, by the Graduate School of the Darmstadt University of Applied Sciences, and by a mid-level faculty position at Darmstadt University of Applied Sciences.

References

1. H. Gruber, The learning curve in the production of semiconductor memory chips, Appl. Econ., 1992, 24, 885–894.
2. X. Hu, P. Krull, B. de Graff, K. Dowling, J. A. Rogers and W. J. Arora, Stretchable inorganic-semiconductor electronic systems, Adv. Mater., 2011, 23, 2933–2936.
3. A. Tricoli, M. Righettoni and A. Teleki, Semiconductor gas sensors: dry synthesis and application, Angew. Chem., Int. Ed., 2010, 49, 7632–7659.
4. L. Wang, J. Zhao, H. Liu and J. Huang, Design, modification and application of semiconductor photocatalysts, J. Taiwan Inst. Chem. Eng., 2018, 93, 590–602.
5. I. V. Martynenko, A. P. Litvin, F. Purcell-Milton, A. V. Baranov, A. V. Fedorov and Y. K. Gun’ko, Application of semiconductor quantum dots in bioimaging and biosensing, J. Mater. Chem. B, 2017, 5, 6701–6727.
6. L. M. Peter, Towards sustainable photovoltaics: the search for new materials, Philos. Trans. R. Soc., A, 2011, 369, 1840–1856.
7. F. Cao, W. Liu, L. Zhou, R. Deng, S. Song, S. Wang, S. Su and H. Zhang, Well-defined Sb₂S₃ microspheres: high-yield synthesis, characterization, their optical and electrochemical hydrogen storage properties, Solid State Sci., 2011, 13, 1226–1231.
8. S. Shaji, A. Arato, J. J. O'Brien, J. Liu, G. A. Castillo, M. I. M. Palma, T. K. D. Roy and B. Krishnan, Chemically deposited Sb₂S₃ thin films for optical recording, J. Phys. D: Appl. Phys., 2010, 43, 75404.
9. R. Tang, X. Wang, C. Jiang, S. Li, G. Jiang, S. Yang, C. Zhu and T. Chen, Vacuum assisted solution processing for highly efficient Sb₂S₃ solar cells, J. Mater. Chem. A, 2018, 6, 16322–16327.
10. X. Wang, R. Tang, C. Wu, C. Zhu and T. Chen, Development of antimony sulfide–selenide Sb₂(S, Se)₃-based solar cells, J. Energy Chem., 2018, 27, 713–721.
11. I. L. Validžić, V. Janošević and M. Mitrić, Characterization and current-voltage characteristics of solar cells based on the composite of synthesized Sb₂S₃ powder with small band gap and natural dye, Environ. Prog. Sustainable Energy, 2016, 35, 512–516.
12. M. Y. Versavel and J. A. Haber, Structural and optical properties of amorphous and crystalline antimony sulfide thin-films, Thin Solid Films, 2007, 515, 7171–7176.
13. R. K. Sahoo, S. Singh, J. M. Yun, S. H. Kwon and K. H. Kim, Sb₂S₃ Nanoparticles Anchored or Encapsulated by the Sulfur-Doped Carbon Sheet for High-Performance Supercapacitors, ACS Appl. Mater. Interfaces, 2019, 11, 33966–33977.
14. Q. Zhang, Y. Zeng, X. Wang, L. Wang, H. Wang, J. Xiao and X. Li, Sb₂S₃ nanoparticles anchored on N-doped 3D carbon nanofibers as anode material for sodium ion batteries with improved electrochemical performance, J. Alloys Compd., 2021, 881, 160594.
15. M. A. Farhana, A. Manjceevan and J. Bandara, Recent advances and new research trends in Sb₂S₃ thin film based solar cells, J. Sci.: Adv. Mater. Devices, 2023, 8, 100533.
16. X. Li, J. Bai, B. Zhou, X. Yuan, X. Zhang and L. Liu, High Performance of 3D Symmetric Flowerlike Sb₂S₃ Nanostructures in Dye-Sensitized Solar Cells, Chem.–Eur. J., 2018, 24, 11444–11450.
17. W. Wang, F. Strössner, E. Zimmermann and L. Schmidt-Mende, Hybrid solar cells from Sb₂S₃ nanoparticle ink, Sol. Energy Mater. Sol. Cells, 2017, 172, 335–340.
18. H. Hosono, 68.3: Invited Paper: Transparent Amorphous Oxide Semiconductors for High Performance TFT, SID Int. Symp. Dig. Tech. Pap., 2007, 38, 1830–1833.
19. H. Alves, R. M. Pinto and E. S. Maçôas, Photoconductive response in organic charge transfer interfaces with high quantum efficiency, Nat. Commun., 2013, 4, 1842.
20. W. Lou, M. Chen, X. Wang and W. Liu, Novel Single-Source Precursors Approach to Prepare Highly Uniform Bi₂S3 and Sb₂S₃ Nanorods via a Solvothermal Treatment, Chem. Mater., 2007, 19, 872–878.
21. J. Ota, P. Roy, S. K. Srivastava, B. B. Nayak and A. K. Saxena, Morphology Evolution of Sb₂S₃ under Hydrothermal Conditions: Flowerlike Structure to Nanorods, Cryst. Growth Des., 2008, 8, 2019–2023.
22. P. Salinas-Estevané and E. M. Sánchez, Preparation of Sb₂S₃ Nanostructures by the Ionic Liquid-Assisted Sonochemical Method, Cryst. Growth Des., 2010, 10, 3917–3924.
23. A. M. Salem and M. S. Selim, Structure and optical properties of chemically deposited Sb₂S₃ thin films, J. Phys. D: Appl. Phys., 2001, 34, 12–17.
24. G. Murtaza, M. Akhtar, M. Azad Malik, P. O'Brien and N. Revaprasadu, Aerosol assisted chemical vapor deposition of Sb₂S₃ thin films: environmentally benign solar energy material, Mater. Sci. Semicond. Process., 2015, 40, 643–649.
25. A. K. Dutta, S. K. Maji, K. Mitra, A. Sarkar, N. Saha, A. B. Ghosh and B. Adhikary, Single source precursor approach to the synthesis of Bi₂S₃ nanoparticles: a new amperometric hydrogen peroxide biosensor, Sens. Actuators, B, 2014, 192, 578–585.
26. R. Piras, M. Aresti, M. Saba, D. Marongiu, G. Mula, F. Quochi, A. Mura, C. Cannas, M. Mureddu, A. Ardu, G. Ennas, V. Calzia, A. Mattoni, A. Musinu and G. Bongiovanni, Colloidal synthesis and characterization of Bi₂S₃ nanoparticles for photovoltaic applications, J. Phys.: Conf. Ser., 2014, 566, 12017.
27. I. Uddin, S. M. Abzal, K. Kalyan, S. Janga, A. Rath, R. Patel, D. K. Gupta, T. R. Ravindran, H. Ateeq, M. S. Khan and J. K. Dash, Starch-Assisted Synthesis of Bi₂S₃ Nanoparticles for Enhanced Dielectric and Antibacterial Applications, ACS Omega, 2022, 7, 42438–42445.
28. M. Abulikemu, S. Del Gobbo, D. H. Anjum, M. A. Malik and O. M. Bakr, Colloidal Sb₂S₃ nanocrystals: synthesis, characterization and fabrication of solid-state semiconductor sensitized solar cells, J. Mater. Chem. A, 2016, 4, 6809–6814.
29. M. Joschko, F. Y. Fotue Wafo, C. Malsi, D. Kisić, I. Validžić and C. Graf, Revealing the formation mechanism and band gap tuning of Sb₂S₃ nanoparticles, Beilstein J. Nanotechnol., 2021, 12, 1021–1033.
30. N. Maiti, S. H. Im, Y. H. Lee and S. I. Seok, Urchinlike nanostructure of single-crystalline nanorods of Sb₂S₃ formed at mild reaction condition, ACS Appl. Mater. Interfaces, 2012, 4, 4787–4791.
31. J. Chao, B. Liang, X. Hou, Z. Liu, Z. Xie, B. Liu, W. Song, G. Chen, D. Chen and G. Shen, Selective synthesis of Sb₂S₃ nanoneedles and nanoflowers for high performance rigid and flexible photodetectors, Opt. Express, 2013, 21, 13639–13647.
32. J. Ma, X. Duan, J. Lian, T. Kim, P. Peng, X. Liu, Z. Liu, H. Li and W. Zheng, Sb₂S₃ with various nanostructures: controllable synthesis, formation mechanism, and electrochemical performance toward lithium storage, Chem.–Eur. J., 2010, 16, 13210–13217.
33. K. V. Kravchyk, M. V. Kovalenko and M. I. Bodnarchuk, Colloidal Antimony Sulfide Nanoparticles as a High-Performance Anode Material for Li-ion and Na-ion Batteries, Sci. Rep., 2020, 10, 2554.
34. H. Wang, Y.-N. Lu, J.-J. Zhu and H.-Y. Chen, Sonochemical fabrication and characterization of stibnite nanorods, Inorg. Chem., 2003, 42, 6404–6411.
35. A. House, A. Kuna, D. Hastings, N. Rodriguez, M. Schoenitz, E. L. Dreizin and M. Guvendiren, Effect of particle shape on rheology and printability of highly filled reactive inks for direct ink writing, Prog. Addit. Manuf., 2023, 8, 1573–1585.
36. L. Zhang, G. Feng, Z. Zeravcic, T. Brugarolas, A. J. Liu and D. Lee, Using shape anisotropy to toughen disordered nanoparticle assemblies, ACS Nano, 2013, 7, 8043–8050.
37. E. Enríquez, J. J. Reinosa, V. Fuertes and J. F. Fernández, Advances and challenges of ceramic pigments for inkjet printing, Ceram. Int., 2022, 48, 31080–31101.
38. Y. Huang, L. Jiang, B. Li, P. Premaratne, S. Jiang and H. Qin, Study effects of particle size in metal nanoink for electrohydrodynamic inkjet printing through analysis of droplet impact behaviors, J. Manuf. Process., 2020, 56, 1270–1276.
39. Q. Wei, D. Chang, Z. Ye, X. Li, L. Zan, L. Gao, F. Fu and D. Yang, Giant improvement of performances of perovskite solar cells via component engineering, J. Colloid Interface Sci., 2021, 588, 393–400.
40. H. Kamiya, K. Gotoh, M. Shimada, T. Uchikoshi, Y. Otani, M. Fuji, S. Matsusaka, T. Matsuyama, J. Tatami, K. Higashitani, K. Kurihara, N. Ishida, M. Suzuki, H. Abe, Y. Otsubo and M. Miyahara, Characteristics and Behavior of Nanoparticles and its Dispersion Systems, Elsevier, Amsterdam, 2008.
41. M. Baalousha, A. Manciulea, S. Cumberland, K. Kendall and J. R. Lead, Aggregation and surface properties of iron oxide nanoparticles: influence of pH and natural organic matter, Environ. Toxicol. Chem., 2008, 27, 1875–1882.
42. Z. Somosi, M. Pavlovic, I. Pálinkó and I. Szilágyi, Effect of Polyelectrolyte Mono- and Bilayer Formation on the Colloidal Stability of Layered Double Hydroxide Nanoparticles, Nanomater, 2018, 8, 986.
43. Y. Zhu, F. Y. Jiang, K. Chen, F. Kang and Z. K. Tang, Size-controlled synthesis of monodisperse superparamagnetic iron oxide nanoparticles, J. Alloys Compd., 2011, 509, 8549–8553.
44. J. Park, K. An, Y. Hwang, J.-G. Park, H.-J. Noh, J.-Y. Kim, J.-H. Park, N.-M. Hwang and T. Hyeon, Ultra-large-scale syntheses of monodisperse nanocrystals, Nat. Mater., 2004, 3, 891–895.
45. V. Pawlik, S. Zhou, S. Zhou, D. Qin and Y. Xia, Silver Nanocubes: From Serendipity to Mechanistic Understanding, Rational Synthesis, and Niche Applications, Chem. Mater., 2023, 35, 3427–3449.
46. W. H. Eisa, Y. K. Abdel-Moneam, Y. Shaaban, A. A. Abdel-Fattah and A. M. Abou Zeid, Gamma-irradiation assisted seeded growth of Ag nanoparticles within PVA matrix, Mater. Chem. Phys., 2011, 128, 109–113.
47. A. Alexandrov, L. Smirnova, N. Yakimovich, N. Sapogova, L. Soustov, A. Kirsanov and N. Bityurin, UV-initiated growth of gold nanoparticles in PMMA matrix, Appl. Surf. Sci., 2005, 248, 181–184.
48. T. Di Luccio, A. M. Laera, L. Tapfer, S. Kempter, R. Kraus and B. Nickel, Controlled nucleation and growth of CdS nanoparticles in a polymer matrix, J. Phys. Chem. B, 2006, 110, 12603–12609.
49. J. Ibáñez, J. A. Sans, C. Popescu, J. López-Vidrier, J. J. Elvira-Betanzos, V. P. Cuenca-Gotor, O. Gomis, F. J. Manjón, P. Rodríguez-Hernández and A. Muñoz, Structural, Vibrational, and Electronic Study of Sb₂S₃ at High Pressure, J. Phys. Chem. C, 2016, 120, 10547–10558.
50. Y. F. Zhu, D. H. Fan and W. Z. Shen, Chemical conversion synthesis and optical properties of metal sulfide hollow microspheres, Langmuir, 2008, 24, 11131–11136.
51. J. Pan, S. Xiong, B. Xi, J. Li, J. Li, H. Zhou and Y. Qian, Tartatric Acid and L-Cysteine Synergistic-Assisted Synthesis of Antimony Trisulfide Hierarchical Structures in Aqueous Solution, Eur. J. Inorg. Chem., 2009, 2009, 5302–5306.
52. B. D. Viezbicke, S. Patel, B. E. Davis and D. P. Birnie, Evaluation of the Tauc method for optical absorption edge determination: ZnO thin films as a model system, Phys. Status Solidi B, 2015, 252, 1700–1710.
53. J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J.-Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Fiji: an open-source platform for biological-image analysis, Nat. Methods, 2012, 9, 676–682.
54. U. Holzwarth and N. Gibson, The Scherrer equation versus the ‘Debye-Scherrer equation’, Nat. Nanotechnol., 2011, 6, 534.
55. P. Kubelka and F. Munk, An Article on Optics of Paint Layers, Z. Tech. Phys., 1931, 12, 593–601.
56. J. Tauc, R. Grigorovici and A. Vancu, Optical Properties and Electronic Structure of Amorphous Germanium, Phys. Status Solidi B, 1966, 15, 627–637.
57. E. A. Davis and N. F. Mott, Conduction in non-crystalline systems V. Conductivity, optical absorption and photoconductivity in amorphous semiconductors, Philos. Mag., 1970, 22, 903–922.
58. H. Lei, T. Lin, X. Wang, S. Zhang, Q. Cheng, X. Chen, Z. Tan and J. Chen, A novel in situ hydrothermal preparation route for Sb₂S₃ and its solar cell application, Mater. Lett., 2018, 233, 90–93.
59. G. Wang and C. L. Cheung, Building crystalline Sb₂S₃ nanowire dandelions with multiple crystal splitting motif, Mater. Lett., 2012, 67, 222–225.
60. Q. Han, S. Sun, D. Sun, J. Zhu and X. Wang, Room-temperature synthesis from molecular precursors and photocatalytic activities of ultralong Sb₂S₃ nanowires, RSC Adv., 2011, 1, 1364.
61. C. Gao, J. Huang, H. Li, K. Sun, Y. Lai, M. Jia, L. Jiang and F. Liu, Fabrication of Sb₂S₃ thin films by sputtering and post-annealing for solar cells, Ceram. Int., 2019, 45, 3044–3051.
62. F. Perales, G. Lifante, F. Agulló-Rueda and C. d. l. Heras, Optical and structural properties in the amorphous to polycrystalline transition in Sb₂S₃ thin films, J. Phys. D: Appl. Phys., 2007, 40, 2440–2444.
63. N. Ţigau, C. Gheorghieş, G. I. Rusu and S. Condurache-Bota, The influence of the post-deposition treatment on some physical properties of Sb₂S₃ thin films, J. Non-Cryst. Solids, 2005, 351, 987–992.
64. R. Vadapoo, S. Krishnan, H. Yilmaz and C. Marin, Self-standing nanoribbons of antimony selenide and antimony sulfide with well-defined size and band gap, Nanotechnology, 2011, 22, 175705.
65. M. R. Filip, C. E. Patrick and F. Giustino, GW quasiparticle band structures of stibnite, antimonselite, bismuthinite, and guanajuatite, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 205125.
66. Y. Su, E. P. Hessou, E. Colombo, G. Belletti, A. Moussadik, I. T. Lucas, V. Frochot, M. Daudon, S. Rouzière, D. Bazin, K. Li, P. Quaino and F. Tielens, Crystalline structures of L-cysteine and L-cystine: a combined theoretical and experimental characterization, Amino acids, 2022, 54, 1123–1133.
67. O. S. Urgut, I. I. Ozturk, C. N. Banti, N. Kourkoumelis, M. Manoli, A. J. Tasiopoulos and S. K. Hadjikakou, Addition of tetraethylthiuram disulfide to antimony(III) iodide; synthesis, characterization and biological activity, Inorg. Chim. Acta, 2016, 443, 141–150.
68. J. A. Tossell, The speciation of antimony in sulfidic solutions: a theoretical study, Geochim. Cosmochim. Acta, 1994, 58, 5093–5104.
69. C. Wesdemiotis, K. N. Williams-Pavlantos, A. R. Keating, A. S. McGee and C. Bochenek, Mass spectrometry of polymers: a tutorial review, Mass Spectrom. Rev., 2024, 43, 427–476.
70. L. Dostál, R. Jambor, A. Růžička, A. Lyčka, J. Brus and F. de Proft, Synthesis and Structure of Organoantimony(III) Compounds Containing Antimony−Selenium and −Tellurium Terminal Bonds, Organometallics, 2008, 27, 6059–6062.
71. I. I. Ozturk, C. N. Banti, N. Kourkoumelis, M. J. Manos, A. J. Tasiopoulos, A. M. Owczarzak, M. Kubicki and S. K. Hadjikakou, Synthesis, characterization and biological activity of antimony(III) or bismuth(III) chloride complexes with dithiocarbamate ligands derived from thiuram degradation, Polyhedron, 2014, 67, 89–103.
72. M. Tella and G. S. Pokrovski, Antimony(III) complexing with O-bearing organic ligands in aqueous solution: an X-ray absorption fine structure spectroscopy and solubility study, Geochim. Cosmochim. Acta, 2009, 73, 268–290.
73. I. M. Weiss, C. Muth, R. Drumm and H. O. K. Kirchner, Thermal decomposition of the amino acids glycine, cysteine, aspartic acid, asparagine, glutamic acid, glutamine, arginine and histidine, BMC Biophys., 2018, 11, 2.
74. F. Jamal, A. Rafique, S. Moeen, J. Haider, W. Nabgan, A. Haider, M. Imran, G. Nazir, M. Alhassan, M. Ikram, Q. Khan, G. Ali, M. Khan, W. Ahmad and M. Maqbool, Review of Metal Sulfide Nanostructures and their Applications, ACS Appl. Nano Mater., 2023, 6, 7077–7106.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4na00020j

---