Green-chemistry synthesis and optical properties of lead-free Cs₂AgSbCl₆ double perovskite by a mechanochemical method

Abstract

Cs₂AgSbCl₆ double perovskite (DP) has been synthesized through many solid-state and solution routes. Still, using unsustainable solvents and complicated synthesis processes are unattractive for large-scale manufacturing. The synthesis of Cs₂AgSbCl₆ using a green approach, mechanosynthesis, offers a sustainable alternative to traditional methods, reducing the environmental impact of solvents and complex processes. X-ray diffraction confirms its double perovskite cubic structure with the space group Fm3̄m (225) and unit cell parameter a = 10.674(2) Å. Diffuse reflectance measurements indicate a slightly smaller indirect band gap (2.61 eV) than chemically synthesized perovskites. The compound demonstrates stability in air and under light. The electronic structure and optical properties of the host material are calculated using quasi-particle theory GW approximation and the Bethe–Salpeter equation (BSE), including the spin–orbit coupling (SOC); the latter is responsible for the emergence of an intermediate conduction band. These findings suggest that double halide perovskite semiconductors, exemplified by the Cs₂AgSbCl₆ DP, can be an eco-friendly alternative to lead halide perovskite semiconductors.

---

Lead-based perovskites remain at the forefront of materials used in cutting-edge devices like light-emitting diodes (LEDs),^1,2 solar cells,³ lasers,² and photodetectors⁴ due to their exceptional efficiency.^4–6 However, their commercial viability and widespread adoption face a significant challenge in the form of lead toxicity. To address this concern, researchers have developed an intriguing alternative: lead-free halide double perovskites, characterized by the general chemical formula A₂M′M′′X₆, where A represents a monovalent metal cation (typically Cs⁺), M′ stands for a monovalent cation (such as Ag⁺ or Cu⁺), M′′ represents a trivalent metal cation (e.g., Sb³⁺, In³⁺, and Bi³⁺), and X denotes a halide anion (like Cl⁻, Br⁻, or I⁻).⁴ Lead-free halide double perovskites present a diverse array of characteristics that position them as strong contenders against lead-based perovskites, boasting attributes such as extended recombination lifetimes at room temperature, enhanced resilience to heat and moisture, and more sustainability.^7,8

The first Cs₂AgSbCl₆ (CASC) lead-free halide double perovskite was synthesized via a solution-state reaction aiming at promising photovoltaic absorber applications with an optical band gap of 2.6 eV.⁹ After that, colloidal Cs₂AgInCl₆ (CAIC) and Cs₂AgSbCl₆ nanocrystals were synthesized by injecting acyl halides into a metal acetate solution under atmospheric conditions and relatively mild temperatures. The Tauc analysis of concentrated nanocrystal absorption spectra results in band gaps with an indirect gap of 2.57 ± 0.05 eV for Cs₂AgSbCl₆ and a direct gap of 3.57 ± 0.03 eV for CAIC;¹⁰ Zhou et al. reported Cs₂AgSbCl₆ microcrystals synthesized by a hydrothermal method in a stainless steel Parr autoclave, which showed stability in air for several weeks.⁸ Nowadays, halide double perovskites can be synthesized in various ways, such as colloidal, mechanochemical, anti-solvent reprecipitation, hot injection, and solvothermal methods.⁴ However, as far as we are concerned, no green synthesis reports exist in the literature for Cs₂AgSbCl₆ compounds. In this context, we adopted a mechanochemical method to synthesize Cs₂AgSbCl₆ polycrystals as an alternative synthesis route to evaluate the structural changes promoted by milling times.

Mechanochemistry involves the initiation of chemical reactions through the application of mechanical energy, which can be generated by various forces and operating modes, including impact, compression, or shear.¹¹ It has several advantages over the most commonly used solution-based processes, such as lower inherent toxicity, little or no solvent participation in the synthesis, and secondary phase suppression.^3,11,12 Further advantages are the formation of high-purity phases with outstanding stability in lead-based perovskites, rapidity, simplicity, and reproducibility, coupled with significant potential for expanding the method to design diverse structures.^11,13 Mechanochemical synthesis (MCS) has proven effective in producing a diverse range of quantum dots (QDs),^14–16 encompassing all-inorganic and organohalide perovskites^12,17,18 and double perovskite (DP) configurations.^3,19,20 MCS proved to be a promising synthesis route for the production of halide double perovskites such as Cs₂AgBiBr₆ (CABB); such powders were successfully prepared by mechanochemical synthesis by Kubicki et al. They synthesized a wide range of mixed-halide Cs₂AgBiX₆ (X = Cl, Br, and I) double perovskites and employed solid-state ¹³³Cs MAS NMR to identify the miscibility limits of the different halides.²⁰ The work of Rodkey et al. demonstrated the estimated mass fractions of different phases formed in each milling stage until the formation of the pure Cs₂AgBiBr₆ phase (derived from Rietveld refinements using powder XRD data) and the band gap evolution as a function of grinding time.³

The Cs₂AgSbCl₆ double perovskite has a face-centered cubic structure (space group Fm3̄m), with a unit cell parameter a = 10.6682(1) Å.^9,21 It exhibits a semiconducting behavior with an indirect band gap of 2.7 eV,^21,22 which limits applications in some photovoltaic and optoelectronic devices due to moderate solar spectrum absorption.^22,23

In this work, we demonstrate the synthesis of a lead-free inorganic double perovskite phase based on Cs₂AgSbCl₆ by mechanochemistry with different milling times. The structural characteristics showed that the milling time plays a fundamental role in forming the monophasic polycrystalline compound. We present a phase diagram formation derived from Rietveld refinements of powder XRD data. Also, we have calculated the electronic structure and the optical properties of Cs₂AgSbCl₆ using state-of-the-art quasi-particle methods such as GW and BSE.

1 Methods

1.1 Materials

CsCl (Inlab Confiança, 99.9%, 168.36 g mol⁻¹), AgCl (Alfa Aesar, 99.5%, 143.32 g mol⁻¹), SbCl₃ (Alfa Aesar, 99%, 228.12 g mol⁻¹), and HCl (Synth 38 wt% in water) were purchased and used as received without further purification.

1.2 Synthesis of Cs₂AgSbCl₆ polycrystals

The inorganic Cs₂AgSbCl₆ double perovskite powder was first synthesized by mechanochemical grinding (i.e., ball milling) following previously reported methods for lead halide perovskites.^11,20 The ball milling process used 1 μL HCl as solvent. CsCl, AgCl, and SbCl₃ were mixed in a 2 : 1 : 1 molar ratio. Ball milling was carried out at 30 Hz for different times (2, 5, 10, 15, and 60 minutes) to produce Cs₂AgSbCl₆ (for more details see the ESI†).

1.3 Characterization

Room-T powder X-ray diffraction (PXRD) data were collected on an STADI-P (STOE^®, Darmstadt, Germany) diffractometer operating in transmission mode to confirm the phase purity and/or the mass fractions of the different phases formed at each stage. We used monochromatic Cu Kα₁ (λ = 1.5406 Å) radiation selected using a curved Ge(111) monochromator, operating at a tube voltage of 40 kV and a current of 40 mA. Data were recorded with a Mythen 1K (Dectris^®, Baden, Switzerland) from 10° to 90° (2θ), in steps of 0.015°, and a counting time of 100 s at each 1.05°. Data have been analyzed using the Rietveld method^24,25 implemented in the program TOPAS-Academic v.7.²⁶ Morphological studies and elemental analysis of materials were carried out by scanning electron microscopy (SEM) (JEOL JSM-6010LA, Pleasanton, CA, USA). The average SEM particle sizes were evaluated with ImageJ software.²⁷ Crystallographic and structural investigations of the perovskite samples were also carried out using high-resolution transmission electron microscopy (HRTEM) (TEM-Thermo Fischer Talos F200X-G2) operating at 200 kV accelerating voltage using a field emission gun (X-FEG). The HRTEM image and electron diffraction patterns obtained from TEM analysis of the Cs₂AgSbCl₆ samples were indexed using Single Crystal Software (Java Electron Microscopy Software). The optical diffuse reflectance spectra were recorded on a UV-Vis-NIR spectrophotometer (Varian Cary 5000, Santa Clara, CA, USA) equipped with an integrating sphere; BaSO₄ was used as a reference standard.

1.4 Electronic structure and optical property computational setup

Spin-polarized first-principles density functional theory (DFT) calculations, including the spin–orbit coupling (SOC), were carried out using the Vienna Ab initio Simulation Package (VASP).^28,29 For the exchange-correlation energy functional, we used the generalized gradient approximation (GGA) and its PBEsol parametrization.³⁰ The projector augmented wave³¹ atomic reference configurations to describe the valence electrons were Cs: 5s²5p⁶6s¹, Ag: 4d¹⁰5s¹, Sb: 5s²5p³ and Cl: 3s²3p⁵. During all calculations, we maintained an energy cut-off of 340 eV and 324 conduction bands, and a stopping criterion of 10⁻⁸ eV for the electronic minimization loop. The Brillouin zone (BZ) was sampled with a uniformly spaced 4 × 4 × 4 k-grid centered at Γ and a Gaussian smearing of 0.01 eV.

To obtain the excited states, quasi-particle (QP) gap, and optical properties, we have used many-body perturbation theory within the G₀W₀ approximation^32–34 and the Bethe–Salpeter equation (BSE) within the Tamm–Dancoff approximation.^35–37 To perform the G₀W₀ calculations, we have kept the same input setup but with different projector augmented wave atomic reference configurations especially designed to produce accurate high-energy scattering properties above the vacuum level, and finally the number of frequency points used was 360. To record the absorption spectrum (the imaginary part of the frequency-dependent dielectric function) including the electron–hole (e–h) interaction (excitonic properties), the BSE Hamiltonian was set with 12 valence and 12 conduction bands, respectively.

2 Results

White to almost yellow-colored powders were obtained for different milling times and then subjected to heat treatment at 100 °C for 12 h (see Fig. 1(a)).

Fig. 1 (a) Photographs and (b) the phase concentration for the Cs₂AgSbCl₆ double perovskite after varying ball-milling times, derived from Rietveld refinements using XRPD data.

The crystal structure evolution of the samples as a function of the mixing time was studied by PXRD. The mass fractions of the different phases by increasing milling times are shown in Fig. 1(b), which were derived from Rietveld refinements using PXRD data, as illustrated in the ESI.†. It is possible to observe that the binary precursors react very quickly in the first few minutes, and their phases are suppressed after 10 minutes. After 2 minutes of milling, we observed a white powder related to the CsAgCl₂ (ICSD 1509264) bimetallic halide phase.³⁸ However, this phase is not observed with increasing milling times, suggesting that the reaction occurs preferentially for other phases. Below a milling time of 20 minutes, the samples contain a mixture of a cubic AgCl-phase (ICSD 56538), the 2D-Cs₃Sb₂Cl₉ (ICSD 22075) perovskite, and the Cs₂AgSbCl₆ (ICSD 244674) double perovskite, a behavior similar to that reported by Rodkey et al.,³ which suggests that CsCl and SbCl₃ precursors are the first to be incorporated into the Cs₂AgSbCl₆ phase and AgCl is the last one. Motivated by this observation, we propose a possible mechanochemical reaction for milling times above 20 minutes.

CsCl + AgCl → CsAgCl₂ (1)

3CsCl + 2SbCl₃ → Cs₃Sb₂Cl₉ (2)

Cs₃Sb₂Cl₉ + CsAgCl₂ + AgCl → 2Cs₂AgSbCl₆ (3)

As shown in the powder X-ray diffractograms (Fig. 2), as the milling time increases, the AgCl (0.16 wt% after 60 minutes of milling) and the Cs₃Sb₂Cl₉ concentrations decrease until the primary phase is formed. It can be seen that the Cs₂AgCl₆ phase is already formed in 2 minutes of milling, coexisting with other phases (see Fig. 1(b)). The various chemical reactions described in eqn (1)–(3) promoted by the mechanical energy of the mixer mill contribute significantly to the formation of the Cs₂AgSbCl₆ pure phase.

Fig. 2 PXRD patterns of the Cs₂AgSbCl₆ double perovskite polycrystals obtained with different milling times.

Our exhaustive grinding tests revealed that AgCl was always present in the final compound in amounts as high as 6 wt%. We then realized to add an HCl droplet (1 μL) close to 60 minutes of grinding, i.e., 5 minutes before finishing the grinding process, and we opened the microtube and pipetted 1 μL of HCl into the mechanosynthesized powders, closed the microtube, and continued grinding for another 5 minutes. We used this solvent, as it is widely used in hydrothermal synthesis, to obtain Cs₂AgSbCl₆. In the work of Zhou et al., the amount of solvent was varied to evaluate the band gap of Cs₂AgSbCl₆. They found that their samples had excellent stability, and the analysis of the X-ray diffractograms from samples measured after one month of storage (in the ambient atmosphere) showed no evidence of the material's decomposition, thus indicating stability.⁸

It is possible to observe different XRD patterns for samples with the same stoichiometry (main phase) and under the same experimental conditions: one with neat grinding and the other with liquid-assisted grinding (LAG); see Fig. S6 and S8 (ESI).† In Fig. S6,† one can observe the presence of the Cs₂AgSbCl₆, AgCl and Cs₃Sb₂Cl₉ phases. Before finishing the grinding process (about 5 min before), 1 μL of HCl was added in an attempt to suppress the AgCl phase, and the rest of the grinding was completed. On the other hand, in Fig. S8,† after adding the HCl droplet, the 2D perovskite (Cs₃Sb₂Cl₉) disappeared and the amount of AgCl decreased. We believe that the addition of HCl, by decreasing the AgCl amount, would interfere with the stoichiometry of the main phase, by decreasing the Ag content and also decreasing the Cl content of AgCl. However, additional work has to be performed, using synchrotron high-resolution powder X-ray diffraction, to obtain confident site occupancies and isotropic displacement parameters. We have provided magnified regions of the diffractograms obtained without (Fig. S7) and with (Fig. S9) (ESI)† the addition of the HCl droplet. One can notice that we can unequivocally identity the presence of the Cs₃Sb₂Cl₉ phase in regard to the main Cs₂AgSbCl₆ phase.

Fig. 3 displays the room-temperature Rietveld plot for the Cs₂AgSbCl₆ sample after 1 hour of milling. We found that all peaks of the pattern were successfully indexed to a cubic crystal system with the space group Fm3̄m (225); the unit cell parameter a = 10.674(2) Å, g_of = 1.98, R_wp = 7.47%, and R_Bragg = 2.91% are in agreement with previous results.^9,21

Fig. 3 Room-T Rietveld plot of the powdered Cs₂AgSbCl₆ sample obtained after 1 hour of milling. The observed (black line), calculated (red line), and the difference (blue line) between the observed and calculated patterns revealing good visual agreement. The magenta and gray vertical bars indicate the primary and the minor AgCl (0.16 wt%) phase.

Fig. 4 shows the conventional unit cell of Cs₂AgSbCl₆ in the space group Fm3̄m; the fractional atomic coordinates are displayed in Table 1. Chlorine atoms (Cl) form a regular octahedron occupying the Wyckoff sites 24e. The Cs₂AgSbCl₆ cubic unit cell consists of a three-dimensional framework composed of corner-sharing alternating [AgCl₆] and [SbCl₆] octahedra. The Cs atoms are situated within the interstitial spaces created by these octahedra, leading to a doubled cell structure reminiscent of the elpasolite K₂NaAlF₆ arrangement.³⁹ Silver (Ag) and antimony (Sb) atoms occupy their unique Wyckoff sites (4b and 4a, respectively) as indicated in Table 1. The Ag and Sb atoms are located in the center of the octahedron and are equidistant from the 6 Cl atoms. The Ag–Cl and Sb–Cl interatomic distances are ∼2.648(2) Å and ∼2.694(8) Å, respectively. The Cs atoms are located in the cavities formed between the octahedra with Cs–Cl interatomic distances of 3.774(1) Å.

Fig. 4 Conventional unit cell of Cs₂AgSbCl₆ (space group Fm3̄m) showing the octahedra of the Sb (purple) and Ag (gray) sites; Cs (blue) shows the pseudo-octahedron. The interatomic distances of each Cs₂AgSbCl₆ element are extracted from Rietveld refinements.

Table 1 Fractional atomic coordinates and isotropic displacement parameters (Ų) of Cs₂AgSbCl₆

Atom	Wyckoff site	x	y	z	B iso
Cs	8c	1/4	1/4	1/4	5.67
Ag	4b	1/2	1/2	1/2	4.56
Sb	4a	0	0	0	4.15
Cl	24e	0.247(5)	0	0	5.84

---

No decomposition of the Cs₂AgSbCl₆ powder was identified; after 365 days, the same structure was observed (see Fig. S3†), but the color changed from yellow to pale yellow.

2.1 SEM measurements

For polycrystalline Cs₂SbAgCl₆, the scanning electron microscopy (SEM) image (Fig. 5) reveals a heterogeneous morphology of massive particles with clusters (5–10 μm) of fragments of undefined shapes. However, on a higher magnification image (Fig. 5), it is possible to observe that each particle is, in fact, formed by an agglomeration of much smaller grains of typically 0.5–1 μm. As illustrated in Fig. S10 (ESI),† the occurrence of particles with diverse shapes and the formation of larger aggregated clusters are frequent outcomes during the application of this mechanosynthesis method. In MAP-EDS, it was observed that the homogeneity in the powders suggests the absence of secondary phases after 60 minutes of grinding.

Fig. 5 SEM image of the Cs₂SbAgCl₆ polycrystalline material. The scale bar at the lower right of the SEM image is between 5 μm on a 3.700× magnification scale.

The elemental composition of the film determined by EDS, as shown in Table 2, was 19.68% Cs, 10.52% Ag, 10.94% Sb, and 61.8% Cl, the same as the expected composition of Cs₂AgSbCl₆ (20% Cs, 10% Ag, 10% Sb, and 60% Cl) within the EDS error.

Table 2 Energy dispersive scanning EDS for Cs₂AgSbCl₆

Atom	Mass%	mol%
Cl	29.11	58.86
Ag	15.83	10.52
Sb	18.57	10.94
Cs	36.49	19.68

---

2.2 HRTEM measurements

Fig. 6(a and b) show, respectively, low-magnification and high-resolution TEM (HRTEM) images of spherical nanoparticles of uniform size of the Cs₂AgSbCl₆ double perovskite.

Fig. 6 (a) Low-magnification and SAED pattern (inset) and (b) high-resolution transmission electron microscope images of a Cs₂AgSbCl₆ nanoparticle.

The FFT reveals the in-plane hexagonal atomic arrangement oriented along the 214 zone axis. The measured d spacings (see Table 3) for (242), (240), and (402) planes were observed from FFT presented as an inset in Fig. 6(b). The selected-area electron diffraction (SAED) pattern obtained over a large area (in the Fig. 6(a) inset) reveals the correspondence with the PXRD patterns in Fig. 3, indicating structural stability after treatment/synthesis.

Table 3 The interplanar spacing between the families of planes

Spot	d (Å)	d* (1 Å^−1)	Families of planes
1	2.132(43)	0.4690	(242)
2	2.318(46)	0.4314	(402)
3	2.424(48)	0.4126	(240)

---

2.3 UV-vis measurement

Fig. 7(a) depicts the optical absorption coefficient for the Cs₂AgSbCl₆ powdered sample related to the Kubelka–Munk function (F(R) = a = (1 − R)²/2R; R is the reflectance) versus energy (eV).

Fig. 7 Optical Properties of Cs₂AgSbCl₆ polycrystals. (a) UV-vis absorption spectra of Cs₂AgSbCl₆, with peaks centered at 376 and 275 nm and the (b) Tauc-plot for an indirect forbidden transition (fuchsia line) with a linear fit in the region of 2.6–3 eV.

The extrapolation of the linear region to the abscissa gives an indirect band gap; see the magenta line in Fig. 7(b). The value obtained for Cs₂AgSbCl₆ (∼2.61(3) eV) is in agreement with data reported in the literature for its band gap at room temperature^8–10,21,40

2.4 Electronic structure and optical properties

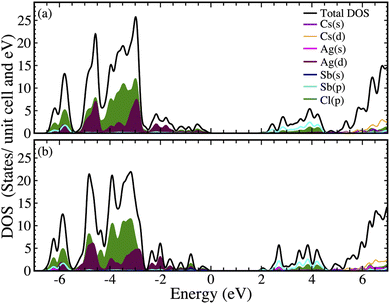
Fig. 8(a and b) show the QP dispersion relation for Cs₂AgSbCl₆ with and without SOC, respectively. The valence band maximum (VBM) and the conduction band minimum (CBM) are localized at the X and L points of the first-Brillouin zone (FBZ), respectively. The indirect calculated QP gaps are 2.22 eV and 2.26 eV with and without SOC, and the gaps at Γ are 4.59 and 4.23 eV. Furthermore, the calculated hole effective masses are −0.198 and −0.647 along the X–Γ and X–M directions without SOC, whereas they are −0.197 and −0.635, including SOC. On the other hand, the electron effective masses without SOC are 0.348 and 0.4 along the L–W and L–Γ directions, respectively, and with SOC, the obtained values are 0.355 and 0.413. Thus, the curvature of the dispersion relation in the neighborhood of the VBM and CBM is very similar with and without SOC. However, the main difference in the topology of the dispersion relation due to SOC is observed at the first bottom conduction bands (CBs), where the degeneracy is entirely left in the whole FBZ, except at Γ, where it is partially left. Furthermore, the SOC exposes an intermediate CB with a small width of 1.16 eV, then another two intermediate CBs that are degenerated at Γ with a width of 1.4 eV and then at higher energies are located the major contribution of the CBs. The presence of these intermediate bands can enhance the absorption of photons with lower energy by additional optical transitions, the first one from the valence band to the intermediate CBs and a second transition from the intermediate CBs to the main CBs, thus opening the prospect to improve thin-film solar cells efficiency exceeding the Shockley–Queisser limit.⁴¹

Fig. 8 Cs₂AgSbCl₆ QP dispersion relation (a) without and (b) including SOC.

The total and partial density of states (DOS) with and without SOC are shown in Fig. 9. The lower three valence bands (VBs) located between −6.5 to −5.4 eV are built up by the hybridization of Cl and Sb p-states with Ag d-states, and then the middle VBs situated across −5.2 eV to −2.6 eV are formed by the hybridization of Cl p and Ag d-states. The top three VBs placed between −2.8 to 0 eV show different orbital contributions, with the low band made up mainly of Ag d-states, and the two top VBs are the result of the hybridization of Cl p, Ag d, and Sb s-states. On the other hand, the bottom CBs are built up mainly by Sb p-states, and the next two intermediate CBs are formed by the hybridization of Sb p and Cl p-states with Ag s-states. Finally, the higher CBs are made from Cs s and Cl p-states.

Fig. 9 Cs₂AgSbCl₆ total and projected DOS (a) without and (b) including SOC.

Fig. 10 presents the imaginary part of the dielectric function (ε₂) calculated at the level of the independent-particle approximation (IPA) and including the electron–hole (e–h) interaction (BSE). First, we discuss the obtained results without the SOC; it is observed that the onset of the IPA spectrum starts around 3.4 eV and then there are four well-defined peaks around 3.87, 4.47, 4.59, and 5.02 eV; these peaks are attributed mainly to the transition between Sb-p to Ag-d and Sb-p to Sb-states for the first two peaks, and Sb-p to Ag-d-states for the following two peaks. The inclusion of the e–h interaction causes the redistribution of the spectral weight and the oscillator strength. Now the onset and the main peaks are considerably moved toward lower energies (redshift), and the onset begins at 3.0 eV, and the first and second peaks are around 3.3 and 4.05 eV and show a considerable increment in their oscillator strength. Second, the calculated ε₂ by IPA and including SOC shows some difference with the previous results; there is, in general, a redshift of the whole spectrum, with the onset starting at 3.0 eV and showing four well-defined peaks located around 3.5, 4.21, 4.69 and 4.99 eV. Moreover, there are two prominent shoulders around 3.8 and 3.9 eV caused by the splitting of the intermediate bands. Finally, the calculated ε₂ using BSE and SOC shows more remarkable features. A redshift of the spectrum and an appreciable redistribution of the spectral weight are observed; the onset now starts around 2.6 eV, and the more prominent peaks are placed around 3.05, 3.81, 4.18, and 4.32 eV, and most significantly there is a continuous excitonic feature at 2.7 eV due to the inclusion of the e–h interaction.

Fig. 10 Cs₂AgSbCl₆ imaginary dielectric function calculated using the independent-particle approximation G₀W₀ – IPA (red dashed line) and BSE (blue line) (a) without and (b) including SOC.

3 Discussion

This study introduces an innovative method for synthesizing Cs₂AgSbCl₆ powders, emphasizing its advantages in sustainability and scalability for industrial use. The new synthesis technique surpasses traditional methods during extended grinding periods exceeding 1 hour, resulting in Cs₂AgSbCl₆ powders that exhibit exceptional stability lasting at least 365 days.

The characterization of the powders reveals a non-uniform distribution of particles with an average size of 10 μm, presenting characteristic clusters associated with mechanosynthesis. In order to check potential optoelectronic application, we dispersed the powders and prepared a solution that was used in the ancillary investigation using electron diffraction, demonstrating the presence of particles as small as 5–15 nm, exhibiting interplanar distances approaching 2.4 Å, which agrees with the (240) crystal plane as determined by powder X-ray diffraction (PXRD).

To manufacture films, we need to optimize the surface with homogeneous particle sizes, and the solution demonstrated that it is possible to separate the agglomerates while preserving the structural properties.

Furthermore, the synthesized powders exhibit optical properties akin to those found in polycrystalline samples in the literature, showcasing an indirect band gap of 2.8 eV (ref. 9 and 21) to 2.61(3) eV (this work). This remarkable consistency highlights the potential of mechanosynthesis as a promising avenue for producing perovskite halide powders with complex stoichiometries, offering possibilities for their application in advanced technologies such as thin-film technology and other cutting-edge applications.

Theoretical results agree with the existing literature,⁴² even though a larger value of the indirect gap was reported using the HSE06 hybrid functional,^8,21 but none of them include explicitly quasi-particle corrections to obtain the electronic dispersion relation and the e–h interaction (excitonic effects) to calculate the optical spectrum. Here, taking into account the SOC, it does not affect significantly the calculated band gaps; however, the degeneracy of the intermediate CBs is left, and a full splitting of those bands is observed. On the other hand, the inclusion of the e–h interaction in the BSE Hamiltonian predicts that this effect leads to the redistribution of the spectral weight and the oscillator strength of ε₂, showing a redshift of the spectrum with the onset of the absorption at 2.6 eV and a prominent continuous excitonic feature at 2.7 eV. These calculated values from the optical spectrum agrees exceptionally well with the value of the band-gap obtained experimentally.

A solar photon of energy equal to 2.7 eV is absorbed by an electron at the valence band (VB), which is promoted to the conduction band (CB), creating an electron–hole pair. Higher energy photons cause the VB → CB transition as well; however, the excess energy is given to the lattice in the form of heat when the carriers migrate to lower energy states, causing phonon emission. By the effect of the SOC, the degeneration of the CBM is left and intermediate bands appear, allowing the e–h pair to be generated by the simultaneous absorption of photons in the two sub-band gap transitions.⁴¹

Since the static dielectric constant of Cs₂AgSbCl₆ is small, the charge carrier recombination rate is high, thus affecting the overall performance of Cs₂AgSbCl₆-based devices⁴³ for potential photovoltaic applications.

4 Conclusions

We have successfully synthesized Cs₂AgSbCl₆via an efficient mechanochemical route, making it highly appealing to industrial applications. Cs₂AgSbCl₆ exhibits superior stability compared to lead halide perovskites, with its structural and optical properties aligning closely with documented literature findings. Finally, it is established that the correct theoretical scheme to describe the optical properties of this material has to take into account the SOC and the continuous excitonic effects due to the e–h interaction, where an excellent agreement between the calculated and experimental gap is found.

Author contributions

The manuscript was written through contributions of all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the São Paulo Research Foundation (proc. FAPESP 2021/03640-7 and 2023/01502-1), the Brazilian National Council for Scientific and Technological Development (CNPq proc. no. 305661/2019-9), the Coordination for the Improvement of Higher Education Personnel (CAPES finance code 001), Colombian MINCIENCIAS (Convocatoria doctorados nacionales No. 757 de 2016) and FCEN-Universidad de Antioquia (Colombia). The authors thank the Multiuser Experimental Center (UFABC) for the experimental support.

Notes and references

1. J. Luo, X. Wang, S. Li, J. Liu, Y. Guo, G. Niu, L. Yao, Y. Fu, L. Gao, Q. Dong, C. Zhao, M. Leng, F. Ma, W. Liang, L. Wang, S. Jin, J. Han, L. Zhang, J. Etheridge, J. Wang, Y. Yan, E. H. Sargent and J. Tang, Nature, 2018, 563, 541–545.
2. X.-G. Zhao, D. Yang, J.-C. Ren, Y. Sun, Z. Xiao and L. Zhang, Joule, 2018, 2, 1662–1673.
3. N. Rodkey, S. Kaal, P. Sebastia-Luna, Y. A. Birkhölzer, M. Ledinsky, F. Palazon, H. J. Bolink and M. Morales-Masis, Chem. Mater., 2021, 33, 7417–7422.
4. S. Ghosh, H. Shankar and P. Kar, Mater. Adv., 2022, 3, 3742–3765.
5. T. Fang, T. Wang, X. Li, Y. Dong, S. Bai and J. Song, Sci. Bull., 2021, 66, 36–43.
6. W. S. Yang, B.-W. Park, E. H. Jung, N. J. Jeon, Y. C. Kim, D. U. Lee, S. S. Shin, J. Seo, E. K. Kim, J. H. Noh and S. I. Seok, Science, 2017, 356, 1376–1379.
7. A. H. Slavney, T. Hu, A. M. Lindenberg and H. I. Karunadasa, J. Am. Chem. Soc., 2016, 138, 2138–2141.
8. J. Zhou, X. Rong, M. S. Molokeev, X. Zhang and Z. Xia, J. Mater. Chem. A, 2018, 6, 2346–2352.
9. W. Deng, Z.-Y. Deng, J. He, M. Wang, Z.-X. Chen, S.-H. Wei and H.-J. Feng, Appl. Phys. Lett., 2017, 111, 151602.
10. J. C. Dahl, W. T. Osowiecki, Y. Cai, J. K. Swabeck, Y. Bekenstein, M. Asta, E. M. Chan and A. P. Alivisatos, Chem. Mater., 2019, 31, 3134–3143.
11. F. Palazon, Y. El Ajjouri and H. J. Bolink, Adv. Energy Mater., 2020, 10, 1902499.
12. D. Prochowicz, M. Saski, P. Yadav, M. Grätzel and J. Lewiński, Acc. Chem. Res., 2019, 52, 3233–3243.
13. A. D. Jodlowski, A. Yépez, R. Luque, L. Camacho and G. de Miguel, Angew. Chem., Int. Ed., 2016, 55, 14972–14977.
14. Z.-Y. Zhu, Q.-Q. Yang, L.-F. Gao, L. Zhang, A.-Y. Shi, C.-L. Sun, Q. Wang and H.-L. Zhang, J. Phys. Chem. Lett., 2017, 8, 1610–1614.
15. T. Tsuzuki and P. G. McCormick, Appl. Phys. A: Mater. Sci. Process., 1997, 65, 607–609.
16. D. Rambabu, S. Bhattacharyya, T. Singh, M. L. Chakravarthy and T. K. Maji, Inorg. Chem., 2020, 59, 1436–1443.
17. F. Palazon, Y. El Ajjouri, P. Sebastia-Luna, S. Lauciello, L. Manna and H. J. Bolink, J. Mater. Chem. C, 2019, 7, 11406–11410.
18. M. Saski, D. Prochowicz, W. Marynowski and J. Lewiński, Eur. J. Inorg. Chem., 2019, 2019, 2680–2684.
19. G. García-Espejo, D. Rodríguez-Padrón, R. Luque, L. Camacho and G. de Miguel, Nanoscale, 2019, 11, 16650–16657.
20. D. J. Kubicki, M. Saski, S. MacPherson, K. Galkowski, J. Lewiński, D. Prochowicz, J. J. Titman and S. D. Stranks, Chem. Mater., 2020, 32, 8129–8138.
21. J. E. F. S. Rodrigues, C. A. Escanhoela, B. Fragoso, G. Sombrio, M. M. Ferrer, C. Álvarez-Galván, M. T. Fernández-Díaz, J. A. Souza, F. F. Ferreira, C. Pecharromán and J. A. Alonso, Ind. Eng. Chem. Res., 2021, 60, 18918–18928.
22. A. Karmakar, M. S. Dodd, S. Agnihotri, E. Ravera and V. K. Michaelis, Chem. Mater., 2018, 30, 8280–8290.
23. Q. Liao, J. Chen, L. Zhou, T. Wei, L. Zhang, D. Chen, F. Huang, Q. Pang and J. Z. Zhang, J. Phys. Chem. Lett., 2020, 11, 8392–8398.
24. H. M. Rietveld, Acta Crystallogr., 1967, 22, 151–152.
25. H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71.
26. A. Coelho, Coelho Software, Brisbane, 2012.
27. C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675.
28. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
29. D. Hobbs, G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 11556–11570.
30. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
31. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
32. M. S. Hybertsen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 5390–5413.
33. L. Hedin, Phys. Rev., 1965, 139, A796–A823.
34. M. Shishkin, M. Marsman and G. Kresse, Phys. Rev. Lett., 2007, 99, 246403.
35. M. Rohlfing and S. G. Louie, Phys. Rev. Lett., 1998, 81, 2312–2315.
36. S. Albrecht, L. Reining, R. Del Sole and G. Onida, Phys. Rev. Lett., 1998, 80, 4510–4513.
37. T. Sander, E. Maggio and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 045209.
38. Z. Zhang, R. Zhao, S. Teng, K. Huang, L. Zhang, D. Wang, W. Yang, R. Xie and N. Pradhan, Small, 2020, 16, 2004272.
39. L. R. Moras, J. Inorg. Nucl. Chem., 1974, 36, 3876–3878.
40. T. T. Tran, J. R. Panella, J. R. Chamorro, J. R. Morey and T. M. McQueen, Mater. Horiz., 2017, 4, 688–693.
41. A. Luque, A. Martí and C. Stanley, Nat. Photonics, 2012, 6, 146–152.
42. M. Babaei, V. Ahmadi and G. Darvish, J. Phys. Chem. Solids, 2022, 169, 110880.
43. X. Liu, B. Xie, C. Duan, Z. Wang, B. Fan, K. Zhang, B. Lin, F. J. Colberts, W. Ma and R. A. Janssen, et al. , J. Mater. Chem. A, 2018, 6, 395–403.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mr00024a

---