Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Supersensitive visual pressure sensor based on the exciton luminescence of a perovskite material†
Marcin
Runowski
 *a,
Przemysław
Woźny
*a,
Przemysław
Woźny
 a,
Kevin
Soler-Carracedo
a,
Agata
Lazarowska
a,
Kevin
Soler-Carracedo
a,
Agata
Lazarowska
 b,
Mikołaj
Kamiński
b,
Mikołaj
Kamiński
 b,
Natalia
Majewska
b,
Alfonso
Muñoz
b,
Natalia
Majewska
b,
Alfonso
Muñoz
 c,
Jan
Moszczyński
a,
Szymon
Sobczak
c,
Jan
Moszczyński
a,
Szymon
Sobczak
 a,
Kashyap
Dave
d,
Wen-Tse
Huang
d,
Ru-Shi
Liu
a,
Kashyap
Dave
d,
Wen-Tse
Huang
d,
Ru-Shi
Liu
 d and
Sebastian
Mahlik
d and
Sebastian
Mahlik
 *b
*b
aFaculty of Chemistry, Adam Mickiewicz University, Uniwersytetu Poznańskiego 8, 61-614 Poznań, Poland. E-mail: runowski@amu.edu.pl
bInstitute of Experimental Physics, Faculty of Mathematics, Physics and Informatics, University of Gdansk, Wita Stwosza 57, 80-308 Gdansk, Poland. E-mail: sebastian.mahlik@ug.edu.pl
cDepartamento de Física, IUdEA, IMN & MALTA Consolider Team, Universidad de La Laguna, Apdo. Correos 456, E-38200 San Cristóbal de La Laguna, Santa Cruz de Tenerife, Spain
dDepartment of Chemistry, National Taiwan University, Taipei 106, Taiwan
First published on 4th September 2024
Abstract
Accurate, rapid, and remote detection of pressure, one of the fundamental physical parameters, is vital for scientific, industrial, and daily life purposes. However, due to the limited sensitivity of luminescent manometers, the optical pressure monitoring has been applied mainly in scientific studies. Here, we developed the first supersensitive optical pressure sensor based on the exciton-type luminescence of the Bi3+-doped, double perovskite material Cs2Ag0.6Na0.4InCl6. The designed luminescent manometer exhibits an extremely high sensitivity, i.e. dλ/dp = 112 nm GPa−1. It also allows multi-parameter sensing, using both blue-shift and rarely observed band narrowing with pressure. Importantly, this material has small temperature dependence for the manometric parameter used, i.e. spectral shift, allowing detection under extreme pressure and temperature conditions. The developed sensor operates in the visible range, and its emission shifts from orange to blue with pressure. This approach allowed us to demonstrate the real-world application of this sensor in detecting small changes in pressure with a designed uniaxial pressure device, with unprecedented resolution of the order of a few bars, demonstrating the technological potential of this sensor for remote, online monitoring of cracks and strains in heavy construction facilities.
New conceptsNowadays, the utilization of extreme conditions, i.e. pressure and temperature, to manipulate the inherent characteristics of materials attracts increasing attention. Especially, pressure exhibits profound influence on diverse fields of material synthesis, scientific research, industrial production, light generation, etc., so its real-time monitoring with fast response and visual features is required. Here, we developed the first exciton-type optical pressure sensor exhibiting unprecedented sensitivity, associated with exotic emission of the self-trapped exciton (STE) of perovskite material Cs2Ag0.6Na0.4InCl6 doped with Bi3+. The designed luminescent manometer exhibits a breakthrough susceptibility to pressure changes of 112 nm GPa−1, which is significantly higher than that of commonly used optical sensors. So, it is classified as the most sensitive optical manometer reported to date. This colossal sensitivity of the developed optical manometer was directly used in uniaxial pressure measurements, resulting in an exceptional pressure resolution of 10 bar, confirming its real-world application potential for remote pressure monitoring in industry and daily life. Moreover, this work opens completely new horizons of visual pressure sensing in real-world situations, allowing early detection of strains and cracks by visual pressure monitoring in ultra-heavy construction facilities, e.g. for prevision of industrial and natural disasters. |
Introduction
Pressure and temperature are fundamental state functions governing all-natural and artificial processes occurring worldwide, so their rapid, accurate, and remote detection is crucial in science, industry, and daily life. Temperature can be quickly and remotely monitored using optical sensors, such as pyrometers or numerous well-established luminescent thermometers, allowing detection with resolutions less than 0.1 K.1 However, in the case of high pressure, the only method of remote detection is the use of optical sensors based on luminescent materials, such as the commonly applied ruby-based sensors (Al2O3:Cr3+), which permit resolving pressure values differing by at least hundreds of bars, being unsatisfactory from the point of view of industrial and daily life applications.2–8 It is worth noting that remote pressure detection is crucial for ensuring safety in hazardous environments, providing high accuracy and reliability unaffected by electromagnetic interference, and enabling real-time monitoring from a distance. Additionally, these remote sensors offer versatility across industries, require minimal maintenance, and contribute to environmental sustainability through reduced power consumption and waste.To overcome these limitations, in the last decade, researchers have started to extensively search for new promising phosphor materials whose photoluminescence is susceptible to pressure changes, which could work as alternative pressure sensor materials.9–45 The candidates for new sensors are typically based on optical materials activated with lanthanides, d-block metal ions, quantum dots or organic dyes and complexes, which, upon UV excitation, may generate visible or NIR light. The operating principle of the vast majority of optical manometers is based on monitoring the spectral shift of their emission band, with typical pressure sensitives (Δλ/Δp) oscillating at 1 nm GPa−1, i.e. 0.1 nm kbar−1 for recently reported materials.15–17,19,26,42 In contrast, the sensitivity is as low as 0.0365 nm kbar−1 for the pioneering ruby sensor.3 Fortunately, in the last few years, several reports on luminescent manometers exhibiting higher sensitivities have been published, reaching 1 nm kbar−1 for visual sensors35 or even slightly exceeding 2 nm kbar−1 for NIR sensors.33 However, another problem with such luminescent manometers is the dependence of their emission on both pressure and temperature, so the change in the temperature gradient in the system in most cases may strongly affect the manometric parameters used, and bias the pressure readouts.16,18,25,26,36 Moreover, each sensor has some merits and drawbacks, such as limited sensitivity, significant temperature dependence of the sensing parameter, non-monotonic changes in the manometric parameters in the low-pressure regime, low structural stability, inability to visually monitor pressure (via UV and NIR sensors), and the necessity of using a reducing atmosphere during synthesis (e.g. in the case of divalent lanthanides).
Metal halide perovskites based on lead, with the general formula MPbX3 (M = Rb+, Cs+; [CH3NH3]+; X = I−, Br−, Cl−), are extensively studied due to their large absorption cross-section, the great mobility of charge carriers (long diffusion lengths), high tolerance to crystal defects, appropriate bandgap and low trap states, implying their application in photovoltaics, new light sources, including lasers and LEDs, scintillators and photodetectors, advanced optoelectronics and numerous clean energy applications.46–51 However, due to their intrinsic toxicity, structural instability, and susceptibility to heat and moisture, lead-free halide double perovskites have recently been considered alternatives to conventional perovskite materials.52–56 Such double perovskites are usually based on Cs2AgInX6, Cs2NaInCl6, and Cs2AgBiCl6 (X = I−, Br−, Cl−), which may exhibit bright photoluminescence upon UV excitation associated with broadband emission of self-trapped exciton (STE), which is an unconventional form of light generation.57–61 These materials benefit from highly symmetrical cubic systems, rich substitutional chemistry, enhanced structural stability, improved absorption (light harvesting materials), large Stokes shifts, resistance to various environmental factors, nontoxicity, and have great application potential in photovoltaics and optoelectronics.62–65
Here, we report the development of the first optical pressure sensor based on exciton emission in a double-perovskite luminescent material. Based on our previous research and literature reports, we designed and synthesized an optimized double perovskite structure that combines the benefits of the abovementioned materials, namely, Cs2Ag0.6Na0.4In0.996Bi0.004Cl6.57,59,66,67 By introducing Na and Bi dopings, we achieved bright photoluminescence with high quantum yield, QY ≈ 74% (λex = 325 nm), by partially relaxing the selection rules. This involves breaking the inversion symmetry and allowing observation of the parity-forbidden transitions. Moreover, doping reduces vacancy defects and suppresses nonradiative recombination loss, improving crystal quality and enhancing PL intensity.59
Its structural stability under extreme pressure conditions was theoretically and experimentally confirmed, and the use of high-pressure luminescence spectroscopy revealed its breakthrough susceptibility to pressure changes, i.e. Δλ/Δp = 112 nm GPa−1 (11.2 nm kbar−1). The additional benefits of the developed double-perovskite manometer include the narrowing of the emission band with pressure, the possibility of multi-parameter sensing, and low-temperature dependence with respect to pressure. The colossal sensitivity of the developed optical manometer was directly used in uniaxial pressure measurements, allowing resolving pressures on the order of 10 bar, confirming its real-world application potential in industry and daily life, e.g. for visual monitoring of strains/defects in heavy constructions, food preservation techniques, studies of elastic and plastic properties of materials.
Methods
Materials
The following reagents were utilized in the synthesis process: CsCl (99.9%) was purchased from Sigma Aldrich; NaCl (99%) was obtained from J. T. Baker; and AgCl (99.9%), InCl3 (99.9%), and BiCl3 (99.9%) were obtained from Alfa Aeaser. HCl (37%) was procured from Merck, and anhydrous ethanol (99.9%) was acquired from ECHO.Synthesis
The compound was synthesized using acid precipitation, with modifications based on previous methods.57,68 To accomplish this, 0.6 mmol of AgCl, 0.4 mmol of NaCl, 0.996 mmol of InCl3, and 0.004 mmol of BiCl3 were mixed with 3 mL of HCl. The mixture was stirred for 20 minutes while maintaining a temperature of 70–80 °C. Next, 2 mmol of CsCl was added to the solution to initiate the final reaction. The reaction mixture was stirred for an additional 20 minutes at 70–80 °C. Once the stirring was complete, the reaction was allowed to cool to room temperature, after which the mixture was subsequently centrifuged with ethanol three times. The resulting sediment was washed and then dried at 60 °C for 24 hours.Characterization
Synchrotron powder X-ray diffraction (XRD) data at room conditions were obtained from the National Synchrotron Radiation Research Center (NSRRC) in Taiwan. The measurements were conducted at room temperature using the BL01C2 beamline and a Debye–Scherrer camera with a wavelength of 0.77491 Å. The diffraction pattern obtained was subjected to Rietveld analysis using Total Pattern Analysis Solutions software (TOPAS 4.2). The high-pressure XRD patterns were recorded in a Merrill Bassett diamond anvil cell (DAC) using a four-circle Xcalibur diffractometer with a MoKα X-ray source (λ = 0.7107 Å) and equipped with a EOS CCD detector. Thermogravimetric (TG) analysis was run on a SDT Q600 apparatus provided by the TA Instruments. Sample of perovskite (∼11 mg) were loaded into Al crucible and heat treated in the temperature range 25–1100 °C using the heating rate 10 °C min−1 and at the rate of argon gas flow equal to 100 cm3 min−1. In addition, a photoluminescence study was conducted using an Edinburg fluorometer equipped with a 1 nm excitation slit width and a 1 nm emission slit width. The internal quantum efficiency was determined using a Hamamatsu Quantaurus instrument. Before taking specimen measurements, the system was calibrated using YAG:Ce3+.Absorption spectra were acquired in diffuse-reflection mode using a JASCO V-770 UV-Vis/NIR spectrophotometer with an ILN-925 spherical integrator (150 mm diameter). Raman spectra were recorded in backscattering geometry with a Renishaw InVia confocal micro-Raman system using a grating with 1200 grooves per mm and a power-controlled 100 mW 532 nm laser diode. The laser beam was focused using an Olympus ×20 SLMPlan N long working distance objective. Scanning electron microscopy (SEM) images were taken with an FEI Quanta 250 FEG instrument equipped with an EDAX detector.
Photoluminescence excitation and emission spectra were acquired using a FluoroMax-4P TCSPC spectrofluorometer produced by Horiba. Steady-state luminescence spectra were obtained with a He–Cd laser at a wavelength of 325 nm and with a continuous wave 375 nm UV laser (max output power of 50 mW). The spectra under high-pressure and temperature conditions were measured with Andor SR-750-D1 and Shamrock 500 spectrometers equipped with Peltier-cooled DU420A-OE type and Andor Indus silicon CCD cameras, respectively. All spectra were corrected for the apparatus response. The sample was cooled by a closed-cycle optical cryostat DE-204 SI. To follow the luminescence kinetics, we used a PL 2143 A/SS laser system and a PG 401/SH parametric optical generator as an excitation source. The sample was cooled by a closed-cycle optical cryostat DE-204 SI. The emission signals were analyzed by a 2501S (Bruker Optics) spectrometer and a Hamamatsu Streak Camera model C4334-01. High hydrostatic pressure in all experiments at elevated pressure was applied in a DAC. Polydimethylsiloxane oil and methanol/ethanol/water (16/3/1) were used as the pressure-transmitting media, and the pressure was measured by the shift of the luminescence lines of ruby. Temperature measurements were obtained using a THMSG600 temperature controller Linkam stage combined with an LNP95 liquid nitrogen cooling pump system.
Results and discussion
Properties of the synthesized perovskite at ambient conditions
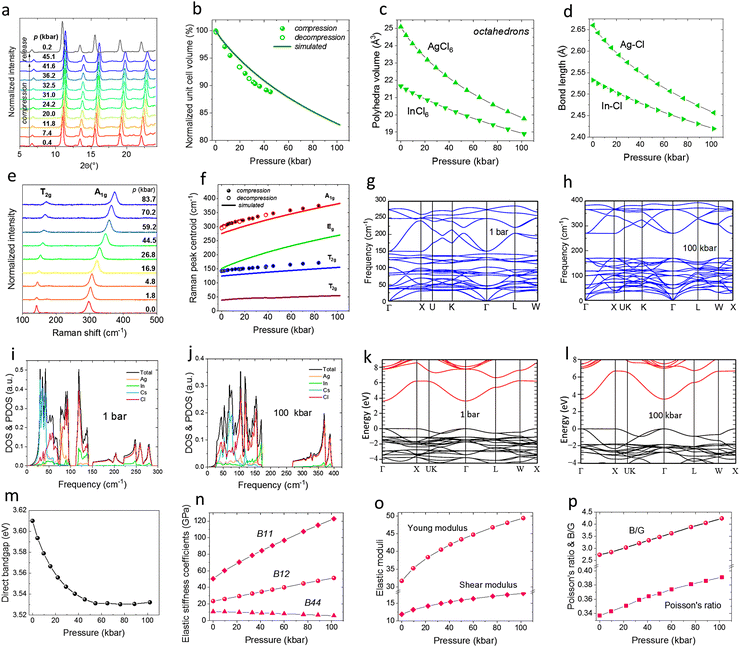
We conducted synchrotron powder X-ray diffraction (XRD) to investigate the crystal structure of the synthesized Cs2Ag0.6Na0.4In0.996Bi0.004Cl6 perovskite material. The obtained diffractogram was indexed using the cubic crystal system with the Fm3m space group of the reference Cs2AgInCl6 (card no. ICSD11524).62,63 The Rietveld refinement (Fig. 1a) confirmed that Ag+ ions were successfully substituted with Na+, whereas In3+ ions were substituted with Bi3+ ions. However, we observed a small amount of unreacted precursor, i.e. AgCl at ≈1%. All refinement parameters are listed in Tables S1 and S2 (ESI†). The framework of the Cs2Ag0.6Na0.4In0.996Bi0.004Cl6 perovskite (Fig. 1b) consists of corner-sharing AgCl6 and InCl6 coordination octahedral, with the counter cations confined within the cavities. The synthesized material is composed of micron-sized crystals, ranging from ca. 1 to 5 μm confirmed by the SEM image (Fig. 1c). The low phonon energy of the material studied is beneficial for its luminescence performance (limited multiphonon quenching), as demonstrated by the Raman spectrum in Fig. 1d. Two most notable Raman modes, A1g and T2g, corresponding to internal oscillations of the octahedra were located at 141 and 299 cm−1, respectively.69 The energy dispersive X-ray analysis (EDX) spectrum (Fig. 1e) additionally confirmed the elemental composition of the perovskite, whereas the obtained atomic percentage composition (shown as an inset in Fig. 1e and listed in details in Table S3, ESI†) confirmed that the real composition of the synthesized material match the expected one. The photoluminescence excitation spectrum (λem = 600 nm) of the Cs2Ag0.6Na0.4In0.996Bi0f.004Cl6 perovskite is shown in Fig. 1f. From our previous work,57,58 using photocurrent and spectroscopic measurements, we managed to determine the appropriate transitions in this type of materials. The most prominent feature in the excitation spectra is denoted as “C”, which is assigned to the direct absorption of the free exciton (FE) state. The “B” band component is plausibly related to the charge transfer transition from the ground state of Bi3+ to the conduction band or between the local state of Bi3+ (1S0–3PJ), which in this case degenerates with the conduction band. The “A” component band is related to host absorption from the valence band (VB) to the conduction band (CB). All these absorption transitions result in the yellow-orange photoluminescence in the form of broadband centered at ≈600 nm (Fig. 1f). The observed significant Stokes shift results from the strong coupling of the excitons to the crystal lattice.53 The broadband character of this perovskite emission is associated with the self-trapped exciton (STE) emission, caused by the strong coupling of the exciton to the lattice.62,63 A simplified energy level diagram for the studied perovskite depicts the observed luminescence mechanism, with the indicated radiative and nonradiative transitions presented in Fig. 1g. The absorption spectrum presented in Fig. 1h shows two absorption bands at ≈315 nm and 380 nm. Compared with the excitation spectrum, the lowest energy band (380 nm) can be associated with the inclusion of bismuth. The second band centered at 315 nm is the host absorption, resulting in the absorption threshold at ≈340 nm, and the corresponding Tauc plot (inset) reveals that the energy of its direct bandgap is 3.61 eV. It is worth nothing, that an apparent mismatch between the absorption and excitation spectra, results from the presence of photoinduced charge carriers in the CB. The excitation involving A and B bands is mediated through the CB. Electrons from the conduction band are only partially captured by the FE state, from where the STE state is excited. The rest are trapped in various lattice defects always present in the crystal structure. On the other hand, the excitation directly to the FE state (C band) results in very efficient nonradiative relaxation to the STE state, suppressing the photoelectrons in CB generation.Structural stability under high-pressure conditions
To investigate the structural stability of the synthesized perovskite Cs2Ag0.6Na0.4In0.996Bi0.004Cl6 under high-pressure conditions, we conducted in situ XRD measurements during compression and decompression cycles (Fig. 2a). The observed shift of the reflexes to higher 2θ angles under high-pressure conditions indicates a reduction of the interplanar distances in the crystal lattice. The unit-cell volume compresses monotonically (Fig. 2b), with no signs of phase transition up to 45 kbar at least (see absolute values in Fig. S1, ESI†). To further elucidate the pressure-induced changes on the physicochemical properties of this double perovskite, we performed comprehensive density functional theory (DFT) simulations on the prototypic Cs2AgInCl6 up to 100 kbar to further investigate the influence of the high pressure on the structure of the perovskite (Fig. 2b–d and f–p). Our quantum-mechanical predictions align closely with experimental data measured for the Cs2Ag0.6Na0.4In0.996Bi0.004Cl6 material at high pressure, showing slight (≈3%) deviations in the unit-cell parameters (Fig. 2b and Fig. S2a, ESI†). The absolute values of the lattice constants, i.e. unit-cell parameter (a) and the unit-cell volume (V) for the material under compression are listed in Table S4 (ESI†). The theoretically calculated bulk modulus (B0) of 32.45 GPa is higher than the experimentally determined B0 = 21.5 GPa for the co-doped material. Such difference suggests that replacing the Ag+ cations with smaller Na+ ions increases the susceptibility of the material to compression. Thus, the predominant effect on mechanical properties of this perovskite can be connected to the contraction of much softer AgCl6 and NaCl6 coordination octahedra (Fig. 2c) of the polyanionic perovskite framework, which is related to the bonds shortening Ag–Cl and In–Cl (Fig. 2d). Interestingly, the compression experiments above 3.5 GPa show that the compressibility of the Cs2Ag0.6Na0.4In0.996Bi0.004Cl6 decreases significantly, suggesting that all free-voids in the structure have been limited. This correlates well with a significant change of the bulk modulus with pressure, which increases by ≈2.3 times at around 100 kbar, compared to the B0 value at ambient conditions (Fig. S2b, ESI†).Corroborating these findings, the high-pressure Raman spectroscopy (Fig. 2e) shows that the high-energy A1g mode undergoes a significant shift at 1.2 cm−1 kbar−1 rate, while the low-energy T2g mode shifting at a rate of ca. 0.35 cm−1 kbar−1 (Fig. 2f). The increase in Raman mode energies at compression supports our XRD experiments, as it usually results from the bond shortening due to the reduction of interatomic distances in a compressed structure. Additionally, the Raman spectra analysis confirms the absence of phase transitions within the studied pressure range, as indicated by the consistent shape of the spectra and the lack of new Raman bands. The simulated (continuous lines) pressure evolutions of four active Raman modes (T2g, Eg, and A1g) agree well with the experimental results (two most intense, observable modes), as they shift with a similar rate toward higher energies, i.e. wavenumbers (Table S5, ESI†). To investigate the lattice dynamics, including the dynamic stability of the compressed perovskite structure, we simulated the phonon dispersions along the high-symmetry direction of the Brillouin zone under ambient conditions and at 100 kbar (Fig. 2g and h). As expected, in the case of the compressed structure, phonon bands are shifted toward higher frequencies following the pressure evolution of the determined Raman modes. Although the obtained bands are quite uneven, there are no imaginary frequencies in either case (no negative phonon branches in the spectra), indicating the dynamic stability of the perovskite crystals under ambient and high-pressure conditions. As in the low-energy region (0–150 cm−1) an increase in the density of vibrational modes was observed, we calculated the total density of states (DOS) and partial density of states (PDOS) at ambient pressure and at 100 kbar (Fig. 2i and j) to determine the exact role of each atomic species in the vibrational spectra. In both situations, the bands associated with Cl atoms are located throughout the whole spectrum, from 0 to 280 cm−1 at ambient conditions and from 0 to 390 cm−1 under pressure. The bands related to Cs, Ag, and In are located mainly in the low-frequency region, from 0 to ≈150 cm−1, with an apparent pressure-induced shift toward higher frequencies. Moreover, the intensities of the compressed materials decreased, and the band shape was altered, which can be linked to the significant contraction of the material subjected to pressure, i.e. high compressibility of the soft perovskite structure.
To examine the impact of pressure on the electronic properties of the material, we calculated the evolution of the electronic band structure of this perovskite in the high-symmetry directions in the first Brillouin zone, at ambient pressure and at 100 kbar (Fig. 2k and l). As presented, the investigated double perovskite is a direct semiconductor material, as the minimum (bottom) of the CB is located at the same point (Γ) as the maximum (top) of the VB, both at ambient and under high-pressure conditions. The plots showing the electronic band structures at intermediate pressures are shown in Fig. S3 (ESI†). The corresponding direct band gap slightly narrows from 3.61 eV under ambient conditions to 3.53 eV at 100 kbar (Fig. 2m). Specifically, the VB hardly changes at point Γ for the initial and compressed structures, whereas the edge of the CB shifts toward lower energies with pressure. Moreover, the band structure is more dispersive for the compressed material, indicating the enhanced covalent character of the bonds, which agrees well with the narrowing of the band gap with pressure. In summary, the obtained band structure resembles the distribution typical of semiconductors with mixed ionic-covalent chemical bonds in the double perovskite structure, as the bands are neither flat nor uneven, and their dispersion is moderate.
To describe the elastic properties of this perovskite, we determined the corresponding elastic stiffness coefficients (Bij), which should be used instead of the elastic constants (Cij) when a crystal is subjected to non-zero uniform stress. In contrast, at zero pressure, the Bij values can be reduced to the Cij constants (see details in ESI†).70 At ambient pressure, this perovskite fulfills the abovementioned conditions. However, when crystals are subjected to isostatic stress, modified Born stability criteria should be applied, considering the elastic stiffness coefficients. A compressed material is mechanically stable if the matrix representation of the elastic stiffness tensor (Bij) is positive-definite.71 In the case of the perovskite studied, all of the eigenvalues of the matrices Bij are positive because the B11, B12, and B14 parameters are always greater than zero in the analyzed pressure range (Fig. 2n), so this material is mechanically stable, at least up to 100 kbar.
To investigate in detail the elastic properties of the developed perovskite material, we also determined other basic elastic moduli, i.e. the shear modulus (G) and Young's modulus (E), as well as the B/G ratio and Poisson's ratio (v). These parameters were determined based on the elastic stiffness parameters72,73 using the analytical expressions given in ref. 74 and Voigt's approximation. Notably, the B/G ratio is greater than 2.7 in the studied pressure range (Fig. 2p), confirming that such perovskite is ductile and should be more resistant to volume compression than shear deformation.75 An increase in the B/G ratio from ≈2.7 under ambient conditions to 4.2 at 100 kbar manifests improved ductility under high-pressure conditions. On the other hand, the v parameter falls within the range of 0–0.5 as it increases from ≈0.34 to 0.39 with pressure (Fig. 2p), which means that the compressed structure has typical elastic characteristics and recovers to the initial state upon pressure release (decompression). An increase in the Poisson's ratio with pressure indicates that the compressed perovskite is more elastic than the uncompressed structure under ambient conditions. Additionally, we presented in Fig. S4 (ESI†) the 3D representations of the investigated crystal structures at ambient pressure and at 100 kbar, confirming the uniform compression of the perovskite crystal lattice in all crystallographic directions.
Luminescence properties under extreme conditions
The excitation spectra (λem = 600 nm) of the Cs2Ag0.6Na0.4In0.996Bi0.004Cl6 perovskite measured at increasing pressure are shown in Fig. 3a. With increasing pressure, there is almost no spectral shift in the excitation bands, and only a gradual decrease in the band stretching from ca. 357 nm (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) to 400 nm (28
000 cm−1) to 400 nm (28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) is observable.
000 cm−1) is observable.
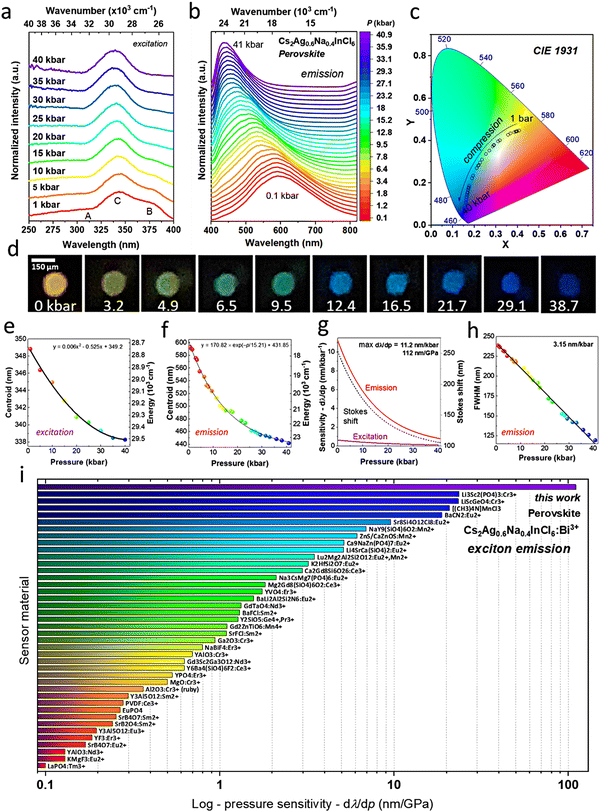 | ||
| Fig. 3 The effect of pressure on the exciton emission – luminescence properties of the perovskite material under high-pressure conditions. (a) Excitation spectra (λem = 600 nm) of the compressed Cs2Ag0.6Na0.4In0.996Bi0.004Cl6 perovskite. (b) Emission spectra (λex = 325 nm) of the material studied measured at increasing pressure (up to ≈40 kbar). (c) The corresponding pressure-related chromaticity coordinates depicted in the CIE diagram, showing the emission color change from orange to blue upon material compression. (d) Digital photographs at selected pressure values (in kbar) showing the effect of pressure on the photoluminescence color visually observed in the DAC chamber; the scale bar (150 μm) presented is valid for all photographs. (e) Determined excitation band centroid as a function of pressure. (f) Emission band centroid as a function of pressure. (g) The calculated absolute pressure sensitivity for the excitation and emission band shifts and Stokes shift as a function of pressure, indicating the maximal pressure sensitivity in the emission mode of 11.2 nm kbar−1. (h) The corresponding emission bandwidth (FWHM) as a function of pressure, showing pressure sensitivity of 3.15 nm kbar−1 in the FWHM mode. (i) Pressure sensitivity of different commonly used and most sensitive luminescent manometers available in the literature, which are based on the spectral shift of the emission band. The corresponding references and numerical data are given in Table S4 in the ESI.† | ||
On the other hand, the emission spectra (λex = 325 nm) of the studied perovskite (Fig. 3b) exhibit an extremely large shift with pressure toward shorter wavelengths (higher energies). The observed phenomenon is triggered by the pressure-induced decrease in the self-trapping, electron-lattice, and lattice deformation energies due to the decreasing distance between the ions in the compressed structure. Moreover, doping the double perovskite crystal lattice with Bi3+ ions significantly enhances their pressure sensitivity, compared to other perovskite materials.62,63 The large spectral shift is manifested in a significant change of the photoluminescence color, from orange under ambient conditions to blue at 40 kbar, as quantitatively expressed by the determined chromaticity coordinates shown in Fig. S5 (ESI†) (including the calculated pressure sensitivities for multi-parameter sensing) and in the CIE diagram in Fig. 3c. These results agree well with the visual observations during the compression process of the light emitted from the DAC chamber, as clearly shown in the photographs in Fig. 3d.
The determined wavelength values for the band centroids of both the excitation and emission spectra as a function of pressure can be correlated with pressure using simple 2nd-order polynomial and exponential functions (phenomenological), as presented in Fig. 3e and f, respectively. In the case of the excitation spectra, the band centroid blueshifts from ≈349 nm (28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 653 cm−1) at ambient pressure to 338 nm (29
653 cm−1) at ambient pressure to 338 nm (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 586 cm−1) at 40 kbar. A slight spectral shift of the excitation bands implies that the energy gap marginally changes with the applied pressure. Meanwhile, the emission band centroid blueshifts from ca. 600 nm (16
586 cm−1) at 40 kbar. A slight spectral shift of the excitation bands implies that the energy gap marginally changes with the applied pressure. Meanwhile, the emission band centroid blueshifts from ca. 600 nm (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 667 cm−1) to 440 nm (22
667 cm−1) to 440 nm (22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 727 cm−1) in the same pressure range, manifesting a significant pressure-induced increase in the STE energy. Notably, in the same pressure range, the energy of the emission band increases ≈6.5 times more than the energy of the excitation band. Such difference indicates a substantial decrease in the Stokes shift with pressure, i.e., from 253 to 105 nm (Fig. 3g), due to the reduction of the energy distance between the FE state (directly excited) and the STE emission state. Moreover, the lattice relaxation energy for the STE state, i.e. electron–phonon coupling, decreases slightly.
727 cm−1) in the same pressure range, manifesting a significant pressure-induced increase in the STE energy. Notably, in the same pressure range, the energy of the emission band increases ≈6.5 times more than the energy of the excitation band. Such difference indicates a substantial decrease in the Stokes shift with pressure, i.e., from 253 to 105 nm (Fig. 3g), due to the reduction of the energy distance between the FE state (directly excited) and the STE emission state. Moreover, the lattice relaxation energy for the STE state, i.e. electron–phonon coupling, decreases slightly.
Using the fitting functions applied for the excitation and emission band centroids, we calculated the absolute pressure sensitivity for the manometric parameters based on the excitation and emission band shifts, which are shown in Fig. 3g. In both cases, the maximal sensitivity is obtained in the low-pressure regime, reaching ≈0.6 nm kbar−1 for the excitation band and 11.2 nm kbar−1 for the emission band shift. The sensitivity of pressure sensors based on the emission band shift is typically expressed in nm GPa−1. Hence, for example, for the commonly applied ruby-based pressure sensor dλ/dp = 0.365 nm GPa−1, the obtained value of material studied in this paper is significantly higher, i.e. dλ/dp = 112 nm GPa−1. The obtained results classify the developed perovskite-based sensor as a truly supersensitive manometer, undoubtedly making it the most pressure-susceptible material reported. To visualize this achievement, we gathered the performance of all reported, most sensitive luminescent manometers in Fig. 3i.9–45,76–87 Currently, the second and third most sensitive sensors, which operate in a low-energy NIR range (inappropriate for visual pressure monitoring), exhibit 5-fold lower sensitivity than our optical manometer.83–87 A detailed comparison of the sensor performances is given in Table S6 (ESI†).
Another very appealing feature for sensing, which is rarely observed, is the effect of pressure-induced narrowing of the emission band (Fig. 3b), caused by a decrease in the lattice relaxation energy in the perovskite structure.62 Moreover, the full width at half maximum (FWHM) of the emission band changes linearly with pressure, i.e. it decreases from ca. 235 nm at an ambient pressure down to 115 nm at 40 kbar, at a rate of 3.15 nm kbar−1 (31.5 nm GPa−1) shown in Fig. 3h. This means that the significant change in the FWHM can also be used as a manometric parameter, classifying the developed sensor as the most sensitive luminescent manometer operating in bandwidth mode (Table S7, ESI†).
To comprehend the high-pressure luminescence analysis of the perovskite material, we examined the effect of the excitation wavelength (λex) on its emission characteristics under ambient conditions (Fig. 4a and b) and under high pressure (Fig. 4c). The magnified emission spectra recorded at different λex values (Fig. 4a), ranging from 305 to 385 nm, indicate the effect of λex on the spectral position of the band. The determined emission band centroid values (Fig. 4b) reveal that exciting from ca. 300 to 320 nm and from 360 to 380 nm, the centroids are initially located at ≈600 nm, whereas exciting from ca. 325 to 350 nm, they shift toward slightly shorter wavelengths. This variance is attributed to the excitation of different band components (A–C), as earlier discussed (Fig. 3a). Note, that the most effective excitation of the STE state is the excitation through the FE state at wavelengths of 325–350 nm (C). In this situation, there is no excitation of electrons into the CB. Through the excitation involving the CB (A and B) trap states are created, which most likely influence the STE state, increasing the spin–orbit coupling and/or increasing the lattice deformation energy.
Apparently, the λex also slightly affects the bandwidth, as shown in the same graph (Fig. 4b; bottom). Hence, we decided to investigate whether λex impacts the spectral shift rate with pressure, which could hamper straightforward pressure monitoring with different optical setups. Fortunately, there was no change in the pressure-related shift rate, and the observed changes in the band centroid were fully reversible, as confirmed by the performed cycling experiments and decompression data shown in Fig. 4c, where the results for three different λex (325, 350 and 375 nm) are presented. The additional cycling data for the emission band centroid for more compression-decompression cycles are presented in Fig. S6 (ESI†).
To further investigate the luminescence kinetics of the exciton emission under high-pressure conditions, we recorded the luminescence decay profiles and determined the decay times as a function of pressure; the results are shown in Fig. 4d and e, respectively. It is observed that the exciton emission decay profiles significantly shorten with pressure. Since the recorded profiles are not single exponential, to estimate the average lifetime (τavg), the following formula was used:
 | (1) |
In Fig. 4f the luminescence intensity of the sample is plotted against pressure. No noticeable pattern relating to the change in intensity is observed, and up to ≈30 kbar the intensity remains nearly constant. Any slight deviations noted fall within the error margin, which is typical for high-pressure measurements in a DAC. With a further increase of pressure, the luminescence intensity decreases to half of its initial value, due to the quenching processes, most likely autoionization. This includes a relaxation of the coupling strength between excitons and phonons in the compressed structure.
The effect of high-pressure compression on the energy level structure and exciton emission in this perovskite is presented in Fig. 4g. The exciton emission's energy significantly increases with pressure (orange and blue arrows), resulting in a blueshift of the STE emission while the energy of the FE state (purple arrow) increases only slightly with increasing pressure, i.e. from 349 to 338 nm. As a consequence, the STE state is moving closer to the FE state, while the activation energy (EA) of the non-radiative processes, associated with a direct transition to the ground state, is increasing.
Developing a new optical pressure sensor is essential for investigating the effect of temperature on emission characteristics to provide reliable pressure readouts both at room and variable temperatures. Hence, we measured the emission spectra (Fig. 5a) of the perovskite in a broad T-range (100–550 K). There are no significant changes in the spectral position of the emission band. Up to 200 K, the band centroid remains constant. Then it starts to slightly shift toward longer wavelengths (Δλ/ΔT = 0.065 nm K−1), reaching a plateau at room temperature, and with further temperature elevation (>400 K) shifts back to shorter wavelengths (Fig. 5b). This may lead to only small variations in pressure readouts, i.e. ≈6 bar K−1, being over 30-times lower than for the conventional ruby-based sensors. A more detailed quantitative analysis and discussion on the impact of temperature on the pressure readouts are given in Table S4 and in the text of the ESI.†
On the other hand, with increasing temperature, starting at 100 K, there is a linear broadening of the band, i.e. the FWHM in nm scale, which increases from ca. 165 nm at 100 K to 235 nm at ≈400 K (ΔFWHM/Δp = 0.2547 nm K−1), and with further temperature increase, the FWHM remains almost constant. The linear increase in the FWHM indicates the potential of this material for application in luminescence thermometry. The effect of thermal broadening of the emission band is opposite to that observed under pressure (band narrowing) and results from two main factors: (I) increasing the lattice relaxation energy with temperature; and (II) enhancing the electron–phonon coupling. According to the coordinate configurational model, the second factor is caused by improved electron–phonon interactions and differences between the initial and final states of the transitions, which leads to thermal broadening of the emission band.88 In order to show a minor effect of the temperature on the observed luminescence color we calculated the CIE coordinates based on the recorded temperature-dependent emission spectra, and are plotted in the CIE diagram shown in Fig. S7 (ESI†). In whole investigated T-range (100–560 K) the chromaticity coordinates are located in the range of the orange color of the CIE diagram, changing from (x = 0.499; y = 0.464) at 100 K to (x = 0.435; y = 0.450) at 560 K. The observed shift of the coordinates (mostly x) is associated alike with small spectral shift and broadening of the emission band with temperature.
As shown in Fig. 5d, the luminescence intensity decreases with temperature, reaching at room temperature ≈70% of its initial intensity. A more significant deterioration in intensity is observed with increasing temperature, reaching ≈20% of the initial value at 500 K. To model the temperature dependence of emission intensity, the following formula (eqn (2)), accounting for the single deexcitation process, was employed:
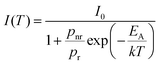 | (2) |
 , and EA = 1210 ± 10 cm−1. There are two main plausible mechanisms governing the observed thermal quenching of the exciton emission: (I) thermally induced photoionization, where the excited electron is transferred to the FE and next to CB state; and (II) a crossover mechanism, where the provided thermal activation energy releases the trapped exciton by ejecting (promoting) it from the excited STE to ground states. From the configurational diagram depicted in Fig. 4g, it is evident that the energy required for autoionization should be significantly higher (∼6000 cm−1). This indicates that the quenching of luminescence is associated with the intersection of the excited and ground states of STE. To ensure that the quenching of luminescence is not associated with the degradation of the perovskite material, we carried out thermogravimetric (TG) analysis of the sample (see Fig. S8, ESI†). The weight loss observed at around 800 K confirms that the perovskite material is stable at least up to this temperature.
, and EA = 1210 ± 10 cm−1. There are two main plausible mechanisms governing the observed thermal quenching of the exciton emission: (I) thermally induced photoionization, where the excited electron is transferred to the FE and next to CB state; and (II) a crossover mechanism, where the provided thermal activation energy releases the trapped exciton by ejecting (promoting) it from the excited STE to ground states. From the configurational diagram depicted in Fig. 4g, it is evident that the energy required for autoionization should be significantly higher (∼6000 cm−1). This indicates that the quenching of luminescence is associated with the intersection of the excited and ground states of STE. To ensure that the quenching of luminescence is not associated with the degradation of the perovskite material, we carried out thermogravimetric (TG) analysis of the sample (see Fig. S8, ESI†). The weight loss observed at around 800 K confirms that the perovskite material is stable at least up to this temperature.
To investigate how temperature affects the kinetics of exciton emission, we measured the temperature-dependent luminescence decay profiles (Fig. 5e) and calculated the corresponding average decay times (Fig. 5f). With increasing temperature, the decay time gradually shortens from ≈10 μs at 100 K to 0.1 μs at 500 K. The temperature dependence of decay time was modeled using formula (eqn (3)):
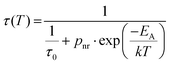 | (3) |
To show the real-world application potential of the developed sensor material based on exciton emission and owing to its colossal spectral shift with pressure, we performed uniaxial low-pressure measurements using the custom-built experimental setup depicted in Fig. 6a. In contrast to the isostatic measurements in a DAC, for the uniaxial pressure experiments, the amount (thickness) of the material studied may affect the spectral position of the emission band centroid, so the observed shift rate during compression (Fig. 6b). The experimental details and differences in pressure evolution for different sample loadings are discussed in detail in the ESI.† Having in hand the relation between the spectral position of the band and pressure (Fig. 3f and g) determined for the developed sensor in a DAC, we plotted a theoretical evolution of the emission band centroid as a function of isostatic pressure (dashed line in Fig. 6b). The plotted line agrees reasonably well with the experimental data points for the intermediate amounts/thicknesses of the loading samples. These results indicate that, in contrast to conventional photoluminescence, the use of exciton emission for optical pressure sensing allows resolving pressure values differing by only ≈10 bar, which had been impossible so far using existing sensor materials. Representative spectra, cycling test results, and decompression data are given in the ESI† (Fig. S9). Fig. 6c schematically represents the concept of visual pressure monitoring in heavy constructions for early detection of cracks/strains (under non-isostatic pressure). When irradiating with a UV light (laser or lamp), the perovskite material appropriately combined (embedded) with an inspected object, will illuminate with a characteristics color, depending on the local pressure in the examined system. The appearance of any fractures, cracks and strains should affect the pressure gradient in the system, introducing some non-uniformities in the emitted light from the irradiated area. In other words, any deviations and inconsistencies from the expected emission color (spectral characteristics) from the inspected object may be used as an alert of the local pressure increase (blueshift) in a given construction facility. On the other hand, Fig. 6d demonstrates application of the sensor in high-pressure luminescence manometry in a DAC assembly, i.e. its usage as an accurate remote pressure gauge.
Conclusions
Here, we developed a novel pressure sensor material with a colossal sensitivity (Δλ/Δp = 112 nm GPa−1) based on a double-perovskite structure, which is significantly higher than that of currently used optical manometers. This was possible by the use of photoluminescence associated with self-trapped exciton (STE) emission in the synthesized lead-free, double perovskite Cs2Ag0.6Na0.4InCl6 doped with Bi3+ ions observed upon UV excitation. This is because the soft lattice of perovskites favors STE photoluminescence, characterized by broadband emission and a significant Stokes shift due to strong exciton–phonon coupling. The low-energy STE emission band, initially located at ≈600 nm under ambient conditions, shifts toward higher energies (shorter wavelengths) upon high-pressure compression, reaching ≈440 nm at 4 GPa (40 kbar). Such an enormous spectral shift from orange to blue has not been previously reported for any other type of material or emission in such a small pressure range. The colossal pressure-induced spectral shift and significant increase in the energy of the emitted photons are associated with the high susceptibility of the self-trapping, electron-lattice interaction energy and lattice deformation energy to pressure changes, and their significant decrease upon compression of the perovskite structure. Due to the small pressure dependence of the excitation spectra, the corresponding Stokes shift also significantly decreases with pressure, i.e. from 200 to 90 nm in the mentioned pressure range. Moreover, the synthesized sensor material exhibits abnormal and rarely observed pressure-induced narrowing of the emission band (FWHM linearly decreases from 235 to 115 nm), allowing multi-parameter pressure sensing. On the other hand, the material studied exhibits small (compared to pressure) temperature effect on the spectral position of the STE emission band, which is crucial for sensing under extreme conditions. Theoretical calculations and experimental studies, including high-pressure XRD and Raman spectroscopy, confirmed the structural stability of the developed sensor material under pressure. Finally, we used the developed sensor for optical detection and resolving small pressure gradients on the order of only 10 bars, confirming its utility in real-world applications by performing uniaxial pressure measurements. The low-pressure experiments conducted in a natural, non-idealized environment (in contrast to the isostatic conditions of the DAC chamber) indicate the possibility of visual pressure monitoring in heavy constructions for early detection of strains and cracks, opening new horizons in remote pressure sensing.Data availability
The data that support the results presented in this paper and other findings are available in a public repository (Zenodo) at https://zenodo.org/records/11057922, with DOI: https://doi.org/10.5281/zenodo.11057922.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by the National Science Centre, Poland (grants no. 2023/50/E/ST5/00021 and 2019/33/B/ST3/00406) and the National Centre for Research and Development Poland Grant (No. PL-TW/VIII/1/2021). A. M. acknowledges the financial support of the Spanish Ministerio de Ciencia e Innovación and the Agencia Estatal de Investigaci'on MCIN/AEI/10.13039/501100011033 as part of the MALTA Consolider Team Network (RED2022-134388-T), the I+D+i project, and the PID2022-138076NB-C44 co-financed by EU FEDER funds. RSL is financially supported by the Ministry of Science and Technology in Taiwan (Contract No. NSTC 112-2113-M-002-020 and NSTC 113-2923-M-002-006).References
- C. D. S. Brites, R. Marin, M. Suta, A. N. Carneiro Neto, E. Ximendes, D. Jaque and L. D. Carlos, Adv. Mater., 2023, 35, 2302749 CrossRef CAS PubMed.
- L. Marciniak, P. Woźny, M. Szymczak and M. Runowski, Coord. Chem. Rev., 2024, 507, 215770 CrossRef CAS.
- H. K. Mao, J. Xu and P. M. Bell, J. Geophys. Res., 1986, 91, 4673–4676 CrossRef CAS.
- J. A. Xu, H. K. Mao and P. M. Bell, Science, 1986, 232, 1404–1406 CrossRef CAS PubMed.
- T. Tröster, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner, J.-C. G. Bünzli and V. K. Pecharsky, Elsevier, North-Holland, 2003, vol. 33, pp. 515–589 Search PubMed.
- U. F. Rodríguez, R. Valiente, V. Lavín and R. Rodríguez-Mendoza, An Introduction to High-Pressure Science and Technology, CRC Press, Boca Raton, 1st edn, 2015, pp. 229–274 Search PubMed.
- A. Katrusiak, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2019, 75, 918–926 CrossRef CAS PubMed.
- M. Runowski, in Handbook of Nanomaterials in Analytical Chemistry, ed. C. M. Hussain, Elsevier, 2020, pp. 227–273 Search PubMed.
- D. M. Trots, A. Kurnosov, T. B. Ballaran, S. Tkachev, K. Zhuravlev, V. Prakapenka, M. Berkowski and D. J. Frost, J. Geophys. Res., 2013, 118, 5805–5813 CrossRef CAS.
- S. V. Rashchenko, A. Kurnosov, L. Dubrovinsky and K. D. Litasov, J. Appl. Phys., 2015, 117, 145902 CrossRef.
- T. Zheng, M. Runowski, P. Woźny, S. Lis and V. Lavín, J. Mater. Chem. C, 2020, 8, 4810–4817 RSC.
- M. Runowski, N. Stopikowska and S. Lis, Dalton Trans., 2020, 49, 2129–2137 RSC.
- S. Goderski, M. Runowski, P. Woźny, V. Lavín and S. Lis, ACS Appl. Mater. Interfaces, 2020, 12, 40475–40485 CrossRef CAS PubMed.
- Y. Masubuchi, S. Nishitani, S. Miyazaki, H. Hua, J. Ueda, M. Higuchi and S. Tanabe, Appl. Phys. Express, 2020, 13, 042009 CrossRef CAS.
- Y. Wang, T. Seto, K. Ishigaki, Y. Uwatoko, G. Xiao, B. Zou, G. Li, Z. Tang, Z. Li and Y. Wang, Adv. Funct. Mater., 2020, 30, 2001384 CrossRef CAS.
- M. A. Antoniak, S. J. Zelewski, R. Oliva, A. Żak, R. Kudrawiec and M. Nyk, ACS Appl. Nano Mater., 2020, 3, 4209–4217 CrossRef CAS.
- M. Runowski, T. Zheng, P. Woźny and P. Du, Dalton Trans., 2021, 50, 14864–14871 RSC.
- T. Zheng, M. Sójka, M. Runowski, P. Woźny, S. Lis and E. Zych, Adv. Opt. Mater., 2021, 9, 2101507 CrossRef CAS.
- M. Sójka, M. Runowski, P. Woźny, L. D. Carlos, E. Zych and S. Lis, J. Mater. Chem. C, 2021, 9, 13818–13831 RSC.
- M. Runowski, P. Woźny and I. R. Martín, J. Mater. Chem. C, 2021, 9, 4643–4651 RSC.
- M. Runowski, J. Marciniak, T. Grzyb, D. Przybylska, A. Shyichuk, B. Barszcz, A. Katrusiak and S. Lis, Nanoscale, 2017, 9, 16030–16037 RSC.
- D. Zhang, B. Zheng, Z. Zheng, L. Li, Q. Yang, Y. Song, B. Zou and H. Zou, Chem. Eng. J., 2022, 431, 133805 CrossRef CAS.
- B. Zheng, X. Zhang, D. Zhang, F. Wang, Z. Zheng, X. Yang, Q. Yang, Y. Song, B. Zou and H. Zou, Chem. Eng. J., 2022, 427, 131897 CrossRef CAS.
- Q. Lv, C. Wang, S. Chen, H. Zheng, E. Dong and G. Zhu, Inorg. Chem., 2022, 61, 3212–3222 CrossRef CAS PubMed.
- T. Zheng, M. Sójka, P. Woźny, I. R. Martín, V. Lavín, E. Zych, S. Lis, P. Du, L. Luo and M. Runowski, Adv. Opt. Mater., 2022, 10, 2201055 CrossRef CAS.
- T. Zheng, L. Luo, P. Du, S. Lis, U. R. Rodríguez-Mendoza, V. Lavín and M. Runowski, Chem. Eng. J., 2022, 446, 136839 CrossRef CAS.
- T. Zheng, L. Luo, P. Du, S. Lis, U. R. Rodríguez-Mendoza, V. Lavín, I. R. Martín and M. Runowski, Chem. Eng. J., 2022, 443, 136414 CrossRef CAS.
- T. Zheng, M. Runowski, P. Rodríguez-Hernández, A. Muñoz, F. J. Manjón, M. Sójka, M. Suta, E. Zych, S. Lis and V. Lavín, Acta Mater., 2022, 231, 117886 CrossRef CAS.
- K. Su, L. Mei, Q. Guo, P. Shuai, Y. Wang, Y. Liu, Y. Jin, Z. Peng, B. Zou and L. Liao, Adv. Funct. Mater., 2023, 2305359 CrossRef CAS.
- M. Pieprz, W. Piotrowski, P. Woźny, M. Runowski and L. Marciniak, Adv. Opt. Mater., 2024, 12, 2301316 CrossRef CAS.
- M. Szymczak, M. Runowski, V. Lavín and L. Marciniak, Laser Photon. Rev., 2023, 17, 2200801 CrossRef CAS.
- M. Runowski, A. Shyichuk, A. Tymiński, T. Grzyb, V. Lavín and S. Lis, ACS Appl. Mater. Interfaces, 2018, 10, 17269–17279 CrossRef CAS PubMed.
- M. Szymczak, M. Runowski, M. G. Brik and L. Marciniak, Chem. Eng. J., 2023, 466, 143130 CrossRef CAS.
- Q. Zeng, M. Runowski, J. Xue, L. Luo, L. Marciniak, V. Lavín and P. Du, Adv. Sci., 2024, 11, 2308221 CrossRef CAS PubMed.
- T. Zheng, M. Runowski, J. Xue, L. Luo, U. R. Rodríguez-Mendoza, V. Lavín, I. R. Martín, P. Rodríguez-Hernández, A. Muñoz and P. Du, Adv. Funct. Mater., 2023, 33, 2214663 CrossRef CAS.
- T. Zheng, M. Runowski, I. R. Martín, K. Soler-Carracedo, L. Peng, M. Skwierczyńska, M. Sójka, J. Barzowska, S. Mahlik, H. Hemmerich, F. Rivera-López, P. Kulpiński, V. Lavín, D. Alonso and D. Peng, Adv. Mater., 2023, 35, 2304140 CrossRef CAS PubMed.
- M. Szymczak, P. Woźny, M. Runowski, M. Pieprz, V. Lavín and L. Marciniak, Chem. Eng. J., 2023, 453, 139632 CrossRef CAS.
- M. Pieprz, M. Runowski, P. Woźny, J. Xue and L. Marciniak, J. Mater. Chem. C, 2023, 1, 3777 Search PubMed.
- M. Szymczak, J. Jaśkielewicz, M. Runowski, J. Xue, S. Mahlik and L. Marciniak, Adv. Funct. Mater., 2024, 2314068 CrossRef CAS.
- M. Runowski, P. Woźny, V. Lavín and S. Lis, Sens. Actuators, B, 2018, 273, 585–591 CrossRef CAS.
- J. Barzowska, T. Lesniewski, S. Mahlik, H. J. Seo and M. Grinberg, Opt. Mater., 2018, 84, 99–102 CrossRef CAS.
- M. Runowski, P. Woźny, N. Stopikowska, Q. Guo and S. Lis, ACS Appl. Mater. Interfaces, 2019, 11, 4131–4138 CrossRef CAS PubMed.
- C. Hernandez, S. K. Gupta, J. P. Zuniga, J. Vidal, R. Galvan, M. Martinez, H. Guzman, L. Chavez, Y. Mao and K. Lozano, Sens. Actuators, A, 2019, 298, 111595 CrossRef CAS.
- K. Soler-Carracedo, I. R. Martin, M. Runowski, L. L. Martín, F. Lahoz, A. D. Lozano-Gorrín and F. Paz-Buclatin, Adv. Opt. Mater., 2020, 8, 2000678 CrossRef CAS.
- M. Runowski, P. Woźny, S. Lis, V. Lavín and I. R. Martín, Adv. Mater. Technol., 2020, 5, 1901091 CrossRef CAS.
- G. Xiao, Y. Cao, G. Qi, L. Wang, C. Liu, Z. Ma, X. Yang, Y. Sui, W. Zheng and B. Zou, J. Am. Chem. Soc., 2017, 139, 10087–10094 CrossRef CAS PubMed.
- Z. Ma, Z. Liu, S. Lu, L. Wang, X. Feng, D. Yang, K. Wang, G. Xiao, L. Zhang, S. A. T. Redfern and B. Zou, Nat. Commun., 2018, 9, 4506 CrossRef PubMed.
- S. D. Stranks and H. J. Snaith, Nat. Nanotechnol., 2015, 10, 391–402 CrossRef CAS PubMed.
- O. Malinkiewicz, A. Yella, Y. H. Lee, G. M. Espallargas, M. Graetzel, M. K. Nazeeruddin and H. J. Bolink, Nat. Photonics, 2014, 8, 128–132 CrossRef CAS.
- W. Yin, T. Shi and Y. Yan, Adv. Mater., 2014, 26, 4653–4658 CrossRef CAS PubMed.
- M. A. Green, A. Ho-Baillie and H. J. Snaith, Nat. Photonics, 2014, 8, 506–514 CrossRef CAS.
- Q. Li, Y. Wang, W. Pan, W. Yang, B. Zou, J. Tang and Z. Quan, Angew. Chem., Int. Ed., 2017, 56, 15969–15973 CrossRef CAS PubMed.
- L. Zhang, Y. Fang, L. Sui, J. Yan, K. Wang, K. Yuan, W. L. Mao and B. Zou, ACS Energy Lett., 2019, 4, 2975–2982 CrossRef CAS.
- J. Zhou, Z. Xia, M. S. Molokeev, X. Zhang, D. Peng and Q. Liu, J. Mater. Chem. A, 2017, 5, 15031–15037 RSC.
- X.-G. Zhao, D. Yang, J.-C. Ren, Y. Sun, Z. Xiao and L. Zhang, Joule, 2018, 2, 1662–1673 CrossRef CAS.
- L. Chu, W. Ahmad, W. Liu, J. Yang, R. Zhang, Y. Sun, J. Yang and X. Li, Nano-Micro Lett., 2019, 11, 16 CrossRef PubMed.
- K. Dave, W.-T. Huang, T. Leśniewski, A. Lazarowska, D. Jankowski, S. Mahlik and R.-S. Liu, Dalton Trans., 2022, 51, 2026–2032 RSC.
- K. Dave, W.-T. Huang, T. Leśniewski, A. Lazarowska, M. Grzegorczyk, S. Mahlik, G. Leniec, S. M. Kaczmarek and R.-S. Liu, Nanoscale, 2022, 14, 17735–17742 RSC.
- J. Luo, X. Wang, S. Li, J. Liu, Y. Guo, G. Niu, L. Yao, Y. Fu, L. Gao, Q. Dong, C. Zhao, M. Leng, F. Ma, W. Liang, L. Wang, S. Jin, J. Han, L. Zhang, J. Etheridge, J. Wang, Y. Yan, E. H. Sargent and J. Tang, Nature, 2018, 563, 541–545 CrossRef CAS PubMed.
- M. D. Smith and H. I. Karunadasa, Acc. Chem. Res., 2018, 51, 619–627 CrossRef CAS PubMed.
- Q. Hu, G. Niu, Z. Zheng, S. Li, Y. Zhang, H. Song, T. Zhai and J. Tang, Small, 2019, 15, 1903496 CrossRef CAS PubMed.
- A. Chen, X. Jing, T. Wang, T. Zhao, Y. Zhang, D. Zhou, R. Sun, X. Zhang, R. Liu, B. Liu, Q. Li and B. Liu, Inorg. Chem., 2022, 61, 6488–6492 CrossRef CAS PubMed.
- Z. Ma, Q. Li, J. Luo, S. Li, L. Sui, D. Zhao, K. Yuan, G. Xiao, J. Tang, Z. Quan and B. Zou, J. Am. Chem. Soc., 2021, 143, 15176–15184 CrossRef CAS PubMed.
- A. Bibi, I. Lee, Y. Nah, O. Allam, H. Kim, L. N. Quan, J. Tang, A. Walsh, S. S. Jang, E. H. Sargent and D. Ha Kim, Mater. Today, 2021, 49, 123–144 CrossRef CAS.
- H. Tang, Y. Xu, X. Hu, Q. Hu, T. Chen, W. Jiang, L. Wang and W. Jiang, Adv. Sci., 2021, 8, 2004118 CrossRef CAS PubMed.
- Y. Liu, A. Nag, L. Manna and Z. Xia, Angew. Chem., 2021, 60, 11592–11603 CrossRef CAS PubMed.
- J. Zhou, X. Rong, P. Zhang, M. S. Molokeev, P. Wei, Q. Liu, X. Zhang and Z. Xia, Adv. Opt. Mater., 2019, 7, 1801435 CrossRef.
- N. K. Nandha and A. Nag, Chem. Commun., 2018, 54, 5205–5208 RSC.
- J. A. Steele, P. Puech, M. Keshavarz, R. Yang, S. Banerjee, E. Debroye, C. W. Kim, H. Yuan, N. H. Heo, J. Vanacken, A. Walsh, J. Hofkens and M. B. J. Roeffaers, ACS Nano, 2018, 12, 8081–8090 CrossRef CAS PubMed.
- D. C. Wallace and H. Callen, Am. J. Phys., 1972, 40, 1718–1719 CrossRef.
- D. C. Wallace, Phys. Rev., 1967, 162, 776–789 CrossRef CAS.
- J. Wang, J. Li, S. Yip, S. Phillpot and D. Wolf, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 12627–12635 CrossRef CAS PubMed.
- Z. Zhou and B. Joós, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 3841–3850 CrossRef CAS PubMed.
- O. Gomis, D. Santamaría-Pérez, R. Vilaplana, R. Luna, J. A. Sans, F. J. Manjón, D. Errandonea, E. Pérez-González, P. Rodríguez-Hernández, A. Muñoz, I. M. Tiginyanu and V. V. Ursaki, J. Alloys Compd., 2014, 583, 70–78 CrossRef CAS.
- S. F. Pugh, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45, 823–843 CrossRef CAS.
- L. Nataf, F. Rodríguez, R. Valiente and J. González, High Pressure Res., 2009, 29, 653–659 CrossRef CAS.
- Z. Zheng, Y. Song, B. Zheng, Y. Zhao, Q. Wang, X. Zhang, B. Zou and H. Zou, Inorg. Chem. Front., 2023, 10, 2788–2798 RSC.
- H. Chen, T. Seto and Y. Wang, Inorg. Chem. Front., 2022, 9, 1644–1654 RSC.
- P. Zhou, Q. Zhang, F. Peng, B. Sun, X. Dou, B. Liu, D. Han, Y. Xue and K. Ding, J. Rare Earths, 2022, 40, 870–877 CrossRef CAS.
- P. Comodi and P. F. Zanazzi, J. Appl. Crystallogr., 1993, 26, 843–845 CrossRef CAS.
- B. Lorenz, Y. R. Shen and W. B. Holzapfel, High Pressure Res., 1994, 12, 91–99 CrossRef.
- T. P. Beales, C. H. L. Goodman and K. Scarrott, Solid State Commun., 1990, 73, 1–3 CrossRef CAS.
- J. D. Barnett, S. Block and G. J. Piermarini, Rev. Sci. Instrum., 1973, 44, 1–9 CrossRef.
- S. F. León-Luis, J. E. Muñoz-Santiuste, V. Lavín and U. R. Rodríguez-Mendoza, Opt. Express, 2012, 20, 10393 CrossRef PubMed.
- N. J. Hess and G. J. Exarhos, High Pressure Res., 1989, 2, 57–64 CrossRef.
- G. Chen, J. Hölsä and J. R. Peterson, J. Phys. Chem. Solids, 1997, 58, 2031–2037 CrossRef CAS.
- F. Datchi, R. LeToullec and P. Loubeyre, J. Appl. Phys., 1997, 81, 3333–3339 CrossRef CAS.
- W. Hayes, J. Mod. Opt., 1990, 37, 1149–1150 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh00871e |
| This journal is © The Royal Society of Chemistry 2024 |