Effect of Sc spatial distribution on the electronic and ferroelectric properties of AlScN

Abstract

While aluminum scandium nitride based ferroelectric materials have shown significant promise for non-volatile memory applications, difficulties relating challenges in device performance, such as electrical leakage, to structural characteristics motivate improved understanding of the fundamental structure–property relationship. Spinodal decomposition has been reported in this material system, consistent with our observation of compositional segregation in AlScN films grown by reactive sputter epitaxy. To better understand the effects of spatially non-uniform Sc concentrations, the electronic and ferroelectric (FE) properties of AlScN as a function of Sc distribution are studied using density functional theory (DFT). We explore the impact of Sc-rich atomic planes in wurtzite AlScN with Sc concentration ranging from 0 to 44 at% through a supercell approach. We find that while spontaneous polarization decreases with Sc concentration (∼133 to 102 μC cm⁻²), periodic Sc-rich planar clusters slow this effect, suggesting that phase segregation counters the effects of increasing Sc composition. Furthermore, the FE switching barrier per formula unit (f.u.) as a function of composition exhibits a local maximum of 0.60 eV f.u.⁻¹ at 25% Sc concentration in the presence of Sc-rich planes but decreases monotonically (0.51 to 0.28 eV f.u.⁻¹) if Sc is uniformly distributed, suggesting that the spatial distribution of Sc plays an important role in the optoelectronic properties of the material by changing the energy landscape. Sc clustering also decreases the bandgap of the material. This study shows that the structural complexity arising from spatial composition modulation provides tunability of ferroelectric properties in AlScN ferroelectrics.

---

New concepts

Recent interests in ferroelectric AlScN for non-volatile memory applications stem from high remanent polarization and a wide memory window. However, structural complexity in these materials, including the tendency for compositional segregation, obfuscates the structure–property relationship. We find that compositional order/disorder in these materials plays an important role in the free energy landscape for ferroelectric switching, suggesting that the influence of compositional order/disorder on ferroelectric properties in this class of materials merits further study.

Recent reports of wurtzite AlScN ferroelectrics show that these materials are promising for non-volatile memory applications such as ferroelectric random-access memory (FeRAM).^1–7 These materials exhibit high remanent polarization but are known to suffer from electrical leakages that have been hypothesized to originate from point defects such as vacancies.⁸ While AlScN adopts a wurtzite structure for lower Sc concentrations, a phase transition to a rocksalt structure begins at ∼30 at% Sc.⁵ There is a miscibility gap between the Al-rich wurtzite and Sc-rich rocksalt phases, and the heat of mixing of AlN and ScN is positive:⁹ as a result, at certain temperatures, the free energy change resulting from a compositional fluctuation will be negative, giving rise to a phase instability. While spinodal decomposition in AlScN has been reported,¹⁰ its effects on the ferroelectric behavior are not known. On the one hand, compositional modulation in AlScN multilayer structures has been shown to increase the electric field at which dielectric breakdown occurs.¹¹ One motivation for this approach to ferroelectric materials comes from interface physics.^12–15 On the other hand, uniformity of Sc spatial distribution in AlScN can be thought of as another structural parameter related to compositional order/disorder. While ordering in metal alloys is well-known,^16,17 this phenomenon in wurtzite solid solutions based on AlN has not been explored in detail.

To illustrate the importance of Sc spatial distribution, we show scanning transmission electron microcopy (STEM) data from epitaxial AlScN(0001) thin films grown on Si(111) substrates exhibiting compositional segregation. These films (approximately 20 at% Sc) are synthesized by ultra-high vacuum reactive sputtering, which has been reported elsewhere (further experimental details are provided in the ESI†).⁵Fig. 1a shows a high-angle annular dark field (HAADF) STEM image, which is highly sensitive to the atomic number.¹⁸ At atomic resolution, this compositional non-uniformity is observed using electron energy loss spectroscopy (EELS). High resolution STEM HAADF images (Fig. 1a and b) show significant disorder at the Si/AlScN interface as well as mosaic spread as observed through lattice fringe tilt in the AlScN film (Fig. 1b). STEM-EELS spectra collected from Sc- and Al-rich regions (regions 1 and 2, respectively) and the Si substrate (region 3) are shown in Fig. 1c. Fitting the total spectrum as a linear combination of the spectra in these regions using the multi-linear least squares (MLLS) method yields fit coefficient plots (Fig. 1d–f) that are consistent with STEM-EDS maps (Fig. 1g–j). Experimental evidence of compositional segregation in wurtzite AlScN motivates a deeper look at the effects of compositional order/disorder in this material. Confirmation of ferroelectric behavior in these films is given in the ESI† (Fig. S5).

Fig. 1 (a) Atomic resolution HAADF STEM image and (b) inset (blue rectangle) of an epitaxial AlScN film on a Si(111) substrate with Si atomic columns and AlScN lattice fringes marked; (c) EELS spectrum from regions 1, 2, and 3 in (a); STEM-EELS (d)–(f) and STEM-EDS maps (g)–(j) of the orange rectangle in (a) showing MLLS fit coefficients for the spectra from regions (d) 1, (e) 2, and (f) 3; STEM-EDS signals from (g) Al, (h) Sc, (i) N, and (j) Si.

We study Sc composition distribution effects on ferroelectric behavior in wurtzite AlScN by performing density functional theory (DFT) calculations of the band structure and polarization (further simulation details are provided in the ESI†). To do this, we generate two configurations of AlScN supercells: (1) in which Sc atoms are crowded into a single basal plane, forming a Sc-rich planar cluster and (2) in which Sc atoms are distributed approximately evenly among all basal planes in the supercell (Fig. S1, additional details in the ESI†). There are several proposed switching mechanisms in wurtzite ferroelectrics. The wurtzite structure belongs to the non-centrosymmetric space group p6₃mc and possesses an intrinsic spontaneous polarization along the c-axis that comes from the separation of Al and N atoms in basal planes.¹ Because of the strong bonding in tetrahedrally coordinated cations and anions, it was long thought that these materials are not susceptible to reversible polarization switching through an external electric field below the dielectric breakdown limit.^19,20 However, one can envision a Gedanken experiment in which symmetry-equivalent states of opposite polarity are obtained by displacing cations relative to anions along the c-axis direction. In this process, the structure passes through a centrosymmetric paraelectric state having the h-BN structure (space group: P6₃mmc) midway, as shown in Fig. 2, which shows a schematic illustration of three virtual states of AlN as it undergoes polarization switching (see also Fig. S2, ESI†). If the potential energy barrier in switching from one polar state to the other is sufficiently small, it is possible to induce a polarization reversal by the application of electric field.^21,22 Recently, different transition states in FE switching of wurtzite ferroelectrics have been reported, suggesting a significantly more complex, multi-step switching mechanism.^23–26 In our simplified picture, the switching occurs for each unit cell simultaneously between N-polar and III-polar in a series of virtual states that traverses through the centrosymmetric h-BN structure, termed collective switching. However, a more complex approach in which tetrahedra switch independently has been proposed.²³ Atomic displacements during the switching can be thought of in terms of lattice vibrations of the h-BN reference structure. In the transverse optical (TO) A_2u mode,^27,28 neighboring atoms move alternately up and down in the out-of-plane direction, consistent with collective switching. On the other hand, coupling to lower energy, long wavelength (e.g. acoustic) phonons could generate a structure consistent with more pronounced switching in some regions compared to others. This provides physical insight for the observation of lower energy barrier to individual as compared to collective switching. We investigate the effect of compositionally segregated Sc-rich planar clusters (similar to experimentally observed Al- and Sc-rich lamellae in Fig. 1) in the AlScN supercell on the FE properties. At the same time, we observe changes in the electronic properties of the system due to the in-plane clustering of Sc atoms. Because, for x > 0.46, the crystal structure of Al_1−xSc_xN changes to the centrosymmetric rock-salt structure (no FE properties), we have kept the Sc content in the system ranging from 0 at% to 43 at%.²⁹ Details of the lattice parameter calculations are provided in the ESI† (Fig. S3).

Fig. 2 AlN crystal structure change from (a) N-polar to (b) non-polar layered hexagonal to (c) Al-polar configuration during polarization switching from P⃑ to −P⃑.

The electronic band structure of AlScN along selected high symmetry directions in the first Brillouin zone and density of states (DOS) are shown in Fig. 3 and Fig. S3 (ESI†). In Fig. 3(a), the band structure of pure AlN is shown. Fig. 3(b) and (c) show the band structure of Al_0.5625Sc_0.4375N with and without Sc-rich planes, respectively. The corresponding changes in the DOS are shown in Fig. S4 (ESI†). Fig. 4 illustrates the band gap of AlScN as a function of both Sc concentration and in-plane Sc clustering. We find that the band gap of AlScN is greatest when no Sc is present with a bandgap of around 4 eV, significantly lower than the experimental value³⁰ (6.2 eV). While a systematic underestimation of band gap is expected due to intrinsic DFT error stemming from the ability of the exchange correlation functional to describe the behavior of electronic interactions in the system,³¹ useful information can still be obtained from the calculated band gap variation as a function of Sc concentration. Comparing Fig. 3(b) and (c), it is observed that in-plane Sc clustering lowers the bandgap and changes the band structure of the system. In pure AlN and for the systems in which there is no in-plane clustering, there exists a parabolic band at the conduction band edge at the Γ-point as shown in Fig. 3(a); the curvature of this band decreases as a result of Sc clustering. Sc clustering also results in the conduction band minimum bearing a band with lower curvature between the high-symmetry H and K points as shown in Fig. 3(b) and (c). The occurrence of the lower curvature in the conduction band edge might decrease electrical conductivity and charge carrier mobility because electron effective mass is larger in those bands. This could be consistent with the experimental observation of improved dielectric breakdown properties in compositionally modulated AlScN multilayers.¹¹ With increasing Sc concentration, the band gap decreases continuously (Fig. 4) and, for each given Sc concentration, Sc-clustering further lowers the band gap. This lowering is more pronounced at lower Sc concentrations.

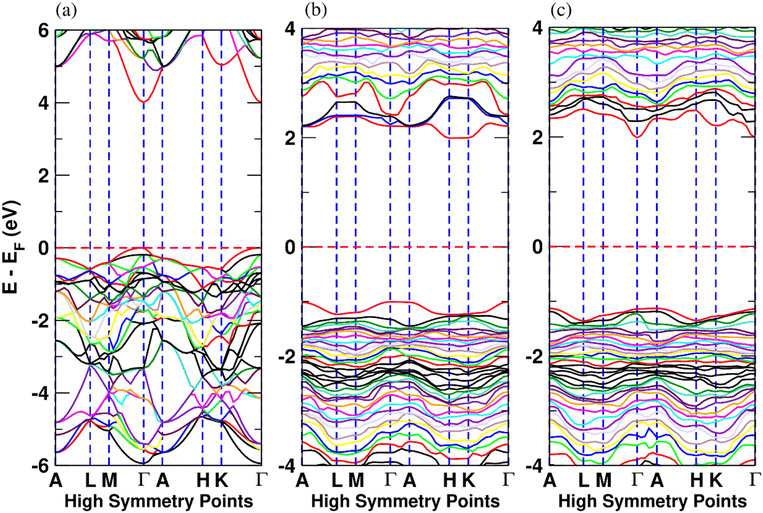Fig. 3 Band structure of (a) AlN and Al_0.5625Sc_0.4375N (b) with and (c) without in-plane Sc clustering. The vertical axis is the energy in reference to the Fermi energy (E_F).

Fig. 4 Calculated band gaps of Al_1−xSc_xN. The blue and red traces represent the system with and without in-plane Sc clustering, respectively.

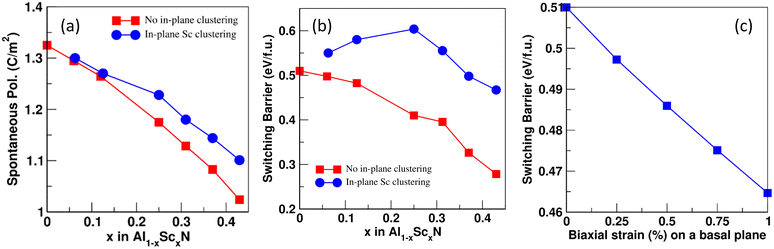
We have calculated spontaneous polarization (P_s) and the potential energy barrier (E_b) for FE switching as a function of both Sc concentration and the spatial distribution of Sc (uniform vs. Sc-rich planar clusters). The spontaneous polarization of pure AlN is 1.326 C m⁻² with a FE switching barrier of 0.51 eV f.u.⁻¹ This value of P_s is in close agreement with previously calculated values: 1.35, 1.34, and 1.33 C m⁻².^25,32,33 Also, the FE switching barrier energy is also consistent with previous reports (0.51 eV f.u.⁻¹).³⁴ The calculated polarization branches³⁵ and relative energies associated with each intermediate distortion for pure AlN are shown in Fig. 5. Here, points A and B are the polarization values calculated for the N-polar and Al-polar wurtzite structures whose values are −0.087 C m⁻² and 0.087 C m⁻² and fall on the polarization branches^35,36 corresponding to n = 3 and n = −3, respectively; polarization branches arise due to the calculation of the polarization as a Berry phase and refer to periodicity of the calculated polarization with respect to integer multiples of the polarization quantum of the system originating from translational symmetry. Similarly, point C corresponds to the reference centrosymmetric structure where the value of polarization is 0.000 C m⁻². The polarization quantum for this system (the separation between polarization branches) is equal to 0.471 C m⁻². So, using eqn (S2) (ESI†) we get P_s = ∓ 0.087 ± 3 × 0.471 − 0 = ± 1.326 C m⁻². It is important to note here that the points of interest for the system are only A, B, and C, but to find the value of n we need to calculate the polarization at several intermediate values of the internal structural parameter u. The same process is used to calculate FE polarization for all the structures considered. In Fig. 6, the energy barrier (in reference to the wurtzite structure) as well as the double-well energy landscape for AlScN FE switching is shown as a function of Sc composition, x, for an approximately uniform spatial composition distribution. The graph shows that the energy is lowest in the wurtzite phase and increases as it reaches a maximum at the centrosymmetric nonpolar structure. Fig. 7(a) and (b) shows that the increase in Sc concentration is associated with a decrease in both spontaneous polarization and the energy barrier for switching. There is no significant impact of in-plane Sc clustering on the value of spontaneous polarization. However, a substantial increase in the energy barrier for FE switching at intermediate Sc concentrations is observed when Sc-rich atomic planes are present. At 25 at% Sc concentration, the energy barrier for FE switching increases from 0.41 eV f.u.⁻¹ to a local maximum of 0.60 eV f.u.⁻¹ There is a subsequent decrease in switching barrier energy when Sc concentrations increase above 25 at%. This result is consistent with the continuous decrease in switching barrier for AlScN systems with approximately uniform Sc spatial distributions. One possible consequence is that if Sc/Al can diffuse locally, Fig. 6 and 7 indicate that high Sc concentrations may appear at domain wall boundaries of positive and negative polarization domains to reduce the switching barrier. We hypothesize that, at long timescales, a strong trend for Sc compositional segregation could potentially form ordered states/structures, which can be investigated using larger size DFT. We note that we perform this calculation for Sc concentrations ranging from 0 at% to 43 at%; within this range, we observe a consistent Sc clustering induced increase in ferroelectric switching barrier. At higher Sc concentrations, the wurtzite structure is not thermodynamically stable – in fact, phase segregation is observed at as low as 30 at% Sc.⁵

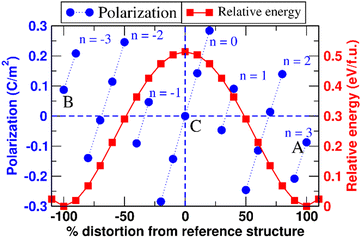Fig. 5 Polarization and relative energy of AlN in the centrosymmetric reference (see Fig. 2b), wurtzite (see Fig. 2a/c), and intermediate structures. The parallel blue traces are polarization branches.

Fig. 6 Double well potential and energy barrier for FE switching of Al_1−xSc_xN for some Sc concentrations in a system with approximately uniform Sc spatial distribution.

Fig. 7 Effect of Sc concentration on the (a) spontaneous polarization and (b) switching barrier energy of Al_1−xSc_xN. The blue trace corresponds to AlScN exhibiting basal plane Sc clustering; the red trace corresponds to AlScN with approximately uniform Sc spatial distribution. (c) Effect of biaxial strain on the ferroelectric switching energy barrier in AlN.

The present data also suggest that the in-plane clustering of Sc atoms renders the system more resistant to FE switching and implies that there exists a range of values for the switching barrier that the system can take at any given concentration of the substitutional Sc atoms. We also note that while basal plane Sc clustering is chosen, there is no particular reason either for or against Sc clustering in a different crystallographic orientation or geometry. We have repeated the calculations for Sc clustering perpendicular to the c-axis and similarly obtained an increase in ferroelectric switching barrier albeit with a smaller magnitude (Fig. S6, ESI†). Finally, it has been observed that the application of biaxial tensile strain in the basal plane of wurtzite ZnO has effectively reduced the ferroelectric switching energy barrier.²¹ To confirm whether a similar effect exists in AlScN, we also investigate the effect of biaxial basal plane strain in pure AlN on the switching barrier. A 1% biaxial tensile strain applied on pure AlN (Poisson's ratio, ν = 0.287)³⁷ slightly reduces the energy barrier for FE switching (Fig. 7c) similar to that observed in ZnO. Our result that in-plane Sc clustering increases the FE switching barrier can also be thought of as follows: Sc clustering causes the in-plane lattice parameter to decrease (Fig. S3a), and the resulting biaxial compression increases the switching barrier.

In summary, the electronic properties and electrical polarization of AlScN as a function of Sc concentration and Sc spatial distribution are studied using DFT. We find that increased Sc concentration decreases the bandgap, the spontaneous polarization, and the FE switching barrier in agreement with previous reports. All of these properties are affected by the spatial distribution of Sc. In particular, the switching barrier is significantly increased when Sc-rich atomic planes are present in AlScN. While the bandgap is not strongly affected by Sc segregation, the band structure changes qualitatively due to Sc planar clusters. These changes can be thought of as a response to compositional order/disorder in AlScN. Our results are also consistent with the correlation between FE switching barrier and in-plane strain. The connection of the ferroelectric properties of AlScN to Sc distribution and the detailed length-scales may provide new insights into the structure–property relationship in these materials. The present results are important because they suggest that compositional segregation in AlScN, which has been experimentally observed, needs to be better controlled, as it affects the functional properties in a complex manner.

Author contributions

B. Bhattarai: writing – original draft, writing – review and editing, investigation – simulations, methodology, formal analysis; X. Zhang: writing – review and editing, investigation – synthesis, methodology, formal analysis; W. Xu: writing – reviewing and editing, investigation – piezoresponse force microscopy; Y. Gu: writing – review and editing, methodology, formal analysis; W. J. Meng: writing – review and editing, investigation, methodology, formal analysis, funding acquisition. A. C. Meng: conceptualization, writing – original draft, writing – reviewing and editing, investigation – simulations, electron microscopy, methodology, formal analysis, funding acquisition. The manuscript was written through contributions of all authors.

Data availability

The data supporting this article are either provided in the main text or included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded in part by the NSF EPSCoR program, under awards OIA-1541079 and OIA-1946231, and by the Missouri Research Council, under award URC-23-012. The use of experimental facilities at the LSU Shared Instrumentation Facility (SIF), a part of the Louisiana Core User Facilities (CUF), is acknowledged. The use of experimental facilities at the MU Electron Microscopy Core (EMC) Facilities is acknowledged.

Notes and references

1. S. Fichtner, N. Wolff, F. Lofink, L. Kienle and B. Wagner, J. Appl. Phys., 2019, 125, 114103.
2. P. Wang, D. Wang, N. M. Vu, T. Chiang, J. T. Heron and Z. Mi, Appl. Phys. Lett., 2021, 118, 223504.
3. K. Yazawa, J. S. Mangum, P. Gorai, G. L. Brennecka and A. Zakutayev, J. Mater. Chem. C, 2022, 10, 17557–17566.
4. K. D. Kim, Y. B. Lee, S. H. Lee, I. S. Lee, S. K. Ryoo, S. Byun, J. H. Lee, H. Kim, H. W. Park and C. S. Hwang, Adv. Electron. Mater., 2023, 9, 2201142.
5. X. Zhang, E. A. Stach, W. J. Meng and A. C. Meng, Nanoscale Horiz., 2023, 8, 674–684.
6. X. Zhang, W. Xu, W. J. Meng and A. C. Meng, CrystEngComm, 2024, 26, 180–191.
7. R. Ota, S. Yasuoka, R. Mizutani, T. Shiraishi, K. Okamoto, K. Kakushima, T. Koganezawa, O. Sakata and H. Funakubo, J. Appl. Phys., 2023, 134, 214103.
8. J. Kataoka, S.-L. Tsai, T. Hoshii, H. Wakabayashi, K. Tsutsui and K. Kakushima, Jpn. J. Appl. Phys., 2021, 60, 030907.
9. B. Alling, A. Karimi and I. A. Abrikosov, Surf. Coat. Technol., 2008, 203, 883–886.
10. K. R. Talley, S. L. Millican, J. Mangum, S. Siol, C. B. Musgrave, B. Gorman, A. M. Holder, A. Zakutayev and G. L. Brennecka, Phys. Rev. Mater., 2018, 2, 063802.
11. J. X. Zheng, D. Wang, P. Musavigharavi, M. M. A. Fiagbenu, D. Jariwala, E. A. Stach and R. H. Olsson, III, J. Appl. Phys., 2021, 130, 114101.
12. S. Zhao, B. Li, Y. Guo and H. Li, Appl. Phys. Lett., 2022, 120, 012904.
13. D. A. Dalba, X. Zhang, W. Xu, B. Bhattarai, D. M. Gamachchi, I. M. Karunarathne, W. J. Meng and A. C. Meng, ACS Appl. Electron. Mater., 2024 DOI:10.1021/acsaelm.4c00281.
14. M. Si, X. Lyu and P. D. Ye, ACS Appl. Electron. Mater., 2019, 1, 745–751.
15. F. Huang, B. Saini, Z. Yu, C. Yoo, V. Thampy, X. He, J. D. Baniecki, W. Tsai, A. C. Meng, P. C. McIntyre and S. Wong, ACS Appl. Mater. Interfaces, 2023, 15, 50246–50253.
16. W. J. Meng, P. R. Okamoto, L. J. Thompson, B. J. Kestel and L. E. Rehn, Appl. Phys. Lett., 1988, 53, 1820–1822.
17. Y. Wang, D. Banerjee, C. C. Su and A. G. Khachaturyan, Acta Mater., 1998, 46, 2983–3001.
18. P. D. Nellist and S. J. Pennycook, in Advances in Imaging and Electron Physics, ed. P. W. Hawkes, Elsevier, 2000, vol. 113, pp. 147–203.
19. F. Bernardini, V. Fiorentini and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, R10024.
20. A. Malashevich and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 045106.
21. A. Konishi, T. Ogawa, C. A. J. Fisher, A. Kuwabara, T. Shimizu, S. Yasui, M. Itoh and H. Moriwake, Appl. Phys. Lett., 2016, 109, 102903.
22. H. Moriwake, A. Konishi, T. Ogawa, K. Fujimura, C. A. J. Fisher, A. Kuwabara, T. Shimizu, S. Yasui and M. Itoh, Appl. Phys. Lett., 2014, 104, 242909.
23. C.-W. Lee, K. Yazawa, A. Zakutayev, G. L. Brennecka and P. Gorai, Sci. Adv., 2024, 10, eadl0848.
24. S. Calderon, J. Hayden, S. M. Baksa, W. Tzou, S. Trolier-McKinstry, I. Dabo, J.-P. Maria and E. C. Dickey, Science, 2023, 380, 1034–1038.
25. Z. Liu, X. Wang, X. Ma, Y. Yang and D. Wu, Appl. Phys. Lett., 2023, 122, 122901.
26. G. Schönweger, N. Wolff, M. R. Islam, M. Gremmel, A. Petraru, L. Kienle, H. Kohlstedt and S. Fichtner, Adv. Sci., 2023, 10, 2302296.
27. B. Gil, G. Cassabois, R. Cusco, G. Fugallo and L. Artus, Nanophotonics, 2020, 9, 3483–3504.
28. J. S. Ginsberg, M. M. Jadidi, J. Zhang, C. Y. Chen, N. Tancogne-Dejean, S. H. Chae, G. N. Patwardhan, L. Xian, K. Watanabe, T. Taniguchi, J. Hone, A. Rubio and A. L. Gaeta, Nat. Commun., 2023, 14, 7685.
29. S.-L. Tsai, T. Hoshii, H. Wakabayashi, K. Tsutsui, T.-K. Chung, E. Y. Chang and K. Kakushima, Appl. Phys. Lett., 2021, 118, 082982.
30. W. M. Yim, E. J. Stofko, P. J. Zanzucchi, J. I. Pankove, M. Ettenberg and S. L. Gilbert, J. Appl. Phys., 1973, 44, 292–296.
31. Á. Morales-García, R. Valero and F. Illas, J. Phys. Chem. C, 2017, 121, 18862–18866.
32. K. Furuta, K. Hirata, S. A. Anggraini, M. Akiyama, M. Uehara and H. Yamada, J. Appl. Phys., 2021, 130, 024104.
33. C. E. Dreyer, A. Janotti, C. G. Van de Walle and D. Vanderbilt, Phys. Rev. X, 2016, 6, 021038.
34. H. Wang, N. Adamski, S. Mu and C. G. Van de Walle, J. Appl. Phys., 2021, 130, 104101.
35. L. D. Filip, N. Plugaru and L. Pintilie, Modell. Simul. Mater. Sci. Eng., 2019, 27, 045008.
36. T. E. Smidt, S. A. Mack, S. E. Reyes-Lillo, A. Jain and J. B. Neaton, Sci. Data, 2020, 7, 72.
37. R. Thokala and J. Chaudhuri, Thin Solid Films, 1995, 266, 189–191.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh00551a

---