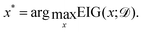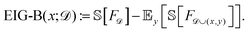Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Probabilistic prediction of material stability: integrating convex hulls into active learning†
Andrew
Novick‡
 *a,
Diana
Cai‡
*a,
Diana
Cai‡
 b,
Quan
Nguyen
c,
Roman
Garnett
c,
Ryan
Adams
d and
Eric
Toberer
b,
Quan
Nguyen
c,
Roman
Garnett
c,
Ryan
Adams
d and
Eric
Toberer
 a
a
aDepartment of Physics, Colorado School of Mines, Golden, Colorado, USA. E-mail: novick@mines.edu
bCenter for Computational Mathematics, Flatiron Institute Address, New York, New York, USA
cDepartment of Computer Science and Engineering, Washington University in St. Louis, St. Louis, Missouri, USA
dDepartment of Computer Science, Princeton University, New Jersey, USA
First published on 5th August 2024
Abstract
Active learning is a valuable tool for efficiently exploring complex spaces, finding a variety of uses in materials science. However, the determination of convex hulls for phase diagrams does not neatly fit into traditional active learning approaches due to their global nature. Specifically, the thermodynamic stability of a material is not simply a function of its own energy, but rather requires energetic information from all other competing compositions and phases. Here we present convex hull-aware active learning (CAL), a novel Bayesian algorithm that chooses experiments to minimize the uncertainty in the convex hull. CAL prioritizes compositions that are close to or on the hull, leaving significant uncertainty in other compositions that are quickly determined to be irrelevant to the convex hull. The convex hull can thus be predicted with significantly fewer observations than approaches that focus solely on energy. Intrinsic to this Bayesian approach is uncertainty quantification in both the convex hull and all subsequent predictions (e.g., stability and chemical potential). By providing increased search efficiency and uncertainty quantification, CAL can be readily incorporated into the emerging paradigm of uncertainty-based workflows for thermodynamic prediction.
New conceptsThe dominant research paradigm in computational thermodynamics involves producing increasingly high-fidelity surrogate models such as machine-learned interatomic potentials or cluster expansions. Here, we take the complementary approach by minimizing the number of thermodynamic calculations necessary to evaluate stability and solubility. This acceleration relies on efficiently resolving the convex hull. With Gaussian processes, we propagate uncertainty in the energy surface of each phase to the resulting convex hull. As such, thermodynamic calculations are chosen that minimize the information entropy of the probabilistic convex hull. By applying a Bayesian approach, we make the uncertainty explicit in our hull predictions as well as any subsequent calculations derived from the hull. Such a framework can be complemented with Bayesian surrogate models, enabling end-to-end uncertainty quantification. |
1 Introduction
Understanding thermodynamic stability is foundational to chemical and materials design. Phase relations provide mechanistic insight and accelerate discovery in disparate areas such as drug solubility,1,2 polymer blend stability,3–5 and phase transitions in metallic alloys.6,7 To accelerate stability predictions, computational research often focuses on producing high-fidelity surrogate models.8–13 However, phase stability prediction remains a persistent challenge for complex systems without effective surrogate models; examples include high-entropy materials,14–18 liquids and glasses,19–21 materials at high temperatures,22 and highly correlated materials.23–27 In this work, we address the frontiers of phase stability prediction by constructing an active learning approach that directly learns about the convex hull.Phase transitions often occur across length- and time-scales too large to be directly observed using simulations. Instead, thermodynamic potentials need to be evaluated across a vast space of competing compositions and phases. The outcome of this competition is encapsulated in the convex hull: a single mathematical object that wraps the energy surface and defines the set of stable phase–composition pairs. Convex hulls are often associated with predicting the stability of compounds without external fields at 0 K,28–36 but they have also been used to calculate phase transitions induced by temperature,22 pressure,37–39 anisotropic stresses in thin films,40,41 magnetic fields,42,43 and applied voltages in battery materials.44,45 Indeed, the convex hull formalism can be used to predict stability under any set of thermodynamic conjugate variables.46,47 Beyond phase diagrams, convex hulls have been recently leveraged in understanding chemical reaction networks and synthesis pathways.48–51
The global nature of convex hulls implies that it is not obvious which composition–phase pairs will reside on the hull. For instance, it is possible for the exact value of the energy to be certain, while still being uncertain that the composition is on the hull. A brute force approach to predicting the convex hull would require calculating the energy for all competing phases and compositions. However, when the cost of individual energy evaluations is large, or the space of possible competing compositions is high-dimensional, exhaustively evaluating the energies is prohibitively expensive. Thus, there are two complimentary modes of acceleration: efficiently producing surrogate models that lower the cost of energy calculations and minimizing the number of energy evaluations necessary to define the convex hull. Both approaches can leverage active learning,52 since it is a natural method for selecting expensive data points that are expected to maximally increase the information about a function.
To optimize the information gain about a surrogate energy function, active learning has been used to iteratively select first-principles calculations that minimize uncertainty in the surrogate model. Surrogate models like cluster expansion53 and interatomic potentials54 have been trained with active learning; they were then leveraged to conduct numerous energy evaluations for predicting the underlying convex hull. Active learning has also been biased to identify phase–composition pairs that are expected to be on or near the convex hull.55–57 While these approaches have been shown to be more efficient than random and grid-based search procedures, the active learning was only biased using proxies that incorporate a local view of the hull rather than directly reasoning about the entire convex hull as a singular, global object.
In this paper, we develop convex hull-aware active learning (CAL) to accelerate stability predictions. CAL distinguishes itself from more conventional Bayesian approaches by reasoning directly about the entire convex hull. CAL uses separate Gaussian process regressions to model the energy surfaces of phases across the composition space. From the Gaussian processes, a posterior belief is produced over possible convex hulls. This induced posterior enables the algorithm to identify composition–phase pairs that are expected to minimize the uncertainty in the convex hull itself, not the constituent energy surfaces. By focusing exclusively on the convex hull, it is possible to make more effective decisions on what compositions to consider.
We start with illustrating the CAL algorithm in one dimension for clarity. The evolution of the convex hull distribution is seen with increasing observations, and both stability predictions and chemical potentials are derived. From there, we explore complex ternary composition spaces with three competing phases. This allows us to quantitatively demonstrate the efficiency of CAL against a baseline active learning procedure and explore analysis techniques for probabilistic hulls. Finally, we demonstrate how CAL can be implemented when there is prior knowledge about line-compounds, as is often the case.
2 Approach
The overall goal is to establish a methodology that approximates the convex hull with minimal observed data. We begin by establishing a probabilistic view of the hull (Fig. 1) and then present the policy for determining the next observation (Fig. 2). We provide additional details on both the model and policy in the Methods section.2.1 Probabilistic view of the hull
In this and all subsequent examples, the energy surfaces are assumed to be continuous and differentiable across alloy compositions. We also assume that there is a finite set of candidate compositions that represent a dense subset of the space. In our first example, we begin with a single phase for which we have observed the energies of the parent compounds and three alloy compositions. As an aside, since CAL is not exclusively built for crystalline matter, we adopt the more general term “phase” rather than “structure-type”. These observations are denoted as![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) = {(xn,yn)}Nn=1, with xn taking values in composition space and yn being energies.
= {(xn,yn)}Nn=1, with xn taking values in composition space and yn being energies.
We model the energy surface with a Gaussian process (GP), which provides a prior on energy surfaces specified by a mean and covariance function.58,59 Conditioning on the observations ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) results in a posterior distribution over energy surfaces that is itself a Gaussian process (eqn (2) and (3)). Let F
results in a posterior distribution over energy surfaces that is itself a Gaussian process (eqn (2) and (3)). Let F![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) be the random function associated with the posterior on energy surfaces; then H
be the random function associated with the posterior on energy surfaces; then H![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) =
= ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) [F
[F![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ] is the induced random (lower) convex hull, where
] is the induced random (lower) convex hull, where ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) is the convex hull operator. The random function H
is the convex hull operator. The random function H![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) is the object of primary interest in this work.
is the object of primary interest in this work.
As we are only considering a finite set of candidate compositions, it is possible to generate samples from this induced posterior by (1) drawing a sample from the multivariate Gaussian distribution resulting from the GP posterior, and (2) using a standard algorithm such as QuickHull60 for computing the lower convex hull of a set of points. Fig. 1a shows a posterior distribution over the energy surface, F![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) , and Fig. 1b depicts three posterior samples and their associated convex hulls.
, and Fig. 1b depicts three posterior samples and their associated convex hulls.
Our epistemic uncertainty about the true convex hull is captured by the random function H![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ; the Shannon entropy
; the Shannon entropy 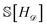 then quantifies our (lack of) knowledge about the convex hull. By framing our problem as one of minimizing
then quantifies our (lack of) knowledge about the convex hull. By framing our problem as one of minimizing  , we can more rapidly gain information about the structure in which we are most interested.
, we can more rapidly gain information about the structure in which we are most interested.
In addition to the hull itself, various properties of interest can be derived from H![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) , so we can reason about their posterior distributions as well. For example, the (random) set
, so we can reason about their posterior distributions as well. For example, the (random) set
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) := {x:F := {x:F![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (x) = H (x) = H![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (x)} (x)} |
Fig. 1c shows 20 samples of stable sets after the 3 iterations in Fig. 1b. These binary classifications can be averaged to estimate the marginal probability that any given composition is on the hull, i.e., is stable (Fig. 1d). Note that these marginal probabilities reveal an important way in which this problem is different from conventional Bayesian optimization and active learning tasks: the global nature of the convex hull means there is uncertainty about stability even for compositions in which the energy has been noiselessly observed. In this example, the observed compositions are marked with dashed vertical lines in Fig. 1d and there is uncertainty about the stability in two of the three cases.
2.2 Refining the convex hull
With a probabilistic view of convex hulls in place, our goal in each iteration of the search is to identify the candidate observation x*, which is expected to minimize the Shannon entropy . This objective can be viewed as a Bayesian experimental design procedure in which the policy is to greedily maximize the information gain (Fig. 2).
. This objective can be viewed as a Bayesian experimental design procedure in which the policy is to greedily maximize the information gain (Fig. 2).
Like many Bayesian optimization and search algorithms, the selection of x* requires approximating the expected information gain (EIG) across the space of possible designs, which in our case is the set of compositions.61,62 The EIG is simply the difference between the Shannon entropy of the current state (reflected in the observed data, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ) and the expected Shannon entropy after making an observation at an unobserved composition x. Of course, the energy value y is unknown at this point and so the new set of observations
) and the expected Shannon entropy after making an observation at an unobserved composition x. Of course, the energy value y is unknown at this point and so the new set of observations ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ∪ (x,y) is considered in expectation:
∪ (x,y) is considered in expectation:
 | (1) |
Finally, the expected information gain is used within each iteration to select x*, the candidate composition to be evaluated:
Fig. 2 illustrates how the EIG is evaluated in practice. In Fig. 2a, we start with a GP conditioned on some data, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) . Energy surfaces are sampled from the resulting posterior distribution, convex hulls are calculated, and the Shannon entropy of state
. Energy surfaces are sampled from the resulting posterior distribution, convex hulls are calculated, and the Shannon entropy of state ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) is calculated, giving us the first term in eqn (1).
is calculated, giving us the first term in eqn (1).
For a given candidate composition x, we sample from the conditional Gaussian process posterior at x to obtain a set of K possible energy values, denoted yk. In other words, these yk values correspond to different energies for composition x given the current uncertainty within our energy model. For each of these K samples, the entropy  is estimated in three steps. (1) The Gaussian process is conditioned on this “fantasized” pair of observations (x,yk), and energy surfaces for all considered compositions are sampled from the resulting distribution. (2) For each of these sampled energy surfaces, a convex hull is computed. (3) The convex hull samples are used to estimate the Shannon entropy (eqn (4)), as detailed in the Methods. The expectation value of the Shannon entropy is then calculated by averaging the K entropy estimates (eqn (6)), resulting in an estimate of the second term in eqn (1), thereby completing our evaluation of the EIG.
is estimated in three steps. (1) The Gaussian process is conditioned on this “fantasized” pair of observations (x,yk), and energy surfaces for all considered compositions are sampled from the resulting distribution. (2) For each of these sampled energy surfaces, a convex hull is computed. (3) The convex hull samples are used to estimate the Shannon entropy (eqn (4)), as detailed in the Methods. The expectation value of the Shannon entropy is then calculated by averaging the K entropy estimates (eqn (6)), resulting in an estimate of the second term in eqn (1), thereby completing our evaluation of the EIG.
We continue to illustrate this algorithm in panels Fig. 2b where three hypothetical energy values for composition x lead to three different hull distributions. For contrast, a different composition is selected for Fig. 2c, resulting in visibly greater variation in the hulls and thus a higher expected Shannon entropy. In Fig. 2d, the process is repeated across composition space to determine the composition with the maximum EIG (i.e., x*). (For panel b, the optimal value x* was intentionally selected to visually emphasize the impact that sampling at x* would have.) Finally, an observation is made at x* to update ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) and the algorithm repeats to refine the convex hull. We reiterate that this approach seeks to minimize the Shannon entropy in the convex hull, not simply observe points that are on the hull. Here, observing the composition x* is advantageous because regardless of its energy, the resulting distribution in possible convex hulls narrows significantly.
and the algorithm repeats to refine the convex hull. We reiterate that this approach seeks to minimize the Shannon entropy in the convex hull, not simply observe points that are on the hull. Here, observing the composition x* is advantageous because regardless of its energy, the resulting distribution in possible convex hulls narrows significantly.
2.3 Application of the convex hull
Having sufficiently iterated to build an accurate hull, relevant thermodynamic intensive variables can be directly calculated. For example, the elemental chemical potentials can be determined by combining the tangent and energy value of the hull. Fig. 3a highlights that the elemental chemical potentials can be directly read off the y-intercepts of the composition boundaries (i.e., x = 0 and x = 1). Here, the energy surface is a single sample from a GP with an associated convex hull. Sweeping over the derivative of the convex hull changes the elemental chemical potentials, as shown in Fig. 3b. All compositions within the two-phase region are in thermodynamic equilibrium, and as such, the chemical potentials stay constant. Fig. 3c shows the mean chemical potential and affiliated uncertainty (±2σ) associated with a distribution of convex hulls.Elemental chemical potentials are critical in predicting defect concentrations, as defect creation involves exchanges with element and charge reservoirs. For example, in LiZnSb, the limited chemical potential window of Li renders the compound significantly Li-deficient even in the presence of secondary phases with excess Li (e.g. Li3Sb).63 Chemical potentials of charged species can also be leveraged to produce intercalation voltage curves in battery materials,45 as was done for LixCoO2.44 Lastly, pressure is an intensive variable that can be determined from the convex hull of an energy surface that is a function volume.37–39 For example, the impact of volumetric confinement on the freezing point of water can be readily determined from the hull.64
2.4 Multiple phases
CAL can be naturally expanded to search across multiple competing phases. In such cases, the n phases are modeled with n independent GPs. By adopting separate GPs, we make no assumptions concerning correlations between the energy surfaces of different phases. For further efficiency, the set of n phases could be described with a joint GP, as mentioned in the Discussion. To construct the corresponding convex hull distribution, each GP is sampled s times, resulting in sn permutations of n energy surfaces. For a given permutation, the n energy surfaces, corresponding to the n phases, can once again be wrapped with a single convex hull. From the convex hull we can predict the probability that a given phase–composition pair is on the hull, as will be shown in Fig. 4. The search process extends gracefully to multiple phases; the expected information gain is evaluated for each phase–composition pair.3 Results
3.1 Case example I: 1D, 2 phases
To see this methodology applied to an iterative loop, we consider the case of a 1-dimensional binary composition space with two competing phases. Fig. 4a shows how the initial energy surfaces are ambiguous and this uncertainty propagates to the convex hull. The probability of any composition being on the hull is then derived from the convex hull distribution. In Fig. 4b and c, increasing observations leads to a tightening of the energy and convex hull distributions. However, CAL leaves significant ambiguity in the energy surfaces when they are well above the hull. The probability of a given phase being on the hull is shown across Fig. 4d–f; these curves quantify the evolving uncertainty in the stability predictions. A similar evolution is seen in the elemental chemical potentials (Fig. 4g–i).As previously mentioned, CAL acquires observations that minimize the uncertainty in the convex hull distribution. The behavior of the algorithm can be characterized by two steps. In the first few iterations when there is large uncertainty, Fig. 4b shows that the algorithm tends to explore the energy surface, producing a coarse estimate for the convex hull. As the estimate of the convex hull develops, the algorithm focuses its next iterations increasingly on regions that are purportedly on the hull or close to it. These subtle refinements to the convex hull distribution are reflected in Fig. 4c, where the convex hull samples converge.
3.2 Quantitative performance assessment
Hulls are intriguing objects as they involve both classification and quantitative prediction. In part, we seek to classify if a given composition is on the hull. Knowing about the energies and slopes of the hull are also important for deriving intensive variables and quantifying the energy above the hull for an unstable composition. For this reason, we use three metrics in order to assess these dual aims: mean absolute error (MAE) for the energy of the convex hull, true positive rate (TPR), and false positive (FPR). Here, TPR refers to the percentage of stable compositions that are correctly identified as being on the hull, while FPR is the percentage of unstable compositions that are incorrectly identified as being on the hull. Mathematical definitions for these metrics can be found in the Methods.In low dimensions, producing an accurate hull can be achieved via brute force. However, the necessity for efficient hull construction emerges in spaces that involve multiple competing phases and large composition spaces. To test the efficiency of CAL in such a space, we pit it against two opponents: a baseline algorithm (BASE), and farthest point sampling (FPS). BASE still models the energy surfaces using a Gaussian process. However, BASE seeks to minimize the uncertainty in the energy surfaces and has no knowledge of convex hulls. See the Methods for further information about the BASE policy. FPS does not leverage a Gaussian process – indeed, it is not aware of any energetic outcome. Rather, FPS simply chooses the composition that is farthest away from all observed compositions.
3.3 Case example II: ternary composition space with three phases
Here we highlight a ternary composition space of the form A1−x−yBxCy with three different competing phases. This example is chosen to show how CAL navigates multiple dimensions and prioritizes phases that are more relevant to the convex hull. With composition steps of 0.1, the search space consists of 66 discrete compositions and 198 phase–composition pairs. We repeat the search process for 40 different sets of energy surfaces to reveal the typical differences between the two policies.Across all three metrics shown in Fig. 5, CAL outperforms BASE and FPS. For CAL, the mean absolute error (MAE) is nearly zero by 50 iterations. Similar convergence is found for the true positive and false positive rates. Together, these metrics indicate that by 50 iterations (i.e., 25% of the search space), CAL is able to predict the energy of the convex hull as well as classify which compositions are on and off the hull. BASE, however, takes significantly longer to come to these conclusions. Considering that there only 198 phase–composition pairs in this space, BASE requires observing nearly 100 phase–composition pairs to understand the convex hull. Not only does BASE finish far slower, but its rate of learning is consistently lower through the search process, as shown by its smaller slopes in Fig. 5a–c. From the width of the shaded regions, we conclude that BASE is much more variable than CAL. FPS learns far slower than both CAL and BASE, and it is also more variable, underlying the importance of using Gaussian processes to determine the hull.
Fig. 6 shows a representative example from Fig. 5 to understand the root of how CAL so efficiently and consistently reveals the hull. The true energetic landscape is shown in panel (a) with energy surfaces corresponding to the three distinct phases. A slice through these energy surfaces is shown in (e); here, we show from B to intermediate composition AC. Additionally, a slice of the true convex hull is included below in grey. In panel (i), the complete convex hull is projected onto two dimensions as a ternary phase diagram. The distribution of energies relative to the hull is included in Section S1 of the ESI.† The three energy surfaces are similar in energy, resulting in a fairly complex phase diagram. As such, this is a challenging task for hull determination.
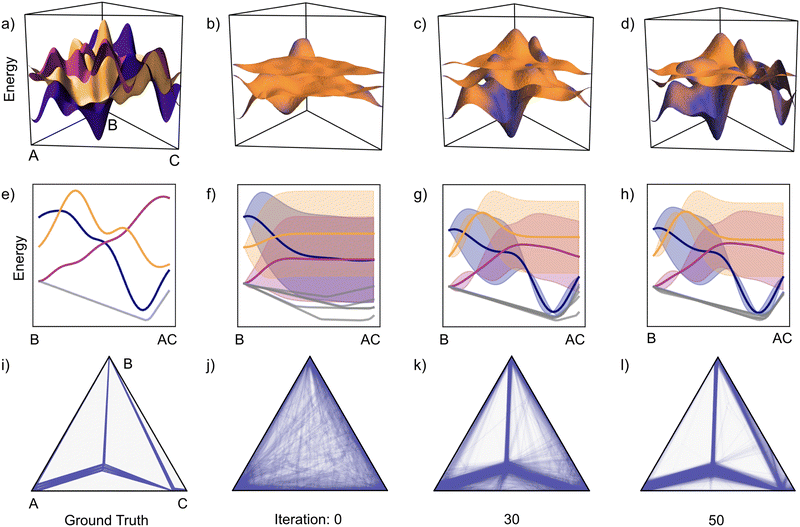 | ||
| Fig. 6 The evolution of the CAL performance is shown quantitatively in Fig. 5; further insight can be gained by visualizing the evolution of the GP and the associated hull for a single set of energy surfaces. To investigate how CAL performs with three phases spanning a ternary composition space (continuing Fig. 5), a single example is considered with increasing observations. (a) Each phase has an energy surface that spans the composition space. (e) A slice of the ternary space from B to AC shows the energies of these competing phases and a corresponding slice of the convex hull. (i) The full convex hull is represented as a ternary phase diagram. (b) After 10 iterations of CAL, the three Gaussian processes are illustrated by plotting their means and coloring the surfaces with their associated uncertainties. (c) and (d) With increasing iteration, CAL prioritizes learning about phase–composition pairs that are relevant to the convex hull, resulting in regions transitioning from high (orange) to low (purple) uncertainty. (f)–(h) A similar progression can be seen in the slice from B to AC. Ultimately, we are interested in predictions of the hull and the associated phase diagram. (j) Before making any observations (iteration 0), the uncertainty in the convex hull distribution is represented by overlaying 100 convex hull samples on a ternary phase diagram. (k) and (l) With increasing iteration, the distribution tightens and converges around the true convex hull. | ||
We model the three energy surfaces using separate Gaussian processes and conduct a total of 50 observations within this system. In panels (b)–(d), we show the mean of each GP and color the three surfaces by their standard deviation. In (b), before any observations, all energy surfaces have significant uncertainty and are thus orange. With increasing iteration, both the mean energies evolve and the uncertainties decrease for select composition regions; it will be made clear that these regions are targeted by CAL for their relevance to the convex hull. The evolution of energetic uncertainties can be clearly seen in the B–AC slice. Composition–phase pairs near the hull show evidence of significant observation and an associated reduction in uncertainty. It is important to note that only observing the lowest energy phase would not have been an optimal solution – different phases affect the hull in different regions.
In panels (j)–(l), 100 hulls are projected and overlaid onto the ternary phase diagram. As expected, no coherent expectation for the hull is present initially. By 30 iterations, most of the single-phase regions have been identified, but there is still significant uncertainty. As such, some unstable compositions are classified as having a non-zero probability of being on the hull, resulting in a smearing out of the ternary phase diagram. Finally, after 50 iterations, much of the lingering uncertainty has dissipated and the convex hull is well understood.
4 Discussion
The above case examples demonstrate CAL as a fundamentally distinct approach to resolving phase diagrams. There are a variety of ways in which the general method presented can be adjusted to specific search problems. Herein, we consider joint Gaussian processes as tools for capturing correlations between separate phases. As a natural extension of joint Gaussian processes, we discuss conducting CAL simultaneously over a variety of temperatures. We then list ways in which the computational cost of CAL can be reduced for truly vast composition spaces.It is also explained how our method may play a role in a broader uncertainty-based thermodynamic workflow. First, the importance of uncertainty quantification is discussed, then we consider how CAL may interact with sources of uncertainty that precede it in a workflow. Finally, we talk through how the uncertainty in CAL predictions is propagated forward to other thermodynamic predictions.
4.1 Correlated energy surfaces
For simplicity, we used separate GPs for modeling the energy surface of each competing phase. If there are compositional correlations between energy surfaces, the set of GPs are not learning from them. For systems where strong compositional correlations are expected, it would be advantageous to use observations of one phase–composition pair to help inform the beliefs about a separate phase for similar compositions.Joint Gaussian processes are well-suited for incorporating compositional correlations into the energy model.65,66 In a joint Gaussian process, the energy surface of each phase would be modeled simultaneously; the inputs for such a model would be observations across all phases, and the outputs would be the energy surfaces for each phase. Incorporating joint GPs into CAL would leave the acquisition function unchanged.
4.2 Temperature
Often, it is favorable to produce phase diagrams over a range of temperatures; example applications include tuning synthesis conditions or identifying phase transitions that limit the operating conditions for a material. To incorporate temperature into the CAL workflow, the free energy surface could be modeled as a function of both composition and temperature. Such an approach would allow for the GP to explicitly learn the relationship between free energy surfaces at differing temperatures. As a terminology note, here we use the term “free energy” to explicitly denote the temperature dependence of the thermodynamic potential.The policy for determining the next optimal observation would need to be extended in order to account for temperature as an added dimension in the design space. The added complexity derives from the free energy convex hull only being defined over composition space at a single temperature. As such, the total expected information gain for a single phase–composition–temperature triplet would need to be assessed as a sum over the expected information gains across temperatures of interest. In practice, the temperature range would need to be discretized to make evaluating the total information gain feasible.
A special case of temperature-dependent search involves thermodynamic methods where calculating the enthalpy of formation is the computationally limiting factor and the entropy can be approximated analytically.67–69 As such, with these methods the free energy can be predicted at multiple temperatures with no additional cost. The ramifications of this set of observations would need to be incorporated into the acquisition function.
4.3 Computational scaling
The computational cost of CAL will often be dwarfed by that of first-principles calculations. However, there is some cost to CAL, especially when moving to multi-dimensional composition spaces with many possible phase–composition pairs. Concerning additional alloy phases, the scaling of CAL is linear in the regime where calculating the hull is the primary cost due to the increase in the number of phase–composition pairs that are considered for EIG evaluation. When sampling the Gaussian process is the primary computational cost, the scaling with respect to the number of phases is approximately quadratic. Here, the number of expected information gain calculations grows linearly withe number of phases, and for each EIG calculation, the cost of producing samples also grows linearly with the number of GPs used. As shown in Section S3 of the ESI,† we find that ternaries with 66 compositions (as shown in this work) fall within the regime where cost scales linearly with the number of phases.A more important consideration is the number of compositions considered. Sampling from a GP scales cubically with the number of compositions. In Section S3 of the ESI,† we demonstrate that computational cost scales cubically with the number of compositions. This highlights the potential for efficiency gains through adaptive composition selection.
4.4 Cutting cost
If the cost of CAL is unacceptably large compared to the energy evaluations, there are multiple shortcuts for speeding up the algorithm. Evaluating the expected information gain (EIG) across phase–composition pairs is the main source of cost for CAL. Indeed, one could use Bayesian optimization to efficiently find the optimal phase–composition pair that maximizes the EIG. One could also imagine using a coarse grid of compositions to begin with and then iteratively increasing the granularity of the composition grid as the convex hull distribution continues to tighten.In truly large spaces, one may want to prioritize composition sub-regions. The acquisition function can be readily altered to exclusively focus on such regions. Here, the expected information gain would only reflect minimizing the uncertainty for the convex hull in those prioritized regions. The resulting efficiency gain will be dependent on how many different multi-phase regions enclose the specified compositions.
Other approaches center around decreasing the cost of the EIG. For instance, the EIG could be calculated with fewer convex hull samples. Another approach would employ BASE in the beginning of the search and CAL only after some number of iterations. Since CAL is more expensive, it would be reserved for later in the search when there is sufficient information about the hull such that the CAL policy results in significantly different decisions from BASE. Finally, one could approximate the joint entropy as a sum of the entropies across individual compositions. This is a strong approximation for the entropy and should be taken with caution since it assumes convex hulls have no correlations between compositions. All these shortcuts add parameters requiring tuning to negotiate between speed and quality.
4.5 Opportunities for uncertainty-based workflows
Understanding how uncertainty propagates throughout a workflow allows for the rational prioritization of certain segments of the workflow. Thermodynamic stability prediction is one such workflow – it often involves a series of convoluted steps, and at each step there is opportunity to estimate and propagate uncertainty. Such uncertainties could be produced from first-principles calculations,70 fitting surrogate models,53,71 or numerical approaches to approximating free energies.67 The GP within CAL could incorporate uncertainties from previous steps as noise in its observations. Such noise would be reflected in the convex hull distribution and resulting predictions.In an uncertainty-based thermodynamic workflow, CAL could be useful in iteratively training surrogate models with energetic uncertainties like the Bayesian approach to cluster expansion.53,71–74 Here, completing the necessary first-principles calculations to train such models is the limiting factor. Such training would be focused on minimizing the uncertainty in the convex hull rather than predicting energies.
Specifically, instead of the GP used in our work, the surrogate model would be leveraged to produce uncertainty in the convex hull distribution before and after a potential observation. The simplicity of such an inexpensive surrogate makes it computationally feasible to retrain numerous times, which is necessary for choosing the optimal observation. Once an optimal composition is identified by CAL, its energy would be calculated using first-principles, and the result would be included in the training set for the surrogate model.
4.6 Ultra-fine convex hulls
Bayesian modeling also allows for propagating uncertainty to subsequent steps in the thermodynamic workflow. We have shown such propagation for both stability predictions and chemical potentials, and herein we highlight one more example – the production of ultra-fine convex hulls from coarse-grid composition spaces. Producing fine-grained convex hulls is advantageous due to their ability to resolve single-phase regions, but conducting CAL on ultra-fine composition grids heavily increases its computational cost. As such, we use CAL to conduct search on coarse grids and use post-processing to produce the fine-grained convex hulls shown in Fig. 6j–l. Specifically, a new GP is trained on the existing energy observations from the coarse grid and produces energetic predictions over a fine composition space. The resulting convex hull distribution is subsequently derived. The associated uncertainty with interpolating to fine grids is naturally included in the convex hull predictions.4.7 Compounds
Throughout this work, we have shown energy as a continuous, smooth function over composition. Indeed, for systems like alloys, liquids, and colloids, this is a useful representation. However, in cases where the energy surface changes drastically over small composition ranges (e.g., line compounds), it is challenging to employ a Gaussian process. In such a case, the length scale of the Gaussian process kernel function would need to be incredibly small to properly capture such abrupt energy fluctuations. The amount of information obtained from a single energy evaluation would therefore be vanishingly small, rendering an active learning process infeasible.Due to the low computational cost of calculating compound energies, we suggest that these observations are conducted before using CAL. Subsequently, CAL would be employed to suggest calculations for highly expensive free energy evaluations, like those required for alloys. Such an example is illustrated in Fig. 7, where at iteration 0 (before CAL has been used) we start with knowing the energy of the parent compounds and two line compounds with compositions x = 0.2 and x = 0.5 (red points). The compounds do not play a role in training the Gaussian processes. However, they are important for determining the convex hull distribution. Here, each of the three GPs is sampled and the convex hull is calculated for those three surfaces and the compounds. As before, CAL makes observations to minimize the uncertainty in the convex-hull distribution. Due to the low-energy compound at x = 0.2, the first three observations are heavily biased to the right (i.e., B-rich compositions) since that composition region is the only portion with remaining hull uncertainty. Once that region is pinned down, CAL makes additional observations towards the left to remove any remaining uncertainty in the hull. After 6 iterations, the convex hull distribution is pinned down, as made clear by the almost perfect overlap of the convex hull samples. Finally, it is worth noting that since the orange phase was too high in energy to affect the convex hull, no observations were made for that phase.
In the above example, we treat the compound energetics as having no uncertainty. However, there can be uncertainty in compound energetics; these uncertainties can be propagated to the convex hull distribution as well, allowing for an active learning process. Uncertainty in compound energies is valuable when dealing with particularly expensive systems where lower-fidelity models are used and the uncertainty in those low-fidelity models can be approximated.
5 Conclusion
Efficient, scalable calculations coupled with end-to-end uncertainty predictions are critical for the next generation of computational materials design. Here, CAL provides a crucial component of this workflow with the ability to efficiently and accurately predict thermodynamic stability. This enhancement comes from developing an acquisition function for active learning that is focused on minimizing the uncertainty of the convex hull. Rather than attempt to characterize the entire space, CAL prioritizes observing compositions that are on or near the hull. As a result, we see a factor of two gain in search efficiency for complex ternary spaces. While we focus on ternary spaces, our approach generalizes across dimensions; thus, it can be applied to pernicious problems such as generating phase diagrams for high-entropy alloys. Uncertainty quantification of both phase stability and associated intensive variables emerges naturally from this hull-aware Bayesian method. Such intensive variables (e.g., pressure, chemical potential, voltage) are critical for linking CAL's results into a predictive workflow for informing experimental campaigns.6 Methods
6.1 Gaussian process model
Let denote the composition space; we assume that the composition space is a discrete set. We model the energy surface using a Gaussian process prior:
denote the composition space; we assume that the composition space is a discrete set. We model the energy surface using a Gaussian process prior:| F(x) ∼ GP(m(x),k(x,x′)), |
![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) , the corresponding energy is y = F(x).
, the corresponding energy is y = F(x).
The convex hull operator ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) takes an energy function F and returns its lower convex envelope H =
takes an energy function F and returns its lower convex envelope H = ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) (F). Thus, the GP prior on the energy function F implies a prior on its convex hull H.
(F). Thus, the GP prior on the energy function F implies a prior on its convex hull H.
Given N observations ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) = {(xn,yn)}Nn=1, the posterior of the energy function p(F|
= {(xn,yn)}Nn=1, the posterior of the energy function p(F|![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ) is also a Gaussian process. Define the vector of energies Y = [y1,…,yN]T and the matrix X whose rows consist of the elements {xn}Nn=1. The posterior of the energy function is p(F|
) is also a Gaussian process. Define the vector of energies Y = [y1,…,yN]T and the matrix X whose rows consist of the elements {xn}Nn=1. The posterior of the energy function is p(F|![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ) = GP(
) = GP(![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) (x),
(x),![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) (x,x′)) with mean and covariance function of the form
(x,x′)) with mean and covariance function of the form
![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) (x) = m(x) + kxXkXX−1(Y − mX) (x) = m(x) + kxXkXX−1(Y − mX) | (2) |
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) (x,x′) = k(x,x′) − kxXkXX−1kXx′ (x,x′) = k(x,x′) − kxXkXX−1kXx′ | (3) |
In practice, we represent F (and H) using a dense grid of c candidate compositions. In this case, the posterior of the energy values on this grid becomes a multivariate Gaussian distribution with a mean and covariance matrix arising from ![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) (eqn (2)) and
(eqn (2)) and ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) (eqn (3)) evaluated at those points.
(eqn (3)) evaluated at those points.
The posterior over the energy surface F induces a posterior over the convex hull function p(H|![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ). To generate a random function from this posterior, i.e., H
). To generate a random function from this posterior, i.e., H![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ∼ p(H|
∼ p(H|![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ), we first sample F
), we first sample F![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) from p(F|
from p(F|![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ) and then construct its convex hull, i.e., H
) and then construct its convex hull, i.e., H![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) =
= ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) (F
(F![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ).
).
6.2 Expected information gain computation
For a given composition, CAL calculates the change in entropy for a variety of possible outcomes and averages them together to produce the expected information gain. Herein, we detail how the EIG is calculated.Recall that to compute the EIG for the random hull H![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ∼ p(H|
∼ p(H|![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ) (eqn (1)), we need to compute the entropy
) (eqn (1)), we need to compute the entropy 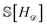 and the expected entropy
and the expected entropy  , where y is the (unobserved) energy of a new candidate composition x. The entropy
, where y is the (unobserved) energy of a new candidate composition x. The entropy  is defined as
is defined as
 | (4) |
A key challenge is to estimate the entropy since it is not available analytically. In particular, in large and high-dimensional composition spaces, the expectation in eqn (4) involves a high-dimensional integral and a high-dimensional log hull density, both of which are challenging to estimate accurately and efficiently using numerical methods.
To address this computational issue, we approximate the hull distribution in a way that allows us to compute eqn (4) in closed form. We assume that random values of the convex hull (evaluated on a dense grid of c elements) follow a multivariate Gaussian distribution with covariance Σ. It is common to use Gaussian approximations to approximate challenging posterior distributions (e.g., Laplace approximation,76 variational inference77–79), and they can be useful even if the posterior is non-Gaussian. Ultimately, the entropy is used in ranking potential observations; exact calculations of the entropy are neither feasible nor necessary.
For the entropy of a multivariate Gaussian, the only unknown value that needs to be computed is the covariance matrix, which can be estimated empirically from m convex hull samples. Hj ∼ p(H|![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ), here, each Hj is a vector of length c, and we use those vectors to construct the covariance matrix:
), here, each Hj is a vector of length c, and we use those vectors to construct the covariance matrix:
 | (5) |
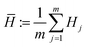 is the vector obtained from averaging over the components of each hull vector Hj. It is worth noting that the number of convex hull samples must satisfy m > c in order to ensure the covariance matrix is full-rank.
is the vector obtained from averaging over the components of each hull vector Hj. It is worth noting that the number of convex hull samples must satisfy m > c in order to ensure the covariance matrix is full-rank.
The entropy of the multivariate Gaussian, which only depends on the covariance Σ, can be computed in closed form:
 | (6) |
For the expected entropy  , we compute a Monte Carlo estimate of the expectation:
, we compute a Monte Carlo estimate of the expectation:
 | (7) |
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ) for a given composition x, and the entropy estimates
) for a given composition x, and the entropy estimates 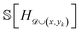 are computed using eqn (6).
are computed using eqn (6).
6.3 Farthest point sampling
Like the name indicates, in farthest point sampling (FPS), the algorithm picks the composition that is farthest from all observed compositions. This distance is defined as the minimum distance a potential composition is from any other observed composition. The point with the largest minimum distance is chosen in each successive iteration.6.4 Implementation and evaluation details
All policies start with the same prior knowledge of the hull, namely, only information about the end members. To ensure a fair comparison, both CAL and BASE use the same hyperparameters for their Gaussian processes. The Gaussian process model and active search algorithm were implemented using JAX80 and the GPJax library.81 For simplicity and consistency, a radial basis function (RBF) kernel with a length scale of 0.2 was used throughout the paper. This length scale was chosen as it gave energy curves that generally agreed with other thermodynamic potentials. The “true” energy surfaces were generated using an RBF kernel with a length scale of 0.2 as well.All observations had no noise associated with them, although observational noise can readily be incorporated. Shaded regions in the GP plots show two standard deviations from the mean prediction. Convex hulls were generated using the qhull algorithm60 within the scipy library.82 Custom code was built to isolate the lower bound of the hull, which is the portion of interest for thermodynamics.
Here we discuss the specific sampling parameters used in the work. In the 1D search evolution shown in Fig. 4, there were 21 compositions in the space. For the ternary search in Fig. 5 and 6, there were 66 total compositions. For both the 1D and 2D search, 200 energy and convex hull samples were used for each entropy calculation, and 10 possible y-values were used to build the expected information gain (i.e., m = 200, K = 10). We find that performance varies slightly with the choice of m and K, but not significantly (see Section S2 in the ESI†). As a general rule, K can be fairly low (i.e., 10) since K is being used to approximate a one-dimensional integral. However, m needs to be larger to empirically compute the covariance matrix of a high-dimensional Gaussian (where c is the number of dimensions). Here we set m > 3c for all systems. Users are encouraged to conduct their own convergence testing.
The baseline active learning algorithm, which also uses a GP model for the energy surface, selected compositions to maximize the information gained about the energy surface. Specifically, BASE maximized the EIG with respect to the energy function (EIG-B):
When multiple phases were present, BASE chose the composition–phase pair that maximized the EIG. In Fig. 5, the policy resulted in BASE alternating evenly between phases. BASE used the same GP hyperparameters as CAL to control for hyperparameter tuning.
The performance of each policy was assessed using the mean absolute error (MAE) for the energy of the convex hull, the true positive rate (TPR), and false positive rate (FPR). The MAE here is defined by:
 | (8) |
The true positive rate is the percentage of the points that are on the hull that are correctly identified:
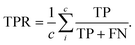 | (9) |
The FPR refers to the percentage of the points that are off the hull that were incorrectly identified:
 | (10) |
FP is the number of false positives, which is the number of compositions that were incorrectly identified as being on the convex hull. TN stands for true negative, and is the number of compositions that were correctly identified as being off the hull. The FPR is also calculated for each hull sample and then averaged across all samples.
For both CAL and BASE, 200 hulls were used to evaluate the MAE, TPR, and FPR for a given iteration. A composition was defined as being on the hull if its energy was within 10−3 of the energy of the hull.
Data availability
All data and methods used to produce this paper are available in the Github repository: https://github.com/PrincetonLIPS/active-phase-mapping.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported under NSF OAC 2118201. Additional support came from NSF OAC 1940199 (AN and ET), NSF IIS 1845434, NSF IIS 2007278 and NSF OAC 1940224 (QN and RG), NSF IIS 2007278 (RA), and a Google PhD Fellowship in Machine Learning (DC).Notes and references
- H. D. Williams, N. L. Trevaskis, S. A. Charman, R. M. Shanker, W. N. Charman, C. W. Pouton and C. J. Porter, Pharmacol. Rev., 2013, 65, 315–499 CrossRef PubMed.
- S. Baghel, H. Cathcart and N. J. O'Reilly, J. Pharm. Sci., 2016, 105, 2527–2544 CrossRef CAS PubMed.
- L. M. Robeson, Polymer blends, Hanser Gardner Publications, 2007, vol. 641.
- D. R. Paul, Polymer Blends, Elsevier, 2012, vol. 1 Search PubMed.
- K. Zhou, K. Xian, R. Ma, J. Liu, M. Gao, S. Li, T. Liu, Y. Chen, Y. Geng and L. Ye, Energy Environ. Sci., 2023, 16, 5052–5064 RSC.
- H. Okamoto, T. Massalskiet al., Binary Alloy Phase Diagrams, ASM International, Materials Park, OH, USA, 2nd edn, 1990.
- J. Chen, X. Zhou, W. Wang, B. Liu, Y. Lv, W. Yang, D. Xu and Y. Liu, J. Alloys Compd., 2018, 760, 15–30 CrossRef CAS.
- S. Batzner, A. Musaelian and B. Kozinsky, Nat. Rev. Phys., 2023, 5, 437–438 CrossRef CAS.
- R. Drautz, Phys. Rev. B, 2019, 99, 014104 CrossRef CAS.
- A. van de Walle and G. Ceder, J. Phase Equilib., 2002, 23, 348 CrossRef CAS.
- S. Kadkhodaei and J. A. Muñoz, JOM, 2021, 73, 3326–3346 CrossRef.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- A. P. Bartók and G. Csányi, Int. J. Quantum Chem., 2015, 115, 1051–1057 CrossRef.
- B. Cantor, I. Chang, P. Knight and A. Vincent, Mater. Sci. Eng. A, 2004, 375, 213–218 CrossRef.
- E. P. George, D. Raabe and R. O. Ritchie, Nat. Rev. Mater., 2019, 4, 515–534 CrossRef CAS.
- C. Oses, C. Toher and S. Curtarolo, Nat. Rev. Mater., 2020, 5, 295–309 CrossRef CAS.
- G. L. Hart, T. Mueller, C. Toher and S. Curtarolo, Nat. Rev. Mater., 2021, 6, 730–755 CrossRef.
- S. S. Aamlid, M. Oudah, J. Rottler and A. M. Hallas, J. Am. Chem. Soc., 2023, 145, 5991–6006 CAS.
- B. Zhuang, G. Ramanauskaite, Z. Y. Koa and Z.-G. Wang, Sci. Adv., 2021, 7, eabe7275 CrossRef CAS PubMed.
- D. D. Mahanta, D. R. Brown, S. Pezzotti, S. Han, G. Schwaab, M. S. Shell and M. Havenith, Chem. Sci., 2023, 14, 7381–7392 RSC.
- F. Therrien, E. B. Jones and V. Stevanović, Appl. Phys. Rev., 2021, 8, 031310 CAS.
- S. D. Griesemer, Y. Xia and C. Wolverton, Nat. Comput. Sci., 2023, 3, 934–945 CrossRef PubMed.
- E. Dagotto, Science, 2005, 309, 257–262 CrossRef CAS PubMed.
- B. Keimer and J. Moore, Nat. Phys., 2017, 13, 1045–1055 Search PubMed.
- F. Yu, X. Zhu, X. Wen, Z. Gui, Z. Li, Y. Han, T. Wu, Z. Wang, Z. Xiang, Z. Qiao, J. Ying and X. Chen, Phys. Rev. Lett., 2022, 128, 077001 CrossRef CAS PubMed.
- J. M. An, S. V. Barabash, V. Ozolins, M. van Schilfgaarde and K. D. Belashchenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 064105 CrossRef.
- V. Meschke, P. Gorai, V. Stevanovic and E. S. Toberer, Chem. Mater., 2021, 33, 4373–4381 CrossRef CAS.
- S. Curtarolo, W. Setyawan, G. L. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang, O. Levy, M. J. Mehl, H. T. Stokes, D. O. Demchenko and D. Morgan, Comput. Mater. Sci., 2012, 58, 218–226 CrossRef CAS.
- C. Oses, E. Gossett, D. Hicks, F. Rose, M. J. Mehl, E. Perim, I. Takeuchi, S. Sanvito, M. Scheffler, Y. Lederer, O. Levy, C. Toher and S. Curtarolo, J. Chem. Inf. Model., 2018, 58, 2477–2490 CrossRef CAS PubMed.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, JOM, 2013, 65, 1501–1509 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- C. J. Bartel, J. Mater. Sci., 2022, 57, 10475–10498 CrossRef CAS.
- A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Nature, 2023, 1–6 Search PubMed.
- V. I. Hegde, M. Aykol, S. Kirklin and C. Wolverton, Sci. Adv., 2020, 6, eaay5606 CrossRef CAS PubMed.
- S. Pandey, J. Qu, V. Stevanović, P. S. John and P. Gorai, Patterns, 2021, 2, 100361 CrossRef PubMed.
- J. Laakso, M. Todorović, J. Li, G.-X. Zhang and P. Rinke, Phys. Rev. Mater., 2022, 6, 113801 CrossRef CAS.
- M. Yin and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 5668 CrossRef CAS.
- J.-H. Lee, A. Jaffe, Y. Lin, H. I. Karunadasa and J. B. Neaton, ACS Energy Lett., 2020, 5, 2174–2181 CrossRef CAS.
- J. E. Jaffe, J. A. Snyder, Z. Lin and A. C. Hess, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 1660 CrossRef CAS.
- F. Xue, Y. Li, Y. Gu, J. Zhang and L.-Q. Chen, Phys. Rev. B, 2016, 94, 220101 CrossRef.
- F. Xue, Y. Ji and L.-Q. Chen, Acta Mater., 2017, 133, 147–159 CrossRef CAS.
- M. Kuz’min, Y. Skourski, D. Eckert, M. Richter, K.-H. Müller, K. Skokov and I. Tereshina, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 172412 CrossRef.
- D. Gorbunov, M. Kuz’min, K. Uhlířová, M. Žáček, M. Richter, Y. Skourski and A. Andreev, J. Alloys Compd., 2012, 519, 47–54 CrossRef CAS.
- A. Van der Ven, M. K. Aydinol and G. Ceder, J. Electrochem. Soc., 1998, 145, 2149 CrossRef CAS.
- A. Van der Ven, Z. Deng, S. Banerjee and S. P. Ong, Chem. Rev., 2020, 120, 6977–7019 CrossRef CAS PubMed.
- R. A. Alberty, Pure Appl. Chem., 2001, 73, 1349–1380 CrossRef CAS.
- W. Sun, M. J. Powell-Palm and J. Chen, The geometry of high-dimensional phase diagrams: I. Generalized Gibbs Phase Rule, 2024, https://arxiv.org/abs/2105.01337.
- M. Wen, E. W. C. Spotte-Smith, S. M. Blau, M. J. McDermott, A. S. Krishnapriyan and K. A. Persson, Nat. Comput. Sci., 2023, 3, 12–24 CrossRef PubMed.
- M. J. McDermott, B. C. McBride, C. E. Regier, G. T. Tran, Y. Chen, A. A. Corrao, M. C. Gallant, G. E. Kamm, C. J. Bartel, K. W. Chapman, P. G. Khalifah, G. Ceder, J. R. Neilson and K. A. Persson, ACS Cent. Sci., 2023, 9, 1957–1975 CrossRef CAS PubMed.
- C. L. Rom, A. Novick, M. J. McDermott, A. A. Yakovenko, J. R. Gallawa, G. T. Tran, D. C. Asebiah, E. N. Storck, B. C. McBride, R. C. Miller, A. L. Prieto, K. A. Persson, E. Toberer, V. Stevanović, A. Zakutayev and J. R. Neilson, J. Am. Chem. Soc., 2024, 146, 4001–4012 CrossRef CAS PubMed.
- J. Chen, S. R. Cross, L. J. Miara, J.-J. Cho, Y. Wang and W. Sun, Nat. Synth., 2024, 1–9 Search PubMed.
- B. Settles, Active learning literature survey, Computer Sciences Technical Report, No. 1648, University of Wisconsin–Madison, 2009 Search PubMed.
- H. Chen, S. Samanta, S. Zhu, H. Eckert, J. Schroers, S. Curtarolo and A. van de Walle, Comput. Mater. Sci., 2024, 231, 112571 CrossRef CAS.
- K. Gubaev, E. V. Podryabinkin, G. L. Hart and A. V. Shapeev, Comput. Mater. Sci., 2019, 156, 148–156 CrossRef CAS.
- A. Seko and S. Ishiwata, Phys. Rev. B, 2020, 101, 134101 CrossRef CAS.
- F. Kuroda, S. Hagiwara and M. Otani, Phys. Rev. Mater., 2023, 7, 115402 CrossRef CAS.
- A. Vasylenko, B. M. Asher, C. M. Collins, M. W. Gaultois, G. R. Darling, M. S. Dyer and M. J. Rosseinsky, J. Chem. Phys., 2024, 160, 054110 CrossRef CAS PubMed.
- C. E. Rasmussen, C. K. Williams, Gaussian processes for machine learning, Springer, 2006, vol. 1 Search PubMed.
- V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Chem. Rev., 2021, 121, 10073–10141 CrossRef CAS PubMed.
- C. B. Barber, D. P. Dobkin and H. Huhdanpaa, ACM Trans. Math. Software, 1996, 22, 469–483 CrossRef.
- D. J. C. MacKay, Neural Comput., 1992, 4, 590–604 CrossRef.
- D. J. C. MacKay, Neural Comput., 1992, 4, 720–736 CrossRef.
- P. Gorai, A. Goyal, E. S. Toberer and V. Stevanović, J. Mater. Chem. A, 2019, 7, 19385–19395 RSC.
- M. J. Powell-Palm, B. Rubinsky and W. Sun, Commun. Phys., 2020, 3, 39 CrossRef.
- M. A. Álvarez, L. Rosasco and N. D. Lawrence, Foundations and Trends in Machine Learning, 2012.
- R. Garnett, Bayesian optimization, Cambridge University Press, 2023 Search PubMed.
- A. Novick, Q. Nguyen, R. Garnett, E. Toberer and V. Stevanović, Phys. Rev. Mater., 2023, 7, 063801 CrossRef CAS.
- A. Zunger, S.-H. Wei, L. Ferreira and J. E. Bernard, Phys. Rev. Lett., 1990, 65, 353 CrossRef CAS PubMed.
- W. Chen, A. Hilhorst, G. Bokas, S. Gorsse, P. J. Jacques and G. Hautier, Nat. Commun., 2023, 14, 2856 CrossRef CAS PubMed.
- A. Wang, R. Kingsbury, M. McDermott, M. Horton, A. Jain, S. P. Ong, S. Dwaraknath and K. A. Persson, Sci. Rep., 2021, 11, 15496 CrossRef CAS PubMed.
- D. E. Ober and A. V. der Ven, Thermodynamically Informed Priors for Uncertainty Propagation in First-Principles Statistical Mechanics, 2023, https://arxiv.org/abs/2309.12255.
- T. Mueller and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 024103 CrossRef.
- J. Kristensen and N. J. Zabaras, Comput. Phys. Commun., 2014, 185, 2885–2892 CrossRef CAS.
- M. Aldegunde, N. Zabaras and J. Kristensen, J. Comput. Phys., 2016, 323, 17–44 CrossRef CAS.
- P. Hennig, M. A. Osborne and H. P. Kersting, Probabilistic Numerics: Computation as Machine Learning, Cambridge University Press, 2022 Search PubMed.
- Z. Shun and P. McCullagh, J. R. Stat. Soc. Series B: Stat. Methodol., 1995, 57, 749–760 CrossRef.
- D. M. Blei, A. Kucukelbir and J. D. McAuliffe, J. Am. Stat. Assoc., 2017, 112, 859–877 CrossRef CAS.
- R. Ranganath, S. Gerrish and D. Blei, Artificial Intelligence and Statistics, 2014, pp. 814–822 Search PubMed.
- D. Cai, C. Modi, L. Pillaud-Vivien, C. Margossian, R. Gower, D. Blei and L. Saul, International Conference on Machine Learning, 2024.
- J. Bradbury, R. Frostig, P. Hawkins, M. J. Johnson, C. Leary, D. Maclaurin, G. Necula, A. Paszke, J. VanderPlas, S. Wanderman-Milne and Q. Zhang, JAX: Composable transformations of Python+NumPy programs, 2018, https://github.com/google/jax.
- T. Pinder and D. Dodd, J. Open Source Software, 2022, 7, 4455 CrossRef.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. Vander-Plas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh00432a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |