Open Access Article
Open Access ArticleShear-induced structural and viscosity changes of amphiphilic patchy nanocubes in suspension
Takahiro
Ikeda
 ,
Yusei
Kobayashi
,
Yusei
Kobayashi
 * and
Masashi
Yamakawa
* and
Masashi
Yamakawa
Faculty of Mechanical Engineering, Kyoto Institute of Technology, Matsugasaki, Sakyo-ku, Kyoto 606-8585, Japan. E-mail: kobayashi@kit.ac.jp
First published on 18th January 2024
Abstract
Structure formation and rheological properties of amphiphilic patchy nanocubes in equilibrium and under shear were investigated using hybrid molecular dynamics simulations combined with multiparticle collision dynamics that consider hydrodynamic interactions. The relationship between complex self-assembled structures and the resulting macroscopic properties has not yet been examined because of the computational complexity these multiscale problems present. The number and location of solvophobic patches on the amphiphilic nanocubes were varied at several colloid volume fractions in the liquid regime. For a pure suspension of one-patch cubes, the nanocubes self-assemble into dimers in the equilibrium state because bonded one-patch cubes have no exposed solvophobic surfaces. At low shear rates, small dimers undergo shear-induced alignment along the flow direction. This results in shear-thinning accompanied by slightly higher shear viscosity (≈15%) than homoparticle dispersions of the same concentration. As the shear rate increases further, the suspensions exhibit Newtonian-like behavior until the cluster disintegrates, followed by shear thinning with breakdown into individual cubes. For binary mixtures of one- and two-patch nanocubes, the resulting cluster shapes, which include elongated rods and fractal objects, can be controlled by the patch arrangements on the two-patch cubes. Interestingly, despite the differences in the shape and resistance of the clusters, two different mixtures undergo a similar increase in the shear viscosity (≈35%) compared to the homoparticle dispersions, to essentially exhibit rheological behavior similar that of a pure suspension of one-patch cubes. Our findings provide new insights into the correlation between microscopic (design of patchy cubes), mesoscopic (self-assembled structures), and macroscopic (viscosity) properties, and are also valuable for identifying the synthesis conditions required to realize novel materials with the desired properties and functionalities.
Design, System, ApplicationRecent advances in the controlled synthesis of nanoparticles have resulted in a large variety of anisotropic nanoparticles with both highly tailored interactions (patches) and strict shape control. The combination of interaction and shape anisotropy is a powerful approach for achieving targeted self-assembled structures and accessing emerging materials. Our study demonstrates the correlation between the design of patchy nanocubes, their self-assembled structures including shear-induced structural changes, and the rheological properties of suspensions. For binary mixtures of one- and two-patch nanocubes, the resulting cluster shapes, which include elongated rods and fractal objects, can be controlled by the patch arrangements on the two-patch cubes. We found a significant correlation between the rheological properties of patchy nanocubes and both the cluster size and the orientational ordering of clusters. The unique aggregation morphologies and rheological behaviors of such patchy nanocubes cannot be achieved not only with purely repulsive or attractive nanocubes, but also with patchy spheres or nanorods. The identified relationship between self-assembly and rheological property contributes to the development of advanced functional materials such as viscosity modifiers and emulsion stabilizers at the molecular-level. Our findings are also valuable for identifying the synthesis conditions required to realize novel materials with the desired properties and functionalities. |
1 Introduction
Colloidal self-assembly has attracted much attention in both science and industry owing to their potential applications, e.g., oil recovery,1–3 drug delivery,4–6 catalysis,7–9 and biosensing.10–12 The collective and enhanced dynamics and properties of these materials arise not only from the chemical nature of the nanoparticles, but also from their complex self-assembled structures. Therefore, it is important to clarify the relationship between the self-assembled structures and the resulting macroscopic properties to produce materials with the desired properties and functionalities.A promising method for controlling the self-assembled structure of colloidal particles is to introduce anisotropy into the interaction forces. Recent advances in the controlled synthesis of nanoparticles have resulted in nanoparticles with highly localized and tailored interactions. A general approach toward this end involves the formation of nanoparticles with highly selective directional interactions by grafting complementary DNA chains onto a particle surface.13–17 Alternatively, surface patterning via site-selective surface modification is a versatile strategy for inducing directional interparticle interactions.18–21 These colloidal particles with site-specific directional interactions are referred to as “patchy particles” and their patches serve as a program for self-assembly defined by the pattern on the surface of the particle.22,23 For example, metallic nanoparticles with regioselective DNA patches self-assemble into dimers, trimers, and pentamers, which is not observed for isotropic particles.24 Binary mixtures of two different types of patchy tetrahedral particles can thermodynamically and kinetically enhance the formation of diamond lattices.25
Shape anisotropy is a key factor in colloidal self-assembly.26–28 Nonspherical particles are ubiquitous in nature, such as discotic montmorillonite29,30 and rod-shaped tobacco mosaic viruses,31,32 and have been well studied as model shapes. Numerous efforts have been made to develop synthetic strategies for anisotropic colloids with nonspherical shapes, which allow the preparation of a large variety of anisotropic colloids with strict size and shape control.26,33 Faceted nanoparticles are attractive candidates for the fabrication of unique and complex nanostructures.34–37 Among these, a nanocube is one of the simplest shapes and a prime example of a space-filling polyhedron. The structural formation and physical properties of purely repulsive hard cubes have been studied extensively.38–41 For instance, Cwalina et al. investigated the rheology of concentrated suspensions of cubic aluminosilicate zeolite particles, and related their measured properties to suspensions of spherical particles.41
The combination of interaction and shape anisotropy is a powerful approach for achieving targeted self-assembled structures and accessing emerging materials. Various approaches such as the DNA origami technique42–44 and grafting DNA chains onto the surface of a nanocube45,46 have been proposed experimentally for the realization of nanocubes with patterned surfaces. However, a large number of parameters influence the self-assembly of patchy nanocubes, e.g., the interaction potential, interaction strength, number and location of patches, and concentration. Therefore, the systematic experimental exploration of an enormous parameter space would be highly challenging. In this regard, coarse-grained molecular simulations are powerful tools that can provide molecular-level interpretations of experimental results and allow efficient exploration of the parameter space. For example, Monte Carlo (MC) simulations of polymer-grafted nanocubes were performed to investigate the assembly mechanism in detail, and it was found that the free energy barriers between metastable states depend on the interaction strength and surface roughness of the nanocubes and steric repulsion from the grafts.47,48 In addition, we recently investigated the equilibrium self-assembly of amphiphilic cubes and the assembly dynamics under shear using a combination of molecular dynamics (MD) and kinetic MC simulations.49,50 Previous studies have focused on the self-assembly behavior induced by the design of nanocubes, but have not investigated the relationship between complex self-assembled structures and the resulting macroscopic properties owing to the computational complexity multiscale problems involve.
In this study, we performed hybrid MD simulations combined with multiparticle collision dynamics (MPCD) to investigate the structural formation and rheological properties of amphiphilic patchy nanocubes at equilibrium and under shear conditions. We systematically varied the number and location of solvophobic patches on amphiphilic nanocubes at different colloidal volume fractions in the liquid regime of the phase diagram and analyze the correlation between the microscopic (design of patchy cubes), mesoscopic (self-assembled structures), and macroscopic (viscosity) phenomena.
2 Methods and models
We use the MD simulations coupled to the MPCD.51–53 Based on our previous works,49,50 a discrete particle model was used for the nanocubes, which can be considered as coarse-grained models for DNA-functionalized nanoparticles, allowing only face-to-face interactions (Fig. 1(a)). Note that here, the possibility exists that the coarse-graining procedures such as our simulation models instead of precision macromolecules called “giant molecules”,54 may not be suitable for understanding protein self-assembly, because the behaviors of proteins, e.g., protein–protein complex and their assembling process are more complex than that of DNA-functionalized nanoparticles. Each nanocube consists of Nv vertex particles of diameter av and mass mv. The vertex particles are placed on the cube surface on a quadratic lattice and connected to their nearest neighbors and with the diametrically opposite particle through a harmonic potential Ub: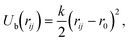 | (1) |
 | ||
| Fig. 1 (a) Discrete particle model of a (one-patch) cubic cube with diameter d = 5av. The Nv vertex particles and bonds between nearest neighbors are shown (diametric bonds have been omitted for clarity). (b–d) Unfolded representations of terminal one-patch cube and two-patch cubes. In all panels, solvophilic patches are colored in purple and solvophobic ones in yellow. Snapshot rendered using Visual Molecular Dynamics (version 1.9.4).56 | ||
As shown in Fig. 1(b and c), we consider suspensions of (nearly) hard colloidal cubes, with between one and two solvophobic faces (so-called “patches”) while the remaining faces are solvophilic. Each solvophobic patch comprised 16 vertex particles (Fig. 1(a)). A total of six and 15 different possibilities exist for arranging the hydrophobic patches on one- and two-patch cubes, respectively; however, only a small subset of patch arrangements is geometrically distinct. In the following, we refer to the two different realizations as type I and II, as indicated in Fig. 1(c) and (d). We introduce the standard Lennard-Jones potential (ULJ) between the vertex particles of solvophobic patches to mimic the (effective) solvent-mediated attraction, and ULJ is given as
 | (2) |
 | (3) |
To focus on the self-assembly of amphiphilic patchy nanocubes into finite-sized aggregates, we simulated binary mixtures of amphiphilic nanocubes, that is, systems consisting of a fraction f of two-patch cubes, with the remaining fraction 1 − f consisting of one-patch cubes. In this study, two different fractions, namely f = 0.0 and f = 0.5 are considered. The edge length of the cubic simulation box was set to L = 80av = 16d and periodic boundary conditions were applied in all three Cartesian directions to mimic the bulk conditions. The initial configurations were prepared by placing the nanocubes at random positions and orientations in the simulation box, while avoiding any overlap between the constituent particles. Three different volume fractions, ϕ ≡ Nvd3/L3 = 0.028 (115), 0.056 (230), and 0.112 (459), where the numbers in parentheses denote the total number of nanocubes in the simulation box.
In the MPCD technique, the solvent is modeled as point particles of unit mass ms propagated by sequential streaming and stochastic collision steps. During the streaming step, the solvent particles move ballistically for a period ΔtMPCD according to the following equation of motion:
| ri(t + ΔtMPCD) = ri(t) + vi(t)ΔtMPCD, | (4) |
| vi(t + ΔtMPCD) = u(t) + Ω(vi(t) − u(t)). | (5) |
The choice of MPCD parameters in this study was inspired by our previous work.50,61,62 Thus, the (average) solvent number density, collision angle, and time step for the MPCD algorithm were set as ρ = 10av−3, α = 130°, and ΔtMPCD = 0.1τ, respectively. The temperature was maintained at kBT = 1 by using a cell-level Maxwellian thermostat.58 For the conventional MD step, we used a Verlet integration scheme63 with a time step ΔtMPCD = 0.005τ and a unit of time 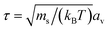 . The mass of the vertex particles was set to the (average) mass of a collision cell filled with solvent particles only; thus, m = msρsav3 = 10ms. These MPCD parameters provided a solvent viscosity of ηs = 8.72ετ/av3. Periodic boundary conditions were applied to all three dimensions. All simulations were performed using the HOOMD-blue software package (v. 2.9.6)64–67 with the “azplugins” extension (v. 0.6.2)68 for generating shear flow.
. The mass of the vertex particles was set to the (average) mass of a collision cell filled with solvent particles only; thus, m = msρsav3 = 10ms. These MPCD parameters provided a solvent viscosity of ηs = 8.72ετ/av3. Periodic boundary conditions were applied to all three dimensions. All simulations were performed using the HOOMD-blue software package (v. 2.9.6)64–67 with the “azplugins” extension (v. 0.6.2)68 for generating shear flow.
3 Results and discussion
3.1 Homoparticle dispersions
To validate our algorithms, we begin with homogeneous (without patchy faces) nanocubes and compare the zero-shear viscosity η0 of homogeneous cubic dispersions with the predicted data from the estimated regression equations. In principle, the Green–Kubo relations can be used to determine η0 through equilibrium simulations. However, our previous simulations of spherical colloid dispersions61 indicated that applying a weak shear resulted in a significantly improved signal-to-noise ratio. Thus, we employed the reverse perturbation method69 to generate shear flow in the system. In this technique, the simulation box is first subdivided into equally sized slabs in the gradient (z) direction of the flow. Subsequently, the most negative momentum of the particles in the z = +Lz/4 slab and the most negative momentum of the particles in the z = −Lz/4 slab were swapped. The shear strength can be controlled by tuning the number of momentum swaps in a step or the momentum swap frequency Δtswap. The resulting shear viscosity η is obtained by | (6) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the shear rate calculated from the slope of the linear velocity profile that develops in the steady state, and σxz is the shear stress given by
is the shear rate calculated from the slope of the linear velocity profile that develops in the steady state, and σxz is the shear stress given by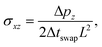 | (7) |
| η0 = ηs(1 + kEϕ + kHϕ2 + higher order terms), | (8) |
In addition, the flow behavior of suspensions of shape-anisotropic particles has recently been studied. For instance, Mallavajula et al.73 studied through simulations and experiments the dilute dispersions of Fe3O4 nanocubes in the dilute limit and found a modified Einstein coefficient that is independent of the particle size and size distribution:
| η0 = ηs(1 + 3.1ϕ). | (9) |
| η0 = ηs(1 + (3.5 ± 0.2)ϕ + (23.7 ± 3.0)ϕ2). | (10) |
Fig. 2 shows the measured viscosities of the dispersions of homogeneous nanocubes as a function of ϕ compared with the predicted data obtained using eqn (9) and (10). Even at ϕ = 0.028 we can observe an overestimation of the simulation data compared with the data predicted by eqn (9). It is also clear that the difference increases with an increase ϕ. The reason for this discrepancy between our simulations and the predicted data is that the interactions between the suspended cubes were ignored in the derivation of eqn (9). The particle interactions become more important with increasing ϕ, such that nonlinear effects need to be considered. In this regard, our simulation results are in good agreement with eqn (10) within the error bars. Based on this plot, we conclude that our method, including the discrete nanocube model, is suitable for studying flow behaviors.
 | ||
| Fig. 2 Normalized zero-shear viscosity, η0/ηs, of homogeneous cubic dispersions as a function of cube volume fraction, ϕ. Symbols show our simulation data. Solid and dashed lines correspond to regression equation of η0/ηs–ϕ curve estimated by eqn (9) from ref. 73 and eqn (10) from ref. 41, respectively. | ||
3.2 Patchy nanocubes in suspensions
Pe = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) d2/D0, d2/D0, | (11) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , ranged from 5.2 × 10−5τ−1 to 1.4 × 10−2τ−1 thus, Pe ranged from 2 to 680.
, ranged from 5.2 × 10−5τ−1 to 1.4 × 10−2τ−1 thus, Pe ranged from 2 to 680.
Fig. 3(a) shows the relative shear viscosity ηr as a function of Pe at ϕ = 0.112. Here, ηr is defined as the ratio of the viscosity of the suspensions of patchy nanocubes to the zero-shear viscosity η0 of dispersions of homogeneous nanocubes at the same volume fraction ϕ. By introducing ηr, we can extract only the effect of self-assembly on the viscosity changes while excluding the viscosity increase due to the increase in ϕ (see Fig. 2). At low shear rates, Pe ≲ 5, the suspensions exhibited a Newtonian shear response with ηr(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → 0) = 1.15 ± 0.24 but then showed distinct shear thinning for 5 ≲ Pe ≲ 50. When Pe was further increased (50 ≲ Pe ≲ 300), ηr remained approximately constant, followed by shear thinning again with ηr → 1 at high shear (Pe ≳ 300).
→ 0) = 1.15 ± 0.24 but then showed distinct shear thinning for 5 ≲ Pe ≲ 50. When Pe was further increased (50 ≲ Pe ≲ 300), ηr remained approximately constant, followed by shear thinning again with ηr → 1 at high shear (Pe ≳ 300).
In an attempt to more clearly understand the shear-induced viscosity changes in a pure suspension of one-patch cubes, we computed the mean aggregation number  , where P(M) is the probability of finding a nanocube in an aggregate of M cubes. The cluster size distribution P(M) was quantified by performing a cluster analysis using the density-based spatial clustering algorithm (DBSCAN).74 Based on previous studies,49,50 nanocubes were assigned to the same cluster if the distance between the centers-of-mass of their solvophobic patches was less than 1.5av. We also computed the second Legendre polynomial S to investigate the effect of the alignment of the anisotropic clusters caused by the applied shear on the shear viscosity of the suspensions:
, where P(M) is the probability of finding a nanocube in an aggregate of M cubes. The cluster size distribution P(M) was quantified by performing a cluster analysis using the density-based spatial clustering algorithm (DBSCAN).74 Based on previous studies,49,50 nanocubes were assigned to the same cluster if the distance between the centers-of-mass of their solvophobic patches was less than 1.5av. We also computed the second Legendre polynomial S to investigate the effect of the alignment of the anisotropic clusters caused by the applied shear on the shear viscosity of the suspensions:
 | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi) is the second Legendre polynomial, given by
θi) is the second Legendre polynomial, given by | (13) |
The steady-state morphologies and viscosity behavior under shear are then discussed. Fig. 5(a and b) shows the relative shear viscosity, ηr, and mean aggregation number, 〈M〉 of mixtures of one- and two-patch cubes (type I) at f = 0.5 as a function of the Péclet number, Pe. At low particle concentrations, ϕ = 0.028 and ηr remained approximately constant for Pe ≲ 300 and weak shear-thinning appeared for Pe ≳ 300. Interestingly, although the suspension behaved as a Newtonian fluid for the entire range of Pe, the mean aggregation number decreased from 〈M〉 ≈ 4 to 〈M〉 ≈ 2, indicating that the decomposition of the cluster into dimers from small rod-shaped clusters (〈M〉 ≈ 4) had no significant effect on ηr. At higher particle concentrations (ϕ = 0.056), the suspensions exhibit Newtonian-like behavior for Pe ≲ 10. We observed the first shear-thinning regime at 10 ≲ Pe ≲ 60 with a slight decrease in 〈M〉. For 60 ≲ Pe ≲ 300, the suspension behaved as a Newtonian fluid, as shown at ϕ = 0.028. For stronger shear, Pe ≳ 300, a second regime of shear-thinning appeared with a decreasing cluster size from 〈M〉 ≈ 2 (small dimers) to 〈M〉 ≈ 1 (free cubes). Although the mean aggregation number increased slightly from 〈M〉 ≈ 4.5 at ϕ = 0.056 to 〈M〉 ≈ 6.6 at ϕ = 0.112, the dense system with ϕ = 0.112 exhibited different behavior, particularly for a small Pe ≲ 10. We can see an obvious increase in ηr ≈ 1.35 compared with the more dilute systems, as shown in Fig. 5(a). To investigate in detail why a ϕ-dependent increase in ηr occurred, we plotted P(M) at ϕ = 0.112 for various Pe values in Fig. 6. Even under weak shear (Pe ≲ 10), the peak of P(M) in the relatively large rod-shaped clusters (M ≳ 10) remained [cf.Fig. 4(a) and (b)]. The shape anisotropy of these large clusters potentially leads to stronger shear resistance at low Pe.75,76 Interestingly, although the size and shape of the clusters remain unchanged when Pe ≲ 10, the relative viscosity gradually decreases to ηr ≈ 1.2. To understand the first shear-thinning regime, we plotted it in Fig. 5(c), the second Legendre polynomial S as a function of Pe. Here, Ω is defined as the unit vector connecting two different patches of a nanocube in a type I patch arrangement. As the shear increased to Pe ≈ 10, the clusters gradually became oriented parallel to the flow direction from a random orientation (purple dashed line in Fig. 5(c)). The values of saturated S in the binary mixtures were also found to be larger than those for the pure suspension of one-patch cubes (cf.Fig. 3(b) and 5(c), respectively). This indicates that the longer rod-like clusters attain a more aligned configuration until cluster break-up, which is largely the same behavior as previous observations.61 We also observed shear-induced alignment of clusters in a more dilute suspension (ϕ = 0.056), but shear-thinning did not appear. We surmise that the effect of the alignment on ηr was not observed for ϕ ≲ 0.056 because of the lack of formation of large rod-like clusters (M > 15). For 10 ≲ Pe ≲ 70, we observe a gradual breakup of the clusters accompanied by shear-thinning. In this flow regime, the peak of P(M) shifts to lower M values as Pe increases, as shown in Fig. 6. A distinct peak exists at M = 2 until it breaks up into single cubes, indicating the high stability of the dimer clusters against shear. When Pe was further increased, the suspensions showed essentially the same behavior as the dilute suspensions, that is, a nearly Newtonian response for 70 ≲ Pe ≲ 300 and shear-thinning with breakage into single cubes for Pe ≳ 300.
 | ||
| Fig. 6 Cluster size distributions, P(M), in sheared mixtures of one- and two-patch cubes (type I) at ϕ = 0.112 for various Péclet numbers, Pe, as indicated. | ||
We continue our discussion using a mixture of one- and two-patch cubes (type II). Fig. 7(a) and (b) show ηr and 〈M〉 as functions of Pe, respectively. For ϕ ≤ 0.056, the suspensions exhibited Newtonian-like behavior for the entire range of Pe numbers and shear-thinning behavior for Pe ≳ 300, similar to the previously discussed type I patch arrangement.
 | ||
| Fig. 7 Same as Fig. 5 but for mixtures of one- and two-patch cubes (type II). | ||
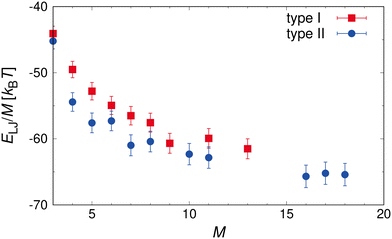
For higher particle concentrations (ϕ = 0.112), the increase was ≈35% in ηr, which was almost the same as that for the type I patch arrangement. These results indicate that the increase in ηr appears to be largely independent of the shape of the clusters for all investigated ϕ. A comparison of Fig. 5(b) and 7(b), informs us that M of the mixture with type II cubes remains constant for a wider range of Pe. To obtain a detailed understanding of the differences in cluster stability, we performed additional simulations of isolated clusters consisting of M amphiphilic nanocubes of both types (50 independent runs per M). Fig. 8 shows the bonding energy per nanocubes ELJ/M for aggregates composed of M nanocubes. For both types, ELJ/M decreases with increasing M, and then does not decrease significantly for larger clusters M > 10. We also found that ELJ/M of type II cubes is consistently higher than that of type I cubes, indicating that clusters composed of type II cubes are more resistant to shear. The suspensions at ϕ = 0.112 exhibited shear-thinning for Pe ≲ 7 and then a Newtonian-like response for 7 ≲ Pe ≲ 20, although 〈M〉 remained unchanged. Similar to type I, the possibility exists that the shear-induced alignment of clusters along the flow direction leads to shear-thinning. We also observed that dimer clusters, which can lead to weak shear thinning (see Fig. 3) are the most abundant in the system, as shown in Fig. 9. In Fig. 7(c), we plotted S of clusters, where the orientation of the clusters is defined as the eigenvector with the largest eigenvalue of the gyration tensor. The values of saturated S in binary mixtures with type II cubes were also found to be lower than those in mixtures with type I cubes, which was attributed to the low shape anisotropy of clusters composed of type II cubes compared to complete rod assemblies composed of type I cubes. From these results, we conclude that the first regime of shear-thinning at Pe ≲ 7 is primarily due to shear-induced alignment of the clusters. However, the alignment effect is weaker than that of the longer rods, as seen in the type I case, thus the decrease in ηr is limited to 10%, followed by Newtonian-like behavior for 7 ≲ Pe ≲ 20. For Pe ≳ 20, we again observed shear-thinning accompanied by a gradual breakup of clusters. This observation is consistent with the previous findings for mixtures with type I cubes.
4 Conclusions
We employed hybrid molecular dynamics (MD) simulations combined with multiparticle collision dynamics (MPCD) to investigate the structure formation and rheological properties of amphiphilic patchy nanocubes at equilibrium and under shear. We studied a pure suspension of one-patch nanocubes and two binary mixtures of one- and two-patch nanocubes with different patch arrangements at three volume fractions (ϕ = 0.028, 0.056, and 0.112) in the liquid regime of the phase diagram.For a pure suspension of one-patch cubes, we found three different regimes of shear-induced structure formation, associated with the mean aggregation number, 〈M〉, and the order parameter. First, at a low shear rate, the dimers composed of one-patch cubes maintain their shape and size (〈M〉 = 2), and tend to align along the flow direction as the shear is increased. The resulting shear-thinning behavior was mainly due to the shear-induced alignment of the dimers. The alignment then became saturated, resulting in Newtonian-like behavior. Finally, the dimers break up into free particles when strong shear is applied, and the anisotropic shape characteristics are lost. In this regime, the shear viscosity of the dispersion correlates strongly with 〈M〉; thus, shear-thinning occurs again.
For binary mixtures of one- and two-patch nanocubes, the resulting cluster shapes, including elongated rods and fractal objects, could be controlled by patch arrangements on the two-patch cubes. In the sheared mixtures, the rod-shaped clusters were more aligned with the flow direction than the fractal-shaped clusters, resulting in distinct shear-thinning for weak shear. Fractal-shaped clusters were also found to be more resistant to shear than rod-shaped clusters. Interestingly, despite the differences in the shape and resistance of the clusters, both suspensions exhibited a similar increase in shear viscosity (≈35%) compared with the homoparticle dispersions. We also found that the binary mixtures exhibited rheological behavior essentially similar to that of a pure suspension of one-patch cubes; therefore, the relationship between structure formation and viscosity obtained in a pure suspension of one-patch cubes is also applicable to binary mixtures of one- and two-patch cubes. This indicates that the design of the patch arrangements on the two-patch cubes primarily affects the flow behavior at low shear rates.
Overall, this study demonstrated the correlation between the rheological properties of suspensions and the design of patchy nanocubes and their self-assembled structures, including shear-induced structural changes. In contrast to systems consisting of patchy spheres or nanorods, the rheological properties of patchy nanocubes are of particular interest because of their significant correlation not only with the cluster size but also with the orientational ordering of clusters. The unique aggregation morphologies and rheological behaviors of such patchy nanocubes cannot be achieved using purely repulsive or attractive nanocubes. The information presented in this paper is also valuable for identifying the synthesis conditions required to obtain novel materials with desired properties and functionalities. In future studies, we aim to extend this approach to and test it on anisotropic particles with other shapes, as other faceted nanoparticles such as tetrahedrons or icosahedrons may also exhibit undiscovered aggregation morphologies and peculiar transport properties through the introduction of patches.
Author contributions
Takahiro Ikeda: investigation, formal analysis, visualization, writing – original draft. Yusei Kobayashi: investigation, methodology, conceptualization, project administration, visualization, writing – original draft, writing – review & editing. Masashi Yamakawa: writing – review & editing, supervision.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This study was supported by a grant from Japan Science and Technology Agency (JST), Support for Pioneering Research Initiated by the Next Generation (SPRING) Grant Number JPMJSP2107. Y. K. acknowledges the support of KIT Grants-in-Aid for Early-Career Scientists.References
- C. Dai, Y. Huang, X. Lyu, L. Li, Y. Sun, M. Zhao, G. Zhao and Y. Wu, Chem. Eng. Sci., 2019, 195, 51–61 CrossRef CAS.
- F. Shi, J. Wu and B. Zhao, Materials, 2019, 12, 1093 CrossRef CAS PubMed.
- Z. Hu, L. Al-Ameri, J. Gardy, M. Alhreez and D. Wen, Energy Fuels, 2022, 36, 12986–12996 CrossRef CAS PubMed.
- Z. Shen, D. T. Loe, J. K. Awino, M. Kröger, J. L. Rouge and Y. Li, Nanoscale, 2016, 8, 14821–14835 RSC.
- J. Xie, Q. Shen, K. Huang, T. Zheng, L. Cheng, Z. Zhang, Y. Yu, G. Liao, X. Wang and C. Li, ACS Nano, 2019, 13, 5268–5277 CrossRef CAS PubMed.
- S. Sivagnanam, K. Das, M. Basak, T. Mahata, A. Stewart, B. Maity and P. Das, Nanoscale Adv., 2022, 4, 1694–1706 RSC.
- E. Ortel, S. Sokolov, C. Zielke, I. Lauermann, S. Selve, K. Weh, B. Paul, J. Polte and R. Kraehnert, Chem. Mater., 2012, 24, 3828–3838 CrossRef CAS.
- B. Yang, L. Leclercq, V. Schmitt, M. Pera-Titus and V. Nardello-Rataj, Chem. Sci., 2019, 10, 501–507 RSC.
- K. Xiao, J. Cheng, X. Xie, M. Wang, S. Xing, Y. Liu, T. Hartman, D. Fu, K. Bossers, M. A. van Huis, A. van Blaaderen, Y. Wang and B. M. Weckhuysen, Nat. Mater., 2022, 21, 572–579 CrossRef PubMed.
- R. Lanfranco, P. K. Jana, G. Bruylants, P. Cicuta, B. M. Mognetti and L. D. Michele, Nanoscale, 2020, 12, 18616–18620 RSC.
- W. G. Kim, J. M. Lee, Y. Yang, H. Kim, V. Devaraj, M. Kim, H. Jeong, E. J. Choi, J. Yang, Y. Jang, T. Badloe, D. Lee, J. Rho, J. T. Kim and J. W. Oh, Nano Lett., 2022, 22, 4702–4711 CrossRef CAS PubMed.
- T. Sato, K. Esashika, E. Yamamoto, T. Saiki and N. Arai, Int. J. Mol. Sci., 2022, 23, 8807 CrossRef CAS PubMed.
- Y. Wang, Y. Wang, D. R. Breed, V. N. Manoharan, L. Feng, A. D. Hollingsworth, M. Weck and D. J. Pine, Nature, 2012, 491, 51–55 CrossRef CAS PubMed.
- L. Feng, R. Dreyfus, R. Sha, N. C. Seeman and P. M. Chaikin, Adv. Mater., 2013, 25, 2779–2783 CrossRef CAS PubMed.
- A. J. A. Diaz, J. S. Oh, G. R. Yi and D. J. Pine, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 10645–10653 CrossRef PubMed.
- G. Yao, J. Li, Q. Li, X. Chen, X. Liu, F. Wang, Z. Qu, Z. Ge, R. P. Narayanan, D. Williams, H. Pei, X. Zuo, L. Wang, H. Yan, B. L. Feringa and C. Fan, Nat. Mater., 2020, 19, 781–788 CrossRef CAS PubMed.
- R. Khalaf, A. Viamonte, E. Ducrot, R. Mérindol and S. Ravaine, Nanoscale, 2023, 15, 573–577 RSC.
- Q. Chen, S. Bae and S. Granick, Nature, 2011, 469, 381–384 CrossRef CAS PubMed.
- Y. Taniguchi, M. A. B. Sazali, Y. Kobayashi, N. Arai, T. Kawai and T. Nakashima, ACS Nano, 2017, 11, 9312–9320 CrossRef CAS PubMed.
- Y. Taniguchi, T. Takishita, Y. Kobayashi, N. Arai, T. Kawai and T. Nakashima, Europhys. Lett., 2017, 118, 68001 CrossRef.
- D. Zámbó, D. Kovács, G. Södi and A. Deák, Part. Part. Syst. Charact., 2023, 40, 2200197 CrossRef.
- L. Cademartiri and K. Bishop, Nat. Mater., 2015, 14, 2–9 CrossRef CAS PubMed.
- H. Tanaka, T. Dotera and S. T. Hyde, ACS Nano, 2023, 17, 15371–15378 CrossRef CAS PubMed.
- L. Liang, L. Wu, P. Zheng, T. Ding, K. Ray and I. Barman, JACS Au, 2023, 3, 1176–1184 CrossRef CAS PubMed.
- A. Neophytou, D. Chakrabarti and F. Sciortino, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2109776118 CrossRef CAS PubMed.
- S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557 CrossRef PubMed.
- M. Jones, R. Macfarlane, B. Lee, J. Zhang, K. L. Young, A. J. Senesi and C. A. Mirkin, Nat. Mater., 2010, 9, 913–917 CrossRef CAS PubMed.
- T. Wang, J. Zhuang, J. Lynch, O. Chen, Z. Wang, X. Wang, D. Lamontagne, H. Wu, Z. Wang and Y. C. Cao, Science, 2012, 338, 358–363 CrossRef CAS PubMed.
- G. Lagaly and S. Ziesmer, Adv. Colloid Interface Sci., 2003, 100–102, 105–128 CrossRef CAS.
- L. J. Michot, I. Bihannic, K. Porsch, S. Maddi, C. Baravian, J. Mougel and P. Levitz, Langmuir, 2004, 20, 10829–10837 CrossRef CAS PubMed.
- M. W. Beijerinck, Verhandelingen der Koninklijke Nederlandsche Akademie van Wetenschappen. Afdeeling Natuurkunde, Sectie 2. Amsterdam, 1898, 5, 3–21 Search PubMed.
- F. C. Bawden, N. W. Pirie, J. D. Bernal and I. Fankuchen, Nature, 1936, 138, 1051 CrossRef.
- J. W. Kim, R. J. Larsen and D. A. Weitz, J. Am. Chem. Soc., 2006, 128, 14374–14377 CrossRef CAS PubMed.
- K. Bian, H. Schunk, D. Ye, A. Hwang, T. S. Luk, R. Li, Z. Wang and H. Fan, Nat. Commun., 2018, 9, 2365 CrossRef PubMed.
- Y. H. Lee, C. L. Lay, W. Shi, Y. Lee, H. K. Yang, S. Li and X. Y. Ling, Nat. Commun., 2018, 9, 2769 CrossRef PubMed.
- A. Bo, Y. Liu, B. Kuttich, T. Kraus, A. Widmer-Cooper and N. de Jonge, Adv. Mater., 2022, 34, 2109093 CrossRef CAS PubMed.
- D. Gandia, L. Gandarias, L. Marcano, I. Orue, D. Gil-Cartón, J. Alonso, A. García-Arribas, A. Muela and M. L. Fdez-Gubieda, ACS Nano, 2022, 16, 7398–7408 CrossRef PubMed.
- B. S. John, A. Stroock and F. A. Escobedo, J. Chem. Phys., 2004, 120, 9383 CrossRef CAS PubMed.
- R. Ni, A. P. Gantapara, J. de Graaf, R. van Roij and M. Dijkstra, Soft Matter, 2012, 8, 8826–8834 RSC.
- F. Smallenburg, L. Filion, M. Marechal and M. Dijkstra, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 17886–17890 CrossRef CAS PubMed.
- C. D. Cwalina, K. J. Harrison and N. J. Wagner, Soft Matter, 2016, 12, 4654–4665 RSC.
- J. Chen and N. Seeman, Nature, 1991, 350, 631–633 CrossRef CAS PubMed.
- Y. Zhang, F. Lu, K. G. Yager, D. van der Lelie and O. Gang, Nat. Nanotechnol., 2013, 8, 865–872 CrossRef CAS PubMed.
- K. J. Si, D. Sikdar, Y. Chen, F. Eftekhari, Z. Xu, Y. Tang, W. Xiong, P. Guo, S. Zhang, Y. Lu, Q. Bao, W. Zhu, M. Premaratne and W. Cheng, ACS Nano, 2014, 8, 11086–11093 CrossRef CAS PubMed.
- F. Lu, T. Vo, Y. Zhang, A. Frenkel, K. G. Yager, S. Kumar and O. Gang, Sci. Adv., 2019, 5, eaaw2399 CrossRef CAS PubMed.
- G. Chen, K. J. Gibson, D. Liu, H. C. Rees, J. H. Lee, W. Xia, R. Lin, H. L. Xin, O. Gang and Y. Weizmann, Nat. Mater., 2019, 18, 169–174 CrossRef CAS PubMed.
- B. H. Lee and G. Arya, Nanoscale, 2019, 11, 15939–15957 RSC.
- B. H. Lee and G. Arya, Nanoscale, 2022, 14, 3917–3928 RSC.
- Y. Kobayashi and A. Nikoubashman, Langmuir, 2022, 38, 10642–10648 CrossRef CAS PubMed.
- T. Yokoyama, Y. Kobayashi, N. Arai and A. Nikoubashman, Soft Matter, 2023, 19, 6480–6489 RSC.
- A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605–8613 CrossRef CAS.
- G. Gompper, T. Ihle, D. Kroll and R. G. Winkler, Adv. Polym. Sci., 2009, 221, 1–87 CAS.
- M. P. Howard, A. Nikoubashman and J. C. Palmer, Curr. Opin. Chem. Eng., 2019, 23, 34–43 CrossRef.
- W.-B. Zhang, X.-L. Wu, G.-Z. Yin, Y. Shao and S. Z. D. Cheng, Mater. Horiz., 2017, 4, 117–132 RSC.
- Y. M. Wani, P. G. Kovakas, A. Nikoubashman and M. P. Howard, J. Chem. Phys., 2022, 156, 024901 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- H. C. Andersen, D. Chandler and J. D. Weeks, J. Chem. Phys., 1972, 56, 3812–3823 CrossRef CAS.
- C.-C. Huang, A. Chatterji, G. Sutmann, G. Gompper and R. G. Winkler, J. Comput. Phys., 2010, 229, 168 CrossRef CAS.
- V. Dahirel, X. Zhao, B. Couet, G. Batôt and M. Jardat, Phys. Rev. E, 2018, 98, 053301 CrossRef CAS.
- T. Ihle and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 020201 CrossRef CAS PubMed.
- Y. Kobayashi, N. Arai and A. Nikoubashman, Soft Matter, 2020, 16, 476–486 RSC.
- Y. Kobayashi, N. Arai and A. Nikoubashman, Langmuir, 2020, 36, 14214–14223 CrossRef CAS PubMed.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, USA, 1989 Search PubMed.
- J. A. Anderson, C. D. Lorenz and A. Travesset, J. Comput. Phys., 2008, 227, 5342–5359 CrossRef.
- J. Glaser, T. D. Nguyen, J. A. Anderson, P. Liu, F. Spiga, J. A. Millan, D. C. Morse and S. C. Glotzer, Comput. Phys. Commun., 2015, 192, 97–107 CrossRef CAS.
- M. P. Howard, A. Z. Panagiotopoulos and A. Nikoubashman, Comput. Phys. Commun., 2018, 230, 10–20 CrossRef CAS.
- J. A. Anderson, J. Glaser and S. C. Glotzer, Comput. Mater. Sci., 2020, 173, 109363 CrossRef CAS.
- https://github.com/mphoward/azplugins .
- F. Müller-Plathe, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 4894–4898 CrossRef PubMed.
- V. Doyeux, S. Priem, L. Jibuti, A. Farutin, M. Ismail and P. Peyla, Phys. Rev. Fluids, 2016, 1, 043301 CrossRef.
- A. Einstein, Ann. Phys., 1906, 324, 289 CrossRef.
- A. Einstein, Ann. Phys., 1911, 339, 591 CrossRef.
- R. K. Mallavajula, D. L. Koch and L. A. Archer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 052302 CrossRef PubMed.
- M. Ester, H.-P. Kriegel, J. Sander and X. Xu, Proc. Second Int. Conf. Knowl. Discov. Data Min., 1996, vol. 96, p. 226 Search PubMed.
- C. Lang, J. Kohlbrecher, L. Porcar, A. Radulescu, K. Sellinghoff, J. K. G. Dhont and M. P. Lettinga, Macromolecules, 2019, 52, 9604–9612 CrossRef CAS.
- C. Lang and M. P. Lettinga, Macromolecules, 2020, 53, 2662–2668 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |