Geometric deep learning-guided Suzuki reaction conditions assessment for applications in medicinal chemistry
Kenneth
Atz†
 *a,
David F.
Nippa†
*a,
David F.
Nippa†
 a,
Alex T.
Müller
a,
Alex T.
Müller
 a,
Vera
Jost
a,
Andrea
Anelli
a,
Vera
Jost
a,
Andrea
Anelli
 a,
Michael
Reutlinger
a,
Michael
Reutlinger
 a,
Christian
Kramer
a,
Christian
Kramer
 a,
Rainer E.
Martin
a,
Rainer E.
Martin
 a,
Uwe
Grether
a,
Uwe
Grether
 a,
Gisbert
Schneider
a,
Gisbert
Schneider
 *b and
Georg
Wuitschik
*b and
Georg
Wuitschik
 *a
*a
aRoche Pharma Research and Early Development (pRED), Roche Innovation Center Basel, F. Hoffmann-La Roche Ltd., Grenzacherstrasse 124, 4070 Basel, Switzerland. E-mail: kenneth.atz@roche.com; georg.wuitschik@roche.com
bDepartment of Chemistry and Applied Biosciences, ETH Zurich, Vladimir-Prelog-Weg 4, 8093 Zurich, Switzerland. E-mail: gisbert@ethz.ch
First published on 31st May 2024
Abstract
Suzuki cross-coupling reactions are considered a valuable tool for constructing carbon–carbon bonds in small molecule drug discovery. However, the synthesis of chemical matter often represents a time-consuming and labour-intensive bottleneck. We demonstrate how machine learning methods trained on high-throughput experimentation (HTE) data can be leveraged to enable fast reaction condition selection for novel coupling partners. We show that the trained models support chemists in determining suitable catalyst-solvent-base combinations for individual transformations including an evaluation of the need for HTE screening. We introduce an algorithm for designing 96-well plates optimized towards reaction yields and discuss the model performance of zero- and few-shot machine learning. The best-performing machine learning model achieved a three-category classification accuracy of 76.3% (±0.2%) and an F1-score for a binary classification of 79.1% (±0.9%). Validation on eight reactions revealed a receiver operating characteristic (ROC) curve (AUC) value of 0.82 (±0.07) for few-shot machine learning. On the other hand, zero-shot machine learning models achieved a mean ROC-AUC value of 0.63 (±0.16). This study positively advocates the application of few-shot machine learning-guided reaction condition selection for HTE campaigns in medicinal chemistry and highlights practical applications as well as challenges associated with zero-shot machine learning.
1. Introduction
The synthesis of novel compounds remains a crucial challenge in small molecule drug discovery, often being the critical bottleneck impacting time and cost.1 In the pursuit of expediting and enhancing the design-make-test-analysis (DMTA) cycle, efficient utilization of chemical transformations to access novel molecular entities is paramount.2,3 In particular, increasing the success rate of heavily utilized cross-coupling reactions, which are instrumental in establishing structure–activity relationships (SAR), can contribute to the acceleration of the make step.4,5 Among those transformations, the Suzuki reaction is known as one of the most powerful methods to aid carbon–carbon (C–C) bond formation, serving as a versatile tool to construct complex molecular architectures.6–8 Suzuki reactions are generally catalyzed by palladium complexes and connect a (hetero-)aryl boronate with a (pseudo)halide, demonstrating versatility in creating diverse chemical entities.9 However, the assembly of novel chemical matter often requires the utilization of Suzuki couplings with limited or even unknown literature precedent, leading to a multi-dimensional optimization problem.10–16High-throughput experimentation (HTE) presents numerous benefits that simplify the process of developing and refining chemical transformations.10,17–19 Most importantly, it enables the efficient identification of suitable reaction conditions through parallel screening of different catalysts, bases, additives or solvents, thereby aiding in the swift enhancement of synthetic procedure optimization.20,21 In addition, HTE generates large and consistent data sets covering both positive and, importantly, negative reaction outcomes for chemical transformations.22,23 In line with the large amount of data generated, addressing the challenge of data sharing, adopting standardized formats and employing both human- and machine-readable reaction data formats24 has become crucial. Repositories such as the Open Reaction Database (ORD)25 and the Unified Data Model (UDM)26 have already improved access to diverse data sets of reactions.
Consequently, HTE serves as an invaluable tool for generating high-quality reaction data, that are needed to allow for broader applications of machine learning models in reaction development.27,28
Deep learning methodologies, integrated into medicinal chemistry workflows, aim to expedite the DMTA cycle, thereby delivering superior molecules more rapidly.29–31 While substantial research in machine learning applications has focused on the deployment of generative methods32–36 and structure-based scoring functions for bioactivity prediction,37–42 the development of machine learning methods for efficient synthesis planning of complex molecules has emerged as another challenge in the field of drug discovery.43,44 Especially, graph-based machine learning methods, facilitating efficient learning on three-dimensional (3D) molecular models, have proven instrumental in various domains of chemistry.45–47 Beyond their notable applications in quantum chemistry,48–52 graph neural network (GNN) methodologies have been tailored for forward reaction prediction, originating from small substrates and culminating in the synthesis of complex drug molecules.53–55 Additional efforts in data set generation and GNN model development have demonstrated the advantages of integrating quantum chemical and electronic information for predicting specific reaction outcomes.56–60 A recent extension of GNN application includes predicting the reaction yield and regioselectivity in C–H borylation reactions.61 In a similar context, a recent investigation has showcased the effectiveness of hybrid machine learning models enriched with quantum chemical insights into transition states, demonstrating accurate predictions of regioselectivity for iridium-catalyzed borylation reactions, even when confronted with limited data.62 Comparable GNN methodologies have been introduced for the prediction of late-stage C–H alkylation and oxidation chemistries, specifically in the context of reaction yield prediction.63 Furthermore, recent research has illustrated the application of trained GNNs for in silico reaction screening, successfully identifying suitable substrates for Minisci-type alkylation reactions with high success rates.64
Although cross-coupling reactions are heavily utilized in medicinal and process chemistry, determining optimal reaction conditions – including catalysts, solvents and bases, along with their respective loadings and concentrations for specific substrates – remains a formidable challenge.65 In this study, we demonstrate the use of machine learning methods for the precise identification of optimal combinations of catalysts, solvents, and bases. We present an algorithm tailored for the design of 96-well plates to streamline initial HTE screening, focusing on Suzuki reaction conditions for novel substrates. We showcase the application of this algorithm in ranking and selecting reaction conditions achieving high accuracy in pinpointing the top-10% of conditions. We demonstrate the efficacy of our approach in predicting reaction yields and binary reaction outcomes. Furthermore, we discuss the advantages of employing few-shot learning over zero-shot learning scenarios.
2. Results and discussion
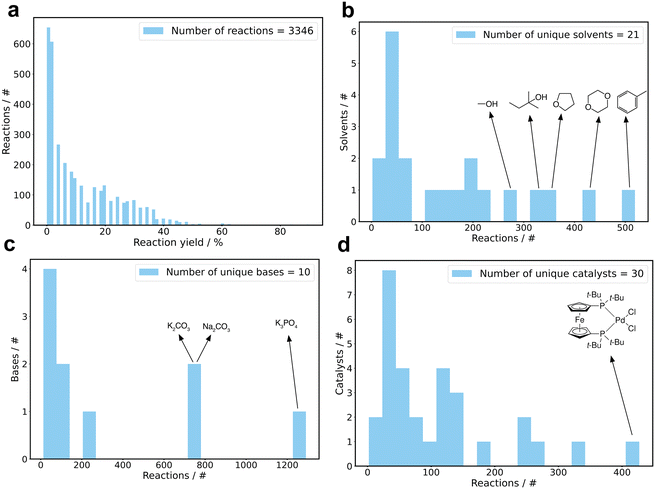
The data set used to train the machine learning models comprised 3346 unique Suzuki reactions, covering 790 distinct conditions (Table 1). Reaction conditions were defined by the combination of catalyst, solvent and base. The data set encompassed 30 catalysts, 21 solvents, and 10 bases. For inclusion in the training data set, each component had to be present in at least 40 reactions. Fig. 1a depicts the distribution of reaction yields, highlighting 645 (19.5%) unsuccessful reactions with yields below 1% and 2692 (80.5%) successful reactions with yields of 1% or higher. Additionally, the frequency distribution of reactions for the individual components is depicted in Fig. 1b–d. The most prevalent solvents were toluene, dioxane, tetrahydrofuran, 2,2-dimethyl-1-propanol and methanol, while the most common bases were K3PO4, Na2CO3 and K2CO3. The catalyst with the highest occurrence was [1,1′-bis(di-tert-butylphosphino)ferrocene]dichloropalladium(II) (PdCl2(dtbpf)). The data set also encompassed a total of 52 halogens, 47 boronic acids and 55 products (Table 1).| Unique entity | Occurrence/# |
|---|---|
| Halogens | 52 |
| Boronic acids | 47 |
| Products | 55 |
| Bases | 10 |
| Solvents | 21 |
| Catalysts | 30 |
| Conditions | 790 |
| Reactions | 3346 |
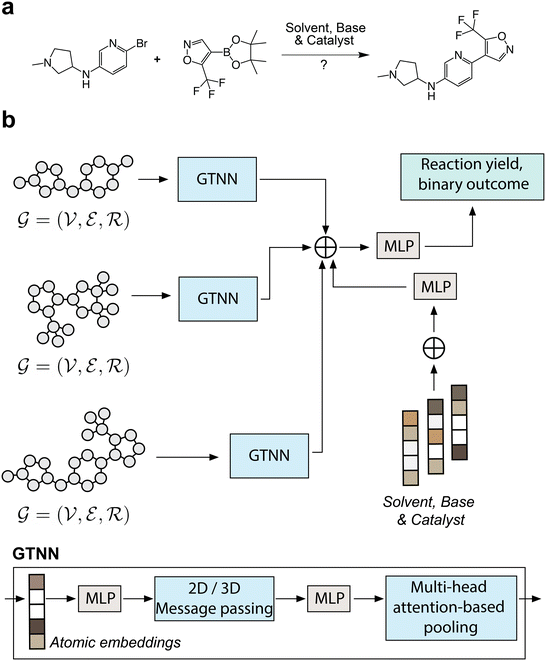
Graph Transformer Neural Networks (GTNNs) were designed to enable the prediction of reaction yields for Suzuki transformations, given the substrates (i.e., halogen and boronic acid), the desired product and the conditions (i.e., catalyst, solvent and base) as shown in Fig. 1a. Substrates and desired products are represented as either 2D or 3D molecular graphs, while conditions are represented by one-hot encodings, as depicted in Fig. 2. The machine learning model embeds the six inputs into individual latent spaces, concatenates them and then maps them to the desired output through a multilayer perceptron (MLP). The GTNN models were compared to a neural network that uses Extended Connectivity Fingerprint (ECFP) vectors as inputs instead of molecular graphs, referred to as ECFPNN, as shown in Table 2. Binary reaction outcomes were considered “successful” if the reaction condition with the chosen substrate yielded the desired product that could be confirmed by liquid chromatography-mass spectrometry (LCMS) with a corresponding conversion of ≥1%, or “unsuccessful” if the desired transformation was not traceable with LCMS. Equivalently, the category covering the lowest conversion for three-category classification was defined as ≥1%.
| Method (model size)/% | Accuracy (3 bins) | Binary accuracy | F 1-score | MAE (reaction yield)/% | Correlation coefficient (reaction yield)/% |
|---|---|---|---|---|---|
| ECFPNN (145 k) | 74.8 (±0.2) | 91.2 (±0.1) | 72.3 (±0.1) | 4.86 (±0.04) | 0.776 (±0.003) |
| ECFPNN (380 k) | 75.5 (±0.3) | 91.2 (±0.1) | 73.0 (±0.5) | 4.74 (±0.02) | 0.777 (±0.001) |
| ECFP-XGBoost | 76.0 (±0.3) | 91.3 (±0.3) | 76.0 (±0.1) | 4.93 (±0.01) | 0.706 (±0.004) |
| GTNN2D (420 k) | 76.2 (±0.2) | 92.1 (±0.2) | 77.1 (±0.8) | 4.86 (±0.02) | 0.761 (±0.0003) |
| GTNN3D (530 k) | 75.7 (±0.4) | 92.0 (±0.3) | 76.6 (±0.6) | 4.82 (±0.03) | 0.762 (±0.003) |
| GTNN2D (4.1 M) | 76.2 (±0.4) | 92.7 (±0.3) | 79.1 (±0.9) | 4.81 (±0.03) | 0.760 (±0.005) |
| GTNN3D (4.5 M) | 76.3 (±0.2) | 92.6 (±0.1) | 78.9 (±0.2) | 4.81 (±0.03) | 0.758 (±0.003) |
For comparison, the models were employed in a few-shot learning scenario, incorporating a randomly selected 20% of each transformation from the data set during model training. Each neural network underwent the same three-fold cross-validation, utilizing three different subsets of 20%. A comparison between the eight different neural networks, with varying numbers of trainable hyperparameters (ranging from 145 k to 4.5 M), revealed that ECFPNNs slightly outperformed GTNNs in terms of mean absolute error (MAE) and Pearson correlation coefficient (r) for reaction yield prediction, with scores of 4.74 (±0.01) vs. 4.81 (±0.03) and 0.777 (±0.001) vs. 0.758 (±0.003), respectively. Conversely, GTNNs slightly outperformed ECFPNNs in binary accuracy with F1-scores of 78.9% (±0.2%) vs. 73.0% (±0.5%) and in accuracy across three categories with 76.3% (±0.2%) vs. 75.5% (±0.2%). Additionally, an extreme gradientboosting (XGBoost) baseline model trained on reaction fingerprints using ECFP has shown comparable performance in all investigated tasks. Although the ECFP-XGBoost performs poorly on absolute reaction yield prediction (91.3% (±0.3%) and r = 0.706 (±0.004)), close to state-of-the arte performance is achieved for three-category accuracy (76.0% (±0.3%)) and binary accuracy (F1-scores = 76.0% (±0.1%)). Comparing the achieved accuracies in reaction yield prediction reveals a substantial improvement from the mean absolute deviation (MAD) of the data set, i.e., 9.96%. Increasing the model size for GTNN architectures from approximately 500 k to 4 M parameters has yielded improvements in both the MAE for yield prediction and accuracy for binary and three-category classification tasks. On the other hand, incorporating 3D information into the input molecular graph structures has not resulted in performance enhancements.
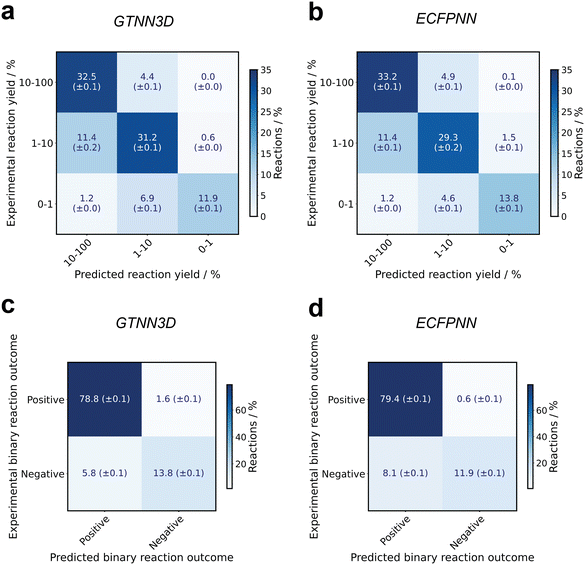
Fig. 3 illustrates the accuracy of the best-performing GTNN, specifically the GTNN3D with 4.5 M parameters and the ECFNN baseline model, in terms of three-category and binary classification accuracy. For the three-category classification, the reaction yields were divided into three categories: no reaction (<1%), medium yield (≥1% to 10%) and high yield (≥10%). The GTNN3D model accurately classified 76.3% (±0.2%) of the reactions into the correct bin, achieving an MAE of 4.81% (±0.03%) and a correlation coefficient of r = 0.758 (±0.003). For binary classification, the GTNN3D model achieved an absolute accuracy of 92.6% (±0.1%), i.e., an F1-s-score of 78.9% (±0.2%).
A framework was designed to enable in silico reaction condition screening and HTE plate design for substrates involved in a novel Suzuki reaction. The trained GTNNs were utilized to predict the reaction yield for each reaction within the specified condition space, i.e., the space comprising combinations of 31 catalysts, 21 solvents and 10 bases (Fig. 4a). These predictions were applied to known reaction conditions, namely the 790 reaction conditions in the data set, or to each of the individual combinations among the three components, amounting to 6300 reaction conditions. The applied models resulted in predicted reaction outcomes for each combination, with predicted yields ranging from 0 to 25% for the exemplary reaction shown in Fig. 2a as depicted in the histogram in Fig. 4b. The conditions that resulted in the highest reaction yields were subsequently selected for in silico plate design aiming to deliver the HTE plate with maximized reaction yields. Fig. 4c illustrates the plate configuration derived from the predictions shown in Fig. 4b. To populate a 96-well plate, the top-8 catalysts and the top-12 solvent-base combinations were selected.
 | ||
| Fig. 4 Plate design workflow. a: Illustration of the reaction condition space as a three-dimensional grid. While fully enumerated combinations cover 6300 conditions, the explored conditions for Suzuki cross-couplings in the Roche HTE data set cover 790 conditions. b: Reaction yield predictions illustrated in a histogram. The substrates used for the prediction are shown in Fig. 2a. c: The reaction yield predictions are then used to select conditions and design a plate for initial high-throughput experimentation (HTE) screening. The plate illustrates the top-8 catalysts on the y-axis, the top-12 base-solvent combinations on the x-axis and the predicted reaction yields on the 2D grid for each combination. The colors illustrate binned reaction yields, i.e., purple for ≥5–15% and green for ≥15–30%. Catalysts: AmPhos_Pd(crotyl)Cl: [4-[bis(1,1-dimethylethyl)phosphino-κP]-N,N-dimethylbenzenamine][(1,2,3-η)-(2E)-2-buten-1-yl]chloropalladium, CatacxiumA_Pd_G3: mesylate[(di(l-adamantyl)-n-butylphosphine)-2-(2′-amino-1,1′-biphenyl)]palladium(II), P(tBu)3_Pd(crotyl)Cl: [(1,2,3-η)-(2E)-2-buten-1-yl]chloro[tris(1,1-dimethylethyl)phosphine]palladium, SPhos_Pd(crotyl)Cl: [(1,2,3-η)-2-buten-1-yl]chloro[dicyclohexyl(2′,6′-dimethoxy[1,1′-biphenyl]-2-yl)phosphine-κP]palladium, Xantphos_Pd(allyl)Cl: palladium-chloro[(9,9-dimethyl-9H-xanthene-4,5-diyl)bis[diphenylphosphine-κP]](η3-2-propenyl), dppfPdCl2: dichloro[1,1′-bis(diphenylphosphine)ferrocene]palladium(II), dtbpfPdCl2: [1,1′-bis(di-tert-butylphosphino)ferrocene]dichloropalladium(II), meCgPPh_Pd_G32: [2′-(amino-κN)[1,1′-biphenyl]-2-yl-κC](methanesulfonato-κO)(1,3,5,7-tetramethyl-8-phenyl-2,4,6-trioxa-8-phosphatricyclo[3.3.1.13,7]decane-κP8)palladium. Bases: Cs2CO3: caesium carbonate, K2CO3: potassium carbonate, K3PO4: tripotassium phosphate, Na2CO3: sodium carbonate. Solvents: tAmOH: tert-amyl alcohol, MeCN: acetonitrile, THF: tetrahydrofuran, MeTHF: 2-methyltetrahydrofuran, PhMe: toluene. | ||
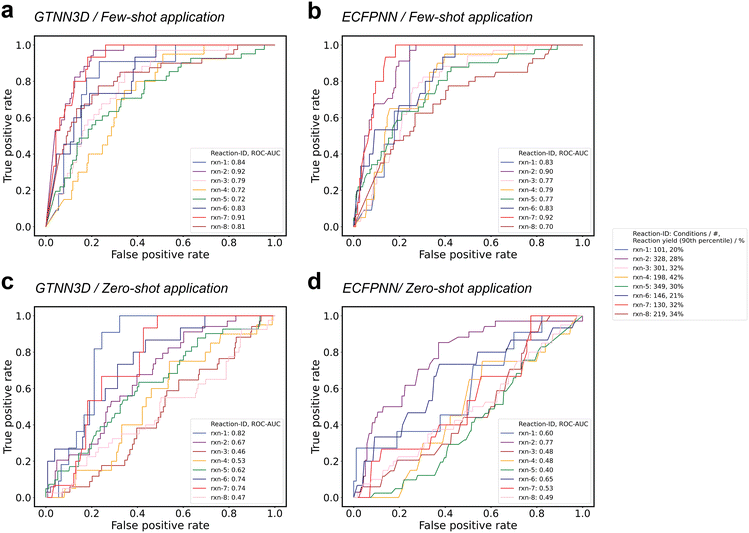
To assess the efficacy of the machine learning-guided reaction condition selection algorithm, eight Suzuki reaction substrates were chosen for validation. Each substrate has been characterized by reaction yields for ≥96 reaction conditions (i.e., 101–349 different catalyst-base-solvent combinations) as well as measured reaction yields ≥20% for the 90th percentile of the tested reaction conditions (i.e., 20–42%). To retrospectively evaluate the model's capability in identifying the reaction condition that delivered the highest reaction yields, the top-10% of reaction conditions were designated as “positive”, while the remaining 90% were categorized as “negative”. Models were trained in a zero- and few-shot-like scenario, either excluding all reactions for each of the individual substrates from training (i.e., zero-shot), or including a randomly selected 20% of the reactions for each of the substrates (i.e., few-shot). The excluded conditions for each of the eight test reactions, specifically 100% for zero-shot applications and 80% for few-shot applications, were subsequently used to rank the conditions and identify the top-10% achieving the highest reaction yields (Table 4). For each data set, the area under the receiver operating characteristic (ROC) curve (AUC) was calculated, with values ranging from 0.46 to 0.82 for zero-shot learning applications, averaging at 0.63 (±0.12), and from 0.73 to 0.92 for few-shot learning applications, averaging at 0.82 (±0.07). While perfect discrimination would correspond to an AUC of 1.0, a model performing at the chance level would exhibit an AUC of 0.5. Fig. 5 illustrates the true positive rates (TPRs) plotted against the false positive rates (FPRs) for various threshold settings across the eight test scenarios for the best-performing GTNN3D model and the ECFPNN baseline method. The ECFPNN baseline method achieves similar performance with values ranging from 0.40 to 0.77 for zero-shot learning applications, averaging at 0.55 (±0.11), and from 0.70 to 0.92 for few-shot learning applications, averaging at 0.81 (±0.06). Moreover, for each of the zero- and few-shot applications, the structural similarity (i.e., Tanimoto similarity using binary ECFP vectors) of the investigated molecules for halogens, boronic acids, and products were analysed (Table 3). The observed similarities to the most similar molecule in the training set ranged from 0.243 to 0.519 for halogens, 0.066 to 0.301 for boronic acids, and 0.300 to 0.657 for products.
| ID | Yield/% | Reactions/# | Similarity/halogens | Similarity/boronic acids | Similarity/products | |||
|---|---|---|---|---|---|---|---|---|
| Average | Max. | Average | Max. | Average | Max. | |||
| rxn-1 | 20 | 101 | 0.149 | 0.292 | 0.109 | 0.301 | 0.142 | 0.540 |
| rxn-2 | 28 | 328 | 0.128 | 0.194 | 0.103 | 0.259 | 0.124 | 0.422 |
| rxn-3 | 32 | 301 | 0.122 | 0.519 | 0.097 | 0.185 | 0.154 | 0.523 |
| rxn-4 | 42 | 198 | 0.116 | 0.243 | 0.087 | 0.217 | 0.127 | 0.300 |
| rxn-5 | 30 | 349 | 0.100 | 0.380 | 0.018 | 0.066 | 0.110 | 0.541 |
| rxn-6 | 21 | 146 | 0.135 | 0.292 | 0.109 | 0.173 | 0.131 | 0.657 |
| rxn-7 | 32 | 130 | 0.151 | 0.379 | 0.091 | 0.187 | 0.131 | 0.454 |
| rxn-8 | 34 | 219 | 0.131 | 0.612 | 0.075 | 0.160 | 0.126 | 0.523 |
| ID | ROC-AUC/GTNN3D | ROC-AUC/ECFPNN | ||
|---|---|---|---|---|
| Zero-shot | Few-shot | Zero-shot | Few-shot | |
| rxn-1 | 0.82 | 0.84 | 0.60 | 0.83 |
| rxn-2 | 0.67 | 0.92 | 0.77 | 0.90 |
| rxn-3 | 0.46 | 0.79 | 0.48 | 0.77 |
| rxn-4 | 0.53 | 0.73 | 0.48 | 0.79 |
| rxn-5 | 0.62 | 0.73 | 0.40 | 0.77 |
| rxn-6 | 0.74 | 0.83 | 0.65 | 0.83 |
| rxn-7 | 0.74 | 0.92 | 0.53 | 0.92 |
| rxn-8 | 0.47 | 0.81 | 0.49 | 0.70 |
| Mean | 0.63 ± 0.12 | 0.82 ± 0.07 | 0.55 ± 0.11 | 0.81 ± 0.06 |
3. Conclusions
The applicability of machine learning algorithms for identifying suitable reaction conditions in Suzuki cross-coupling reactions were demonstrated. We revealed insights into our Suzuki reaction data set comprising 3346 unique reactions and 790 distinct conditions as well as a diverse range of catalysts, solvents and bases, with a substantial portion of the reactions achieving desired product formation above 1%. We show that training of machine learning models on the described data set enables prediction of reaction yields with high accuracy, i.e., 76.3% (±0.2%) for three-category classification and 92.1% (±0.3%) for binary classification.Our findings suggest that GTNNs as well as fingerprint-based neural networks enable binary and multi-class classification tasks, as well as reaction yield prediction with high accuracy underscoring the effectiveness of neural networks in categorizing reaction outcomes. Consistent with previous research investigating reaction yield prediction and classification,61,63 incorporating 3D molecular graph information did not enhance the model performance, affirming that 2D representations are adequate for extracting pertinent reactivity information in the case of Suzuki reactions. Remarkably, while ECFPNN models exhibited higher accuracy in reaction yield prediction, GTNN models demonstrated superior accuracy in binary and three-category classification. Such a scenario occurs when overall higher predictive accuracy is achieved, although lower accuracy is observed at the edges of the different categories, i.e., around 1% and 10%. We introduced a machine learning-guided plate design framework facilitating the generation of proposals for 96-well plates through the in silico screening of thousands of reaction conditions. Validation of the algorithm with eight Suzuki reaction substrates affirmed its proficiency in identifying high-yield conditions. The disparities observed between few- and zero-shot applications underscored the superiority of few-shot learning. ROC-AUC values for few-shot applications ranged from 0.72 to 0.92, indicating robust discrimination between top-performing and low-yielding reaction conditions.
Furthermore, it is worth noting that zero-shot learning demonstrated utility, achieving ROC-AUC values surpassing 0.5 (better than random condition selection) for five out of the eight cases studied. This underscores both the practical applications and challenges associated with zero-shot learning in identifying suitable starting points for reaction conditions. Additionally, the calculated structural similarities revealed extensive diversity within the data set, with no compounds exhibiting Tanimoto-Jaccard similarity values greater than 0.7, emphasizing the absence of structural analogs or structurally similar reaction substrates. Notably, reactions rxn-1 (0.86 vs. 0.85) and rxn-7 (0.92 vs. 0.90) illustrate almost identical performance in zero- and few-shot applications. Such a scenario indicates that this could result from the fact that training on all other reaction data properly describes the two substrates.
In conclusion, our study showcases the potential of machine learning methods to accelerate the initial screening process in medicinal and process chemistry by efficiently identifying top-yielding reaction conditions. The integration of machine learning algorithms into the design of HTE plates facilitates streamlining the discovery and optimization of chemical reactions, thereby potentially accelerating the development of new compounds and materials.
4. Methods
Training details
PyTorch Geometric (2.0.2)67 and PyTorch (1.10.1+cu102)68 functionalities were used for neural network training. Training was performed on a graphical processing unit GPU (NVIDIA A100 Tensor Core GPU, 40 GB) for four hours, using a batch size of 16 samples. The Adam stochastic gradient descent optimizer was employed,69 with a learning rate of 10−4, mean squared error (MSE) loss on the training set, a decay factor of 0.5 applied after 100 epochs and an exponential smoothing factor of 0.9. The final model was stored after 300 epochs. All the models considered in this study were trained on the Roche computing cluster located in Kaiseraugst, Switzerland.Deep learning
Fig. 2b displays the neural network based model used with all its components. The properties of each atom (i.e. node), i, described in detail in the next section, were densely embedded using two pre-message-passing multilayer Perceptrons (MLPs) for the three input graphs, i.e., boronic acid (g = B), halogen (g = H) and the product (g = P). The individual embeddings the result in the node features h0g, i. Inter-atomic distance between the nodes of the molecule graph, rij, were represented in terms of Fourier features, using a sine- and cosine-based encoding,70![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) , resulting in the edge features hP,ij =
, resulting in the edge features hP,ij = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (rij).
(rij).
For each of the three input graphs, i.e., g = B, g = H and g = P the same message-passing description is applied (herein denoted as X). In each message-passing step, the node representations were updated via (eqn (1)):
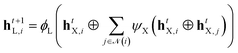 | (1) |
 | (2) |
ψ X is representative for the three MLP modules for halogens, boronic acids and products, i.e., ψB, ψH, ψP, transforming node features into message features between nodes connected via an edge.
These message features were aggregated using permutation-invariant pooling (i.e. sum operator in this instance) of the node-neighborhood, ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (i), which consists of all nodes j connected by an edge to node i.
(i), which consists of all nodes j connected by an edge to node i.
The outputs of the message passing step for each node are obtained by utilizing ϕH, ϕBϕP, which are MLPs. These MLPs make use of the aggregated message features along with the node features from the previous step. For a comprehensive understanding of message-passing neural networks and a detailed examination of their various components, we recommend referring to ref. 71. It provides both a general overview and an in-depth exploration of these networks.
After T = 3 message-passing steps, the node features resulting from all three steps were transformed via graph-specific post-message-passing MLPs, ρH, ρB and ρP, resulting in the final node features via (eqn (3)):
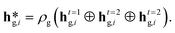 | (3) |
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) L and
L and ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) P, of each graph via graph-specific graph multiset transformers (GMT)72via (eqn (4)):
P, of each graph via graph-specific graph multiset transformers (GMT)72via (eqn (4)):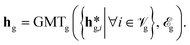 | (4) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) H,
H, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) B and
B and ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) P. Unlike the commonly used sum-pooling of node features, the GMT-pooling operation leverages the inherent graph structure. This distinction gives it the potential to attain a more potent global graph representation.72
P. Unlike the commonly used sum-pooling of node features, the GMT-pooling operation leverages the inherent graph structure. This distinction gives it the potential to attain a more potent global graph representation.72
In parallel, the three reaction conditions were densely embedded resulting in three individual latent spaces i.e., catalyst CC, solvent CS and base CB. The three latent spaces were concatenated and transformed via an MLP θ resulting in an condition representation: hCvia (eqn (5)):
| θ(CC ⊕ CS ⊕ (CB)) = hC | (5) |
| ŷLP = ζ(hH ⊕ hB ⊕ hP ⊕ hC). | (6) |
Molecular representation
Node features of atomic properties of molecular graphs were encoded in terms of the following embeddings.1. 10 atom types [H, C, N, O, F, P, S, Cl, Br, I].
2. 2 ring types [True, False].
3. 2 aromaticity types [True, False].
4. 4 hybridisation types [sp3, sp2, sp, s].
Reaction condition representation
Reaction conditions were encoded in terms of the following number of embeddings, i.e., 30 catalysts, 21 solvents and 10 bases.Number of hyperparameters
Metric for model validation
For model validation and optimization mean absolute error was used for reaction yield prediction. For predicting binary reaction outcomes the models were validated using absolute accuracy and the F-score metric. The F-score (F1) is used as a measure for unbalanced data sets and is calculated by the mean of precision and recall (eqn (7)):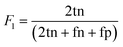 | (7) |
Data set split
For model validation and testing of the individual neural network architectures, i.e., GTNN and ECFPNN with different numbers of hyperparameters, the data set was divided using a four-fold cross-validation (refer to Table 2 and Fig. 3). A substrate-based split was employed, involving all reactions except one in the training set. The excluded reaction was subsequently applied for testing. To allow for validation scenarios where more than 96 reaction conditions were screened (i.e., more than a 96-well plate), all reactions with ≥96 conditions (i.e., eight reactions including 101–349) were selected for model validation. The excluded reaction was subsequently reserved for testing purposes. Two machine learning procedures, i.e., zero-shot and few-shot learning, were employed based on different training and test-set splitting methods. In zero-shot learning, 0% of the conditions of the test reactions were included for training. In few-shot learning, 20% of the reaction conditions of the test set reactions were included for training. The 20% of reaction conditions were randomly selected. Training of few-shot models was conducted in a one-step process where the whole training data was included. Fig. 5 illustrates the results using the described substrate-based approach for both few- and zero-shot learning.Plate design
Following the reaction yield predictions of a new Suzuki transformation, the top-8 catalysts as well as the top-12 base-solvent combinations are used for the plate design of a 96-well plate. Fig. 3c illustrates the top-8 catalysts on the y-axis, the top-12 base-solvent combinations on the x-axis and the binned predicted reaction yields on the 2D grid for each combination.Determination of reaction yield
The calculation of yields was performed based on the peak area ratio of the product relative to an internal standard, as well as the recorded weight ratio of the limiting starting material to the internal standard present in each vial. In the majority of instances, a product reference was not available to standardize these relative yields for comparability between reactions. Consequently, the assignment of absolute yield to the most promising hits of each reaction was based on the visual appearance of the reaction chromatograms.Data set composition and preprocessing
The data set, comprising 3346 Suzuki cross-coupling reactions with 790 unique conditions as described in Table 1, originates from the high-throughput experimentation (HTE) conducted in Roche's Process Chemistry Department covering reaction data from HTE campaigns conducted over the past three years. Initially encompassing 6799 reactions, those involving catalysts, solvents, and bases occurring in fewer than 40 reactions were excluded to ensure high-quality embedded learning for catalysts, solvents, and bases. A cut-off threshold was applied to ensure the quality of learned embeddings. While a cut-off of 40 reactions yielded 3346 reactions, cut-offs of 80 and 5 yielded totals of 2599 and 3696 reactions, respectively. A cut-off of 40 was found to strike a good balance between retaining enough reactions to encompass most of the data set and enabling high-quality condition embeddings.Code availability
A reference implementation of the geometric machine learning platform based on PyTorch68 and PyTorch Geometric67 is available at https://github.com/ETHmodlab/minisci (rep. DOI: https://doi.org/10.5281/zenodo.8344587, https://zenodo.org/record/8344587) and https://github.com/ETHmodlab/lsfml (rep. DOI: https://doi.org/10.5281/zenodo.8118845, https://zenodo.org/record/8118845).Data availability
The data set covering 3346 Suzuki reactions is proprietary and owned by F. Hoffmann-La Roche Ltd. and is not publicly available. Researchers interested in accessing the data set may contact the corresponding author for more information. Other reference data sets to train and apply the geometric machine learning models are available at https://reaction-surf.com.Author contributions
Kenneth Atz: conceptualization, methodology, experiments, software development and validation, formal analysis, data curation, writing – original draft. David F. Nippa: conceptualization, methodology, experiments, formal analysis, data curation, writing – original draft. Alex T. Müller: conceptualization, methodology, experiments, software development and validation, formal analysis, writing – review and editing. Vera Jost: conceptualization, methodology, experiments, writing – review and editing. Andrea Anelli: formal analysis, writing – review and editing. Michael Reutlinger: conceptualization, formal analysis, writing – review and editing. Christian Kramer: conceptualization, formal analysis, writing – review and editing. Rainer E. Martin: conceptualization, formal analysis, investigation, methodology, writing – review and editing. Uwe Grether: conceptualization, formal analysis, investigation, methodology, writing – review and editing. Gisbert Schneider: conceptualization, formal analysis, investigation, methodology, writing – review and editing. Georg Wuitschik: conceptualization, formal analysis, methodology, writing – review and editing. All authors discussed the results and gave their approval of the final version.Conflicts of interest
G. S. declares a potential financial and non-financial conflict of interest as co-founder of https://inSili.com LLC, Zurich and in his role as a scientific consultant to the pharmaceutical industry. K. A., D. F. N., A. T. M., V. J., M. R. U. G., R. E. M., C. K. and G. W. declare a potential financial and non-financial conflict of interest as full employees of F. Hoffmann-La Roche Ltd.Notes and references
- D. C. Blakemore, L. Castro, I. Churcher, D. C. Rees, A. W. Thomas, D. M. Wilson and A. Wood, Nat. Chem., 2018, 10, 383–394 CrossRef CAS PubMed.
- E. J. Corey, Angew. Chem., Int. Ed. Engl., 1991, 30, 455–465 CrossRef.
- E. J. Corey and W. T. Wipke, Science, 1969, 166, 178–192 CrossRef CAS PubMed.
- D. G. Brown and J. Bostrom, J. Med. Chem., 2016, 59, 4443–4458 CrossRef CAS PubMed.
- J. Boström, D. G. Brown, R. J. Young and G. M. Keserü, Nat. Rev. Drug Discovery, 2018, 17, 709–727 CrossRef PubMed.
- A. Suzuki, J. Org. Chem., 1999, 576, 147–168 CrossRef CAS.
- S. B. Blakey and D. W. MacMillan, J. Am. Chem. Soc., 2003, 125, 6046–6047 CrossRef CAS PubMed.
- A. Fihri, M. Bouhrara, B. Nekoueishahraki, J.-M. Basset and V. Polshettiwar, Chem. Soc. Rev., 2011, 40, 5181–5203 RSC.
- L.-C. Campeau and N. Hazari, Organometallics, 2018, 38, 3–35 CrossRef PubMed.
- S. W. Krska, D. A. DiRocco, S. D. Dreher and M. Shevlin, Acc. Chem. Res., 2017, 50, 2976–2985 CrossRef CAS PubMed.
- W. F. Hoffman, R. L. Smith and A. K. Willard, Antihypercholesterolemic compounds, US Pat., 4444784, 1984 Search PubMed.
- J. Y. Chung, C. Cai, J. C. McWilliams, R. A. Reamer, P. G. Dormer and R. J. Cvetovich, J. Org. Chem., 2005, 70, 10342–10347 CrossRef CAS PubMed.
- C. Cai, J. Y. Chung, J. C. McWilliams, Y. Sun, C. S. Shultz and M. Palucki, Org. Process Res. Dev., 2007, 11, 328–335 CrossRef CAS.
- P. Grongsaard, P. G. Bulger, D. J. Wallace, L. Tan, Q. Chen, S. J. Dolman, J. Nyrop, R. S. Hoerrner, M. Weisel and J. Arredondo, et al. , Org. Process Res. Dev., 2012, 16, 1069–1081 CrossRef CAS.
- G. W. Stewart, P. E. Maligres, C. A. Baxter, E. M. Junker, S. W. Krska and J. P. Scott, Tetrahedron, 2016, 72, 3701–3706 CrossRef CAS.
- R. T. Ruck, N. A. Strotman and S. W. Krska, ACS Catal., 2022, 13, 475–503 CrossRef.
- S. M. Mennen, C. Alhambra, C. L. Allen, M. Barberis, S. Berritt, T. A. Brandt, A. D. Campbell, J. Castañón, A. H. Cherney and M. Christensen, et al. , Org. Process Res. Dev., 2019, 23, 1213–1242 CrossRef CAS.
- M. Shevlin, ACS Med. Chem. Lett., 2017, 8, 601–607 CrossRef CAS PubMed.
- D. F. Nippa, R. Hohler, A. F. Stepan, U. Grether, D. B. Konrad and R. E. Martin, Chimia, 2022, 76, 258–258 CrossRef CAS.
- C. L. Allen, D. C. Leitch, M. S. Anson and M. A. Zajac, Nat. Cat., 2019, 2, 2–4 CrossRef.
- E. S. Isbrandt, R. J. Sullivan and S. G. Newman, Angew. Chem., Int. Ed., 2019, 58, 7180–7191 CrossRef CAS PubMed.
- B. Mahjour, Y. Shen and T. Cernak, Acc. Chem. Res., 2021, 54, 2337–2346 CrossRef CAS PubMed.
- F. Strieth-Kalthoff, F. Sandfort, M. Kühnemund, F. R. Schäfer, H. Kuchen and F. Glorius, Angew. Chem., Int. Ed., 2022, 61, e202204647 CrossRef CAS PubMed.
- D. F. Nippa, A. T. Müller, K. Atz, D. B. Konrad, U. Grether, R. E. Martin and G. Schneider, ChemRxiv, 2024, preprint, DOI:10.26434/chemrxiv-2023-nfq7h-v2.
- S. M. Kearnes, M. R. Maser, M. Wleklinski, A. Kast, A. G. Doyle, S. D. Dreher, J. M. Hawkins, K. F. Jensen and C. W. Coley, J. Am. Chem. Soc., 2021, 143, 18820–18826 CrossRef CAS PubMed.
- J. Tomczak, E. Herzog, M. Fischer, J. Swienty-Busch, F. van den Broek, G. Whittick, M. Kappler, B. Jones and G. Blanke, Pure Appl. Chem., 2022, 94(6), 687–704 CrossRef CAS.
- J. Götz, M. K. Jackl, C. Jindakun, A. N. Marziale, J. André, D. J. Gosling, C. Springer, M. Palmieri, M. Reck and A. Luneau, et al. , Sci. Adv., 2023, 9, eadj2314 CrossRef PubMed.
- A. E. McMillan, W. Wilson, P. L. Nichols, B. Wanner and J. W. Bode, Chem. Sci., 2022, 13, 14292–14299 RSC.
- P. Schneider, W. P. Walters, A. T. Plowright, N. Sieroka, J. Listgarten, R. A. Goodnow, J. Fisher, J. M. Jansen, J. S. Duca and T. S. Rush, et al. , Nat. Rev. Drug Discov., 2020, 19, 353–364 CrossRef CAS PubMed.
- J. Jiménez-Luna, F. Grisoni and G. Schneider, Nat. Mach. Intell., 2020, 2, 573–584 CrossRef.
- S. Allenspach, J. A. Hiss and G. Schneider, Nat. Mach. Intell., 2024, 6, 124–137 CrossRef.
- A. Gupta, A. T. Müller, B. J. Huisman, J. A. Fuchs, P. Schneider and G. Schneider, Mol. Inf., 2018, 37, 1700111 CrossRef PubMed.
- A. T. Muller, J. A. Hiss and G. Schneider, J. Chem. Inf. Model., 2018, 58, 472–479 CrossRef CAS PubMed.
- F. Grisoni, B. J. Huisman, A. L. Button, M. Moret, K. Atz, D. Merk and G. Schneider, Sci. Adv., 2021, 7, eabg3338 CrossRef CAS PubMed.
- M. Moret, I. Pachon Angona, L. Cotos, S. Yan, K. Atz, C. Brunner, M. Baumgartner, F. Grisoni and G. Schneider, Nat. Commun., 2023, 14, 114 CrossRef CAS PubMed.
- K. Atz, L. Cotos, C. Isert, M. Håkansson, D. Focht, M. Hilleke, D. F. Nippa, M. Iff, J. Ledergerber and C. C. Schiebroek, et al. , Nat. Commun., 2024, 15, 3408 CrossRef CAS PubMed.
- J. Jiménez, M. Skalic, G. Martinez-Rosell and G. De Fabritiis, J. Chem. Inf. Model., 2018, 58, 287–296 CrossRef PubMed.
- L. Möller, L. Guerci, C. Isert, K. Atz and G. Schneider, Mol. Inf., 2022, 41, 2200059 CrossRef PubMed.
- M. Volkov, J.-A. Turk, N. Drizard, N. Martin, B. Hoffmann, Y. Gaston-Mathé and D. Rognan, J. Med. Chem., 2022, 65, 7946–7958 CrossRef CAS PubMed.
- C. Isert, K. Atz, S. Riniker and G. Schneider, RSC Adv., 2024, 14, 4492–4502 RSC.
- A. Tosstorff, M. G. Rudolph, J. C. Cole, M. Reutlinger, C. Kramer, H. Schaffhauser, A. Nilly, A. Flohr and B. Kuhn, J. Comput.-Aided Mol. Des., 2022, 36, 753–765 CrossRef CAS PubMed.
- B. Kuhn, J.-U. Peters, M. G. Rudolph, P. Mohr, M. Stahl and A. Tosstorff, Chimia, 2023, 77, 489–493 CrossRef CAS PubMed.
- C. W. Coley, D. A. Thomas III, J. A. Lummiss, J. N. Jaworski, C. P. Breen, V. Schultz, T. Hart, J. S. Fishman, L. Rogers and H. Gao, et al. , Science, 2019, 365, eaax1566 CrossRef CAS PubMed.
- H. Wang, T. Fu, Y. Du, W. Gao, K. Huang, Z. Liu, P. Chandak, S. Liu, P. Van Katwyk and A. Deac, et al. , Nature, 2023, 620, 47–60 CrossRef CAS PubMed.
- M. M. Bronstein, J. Bruna, T. Cohen and P. Veličković, arXiv, 2021, preprint, DOI:10.48550/arXiv.2104.13478.
- K. Atz, F. Grisoni and G. Schneider, Nat. Mach. Intell., 2021, 3, 1023–1032 CrossRef.
- C. Isert, K. Atz and G. Schneider, Curr. Opin. Struct. Biol., 2023, 79, 102548 CrossRef CAS PubMed.
- O. A. von Lilienfeld, K.-R. Müller and A. Tkatchenko, Nat. Rev. Chem., 2020, 4, 347–358 CrossRef PubMed.
- O. T. Unke, S. Chmiela, M. Gastegger, K. T. Schütt, H. E. Sauceda and K.-R. Müller, Nat. Commun., 2021, 12, 7273 CrossRef CAS PubMed.
- V. G. Satorras, E. Hoogeboom, F. B. Fuchs, I. Posner and M. Welling, Advances in Neural Information Processing Systems, 2021, 34, 4181–4192 Search PubMed.
- A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Nature, 2023, 624, 80–85 CrossRef CAS PubMed.
- C. Zeni, A. Anelli, A. Glielmo, S. de Gironcoli and K. Rossi, Digital Discovery, 2024, 3, 113–121 RSC.
- V. R. Somnath, C. Bunne, C. Coley, A. Krause and R. Barzilay, Adv. Neural. Inf. Process. Syst., 2021, 34, 9405–9415 Search PubMed.
- Y. Guan, C. W. Coley, H. Wu, D. Ranasinghe, E. Heid, T. J. Struble, L. Pattanaik, W. H. Green and K. F. Jensen, Chem. Sci., 2021, 12, 2198–2208 RSC.
- W. Jin, C. Coley, R. Barzilay and T. Jaakkola, Adv. Neural. Inf. Process. Syst., 2017, 30, 2607–2616 Search PubMed.
- T. Stuyver and C. W. Coley, J. Chem. Phys., 2022, 156, 084104 CrossRef CAS PubMed.
- C. Isert, K. Atz, J. Jiménez-Luna and G. Schneider, Sci. Data, 2022, 9, 273 CrossRef CAS PubMed.
- T. Stuyver and C. W. Coley, Chem. – Eur. J., 2023, 29, e202300387 CrossRef CAS PubMed.
- T. Stuyver, K. Jorner and C. W. Coley, Sci. Data, 2023, 10, 66 CrossRef CAS PubMed.
- R. M. Neeser, C. Isert, T. Stuyver, G. Schneider and C. W. Coley, Chem. Data Collect., 2023, 46, 101040 CrossRef CAS.
- D. F. Nippa, K. Atz, R. Hohler, A. T. Müller, A. Marx, C. Bartelmus, G. Wuitschik, I. Marzuoli, V. Jost and J. Wolfard, et al. , Nat. Chem., 2024, 16, 239–248 CrossRef CAS PubMed.
- E. Caldeweyher, M. Elkin, G. Gheibi, M. Johansson, C. Sköld, P.-O. Norrby and J. F. Hartwig, J. Am. Chem. Soc., 2023, 145, 17367–17376 CrossRef CAS PubMed.
- E. King-Smith, F. A. Faber, A. V. Sinitskiy, Q. Yang, B. Liu and D. Hyek, Nat. Commun., 2024, 15, 426 CrossRef CAS PubMed.
- D. F. Nippa, K. Atz, A. T. Müller, J. Wolfard, C. Isert, M. Binder, O. Scheidegger, D. B. Konrad, U. Grether and R. E. Martin, et al. , Commun. Chem., 2023, 6, 256 CrossRef CAS PubMed.
- M. Fitzner, G. Wuitschik, R. Koller, J.-M. Adam and T. Schindler, ACS Omega, 2023, 8, 3017–3025 CrossRef CAS PubMed.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed.
- M. Fey and J. E. Lenssen, International Conference on Learning Representations, 2019 Search PubMed.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein and L. Antiga, et al. , Adv. Neural. Inf. Process. Syst., 2019, 32, 8026–8037 Search PubMed.
- D. P. Kingma and J. Ba, arXiv, 2014, preprint, DOI:10.48550/arXiv.1412.6980.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser and I. Polosukhin, Adv. Neural. Inf. Process. Syst., 2017, 5998–6008 Search PubMed.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, International Conference on Machine Learning, 2017, 1263–1272 Search PubMed.
- M. Baek, F. DiMaio, I. Anishchenko, J. Dauparas, S. Ovchinnikov, G. R. Lee, J. Wang, Q. Cong, L. N. Kinch, R. D. Schaeffer, C. Millán, H. Park, C. Adams, C. R. Glassman, A. DeGiovanni, J. H. Pereira, A. V. Rodrigues, A. A. van Dijk, A. C. Ebrecht, D. J. Opperman, T. Sagmeister, C. Buhlheller, T. Pavkov-Keller, M. K. Rathinaswamy, U. Dalwadi, C. K. Yip, J. E. Burke, K. C. Garcia, N. V. Grishin, P. D. Adams, R. J. Read and D. Baker, Science, 2021, 373, 871–876 CrossRef CAS PubMed.
- K. Atz, C. Isert, M. N. Böcker, J. Jiménez-Luna and G. Schneider, Phys. Chem. Chem. Phys., 2022, 24, 10775–10783 RSC.
- T. Chen and C. Guestrin, International Conference on Knowledge Discovery and Data Mining, 2016, 785–794 Search PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |