Phase transitions in CsPbBr₃: evaluating perovskite behavior over different time scales

Abstract

Halide perovskites have gained relevance in the field of solar cells due to their remarkable electro-optical properties, which enable efficient conversion of solar energy into electricity. Despite their promising characteristics, challenges such as long-term stability and structural complexity demand exceptional attention and dedication in the research on these materials. Their inherent soft nature, high atom mobility (especially of the halides) and the unconventional dynamics of structural motifs (halide octahedra) make them interesting from a fundamental point of view as well. The study focuses on understanding phase transitions in CsPbBr₃ perovskite, considering the importance of the dynamic properties it exhibits. The phase transitions of the CsPbBr₃ perovskite were studied through ab initio NPT molecular dynamics simulations considering several different temperatures. By taking into account the average structures over a simulation time of 45 ps after thermalization, we predict phase transitions between 300 and 325 K, as well as between 400 and 450 K, in line with previous experimental findings reported in the literature. Furthermore, through the analysis of the angles within the octahedron (Br–Pb–Br) and between octahedra (Pb–Br–Pb), the mechanism underlying the phase transitions is understood, and the structural anomalies previously reported [Svirskas et al., J. Mater. Chem. A, 2020, 8, 14015–14022] near 220 K are identified. In addition to the results obtained by performing long-time averages, we also conducted an analysis of the implications of using different time windows when calculating the average properties of interest. In this case, we observed a more complex pattern, where the material exhibits various structures depending on the exposure time and temperature, which aligns with the polymorphic nature of these materials. Our results show that, depending on the type of experiment that is being performed, different analysis, with averages considered over different times, must be performed. Long-time averages can be compared to X-ray diffraction experiments, while short-time averages should be compared to experiments that track the local structure of the material, such as PDF or Raman. Our results also indicate that phase transitions in CsPbBr₃ are not as abrupt as previously considered, posing new challenges for the experimental observation of these features.

---

1 Introduction

Halide perovskites, with the general formula ABX₃, where X can be Cl, Br, or I, have gained prominence in the field of solar cells due to their remarkable electro-optical properties. Applied research on these materials has been extensive, driven by their highly efficient capability to convert solar energy into electricity.^1–5 Despite their promising characteristics, these compounds face significant challenges, especially concerning their long-term stability.

These materials are also well known for their relative soft nature, high mobility of their constituent atoms (mainly the halides) creating complex defects,⁶ and the unconventional dynamics of structural motifs (halide octahedra),⁷ which also contribute to the complexity of these materials. This kind of dynamics and the movement of the ions impact the durability and long-term performance of perovskite-based solar cells.

When analyzing perovskites, whether halides or oxides, structural complexity becomes evident when considering the predominant phase in relation to temperature. At low temperatures, these perovskites exhibit monoclinic, orthorhombic, or tetragonal structures, while at higher temperatures, they adopt a high-symmetry cubic structure (Pm3̄m).^8–14

Taking CsPbBr₃ as an example, there are two well accepted phase transitions. The first occurs at 403 K, marking the transition from a cubic phase to a tetragonal phase (P4/mbm). The second transition takes place at 361 K, transforming the perovskite from the tetragonal phase to the orthorhombic phase (Pmbn).¹³ In a temperature range spanning from 120 K to 450 K, Svirskas et al.¹⁴ conducted a comprehensive investigation into the phase transitions of perovskites, revealing a new anomaly in the dielectric data. This anomaly, confirmed through X-ray diffraction and electron paramagnetic resonance (EPR) studies, could be interpreted as a new phase transition. However, Raman scattering spectra did not indicate any anomalies in the lattice near 220 K.

At an experimental level, one of the most commonly used methods to determine the crystal structure (phase) of a system at different temperatures is X-ray spectroscopy. In this approach, a space-time average of the sample under analysis is performed, and the time required to obtain results is usually significant, typically ranging from minutes to hours of exposure. The standard protocol for such measurements often involves using simple monomorphic unit cells for making the necessary adjustments through Rietveld refinement. Some of the main controversies regarding the crystal structure of these materials comes from an interplay among the long measurement times of X-ray diffraction and the dynamic nature of the halide perovskites. This methodology tracks the average structure of these materials, that many times is not enough to completely describe their optic and electronic properties. The desire to get a minimal unit cell induces a fictitious role in obtaining material's properties.^15–18

In the same vein, but from a computational perspective, there have been proposals to use polymorphous structures to calculate the properties of halide perovskites.¹⁹ However, the most effective way to study dynamic properties involves incorporating finite temperatures into the description. At 0 K, where static properties are studied, the real behavior of the material is not fully captured. That's why in this work, ab initio molecular dynamics simulations (AIMD) were employed to interpret the effect of the soft behavior of CsPbBr₃ perovskite and obtain dynamic information about the system in calculating the possible competing phases that the system may exhibit as a function of temperature.

AIMD is a powerful computational technique employed in the simulation of atomic and molecular systems. Unlike DFT calculations at 0 K, which assume that atoms are in their ground state and lack thermal motion, AIMD takes into account the real dynamic and thermodynamic effects that occur at finite temperatures. This enables a more realistic and detailed study of the properties and behavior of molecular systems. The ability to simulate dynamic phenomena provides a more comprehensive understanding of the chemistry and physics of molecular systems.

The application of methodologies such as ab initio molecular dynamics in the field of perovskites is crucial for properly understanding the behavior of these materials. The soft nature of the lead-halide bonds and the lattice vibrations, demands a detailed approach that considers the dynamics of the movement of their components.

By incorporating the study of molecular dynamics of the octahedra that form perovskites, such as CsPbBr₃, it is possible to explain various structural and electronic properties of the material. Furthermore, this approach allows for understanding the phases that predominate based on temperature variations.

AIMD is presented as a particularly relevant simulation tool in this context. AIMD not only takes into account the structural flexibility of the material but also offers a precise description based on fundamental principles of its electronic structure. Thus, a more faithful and closer representation of the behavior of perovskites is achieved, facilitating the interpretation and prediction of their properties and responses under different conditions.

This methodology has been widely used in the study of perovskites.^20–23 These simulations have been employed to compare different functionals used in ab initio calculations,^24,25 examine the impact of cation mixing,²⁶ and understand local disorder and its influence on experimental observations.^27,28 Furthermore, molecular dynamics simulations have allowed for the tracking of the B–X–B angle,²⁶ analysis of X–B–X tilt angle distributions,^27,29 and investigation of halogen displacements.^24,29,30

With this in mind, ab initio NPT molecular dynamics simulations were conducted at different temperatures with the aim of investigating the phase diagram of CsPbBr₃. Our time-averaged results agree very well with other similar calculations and experimental results, indicating phase transition temperature and averaged properties. We also expand the understanding of the properties of these materials by proposing a novel approach to analyze the behavior of perovskites over time at each temperature and how to compare these results with experimental findings. The concept relies in the type of experiment that is being performed. If the comparison is done with experiments that demand long time exposures, such as X-ray diffraction, one need to calculate averages over long simulation times. However, if experiment tracks structures in shorter times, or instantaneous structures, such as in Raman spectroscopy,³¹ shorter time averages in AIMD simulations must be done. These shorter time averages lead to smoother phase transitions where more than one crystal structure coexist at a give temperature, changing the analysis of the phase diagram of halide perovskites.

2 Theoretical methods

Calculations were performed at the density functional theory (DFT) level³² and performed with the CP2K software,³³ the modified Perdew–Burke–Ernzerhof (PBEsol) exchange–correlation functional,³⁴ and with the standard Goedecker, Teter and Hutterv pseudopotentials.^35–37 Molecularly optimized basis functions DZVP³⁸ and a cutoff of 800 Ry/60 Ry for the finest grid/relative grid for Gaussian mapping were used. The CsPbBr₃ perovskite was simulated with a standard 4 × 4 × 4 supercell with 320 atoms.

Ab initio molecular dynamics were performed within a NPT ensemble, using a completely flexible cell, keeping both the pressure and temperature constants, with a time step of 1 fs. The use of the NPT ensemble is important to allow for the proper dynamics of the octahedra. Several temperature values between 150 and 500 K were considered and the target pressure was kept fixed at zero in all simulations. To make sure that the systems were thermally equilibrated, avoiding possible local minima trapping, two different types of simulations were performed at each temperature. The first type consisted of independent AIMD simulations, each performed at a specific temperature that was kept constant during the whole run, that lasted from 80–100 ps. The constant temperature method always started from a frozen 0 K system (cubic structure). The second type was a temperature ramp. In this case, a AIMD simulation was initiated at 600 K for 15 ps. Upon completing this simulation, the last obtained configuration was taken and used as a starting point for new simulations at lower temperatures, including 500 K, 450 K, and 400 K. Then, from the 400 K simulation, a configuration at approximately 30 ps was extracted and used as the starting point for simulations at 350 K, 325 K, 300 K, and 200 K. Continuing this process, from the 300 K simulation, additional configurations were taken at 12 ps to perform simulations at 275 K and 250 K. Finally, at 50 ps of the 200 K simulation, the configuration was captured and employed to conduct a simulation at 150 K. This strategy is illustrated in Fig. 1.

Fig. 1 Energy as a function of time for different simulation temperatures. The energy corresponds to the system's energy per unit cell, expressed in eV. (A) Energy from simulations using the temperature ramp methodology. (B) Energy from simulations using the constant temperature methodology.

The phonon studies were conducted using the TRAVIS software,³⁹ based on the trajectory obtained from AIMD simulations.

3 Results and discussion

We are initially interested in learning what is the most likely crystal structure of CsPbBr₃ at a given temperature. Looking at different temperatures one can gather information regarding the phase diagram of this material, including phase transition temperatures. To get this type of information, the standard approach is to calculate the average structure over the whole AIMD cycle after thermalization, that in our case lies around 45 ps. In the following we will provide this discussion (long-time averages) but will also provide some analysis of what happens when averages are considered in shorter time scales (from 2 ps to 20 ps). As shown below, results can be very different.

3.1 Long-time average

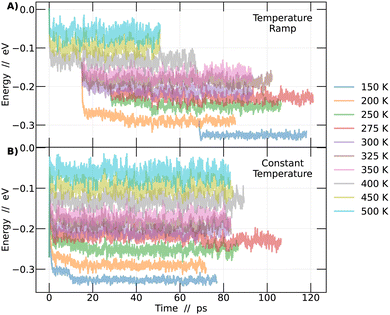
In order to investigate the phase transitions of the CsPbBr₃ perovskite, molecular dynamics simulations were conducted in an NPT ensemble, maintaining constant pressure to allow for system size flexibility. Two different methodologies were employed: constant temperature and temperature ramp. The aim was to support the findings of this study. Molecular dynamics simulations allow for the collection of the system's energy at each step of the simulation. Plotting this energy as a function of time enables the detection of the region where the system reaches a state of dynamic equilibrium. From this point onward, it becomes feasible to obtain reliable information about the system over time, as detailed in Fig. 1.

In Fig. 1A, simulations conducted using the temperature ramp methodology are presented, while in Fig. 1B, simulations conducted at a constant temperature are shown. With this information, the differences between the methodologies become clear. To improve the interpretation of the results in Fig. 1, a normalization of the curves was performed. This process involved subtracting from each point on the curves the energy value at time 0 of the simulation corresponding to the temperature of 500 K in the temperature ramp methodology. Different colors represent different temperatures.

The analysis described in the following were performed always considering the last 45 picoseconds of each simulation. The system is considered adequately converged in this time frame, ensuring that the results obtained are representative of the behavior of perovskites at each temperature studied.

In the previous discussion, we highlighted the importance of ensuring the accuracy of our simulations. The following delves into the analysis of the properties of perovskite that characterize the system and allow us to understand the mechanisms by which perovskite undergoes phase transitions as a function of temperature. First, we investigated the evolution of the lattice parameters in relation to temperature, which allowed us to identify the temperatures at which phase transitions occur, transitioning from an orthorhombic structure to a tetragonal structure and subsequently to a cubic structure as temperature increases.

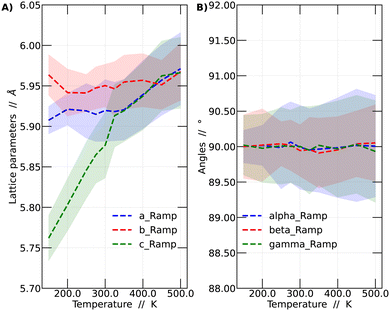
It was observed that the system's volume shows a significant dependence on temperature, as evidenced by variations in the crystal lattice parameters. A detailed analysis of these lattice parameter variations is presented in Fig. 2. The presented results correspond to the temperature ramp methodology.

Fig. 2 (A) Variation of the average lattice parameters (a, b and c) and (B) angles among lattice vectors (alpha, beta and gamma) as a function of temperature for CsPbBr₃. The standard deviation (STD) is depicted using a shaded region.

In Fig. 2A, the variations of the parameters a, b, and c, which monitor the size of the unit cell vectors, are presented. Meanwhile, Fig. 2B shows the temperature-dependent changes in the angles between these vectors. At low temperatures, the vector sizes are all different, indicative of the orthorhombic structure. As the temperature increases, vector c begins to approach the value of vector a. From 325 K onward, vectors a and c vary in a similar fashion but remain distinct from b. This temperature range corresponds to the tetragonal structure. This behavior continues up to 450 K, at which point all vectors possess the same size, resulting in a cubic structure representation. As mentioned before, all these values were obtained by averaging the lattice parameters over the last 45 ps of the simulations. Fig. 2B reports the variation of the angles among lattice vectors. These angles are always around 90 degrees, supporting the interpretation towards the observation of a cubic, tetragonal and orthorhombic lattices at different temperatures.

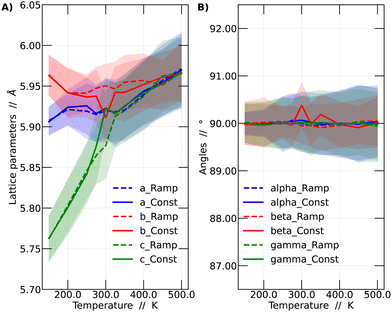
In this context, a comparison was made based on the network parameters of the two methodologies used (ramp and constant temperature). It was observed that both simulation strategies yielded very similar results. This finding suggests that the results presented in this work have adequately converged to dynamic equilibrium. The larger differences between the results of the two simulation strategies arise at intermediate temperatures, especially around 300 and 350 K. These intermediate temperatures are critical since it is in this range where the perovskite in question undergoes phase transitions. The comparison among the different strategies is shown in Fig. 3.

Fig. 3 Comparison between the average lattice parameters as a function of the temperature for the two main dynamics performed in the work: constant temperature and temperature ramp. The a, b and c parameters are shown in (A), while in (B) the alpha, beta and gamma angle is shown. The standard deviation (STD) is depicted using a shaded region.

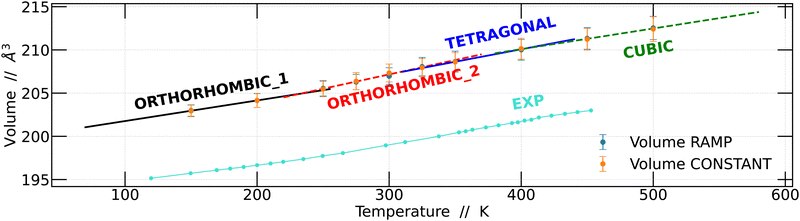
Based on these findings, we proceeded to calculate the unit cell volume from the 4 × 4 × 4 supercell as a function of temperature and compared it with the experimental data previously reported by Svirskas et al.¹⁴ The results obtained in this study show a notable similarity to the experimental data; however, it is worth noting that the volumes calculated in this work were slightly higher than the experimental values. This disparity is a well-recognized challenge that arises due to the choice of the exchange–correlation function in DFT calculations.^40,41 The results obtained for the two simulation strategies are presented in Fig. 4.

Fig. 4 The average volume of the CsPbBr₃ unit cell as a function of temperature, averaged over 45 ps for both temperature ramp and constant temperature. The lines indicate the linear expansion in each region, and structural changes as well as phase transitions can be identified at approximately 315, and 425 K. Furthermore, at 225 K, a change in the slope of the lines is observed, which is not considered a phase transition.

Linear regression analyses were conducted on the volumes obtained using the two strategies, as depicted in Fig. 4. These analyses encompassed all temperature intervals bounded by the structural changes observed. The results obtained are consistent with the previously obtained results.¹⁴ Although the slopes of the regression lines are quite similar, distinctions become apparent for each of the structural changes, whether they are phase transitions or not.

As mentioned earlier, distortions in perovskites play a critical role in both their high photovoltaic performance and stability at different temperatures. In addition to these consequences, tracking these distortions as temperature changes allows us to elucidate mechanisms in the phase transitions studied in perovskite materials.

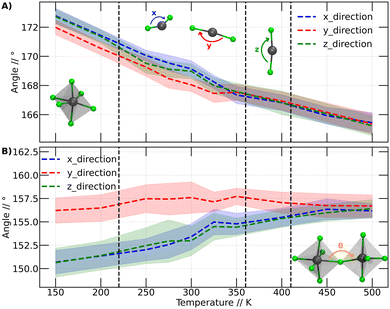
In this context, we have analyzed the behavior of PbBr₆ octahedra in terms of the Br–Pb–Br and Pb–Br–Pb angles. These angles have shown to be important descriptors in halide perovskites.^42,43 The first angles are related to the behavior of the octahedra individually in the three Cartesian directions. In the second analysis (Pb–Br–Pb angle), we assessed the influence of neighboring octahedra. This analysis was conducted over the range of temperatures at which our simulations were performed. Fig. 5A illustrates the variation of the Br–Pb–Br while Fig. 5B displays the variation of the Pb–Br–Pb angle as a function of temperature.

Fig. 5 Representative internal angles as a function of temperature for CsPbBr₃ perovskites. (A) Br–Pb–Br angles, the inset shows one of the octahedrons that make up the CspbBr₃ perovskite. In addition, the 3 directions analyzed in this study stand out, where the colors are related to the graphic lines. (B) Pb–Br–Pb Angles, the inset shows two octahedra and the angle between them. The dashed lines indicate the temperatures at which the phase transitions and anomaly occur at 220 K, as reported by Svirskas et al.

The Br–Pb–Br angles were calculated for each octahedron, distinguishing their behavior in the three dimensions through calculations in the Cartesian coordinates x, y and z. The graphs in Fig. 5A display the angles in the x direction, y direction and z direction, corresponding to the Br–Pb–Br angles in the x, y, and z directions, respectively. Fig. 5A presents the calculated average of the Br–Pb–Br angle for all octahedra at each temperature.

Fig. 5A shows that the Br–Pb–Br angle decreases as the temperature increases. This angle is closely linked to the displacement of the Pb atom out of the center of the octahedron. Wider angles indicate that the Pb atom is further away from the center of the octahedron. At lower temperatures, it is observed that in two directions the angles are comparable, while the angle in the y-direction is smaller. However, above 200 K, a slight change in arrangement is noticeable, evidenced by the divergence of the three angles. We plot a dashed line at this position to make this point clearer. Although these values are within the standard deviation bars, it is important to note that around this temperature, Svirskas et al. identified an anomaly in dielectric data, as well as in X-ray diffraction and electron paramagnetic resonance (EPR) studies. These phenomena were interpreted as a distortion in the perovskite structure, although it is not considered a phase change.¹⁴ Our results support these observations, as a change in the dynamics of angles in different directions could be sufficient to induce alterations in dielectric constants. Indeed, our findings provide a clear structural interpretation for the distortion at 220 K proposed by Svirskas and colleagues.¹⁴ This phenomenon is also visualized in Fig. 4, where, at that temperature, a change in the slope of the points is observed, marked as the transition from orthorhombic_1 to orthorhombic_2.

At temperatures above 350 K, it becomes evident that the Br–Pb–Br angles in the three Cartesian directions converge towards a specific value. As the temperature increases, these angles consistently continue to decrease. This phenomenon coincides with the phase transition from orthorhombic to tetragonal, closely resembling the reported experimental transition temperature (the black line at 360 K corresponds to the orthorhombic to tetragonal phase transition).¹⁴ Thus, we can observe that the behavior of the Br–Pb–Br angles is directly linked to the orthorhombic to tetragonal phase transition. However, when examining the temperature range where the second phase transition occurs, from tetragonal to cubic, no modification in the trend of angles is detected. Therefore, it can be stated that the behavior of these angles does not have a close relationship with this higher temperature phase change.

In Fig. 5B, noticeable differences can be observed in the angle in the y-direction compared to the other two Cartesian directions. The angles in the y-direction show minimal variations at all temperatures, averaging around 156 degrees, while in the other two directions, the distortion gradually decreases, approaching the values observed in the y-direction.

Similar to Fig. 5A, a subtle differentiation between angles in the x and z directions is observed between 200 and 250 K. This implies that the conformational change discussed for the Br–Pb–B angle is also reflected in the Pb–Br–Pb angle. However, unlike the Br–Pb–Br angle, this angle does not elucidate the phase transition from orthorhombic to tetragonal, as no significant variation in the Pb–Br–Pb angle is noted. Nevertheless, this angle plays a crucial role in studying the transition between tetragonal and cubic phases. Between 400 and 450 K, the Pb–Br–Pb angles in all three directions converge at approximately 156 degrees, maintaining this value at higher temperatures.

Based on the analysis presented in Fig. 5, it can be inferred that the phase transitions are intricately linked to the behavior of the octahedra constituting the perovskite structure. This association becomes evident when focusing on an individual octahedron or considering its interactions with neighboring units.

Based on the trajectories obtained from AIMD simulations, we conducted a vibrational analysis as a function of temperature. At this point, we calculated the phonon density spectrum for the entire perovskite as well as the contributions from each of its constituent elements. This approach allows us to observe the impact of atomic vibrations on the system's behavior at different temperatures and their effect on the phase transitions that the system undergoes. This study is presented in Fig. S3 (ESI†).

3.2 Making short-time averages

Up to this point, the reported results were based on averages calculated over our whole AIMD calculations (45 ps). These results are comparable to experiments like X-ray diffraction, that track long-time and space averages of the samples. However, when employing experimental methodologies that do not track the average structure or that involves shorter exposure times, a different computational strategy is needed. As will be evident below, the results obtained for CsPbBr₃ exhibit a high sensitivity to the way in which such averages are taken.

To visualize this phenomenon, lets consider the time evolution of the lattice parameters (a, b, c) as shown in Fig. S1 (ESI†) for T = 150 K. Each lattice parameter is shown in a different color. The lighter colors indicate the AIMD results for the whole simulation (45 ps). The dashed lines indicate the average values considering time windows of 1000 fs. This is performed for the whole simulation. The shaded area indicates the standard deviation for the averages. The important point here is that we have to determine a time window to calculate these averages.

With the aim of investigating the impact of exposure time on the calculation of system properties, the protocol detailed in Fig. S1 (ESI†) was implemented using different window sizes for all temperatures analyzed. As an example, Fig. S2 (ESI†) shows the values of the lattice parameters a, b, and c as a function of temperature using windows of 5000 fs.

In Fig. S2 (ESI†), a significant difference in the sizes of the lattice vectors is highlighted at low temperatures (150 K) throughout the entire simulated period. However, as the temperature increases, a convergence in these sizes is observed. This phenomenon had already been identified in the previous analysis in the section earlier in this work. Fig. S2 (ESI†) explores this trend in relation to temperature, incorporating the study of the mobility of the octahedra that make up the perovskite structure.⁷ This mobility introduces subtle fluctuations in the lattice parameters, resulting in variations in the number of identical vectors over time at certain temperatures. These variations, in turn, influence the phase exhibited by the system. For example, between 200 K and 300 K, in certain temporal regions, the system presents 2 similar vectors or none at all. In contrast, at 325 K, regions with 3 identical vectors, two similar vectors, and even none are observed. As the temperature continues to increase, regions with 3 identical vectors become increasingly predominant.

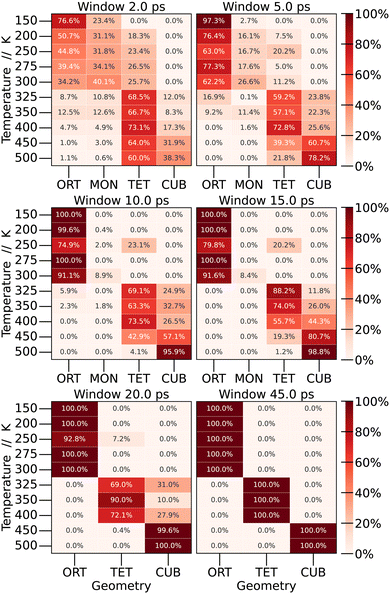
By examining the average values of the parameters within each window, it becomes possible to quantify the frequency of finding each crystal structure (phase) as a function of the time window for calculating the time averages. The results are depicted in Fig. 6.

Fig. 6 Quantification of windows with the same geometry as a function of temperature. Light colors represent percentage values close to zero, while the color darkens as the percentage increases. The values are expressed in percentages.

To start the analysis of the phase dependence at each temperature as a function of window size, the longest window time was examined, corresponding to the time used in the preceding section (45 ps). As expected, abrupt transitions are observed as the temperature increases: at low temperatures the structure exhibits an orthorhombic shape, undergoing the first phase transition in the range of 300 to 325 K, at which point the structure adopts a tetragonal configuration. In the interval from 400 to 450 K, another phase transition occurs, resulting in a cubic structure.

When we perform shorter-time averages, however, we observe a large distribution of different structures through the simulation. For low temperatures, even the monoclinic structure was observed. Depending on the window size, we observe a distribution of probabilities for each structure at each temperature. For 150 K, CsPbBr₃ present the orthorhombic structure 76.6% of the time, and the monoclinic structure 23.4% of the time. As we increase the window size, the percentage of the monoclinic structure decreases until it becomes only orthorhombic. A similar behaviour is observed for other temperatures. This leads to the conclusion that phase transitions are not as sharp as expected, and the crystal structure of the material at a specific temperature should be defined by a linear combination of different crystal structures.

To our knowledge, this kind of analysis is new for halide perovskites and, as discussed below, it has important consequences towards the experimental evaluation of the properties of these materials.

This behavior is not only evident in CsPbBr₃ perovskites, as explored in our study, but also in other perovskites such as FAPbI₃ or MAPbI₃, as reported in the work of Carignano et al.²⁹ They evaluated the temporal evolution of lattice parameters, revealing similarities with the patterns observed in our research.

3.3 Competition among long and short time averages

The analysis provided above clearly shows that running long-time averages and short-time averages changes the conclusions about the structure of halide perovskites at different temperatures, as well as the phase transitions they undergo. A straightforward question should be: which one is correct? The best answer is: both are correct.

As light can exhibit a dual character, both wave-like and particle-like, depending on the experiment conducted, here we have a similar behavior. Perovskites, depending on how an experimental measurement is carried out, should exhibit different behaviors.

The long-time averages, as discussed before, can be directly compared to X-ray diffraction analysis. This kind of analysis is used to provide structural properties such as lattice parameters and atomic positions. These experiments take a long time to be performed, and maps large areas of the sample. The final result is that the atomic positions and lattice parameters are an average of the actual experimental values. This is why the high-symmetry Pm3̄m phase is observed for CsPbBr₃ at high temperatures. However, if one uses these atomic positions for making ab initio calculations, the final calculated properties such as band gaps, segregation energies⁴⁴ and even phonon spectra will be incorrect. Polymorphous structures¹⁹ have been proposed to solve this kind of problem by keeping the cubic lattice vectors but using distorted octahedra to simulate these materials.

The results obtained with short-time averages demand different types of experiments, preferably those that depend on symmetry and that get local properties. This is the case of Raman spectroscopy, that tracks vibrational modes that intrinsically depend on the symmetry of the material. Previous results have reported unexpected vibrational modes in nominally cubic materials. The spectra would not fit the expected peaks of the cubic structure because of the lower symmetry of the material. This kind of methodology was already used to track local polar fluctuations in halide perovskites³¹ and subtle symmetry breaking in EuB₆.⁴⁵

Other powerful technique to track the local structure of a material is the pair distribution function (PDF). This methodology has been used to study MAPbI₃.⁴⁶ The measured PDF for the high symmetry phase (cubic) would not fit the theoretical PDF obtained in a high-symmetry structure. Lower symmetry configurations, in the format of a double well structure, were proposed to explain the results.

The challenge posed here is related to how one could design experiments that would be able to track and differentiate the results shown in Fig. 6. In principle, differential X-ray diffraction or some kind of femtosecond spectroscopy would be good candidates, although this is still to be reported in more detail.

4 Conclusions

Ab initio molecular dynamics calculations were used to evaluate the phase diagram of CsPbBr₃ at different temperatures. We were able to track the time evolution of the structure of this material including volume, lattice parameters, angles among lattice vectors and information regarding different angles among different octahedra and inside octahedra. The predicted structure average over longer 45 ps time range agrees very well with experimental data. We were able to track two very clear phase transitions: the first, around 300 and 325 K, among the orthorhombic and tetragonal structures; the other between 400 and 450 K from the tetragonal towards the cubic one.

Besides these very clear phase transitions, we also obtained some hints regarding a possible phase transition around 220 K, that has been reported by verifying changes in the dielectric constant around this temperature.¹⁴ We observe a change in the angles between different octahedra: for temperatures lower than 220 K we observe that the angles in two directions (x and z) are similar, and start to differ for larger temperatures. Even though we can not classify this exactly as a phase transition, our results can help explain the unusual patterns in the dielectric constant at this temperature.

Besides the results obtained by performing long-time averages, we also made some analysis by decreasing the size of the windows for taking these averages. In this case, we observe a more complex pattern for the structure, where the material change the most stable structure over time for a specific temperature. This result indicate that the phase transitions are not as abrupt as considered before. We discuss that, depending on the type of experiment that is performed, one will obtain results that can be compared to both methodologies: long-time averages and sort-time averages. Designing experiments that can track the results obtained in our short-time average analysis represents a challenge for fully understanding these materials.

Author contributions

L. M. F., F. N. R. and G. M. D. formulated the problem and planned the ab initio calculations. L. M. F. y F. N. R. performed AIMD simulations. L. M. F., F. N. R. and G. M. D. analysed the simulated data. L. M. F. and G. M. D. wrote the manuscript, and all authors commented on it.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been performed within the scope and with funding from the Materials Informatics INCT (National Institute of Science and Technology), CNPq, Brazil. Funding from FAPESP (grant 21/14422-0) is also acknowledged. Computer simulations were performed at the Santos Dumont supercomputer at LNCC, Brazil and CCAD – Universidad Nacional de Córdoba (https://ccad.unc.edu.ar/) at SNCAD – MinCyT, República Argentina. We thank Fernando Pereira Sabino for fruitful discussions on this subject.

Notes and references

1. J. Y. Kim, J.-W. Lee, H. S. Jung, H. Shin and N.-G. Park, Chem. Rev., 2020, 120, 7867–7918.
2. A. K. Jena, A. Kulkarni and T. Miyasaka, Chem. Rev., 2019, 119, 3036–3103.
3. Y. Rong, Y. Hu, A. Mei, H. Tan, M. I. Saidaminov, S. I. Seok, M. D. McGehee, E. H. Sargent and H. Han, Science, 2018, 361, 8235.
4. N.-G. Park, Trans. Electr. Electron. Mater., 2020, 21, 1–15.
5. R. Szostak, A. de Souza Gonçalves, J. N. de Freitas, P. E. Marchezi, F. L. de Araújo, H. C. N. Tolentino, M. F. Toney, F. das Chagas Marques and A. F. Nogueira, Chem. Rev., 2023, 123, 3160–3236.
6. F. P. Sabino, G. M. Dalpian and A. Zunger, Adv. Energy Mater., 2023, 13, 2301539.
7. W. J. Baldwin, X. Liang, J. Klarbring, M. Dubajic, D. Dell’Angelo, C. Sutton, C. Caddeo, S. D. Stranks, A. Mattoni, A. Walsh and G. Csányi, Small, 2024, 20, 2303565.
8. Z. Cheng and J. Lin, CrystEngComm, 2010, 12, 2646–2662.
9. L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Krieg, R. Caputo, C. H. Hendon, R. X. Yang, A. Walsh and M. V. Kovalenko, Nano Lett., 2015, 15, 3692–3696.
10. X. Li, Y. Wu, S. Zhang, B. Cai, Y. Gu, J. Song and H. Zeng, Adv. Funct. Mater., 2016, 26, 2435–2445.
11. F. Palazon, C. Urso, L. De Trizio, Q. Akkerman, S. Marras, F. Locardi, I. Nelli, M. Ferretti, M. Prato and L. Manna, ACS Energy Lett., 2017, 2, 2445–2448.
12. A. Swarnkar, R. Chulliyil, V. K. Ravi, M. Irfanullah, A. Chowdhury and A. Nag, Angew. Chem., 2015, 127, 15644–15648.
13. S. Hirotsu, J. Harada, M. Iizumi and K. Gesi, J. Phys. Soc. Jpn., 1974, 37, 1393–1398.
14. Š. Svirskas, S. Balčiūnas, M. Šimėnas, G. Usevičius, M. Kinka, M. Velička, D. Kubicki, M. E. Castillo, A. Karabanov and V. V. Shvartsman, et al., J. Mater. Chem. A, 2020, 8, 14015–14022.
15. G. Laurita, D. H. Fabini, C. C. Stoumpos, M. G. Kanatzidis and R. Seshadri, Chem. Sci., 2017, 8, 5628–5635.
16. C. Quarti, E. Mosconi, J. M. Ball, V. D'Innocenzo, C. Tao, S. Pathak, H. J. Snaith, A. Petrozza and F. De Angelis, Energy Environ. Sci., 2016, 9, 155–163.
17. M. Houari, B. Bouadjemi, S. Haid, M. Matougui, T. Lantri, Z. Aziz, S. Bentata and B. Bouhafs, Indian J. Phys., 2020, 94, 455–467.
18. Y. Kang and S. Han, Phys. Rev. Appl., 2018, 10, 044013.
19. X.-G. Zhao, G. M. Dalpian, Z. Wang and A. Zunger, Phys. Rev. B, 2020, 101, 155137.
20. J. Wu, J. Yang, Y.-J. Liu, D. Zhang, Y. Yang, Y. Zhang, L. Zhang and S. Liu, Phys. Rev. B, 2023, 108, L180104.
21. X. Ouyang, W. Chen, Y. Zhang, F. Zhang, Y. Zhuang, X. Jie, L. Liu and D. Wang, Phys. Rev. B, 2023, 108, L020103.
22. C.-X. Cui and J.-W. Jiang, J. Phys. Chem. C, 2023, 127, 11760–11766.
23. H.-C. Thong, X. Wang, J. Han, L. Zhang, B. Li, K. Wang and B. Xu, Phys. Rev. B, 2023, 107, 014101.
24. W. Kaiser, M. Carignano, A. A. Alothman, E. Mosconi, A. Kachmar, W. A. Goddard III and F. De Angelis, J. Phys. Chem. Lett., 2021, 12, 11886–11893.
25. E. Fransson, J. Wiktor and P. Erhart, J. Phys. Chem. C, 2023, 127, 13773–13781.
26. D. Ghosh, P. Walsh Atkins, M. S. Islam, A. B. Walker and C. Eames, ACS Energy Lett., 2017, 2, 2424–2429.
27. O. Cannelli, J. Wiktor, N. Colonna, L. Leroy, M. Puppin, C. Bacellar, I. Sadykov, F. Krieg, G. Smolentsev and M. V. Kovalenko, et al., J. Phys. Chem. Lett., 2022, 13, 3382–3391.
28. E. Fransson, P. Rosander, F. Eriksson, J. M. Rahm, T. Tadano and P. Erhart, Commun. Phys., 2023, 6, 173.
29. M. A. Carignano, S. A. Aravindh, I. S. Roqan, J. Even and C. Katan, J. Phys. Chem. C, 2017, 121, 20729–20738.
30. X. Liang, J. Klarbring, W. J. Baldwin, Z. Li, G. Csányi and A. Walsh, J. Phys. Chem. C, 2023, 127, 19141–19151.
31. O. Yaffe, Y. Guo, L. Z. Tan, D. A. Egger, T. Hull, C. C. Stoumpos, F. Zheng, T. F. Heinz, L. Kronik, M. G. Kanatzidis, J. S. Owen, A. M. Rappe, M. A. Pimenta and L. E. Brus, Phys. Rev. Lett., 2017, 118, 136001.
32. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864.
33. J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25.
34. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
35. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703.
36. C. Hartwigsen, S. Gœdecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641.
37. M. Krack, Theor. Chem. Acc., 2005, 114, 145–152.
38. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105.
39. M. Brehm, M. Thomas, S. Gehrke and B. Kirchner, J. Chem. Phys., 2020, 152(16), 164105.
40. S. F. Yuk, K. C. Pitike, S. M. Nakhmanson, M. Eisenbach, Y. W. Li and V. R. Cooper, Sci. Rep., 2017, 7, 43482.
41. A. Paul, J. Sun, J. P. Perdew and U. V. Waghmare, Phys. Rev. B, 2017, 95, 054111.
42. M. R. Filip, G. E. Eperon, H. J. Snaith and F. Giustino, Nat. Commun., 2014, 5, 5757.
43. M. K. Jana, R. Song, Y. Xie, R. Zhao, P. C. Sercel, V. Blum and D. B. Mitzi, Nat. Commun., 2021, 12, 4982.
44. G. M. Dalpian, X.-G. Zhao, L. Kazmerski and A. Zunger, Chem. Mater., 2019, 31, 2497–2506.
45. H. Martinho, C. Rettori, G. M. Dalpian, J. L. F. da Silva, Z. Fisk and S. B. Oseroff, J. Phys.: Condens. Matter, 2009, 21, 456007.
46. A. N. Beecher, O. E. Semonin, J. M. Skelton, J. M. Frost, M. W. Terban, H. Zhai, A. Alatas, J. S. Owen, A. Walsh and S. J. Billinge, ACS Energy Lett., 2016, 1, 880–887.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00216d

---