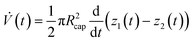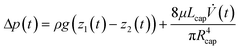DOI:
10.1039/D4LC00178H
(Paper)
Lab Chip, 2024,
24, 2893-2905
Chip-integrated non-mechanical microfluidic pump driven by electrowetting on dielectrics†
Received
25th February 2024
, Accepted 15th April 2024
First published on 24th April 2024
Abstract
A microfluidic pump is presented that generates its pumping action via the EWOD (electrowetting-on-dielectric) effect. The flow is generated by the periodic movement of liquid–vapor interfaces in a large number (≈106) of microcavities resulting in a volume change of approx. 0.5 pl per cavity per pump stroke. The total flow resulting from all microcavities adds up to a few hundred nanolitres per cycle. Passive, topologically optimized, non-mechanical Tesla valves are used to rectify the flow. As a result, the micropump operates without any moving components. The dimensioning, fabrication, and characterization process of the micropump are described. Device fabrication is done using conventional manufacturing processes from microsystems technology, enabling cost-effective mass production on wafer-level without additional assembly steps like piezo chip-level bonding, etc. This allows for direct integration into wafer-based microfluidic or lab-on-a-chip applications. Furthermore, first measurement results obtained with prototypes of the micropump are presented. The voltage- and frequency-dependent pump performance is determined. The measurements show that a continuous flow rate larger than 0.2 ml min−1 can be achieved at a maximum pump pressure larger than 12 mbar.
1 Introduction
Micropumps are vital core components in a wide range of microfluidic systems. Numerous options for realizing micropumps have already been documented and explored in the literature. Comprehensive overviews of common pumping concepts, including a discussion of the advantages and disadvantages of each pumping principle, have been provided by Nguyen,1 Laser and Santiago,2 Woias,3 or Amirouche and Zhou,4 for example. In general, micropumps can be categorized into mechanical and non-mechanical variants. In mechanical pumps, the driving force is generated by the actuation of moving components. Advantages include the ability to achieve high flow rates and pump pressures, as well as the capability to pump gases. The most prevalent type of mechanical micropumps are diaphragm pumps, whereby the periodic deflection of the diaphragm in the pump chamber generates the volume stroke. Various methods can be employed to actuate the diaphragm. For example, electrostatic,5,6 magnetostatic,7 thermopneumatic,8,9 and piezoelectric10,11 diaphragm pumps have been developed. The drawback of mechanical micropumps is that they are typically more difficult to manufacture due to the moving components. For example, the diaphragm pump developed by Meng et al.12 requires the structuring and assembly of a total of three silicon wafers. When piezo actuators are used for actuation, the integration of the actuator into the system is challenging and usually requires serial processes. For example, in the micropump presented by Linnemann et al.,13 the piezo actuators are glued manually to the backside of the diaphragm. While a diverse range of mechanical micropumps is already commercially available, non-mechanical pumps are still relatively uncommon. Due to the absence of moving parts, the manufacturing process is typically much simpler compared to mechanical pumps. However, this advantage is often offset by complicated filling mechanisms or the inability to achieve continuous flow rates. To achieve non-mechanical pumping, hydrostatic,14 electrochemical,15 magnetohydrodynamic,16 electrohydrodynamic,17,18 or capillary19 forces can be utilized. Here, a different approach is presented, based on the utilization of the electrowetting on dielectrics (EWOD) effect. EWOD is a widely used technique for manipulating liquids and soft matter at the microscale.20–22 The electrowetting effect, in general, describes the contact-angle change upon applying an electrical voltage.23–25 An EWOD-driven pump was previously presented by Tang.26 It uses the periodic electrowetting/deelectrowetting on the surface of liquid metals to generate the pumping effect.
A relatively good efficiency and a high maximum achievable flow rate are offset by the disadvantages of a challenging filling process, a nonlinear system behavior, and the limitation that the pump principle only works for liquids with a pH value greater than 6.5. A quite different, easy to fabricate and easy to operate approach is demonstrated here. The basic principle is illustrated in Fig. 1(a). The flow in the pump chamber is caused by the periodic movement of the liquid to be pumped in a large number of microcavities. The micropump is manufactured entirely in silicon, enabling well-established manufacturing processes from microsystems technology to be used. The surface of the microcavities is hydrophobized, preventing the liquid from entering the cavities (i.e., the liquid is in the Cassie–Baxter state27).
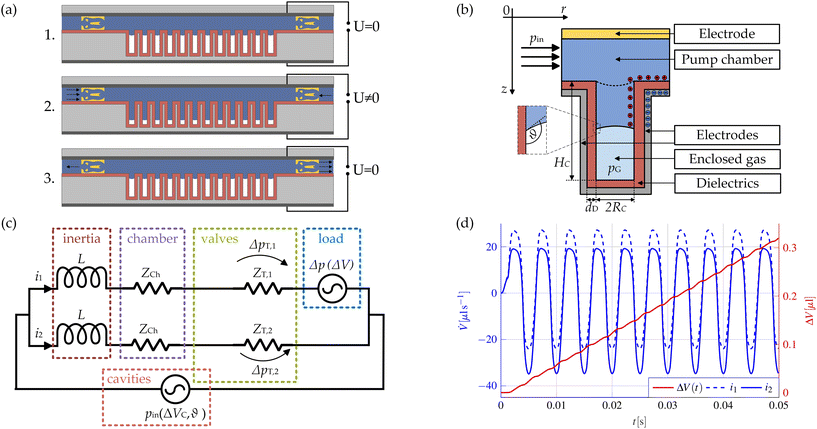 |
| | Fig. 1 (a) Schematic representation of the pump principle. The Tesla valves are shown in yellow, the intermediate dielectric layer in red, the substrates in light gray, and the electrodes in dark gray. From top to bottom: 1. Initial state of the liquid in the pump chamber. The cavities are filled with air, i.e. the liquid is in the Cassie–Baxter state. 2. When a voltage is applied, the liquid partially moves into the microcavities and compresses the enclosed air. Due to the different flow resistances of the Tesla valves, more liquid flows into the chamber from the left than from the right. 3. After switching off the voltage, the initial state is restored: the trapped gas relaxes and the liquid is displaced from the microcavities. Now, due to the different flow resistances of the Tesla valves, more liquid is expelled to the right than to the left. (b) Detailed illustration of a single microcavity. The initial state of the liquid–vapor interface is marked as dashed lines. (c) Fluidic equivalent circuit diagram which is used for modeling the overall pump system. (d) Simulated progression of the two flow rates i1 and i2 and the resulting net pumped volume ΔV(t) over a time interval of 0.05 s. A sinusoidal voltage with a frequency of f0 = 100 Hz and an amplitude of U0 = 100 V is used for actuation. Due to the quadratic dependence of the contact angle on the applied voltage according to eqn (1), the interface oscillates at twice the actuation frequency. | |
By applying a voltage between the liquid and the surrounding electrodes, the wetting properties can be periodically manipulated using EWOD, causing the liquid to move partially into the microcavities while simultaneously compressing the trapped air.28 When the voltage is switched off again, the air relaxes and the initial state is restored, thus the liquid is displaced from the microcavities. This means that a periodic volume stroke can be generated using an alternating voltage for the actuation. The rectification of this volume stroke is achieved using passive non-mechanical Tesla valves. As a result, no moving parts at all are required for the pump to work. An almost continuous flow rate can be achieved with this pump principle. The pump can be integrated directly into lab-on-a-chip applications or used as a standalone component. Customization to specific target applications is possible by adapting a wide range of parameters, achieving a high degree of flexibility.
The paper is structured as follows. Section 2 first discusses the theoretical foundations of the presented pump principle. In subsection 2.1, a method for efficient modeling of the complete pump system is presented. The method allows the direct determination of relevant characteristics, such as the flow rate-dependent pump pressure, and enables the evaluation of the influence of different geometric and actuation parameters. In subsection 2.2, the application potential, but also the limitations of the presented pumping principle are discussed. The manufacturing process is described in detail in the next section 3. Subsequently, the characterization of the main components, i.e., the Tesla valves and the microcavities, is discussed in subsections 4.1 and 4.2, and the characterization of the overall system in subsection 4.3. In each case, relevant measurement results are presented. Finally, the results are summarized, and possible further research paths are outlined in section 5.
2 Fundamentals
2.1 Fluidic equivalent circuit diagram
In the following, we present an efficient method for modeling the micropump system. The equations introduced hereinafter represent only a simplified version of the modeling but are sufficient to understand the ideas. Further details of the modeling, as well as methods for considering the phenomenon of contact angle saturation and the complex wetting behavior close to the edges of the microcavities, are presented in the ESI.† In any case, modeling the entire micropump is a challenge as the large number of microcavities of approx. 106 prevents direct numerical treatment. Even though a detailed simulation of EWOD micropumps is possible using numerical methods as described by Bohm et al.,29 a phenomenological approach is presented here. For this, the main components of the micropump, the Tesla valves and the microcavities, are considered separately. The simulation of the overall system is then carried out using a simplified fluidic equivalent circuit diagram. Modeling the interfacial motion in the microcavities is complicated as it involves the description of a multiphase flow coupled with electrodynamics. A detailed description of this problem and an efficient solution algorithm for such problems were given by Bohm and Runge.30 A simplified description of the movement of the liquid–air interface as introduced by Matsumoto and Colgate31 is chosen here. Each microcavity is modeled as a cylinder with a radius RC and a length HC. It is assumed that the voltage-dependent contact angle θ follows the well-known Young–Lippmann equation:23,25| | 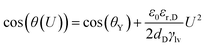 | (1) |
where dD denotes the thickness of the dielectric layer, γlv is the interfacial tension between the liquid and the air inside the microcavities, U is the applied voltage, θY is the Young angle, i.e., the equilibrium contact angle at the triple-phase contact line, ε0 is the vacuum permittivity, and εr,D is the relative permittivity of the dielectric layer. When a voltage is applied between the liquid and the surrounding electrodes, the contact angle decreases according to eqn (1). The decrease in the contact angle leads to a decrease in interface curvature and, as a result, to a change in the Laplace pressure. The resulting pressure gradient drives a flow inside the microcavity. During this movement, the enclosed gas is compressed. The movement of the interface stops when the Laplace pressure pL is equal to the difference of the vapor pressure pG of the enclosed gas minus the applied overpressure at the cavity inlet p0, which results in the equilibrium condition:Assuming that the enclosed gas can be described as an ideal gas, the following applies:| | 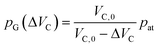 | (3) |
where pat denotes the pressure within an empty cavity which is typically identical to p0, VC,0 is the volume of an empty cavity, and ΔVC describes the volume change of the liquid inside of one single cavity. For a cylindrical cavity with radius RC or a cavity with a square cross-section and side length SC = 2RC, the Laplace pressure is given by:32| | 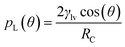 | (4) |
whereby it is assumed that the contact angle is identical on all wetted surfaces and that the actual contact angle is solely determined by the value of the applied voltage, i.e., θ = θ(U). Thus, the Laplace pressure becomes voltage-dependent. In order to consider non-circular cavities, it is useful to introduce the hydraulic diameter DH = 4A/P, where A is the cross-sectional area, and P is the wetted circumference of the cavity.33 So far, the equations have been derived by considering the steady state. If the interface is not in equilibrium, i.e., eqn (2) is not fulfilled, this results in a pressure difference pin at the inlet of the microcavities that drives the flow. However, the equations can also be applied to the description of the time-dependent movement of the liquid–air interface in the microcavities, since the inertia of the liquid within a microcavity is negligible compared to the overall inertia of the liquid inside the pump chamber. Thus, it is a valid assumption that the deformation of the interface follows the external applied voltage instantaneously and can be regarded as quasi-static. This assumption is at least valid for actuation frequencies smaller than 500 Hz and thus, for the experiments presented below. For very high actuation frequencies, however, the time-dependent deformation of the interfaces in the microcavities would have to be considered in order to model the system correctly. This would only be relevant for cases where the inertia of the liquid in the chamber is negligibly small. In the pump system considered here, the pumping effect decreases sharply at higher actuation frequencies, as the inertia of the liquid in the chamber dominates. In addition, the compression of the gas is regarded as isothermal, as the thermal diffusion time with τtherm ≈ S2C/αtherm ≈ 1 μs…5 μs is at least two orders of magnitude smaller than the duration of a single period T = 1/f0 ≫ 1 ms, where αtherm ≈ 22 mm2 s−1 denotes the thermal diffusivity of the enclosed air.34 Typically, the flow within a cavity can be considered to be laminar and dominated by viscous effects as the Reynolds number Re ≈ ρΔVC,maxf0DH/(μA) is typically less than 0.01, where ΔVC,max ≈ 0.5 pl denotes the maximum volume change inside a single cavity, ρ ≈ 1000 kg m−3 is the density of the liquid, A is the cross-sectional area of the cavity and μ ≈ 1 mPa s is the dynamic viscosity of the liquid. Entrance effects inside the cavities can be neglected, as the entrance length of order LE ≈ 0.06ReDH ≈ 1 nm is negligibly small compared to the deflection of the liquid column inside of the cavity. Furthermore, unsteady flow effects can be neglected, since the viscous time scale τunsteady ≈ S2Cρ/μ ≈ 10 μs…50 μs is, similar to the thermal diffusion time τtherm, negligibly small compared to the period duration T. Under the assumptions made, the inlet pressure pin can be calculated by:| | | pin(ΔVC, θ) = pL,0 − pL(θ) + pG(ΔVC) − p0 | (5) |
The pressure driving the flow at the inlet of the microcavities is therefore determined by the applied voltage, but also by the volume change inside the pump chamber. In the following, it is assumed that a sinusoidal voltage U(t) = U0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin (2πf0t) is used for actuation. Each side of the pump is described as a series connection consisting of a non-linear current-, i.e. flow rate-dependent resistor describing the Tesla valve, a linear resistor ZCh modeling the pump chamber, and an inductance L describing the inertia of the liquid. The resulting equivalent circuit diagram is shown in Fig. 1(c). To determine the parameters ZCh and L, a time-dependent simulation of one half of the pump chamber in combination with a single Tesla valve is carried out in COMSOL Multiphysics®35 specifying a sinusoidal oscillating flow rate i(t) ≡
sin (2πf0t) is used for actuation. Each side of the pump is described as a series connection consisting of a non-linear current-, i.e. flow rate-dependent resistor describing the Tesla valve, a linear resistor ZCh modeling the pump chamber, and an inductance L describing the inertia of the liquid. The resulting equivalent circuit diagram is shown in Fig. 1(c). To determine the parameters ZCh and L, a time-dependent simulation of one half of the pump chamber in combination with a single Tesla valve is carried out in COMSOL Multiphysics®35 specifying a sinusoidal oscillating flow rate i(t) ≡ ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) (t) =
(t) = ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πf0t) at the inlet. The total time-dependent pressure drop ΔpTot(t) over the pump chamber and the single valve can be determined from this simulation.
sin(2πf0t) at the inlet. The total time-dependent pressure drop ΔpTot(t) over the pump chamber and the single valve can be determined from this simulation.
In addition, the pressure difference ΔpT,1/2(i) across the valve is determined as a function of the flow rate i(t) by carrying out stationary simulations of a single-valve structure. The flow rate-dependent resistances, i.e. the pressure differences ΔpT,1/2(![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) ), were also determined experimentally for both flow directions and are shown in Fig. 5(b). The parameters ZCh and L are determined by solving the optimization problem:
), were also determined experimentally for both flow directions and are shown in Fig. 5(b). The parameters ZCh and L are determined by solving the optimization problem:
| | 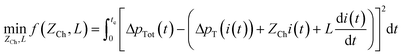 | (6) |
Further details on the optimization procedure and the simulation can be found in the ESI.
† Once the parameters
ZCh and
L are known, the entire pump system can be described using the following non-linear differential equation system:
| | 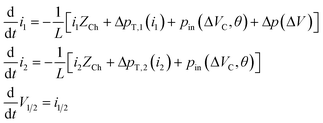 | (7) |
where
i1/2 denote the flow rates through the two fluidic connections of the micropump and
V1/2 the respective total volume changes. The last differential equation is introduced to calculate the volume changes while solving the system numerically in order to be able calculate the volume-dependent pressure terms
pin(Δ
VC,
θ) and Δ
p(Δ
V). Δ
VC describes the volume change of the liquid inside of each cavity, which can be calculated using:
| | 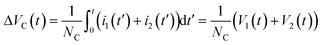 | (8) |
where
NC is the total number of cavities. The additional pressure Δ
p in
eqn (7) is introduced to model external loads. The net pumped volume results from the difference between the two volumes
V1 and
V2 and can therefore be calculated using:
| | 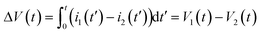 | (9) |
Fig. 1(d) shows an example of the time-dependent flow rates and the resulting pumped volume. It becomes clear that although the flow rates show a complex non-linear time-dependent behavior, an almost constant pump rate with only minor pulsations is achieved.
To calculate the pump characteristic curve, i.e., the flow rate-dependent pump pressure, Δp is set proportional to the net pumped volume, hence Δp = cΔV. With increasing time, the pumped volume and thus the back pressure Δp increases. Finally, the value of ΔV approaches a constant value. To calculate the pump characteristic curve from such a simulation run, the volume curve is first fitted with a polynomial to remove the small oscillations. Then, the time-averaged flow rate is obtained as time derivative of the fitted polynomial. This directly provides the desired relationship of the maximum pump pressure as a function of the flow rate. Examples of the calculated characteristics are shown in Fig. 2 for different cavity sizes and different actuation regimes. The parameters for the simulations were selected in such a way that the simulations can be compared with the measurements on real pump systems presented in section 4.3.
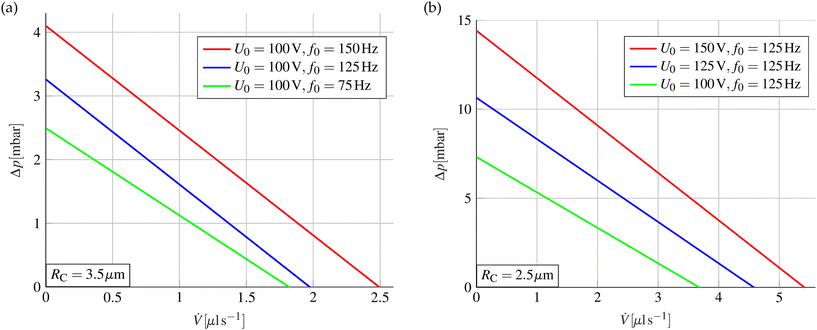 |
| | Fig. 2 Simulated pump characteristic curve for different actuation parameters and cavity sizes. In (a), the actuation frequency is varied for cavity sizes of RC =3.5 μm with the same voltage amplitude. It is clear that the pump performance increases with increasing frequency. In (b), the pump characteristic curve is shown at the same actuation frequency for different voltage amplitudes with a cavity size of RC = 2.5 μm. As expected, the pump performance increases with increasing amplitude of the driving voltage. The comparison between the two diagrams shows the strong dependence of the maximum pressure and the maximum flow rate on the size of the microcavities. Simulation parameters: NC = 550![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, HC = 80 μm, dD = 2.25 μm, εr,D = 2.3, γlv = 0.073 N m−1, θY = 115°, θsat = 70°, UT = 25 V, RE = 0.5 μm. 000, HC = 80 μm, dD = 2.25 μm, εr,D = 2.3, γlv = 0.073 N m−1, θY = 115°, θsat = 70°, UT = 25 V, RE = 0.5 μm. | |
Clearly, the pump-characteristic curves can be well approximated by linear functions. The maximum achievable pressure and the maximum flow rate are mainly determined by the cavity dimensions. This means that the performance can be improved by minimizing the cavity radius RC while maximizing the etch depth HC at the expense of an increasingly difficult fabrication process. However, the simulations show that pump pressures of approx. 15 mbar and flow rates larger than 0.3 ml min−1 can be achieved with cavity dimensions that are comparatively easy to manufacture.
2.2 Application potential and limitations of the pump principle
An important question is which types of liquids can be pumped with the presented pump mechanism. The Young–Lippmann equation used to describe the contact angle, i.e.eqn (1), is valid under the assumption of an ideally conducting liquid. However, this is a very good approximation for aqueous solutions, as they already have a sufficiently high conductivity due to the autoprotolysis of the water. A more detailed discussion of the influence of the finite conductivity of the liquid on the EWOD effect was given by Mugele and Buehrle.36 We note in passing that liquids with vanishing conductivity, such as oils, are more difficult to pump but can also be actuated using dielectrowetting37,38 and therefore, in principle, pumped using the pumping mechanism presented. More important than the conductivity for the function of the pumping principle, however, is the surface tension of the liquid, as the pumping action and the resulting pumping pressure are generated from the manipulation of the surface tension. At the same time, the pressure losses in the chamber etc. increase as viscosity increases, which leads to a decrease in the pumping performance. In summary, the presented EWOD-based pump is expected to work best for low-viscosity liquids with a high surface tension and sufficient conductivity. Fortunately, these criteria are met by most non-biological and many biological aqueous solutions which are used in typical lab-on-a-chip applications.
Shen et al.39 provided a comprehensive review of the use of EWOD for biomedical applications. This paper also discusses numerous major challenges and presents possible mitigation plans. Accordingly, a number of open questions remain to be addressed, if the presented pumping principle is used for pumping biological fluids. For example, the influence of the rather strong electric fields on the cells or biomolecules contained in the liquid need to be investigated. If liquids containing cells are to be pumped, it must also be determined whether the cells contained can clog the microcavities. For example, the diameter of a human red blood cell is in the range of the side length of the microcavities in the pump design presented. In such a case, increasing the diameter of the microcavities may be sufficient to avoid clogging, although this will result in a reduction in pump performance, which may or may not be acceptable depending on the application. However, one of the main challenges with biological fluids is that they tend to adhere to the surface and thus, reduce the hydrophobic properties, an effect that is also known as ‘biofouling’. Dealing with this undesirable effect is particularly important because reversible EWOD actuation is critical to the operation of the micropump. The addition of non-toxic chemical additives, as suggested by Luk et al.40 or Au et al.,41 may be a solution to this problem. The authors showed that the addition of small amounts of pluronic, an amphiphilic additive, to the liquid effectively prevents the adsorption of proteins on the surface. In summary, the application and optimization of the presented pumping principle for the manipulation of biological fluids represents an interesting field for future investigations.
Next, we will briefly discuss the influence of gas solubility on pump performance, because the reversible deflection of the liquid–air interface in the microcavities is essential for the pumping effect. Periodically, the gas pressure in the microcavities is increased, which implies that some gas could possibly be dissolved in the liquid being pumped. However, this effect is typically negligible, as shown by some estimates presented in section 2 of the ESI.†
3 Experimental
The manufacturing process of the micropumps is described next and illustrated schematically in Fig. 3. The production of the micropumps is carried out fully parallelized on wafer level using standard manufacturing processes known from microsystems technology (MEMS). This enables the precise production of valves and cavities in the first place and allows for cost-effective and scalable manufacturing. For each set of pumps, two highly doped silicon wafers (P/B, resistivity < 0.005 Ω cm) with approx. 330 μm thickness are processed. The high doping level is necessary as the silicon functions as electrodes for the EWOD actuation. The pump chamber, the valve structures, and the openings for the fluidic connections are integrated into the lid wafer. These structures are created using two subsequent deep reactive ion etching (DRIE) processes. The pump chamber and valve structures are produced together in one etching process and have a depth of approx. 120 μm. The through-holes for fluidic connections are created from the backside in the second DRIE process. To allow for an electrical contact of the liquid, the surface of the pump chambers is completely coated with a layer of approx. 150 nm gold. An approx. 200 nm thick aluminum layer is deposited on the top, i.e. the outside of the lid wafer, to enable electrical contacting. The individual production steps for the lid wafer and the final layer structure are shown in Fig. 3(a).
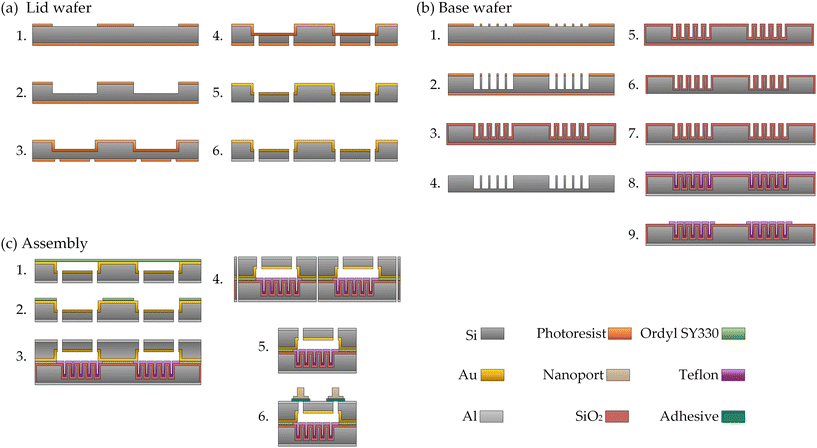 |
| | Fig. 3 Schematic representation of the individual fabrication steps required to manufacture the micropumps. The involved machines, processes, or materials used are indicated in brackets. (a) Processing the lid wafers: 1. UV lithography (Maskaligner MA8e Süss) on the front of the wafer to create the pump chamber and the valve structures. 2. Transferring the structures to the silicon wafer using DRIE (Oxford PlasmaPro 100 Estrelas). 3. UV lithography on the back to create the structures for the fluidic connections. 4. Creating the through-holes for the fluidic connections in the silicon wafer using DRIE. 5. Deposition of a gold layer on the front side of the lid wafer by sputtering (Ardenne CS400). 6. Deposition of an aluminum layer on the backside by sputtering. (b) Fabrication of the base wafers: 1. UV lithography on the front of the wafer to create the microcavities. 2. Transferring the microcavity structures to the silicon wafer using DRIE. 3. Growing a layer of SiO2 on the wafer surface using thermal oxidation to smooth the DRIE scallops (Tempress Omega Junior 2). 4. Wet-chemical removal of the oxide layer using hydrofluoric acid (BOE 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, NH4F buffered HF). The smoothed silicon surface remains. 5. Renewed thermal oxidation to create the dielectric intermediate layer on the wafer surface. 6. Backside removal of the thermal oxide using a wet-chemical process with hydrofluoric acid. 7. Deposition of a thin layer of aluminum on the backside of the base wafer. 8. Hydrophobization of the wafer surface by depositing an approx. 150 nm thick layer of Teflon using dip-coating. 9. Structuring of the Teflon layer using an oxygen plasma to remove it in the areas used for bonding (Oxford PlasmaPro 100 RIE). (c) Assembly of the lid and base wafers: 1. Application of a 30 μm thick layer of the dry film resist Ordyl SY330 on the front side of the lid wafer, which is used for bonding. 2. Structuring of the Ordyl layer using conventional UV lithography. The Ordyl remains around the pump chamber, at the chip edge and on the top of the island structures of the Tesla valves. 3. Bonding of the lid and the base wafer using a thermal bonding process (EVG EV501). 4. Separation of the wafer stack into individual chips using a dicing process (ADT ProVectus 7100). 5. Fully processed pump chip. Up to this point, production is done fully parallelized on wafer level. 6. Nanoports are attached to enable a fluidic connection of the individual chips (adhesive 3M-4926). This is the only serial production step. However, it is only required if the pump is used as a standalone chip. If the pump is integrated directly into microfluidic chips, this step can be omitted if appropriate. 1, NH4F buffered HF). The smoothed silicon surface remains. 5. Renewed thermal oxidation to create the dielectric intermediate layer on the wafer surface. 6. Backside removal of the thermal oxide using a wet-chemical process with hydrofluoric acid. 7. Deposition of a thin layer of aluminum on the backside of the base wafer. 8. Hydrophobization of the wafer surface by depositing an approx. 150 nm thick layer of Teflon using dip-coating. 9. Structuring of the Teflon layer using an oxygen plasma to remove it in the areas used for bonding (Oxford PlasmaPro 100 RIE). (c) Assembly of the lid and base wafers: 1. Application of a 30 μm thick layer of the dry film resist Ordyl SY330 on the front side of the lid wafer, which is used for bonding. 2. Structuring of the Ordyl layer using conventional UV lithography. The Ordyl remains around the pump chamber, at the chip edge and on the top of the island structures of the Tesla valves. 3. Bonding of the lid and the base wafer using a thermal bonding process (EVG EV501). 4. Separation of the wafer stack into individual chips using a dicing process (ADT ProVectus 7100). 5. Fully processed pump chip. Up to this point, production is done fully parallelized on wafer level. 6. Nanoports are attached to enable a fluidic connection of the individual chips (adhesive 3M-4926). This is the only serial production step. However, it is only required if the pump is used as a standalone chip. If the pump is integrated directly into microfluidic chips, this step can be omitted if appropriate. | |
The second wafer, hereinafter referred to as the base wafer, contains the microcavities. These are generated again using DRIE. The cavities have dimensions of approx. 5 μm × 5 μm and a depth of up to 125 μm. Due to the cyclic etching process, so-called scallops with a size of approx. 200 nm form on the side walls of the etched microcavities. These make subsequent hydrophobization of the surface more difficult and lead to increased contact angle hysteresis and must therefore be removed first. For this purpose, an approx. 2.1 μm thick layer of silicon dioxide (SiO2) is created on the wafer surface using thermal oxidation. Since the oxide grows in the direction normal to the wafer surface, the tips of the scallops are oxidized faster than flat surfaces. As a result, the interface between the SiO2 and the underlying silicon gets smoother with increasing thickness of the oxide layer. The SiO2 layer is then removed in a wet chemical process using hydrofluoric acid (HF), leaving behind a smooth silicon surface. The thermal oxidation process is then repeated to produce the dielectric intermediate layer with a thickness of approx. 2.1 μm, which is required for the EWOD effect. The rather large thickness of the oxide layer means that voltage amplitudes in the region of approx. 100 V are required for actuation. This voltage can be significantly reduced at the expense of higher currents if the thickness of the dielectric layer is reduced. However, a thicker dielectric simplifies production, as a pinhole-free layer can be achieved more easily. In the next step, the thermal oxide is removed again on the back of the wafer using a HF-based wet chemical process. An approx. 200 nm thick layer of aluminum is applied directly after the removal of the SiO2-layer to the exposed silicon surface on the backside by sputtering to enable electrical contacting of the base wafer. Finally, the surface of the cavity structures must be hydrophobized. For this purpose, an approx. 150 nm thick layer of Teflon is applied using a dip-coating process. The 6% Teflon AF 1600 solution from CHEMOURS is diluted down to 1.5% with FC-40 solvent and is used for the dip-coating. A retraction speed of 0.1 m min−1 is used and the dip-coating process is repeated twice. After dip-coating, the wafers are baked to evaporate the solvent from the Teflon AF solution (parameters: 20 min @ 50 °C, ramp to 165 °C in 10 min and hold for 20 min, ramp to 200 °C in 10 min and hold for 30 min; the complete process runs at a reduced pressure of 0.25 bar). As the surface of the Teflon layer is not suitable for the subsequent bonding process of the wafers, the Teflon is patterned and removed in the areas outside of the pump chamber using an oxygen plasma. For this, a shadow mask machined from aluminum is used to mask the wafer surface. This eliminates the need for an additional lithography step on the strongly structured wafer surface and prevents the contamination or modification of the Teflon coating by wet chemical processes that would be required for lithography. The summarized fabrication process for the base wafers is shown in Fig. 3(b).
Once the lid and base wafer have been manufactured, they are connected using a thermal bonding process. The valve structures pose a particular challenge here, as an adhesive layer also needs to be created on the top of the small island structures to prevent fluidic bypasses. To achieve this, a layer of 30 μm thick Ordyl SY330 dry resist is applied to the entire front of the lid wafer using lamination covering the pump chambers and the valve structures. This dry resist is then patterned using a conventional UV lithography process. The remaining dry resist serves as an adhesive layer for the bonding process. Bonding takes place at a temperature of 150 °C, a force of 5000 N and in a vacuum at a reduced pressure of 1 μbar for at least 60 min. After the bonding process, the complete wafer stack is separated using a dicing process. In the final step, nanoports are attached to the individual chips as fluidic connections. The individual production steps for the assembly process are shown in Fig. 3(c). An image of a finished lid wafer is shown in Fig. 4(a). The finished base wafer is shown in Fig. 4(b) before hydrophobization and in Fig. 4(c) after hydrophobization. The bonded wafer stack is shown in Fig. 4(d). Stitched microscope images of the cavity structures and the pump chamber with the valve structures are shown in Fig. 4(e). As shown, the pump chamber has a teardrop-like shape with no sharp edges or corners. This shape was chosen to ensure that the pump chamber can be easily filled without bubbles. Diced and ready to use pump chips with the attached nanoports are shown in Fig. 4(f). In the pump chamber, the liquid only gets in contact with the Teflon, the gold and the Ordyl layer. This ensures a high level of bio-compatibility. However, the gold surface in particular can be adapted to special requirements or replaced by other conductive materials. This offers the possibility of further functionalization of the chamber surface for, e.g., certain biological applications.
 |
| | Fig. 4 (a) Finished processed lid wafer. The pump chamber and the valve structures on the front can be seen. The wafer surface was coated with gold to enable electrical contacting. (b) Base wafer before hydrophobization. The microcavities are located in the darker areas. (d) Base wafer after hydrophobization of the surface with Teflon AF. The Teflon was locally removed outside the areas with the microcavities to enable bonding. The different wetting properties in the different areas are illustrated by added water droplets. (e) Bonded wafer stack before separation into individual chips. The back of the lid wafer can be seen, which is coated with an aluminum layer to enable electrical contacting of the lid wafer. (c) Left: Stitched microscope images of the area with microcavities in the base wafer. The red line marks the boundary of the area that is hydrophobized with Teflon AF. Right: Stitched microscope image of a pump chamber with valve structures in the lid wafer. The pump chamber is surrounded by additional structures to homogenize the etching load during the DRIE process. (f) Finished and diced micropump chip with attached Nanoports, which are used for fluidic contacting. | |
4 Results and discussion
The following sections discuss the characterization of the individual system components and the system as a whole. In section 4.1, the dimensioning and measurement of the Tesla valves is discussed first. Subsequently, the characterization of the microcavities is discussed in section 4.2. Finally, the overall pump system is analyzed in section 4.3.
4.1 Tesla valves
The valve structures are a critical component of the pump system. To completely eliminate moving components, passive non-mechanical Tesla valves are used for the rectification of the flow. Due to the comparatively low volume stroke, the low flow rates, and the resulting low Reynolds numbers, the valve structures must be as efficient as possible. However, designing efficient passive valve structures poses a significant challenge. For this reason, the valves were designed via an adapted multistage topological optimization. The method is described in detail by Bohm et al.,42 where reasonable values for all the parameters and weighting factors involved are presented and discussed. In the following, the main concept will be briefly summarized. The idea is to find a valve design that maximizes the following multi-objective function:| | 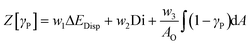 | (10) |
where ΔEDisp describes the ratio of the dissipated energy for both flow directions, Di = ΔpB/ΔpF is the diodicity of the valve, AO is the area of the design domain, and the wi are weighting factors for the partially competing objectives. The energy dissipation ratio is introduced into the objective function in addition to the diodicity to improve the numerical stability of the method.43 This is especially important at the beginning of the optimization, when a good valve geometry is not yet available. The last term in eqn (10) ensures that as much of the design domain is filled with material as possible. This avoids the formation of small structures that are otherwise difficult to fabricate. Combined with the rounded shape of the design domain, this also ensures that the valve structure can be filled without bubbles. The design itself is described by the material distribution function γP. The quantities ΔEDisp and Di are determined not only by the material distribution γP, but also by the flow profiles ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) F/B for the forward and the backward flow directions inside of the valve. In each optimization step, the flow profiles for both flow directions are determined numerically as a solution of the laminar Navier–Stokes equations. All the variables required for evaluating the respective objective function, i.e., ΔEDisp and Di, can then be determined from the calculated flow profiles. For the calculation of the flow profiles, a material-distribution-dependent Darcy force FD = −α(γP)
F/B for the forward and the backward flow directions inside of the valve. In each optimization step, the flow profiles for both flow directions are determined numerically as a solution of the laminar Navier–Stokes equations. All the variables required for evaluating the respective objective function, i.e., ΔEDisp and Di, can then be determined from the calculated flow profiles. For the calculation of the flow profiles, a material-distribution-dependent Darcy force FD = −α(γP)![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) F/B is introduced, coupling the material distribution γP and the flow profiles
F/B is introduced, coupling the material distribution γP and the flow profiles ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) F/B. The function α(γP) = αmaxq(1 − γP)/(q + γP) ensures that the continuous material distribution converges to the values 0 (no material and the liquid can flow freely) or 1 (filled with material) throughout the optimization process, where q and αmax are freely chooseable factors. The factor q controls the convexity of the function α(γP) and αmax determines the porosity of the distributed material. In the individual stages of the optimization, the value of αmax is continuously incremented in order to steadily improve the approximation of a solid that is impermeable to the liquid. In a final stage, the valve design is further optimized by maximizing the following objective function, which takes N
F/B. The function α(γP) = αmaxq(1 − γP)/(q + γP) ensures that the continuous material distribution converges to the values 0 (no material and the liquid can flow freely) or 1 (filled with material) throughout the optimization process, where q and αmax are freely chooseable factors. The factor q controls the convexity of the function α(γP) and αmax determines the porosity of the distributed material. In the individual stages of the optimization, the value of αmax is continuously incremented in order to steadily improve the approximation of a solid that is impermeable to the liquid. In a final stage, the valve design is further optimized by maximizing the following objective function, which takes N![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) different flow rates
different flow rates ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) i into account:
i into account:| | 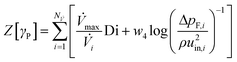 | (11) |
where uin,i are the corresponding inlet velocities used for the simulation and ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) max is the maximum flow rate. In this step, the diodicity can be maximized directly without losing numerical stability, since a good valve geometry already exists at this point in the optimization. Considering several different flows simultaneously results in a more consistent valve performance over the selected flow rate range. After the optimization, the function γP can be transferred directly into a mask design that can be used for the fabrication described previously in section 3. Images of the etched and herein used valve are shown in Fig. 5(a). The flow profiles of the used valve were determined for both flow directions using particle image velocimetry (PIV). The results are shown in Fig. 5(b). In these measurements, the strong asymmetry in the flow profiles becomes directly visible. The resulting difference in the pressures finally leads to the rectification and thus, to the pumping effect. The associated pressure differences for both flow directions and the resulting diodicities were experimentally measured. They are shown in the Fig. 5(c) and (d). It can be seen that the optimized valve design achieves a high diodicity even at very low Reynolds numbers and is therefore suitable for the pump. Nevertheless, it should be noted that the pump principle presented here can also be combined with other valve types, such as mechanical or even actively controlled valves. Furthermore, fully three-dimensionally structured non-mechanical passive valves could also be used in the future, which can achieve an even higher diodicity as shown by Phi et al.44
max is the maximum flow rate. In this step, the diodicity can be maximized directly without losing numerical stability, since a good valve geometry already exists at this point in the optimization. Considering several different flows simultaneously results in a more consistent valve performance over the selected flow rate range. After the optimization, the function γP can be transferred directly into a mask design that can be used for the fabrication described previously in section 3. Images of the etched and herein used valve are shown in Fig. 5(a). The flow profiles of the used valve were determined for both flow directions using particle image velocimetry (PIV). The results are shown in Fig. 5(b). In these measurements, the strong asymmetry in the flow profiles becomes directly visible. The resulting difference in the pressures finally leads to the rectification and thus, to the pumping effect. The associated pressure differences for both flow directions and the resulting diodicities were experimentally measured. They are shown in the Fig. 5(c) and (d). It can be seen that the optimized valve design achieves a high diodicity even at very low Reynolds numbers and is therefore suitable for the pump. Nevertheless, it should be noted that the pump principle presented here can also be combined with other valve types, such as mechanical or even actively controlled valves. Furthermore, fully three-dimensionally structured non-mechanical passive valves could also be used in the future, which can achieve an even higher diodicity as shown by Phi et al.44
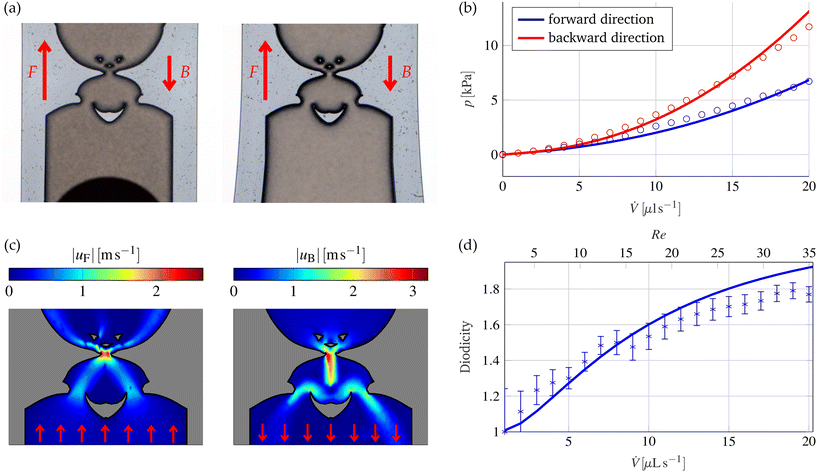 |
| | Fig. 5 (a) Detailed view of the two etched valve structures at both sides of the pump chamber. The forward and backward flow directions are marked with red arrows. (b) Simulated (solid lines) and measured (circles) pressure differences for the valve structure shown in (a) for the two flow directions as a function of the flow rate. (c) Flow profile measured by PIV inside the valve structures for the two flow directions (left: forward, right: backward) at a flow rate of 10 μl s−1. The red arrows indicate the flow direction. (d) Simulated (solid line) and measured (crosses with error bars) diodicity of the valve structure shown in (a) as a function of the flow rate. In addition, the corresponding Reynolds number at the inlet of the valves is shown. | |
4.2 Microcavities
The microcavities, which are responsible for the volume stroke, are the second main component of the pump. In the presence of the external voltage, the EWOD effect forces the liquid–vapor interfaces from the Cassie–Baxter state into an intermediate Wenzel state inside the microcavities. This compresses the air trapped inside the cavities. When the voltage is switched off, the air relaxes and the interface returns to its original state. It is important for the function of the micropump that this process is reversible and that the EWOD actuation shows a low contact angle hysteresis. This depends largely on the quality of the hydrophobic layer on the surface of the microcavities. Preliminary experiments had suggested that layers of Teflon AF on SiO2 applied by dip-coating exhibit a very low contact angle hysteresis. Therefore, they should be well suited for use in the micropump. To test this, EWOD experiments were carried out on flat chips with alternating voltages on water droplets. The layer structure of these chips is identical to the layer structure of the base wafers. The results are shown in Fig. 6(a).
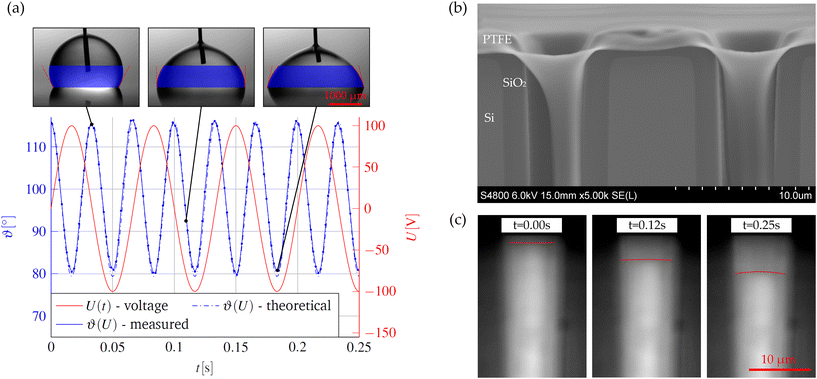 |
| | Fig. 6 (a) Measured contact angle on the Teflon AF surface as a function of time by applying an alternating voltage with an amplitude of 100 V and a frequency of 15 Hz. The mean of the left and right contact angles is shown. In addition, the theoretical contact angle curve according to eqn (1) is shown as blue dashed line. The insets show examples of the drop shape at different times of actuation. (b) SEM image of two microcavities at the cleaved edge of a base wafer. The wafer was cleaved after scribing with a diamond scriber. The dark gray layer shows the SiO2 layer, the light gray area shows the silicon substrate of the base wafer, and the bright layer shows the Teflon. As one can see, the Teflon covers the entire cavity surface as intended. (c) Liquid–air interface within a single microcavity determined by infrared microscopy during actuation at different times. A sinusoidal alternating voltage with an amplitude of 100 V and a frequency of 1 Hz was used for the actuation. For better visualization, the interface is marked in red. The bright areas show the trapped air inside the cavity. The interface in its initial state is shown on the left. The filling process creates a slight overpressure, which partially pushes the interface into the cavity. The interface position at a voltage of approx. 70 V is shown in the center. On the right, the interface is shown when the maximum deflection is reached at a voltage of 100 V. | |
In the case of the micropump, an additional complication is that the side walls of the microcavities must also be homogeneously coated. This is a challenge due to the poor layer adhesion between Teflon and SiO2 and the large aspect ratios of the cavities. To improve the adhesion and achieve a conformal coating, the SiO2 surface is pre-processed using a two-step process: first, the wafer surface is roughened using a HF vapor etching process. The base wafers are heated to 30 °C and placed face down over a container filled with 50 ml of 40% HF for 15 minutes. This results in a nanoscale roughness, which covers the whole wafer surface. In the second step, the wafer surface is coated with a monolayer of hexamethyldisilazane (HMDS C6H19NSi2) directly before the coating process. Although the HMDS does not improve the adhesion between the cured Teflon layer and the SiO2 itself, it does improve the wetting with the FC-40 solvent of the Teflon AF solution. This prevents the Teflon AF solution from accumulating in the corners and at the bottom of the microcavities during the drying process. An SEM image of coated microcavities is shown in Fig. 6(b). The conformal coating of the entire surface and, in particular, also the edges of the microcavities becomes evident. In addition, energy-dispersive X-ray spectroscopy (EDX) measurements are shown in the ESI,† which prove the usefulness of the described pre-treatment. After the demonstration of a low contact-angle hysteresis on flat substrates, a special measuring setup was developed to also verify the reversibility of the EWOD-actuation in the microcavities. It further allows the direct visual observation of the pumping action. Chips were manufactured for this purpose which are identical in layer structure to the base wafers but have only a single row of microcavities close to the chip edge at a distance of approx. 10 μm. The chip edge is then viewed vertically with a microscope using infrared light. A conventional microscope with a broad light source is used for the experiments. A long-pass filter (EDMUND OPTICS Cut-On wavelength 1000 nm) is inserted in the light path to suppress the radiation components in the visible range and an infrared sensitive camera (EHD SCM464-CNIR-TR) is used for the observation. As silicon is transparent in the infrared spectrum, the microcavities in the silicon can be made visible. Example images of the voltage-dependent deflection of the interface in a single microcavity are shown in Fig. 6(c). The fabrication process and the measurement setup are described in more detail in the ESI.† In addition, a video is available online showing the time-dependent periodic deflection in microcavities of different sizes at different amplitudes of the applied AC voltages. These measurements show the predicted periodic deflection of the liquid in the microcavities. The maximum volume stroke per cavity is in the range of approx. 0.5 pl.
4.3 Pump system
A simple but effective measurement setup is used to characterize the entire pump system. For this purpose, glass capillaries are connected to each nanoport of the micropump chip. The pump is then filled with liquid through these capillaries. If an alternating voltage is applied to the chip, the liquid rises in one of the glass capillaries and simultaneously drops in the other capillary. The experiments are carried out with DI water. This proves that even poorly conductive liquids can be pumped with the presented mechanism. For the actuation, a BD300 piezo driver from PIEZODRIVE is used, which can generate a symmetrical sinusoidal voltage with variable amplitude and frequency. As the water level increases, a back pressure due to gravity builds up and the flow rates decrease. If the movement of the interfaces in the glass capillaries is tracked over time, knowing the capillary diameter and density of the liquid, the pump pressure and flow rate can be determined. This allows the pump characteristic curve to be determined directly. For this purpose, the movement in the capillaries is filmed using a conventional camera at 100 fps (SONY 6700 camera, TAMRON 17-70MM F/2.8 lense). The tracking of the interface movement is carried out using the Kanade–Lucas–Tomasi (KLT) tracking algorithm.45,46 Examples of the tracked interfaces in the capillaries at different points in time are shown in Fig. 7(a). The corresponding video showing the interfacial movement is available in the ESI.† The flow rates and the associated pressure differences can be determined directly from the tracked positions z1,2(t) inside the two glass capillaries with radius Rcap. The flow rate is calculated via:| | 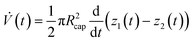 | (12) |
When calculating the associated pressure differences, not only the pressure due to gravity but also the pressure drop caused by the flow in the capillaries is taken into account using the Hagen–Poiseuille law. Thus, the following applies to the total pressure:| | 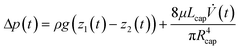 | (13) |
where ρ is the density of the liquid, g is the gravitational acceleration, μ is the dynamic viscosity, and Lcap is the total length of the liquid column in the two capillaries. The resulting pump characteristics are shown in Fig. 7(b) and (c) for different sizes of microcavities and different actuation parameters. In good agreement with the simulation results presented in section 2.1, the pump characteristics can be described well by a linear function. Once again, the strong dependence of the maximum flow rate and the maximum pump pressure on the cavity size becomes clear. A comparison with the simulations shows that the simulation always overestimates the pump performance. This can be explained on the one hand by the simplified modeling and uncertainties in the fabricated geometries and material parameters. Another deviation is caused by the fact that the Young–Lippmann equation, i.e.eqn (1), only describes the contact angle correctly far away from the triple-phase contact line. The local contact angle directly at the triple-phase contact line is independent of the value of the applied voltage and remains unchanged. This phenomenon was first discovered by Buehrle, Herminghaus, and Mugele.36,47 This results in a complicated interface shape and overall to a smaller volume stroke per cavity. A possibility to describe this phenomenon correctly inside the microcavities was presented by Bohm and Runge.30 In summary, the measurements prove the function of the introduced pump principle. The micropump is able to achieve continuous flow rates greater than 0.2 ml min−1 at a maximum pressure larger than 12 mbar. Further improvements seem possible, especially by minimizing the cavity radius, increasing the etch depth of the cavities, and improving the quality of the hydrophobic coating. We believe that pressures of up to 50 mbar and flow rates in the range of 1 ml min−1 can be achieved with reasonable effort optimizing the pump design as well as the fabrication processes.
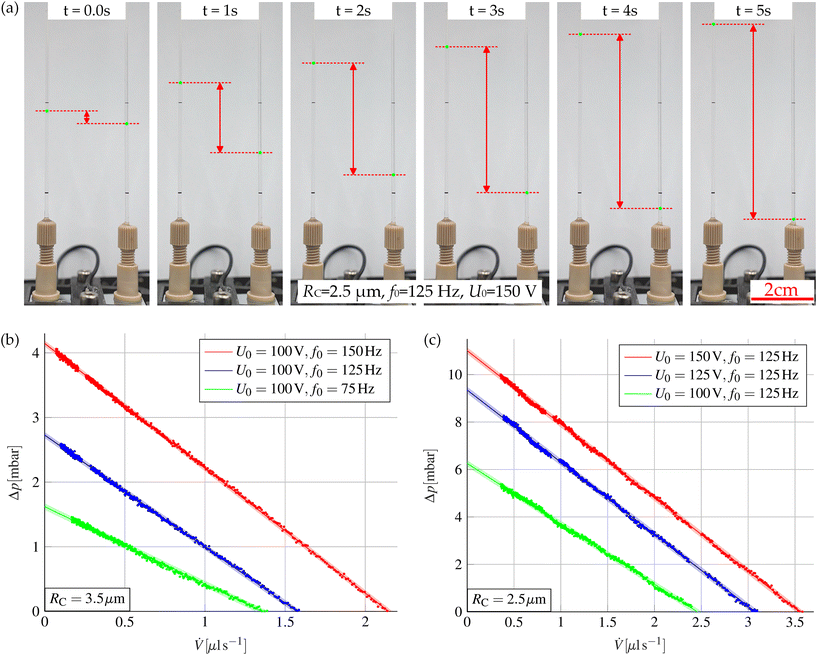 |
| | Fig. 7 (a) Visualization of the pumping action in two glass capillaries connected to the micropump. The deflections z1/2(t) of the interfaces are marked as green dots. When an alternating voltage is applied to the micropump, the liquid rises in the left capillary and drops in the right capillary. The resulting deflection of the liquid–air interfaces in the glass capillaries is marked in red for better visualization. (b) Measured pump characteristic curve for different actuation frequencies with a cavity size of RC = 3.5 μm. (c) Measured pump characteristic curve for different actuation voltages for a cavity size of RC = 2.5 μm. Diagrams (b) and (c) also show a linear fit of the measured pump characteristics together with the 95% prediction intervals. The gaps in the measurement data mark the positions where the interface was behind the black markings on the glass capillaries and, thus, could not be tracked. | |
5 Conclusions
A new type of micropump was presented that utilizes the EWOD effect to achieve an almost continuous flow rate without any moving components. As there are no moving components, fabrication is straightforward, based on standard microsystems technology processes, and is done fully parallelized at wafer level. Here, it was shown how the pump can be set up as a standalone application. However, the manufacturing strategy presented also allows for direct integration of the micropump into lab-on-a-chip applications.
Furthermore, a method for an efficient simulation of the overall system was presented. The method allows the calculation of the relevant pump characteristics and shows good agreement with the measurements. The method can also be used to tailor the pump to the respective target application. In principle, the pump is suitable for pumping all liquids with a certain electrical conductivity, whereby the conductivity of distilled water is already sufficiently high. In particular, aqueous solutions can be pumped, which makes the pump principle interesting for applications involving biological fluids.
Author contributions
SB: software, visualization, writing – original draft, review & editing; HBP: fabrication, writing – review & editing; LD: technology, project administration, writing – review & editing; ER: conceptualization, project administration, writing – review & editing.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We thank the German Federal Ministry for Economic Affairs and Climate Action for the funding of the research project within the framework of the Zentrales Innovationsprogramm Mittelstand (ZIM, funding number: ZF4457306PO9). In addition, we thank the staff of the Zentrum für Mikro- und Nanotechnologien and of the HPC cluster of the Technische Universität for providing an excellent research environment. We thank Ayaka Moriyama (University of Minnesota), supported by the RISE Germany program of the DAAD – German Academic Exchange Service, for the assistance in characterizing the Tesla valves, the group of Christian Cierpka (TU Ilmenau) for support with the Particle Image Velocimetry (PIV) measurements and Björn Müller (TU Ilmenau, Jens Müller group) for performing the Scanning Acoustic Microscope (SAM) measurements presented in the ESI.†
Notes and references
- N.-T. Nguyen, X. Huang and T. K. Chuan, J. Fluids Eng., 2002, 124, 384–392 CrossRef.
- D. J. Laser and J. G. Santiago, J. Micromech. Microeng., 2004, 14, R35–R64 CrossRef.
- P. Woias, Sens. Actuators, B, 2005, 105, 28–38 CrossRef CAS.
- F. Amirouche, Y. Zhou and T. Johnson, Microsyst. Technol., 2009, 15, 647–666 CrossRef CAS.
-
J. Judy, T. Tamagawa and D. Polla, Proceedings. IEEE Micro Electro Mechanical Systems, 1991, pp. 182–186 Search PubMed.
- M. W. Ashraf, S. Tayyaba and N. Afzulpurkar, Int. J. Mol. Sci., 2011, 12, 3648–3704 CrossRef CAS PubMed.
-
T. Pan, E. Kai, M. Stay, V. Barocas and B. Ziaie, The 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 2004, pp. 2639–2642 Search PubMed.
-
J. Folta, N. Raley and E. Hee, Technical Digest IEEE Solid-State Sensor and Actuator Workshop, 1992, pp. 186–189 Search PubMed.
- B. T. Chia, H.-H. Liao and Y.-J. Yang, Sens. Actuators, A, 2011, 165, 86–93 CrossRef CAS.
- J. G. Smits, Sens. Actuators, A, 1990, 21, 203–206 CrossRef.
-
J. Shinohara, M. Suda, K. Furuta and T. Sakuhara, Proceedings IEEE Thirteenth Annual International Conference on Micro Electro Mechanical Systems (Cat. No.00CH36308), 2000, pp. 86–91 Search PubMed.
-
E. Meng, X.-Q. Wang, H. Mak and Y.-C. Tai, Proceedings IEEE Thirteenth Annual International Conference on Micro Electro Mechanical Systems (Cat. No.00CH36308), 2000 Search PubMed.
-
R. Linnemann, P. Woias, C.-D. Senfft and J. Ditterich, Proceedings MEMS 98. IEEE. Eleventh Annual International Workshop on Micro Electro Mechanical Systems. An Investigation of Micro Structures, Sensors, Actuators, Machines and Systems (Cat. No.98CH36176), 1998 Search PubMed.
- X. Wang, D. Zhao, D. T. T. Phan, J. Liu, X. Chen, B. Yang, C. C. W. Hughes, W. Zhang and A. P. Lee, Lab Chip, 2018, 18, 2167–2177 RSC.
- Y. Liu, Q. Yu, L. Ye, L. Yang and Y. Cui, Lab Chip, 2023, 23, 421–436 RSC.
- A. V. Lemoff and A. P. Lee, Sens. Actuators, B, 2000, 63, 178–185 CrossRef CAS.
- S. F. Bart, L. S. Tavrow, M. Mehregany and J. H. Lang, Sens. Actuators, A, 1990, 21, 193–197 CrossRef.
- A. Ramos, J. Phys.: Conf. Ser., 2011, 301, 012028 CrossRef.
- L. Wallman, S. Ekström, G. Marko-Varga, T. Laurell and J. Nilsson, Electrophoresis, 2004, 25, 3778–3787 CrossRef CAS PubMed.
- J. Gong and C.-J. Kim, Lab Chip, 2008, 8, 898 RSC.
- G. J. Shah, A. T. Ohta, E. P.-Y. Chiou, M. C. Wu and C.-J. Kim, Lab Chip, 2009, 9, 1732 RSC.
- C. Peng, Z. Zhang, C.-J. Kim and Y. S. Ju, Lab Chip, 2014, 14, 1117 RSC.
- F. Mugele and J.-C. Baret, J. Phys.: Condens. Matter, 2005, 17, R705–R774 CrossRef CAS.
- F. Mugele, Soft Matter, 2009, 5, 3377 RSC.
- W. C. Nelson and C.-J. C. Kim, J. Adhes. Sci. Technol., 2012, 26, 1747–1771 CrossRef CAS.
- S.-Y. Tang, K. Khoshmanesh, V. Sivan, P. Petersen, A. P. O'Mullane, D. Abbott, A. Mitchell and K. Kalantar-zadeh, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 3304–3309 CrossRef CAS PubMed.
- A. B. D. Cassie, Discuss. Faraday Soc., 1948, 3, 11 RSC.
-
M. Hoffmann, L. Dittrich and M. Bertko, Mikropumpe zur Erzeugung einer Fluidströmung, Pumpensystem und Mikrokanalsystem, DE Pat., DE112011104467B4, 2017 Search PubMed.
-
S. Bohm, L. Dittrich and E. Runge, COMSOL Conference 2020, 2020 Search PubMed.
- S. Bohm and E. Runge, J. Appl. Phys., 2022, 132, 224702 CrossRef CAS.
-
H. Matsumoto and J. E. Colgate, IEEE Proceedings on Micro Electro Mechanical Systems, An Investigation of Micro Structures, Sensors, Actuators, Machines and Robots, 1990, pp. 105–110 Search PubMed.
- E. Delamarche, A. Bernard, H. Schmid, A. Bietsch, B. Michel and H. Biebuyck, J. Am. Chem. Soc., 1998, 120, 500–508 CrossRef CAS.
-
F. M. White, Fluid Mechanics, McGraw Hill Higher Education, Maidenhead, England, 7th edn, 2010 Search PubMed.
- A. N. Salazar, Eur. J. Phys., 2003, 24, 351–358 CrossRef CAS.
-
COMSOL AB, COMSOL Multiphysics® v. 6.1, Stockholm, Sweden, https://www.comsol.com/(2023.12.05) Search PubMed.
- F. Mugele and J. Buehrle, J. Phys.: Condens. Matter, 2007, 19, 375112 CrossRef.
- G. McHale, C. V. Brown, M. I. Newton, G. G. Wells and N. Sampara, Phys. Rev. Lett., 2011, 107, 186101 CrossRef CAS PubMed.
- A. Edwards, C. Brown, M. Newton and G. McHale, Curr. Opin. Colloid Interface Sci., 2018, 36, 28–36 CrossRef CAS.
- H.-H. Shen, S.-K. Fan, C.-J. Kim and D.-J. Yao, Microfluid. Nanofluid., 2014, 16, 965–987 CrossRef CAS.
- V. N. Luk, G. C. Mo and A. R. Wheeler, Langmuir, 2008, 24, 6382–6389 CrossRef CAS PubMed.
- S. H. Au, P. Kumar and A. R. Wheeler, Langmuir, 2011, 27, 8586–8594 CrossRef CAS PubMed.
- S. Bohm, H. B. Phi, A. Moriyama, E. Runge, S. Strehle, J. König, C. Cierpka and L. Dittrich, Microsyst. Nanoeng., 2022, 8, 97 CrossRef PubMed.
- S. Lin, L. Zhao, J. K. Guest, T. P. Weihs and Z. Liu, J. Mech. Des., 2015, 137, 081402 CrossRef.
- H. B. Phi, S. Bohm, E. Runge, L. Dittrich and S. Strehle, Microfluid. Nanofluid., 2023, 27, 55 CrossRef CAS.
-
B. D. Lucas and T. Kanade, Proceedings of the 7th International Joint Conference on Artificial Intelligence, San Francisco, CA, USA, 1981, vol. 2, pp. 674–679 Search PubMed.
-
C. Tomasi and T. Kanade, Detection and Tracking of Point Features, School of Computer Science, Carnegie Mellon Univ., 1991 Search PubMed.
- J. Buehrle, S. Herminghaus and F. Mugele, Phys. Rev. Lett., 2003, 91, 086101 CrossRef PubMed.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *abc,
Hai Binh
Phi
bc,
Lars
Dittrich
bc and
Erich
Runge
*abc,
Hai Binh
Phi
bc,
Lars
Dittrich
bc and
Erich
Runge
 ab
ab

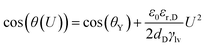
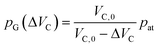
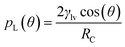
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin (2πf0t) is used for actuation. Each side of the pump is described as a series connection consisting of a non-linear current-, i.e. flow rate-dependent resistor describing the Tesla valve, a linear resistor ZCh modeling the pump chamber, and an inductance L describing the inertia of the liquid. The resulting equivalent circuit diagram is shown in Fig. 1(c). To determine the parameters ZCh and L, a time-dependent simulation of one half of the pump chamber in combination with a single Tesla valve is carried out in COMSOL Multiphysics®35 specifying a sinusoidal oscillating flow rate i(t) ≡
sin (2πf0t) is used for actuation. Each side of the pump is described as a series connection consisting of a non-linear current-, i.e. flow rate-dependent resistor describing the Tesla valve, a linear resistor ZCh modeling the pump chamber, and an inductance L describing the inertia of the liquid. The resulting equivalent circuit diagram is shown in Fig. 1(c). To determine the parameters ZCh and L, a time-dependent simulation of one half of the pump chamber in combination with a single Tesla valve is carried out in COMSOL Multiphysics®35 specifying a sinusoidal oscillating flow rate i(t) ≡ ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) (t) =
(t) = ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πf0t) at the inlet. The total time-dependent pressure drop ΔpTot(t) over the pump chamber and the single valve can be determined from this simulation.
sin(2πf0t) at the inlet. The total time-dependent pressure drop ΔpTot(t) over the pump chamber and the single valve can be determined from this simulation.
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) ), were also determined experimentally for both flow directions and are shown in Fig. 5(b). The parameters ZCh and L are determined by solving the optimization problem:
), were also determined experimentally for both flow directions and are shown in Fig. 5(b). The parameters ZCh and L are determined by solving the optimization problem: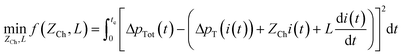
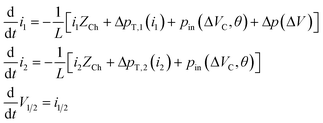
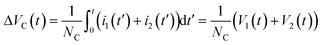
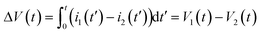
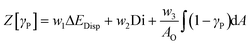
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) F/B for the forward and the backward flow directions inside of the valve. In each optimization step, the flow profiles for both flow directions are determined numerically as a solution of the laminar Navier–Stokes equations. All the variables required for evaluating the respective objective function, i.e., ΔEDisp and Di, can then be determined from the calculated flow profiles. For the calculation of the flow profiles, a material-distribution-dependent Darcy force FD = −α(γP)
F/B for the forward and the backward flow directions inside of the valve. In each optimization step, the flow profiles for both flow directions are determined numerically as a solution of the laminar Navier–Stokes equations. All the variables required for evaluating the respective objective function, i.e., ΔEDisp and Di, can then be determined from the calculated flow profiles. For the calculation of the flow profiles, a material-distribution-dependent Darcy force FD = −α(γP)![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) F/B is introduced, coupling the material distribution γP and the flow profiles
F/B is introduced, coupling the material distribution γP and the flow profiles ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) F/B. The function α(γP) = αmaxq(1 − γP)/(q + γP) ensures that the continuous material distribution converges to the values 0 (no material and the liquid can flow freely) or 1 (filled with material) throughout the optimization process, where q and αmax are freely chooseable factors. The factor q controls the convexity of the function α(γP) and αmax determines the porosity of the distributed material. In the individual stages of the optimization, the value of αmax is continuously incremented in order to steadily improve the approximation of a solid that is impermeable to the liquid. In a final stage, the valve design is further optimized by maximizing the following objective function, which takes N
F/B. The function α(γP) = αmaxq(1 − γP)/(q + γP) ensures that the continuous material distribution converges to the values 0 (no material and the liquid can flow freely) or 1 (filled with material) throughout the optimization process, where q and αmax are freely chooseable factors. The factor q controls the convexity of the function α(γP) and αmax determines the porosity of the distributed material. In the individual stages of the optimization, the value of αmax is continuously incremented in order to steadily improve the approximation of a solid that is impermeable to the liquid. In a final stage, the valve design is further optimized by maximizing the following objective function, which takes N![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) different flow rates
different flow rates ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) i into account:
i into account: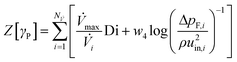
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) max is the maximum flow rate. In this step, the diodicity can be maximized directly without losing numerical stability, since a good valve geometry already exists at this point in the optimization. Considering several different flows simultaneously results in a more consistent valve performance over the selected flow rate range. After the optimization, the function γP can be transferred directly into a mask design that can be used for the fabrication described previously in section 3. Images of the etched and herein used valve are shown in Fig. 5(a). The flow profiles of the used valve were determined for both flow directions using particle image velocimetry (PIV). The results are shown in Fig. 5(b). In these measurements, the strong asymmetry in the flow profiles becomes directly visible. The resulting difference in the pressures finally leads to the rectification and thus, to the pumping effect. The associated pressure differences for both flow directions and the resulting diodicities were experimentally measured. They are shown in the Fig. 5(c) and (d). It can be seen that the optimized valve design achieves a high diodicity even at very low Reynolds numbers and is therefore suitable for the pump. Nevertheless, it should be noted that the pump principle presented here can also be combined with other valve types, such as mechanical or even actively controlled valves. Furthermore, fully three-dimensionally structured non-mechanical passive valves could also be used in the future, which can achieve an even higher diodicity as shown by Phi et al.44
max is the maximum flow rate. In this step, the diodicity can be maximized directly without losing numerical stability, since a good valve geometry already exists at this point in the optimization. Considering several different flows simultaneously results in a more consistent valve performance over the selected flow rate range. After the optimization, the function γP can be transferred directly into a mask design that can be used for the fabrication described previously in section 3. Images of the etched and herein used valve are shown in Fig. 5(a). The flow profiles of the used valve were determined for both flow directions using particle image velocimetry (PIV). The results are shown in Fig. 5(b). In these measurements, the strong asymmetry in the flow profiles becomes directly visible. The resulting difference in the pressures finally leads to the rectification and thus, to the pumping effect. The associated pressure differences for both flow directions and the resulting diodicities were experimentally measured. They are shown in the Fig. 5(c) and (d). It can be seen that the optimized valve design achieves a high diodicity even at very low Reynolds numbers and is therefore suitable for the pump. Nevertheless, it should be noted that the pump principle presented here can also be combined with other valve types, such as mechanical or even actively controlled valves. Furthermore, fully three-dimensionally structured non-mechanical passive valves could also be used in the future, which can achieve an even higher diodicity as shown by Phi et al.44