Effect of in-plane and out-of-plane bifurcated microfluidic channels on the flow of aggregating red blood cells

Abstract

The blood flow through our microvascular system is a renowned difficult process to understand because the complex flow behavior of blood is intertwined with the complex geometry it has to flow through. Conventional 2D microfluidics has provided important insights, but progress is hampered by the limitation of 2-D confinement. Here we use selective laser-induced etching to excavate non-planar 3-D microfluidic channels in glass that consist of two generations of bifurcations, heading towards more physiological geometries. We identify a cross-talk between the first and second bifurcation only when both bifurcations are in the same plane, as observed in 2D microfluidics. Contrarily, the flow in the branch where the second bifurcation is perpendicular to the first is hardly affected by the initial distortion. This difference in flow behavior is only observed when red blood cells are aggregated, due to the presence of dextran, and disappears by increasing the distance between both generations of bifurcations. Thus, 3-D structures scramble in-plane flow distortions, exemplifying the importance of experimenting with truly 3D microfluidic designs in order to understand complex physiological flow behavior.

---

Introduction

Healthy blood circulation through the vascular network is a prerequisite for respiration and transporting materials to tissue.¹ This is, however, a complex process due to the nature of blood as a fluid as well as the geometry of the vascular network blood has to flow through. The flow behavior of blood is convoluted due to the high volume fraction of red blood cells (RBCs) and their tendency to form “rouleaux”, one-dimensional stacks of RBCs, which lead to non-Newtonian behavior.² Factors affecting this aggregate formation have been intensively studied,³ as well as alternative model aggregation agents such as dextran.^4,5 The complexity of the vascular network is due to the huge gradient in length scales, ranging from large arteries to the microvasculature as small as 5 μm in diameter,⁶ smaller than the diameter of RBCs, and the sequence of more or less regular branching events.⁷ The network of microcapillaries at the end of the vasculature network is dense and randomly oriented, especially where it is curved around the surface of the brain, known as cortical penetrating vessels.⁸ In order to gain a bottom-up understanding of blood flow through a complex network such as this brain cortex vasculature, it is therefore essential to control the blood rheology, the geometry, and the interplay between both. In this paper we show how the interplay between RBC aggregation and geometry indeed affects the flow, however, this interplay is very different when geometry is truly three-dimensional instead of purely two dimensional. We achieved this by imaging the flow of aggregated RBCs through 3D geometries excavated in glass that bear similarities with the brain cortex vasculature.

The rheology of blood is both set by the hematocrit volume fraction of RBCs, indicated by Hn where n is the volume fraction in percentage, and the aggregation between the RBCs. Due to the aggregation, blood forms a percolated network at rest, so that a finite stress needs to be applied to induce flow. The presence of this so-called yield stress has important implications for blood flow and may contribute to the development of irregularities in blood flow dynamics.^9,10 The aggregation is caused by the presence of the many macromolecules in the plasma.^4,11,12In vitro, it can be switched off or on by first dispersing RBCs in a physiological buffer, the off state, and then adding dextran,^13,14 a neutral polysaccharide, to induce aggregation. The blood flow can be further tuned by the hematocrit, where higher hematocrit results in bigger clusters.¹⁵ While aggregation is well studied and controlled, this is less the case for mimicking the complex geometries. Advances in the production of microfluidic devices and analyzing tools in the last two decades succeeded to attract more attention toward the problems associated with RBCs flow through the confined geometries. Most research groups use conventional soft lithography to produce patterned micro-structured channels, as it combines high-throughput analysis with physiologically relevant flow conditions projected in 2D structures. This technique has been used to uncover the effect of bifurcations on blood flow, leading to the formation of cell-free layers and cell partitioning,^16,17 the so called Zweifach–Fung effect. This effect causes a very heterogeneous distribution of RBCs in a sequence of many bifurcations.^18,19

In recent years, there has been increasing recognition of the critical importance of developing microfluidic devices that can more accurately replicate the intricate physiological features of the microvasculature.^19,20 This recognition has sparked innovative efforts to push microfluidics beyond conventional designs. One notable advancement in this pursuit has been the shift from rectangular channels to the production of bio-inspired channels with circular cross-sections and planar networks.^21,22 More physiological randomly interconnected structures have been created inside a block of polymeric material²³ although there is limited control over the shape and size of the branches. The crucial step towards more physiological structures is, however, to create three-dimensional non-planar networks. Examples are inducing buckling in 2D soft microchips designed with a planar structure,²⁴ scaffold removable techniques,²⁵ and employing ice patterns as removable geometries to create resin parts with pre-defined features.²⁶ While these advances more closely replicate the physiological aspects of vascular networks, they are mostly based on 2D planar chip designs, except for freeform ice printing, which is limited to a size of 50 μm.²⁶ The use of the multiphoton process is an upcoming technique to fabricate 3D microfluidics in hydrogels. This is achieved by degrading the hydrogels either through acid dissolution of irradiated materials or through fluorescein-excitation driven photoablation.^27–30 These methods have the drawback that local clumps with low-density materials in proximity to the ablation regions remain and post-degradation or decomposition of materials takes place.³¹ Recently, a 3D-printed microfluidic capillary grid using hydrogels was fabricated to replicate the mesh structure of parallel capillaries, perfusing large-scale tissues.³² However, the complete demonstration of optical properties and mechanical stiffness is lacking.

Here we use selective laser induced etching (SLE) as an alternative multiphoton process to fabricate 3D channels. This is a relatively new technique to excavate 3D structures in glass with a resolution of about one micrometer.³³ SLE thus lifts the constraints of conventional planar designs, providing a robust and precise control over the geometry of the channels with full optical accessibility, as demonstrated in recent microfluidic studies.³³ We choose to produce a full 3D microfluidic design that consists of two generations of bifurcations, where the second bifurcation is either in plane or out of plane compared to the first bifurcation, see Fig. 1. This geometry also mimics the cortical vascular network orientation in the human brain, which is composed of parallel-oriented vessels and penetrating branches perpendicular to the cortex surface,^34,35 thus making a next step to understand the effect of physiological shaped geometries on blood flow.

Fig. 1 Schematic design of the 3D microfluidic channels. The design consists of two sets of bifurcations, the second generation of the bifurcations has one in-plane and one out-of-plane bifurcation with respect to the first bifurcation plane. D₁ = 40 μm, D₂ = 32 μm and D₃ = 25 μm refer to the diameters of the channels, which are chosen such that they are flow rate conserving. L indicates the distance between the apex of the two consecutive bifurcations.

The rationale of this choice is to illustrate the impact of the third dimension in a sequence of bifurcations on blood flow. This geometry is prone to show the influence of the third dimension in the structure on blood flow when the distance between the two generations of bifurcations L is smaller than the relaxation length of the fluid,^19,33 defined by the distance after some obstruction where the flow has regained its steady-state flow profile. Therefore, the distance L between the consecutive generations of bifurcations in our 3D geometry will be varied. Moreover, as it has been shown that the state of the RBCs plays an important role in the flow behavior,³⁶ we tuned the complexity of the fluid by varying the hematocrit for non-aggregated, indicated by Hn, and aggregated RBCs, using dextran as indicated by Hn_dex. We will show that 3D flow patterns are distinctly different from their 2D equivalents, but only for aggregated RBCs at high hematocrit.

Results and discussion

Particle imaging velocimetry in 3D bifurcating geometries

We designed and excavated true 3D microfluidic geometries consisting of two generations of bifurcations in glass. The two bifurcations in the second generation have different orientations: one in-plane with the first bifurcation and one out-of-plane bifurcation, which is perpendicular to the first bifurcation, see Fig. 1. The main channel has a round cross section with a diameter of 40 μm. To conserve the flow rate along the direction of the flow, we choose the diameter D₂ of the second-generation downstream channel to follow Murray's law:^37,38where j is the index for the number of channels in the i + 1-th generation. In our case we only have two channels with equal diameter. K is the ratio of mass variation in non-conservative networks which is zero in our case, and the exponent a = 3 for laminar flow. This law is based on minimizing the transport and maintenance cost of the network.³⁹ It is the governing law for biological transporting networks and has been found to be valid for the human vascular system. We produced three chips with lengths L_i = τ_iD₁, τ ∈ 3,6,9 between the first and second bifurcation in order to access the effect of flow relaxation.

In Fig. 2a, we show a typical snapshot for the L = 3D₁ and hematocrit of H_dex = 20, where the subscript indicates addition of dextran to the sample. The case of H_dex = 20 and L = 3D₁ is most prone to show an effect as this is the most complex fluid in the most complex geometry. Fig. 2b represents the velocity vector plot based on the PIV analysis. As we have a crowded system it is not possible to track each particle and apply particle tracking velocimetry (PTV) to generate flow velocity fields, instead we used PIV which measures the mean displacement of groups of particles between two images.

Fig. 2 Blood flow through the microfluidic device and extracted velocity fields. Blood flow through a 3D geometry with hematocrit of H20_dex (20% volume of RBCs and 50 mg ml⁻¹ dextran to induce aggregation) and a flow rate of 10 μl min⁻¹ that matches physiological conditions: (a) bright field microscopy snapshot taken with an exposure time of 100 μs, for exemplary videos see the ESI;† (b) the averaged velocity vector field of the mid-plane obtained from particle image velocimetry (PIV) analysis. The color coding corresponds to the magnitude of the vectors (yellow highest, blue lowest value). The inset is a zoom in of the first bifurcation; (c) the corresponding velocity contour plot, with bullets indicating the location of the maximum velocity in the main channel and the daughter channels. ΔX indicates the skewness of the flow profile: the shift of the maximum velocity from the center line of the channel at each cross-section. Y_max,i and Y_max,o depict the distance of each maximum to the apex of the first bifurcation in the Y direction. The difference between Y_max,i and Y_max,o is defined as ΔY_i−o.

Shift in location of the maximum velocity

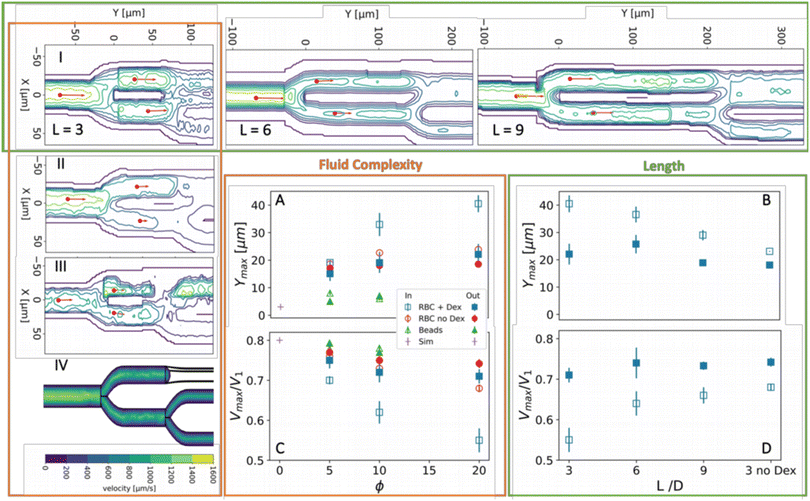
The contour plot of the flow rate discloses a remarkable feature: the location of the maximum velocity after the first bifurcation in the direction of downstream flow, Y_max, is displaced between the two daughter branches, where Y_max is taken relative to the first apex, see Fig. 2c. To test if the relative displacement of the maximum between both branches is due to the complexity of the fluid, we decreased the complexity of the fluid by removing the dextran and therefore aggregation, see Fig. 3II for the contour plot; replacing RBCs by spherical beads, see Fig. 3III; by performing simulations of Newtonian and power-law fluids, see Fig. 3IV.

Fig. 3 Effect of fluid complexity (orange boxes) and geometry (green boxes) on the flow. Left column, top to bottom: contour plots exemplifying decreasing complexity of the fluid with : (I) H20_dex; (II) H10; (III) spherical beads; (IV) simulation of a power law fluid with an exponent of n = 0.6. The resulting effect of the complexity of the fluid for increasing volume fraction on ΔY_i−o (A) and scaled velocity V_max/V₁ (C). The + at ϕ = 0 indicates the simulation of a power law fluid, the green Δ refers to the experiments with 2 μm diameter beads, the ○ and □ stand for H20 and H20_dex, respectively. Top row, left to right: contour plots for increasing length L between bifurcations with H = 20% and 50 mg ml⁻¹ dextran. The resulting effect of the distance between two bifurcations on the ΔY_i−o (B) and scaled velocity V_max/V₁ (D). The □ symbol stands for H20_dex, solid and open symbols refer to out-of-plane and in-plane branches respectively. The error bars are obtained from averaging three different experiments.

The results are quantified in terms of Y_max,i and Y_max,o plotted in Fig. 3A and maximum velocity scaled by the maximum velocity in the mother channel V_max/V₁ plotted in Fig. 3Cvs. the volume fraction ϕ.

The simulations and spherical beads (△) did not show a significant difference between Y_max,i and Y_max,o even at an elevated volume fraction of 10%. Compared to the beads, the morphology of non-aggregated RBCs adds to the complexity of the fluid. This results in a substantial shift of Y_max,i and Y_max,o downstream as compared to the beads, which is slightly larger for Y_max,i, see Fig. 3A. This shift is accompanied by a decrease in V_max, which is again more substantial for the in-plane branch than for the out-of-plane branch, see Fig. 3B. These effects are much more pronounced for aggregated RBCs and enhanced with increasing hematocrit. Flow is strongly hindered in the in-plane branch due to complexity of the fluid as witnessed by the strong decay of V_max,i with increasing hematocrit, while in the out-of-plane the data almost overlay. This is accompanied by a shift in Y_max,i to a position more than half-way to the second bifurcation.

Assuming that the different flow behavior in both branches is caused by the different geometries downstream, which influences the upstream flow behavior, it is of interest to test if these effects disappear when the distance between both bifurcations is increased. Indeed, contour plots for geometries with increasing apex to apex length (L = 6D and 9D) at a fixed H20_dex display a recovery of both V_max,i and Y_max,i towards the values in the out-of-plane branch, see the green row on the top of Fig. 3C and D.

The results we presented above show that the shift between Y_max in both branches and the drop in velocity in the in-plane branch are due to the interplay between aggregation and 3D geometric complexity. An important hint to understand this phenomenon is given by the fact that Y_max,o overlay for the aggregated and non-aggregated RBCs, while Y_max,i and V_max,i deviate with increasing complexity of the fluid and decreasing distance between the bifurcations. This suggests that distortion of the flow by the first bifurcation, which is in the X-direction, is only probed locally downstream by the second bifurcation when this next distortion is in the same plane as the initial distortion. Thus, the difference between the two branches implies that the flow is asymmetric in the X-direction at the second branch. Hence, in the next section the velocity profiles will be examined.

Skewness of flow profile

The different behavior of the in-plane and out-of-plane branches becomes apparent when plotting the velocity profiles along the Y-direction in branches, as shown in Fig. 4a. The profiles are initially asymmetric and blunted. This bluntness in the velocity profiles is typical for shear thinning fluids,^40,41 so we need a fitting model considering the slip condition and asymmetry at walls to obtain the flow profile. Therefore, we parameterize this behavior by fitting the profiles with

v(x) = k(C₁ + C₂x − x²)(1 − σ₁x − σ₂x²), (2)

where k = k(C₁,C₂,σ₁,σ₂), C₁ = C₁(β₁,β₂) and C₂ = C₂(β₁,β₂). σ₁ and σ₂ are two fit parameters that capture the asymmetry of the velocity profile, where σ₁ tunes the curvature of the velocity profile and the σ₂ determines the position of the maximum of the velocity profile.⁴²

Fig. 4 Skewness of the velocity profile for the indicated conditions for the highly aggregated blood sample with 20% hematocrit. (a) Flow profiles with fit (black line) at different positions throughout the most extended geometry. (b) Shift of the location of the maximum velocity with respect to the central line in (X) direction vs. distance from the apex of the first bifurcation for different geometries. The big symbols indicate the locations where the velocity is highest (Y_max), see the red dots in the contour plots of Fig. 2. (c) Skewness of the flow profile in each branch at the location of the maximum velocity Y_max. Negative values represent the out-of-plane branch, and positive values represent the in-plane branch. The error bars are obtained from averaging three different experiments.

The fit shows that the flow rate at the wall is 24 ± 3 s⁻¹, indicating that the RBCs do not display stick behavior, despite the somewhat rough surface in the order of 1.5 μm, see Fig. S3.† Indeed, in the Movie S7† we scarcely see events that could be interpreted as that the motion of the RBC being affected by the wall. Cell migration at the wall, which is known to occur for the used hematocrit and channel width,^43,44 can explain why the moderate roughness of the walls do not cause sticking effects. The skewness was obtained by calculating the difference between the maximum velocity of the fitted curve and the center of the channel, as ΔX = X_center − X_Vmax,fit, see also Fig. 2c. ΔX is plotted vs. distance Y in Fig. 4b for the three different geometries used. For the most complex geometry L = 3D₁, ΔX does not relax to zero in both branches, see the triangles in Fig. 4b. For L = 6D₁ there is a decreasing trend in the ΔX, although the data are quite scattered. For L = 9D₁, a trend towards zero for ΔX for the out-of-plane branch can be identified, while it is still erratic and non-zero for the in-plane branch. In the absence of dextran, so without aggregation, the differences between both branches in terms of the average skewness disappear. This can be seen by comparing the skewness ΔX at the location of the maximum velocity in both branches as indicated by the big symbols in Fig. 4b. Within the error bar, that we again obtain from averaging the three independent contour plots, ΔX is similar in both branches (indicated by the positive and negative value) see Fig. 4c. The only clear outlier is the long branch with dextran induced aggregation, for which the peak in the profile is about a factor of two more shifted away from the center. This suggests that the origin of the skewness is likely due to the complexity of the flow as it is most pronounced for H20_dex.

The direct conclusion we can draw from Fig. 3A is that a complex fluid, like dextran induced aggregated RBCs at high hematocrit, behaves very differently in the in-plane branch than a Newtonian fluid, while the behavior of both fluids in the out-of-plane branch is very comparable. Thus, we infer that there is a cross-talk between the first and second bifurcation, as mediated by the complex fluid, when the bifurcations are in the same plane. This observation is in accordance with earlier experiments performed in planar designed microfluidics. In such 2D geometries, similar to our in-plane second generation bifurcations, RBC partitioning is observed in cascades of bifurcations.^19,45–47 This phenomenon is connected to lingering of RBCs at the apex of the bifurcation, which is more pronounced when RBCs are aggregated.⁴⁸ Similarly, anomalies in the channels structure can alter RBC partitioning at a downstream bifurcation, which is an effect that depends on hematocrit.¹⁷ Here one should also consider that the maximum hematocrit we used of H = 20 complies with the local hematocrit of RBCs in the micro-vasculature,^49,50 given the physiological rates that we applied.

Fig. 3B and 4 show that the memory of the flow distortion by the first bifurcation that causes the crosstalk, fades out over a considerable distance, confirming earlier observations.³⁹ From our experiments on true 3D branching sequences we learn, however, that this memory effect also disappears when a down-stream perturbation of the flow is perpendicular to the initial perturbation, as the flow behavior of the aggregated high hematocrit RBCs in the out-of-plane branch is very similar to the Newtonian flow. Thus, the partitioning due to distortion of the flow, that is typically observed in 2D microfluidic experiments, will mostly be scrambled by downstream distortions in true 3D environments. This effect will most probably also play a role in physiological conditions as daughter branches in, for example, the human brain will almost never have the same orientation as the bifurcation of the mother branch.^51,52 In principle gravity could also play a role, but we tried to prevent this using our density-matching protocol. Still, we have calculated the terminal velocity in the worst case, assuming a cluster of 5 cells and a complete mismatch of 0.1 g cm⁻³. During the residence time in the longest branch, which we estimate to be 0.3 s, the rouleaux would sediment 0.29 μm, which is negligible.

Conclusions

The interplay between true 3D microfluidic geometries and aggregation of red blood cells that we uncovered with our approach, exemplifies the great potential of the novel SLE technique, producing any desired vessel-like structure in glass. Thus, our experimental approach brings microfluidics closer to physiological reality, where flow through truly 3D geometries consisting of channels that are shaped according to physiological confirmed branching can be investigated, using 3D data from the microvasculature extended with any kind of anomaly and pathology of interest. Doing so, one needs to consider that arteries in the human body have a stiffness of 10 to 20 MPa which is three orders of magnitude less than the glass device.⁵³ It is a matter of debate if this plays an important role though, as one should consider that RBCs migrate from the wall and form the cell-free layer. Therefore, they have less interaction with the capillary wall,² mitigating the effect of the different stiffness of the walls. Nonetheless, to mimic more physiological conditions in future works, one could coat the channels with soft bio-polymers such as BSA to generate a soft-layer inside the microchip or even try to grow endothelial cells into the channels. The latter would be a prerequisite to make the next step, having made the step from 2D to 3D microfluidics, namely to produce also active microchannels.

Experimental

Fabrication of microfluidic channel

The microfluidic devices have been produced by selective laser-induced etching (SLE), which is a novel procedure where local two-photon excitation is combined with a chemical etching process for excavating different geometries inside a transparent material such as fused silica. A femtosecond laser irradiates the interior of a polished glass substrate via a multi-photon process. The irradiation of the material leads to the weakening of the bonds in the crystal, so that they would be broken easier and faster when exposed to the etching agent compared to the rest of the material. The laser-irradiated material is preferentially etched by KOH (assisted by ultrasonication at 85 °C). This process is a subtractive 3D printing technique. It was introduced first in 2001 (ref. 54) and later optimized and developed for KOH as an etching agent in ref. 55 and 56.

CATIA software (V5-6) was used as CAD software to design the model, which is then sliced, using Rhino software to generate guidelines for the laser beams to illuminate the bulk material.

Sample preparation

The RBCs were extracted fresh before each experiment from the fingertips of one single donor. Approval was not required for this study, as the blood was collected from the fingertips of the experimentalist, while previous reports on the aggregation behaviour show that dextran-induced aggregation is primarily influenced by the properties of dextran, see Fig. S1,† rather than donor-specific characteristics.⁵⁷ The extracted blood was collected in the ethylenediaminetetraacetic acid (EDTA) coated tubes and 500 μL PBS (phosphate-buffered saline) was added to the tube, then it was mixed by vortexing. Following centrifugation steps the plasma was extracted and exchanged with fresh PBS. This centrifugation and buffer exchange should be repeated three times, see ref. 58 for a detailed procedure. The remaining RBCs were used to make the samples with desired hematocrit (10 or 20%).

To prevent sedimentation and additional agglomeration of RBCs due to gravity, we implemented an approach of density-matching by re-suspending RBCs in PBS and OptiPrep™ (OP, D1556, Merck, Germany), which consists of a 60% solution of iodixanol in water. Aggregation of RBCs was induced by adding the natural polymer 70 kDa dextran (dx, 31390, Merck, Germany) with a final concentration of 50 mg μl⁻¹. It has been shown earlier that the maximum aggregation is obtained with 50 mg μl⁻¹ of dextran.⁵⁹

We chose dextran as aggregation agent is it induces the same level of aggregation of RBCs compared to albumin but less aggregation for platelets.⁶⁰ Moreover, the mechanisms underlying dextran-induced aggregation for RBCs have been well studied, see ref. 4, 57 and 61. An example of the aggregated RBCs with hematocrit of H10 is presented in Fig. 5. Each experiment needs up to 200 μL of the sample. Due to the experimental limitation we were bound to max of 20% hematocrit. Fluoro-Max™ (G0200, Thermo Scientific) 2 μm beads were used to characterize background fluid. The beads were diluted to 30% of the final volume in the density matched solution of OptiPrep and PBS.

Fig. 5 Aggregated RBCs with hematocrit of ten in the presence of dextran (H_dex = 10) at the apex of the bifurcation, imaged using a 100× air objective. The red circles indicate examples of clusters; the scale bar represents 15 μm.

Dynamic viscosity of PBS–Optiprep with and without dextran was measured at 21 °C for a density of 1.09 g cm⁻³ and shear rates between 5 and 100 s⁻¹. The measured value of 4 cp (see Fig. S2†) for PBS–Optiprep with dextran is comparable to the dynamic viscosity of blood plasma (3–5 cp).^62,63

Operation microfluidics

A syringe pump (NEMESYS LOW PRESSURE™, Centoni, Germany) in combination with Hamilton 250 syringes were used to inject the blood mixture through the microfluidic device. The microfluidic chip is connected to the syringe pump using chromatography tubing (natural FEP). To establish a physiological condition for the flow in the microfluidic device, the input flow rate of the channel was set to 30 μL h⁻¹.

Imaging and PIV analysis

To observe the blood flow dynamics inside the microchips, we used an inverted microscope (IX71, Olympus) with a 50× air objective. Considering the red color of the RBCs and different refractive index of RBCs from our background fluid, they are visible under standard Köhler illumination. In order to identify the central plane, we first scanned the channels in the z-direction and selected the plane with the largest cross-section of the channel to perform our measurements.

Since erythrocytes flow at about 2 mm s⁻¹ in microcapillaries,^64,65 short exposure times (200 μs) and high frame rates (about 2000 fps) are required to enable PIV analysis of the recorded data. To this end, an ultra-fast camera Phantom v1610 (Phantom, New Jersey, USA), which meets both requirements, is connected to the microscope and data are recorded with 200 μs exposure time. All images were recorded with a field of view of 295 × 221 μm and 768 × 576 pixel resolution. To probe the full channel, we therefore needed to record tiles with overlap along the channels.

It is not uncommon for biological application to use the native particles as tracers,^40,66–69 especially in blood flow at high hematocrit.^70–77 PIV relates the shift in intensity peaks in two consecutive frames to calculate the local velocities. The timing between the consecutive images is crucial for a successful cross-correlation, as well as the seeding of particles within the interrogation windows. The recorded data were analyzed using the PIVview 2C software (PIVTEC GmbH, Germany). To obtain the velocity vector fields, first iterative 2D cross-correlation of two sequential images was applied with multiple interrogation windows of 96 × 96 pixels (first), 64 × 64 pixels (second) and 32 × 32 pixels (third) with 75% overlap. Standard multi-path FFT correlation was selected to correlate the intensity peaks, with the signal-to-noise ratio of SNR > 3.5. For the peak search the Whittaker reconstruction algorithm was used for reliable PIV.⁷⁸ The procedure results in a spatial resolution of 2.6 μm, which is a factor of four higher than the actual size of the particles, i.e. the beads or RBCs. Thus, adjacent pixels for one PIV analysis would result in adjacent pixels with the same velocity. However, we obtained the final velocity vector field from PIV analysis averaged over 1000 measurements. Given that cells in the middle move with about 1.4 mm s⁻¹, this means that we have about hundred different configurations per measurement and that we oversampled by about a factor of ten. The roughly hundred independent measurements guarantee sub-cell resolution of the velocity. We repeated this procedure three times per experimental condition, which enables us to estimate the error bars in the data we obtain from the parameterization of the velocity vector field, such as the location of the highest velocity.

A Python script was used to post-process the obtained data and generate contour plots, where the K-mean nearest neighbor algorithm has been implemented to detect the maximum velocities in different clusters. The movies we show in the ESI† are only the showcases and represents 2% of the total data. All the tiles have been analysed individually and stitched together posteriori. By assuring there is overlap between tiles we do not have gaps in our velocity fields.

Simulations

The CFD simulation has been carried out using COMSOL software (version 6), the 3D-CAD model (Fig. 1) has been used as the main geometry. Experimentally we experience steady state, steady flow conditions, therefore two different fluids have been simulated using stationary solver with the Stokes flow as governing physics to mimic physiological conditions.⁷⁹

For the COMSOL simulation of the power-law fluid the exponent was set to n = 0.6 and the density of 1005.7 kg m⁻³.

Data availability

All data needed to evaluate the conclusions in the paper are present in the paper and/or the ESI.† All raw data are available from the corresponding author upon reasonable request.

Author contributions

Conceptualization: AG, KD, TD, MPL. Methodology: AG, OK, KD, TD, MPL. Investigation: AG. Visualization: AG, OK. Supervision: KD, TD, MPL. Writing – original draft: AG, KD, TD, MPL. Writing – review & editing: AG, OK, MB, KD, TD, MPL.

Conflicts of interest

Authors declare that they have no competing interests.

Acknowledgements

The authors thank Prof. Stefan Foerster for providing instruments and Daniel Hintzen for his help in designing the microfluidics. We thank Dr Matthew Wade for his critical reviewing. We acknowledge Jolan Wellens for measuring the surface roughness of the etched walls. We acknowledge the funding of this research by Forschungszentrum Jülich.

References

1. T. J. McMahon, Front. Physiol., 2019, 489551.
2. D. A. Fedosov, W. Pan, B. Caswell, G. Gompper and G. E. Karniadakis, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11772–11777.
3. A. R. Pries and T. W. Secomb, Microcirculation, 2008, 15, 753–764.
4. B. Neu, R. Wenby and H. J. Meiselman, Biophys. J., 2008, 95, 3059–3065.
5. S. Chien and K. Jan, Microvasc. Res., 1973, 5, 155–166.
6. H. H. Lipowsky, Microcirculation, 2005, 12, 5–15.
7. B. Schaller, Brain Res. Rev., 2004, 46, 243–260.
8. B. Xiong, A. Li, Y. Lou, S. Chen, B. Long, J. Peng, Z. Yang, T. Xu, X. Yang, X. Li, T. Jiang, Q. Luo and H. Gong, Front. Neuroanat., 2017, 11, 128.
9. R. Mehri, C. Mavriplis and M. Fenech, PLoS One, 2018, 13, e0199911.
10. Y.-F. Wu, P.-S. Hsu, C.-S. Tsai, P.-C. Pan and Y.-L. Chen, Sci. Rep., 2018, 8, 7173.
11. J. K. Armstrong, R. B. Wenby, H. J. Meiselman and T. C. Fisher, Biophys. J., 2004, 87, 4259–4270.
12. K. Lee, M. Kinnunen, M. D. Khokhlova, E. V. Lyubin, A. V. Priezzhev, I. Meglinski and A. A. Fedyanin, J. Biomed. Opt., 2016, 21, 035001.
13. H. J. Meiselman, B. Neu, M. W. Rampling and O. K. Baskurt, Indian J. Exp. Biol., 2007, 9–17.
14. E. Nader, S. Skinner, M. Romana, R. Fort, N. Lemonne, N. Guillot, A. Gauthier, S. Antoine-Jonville, C. Renoux, M.-D. Hardy-Dessources, E. Stauffer, P. Joly, Y. Bertrand and P. Connes, Front. Physiol., 2019, 1329.
15. O. K. Baskurt and H. J. Meiselman, Clin. Hemorheol. Microcirc., 2013, 53, 23–37.
16. V. Leble, R. Lima, R. Dias, C. Fernandes, T. Ishikawa, Y. Imai and T. Yamaguchi, Biomicrofluidics, 2011, 5, 044120.
17. E. Kaliviotis, J. M. Sherwood and S. Balabani, Phys. Fluids, 2018, 30, 030706.
18. J. O. Barber, J. P. Alberding, J. M. Restrepo and T. W. Secomb, Ann. Biomed. Eng., 2008, 36, 1690–1698.
19. A. Mantegazza, F. Clavica and D. Obrist, Biomicrofluidics, 2020, 14, 014101.
20. Q. Gao, Z. Liu, Z. Lin, J. Qiu, Y. Liu, A. Liu, Y. Wang, M. Xiang, B. Chen, J. Fu and Y. He, ACS Biomater. Sci. Eng., 2017, 3, 399–408.
21. M. Abdelgawad, C. Wu, W.-Y. Chien, W. R. Geddie, M. A. S. Jewett and Y. Sun, Lab Chip, 2011, 11, 545–551.
22. M. Stroobach, L. Haya and M. Fenech, Med. Eng. Phys., 2019, 69, 100–108,  DOI:10.1016/j.medengphy.2019.04.008.
23. J.-H. Huang, J. Kim, N. Agrawal, A. P. Sudarsan, J. E. Maxim, A. Jayaraman and V. M. Ugaz, Adv. Mater., 2009, 21 DOI:10.1002/adma.200990132.
24. H. Luan, Q. Zhang, T.-L. Liu, X. Wang, S. Zhao, H. Wang, S. Yao, Y. Xue, J. W. Kwak, W. Bai, Y. Xu, M. Han, K. Li, Z. Li, X. Ni, J. Ye, D. Choi, Q. Yang, J.-H. Kim, S. Li, S. Chen, C. Wu, D. Lu, J.-K. Chang, Z. Xie, Y. Huang and J. A. Rogers, Sci. Adv., 2021, 7, eabj3686.
25. V. Saggiomo and A. H. Velders, Adv. Sci., 2015, 2, 1500125.
26. A. Garg, S. S. Yerneni, P. Campbell, P. R. LeDuc and O. B. Ozdoganlar, Adv. Sci., 2022, 9, 2201566.
27. K. A. Heintz, M. E. Bregenzer, J. L. Mantle, K. H. Lee, J. L. West and J. H. Slater, Adv. Healthcare Mater., 2016, 5, 2153–2160.
28. M. A. Skylar-Scott, M.-C. Liu, Y. Wu and M. F. Yanik, in Advanced Fabrication Technologies for Micro/Nano Optics and Photonics X, SPIE, 2017, vol. 10115, pp. 71–80.
29. N. Brandenberg and M. P. Lutolf, Adv. Mater., 2016, 28, 7450–7456.
30. C. K. Arakawa, B. A. Badeau, Y. Zheng and C. A. DeForest, Adv. Mater., 2017, 29, 1703156.
31. A. Enrico, D. Voulgaris, R. Östmans, N. Sundaravadivel, L. Moutaux, A. Cordier, F. Niklaus, A. Herland and G. Stemme, Adv. Mater., 2022, 34, 2109823.
32. S. Grebenyuk, A. R. Abdel Fattah, M. Kumar, B. Toprakhisar, G. Rustandi, A. Vananroye, I. Salmon, C. Verfaillie, M. Grillo and A. Ranga, Nat. Commun., 2023, 14, 193.
33. V. Calabrese, S. J. Haward and A. Q. Shen, Macromolecules, 2021, 54, 4176–4185.
34. M. G. Báez-Yánez, P. Ehses, C. Mirkes, P. S. Tsai, D. Kleinfeld and K. Scheffler, NeuroImage, 2017, 163, 13–23.
35. P. Blinder, P. S. Tsai, J. P. Kaufhold, P. M. Knutsen, H. Suhl and D. Kleinfeld, Nat. Neurosci., 2013, 16, 889–897.
36. Y. C. Ng, B. Namgung, S. L. Tien, H. L. Leo and S. Kim, Am. J. Physiol., 2016, 311, H487–H497.
37. C. D. Murray, Proc. Natl. Acad. Sci. U. S. A., 1926, 12, 207–214.
38. S. Kim, H. Nam, B. Cha, J. Park, H. J. Sung and J. S. Jeon, Adv. Sci., 2022, 9, 2105809.
39. T. F. Sherman, J. Gen. Physiol., 1981, 78, 431–453.
40. A. Passos, J. M. Sherwood, E. Kaliviotis, R. Agrawal, C. Pavesio and S. Balabani, Phys. Fluids, 2019, 31, 091903.
41. S. Ghosh, Fluids, 2017, 2, 66.
42. A. Merlo, M. Berg, P. Duru, F. Risso, Y. Davit and S. Lorthois, Soft Matter, 2022, 18, 1463–1478.
43. S. Fitzgibbon, A. P. Spann, Q. M. Qi and E. S. G. Shaqfeh, Biophys. J., 2015, 108, 2601–2608.
44. D. Oh, S. Ii and S. Takagi, Fluids, 2022, 7, 96.
45. B. Snyder, D. R. Dantzker and M. J. Jaeger, J. Appl. Physiol., 1981, 51, 598–606.
46. Y. Rashidi, G. Simionato, Q. Zhou, T. John, A. Kihm, M. Bendaoud, T. Krüger, M. O. Bernabeu, L. Kaestner, M. W. Laschke, M. D. Menger, C. Wagner and A. Darras, Biophys. J., 2023, 122, 1526–1537.
47. J. M. Sherwood, D. Holmes, E. Kaliviotis and S. Balabani, PLoS One, 2014, 9, e100473.
48. T. W. Secomb, Annu. Rev. Fluid Mech., 2016, 443–461.
49. J. Perkkiö and R. Keskinen, Bull. Math. Biol., 1983, 45, 41–50.
50. A. R. Pries, K. Ley, M. Claassen and P. Gaehtgens, Microvasc. Res., 1989, 38, 81–101.
51. K. Amunts, C. Lepage, L. Borgeat, H. Mohlberg, T. Dickscheid, M.-É. Rousseau, S. Bludau, P.-L. Bazin, L. B. Lewis, A.-M. Oros-Peusquens, N. J. Shah, T. Lippert, K. Zilles and A. C. Evans, Science, 2013, 340, 1472–1475.
52. A. Hasan, A. Memic, N. Annabi, M. Hossain, A. Paul, M. R. Dokmeci, F. Dehghani and A. Khademhosseini, Acta Biomater., 2014, 10, 11–25.
53. Y. Qiu, D. R. Myers and W. A. Lam, Nat. Rev. Mater., 2019, 4, 294–311.
54. A. Marcinkevičius, S. Juodkazis, M. Watanabe, M. Miwa, S. Matsuo, H. Misawa and J. Nishii, Opt. Lett., 2001, 26, 277–279.
55. M. Hermans, J. Gottmann and F. Riedel, J. Laser Micro/Nanoeng., 2014, 9, 126–131,  DOI:10.2961/jlmn.2014.02.0009.
56. J. Gottmann, M. Hermans, N. Repiev and J. Ortmann, Micromachines, 2017, 8, 110.
57. A. Pribush, D. Zilberman-Kravits and N. Meyerstein, Eur. Biophys. J., 2007, 36, 85–94.
58. O. Korculanin, T. Kochetkova and M. P. Lettinga, Front. Phys., 2021, 721368.
59. G. Barshtein, I. Tamir and S. Yedgar, Eur. Biophys. J., 1998, 27, 177–181.
60. J. Sigurjonsson, D. Hedman, P. Bansch and U. Schött, Perioperative Medicine, 2018, 7, 21.
61. P. Steffen, C. Verdier and C. Wagner, Phys. Rev. Lett., 2013, 110, 018102.
62. R. Khnouf, D. Karasneh, E. Abdulhay, A. Abdelhay, W. Sheng and Z. H. Fan, Biomed. Microdevices, 2019, 21, 80,  DOI:10.1007/s10544-019-0426-5.
63. P. W. Rand, E. Lacombe, H. E. Hunt and W. H. Austin, J. Appl. Physiol., 1964, 19, 117–122.
64. J. Jeong, Y. Sugii, M. Minamiyama and K. Okamoto, Microvasc. Res., 2006, 71, 212–217.
65. M. P. Hilty, P. Guerci, Y. Ince, F. Toraman and C. Ince, Commun. Biol., 2019, 2, 217.
66. H. Petermeier, W. Kowalczyk, A. Delgado, C. Denz and F. Holtmann, Exp. Fluids, 2007, 42, 611–623.
67. G. B. Kim and S. J. Lee, Exp. Fluids, 2006, 41, 195–200.
68. A. Abay, S. M. Recktenwald, T. John, L. Kaestner and C. Wagner, Soft Matter, 2020, 16, 534–543.
69. C. Poelma, A. Kloosterman, B. P. Hierck and J. Westerweel, PLoS One, 2012, 7, e45247.
70. Y. Sugii, S. Nishio and K. Okamoto, Physiol. Meas., 2002, 23, 403.
71. A. Nakano, Y. Sugii, M. Minamiyama and H. Niimi, Clin. Hemorheol. Microcirc., 2003, 29, 445–455.
72. Y. Sugii, R. Okuda, K. Okamoto and H. Madarame, Meas. Sci. Technol., 2005, 16, 1126.
73. A. Nakano, Y. Sugii, M. Minamiyama, J. Seki and H. Niimi, JSME Int. J., Ser. C, 2005, 48, 444–452.
74. R. Lima, S. Wada, M. Takeda, K. Tsubota and T. Yamaguchi, J. Biomech., 2007, 40, 2752–2757.
75. J. Y. Lee, H. S. Ji and S. J. Lee, Physiol. Meas., 2007, 28, 1149.
76. J. Dusting, E. Kaliviotis, S. Balabani and M. Yianneskis, J. Biomech., 2009, 42, 1438–1443.
77. S. M. Choi, W. H. Kim, D. Côté, C.-W. Park and H. Lee, Opt. Express, 2011, 19, 4357–4368.
78. J. Pyeon, K. M. Song, Y. S. Jung and H. Kim, Adv. Sci., 2022, 9, 2104519.
79. Y. Sui, Y. T. Chew, P. Roy, Y. P. Cheng and H. T. Low, Phys. Fluids, 2008, 20, 112106.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lc00151f

---