Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Urine osmolality assessment through the integration of urea hydrolysis and impedance measurement†
Tian Fook
Kong
a,
Xinhui
Shen
a,
Mei Yi
Sim
b,
Jin
Yong
b,
Tze Kiat
Ng
b,
Tsung Wen
Chong
*b and
Marcos
 *a
*a
aSchool of Mechanical and Aerospace Engineering, Nanyang Technological University, 50 Nanyang Avenue, 639798 Singapore. E-mail: marcos@ntu.edu.sg; Tel: +65 67905713
bDepartment of Urology, Singapore General Hospital, 20 College Road, Singapore, 169856, Singapore. E-mail: chong.tsung.wen@singhealth.com.sg
First published on 1st July 2024
Abstract
We present the development and validation of an impedance-based urine osmometer for accurate and portable measurement of urine osmolality. The urine osmolality of a urine sample can be estimated by determining the concentrations of the conductive solutes and urea, which make up approximately 94% of the urine composition. Our method utilizes impedance measurements to determine the conductive solutes and urea after hydrolysis with urease enzyme. We built an impedance model using sodium chloride (NaCl) and urea at various known concentrations. In this work, we validated the accuracy of the impedance-based urine osmometer by developing a proof-of-concept first prototype and an integrated urine dipstick second prototype, where both prototypes exhibit an average accuracy of 95.5 ± 2.4% and 89.9 ± 9.1%, respectively in comparison to a clinical freezing point osmometer in the hospital laboratory. While the integrated dipstick design exhibited a slightly lower accuracy than the first prototype, it eliminated the need for pre-mixing or manual pipetting. Impedance calibration curves for conductive and non-conductive solutes consistently yielded results for NaCl but underscored challenges in achieving uniform urease enzyme coating on the dipstick. We also investigated the impact of storing urine at room temperature for 24 hours, demonstrating negligible differences in osmolality values. Overall, our impedance-based urine osmometer presents a promising tool for point-of-care urine osmolality measurements, addressing the demand for a portable, accurate, and user-friendly device with potential applications in clinical and home settings.
Introduction
Urine osmolality is an important indicator for human health and medical conditions. Physicians often refer to one's urine osmolality to aid them in understanding the patient's renal function such as the kidney's ability to concentrate urine and the hydration state of the patient.1,2 More specifically, urine osmolality reflects the solute-to-water ratio – often expressed in milliosmoles per kilogram of water (mOsm kg−1 water) and depends on the amount of conductive ions and non-conductive molecules dissolved. In a normal urine sample, chloride contributes to ∼19% of urine osmolarity, sodium ∼18%, potassium ∼7%, and urea ∼55%.3–5 Pathological urine may contain glucose, proteins, etc.4 Random urine osmolality values range from 50–1200 mOsm kg−1 water, while 24 hour urine osmolality should be in the range of 500–800 mOsm kg−1 water.6 Urine osmolality can also be used as a means of assessing the hydration status of an individual.7An increased level of urine osmolality could be associated with dehydration, acute kidney injury, congestive heart failure, syndrome of inappropriate antidiuretic hormone secretion (SIADH), adrenal insufficiency, glycosuria, hypernatremia, and a high-protein diet.1,7,8 On the other hand, a decreased level of urine osmolality could be associated with diabetes insipidus, excessive fluid intake, kidney failure, acute renal insufficiency, and glomerulonephritis.1,6,8 With 12–14 hours of water deprivation, the urine osmolality value should be >850 mOsm kg−1 water. If the water deprived urine osmolality is <300 mOsm kg−1 water, the patient is likely to have diabetes insipidus (DI) due to insufficient antidiuretic hormone (ADH) causing large volume discharge of diluted urine.9 Nonetheless, if the urine osmolality is significantly lower at night, the person is likely to have nocturia.10 A clinical trial was carried out to determine the diagnostic utility of the volume and urine osmolality of a single early nocturnal urine sample in detecting nocturnal polyuria. The first nocturnal void can predict a diagnosis of nocturnal polyuria with a reasonably high degree of sensitivity and specificity.11
The current state of the art urine osmometers are laboratory benchtop measurement devices that measure urine osmolality based on the freezing point, membrane, and vapor pressure methods.12–14 Note that osmolality (total number of solutes dissolved in one kilogram of solvent) is often used interchangeably with osmolarity, which is the total number of solutes per litre of solution. The freezing point osmometer determines the urine's osmotic concentration through freezing point depression. The freezing point of the urine solution decreases with increasing amount of solutes in the urine, which enables the determination of urine osmolality. On the other hand, the membrane osmometer correlates the solution osmolality with the osmotic pressure of a solution separated through a semipermeable membrane,15 while the vapour pressure osmometer works based on determining the drop in vapour pressure of urine compared to a standard solution at the same temperature and pressure.16 However, these benchtop osmometers, often not portable, large in size, and laboratory based, require specialized training and involve high cost and time.
In other words, there's a compelling need to develop a tool for patients to measure and keep track of their urine osmolalities to aid physicians to have a more thorough understanding of their body conditions, such as nocturia. At present, measuring urine osmolality requires patients to make a trip to the clinic for laboratory urine testing. These laboratory-based osmometers are usually bulky and expensive, thus limiting the ability for patients to perform 24 hour evaluation of their urine osmolality for their bladder diary at the comfort of their home. Therefore, in this paper, we present our invention of a portable impedance osmometer for patients' urine osmolality measurements through integration of urea hydrolysis and impedance measurement.
Methods and materials
Urine composition
In a normal human urine sample (Table 1), the “non-conductive” urea contributes to ∼55% of urine osmolality, while the “conductive ions” contribute ∼44% (sodium ∼18%, potassium ∼7%, and chloride ∼19%).3 In other words, we can obtain a urine osmolality measurement with an accuracy of up to 99% by simply quantifying the above components present in a urine sample. The osmolality of a urine sample is given by the summation of the total molarity of conductive ions and molarity of non-conductive solutes.| Conductive solute | Non-conductive solute |
|---|---|
| Sodium (Na+) | Urea (H2NCONH2) |
| Potassium (K+) | Creatinine (C4H7N3O) |
| Chloride (Cl−) | Inorganic sulphur (S) |
| Other dissolved ions | Other inorganic and organic compounds |
Implementation/schematics
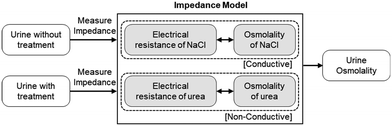
We utilize impedance measurement for urine osmolarity measurement by evaluating the exact concentrations of conductive ions and individual non-conductive solutes after urea hydrolysis with urease enzyme. The procedure for the urine osmolarity calibration and measurement is summarized in Fig. 1. Briefly, we first calibrate and build an impedance (electric resistance) model for both the conductive and non-conductive solutes using sodium chloride (NaCl) and urea solutions prepared at various known concentrations. As urea is non-conductive, we pre-treat the urea solutions with a catalyst, such as urease enzyme, to convert the non-conductive urea to conductive ions. Equipped with the aforementioned impedance model, we are then able to determine the osmolality of a random urine sample through impedance mapping. For each urine sample, the electric resistance of urine is measured twice, one without urease treatment and one after treatment with urease. The electric properties of conductive ions in urine are very similar to those of NaCl. On the other hand, urea is the dominant non-conductive solute in urine. These two facts allow us to estimate the osmolarities of the conductive and non-conductive solutes in urine. The total urine osmolarity level could then be determined.Impedance model and urine osmolality measurement
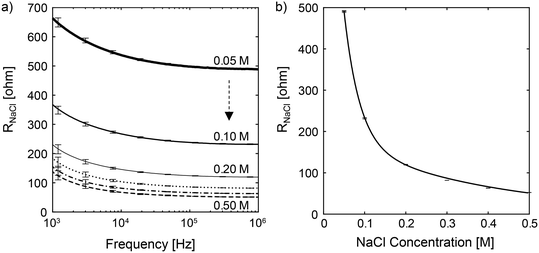
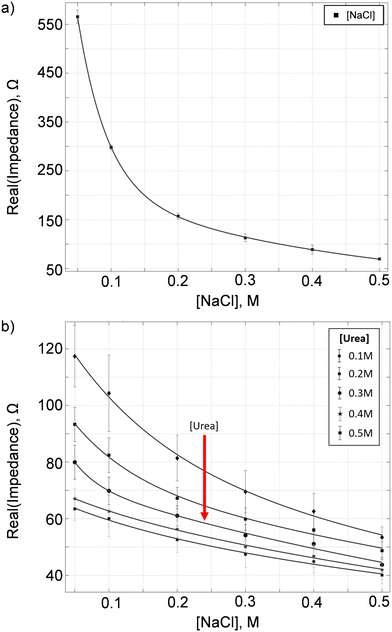
Our calibration phase consists of two measurements – conductive ions and urea. These calibrations allow us to build an impedance (electric resistance) model for both the conductive and non-conductive solutes using sodium chloride (NaCl) and urea solutions prepared at various known concentrations.In the conductive ion calibration, we first determine the optimal frequency for the measurement of NaCl solution with molarities varying from 0.05 M to 0.5 M, which are typical representative concentrations of conductive solutes in urine. For each NaCl sample, we first dilute the sample by 10 fold. We then load 300 μL of the diluted sample to electrode A, as shown in Fig. 2 (left), and incubate it at 60 °C for 2 min. Next, we do a frequency sweep to determine the electric resistance of the NaCl sample, RNaCl. The above-mentioned steps are repeated three times. Fig. 3a shows the mean RNaCl at frequencies ranging from 1 kHz to 1 MHz. The error bars denote the standard deviations of the measurements at the corresponding frequency. We defined the noise-to-signal ratio for each frequency as the summation of the ratio between standard deviation and the average resistance gap (Fig. S1 and S2†), with the aim to minimize the error in the sample measurements while increasing the gap or separation in the mean resistance. The optimal frequency with the lowest noise-to-signal ratio was determined to be f = 724 kHz for the measurement of conductive ions. From Fig. S2,† we observed that increasing the applied frequency above the optimal frequency yielded no additional benefit. Furthermore, it should be noted that the optimal frequency varies with different electrode setups and configurations.
We then determine the relationship between the electric resistance and osmolality of NaCl solution. The osmolality of NaCl solution is equivalent to two times the molar concentration of NaCl, or the sum of the molar concentrations of Na+ and Cl−. In Fig. 3b, we show the electric resistance of NaCl solution as a function of NaCl osmolality at f = 724 kHz. The vertical bars represent the experimental measurements, while the solid line is the interpolated curve. Using the interpolation curve, we can determine the concentration (or the osmolality) of conductive ions, [C]urine, in any given urine sample by measuring the urine electric resistance Rurine and matching the corresponding ion concentration with the fitted line in Fig. 3b. Note that the optimal excitation frequency for the impedance measurement varies for different electrode designs and configurations.
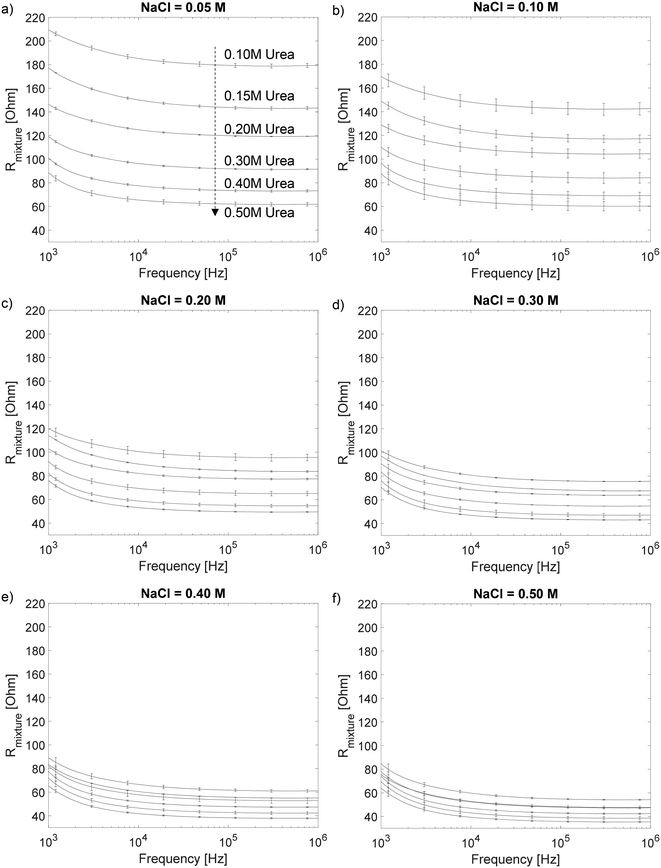
On the other hand, for the urea calibration, we first determine the optimal operating frequency. We prepare sample mixtures containing: NaCl in concentrations of 0.05 M, 0.10 M, 0.20 M, 0.30 M, 0.40 M and 0.50 M; and urea in concentrations of 0.10 M, 0.15 M, 0.20 M, 0.30 M, 0.40 M and 0.50 M, thus, a total of 36 sets of calibration samples. For each sample, we utilize the urease enzyme as a catalyst to convert urea, a non-conductive solute, to conductive ions. The chemical reactions are as follows:
| NH3·H2O ⇌ NH4+ + OH− |
| CO2 + H2O ⇌ H+ + HCO3− |
| HCO3− ⇌ H+ + CO32− |
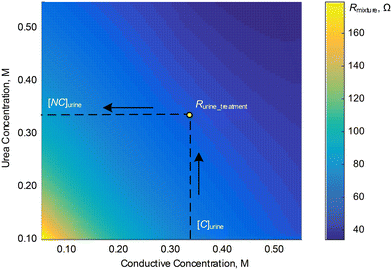 | ||
| Fig. 5 Contour plot for the values of Rmixture for each of the 36 sets of calibration samples at f = 316 kHz. | ||
With the impedance model we obtained from the calibration steps above, we can then determine the urine osmolality for any given sample. First, we measure the electric resistance of urine, Rurine, through electrode A. The concentration (or the osmolality) of conductive ions, [C]urine, is determined from Rurine and the fitting line in Fig. 3b. Subsequently, the electric resistance of the urine sample after treatment with urease enzyme, Rurine_treatment, is measured with electrode B. We then determine the concentration (or osmolality) of non-conductive urea, [NC]urine, in urine from Fig. 5 using the values of [C]urine and Rurine_treatment. Finally, the urine osmolarity of the sample is given by:
| Urine Osmolarity = (2[C]urine + [NC]urine) × 1000 mOsm L−1. |
| Density = (1000 + 58.5[C]urine + 60[NC]urine)/1000, |
| Osmolality = Osmolarity/Density. |
In this work, we utilized urease from Canavalia ensiformis (jack bean) due to its well-characterized properties and commercial availability. Other types of urease enzymes, such as those from soybean, bacterial sources, and fungal sources, may be explored in future studies. Furthermore, to enhance the accuracy of urine osmolality measurements, the concentrations of creatinine and glucose (for patients with glycosuria) can also be determined and incorporated into the analysis scheme.
Fig. S5† compares the conductive concentrations [C]urine with the sum of the sodium and potassium ions ([Na+] and [K+]) of 126 urine samples collected from 31 volunteers. The goodness of fit, at 0.9747, supports the validity of our conductive calibration model for predicting urine osmolality. Nonetheless, as potassium ions have higher ionic mobility than sodium ions, the accuracy of urine osmolality measurements may be reduced for patients with hyperkalemia. Future work can incorporate measurements of sodium and potassium ions using integrated ion-selective electrodes (ISEs) to further improve the accuracy of urine osmolality.
Prototype implementation
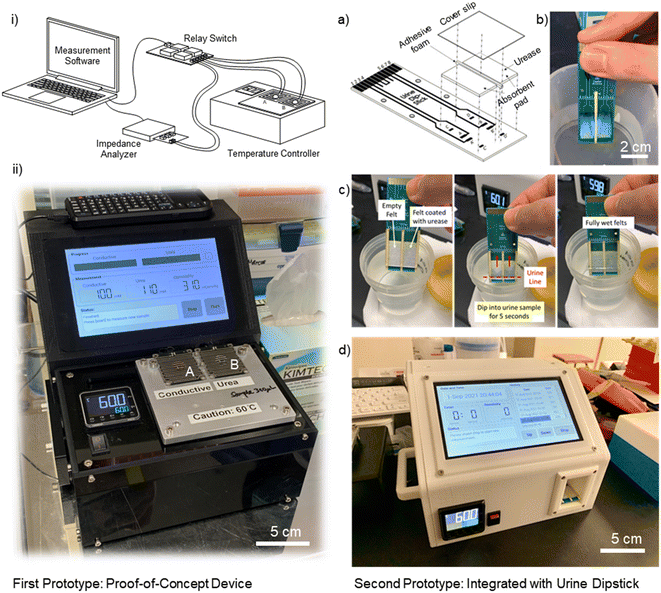
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 units of urease per 10 mL DI water) and left to dry at room temperature. Once the dipstick is fully assembled with two sets of felts (non-coated and coated) using adhesive foams covered with an acrylic PMMA cover slip, the dipstick can be stored and is ready for urine osmolality measurement. After loading the urine sample onto the dipstick, the user simply has to insert the dipstick into the reader unit for urine osmolaliaty measurement (Fig. 2 (right)).
000 units of urease per 10 mL DI water) and left to dry at room temperature. Once the dipstick is fully assembled with two sets of felts (non-coated and coated) using adhesive foams covered with an acrylic PMMA cover slip, the dipstick can be stored and is ready for urine osmolality measurement. After loading the urine sample onto the dipstick, the user simply has to insert the dipstick into the reader unit for urine osmolaliaty measurement (Fig. 2 (right)).
Impedance model for the second prototype with an integrated urine dipstick and a reader unit
We repeated the calibration process for the second prototype with an integrated urine dipstick. Similarly, the calibration phase consists of two measurements – conductive ions and urea. These calibrations allow us to build an impedance (electric resistance) model for both the conductive and non-conductive solutes using sodium chloride (NaCl) and urea solutions prepared at various known concentrations. In the conductive ion calibration, we first determine the optimal frequency for the measurement of NaCl solution with molarities varying from 0.05 M to 0.50 M, which are typical representative concentrations of conductive solutes in urine. Through noise-to-signal ratio characterization, the optimal frequency for the conductive-ion measurement of the second prototype is determined to be 158 kHz. Fig. 6a shows the plot of the real part of impedance with sodium chloride (NaCl) solutions ranging from 0.05–0.50 M at 158 kHz. By knowing the electric resistance of urine, we can determine the conductive ion concentration through interpolation.On the other hand, for the urea calibration of the second prototype, we first determined the optimal operating frequency to be 21.9 kHz. Note that the optimal frequencies for both the conductive ion and urea measurements differ from those of the first prototype due to differences in electrode configurations and gaps. We prepare sample mixtures containing: NaCl in concentrations of 0.05 M, 0.10 M, 0.20 M, 0.30 M, 0.40 M and 0.50 M; and urea in concentrations of 0.10 M, 0.20 M, 0.30 M, 0.40 M and 0.50 M, thus, a total of 30 sets of calibration samples. For each sample, we utilize the urease enzyme as a catalyst to convert urea, a non-conductive solute, to conductive ions. Fig. 6b shows the calibration for [non-conductive] measurement with known samples of NaCl–urea mixtures. Instead of using the contour plot for the second prototype, we used nonlinear models (exponential fit: Aebx + Cedx) to determine the urea concentration. From the data in Fig. 6b, we discretized and interpolated the resistance–urea curves (Fig. S7†) for various NaCl concentrations at increments of 0.01 M. These calibration data are then exported to the C++ program with a graphical user interface (GUI) that controls and operates the prototype in Fig. 2(c).
Clinical trial
We carried out a clinical trial (phase 1 – proof of concept, IRB 2019/2917) at Singapore General Hospital (SGH) to validate the accuracy of the novel portable urine osmometer device compared to the current standard clinical laboratory's gold standard – freezing point osmometer. For the validation of the proof-of concept first prototype, 6 healthy volunteers were recruited, each providing 5 urine samples at different time intervals of the day (6 am, 12 pm, 6 pm, 12 am, and 3 am) for measurements and comparisons (a total of 30 urine samples), both by the developed prototypes and medical grade biochemistry laboratory at SGH. Subsequently, we validate the accuracy of the second prototype with an integrated urine dipstick using 17 urine samples from 13 healthy volunteers.Ethics statement
This study received ethical approval from our institutional review board (SingHealth CRIB 2019/2917). All procedures performed in this study were in accordance with institutional guidelines. Informed consent was obtained from all research subjects who participated in the study.Results and discussion
Proof-of-concept first prototype
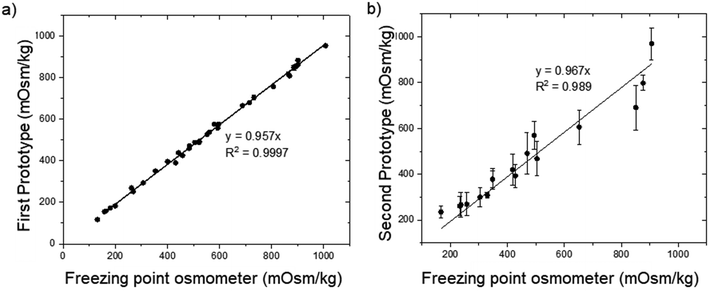
In order to validate our proof-of-concept first prototype, we conducted a clinical trial at SGH. The device was setup in SGH, and a research officer was trained and performed all the urine measurements. Six healthy volunteers were recruited with each of them providing urine samples taken at timings of 0600 h, 1200 h, 1800 h, 0000 h and 0300 h (Table S1†). Fig. 7a summarizes the results of our clinical trial for all the 30 urine samples. Our prototype predicts the urine osmolarity with 95.5 ± 2.4% accuracy as compared to the results obtained from the SGH Biochemistry Diagnostic Laboratory using the gold standard conventional freezing point osmometer, with a goodness of fit of 0.9997.Second prototype with an integrated urine dipstick
Subsequently, a continuation trial was conducted for the second prototype with an integrated urine dipstick. A total of 17 urine samples were obtained from healthy volunteers. Each urine sample measurement was repeated three times (N = 3) for two identical machines (Fig. S8†), except for U2, U4, and U5 due to an insufficient sample volume. The results were compared against the results obtained from the SGH Biochemistry Diagnostic Laboratory which uses the freezing point osmometer (Table 2), the current gold standard for urine osmolality measurements. Nonetheless, the accuracy of U17 was lower than expected. The accuracy may be affected as the sample's urea level is less than 0.1 M and is out of our urea calibration range (0.1 M < urea < 0.5 M). The urine osmolality value was estimated through extrapolation. Overall, our second prototype with a urine dipstick has an average accuracy of 89.9 ± 9.1%. Fig. 7b shows the plot of the second prototype urine osmolality reading vs. osmolality values obtained from the SGH Biochemistry Diagnostic Laboratory using the freezing point osmometer, the current gold standard for urine osmolality measurement. The error bars represent the standard deviation of the prototype urine osmolality values. With the linear intercept set to zero, the gradient of the linear curve fitting obtained is 0.967, with a goodness of fit R2 of 0.989. The lower accuracy compared to the first proof-of-concept prototype is due to the larger than expected standard deviation for urea measurements. While the impedance value for NaCl has a tight standard deviation between repeated measurements, the impedance values for urea exhibits greater variation. We postulate that the large standard deviation is due to the inconsistency in the urease enzyme coating on the absorbent pad (Fig. S9†). Hence, for future development, the consistency of the urea enzyme coating on the felt absorbant pad will have to be improvised to achieve more consistent urine osmolality readings, as well as expand the calibration range of urea below 0.1 M. Another area of improvement could be the utilization of a microfluidics device integrated with microfabricated electrodes17–19 instead of a printed circuit board for on-chip coating of enzyme and measurement of urine impedance.| Sample | Prototype osmolality (mOsm kg−1) | Clinical result | Accuracy (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| L1 | L2 | L3 | R1 | R2 | R3 | Avg | Std | |||
| U1 | 332 | 472 | 518 | 443 | 550 | 492 | 468 | 76 | 504 | 92.9 |
| U2 | 314 | 289 | — | 313 | 316 | — | 308 | 13 | 330 | 93.3 |
| U3 | 325 | 394 | 435 | 434 | 339 | 432 | 393 | 50 | 428 | 91.8 |
| U4 | 627 | 389 | 431 | 507 | 501 | — | 491 | 91 | 469 | 95.3 |
| U5 | 813 | 807 | — | 823 | 749 | — | 798 | 33 | 876 | 91.1 |
| U6 | 234 | 242 | 188 | 322 | 307 | 309 | 267 | 54 | 237 | 87.3 |
| U7 | 351 | 341 | 242 | 266 | 314 | 288 | 300 | 43 | 304 | 98.7 |
| U8 | 357 | 275 | 215 | 271 | 229 | 265 | 269 | 50 | 258 | 95.7 |
| U9 | 223 | 298 | 292 | 255 | 199 | 296 | 261 | 42 | 233 | 88.0 |
| U10 | 658 | 513 | 584 | 528 | 691 | 661 | 606 | 75 | 652 | 92.9 |
| U11 | 350 | 392 | 466 | 532 | 394 | 385 | 420 | 67 | 418 | 99.5 |
| U12 | 389 | 357 | 372 | 415 | 308 | 435 | 379 | 45 | 348 | 91.1 |
| U13 | 892 | 921 | 924 | 1046 | 977 | 1060 | 970 | 70 | 906 | 92.9 |
| U14 | 601 | 526 | 585 | 467 | 617 | 619 | 569 | 61 | 494 | 84.8 |
| U15 | 858 | 633 | 633 | 610 | 757 | 656 | 691 | 97 | 851 | 81.2 |
| U16 | 391 | 314 | 367 | 373 | 414 | 403 | 377 | 36 | 348 | 91.7 |
| U17 | 274 | 198 | 233 | 246 | 237 | 221 | 235 | 25 | 167 | 59.3 |
| Average | 89.9 | |||||||||
| Std dev | 9.1 | |||||||||
We also investigated the effect of storing urine at room temperature for 24 hours. Fig. 8 shows the comparison of the urine osmolality values on day 0 and day 1. From these six-urine samples from two volunteers, there is no significant difference in the urine osmolality values measured on day 0 and day 1 (p-value > 0.05). In other words, the urine osmolality measurements can be performed within a 24 hour period without any significant difference. Our results corroborate the findings from the literature20 indicating that urine osmolality remains stable in a refrigerated environment (7 °C) for up to 7 days and at room temperature for 1 day, while freezing the samples at −20 °C and −80 °C significantly decreases the urine osmolality values.
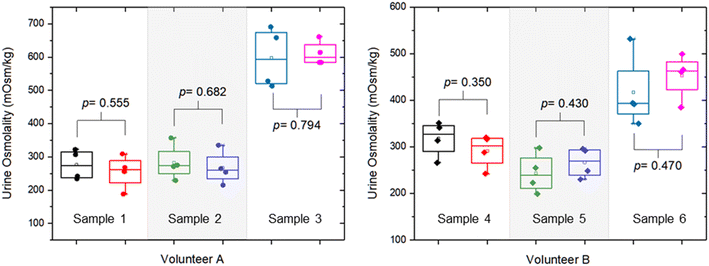 | ||
| Fig. 8 Comparison of the urine osmolality values for readings obtained on day 0 and day 1 (24 hours apart) at room temperature. | ||
Conclusion
In conclusion, we have developed an impedance-based urine osmometer with urea hydrolysis using urease enzyme. The urine osmolality of a urine sample is estimated through the summation of concentrations of the conductive solutes and urea present. An impedance model was developed through known concentrations of NaCl and urea. We carried out clinical trials to validate and evaluate the accuracy of the method of the impedance-based urine osmometer by developing a proof-of-concept first prototype and a second prototype with an integrated urine dipstick. Both prototypes demonstrated an average accuracy of 95.5 ± 2.4% and 89.9 ± 9.1%, respectively, when compared to a clinical freezing point osmometer in the hospital laboratory. A portion of the work has been filed as a PCT patent (PCT/SG2021/050398 WO 2022/015239 A1).Data availability statement
The data that support the findings of this study are openly available in NTU research data repository DR-NTU (Data) at https://doi.org/10.21979/N9/F88FRJ.Author contributions
T. F. Kong, Shen X. H., Sim M. Y. – conceptualization, investigation, methodology, data curation, and writing – original draft. Marcos, Chong T. W., Yong J. and Ng T. K. – conceptualization, writing – review & editing, formal analysis, funding acquisition, resources, and supervision.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The work is supported by SingHealth Duke-NUS Academic Medicine & National Health Innovation Centre Joint MedTech Grant (AM-NHIC/JMT046/2022), Clinician Innovator Award - Investigator Grant (CIAINV22jul-0002), NTUitive Gap Fund (NGF-2020-08-003), and HealthTech NTU – Surgery Academic Clinical Programme Clinical Device Development Programme 2017 (CDD 2017).References
- M. H. Jacobson, S. E. Levy, R. M. Kaufman, W. E. Gallinek and O. W. Donnelly, Arch. Intern. Med., 1962, 110, 83–89 CrossRef CAS PubMed.
- S. M. Shirreffs and R. J. Maughan, Med. Sci. Sports Exercise, 1998, 30, 1598–1602 CrossRef CAS PubMed.
- J. McMurry, D. Ballantine, C. Hoeger and V. Peterson, Fundamentals of General, Organic, and Biological Chemistry, Pearson, 8th edn, 2020 Search PubMed.
- H. J. Yardley, Clin. Chim. Acta, 1958, 3, 280–287 CrossRef CAS PubMed.
- D. F. Putnam, Composition and Concentrative Properties of Human Urine, National Aeronautics and Space Administration, 1971 Search PubMed.
- K. D. Pagana, T. J. Pagana and T. N. Pagana, Mosby's Diagnostic and Laboratory Test Reference, Elsevier, 16th edn, 2022 Search PubMed.
- M. Gray, J. S. Birkenfeld and I. Butterworth, Annu. Rev. Biomed. Eng., 2023, 25, 23–49 CrossRef CAS PubMed.
- H. M. Siragy, Endocr. Pract., 2006, 12, 446–457 CrossRef PubMed.
- C. Capatina, A. Paluzzi, R. Mitchell and N. Karavitaki, J. Clin. Med., 2015, 4, 1448–1462 CrossRef CAS PubMed.
- M. Miller, Chapter 17: Fluid Balance Disorders in the Elderly, American Society of Nephrology, 2010 Search PubMed.
- T. F. Monaghan, J. G. Verbalis, R. Haddad, K. Pauwaert, C. W. Agudelo, A. S. Goessaert, M. A. Denys, J. M. Lazar, D. L. Bliwise, J. Vande Walle, A. J. Wein, J. P. Weiss and K. Everaert, Eur. Urol. Focus, 2020, 6, 738–744 CrossRef PubMed.
- A. Instruments, https://www.aicompanies.com/education/osmolality/advantages-of-freezing-point-depression/ (accessed 23 June 2024).
- M. C. Larkins and A. Thombare, in Osmometer, StatPearls Publishing, Treasure Island (FL), 2023 Search PubMed.
- W. Arneson and J. Brickell, Clinical Chemistry: A Laboratory Perspective, F.A. Davis Company, Philadelphia, 1st edn, 2007 Search PubMed.
- A. Grattoni, G. Canavese, F. M. Montevecchi and M. Ferrari, Anal. Chem., 2008, 80, 2617–2622 CrossRef CAS PubMed.
- M. J. Madden, S. N. Ellis, A. Riabtseva, A. D. Wilson, M. F. Cunningham and P. G. Jessop, Desalination, 2022, 539, 115946 CrossRef CAS.
- T. F. Kong, X. Shen, Marcos, C. Yang and I. H. Ibrahim, Biomicrofluidics, 2020, 14, 054105 CrossRef CAS PubMed.
- T. F. Kong, P. Y. Tan, B. Z. Tay, X. Shen and Marcos, Electrophoresis, 2021, 42, 1070–1078 CrossRef CAS PubMed.
- T. F. Kong, X. Shen, Marcos and C. Yang, Appl. Phys. Lett., 2017, 110, 233501 CrossRef.
- J. D. Adams, S. A. Kavouras, E. C. Johnson, L. T. Jansen, C. Capitan-Jimenez, J. I. Robillard and A. Mauromoustakos, Int. J. Sport Nutr. Exercise Metab., 2017, 27, 18–24 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lc00114a |
| This journal is © The Royal Society of Chemistry 2024 |