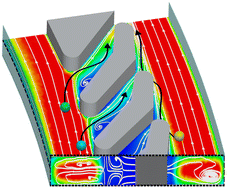
Size-based particle filtration has become indispensable in numerous biomedical and environmental applications. In this study, bioinspired by the filter-feeding mechanism (lobe filtration) of manta rays, we designed a U-shaped biomimetic gill rake filter that combined lobe filtration and Dean flow to filter monodisperse suspensions, bi-disperse suspensions and yeast cells. Compared with other equipment using the inertial focusing technology, our equipment can perform high-throughput (up to 8 mL min−1) and high-efficiency filtration of particles (maximum filtration efficiencies of 96.08% and 97.14% for 10 and 15 μm monodisperse suspensions at the optimum flow rate of 6 mL min−1). The complex velocity field of the micro-fluidic flow within the filter is numerically simulated, and in combination with experiments, a threshold for the flow rate is identified. When the inlet flow rate exceeds the threshold value, the efficiency of particle filtration is increased rapidly. Afterwards, by analysing the filtration mechanism, we develop three novel filtration processes. The equilibrium positions of the particles and yeast cells in the main channel are close to the outer wall at high flow rate, which diminishes the likelihood of particles and yeast cells entering the side channel. This configuration establishes a self-cleaning mechanism, ensuring prolonged and efficient operation of the filter with high-throughput processing. Furthermore, the influence of the filter lobe angle and channel width on the filtration efficiency and outlet flow rate ratio are explored, and an optimisation plan is prepared.