Versatile hybrid technique for passive straight micromixer manufacturing by combining pulsed laser ablation, stereolithographic 3D printing and computational fluid dynamics

Abstract

There is a need to develop new and versatile fabrication methods to achieve efficient mixing of fluids in microfluidic channels using microstructures. This work presents a new technique that combines stereolithography (SLA) and pulsed laser ablation (PLA) to manufacture a straight micromixer for uniform mixing of two samples. Computational fluid dynamics (CFD) simulation is performed to deeply understand the physical mechanisms of the process. The results suggest that this new optical technique holds the potential to become a versatile hybrid technique for manufacturing remarkable mixing microfluidic devices.

---

1. Introduction

Microfluidics is one of the most promising fields in applied science. This interdisciplinary field integrates principles from physics, chemistry, and engineering to achieve precise manipulation of fluid dynamics on a miniature scale, ranging from microliters to millilitres.¹ Microfluidics offers a huge number of advantages, including reduced resource consumption, enhanced reaction efficiency, and minimized waste production. Due to the high control over fluid behaviour, one of the most relevant applications of microfluidics is the controlled mixing and homogenization of chemical reactions.²

However, mixing in microfluidics is a complex issue, due to the prevalence of low Reynolds number (Re) in these systems. At low Reynolds numbers, the inertia of fluid motion is negligible compared to viscous forces, leading to laminar flow profiles. In such laminar flows, the inherent mixing of fluids via diffusion alone is often insufficient to achieve the desired level of homogeneity of the solution or the completeness of the reaction.

To address this limitation, microfluidic researchers have incorporated micromixing strategies inside of microreactors, which play a crucial role in a broad range of applications including synthesis of nanoparticles,^3,4 selective polymerization,^5,6 chemical analysis,⁷ molecular biology^8,9 and point-of-care applications.¹⁰ Consequently, micromixers fall into two main categories: active and passive. On the one hand, active micromixers use external forces or energy sources, such as electric fields, acoustic waves,⁹ or magnetic fields,¹¹ to actively induce mixing in the microfluidic channels. On the other hand, passive micromixers rely on the structural characteristics of the microchannel design to promote mixing without involving external sources. They frequently incorporate microstructures such as ridges,¹² grooves, or serpentines¹³ capable of disrupting the characteristic laminar flow of microscale fluids. In our case of study, we will focus on channels featuring grooves on the bottom, which are classified as slanted micromixers.¹⁴

These passive slanted micromixers are of great interest: they consume minimal power, making them ideal for portable applications; they exhibit robustness, not depending on continuous operation of mechanical or electrical components; and they offer cost-efficiency and easy integration into complex microfluidic systems.

To this end, optical technologies have been essential to accurately manufacture this wide variety of 2D and 3D microstructures capable of creating turbulent flows and enhancing diffusion.^15,16 Until now, photolithography has been the most used optical technology in microfluidics,¹⁷ characterised by complex and time-consuming protocols to micropattern photoresists in 2D, which also produce highly polluting chemical waste. Thereby, in recent years, the rapid developments in lasers have favoured the appearance of different technologies that can be used to microstructure different substrates in a more user-friendly way. This is the case of pulsed laser ablation (PLA) that allows us to achieve outstanding resolutions when micropatterning 2D surfaces, enabling the creation of micro^18–20 and nano²¹ structures with promising results. 3D printers based on the selective stereolithography (SLA) of liquid resins have made it easier to manufacture 3D objects with significant structural complexity (ranging between hundreds of micrometers and millimeters), demonstrating substantial potential in the field of microfluidics^22–24 and, in particular, micromixers.^9,25,26 Both technologies have the potential to overcome the complexities and limitations associated with traditional photolithographic manufacturing methods, in terms of time consumption, scalability, cost and pollution.

Micromixers such as the ones that will be presented in this work have been used to perform chemical reactions in the literature. For instance, Koo et al.¹² proposed the fabrication of a microreactor using a fuse deposition modelling 3D printer. In this work, various printing angles were used to form structures that will be replicated by soft lithography of PDMS creating a groove pattern on the replicas. These authors utilized channels with structures in a similar dimensional range to the one that will be presented in our study (800 μm diameter channels with grooves ranging from 200 to 300 μm), improving the mixing performance of several iodide–iodate reactions (Villermaux–Dushman method²⁷), as the angle and flowrate increased.

Other studies have highlighted the advantages of the slanted groove micromixer positioned on the bottom side of the channel in diverse applications. For instance, Xu et al.²⁸ demonstrated the synthesis of a statistical-copolymer-brush composition gradient of two monomers following the manufacturing protocol of Cabral et al.²⁹ This technique based on frontal photopolymerization of a photoresist sandwiched between two glass slides allows obtaining outward grooves of 190 and 340 μm on the bottom of a 600 μm channel, which is close to the results presented in our work.

In another case, Abonnenc et al.³⁰ fabricated a microreactor through UV-photoablation of a micromachined channel (of 100 μm in width and 35 μm in depth) on a polyethylene terephthalate (PET) sheet, obtaining 45° oriented inward grooves of 35 μm in depth. This device was used to conduct a tagging reaction to enable protein tagging for applications in liquid chromatography-mass spectrometry workflows.

Beyond direct chemical reactions, Moon et al. developed a slanted groove micromixer, obtained by photolithography and replication in PDMS, featuring grooves of 50 μm in width and 10 μm in diameter.³¹ This reactor was applied in their next work to create an enzymatic microreactor for continuous glucose level monitoring via subcutaneous microdialysis in rats.³²

In light of the interest garnered by these devices and their applications, this work presents for the first time, to our knowledge, a novel hybrid technique that combines PLA and SLA to simply manufacture and test straight micromixers featuring different patterns.

2. Materials and methods

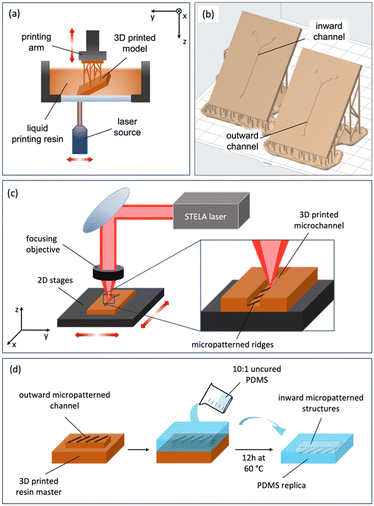
2.1 Manufacturing

The proposed manufacturing process of micromixers consists of two steps, in which each technique (SLA and PLA) is used in its most suitable dimensional range (millimetres and micrometres, respectively).

2.1.1 Stereolithographic 3D printing. A Form 3B (Formlabs, Somerville, Massachusetts, USA) SLA 3D printer was used to produce the substrate (Fig. 1a). This printer features a UV laser (λ = 405 nm, P = 250 mW) and offers an XY resolution of 25 μm and a laser spot size of 85 μm. The resolution in the Z axis depends on the selected resin. Printed substrates featured inward and outward square section (0.55 × 0.55 mm²) channels on their surface. These channels, 25 mm long, incorporate a bifurcation at the beginning, intended to introduce two samples to be mixed (Fig. 1b). Thereby, Y-shaped³³ micromixers were designed using the Computer Aided Design (CAD) software Fusion 360 (Autodesk, San Francisco, California, USA) and then managed with the printer software Preform.

Fig. 1 a) SLA 3D printing principle. b) CAD images of the printed plates featuring Y-shaped microchannels (inward and outward) on the surface. c) Laser setup used for PLA micropatterning of the bottom of the inward channels (the same principle applies for the top of outward channels). d) PDMS soft lithography process for replicating outward channels.

Commercial Model V2 resin from Formlabs was selected as the printing resin given the precision it offers (25 μm in Z)²² and its performance when replicating polymers. In the post curing process, the piece was washed in 2-propanol and cured into a UV chamber for 60 minutes at 60 °C. Moreover, the selected resin offers a very good response to the laser ablation in the infrared (IR) regime.

2.1.2 Pulsed laser ablation. Next, PLA microstructuration of the bottom (top) area of the inward (outward) microchannel was performed (Fig. 1c) using the Santiago TErawatt Laser (STELA) of the Laser Laboratory for Acceleration and Applications (L2A2) facility in Santiago de Compostela. This laser offers an energy of 1 mJ per pulse, a pulse duration of 35 fs, a fixed repetition rate of 1 kHz and a wavelength of 800 nm with a bandwidth of 75 nm. The beam was focused through a microscope objective M Plan APO NIR20X (Mitutoyo, Sakado, Japan) on the 3D printed target. This target was held by a high precision microprocessing system made of two ILS200LM-S stages (Newport, Irvine, California, USA) with an accuracy of 1.5 μm in the X and Y axes and 100 nm in the Z axis.

The design of the patterns was made using Fusion 360 CAD software (Autodesk, San Francisco, California, USA). The target was maintained always at the focal length of the microscope thanks to a collinear laser feedback with a resolution of 0.4 μm. During irradiation of the target, the focal position was automatically readjusted.

2.1.3 Soft lithography of PDMS. Outward channels were employed as the master structures, creating inward channels by replication with soft lithography of polydimethylsiloxane (PDMS). This is one of the most used polymers to fabricate microfluidic devices given its optical transparency, permeability to gases, elasticity, and biocompatibility.^34,35 PDMS was prepared from Sylgard 184 elastomer (Dow Chemical Company, Midland, Michigan, USA). The replication process consisted of the following steps: the uncured (1 : 10 ratio) polymer was deposited on the master fabricated by SLA and micropatterned by PLA and introduced in a vacuum chamber (40 min at 400 mbar) to remove bubbles produced during the mixing process. Finally, the master with the degassed PDMS was cured in an oven for 12 h at 60 °C and easily peeled off (Fig. 1d). After that, PDMS replicas can be easily demolded from the resin master.

2.1.4 Sealing of the channels. Two different approaches were used to seal the channels to introduce flow through them. These two techniques depend on whether the channel is 3D printed (made of resin) or replicated (made of PDMS). 3D printed channels were sealed using transparent PET/acrylic adhesive films (ThermoFisher, Waltham, Massachusetts, USA). The stickers are easy to apply, ensure reliable containment of fluids, prevent contamination, and show optical transparency.

Replicated PDMS channels were punched (to create the fluid entries) and plasma bonded to a microscope glass slide. For this, a Zepto plasma cleaner (Diener Electronics, Ebhausen, Germany) was employed, exposing the surfaces to oxygen plasma. The power was fixed at 20 W, and the pieces were exposed for 20 s. Bonded devices were then thermally treated for 30 min at 90 °C.

2.2 Micromixer testing

Understanding the flow behaviour and mixing efficiency within micromixers is crucial for optimizing their performance and application in various fields. In this section, we delve into the investigation of micromixer flows through two different approaches: peristaltic pump fluid perfusion and CFD simulation.

2.2.1 Flow assays. For testing the real performance of the micromixers, a peristaltic pump and dyes were used. A four channel Minipuls 3 peristaltic pump (Gilson, Middleton, Wisconsin, USA) was employed, allowing us to precisely control the flow rate and ensure consistent flow conditions for accurate measurements and observations. To assess the mixing capabilities of the micromixers, different colour dyes (blue and yellow) were introduced simultaneously into the system. The selection of multiple dyes offers the advantage of visualizing and quantifying the mixing process, as a distinct colour pattern emerges because of efficient or inefficient mixing. The flow was established through 3-stop pump platinum-cured silicone tubing (inner diameter (ID) 1 mm and outer diameter (OD) 3 mm) (Darwin, Paris, France), connected with stopper connectors (BFlow SL, Santiago de Compostela, Spain) and silicon tubing (ID 1 mm and OD 3 mm). Straight connectors (BFlow SL, Santiago de Compostela, Spain) were used to introduce flow in the micromixer. The used caudal was Q = 1 ml min⁻¹, which corresponds to Re = 30.16.

2.2.2 Computer fluid dynamics simulation. Computational fluid dynamics (CFD) allows the analysis of various flow characteristics, such as fluid velocity,³⁶ pressure distribution, and mixing patterns³⁷ employing numerical modelling and simulation of the incompressible Navier–Stokes equations. Its use has been reported in medical disciplines³⁸ and, in particular, micromixers.³⁹ In this work, CFD simulations were used to test the geometries and corresponding performance of the manufactured micromixers, employing ANSYS Fluent (Ansys, Canonsburg, Pennsylvania, USA) software. Numerical simulations were developed considering incompressible fluids, no friction, double precision, laminar flow, transient, the pressure-based solver, implicit volume of fluid, implicit body force, dispersed interface modelling, and two-phase volume of the fluid model with dispersed interface modelling. For the primary phase, we considered liquid water (ρ₁ = 998.2 kg m⁻³ and μ₁ = 0.001003 kg ms⁻¹) and for the secondary phase, we selected a hypothetical fluid with ρ₂ = 997.2 kg m⁻³ and μ₂ = 0.001002 kg ms⁻¹ (the physical properties differ by 0.1% from the water properties) without a surface tension coefficient between the two phases. Another sample was considered to test the adaptability of the micromixers, in that case, an aqueous solution of water with glycerine at 20% was chosen as the first phase (ρ₃ = 1047 kg m⁻³ and μ₃ = 0.00184 kg ms⁻¹), and a hypothetical fluid differing by 0.1% from the first one (ρ₄ = 1046 kg m⁻³ and μ₄ = 0.00183 kg ms⁻¹) was selected as the second phase.

The inlets 1 and 2 were set at Q = 1 ml min⁻¹ and the outlet was set at atmospheric pressure (101 325 Pa). The other surfaces were set as walls with no slip conditions. A tetrahedral mesh refined near the walls was employed to enhance accuracy in regions characterized by high gradients of velocity. Mixtures were considered isothermal and isobaric.

Three meshes of varying grid density and size were considered, comprising 99 668 elements for grid 1, 358 813 elements for grid 2, and 509 873 elements for grid 3. The simulation for a micromixer featuring 20° oriented grooves was conducted on all three grids. When comparing the maximum velocity values to the theoretical value (v = 0.2204 m s⁻¹), grid 2 exhibited a deviation of approximately 5% (grid 1 offered a deviation of 10%), providing good accuracy while requiring less computational effort compared to grid 3. Consequently, all simulation cases were conducted using grids with a number of elements of the order of grid 2 and Q = 0.5, 1, and 2 ml min⁻¹, which correspond to Re = 15, 30, and 60.

Simulations were run until critical convergence of residuals of 1 × 10⁻⁶ under a SIMPLE solution method with 200 steps of 0.01 seconds and maximum interaction/time steps of 20. The spatial discretization includes a least squares cell-based gradient, PRESTO! discretization for pressures, second order upwind momentum, first order upwind volume fraction and first order implicit transient formulation.

2.3 Data collection

Confocal images of the microstructures manufactured on the plates were taken using a 3D optical profilometer S Neox (Sensofar Metrology, Terrassa, Spain). This profilometer allowed us to measure the dimensions (measurements were taken 10 times, obtaining a mean value and its corresponding standard deviation) and to analyse the morphology of the channels. A Nikon MM-400 metallurgic microscope (Nikon Instruments Europe B.V., Amsterdam, The Netherlands) was used to acquire the optical images, using an LU Plan Fluor objective (Nikon Instruments, Melville, USA) with a 5× magnification and a CCD camera Nikon DS-FI2 (Nikon Instruments, Melville, USA).

3. Results and discussion

3.1 Laser parameters for manufacturing

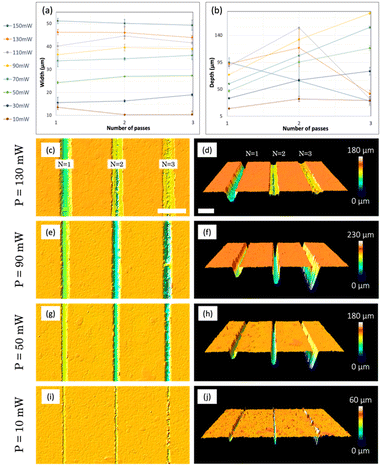
The first step in the experimental section consisted of a comprehensive study focused on the optimization of laser ablation parameters. Specifically, we conducted experiments involving the micropatterning of grooves by PLA on a flat resin surface. During these experiments, we systematically varied the laser power (P) and the number of passes (N) to find the optimal channel results, analysing thermal damage, homogeneity, regular profiles, and dimensions by confocal/optical images (Fig. 2). The velocity of 2D platforms (where the resin plate was placed) was fixed at 1 mm s⁻¹.

Fig. 2 Average a) width and b) depth of the microchannels ablated by PLA on the surface of the resin for different powers (10–130 mW) and laser passes (1–3). Top (left) and 3D (right) confocal images of microchannels obtained for c) and d) 130, e) and f) 90, g) and h) 50 and i) and j) 10 mW, respectively. Scale bars: 100 μm.

First, geometric data were collected using a confocal microscope, which allowed us to measure the width (Fig. 2a) and depth (Fig. 2b) of the fabricated channels. Since these average measurements are not sufficient to describe the real aspect of the channels, the results were cross-checked with confocal images (Fig. 2c–j).

In terms of channel width (W), a clear correlation is observed between this width and the power of the pulses (Fig. 2a): the channels, for a fixed power, are wider than those obtained for lower powers. This is verified for 1, 2 and 3 passes of the laser. However, for each of the powers studied, the number of passes does not always imply an increase in the width of the channel. This behaviour is observed in the results for higher powers (110, 130 and 150 mW) and lower ones (10 mW), and occurs for different reasons: in the case of higher powers, for example 150 mW (Fig. 2c), a deeper channel is obtained for 1 pass, while an inhomogeneous result is observed for 2 and 3 passes. This phenomenon has its origin in the immediate arrival of very energetic second and third pulses, which prevent the ejection and adequate evacuation of the material that is instantly recast in the borders of the channels, reducing its width. For lower powers, for example 10 mW (Fig. 2i), manufactured microchannels present a regular structure for only 1 laser pass. When the number of passes is increased, this low energy value of the pulses is unable to ablate the previously ablated areas in a constant manner, creating small irregular grooves along the channel. In this scenario, the concept of average width does not adequately describe the result, as it varies locally (the same applies for depths, as can be seen in Fig. 2j). For intermediate powers, for example 90 (Fig. 2e) and 50 mW (Fig. 2g), in general terms, a greater number of passes increases the width of the channel, since the energy is enough to allow vaporization and proper elimination of the material after the first laser pass and no recasting is observed.

Regarding the depth (D) of the channels (Fig. 2b), we observe two regimes with very different behaviours. For high powers (150, 130 and 110 mW), as mentioned before, the arrival of the second and third pulses favours the collapse of the walls and the accumulation of the material in the remaining space, which is immediately recast and deposited again inside the channel (Fig. 2d). This favours that for these three powers, when three passes are performed, the depths fall to approximately 20 μm. For two passes, some material can escape, so for 130 and 110 mW, we reach microchannels with a depth of around 100 μm. For lower powers (10–90 mW), we obtain a more effective result, pulses do not block the removal of the material and the depth increases with the number of passes. In this regime, the higher the power, the deeper the channels will be (comparing the same number of passes). The uniformity of channel depths is verified, as evidenced by 3D confocal images for P = 90, 50 mW (Fig. 2f and h) and two passes.

After an extended analysis of the results obtained for different values of power for the ablation, the selected one was 90 mW, combined with 2 passes, with which we can obtain channels with a width of W = 39.6 ± 1.9 μm and a diameter of D = 129.1 ± 2.3 μm. This energy and passes were selected because they are at the intermediate point between high and low powers, producing optimal ablation results (Fig. 2e) and allowing the patterning of regular, homogeneous, and reproducible superficial channels.

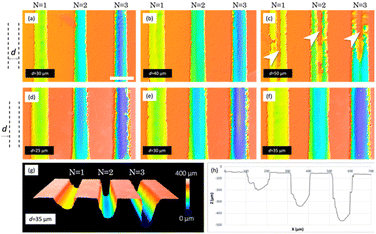
To this point, the obtained channels are within the dimensional range of some reported in the literature,^40,41 suggesting that the fluid penetration into these channels is expected to be sufficient. However, concerning the demolding of PDMS from the master (see section 2.1.3), it is necessary to slightly increase the channel width to prevent any polymer retention within the master. To reach this goal, wider channels are needed, which leads to the following approach: obtaining a wide channel through the ablation of two or more contiguous lines on a flat resin surface. The ablation results of several contiguous lines cannot be directly extrapolated from the results obtained for a single line, so a new study and optimization of parameters were carried out evaluating the ablation results for 2 and 3 contiguous lines depending on the separation distance between them (d) and maintaining the previous ablation parameters: 90 mW, 2 passes and 1 mm s⁻¹.

The results of this study are shown in Fig. 3. In this figure, several confocal images are presented, in the top row, those corresponding to the study of two contiguous lines and in the middle row, those corresponding to three lines. For 2 lines, the energy is very spatially confined, and a big quantity of material is removed, promoting the creation of the deepest channels (D = 330.0 ± 4.2 μm, W = 67.2 ± 3.2 μm) for d = 20 μm and N = 3. These dimensions are significantly greater than those obtained for the study performed for a single line. This is logical since widening the channel allows the material to be eliminated in a larger amount. In this case, the structures have a W/D ratio that has to be increased in order to promote liquid insertion and non-trapping of PDMS during replication, as we mentioned before. For greater separation distances, the energy fails to adequately remove the material in the intermediate region, being especially noticeable in Fig. 3c, where a raised, not ablated region (highlighted with arrows) is observed between the two contiguous lines.

Fig. 3 Confocal images of the obtained laser ablated microchannels on the surface of the resin. The upper row shows the results when 2 lines were ablated contiguously at different separations: a) 30, b) 40 and c) 50 μm. The middle row shows the results when 3 lines were contiguously ablated with separations of d) 25, e) 30 and f) 35 μm, respectively. g) 3D confocal profile and h) cross section of the microchannels obtained in f).

More adequate results are obtained when using three contiguous lines, since the intermediate line grants proper ablation of the intermediate region, thus obtaining a wider channel with a regular bottom. For the lowest separation studied, 25 μm (Fig. 3d), the energy density per area is very high, so the edges are irregular, and some breaks can be observed, especially for N = 3. These results will not grant proper sealing of the channels when using an adhesive film or plasma bonding, and some leakages of fluids can occur. A similar scenario is observed for d = 30 μm. Regarding d = 35 μm (Fig. 3f), we consider that the results obtained for N = 2 are the most appropriate since they allow obtaining a channel with an appropriate size (D = 230.9 ± 4.7 μm, W = 95.5 ± 5.2 μm) for the sample to enter, featuring a homogeneous channel bottom and a regular edge that will favour sealing without leakage. A 3D confocal image of these results can be seen in Fig. 3g, in addition to a cross section profile (Fig. 3h), where regular vertical walls of the channels can be observed.

3.2 Micropatterning results and characterization

Two different protocols were used in the manufacturing process. In protocol 1, PLA was used to micropattern the bottom of inward channels, which were sealed directly using an adhesive film for immediate use. In protocol 2, we employed PLA to micropattern the top of outward channels, with the intention of later replicating them through PDMS soft lithography to obtain the final micromixers. It is worth mentioning that, in this case, walls were added to the masters in order to fill them with PDMS. This protocol makes possible the production of multiple replicas of the micromixers, a feature of great interest for scaling up the production process. In both cases, the following PLA parameters were used: an average power of 90 mW, 3 contiguous lines separated by 35 μm, 2 passes per line, a repetition rate of 1 kHz and a platform velocity of 1 mm s⁻¹.

3.2.1 Inward channels. Various images illustrating the results of protocol 1 are displayed in Fig. 4. One channel was intentionally left unpatterned as a control.

Fig. 4 Optical (top) and confocal (bottom) microscopy images of the micropatterned structures on the bottom of 3D printed microchannels, featuring: a) and e) none, b) and f) 90°, c) and g) 20°, and d and h) 45° oriented grooves, respectively. Scale bar: 300 μm. Magnification: 5×. i) Confocal image of the highlighted area in picture f). j) Picture of the 3D printed resin plate where all structures were micropatterned. An enlarged view of the inner part of one micromixer is shown. The measured groove parameters (W, L, D, p) are also denoted in the image.

In Fig. 4a and e, the printing quality is notorious, as evidenced by the consistent edge regularity and channel straightness. The characteristic roughness of the surfaces printed by SLA was studied in detail in our previous work,²² in which a value of S_a = 1.444 ± 0.247 μm was measured for the employed resin. Subsequently, following the application of PLA with the specified parameters on the bottom of the channel, we can observe the formation of oriented grooves. In these grooves, a set of distinctive parameters (width (W), length (L), depth (D), and period (p)) can be identified and measured using profiles derived from the confocal images. The values obtained are presented in Table 1. In the case of 90° oriented structures, the optical image (Fig. 4b) exhibits no thermal damage and consistent results in terms of structure formation at the bottom of the channel. When assessing their dimensions, we note that the width of these grooves (94.3 ± 8.3 μm) matched what was obtained in the parameter study (95.5 ± 5.2 μm).

Table 1 Measured parameters of the ablated structures at the bottom of the channel

Angle (°)	Width (μm)	Length (μm)	Depth (μm)	Period (μm)
90	94.3 ± 8.3	488.3 ± 8.1	243.5 ± 15.5	235.3 ± 3.3
20	86.6 ± 4.0	1429.3 ± 14.8	253.3 ± 11.1	167.0 ± 4.0
45	89.3 ± 2.5	631.8 ± 14.4	248.3 ± 9.8	189.7 ± 4.0

---

In terms of groove length, it is somewhat shorter than anticipated (designed channels had a 550 × 550 μm² section). This discrepancy arises from the manner in which the printer constructs square-section structures, resulting in a shape closer to a trapezoid,²² with a narrower base width compared to the top. Given that ablation takes place in this specific region, the grooves end up measuring less in length.

Additionally, a minor accumulation of residues is visible along the sides of the channel. This accumulation can be seen in the confocal image (Fig. 4f) and can be attributed to the challenge of effectively removing volatilized debris. The highlighted area in this image is presented in a 3D view in Fig. 4i, helping us to better understand the ablation results and the achieved depths for this orientation (243.5 ± 15.5 μm), which agree with the previously obtained results on a flat surface (230.9 ± 4.7 μm). The difference between the width and the period allows us to determine the width of the ridges, which are structures formed by the resin that is not subjected to ablation. These structures, measuring 140 μm in width, are slightly wider than the grooves and exhibit a squarer section.

Regarding the 20° oriented structures, Fig. 4c displays well-defined grooves that are slightly narrower (86.6 ± 4.0 μm) than those achieved at 90°. This difference is due to the overlapping of the three contiguous lines used in PLA when ablation is performed at a certain angle. Notably, the accumulation of residues in these inward channels is the most significant among all the observed, as evident in the confocal image (Fig. 4g). This can be attributed to the greater length of these structures (1429.3 ± 14.8 μm) in comparison with the others, which favours that a larger amount of material is volatilized and carried towards the edges of the channel during PLA. The period allows us to estimate a closer dimensional similarity between the grooves and ridges, which are approximately 80 μm in width in this case. Finally, these channels show the greatest of the depths obtained (253.3 ± 11.1 μm), due to the greater overlapping of the lines mentioned above.

For channels with 45° oriented structures (Fig. 4d), the width of the ridges (89.3 ± 2.5 μm) is an intermediate point between 0° and 20°, just as happens for the orientation angle. The same applies for the depth of the ridges (248.3 ± 9.8 μm). The confocal image (Fig. 4h) shows a subtle accumulation of debris in certain areas, somewhat distant from the edges of the channel. However, no thermal damage is observed in any case and the results agree with the ones obtained in section 3.1. The period indicates a suitable match between the grooves and ridges, of approximately 90 μm in width. The versatility of the proposed manufacturing technique has also enabled the creation of three micropatterned channels (and two controls) effortlessly and reproducibly on a single multichannel resin plate (Fig. 4j), where five unpatterned channels were printed at first. The total manufacturing time for the three structures has not exceeded fifteen minutes. The integration of these microstructures within the same platform allows for convenient experimentation and direct comparison of their performance. These devices can be used directly by sealing them using an adhesive film.

3.2.2 Outward channels. The outcomes of protocol 2 (corresponding to outward channels) are shown in Fig. 5 and 6, while Table 2 presents the values of the parameters of the structures. Just as in the previous section, we deliberately left the first channel without patterning, as shown in the confocal images (Fig. 5a), which is properly translated to the PDMS replica (Fig. 5e). The previously mentioned surface roughness of the employed resin is evident in the replica. This underscores the remarkable level of detail that PDMS can faithfully replicate, extending down to the micrometer scale.

Fig. 5 Confocal (top) and optical (bottom) microscopy images of the micropatterned structures on the top of printed microchannels (top) (a–d) and their corresponding PDMS replicas (bottom) (e–h), featuring: a) and e) none, b) and f) 90°, c) and g) 20°, and d) and h) 45° oriented grooves. The measured groove parameters (W, L, p) are also shown in the image. Scale bar: 300 μm. Magnification: 5×.

Fig. 6 3D confocal view of the micropatterned structures on the top of printed microchannels (a–c) and their corresponding PDMS (d–f) replicas featuring: a) and d) 90°, b) and e) 20° and c) and f) 45° oriented grooves.

Table 2 Measured dimensions of the ablated structures at the top of the channel and the corresponding dimensions of the PDMS replicas

	Angle (°)	Width (μm)	Length (μm)	Depth (μm)	Period (μm)
Resin master	90	98.3 ± 6.3	502.8 ± 9.5	301.3 ± 9.9	234.0 ± 7.0
	20	87.7 ± 2.1	1438.5 ± 30.7	299.3 ± 17.2	179.0 ± 3.0
	45	88.8 ± 5.6	648.3 ± 14.4	306.5 ± 12.9	182.3 ± 6.6
PDMS replica	90	123.0 ± 4.8	495.0 ± 4.8	293.3 ± 12.4	227.3 ± 4.6
	20	98.0 ± 4.6	1318.5 ± 36.1	299.0 ± 25.0	177.7 ± 16.5
	45	99.8 ± 5.1	690.8 ± 20.8	306.3 ± 39.5	188.3 ± 9.2

---

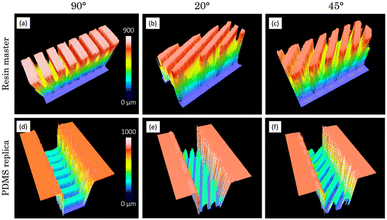
Regarding the channels with 90° oriented structures, the first step consisted of micropatterning the top of outward channels by PLA. Ablation and soft lithography results are shown in Fig. 5b and f and allow us to observe the correct formation of the grooves, featuring W = 98.3 ± 6.3 μm in the master of resin and W = 123.0 ± 3.8 μm in the replica. It is worth mentioning that this difference in size is since it is a replication process, the ridges in master are the structures that form the grooves in the replicas and vice versa. A very simple verification of these outcomes is that the sum of both widths must be equal to the period, which virtually happens within the standard deviations. Furthermore, the periods coincide for both the master and the replica, demonstrating the precision of the soft lithography technique used in this process. Regarding the length, the measured value for outward channels is greater than that of the inward ones. This is because during SLA printing, the outward channels release a larger amount of uncured resin, allowing them to achieve a less trapezoidal shape, closer to a square. The most significant difference compared to the previous case lies in the depth measurement (301.3 ± 9.9 μm), which is 70 μm greater than what was obtained during the parameter study on a flat surface. This increase originates from the ablation being carried out on a structure that is raised above its surroundings (Fig. 6a). As a result, the resin can be volatilized and eliminated without restrictions when surrounded by air. Finally, a more comprehensive 3D confocal view of the proper replication of the master structure into the PDMS replica can be observed in Fig. 6a and d.

For channels featuring structures oriented at 20°, the master grooves exhibit similar dimensions (W = 87.7 ± 2.1 μm and L = 1438.5 ± 30.7 μm) to the PDMS replicas (W = 98.0 ± 4.6 μm and L = 1318.5 ± 36.1 μm) and both are consistent with the study of parameters. Meanwhile, the depth follows the same trend as that obtained for 45°, being significantly greater than that achieved on a flat surface due to increased debris release, so deeper structures are obtained (Fig. 6b) and translated to replicas (Fig. 6e). A very illustrative result of the replication process explored in this section is the production of specular images of the original pattern, so that if the master structure is oriented at 20° (Fig. 5c), with reference to the vertical axis in the photo, the replica will be oriented at −20° (Fig. 5g). After the structures were fabricated and characterized through confocal microscopy, they were recreated using CAD software (Fig. 6g–i) to conduct further simulations.

3.3 Flow assays

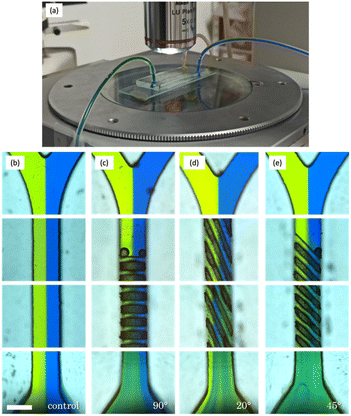
In order to demonstrate the efficiency of the micromixer fabricated, flow experiments were carried out using a peristaltic pump to assess their mixing performance (Fig. 7). Two different dyes (yellow and blue) were simultaneously introduced into the micromixers, representing distinct fluid streams (Fig. 7a). By observing the resulting colour patterns, the efficiency and effectiveness of the mixing process can be evaluated in terms of the homogeneity of the green colour obtained at the outlet. PDMS replicated micromixers were utilized due to their complete transparency. Resin micromixers are expected to yield similar results, but their opaqueness makes it challenging to capture images by optical microscopy.

Fig. 7 a) Experimental setup used in the flow assays where two dyes (blue and yellow) were mixed in the micromixers under an optical microscope. Optical microscopy images (5×) of the mixing test inside manufactured micromixers featuring b) none, c) 90°, d) 20°, and e) 45° oriented grooves. Scale bar: 500 μm.

In the first column (Fig. 7b), it is evident that the blue and yellow dyes remain segregated and do not mix effectively within the 25 mm microchannel. This is primarily due to laminar flow, characterized by flow streams moving in parallel layers with minimal interaction, caused by the absence of microstructures designed to induce turbulent mixing. Moving to the second case with structures oriented at 90°, as depicted in Fig. 7c, notable differences from the first image become apparent.

Initially, trapping is observed when the fluid interacts with the first set of structures. However, this issue seems to be localized, and, overall, the colours significantly mix at the device's outlet. This suggests that the 90° oriented structures do enhance the efficiency of dye mixing compared to the previous configuration without microstructures. Nevertheless, it is worth noting that the presence of blue colour dominance on the right side could be attributed to specific flow patterns or uneven distribution of structures within the device. In the next column, corresponding to structures oriented at 20° (Fig. 7d), effective mixing is also observed at the device's outlet. Nevertheless, visible streams of yellow colour, reminiscent of the blue streams in the previous micromixer, indicate that there are still areas where mixing is not entirely uniform. Finally, the micromixer featuring 45° oriented grooves, as illustrated in Fig. 7e, demonstrates the most promising results, with an extremely homogeneous mixture at the outlet. In this case, the green colour at the output exhibits the greatest uniformity observed, surpassing all other flow configurations.

In summary, the 45° configuration appears to overcome the limitations observed in the previous images, offering a high degree of mixture homogeneity. This makes it a promising choice for fluid mixing applications in micromixers. However, it's important to note that these experimental results are largely qualitative, making it challenging to draw definitive conclusions. As such, quantitative methods are needed to give us a better understanding of the system behaviour.

3.4 Numerical simulations

3.4.1 Simulation of manufactured micromixers. To quantitatively assess the effectiveness of the micromixers, simulations were conducted on the manufactured micromixers (Fig. 8) and mixing histograms were obtained. The water volume fraction is represented in the x-axis for two cross sections located at two distances, starting from the junction: x₁ = −5.1 mm (red histogram) and x₂ = −9.5 mm (blue histogram), arbitrarily chosen. On the other hand, the y-axis illustrates the percentage of counts recorded at these two sections. For the sections, their colour scalebar represents the volume fraction of water in each pixel, which can be interpreted as the degree of mixing. Volume fractions close to green coloured pixels indicate a balanced coexistence of both liquids, while reddish or bluish pixels represent the sole presence of one phase.

Fig. 8 Top view, transversal section, and histograms of the volume fraction (from 0 to 1) of two flow samples inside a) an unpatterned microchannel and manufactured micromixers featuring b) 90°, c) 20° and d) 45° micropatterned grooves. The histograms correspond to two different points of the micromixer, x₁ = −5.1 mm (red) and x₂ = −9.5 mm (blue). The corresponding efficient mixing index (EMI) is presented for each histogram.

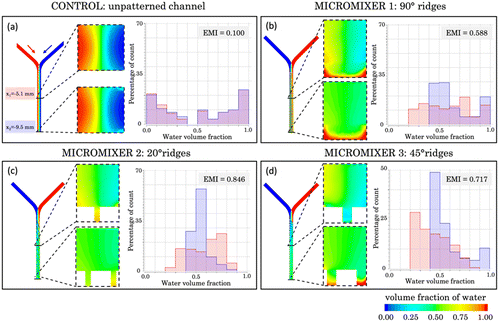
To quantitatively assess the degree of mixing in each histogram, we define the efficient mixing index (EMI) as

Henceforth, the EMI will be calculated at the x₂ cross section, as a higher degree of mixture is expected given the higher distance from the fluids' meeting point.

Fig. 8a shows a transversal section of the micromixer without structural elements at the bottom (acting as a control). The cross sections reveal poor liquid mixing performance, which agrees with the absence of green pixels. The histogram shows nearly identical lateral distributions for both cross sections across the microchannel, separated with a gap corresponding to the range of 0.4–0.5 water volume fraction. An EMI = 0.100 was obtained, implying that complete mixing is not achieved.

Fig. 8b illustrates the initially proposed micromixer featuring angled structures at a 90° orientation, designed to enhance the mixing process. In this configuration, the histograms display a more centralized pattern, signifying that a notorious portion of the sample is in a state of mixing. At position x₁, the majority of data points fall within the range of 0.2 to 0.8 water volume fraction, while at position x₂, the degree of mixture increases reaching an EMI = 0.588. It's worth noting that the histograms show a substantial portion of the sample composed of pure water (between 0.9 and 1), accounting for 15% at x₁ and almost 20% at x₂. This phenomenon is particularly noticeable in the cross-section, where it becomes evident that in the lower region of the mixer, corresponding to the grooves, water becomes trapped. This can be explained by the higher density of the water used in the simulations (ρ₁ = 998.2 kg m⁻³) compared to the other fluid (ρ₂ = 997.2 kg m⁻³), causing the fluid dynamics to promote downward flow and preventing effective interaction between the samples. Nevertheless, if we disregard the region containing the grooves, the mixture is highly favourable at position x₂, as indicated by the green colour in the top region, corresponding to 0.5 water volume fraction. In the case of the micromixer featuring 20° angled structures (Fig. 8c), a significant improvement in mixing performance was observed compared to the two previous cases discussed. At position x₁, the histogram distribution shows a wide profile, and the largest bar of the histogram (27%) corresponds to points clustering around 0.6 and 0.8 water volume fraction.

However, the micromixer demonstrates its most promising outcomes, showcasing an EMI = 0.846 at position x₂, which is closest to achieving complete mixing. This substantial improvement is visually evident in the cross-sectional views, where colour variations persist at x₁ but disappear at x₂, presenting a fully homogeneous distribution. Nevertheless, a phenomenon like the previous case is observed, with the lower structures tending to trap water. Nonetheless, if this lower region is excluded, the results are of total mixture.

Finally, results corresponding to the micromixer with a 45° angled structure (Fig. 8d) position correspond to an intermediate configuration between the results obtained for the 90° and 20° counterparts. Specifically, when examining position x₁, a significant portion of data points falls within the range of 0.2 to 0.4 for the water volume fraction. This performance ameliorates at position x₂, where an EMI = 0.717 was obtained, indicating a high mixing performance. However, like previous cases, unmixed water (accounting for 10%) becomes apparent in x₂, primarily located in the lower region and confined within the microstructures.

These findings emphasize the pivotal role of the structural micromixer design in the mixing process. A closer examination reveals that structures performed at a 20° angle consistently deliver the most favourable outcomes over their counterparts at 90° and 45°, facilitating more thorough and uniform fluid blending. However, these simulations slightly diverge from experimental findings that favour the 45° angle. This can be attributed to not only simulations assuming highly ideal conditions but also experiments involving inherent variability. In terms of simulation, several simplified conditions were employed for computational efficiency, such as no sliding wall (not applicable to PDMS, an elastic material), isothermal and isobaric conditions (where temperature and pressure were not controlled during experiments), use of pure water and a similar sample (compared to dyed water used experimentally), short simulation time, neglect of gravity, and mesh size considerations. Experimentally, deviations arise from roughness resulting from the PDMS soft lithography process. This process transfers both resin and laser generated roughness, leading to less-than-ideal groove edges, a factor neglected in simulations.

Nevertheless, in both cases (simulation and experiments), it is clear that the incorporation of microstructures at the bottom of the mixer significantly enhances mixing compared to a flat channel (EMI = 0.846 in Fig. 8c compared to EMI = 0.100 in Fig. 8a). Among the various angle possibilities, mixing improves as the angle decreases from 90° (perpendicular to the channel).

3.4.2 Simulation of other micromixer configurations. Other micromixer configurations were evaluated to identify optimal conditions for enhancing mixing efficiency. Fig. 9 displays 15 mixing histograms at positions x₁ and x₂ (see Fig. 8), corresponding to different scenarios. Fig. 9a–f feature micromixers where new geometries have been considered, whereas Fig. 9g–o display cases for different Re values.

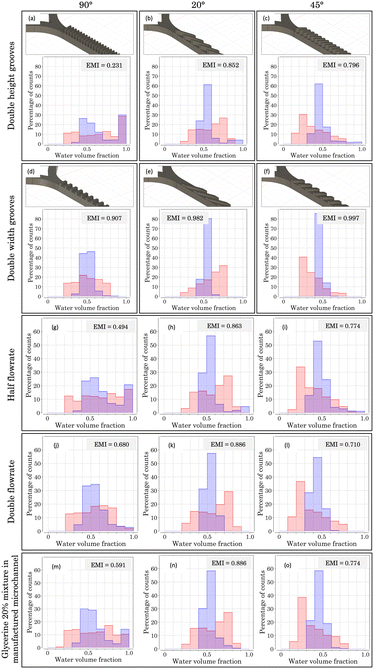Fig. 9 CAD images and mixing histograms of the volume fraction (from 0 to 1) of two flow samples inside a microchannel with a and d) 90°, b and e) 20° and c and f) 45° micropatterned grooves, respectively. Double height (first row) and double width (second row) grooves were considered, with respect to dimensions of micromixers from Fig. 8. Mixing histograms of two flow samples introduced with a halved flowrate (third row) and a doubled flowrate (fourth row) inside a microchannel with g and j) 90°, h and k) 20° and i and l) 45° micropatterned grooves, with respect to those of Fig. 8. Mixing histograms of two glycerine–water 20% mixture samples introduced inside a microchannel with m) 90°, n) 20° and o) 45° micropatterned grooves using the micromixers presented in Fig. 8. The histograms were obtained for two different positions of the micromixer, x₁ = −5.1 mm (red) and x₂ = −9.5 mm (blue). The corresponding EMIs are included.

Starting with Fig. 9a, featuring angled structures at a 90° orientation, poor mixing conditions are achieved, as an EMI = 0.231 indicates. In addition, a noticeable proportion of pure water (volume fraction between 0.9 and 1.0) is observed, reaching almost 30% at both x₁ and x₂ positions. This behaviour aligns with that presented in Fig. 8b: the appearance of a downward flow due to the density difference between the fluids. For the case of double groove height, a heightened blockage of the higher density fluid occurs, intensifying the phenomenon.

Conversely, considering the double width scenario (Fig. 9d), a very promising result is achieved. Doubling the width enables the higher density water not to be blocked onto the groove bottom, allowing the downward fluid to be mixed across the structure. This structural change led to an EMI = 0.907, resulting in a micromixer almost four times more efficient than the previous case.

For Fig. 9b, c, e and f, improvements in the mixing conditions when doubling the width are not so noticeable. For the case of double height grooves, the 20° configuration (Fig. 9b) offers a higher mixing performance, reaching an EMI = 0.852, which surpasses the one obtained for the 45° configuration (0.796), presented in Fig. 9c. In both cases, a minor proportion of downward flow is observed, in a lower percentage compared to the 90° case. These alterations stem from the geometry of the micropattern, since slanted grooves create an asymmetry in the system, fostering the introduction of the fluid coming from the branch most parallel to the grooves. Consequently, the opposite effect occurs on the counter branch. In our simulations, the lower density fluid is introduced through the most parallel branch, easing its mixture with the higher density one retained in the lower region. Therefore, a high degree of mixture is achieved, as can be checked in their corresponding EMIs.

Fig. 9e and f showcase the double width scenario for micromixers with grooves at 20° and 45°, respectively. Under these conditions, the most promising results are achieved, with an almost perfect homogeneous mixture, as indicated by their EMIs (0.982 for 20° and 0.997 for 45°). This remarkable improvement with respect to 90° can be explained considering the geometrical asymmetry present in the system (as mentioned above), which enables the low density fluid to mix favourably with the high density phase, which does not confine on the groove bottom.

Further simulations considering half height and half width grooves were also performed (data not shown), and certain similarities with the previously presented cases can be outlined. For the case of half width, outcomes are comparable to those obtained when the height is doubled, leading to low EMIs, especially for the 90° case (0.423). On the other hand, halving the height fosters the mixing, as checked by the EMIs for the three orientations, reaching values close to 0.900.

What is more, simulations varying Re were carried out to study the mixing properties of the micromixer under different fluid conditions. On the one hand, Fig. 9g–l present the mixing histograms obtained for micromixers with manufactured dimensions (as presented in Fig. 8), where the flow rate has been doubled (Q = 2 ml min⁻¹) or halved (Q = 0.5 ml min⁻¹). For its part, Fig. 9m–o display the results obtained when an aqueous solution of water with glycerine at 20% has been considered (see section 2.2.2).

First, Fig. 9g–i present a half flow rate case (corresponding to a half Re scenario). For the 90° configuration (Fig. 9g), the obtained EMI = 0.494 is almost half that obtained for 20° (0.863) and 45° (0.774). This result can be attributed to an inertia reduction in both phases, which favours the blockage of high density fluid onto the bottom of the grooves. This is depicted in the mixing histogram (Fig. 9g), where a concentration of pure liquid above 20% (corresponding to the 0.9–1 bin) is observed. In the 20° (Fig. 9h) and 45° (Fig. 9i) cases, this phenomenon is not dominant due to the asymmetry of slanted grooves, leading to a behaviour similar to the manufactured micromixer outcomes (Fig. 8c and d): the lower the angle of the grooves, the higher the EMI (0.774 for 45° and 0.863 for 20°).

Fig. 9j–l feature a double flow rate (double Re) scenario. Under these conditions, the mixing performance for the 90° configuration (Fig. 9j) offers a higher EMI than the half flow rate case (0.680 vs. 0.494). This outcome arises from the higher velocity of the fluids (resulting in higher inertia) that decreases the downward fluid and favours the mixing inside the grooves. For the 20° (Fig. 9k) and 45° (Fig. 9l) oriented grooves, the EMIs are similar to the half flow rate scenario, where the 20° case offered a higher EMI (0.886).

Moreover, simulations with a different flow rate on each branch were carried out (data not shown), considering a doubled or halved flowrate only in one of the branches, while keeping the other one at Q = 1 ml min⁻¹. For these 6 possible scenarios, a poor mixing performance was observed, leading in all cases to EMIs around 0.000 and 0.400. These results stem from the remarkable difference in flowrate values, which inhibits the mixing process and clusters the data in the borders of the histogram (pure volume fractions). The following conclusion is obtained from this study: the more similar the flow rate inputs are, the more efficient the mixture is.

Finally, Fig. 9m–o feature simulations considering a water–glycerine sample. These studies revealed a remarkable resemblance between the EMIs and histogram shapes obtained for the manufactured micromixers: 0.591 (Fig. 9m) vs. 0.588 (Fig. 8b) for 90°, 0.886 (Fig. 9n) vs. 0.846 (Fig. 8c) for 20°, and 0.774 (Fig. 9o) vs. 0.717 (Fig. 8d) for 45°. These findings demonstrate the mixing adaptability of our slanted micromixers, capable of yielding comparable outcomes considering various fluid samples, despite alterations in their physical properties. For instance, this versatility is evident when employing glycerine, a substance commonly utilized in microfluidic applications.⁴² Comparing the simulations carried out for the manufactured micromixer (Fig. 8) with new configurations considered in this section (where grooves and Re have been varied), two fundamental conclusions emerge.

First, doubling the width of the grooves results in a favouring scenario for more efficient mixing, leading to an almost perfect mixture. Second, the versatility of the manufactured micromixers is demonstrated when considering diverse physical fluid properties, yielding results closely resembling the original.

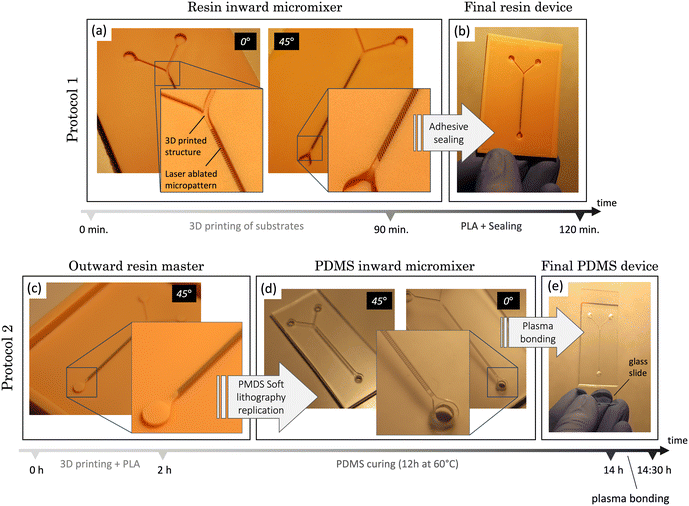
3.5 Final devices

The versatility of this technique has been proved, enabling the straightforward, cost-effective, rapid, and user-friendly production of six distinct slanted micromixers for microfluidic applications. These micromixers feature micropatterns at 20°, 45°, and 90° and are fabricated in resin or PDMS (Fig. 9). Protocol 1 (depicted in Fig. 10a and b) enables the manufacturing of microreactors within a timeframe of less than 2 hours (1 h and 30 min for substrate printing and 30 min for ablation). For its part, protocol 2 (Fig. 10c–e) requires a longer duration, due to the PDMS curing process, which spans approximately 12 hours after printing and PLA. However, it is noteworthy that this replication step is very common in microfluidics workflows and can be seamlessly integrated into the researcher routine by allowing the components to remain in the oven overnight (furthermore, some authors use a shorter curing time⁴³). After that, the final step consists of bonding the PDMS replicas to glass, which takes less than half an hour. Given the diverse nature of research projects, each user must focus on selecting the most suitable protocol in terms of time and resources to achieve optimal results.

Fig. 10 The two proposed protocols for manufacturing microreactors (micromixers in this case). In protocol 1, the sequence begins with the 3D printing of a resin substrate, followed by PLA of inward channels at a) various orientations (e.g., 0°, 45°). These channels can then be b) sealed using an adhesive stick, and the entire process is completed in just 2 hours. Protocol 2 initiates with the c) 3D printing of masters (with added walls to retain the replication polymer) and PLA of outward channels, followed by the d) soft lithography replication of the structures using PDMS. Subsequently, the replicas can be peeled off and e) plasma bonded to a glass slide. This protocol has an approximate duration of 14 h.

In essence, the proposed process in the article represents a significant reduction in manufacturing time compared to photolithography, the predominant technology in microfluidics manufacturing, which can require days to complete. Another advantage of this technique is its capability to easily modify micropatterning designs simply by employing the laser software, virtually in real time. This enhances the prototyping and testing processes for the devices. Moreover, our method is contaminant-free and generates minimal waste as the 3D printer used to fabricate the masters reuses liquid resin that remains unphotopolymerized during the process. In the ablation process, only a negligible amount of dust (vaporized resin) is produced, which is promptly removed by the laser cleaning system.

Conclusions

In this work, a novel hybrid technique combining PLA and SLA is proposed for manufacturing and testing passive slanted micromixers, which are of great interest in the field of microfluidics. For this, an optimization of laser ablation power for microchannel fabrication was carried out. The width and depth of the channels were measured, finding that power is correlated with the channel width, and more passes generally widen the channels. However, high power pulses may cause irregularities. The optimal parameters for regular, homogeneous channels were identified to be 90 mW, a repetition rate of 1 kHz, a platform velocity of 1 mm s⁻¹ and 2 passes, resulting in channels with a width of 39.6 ± 1.9 μm and a depth of 129.1 ± 2.3 μm. To enhance fluid flow and proper PDMS removal, wider channels were desired, achieved by ablating two or more contiguous lines with varying separations. The results showed that ablating three contiguous lines with a 35 μm separation provided the most suitable channels, with a width of 95.5 ± 5.2 μm and a depth of 230.9 ± 4.7 μm.

Using these parameters, two manufacturing protocols were developed, with the goal of manufacturing various groove patterns with different orientations in the channels (that will enhance mixing). Protocol 1 is focused on micropatterning the bottom of inward channels using PLA, to be sealed directly with an adhesive film for immediate use. In the case of 90° oriented structures, optical images revealed consistent groove formation, featuring a width of 94.3 ± 8.3 μm and a depth of 243.5 ± 15.5 μm. For 20° structures, narrower grooves (86.6 ± 4.0 μm) were observed due to overlapping lines and showed a greater depth (253.3 ± 11.1 μm). For 45° structures, an intermediate scenario was obtained. Protocol 2 starts with the creation of grooves on the top of outward channels using PLA for subsequent replication through PDMS soft lithography, facilitating scalable production. For the 90° orientation, proper groove formation (W = 123.0 ± 4.8 μm) is achieved. In this protocol, grooves in the master become ridges in the replicas and vice versa. The depth of master grooves is notably greater (301.3 ± 9.9 μm) than that obtained in protocol 1, since ablation on an elevated structure increases debris release. Figures show a 3D confocal view of successful master-to-replica transfer and show similar surface roughness, demonstrating the high replication capability of PDMS.

Flow experiments were conducted in micromixers with different orientations (90°, 20°, and 45°) using a peristaltic pump and coloured dyes. The 45° orientation presents the most homogeneous mixing, offering promise for fluid mixing applications, but quantitative methods are required for more definitive insights. For this, CFD simulations were used, revealing the following behaviours: in a control micromixer without structures, mixing was ineffective; a micromixer with 90° structures improved mixing, with some trapped water in the grooves; the 20° angled structures demonstrated significant improvement, with more homogeneous mixing capabilities than the others. Finally, the 45° angled structures provided intermediate results. Different scenarios involving new geometries, flowrates and physical properties were introduced, yielding the following conclusions: first, doubling the groove width significantly enhances mixing efficiency, resulting in a nearly perfect mixture. Second, the micromixers demonstrate high versatility when considering various fluid properties (density and viscosity), producing outcomes closely resembling the original conditions.

In brief, the simulation results favoured the 20° structures, while the experiments preferred the 45° ones, but both showed that microstructures enhance mixing compared to flat channels, with lower angles contributing to better mixing.

In summary, a significant advancement for the fabrication of passive micromixers is presented, using a versatile hybrid technique that combines SLA and PLA in their most suitable dimensional range.

Author contributions

Bastián Carnero: methodology, validation, investigation, writing – original draft and review. Yago Radziunas-Salinas: implementation of the computer code, formal analysis, critical review. Bruno Kotksa Rodiño-Janeiro: conceptualization, supervision. Sylvana Varela Ballesta: supervision of the computer code. M. Teresa Flores-Arias: conceptualization, supervision, writing, project administration, funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been supported by contracts: PID2022-138322OB-100 MCIN/AEI/10.13039/501100011033/FEDER, UE and Consellería de Educación Xunta de Galicia/FEDER ED431B 2023/07. B. Carnero acknowledges GAIN/Xunta de Galicia for contract 11-IN606D-2021-2604925. Y. Radziunas-Salinas acknowledges Ministerio de Ciencia, Innovación y Universidades for contract FPU22/01231.

References

1. G. M. Whitesides, Nature, 2006, 442, 368–373.
2. M. Long, M. A. Sprague, A. A. Grimes, B. D. Rich and M. Khine, Appl. Phys. Lett., 2009, 94, 133501.
3. A. Agha, W. Waheed, I. Stiharu, V. Nerguizian, G. Destgeer, E. Abu-Nada and A. Alazzam, Discover Nano, 2023, 18, 18.
4. K. Guo, Y. Chen, Z. Zhou, S. Zhu, Z. Ni and N. Xiang, Electrophoresis, 2022, 43, 2184–2194.
5. F. Bally, C. A. Serra, V. Hessel and G. Hadziioannou, Chem. Eng. Sci., 2011, 66, 1449–1462.
6. D. Ziegenbalg, C. Kompter, F. Schönfeld and D. Kralisch, Green Processes Synth., 2012, 1(2), 211–224.
7. K. Sato, A. Hibara, M. Tokeshi, H. Hisamoto and T. Kitamori, Adv. Drug Delivery Rev., 2003, 55, 379–391.
8. M. A. Burns, B. N. Johnson, S. N. Brahmasandra, K. Handique, J. R. Webster, M. Krishnan, T. S. Sammarco, P. M. Man, D. Jones, D. Heldsinger, C. H. Mastrangelo and D. T. Burke, Science, 1998, 282, 484–487.
9. A. J. Conde, I. Keraite, A. E. Ongaro and M. Kersaudy-Kerhoas, Lab Chip, 2020, 20, 741–748.
10. A. Ganguli, A. Mostafa, J. Berger, M. Y. Aydin, F. Sun, S. A. S. D. Ramirez, E. Valera, B. T. Cunningham, W. P. King and R. Bashir, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 22727–22735.
11. Y. Wang, J. Zhe, B. T. F. Chung and P. Dutta, Microfluid. Nanofluid., 2008, 4, 375–389.
12. D. Koo and H. So, Sci. Rep., 2022, 12, 6346.
13. R. H. Liu, M. A. Stremler, K. V. Sharp, M. G. Olsen, J. G. Santiago, R. J. Adrian, H. Aref and D. J. Beebe, J. Microelectromech. Syst., 2000, 9, 190–197.
14. M. A. Ianovska, P. Mulder and E. Verpoorte, Novel micromixers based on chaotic advection and their application – a review, 2018.
15. A. D. Stroock, S. K. W. Dertinger, A. Ajdari, I. Mezić, H. A. Stone and G. M. Whitesides, Science, 2002, 295, 647–651.
16. L. Zhendong, L. Yangcheng, W. Jiawei and L. Guangsheng, Chem. Eng. J., 2012, 181–182, 597–606.
17. C. S. Carrell, C. P. McCord, R. M. Wydallis and C. S. Henry, Anal. Chim. Acta, 2020, 1124, 78–84.
18. D. Nieto, T. Delgado and M. T. Flores-Arias, Opt. Lasers Eng., 2014, 63, 11–18.
19. K. L. Wlodarczyk, D. P. Hand and M. M. Maroto-Valer, Sci. Rep., 2019, 9, 20215.
20. A. I. Gómez-Varela, R. Sanchez, B. Carnero, L. Diaz-Gomez, M. T. Flores-Arias and C. Bao-Varela, Opt. Express, 2022, 30, 37536.
21. S. Bai, D. Serien, A. Hu and K. Sugioka, Adv. Funct. Mater., 2018, 28, 1706262.
22. B. Carnero, C. Bao-Varela, A. I. Gómez-Varela, E. Álvarez and M. T. Flores-Arias, Mater. Sci. Eng., C, 2021, 129, 112388.
23. C. Turpin, M. L. Apalama, B. Carnero, A. Otero-Cacho, A. P. Munuzuri, M. T. Flores-Arias, E. Vélia, O. Meilhac, E. Bourdon, E. Álvarez and P. Rondeau, Cell, 2022, 11, 2200.
24. A. I. Shallan, P. Smejkal, M. Corban, R. M. Guijt and M. C. Breadmore, Anal. Chem., 2014, 86, 3124–3130.
25. A. P. Kuo, N. Bhattacharjee, Y. Lee, K. Castro, Y. T. Kim and A. Folch, Adv. Mater. Technol., 2019, 4, 1800395.
26. S. Corbel, G. Charles, N. Becheikh, T. Roques-Carmes and O. Zahraa, Virtual Phys. Prototyp., 2012, 7, 203–209.
27. M.-C. Fournier, L. Falk and J. Villermaux, Chem. Eng. Sci., 1996, 51, 5053–5064.
28. C. Xu, S. E. Barnes, T. Wu, D. A. Fischer, D. M. DeLongchamp, J. D. Batteas and K. L. Beers, Adv. Mater., 2006, 18, 1427–1430.
29. J. T. Cabral, S. D. Hudson, C. Harrison and J. F. Douglas, Langmuir, 2004, 20, 10020–10029.
30. M. Abonnenc, L. Dayon, B. Perruche, N. Lion and H. H. Girault, Anal. Chem., 2008, 80, 3372–3378.
31. B.-U. Moon, S. Koster, K. J. C. Wientjes, R. M. Kwapiszewski, A. J. M. Schoonen, B. H. C. Westerink and E. Verpoorte, Anal. Chem., 2010, 82, 6756–6763.
32. B.-U. Moon, M. G. De Vries, C. A. Cordeiro, B. H. C. Westerink and E. Verpoorte, Anal. Chem., 2013, 85, 10949–10955.
33. X. Shi, Y. Xiang, L.-X. Wen and J.-F. Chen, Ind. Eng. Chem. Res., 2012, 51, 13944–13952.
34. Y. Hwang, O. H. Paydar and R. N. Candler, Sens. Actuators, A, 2015, 226, 137–142.
35. H. N. Chan, Y. Chen, Y. Shu, Y. Chen, Q. Tian and H. Wu, Microfluid. Nanofluid., 2015, 19, 9–18.
36. D. D. O. Maionchi, L. Ainstein, F. P. Dos Santos and M. B. De Souza Júnior, Int. J. Heat Mass Transfer, 2022, 194, 123110.
37. S. L. Florez, A. L. Campaña, M. J. Noguera, V. Quezada, O. P. Fuentes, J. C. Cruz and J. F. Osma, Micromachines, 2022, 13, 970.
38. C. Casas-Arozamena, A. Otero-Cacho, B. Carnero, C. Almenglo, M. Aymerich, L. Alonso-Alconada, A. Ferreiros, A. Abalo, C. Bao-Varela, M. T. Flores-Arias, E. Alvarez, A. P. Munuzuri and M. Abal, Sci. Rep., 2021, 11, 23231.
39. J. Aubin, D. F. Fletcher and C. Xuereb, Chem. Eng. Sci., 2005, 60, 2503–2516.
40. S. P. Kee and A. Gavriilidis, Chem. Eng. J., 2008, 142, 109–121.
41. M. S. Williams, K. J. Longmuir and P. Yager, Lab Chip, 2008, 8, 1121.
42. S. Wang, X. Huang and C. Yang, Lab Chip, 2011, 11, 2081.
43. G. V. Kaigala, S. Ho, R. Penterman and C. J. Backhouse, Lab Chip, 2007, 7, 384.

---