Microflow sensing and control using an in-channel birefringent biomembrane

Abstract

This study describes the function, optimization, and demonstration of a new class of passive, low-cost microfluidic flow meters based on birefringent chitosan biomembranes analyzed by polarized microscopy. We subjected the membrane to dynamic flow conditions while monitoring the real-time response of its optical properties. We obtained figures of merit, including the linear response operating range (0 to 65 μL min⁻¹), minimum response time (250 ms), sensitivity (2.03% × 10⁻³ μL⁻¹ min), and minimum sensor longevity (1 week). In addition, possible sources of interference were identified. Finally, we demonstrate the membrane as a low-cost flow rate measurement device for the close loop control of a commercial pressure-driven pump. Preliminary experiments using a basic PID controller with the membrane-based flow rate measurement device showed that stable control could be achieved and the system could reach steady-state behavior in less than 15 seconds. Analysis of fundamental limits to sensor response time indicate the potential for faster steady-state behaviour.

---

Introduction

Monitoring of liquid flow rates and related hydrodynamic properties in microfluidic devices has become increasingly important in biomedical research and analytical chemistry. Examples include flow fractionation of cells and particles,^1–3 implantable drug delivery devices,⁴ nanomaterial synthesis,⁵ and bacteriology and biofilm studies.^6–8 With accurate monitoring comes accurate control of flow rates, which is essential for optimizing various processes and ensuring efficient performance. Flow rate measurements are especially important for an emerging class of pumping systems that require feedback control over the pressurized head space above a liquid reservoir, as opposed to volume-controlled pumps such as syringe, gear, or peristaltic pumps. Though they are more complex to control, pressure-driven flow systems can outperform volumetric systems thanks to their near-instantaneous response time, lack of flow pulsation, and the resulting opportunity for precision and automation. However, until now, one of the major hurdles to wider penetration into the market is the high cost associated with so-called “active” flow meters and the lack of readiness of sensitive passive flow meters.⁹

Commercial flow meters are usually standalone devices that are integrated into the liquid supply flow path usually downstream of the pressure pump. Most of these use an active thermal approach in which a temperature sensor is integrated into the downstream flow path of a heating element within the flow meter. Typically, the sensor is placed in-line with the microfluidic device,¹⁰ so it is important to consider potential thermal effects on samples such as living cells or thermosensitive molecules and materials.¹¹ Another active measurement approach that is gaining interest is based on the Coriolis effect. These flow meters measure both flow rate and liquid density by monitoring motion of a U-shaped channel that contains a conducting layer under the application of a constant magnetic field.^12,13 These systems benefit from a wider range of applicable flow rates and solution properties, but they are even more complicated and costly than thermal sensors.

To overcome drawbacks of cost and complexities related to active flow meters,⁹ it will be necessary to develop new approaches, especially those based on so-called “passive” sensing. Imbedded deformable features (microscale films, cantilevers, and springs)^14–16 are one option, but their integration may complicate the fabrication process.^17–19 The low cost and simplicity of differential pressure flow meters are promising,^20,21 but their dependence on solution parameters and applicability to flow ranges may limit them to point-of-use applications.⁹

Excellent, distortion-free opitical transmisison through most microfluidic devices has led microscope imaging to become a dominant measurement modality in microfluidics.²² As such, approaches to flow rate metering have also included imaging approaches. One example was the inclusion of a flexible membrane that generated interference patterns in an air-gap cavity, serving as a robust optofluidic version of a pressure sensor that can correlate to a wide range of flow rates.²³ While this idea requires detailed device/sensor design considerations along with some restrictions on the dimension of the channel, it paves the way for other microscope-based flow meters that use an optical membrane that responds to flow.

Our group is pursuing the development of functional biomaterials for microfluidic applications.^24,25 Chitosan is a birefringent hydrogel material that is readily available, low in cost, biocompatible and biodegradable and can be formed into membranes²⁶ and nanoparticles.^27,28 Moreover, chitosan can be sourced from marine biowaste and benefits from new techniques to sustainably deacetylate the starting material, chitin.²⁹ The use of microfluidic tools in synthesizing and studying chitosan-based materials is helping to accelerate the pace of their development³⁰ and greatly expands the range of applications.³¹ Like many elastomer hydrogels, chitosan membranes can contain regions in which polymer chains are highly organized, yielding interesting optical properties³² and applications.³³ Indeed, under flow, both dissolved chitosan and solid membranes have demonstrated birefringent properties.^34,35 Recently, birefringent chitosan membranes were successfully assembled and characterized in a microfluidic environment under certain flow conditions.³⁵

In this work, we prepared a birefringent chitosan membrane in an X-shape microfluidic device using the method reported in earlier publications.²⁵ The membrane was observed using an optical microscope with fixed crossed polarizers to measure its relative birefringence (RB), which is defined in the experimental section (eqn (1)).

This contrasts with full birefringence measurements, which require rotation of the crossed polarizers as discussed in the experimental section. We discovered that the relative birefringence intensity depended on the applied flow rate and that this relationship was constant, sensitive to small changes in flow conditions, and repeatable over long durations. As such, we demonstrate the proposed flow meter as a low-cost sensor and feedback element for closed-loop controlled pressure-driven flow systems.

Results

Microfluidic device and system configuration

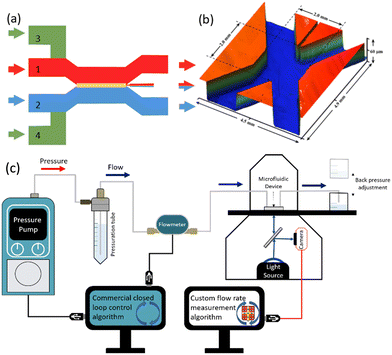
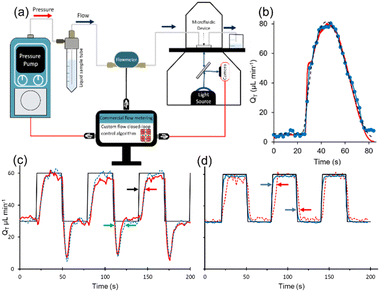
Chitosan membrane synthesis in polydimethylsiloxane (PDMS) microfluidic channels has been previously reported.²⁵ The microfluidic device includes 4 inlets and 3 outlets connected to an X-shape channel (Fig. 1a). The small middle exit channel was centered between the two principal exit channels to help centre and anchor the membrane as demonstrated previously.²⁵ We take advantage of multiple upstream inlets, which allow rapid switching between different membrane precursor solutions and phosphate-buffered saline (PBS, pH 7.4) for real-time control over membrane synthesis, as demonstrated previously.²⁵ In brief, the acidified chitosan solution and the basic NaOH solution were flowed through inlets 1 and 2 at volumetric flow rates Q_C and Q_B, respectively. Due to the more viscous chitosan solution, a flow rate ratio of Q_B/Q_C = 26 was used to position the co-flow interface and the subsequent membrane growth at the center of the channel under a wide range of total flow rates (Q_T = Q_B + Q_C), from Q_T,low = 50 to Q_T,high = 500 μL min⁻¹. This was accomplished while the flow of a phosphate buffered saline (PBS) solution through inlets 3 and 4 was stopped (Q_PBS = 0 μL min⁻¹) (Fig. 1a). When the membrane grew to approximately 40 μm, the precursor solutions were stopped (Q_B = Q_C = 0 μL min⁻¹) and the PBS flow was started (Q_PBS = 100 μL min⁻¹) for 5 min. Membrane thicknesses between 15 μm to 430 μm have been previously obtained by varying the flow rate or pH of the basic solution.²⁵ The dimensions of the middle part of this device are shown in Fig. 1b, was obtained by scanning an open channel device with a 3D optical profilometer (Contour GT-K, Bruker, USA). These include critical dimensions: height, H = 60 μm and total channel width, W = 2 mm.

Fig. 1 (a) Schematic of the X-channel microfluidic device showing the flow paths for the basic solution stream (inlet 1, red), acidified chitosan solution (inlet 2, blue), and PBS solutions (inlets 3 and 4, green). The position of the membrane (yellow) at the aperture between the two sides is formed during flow. Arrows indicate direction of flow. (b) 3D profilometer image of a PDMS device. (c) System setup used for experiments involving a commercial pressure pump with feedback control provided by a commercial flow meter. The chitosan flow meter is located on a microscope and transmission images are transferred to a computer where they are analysed by a custom flow rate measurement algorithm. Backpressure is adjusted by vertical displacement of the output beaker.

The control system was configured for two operational modes. Fig. 1c shows the first setup in which a commercial pressure pump and accompanying flow meter control the flow rate via a commercial closed loop control algorithm. This setup was used to validate the response from the chitosan flow meter. This was accomplished using a custom flow rate measurement algorithm enabling a comparison to the output from the commercial flow meter. A second configuration is discussed later in this work, in which the chitosan membrane was used as a feedback controller for the pressure pump.

Flow synthesis and characterization of the chitosan membrane

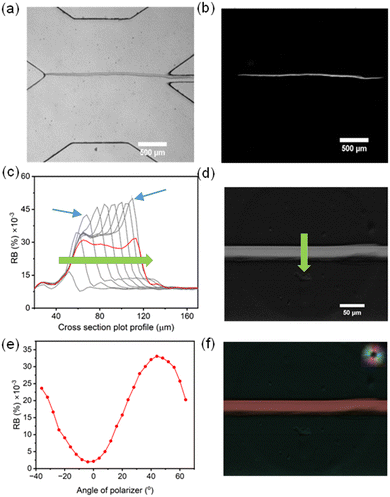
We synthesized a membrane, as shown in the transmission microscope image in Fig. 2a, using a total flow rate of Q_T = 500 μL min⁻¹ before stopping the growth. In most of this work, we preferred a rapid measurement that could be used to track real-time changes to flow rate. This was achieved by introducing two linear polarizers in the light path in a crossed orientation, one above and one below the microfluidic device, to obtain a measurement of the cross-polarized membrane light transmission (Fig. 2b).³⁶ We obtained RB maps during the membrane growth process via time-lapse imaging to understand the distribution of the ordered (anisotropic) regions as a function of space and time. The resulting plot of the RB intensity along the membrane cross-section of a typical thin membrane is shown in Fig. 2c. In this figure, a higher RB is observed at the growing edge (chitosan solution side) during membrane formation, though the intensity subsided after the leading edge advanced away from the former interface positions. We hypothesize that the high RB values were the result of shear-induced alignment of the nascent, pre-solidified chitosan polymer strands that were partially anchored and conformable in the low pH environment at the leading membrane edge. The figure also shows that the RB at the leading edge increased as the membrane grew. We believe this to be at least partially related to small increases to shear stress due to a reduction in the effective channel width during membrane growth.³⁵ However, despite the small changes to the channel dimensions, changes to the RB were rather pronounced. For example, the RB values increased by 22% at the high-sensitivity leading edge while the membrane width increased from 25 to the final width of 60 μm (see blue arrows in Fig. 2c) despite increases to shear stress of only 1.8%. This stronger than expected relationship between shear stress (which relates to channel width as τ ∝ W⁻¹, see eqn (2)) and RB may be related to the previously mentioned effect of local acidic conditions during membrane growth. In contrast, previously deposited chitosan strands away from the shear/growth front can locally relax, resulting in a loss of RB in the deeper portions of the membrane. After washing the membrane with PBS buffer, the previously noted peak in RB at the formerly acidic membrane edge was nearly eliminated (red line in Fig. 2c), likely because of the reduced mobility of chitosan strands above chitosan pK_a. While this rendered the overall RB more uniform across the entire membrane, small increases in RB can be seen at both edges due probably to the direct application of shear stress at those sites. Of interest, the RB intensity at the formerly high pH side was between 10 and 15% lower after application of the 7.4 pH PBS buffer. We propose that the high pH caused membrane densification which could result in higher percent crystallization. To test the role of pH, after membrane synthesis and washing with PBS buffer, we cycled between a 13 pH liquid and the 7.4 pH PBS solution. The resulting RB values oscillated with the PBS/high pH cycling, indicating that the solution pH was causing repeatable changes to the membrane structure (ESI,† Section S1). It should also be noted that the difference between ionic strength of the two solutions (60%) may also played a role in changes to RB. Taken together, the results at different pH values indicate that these membranes may also be efficient sensors of solution pH or salinity.

Fig. 2 (a) A wide-field transmission microscope image and (b) a polarized optical microscopy image showing the chitosan membrane under a total PBS flow rate of Q_T = 20 μL min⁻¹. (c) A series of curves of the cross-sectional plot profile of RB intensity of the chitosan membrane during formation. The red curve represents the cross-sectional plot profile of the membrane after washing the channel with PBS. The blue arrows indicate the growth edge of the membrane RB profile after the membrane grew to 25 and 60 μm (left and right arrows, respectively). (d) Qualitative demonstration of the film birefringence under static conditions. In all cases, the membrane synthesis conditions used a total flow rate of Q_T = 500 μL min⁻¹. The green arrows in (c) and (d) point in the direction of growth, toward the chitosan stream side. (e) RB intensity changes with rotating of the crossed polarizers. (f) Colour coded orientation map of the membrane (the correspondence between colour and orientation is shown on the top right). All experiments were conducted under a total PBS flow rate Q_T = 20 μL min⁻¹ provided though both inlets.

We conducted off-line measurement of a preformed chitosan membrane using a monochrome microscope system to evaluate birefringence values (Fig. 2d). We measured birefringence values under different flow rate condition, from 100 to 800 μL min⁻¹. This image supports our real-time measurements of uniform birefringence properties following washing, with an average birefringence value of 0.0002. As a comparison, the birefringence of chitin (chitosan with no free amino groups) was recently found to be 0.0008.³²

Further tests of the orientation of the ordered regions were conducted using a rotating crossed polarizer and analyzer, which produced variations in the membrane RB intensity from the membrane. As shown in Fig. 2e, a sinusoidal variation in RB intensity was observed as a function of the angle between the flow and the downstream polarizer direction (acting on the light leaving the device before entering the objective lens). In portions where there was no membrane, the isotropic materials in the light path demonstrated no birefringence at any angle, indicating that the effect is only related to the chitosan membrane. Taken together, these experiments demonstrated a preferential orientation of ordered chitosan domains as colinear with the flow direction, as expected. A measurement of molecular orientation was conducted on the same pre-prepared membrane as shown in Fig. 2d, which confirms this conclusion (Fig. 2f) and matches the results from other studies.³⁵

Optimizing membrane flow synthesis parameters

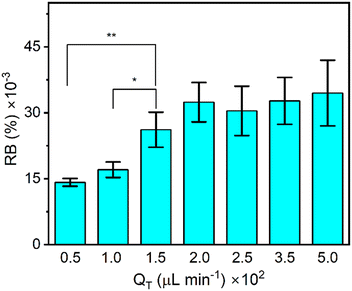
We followed previous studies demonstrating that increased flow rates resulted in the formation of chitosan membranes with higher birefringence resulting from shear alignment of polymer molecules during membrane formation.³⁵ This is similar to previous reports showing shear flow in a microchannel orienting ordered regions in liquid crystal gels.^35,37,38 High shear flow has also been combined with other approaches to create materials with programmable birefringence.³⁹ Therefore, we studied the effect of the chitosan solution flow rate during membrane synthesis to optimize the starting RB intensity of chitosan membranes, as shown in Fig. 3. We prepared 7 chitosan membranes formed under different flow rates while maintaining a flow rate ratio of Q_B/Q_C = 26 to account for the higher viscosity of the chitosan solution over the NaOH trigger solution. After making the membranes, they were washed with a PBS flow (5 min, 100 μL min⁻¹), and then the flow was stopped while the RB was measured. As Q_C increased from 1.8 to 18.5 μL min⁻¹ (and Q_B increased from 48.2 to 481.5 μL min⁻¹), the RB intensity increased until it reached a plateau. We compared the RB after formation at Q_C = 150 μL min⁻¹ to that of all other membranes formed under different flow conditions. We found significantly higher RB than for those membranes that were formed at lower Q_C, with a confidence level of higher than 95% (P ≤ 0.05). Nevertheless, as the average birefringence intensity was larger when formed at Q_T = 200 μL min⁻¹ (P ≤ 0.25), we used this flow rate for synthesis of membranes for later testing.

Fig. 3 The effect of chitosan solution flow rates during membrane formation on the RB intensity of the chitosan membranes. The RB intensity stops increasing with flow rate at a certain value. Statistical significance between RB intensity is shown as *P ≤ 0.05 and **P ≤ 0.01. Each test was repeated 4 times to calculate the average intensity and standard deviation. No flow was applied during data acquisition.

Flow sensitivity of the chitosan membrane

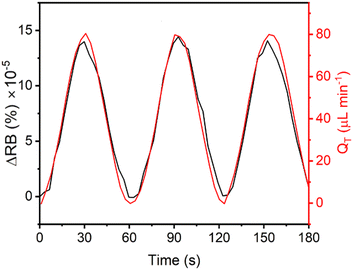
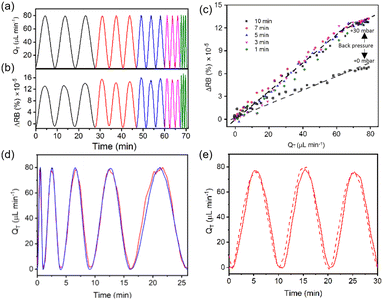
We found that the RB of the formed membranes was sensitive to flow rate and thus proposed its use as a flow rate sensor. To quantitatively investigate the relationship between the RB intensity and flow rate under dynamic conditions, we introduced a sinusoidal flow profile into each side of the X-channel device. Time-varying flow rates at each side of the membrane followed the equation Q(t) = Q_max·sin(Bt), where Q_max = 40 μL min⁻¹ and B is the period. We note that Q_min should reach zero at the beginning of each period (Fig. 4). As an independent measurement of flow rate, we used a commercial thermal flow meter placed upstream in the flow supply tubing for comparison with the results obtained from the on-chip RB measurements of the membrane. Using a commercial programmable pressure pump with feedback control over the flow rate from the supplied flow meter, we applied flow oscillations and observed good fidelity between the actual flow conditions (reported by the commercial flow meter) and those reported by the chitosan membrane flow meter. Due to the low backpressure of our proof-of-principle system, even with an additional 30 mbar applied at the outlet, it was difficult to generate faster oscillations in the flow rate because of the flow inertia, which carried the liquid forward even when the pumping pressure was decreased to zero. Thus, in the rest of the work, we used flow rate oscillation periods that were no less than B = 60 s.

Fig. 4 Measured flow rate using a commercial flow meter (red) and the on-chip chitosan flow meter (black) over 3 cycles using flow oscillations with a period of 60 s. All data were acquired with an additional backpressure of 30 mbar applied at the outlet of the device.

Backpressure sensitivity of the chitosan membrane

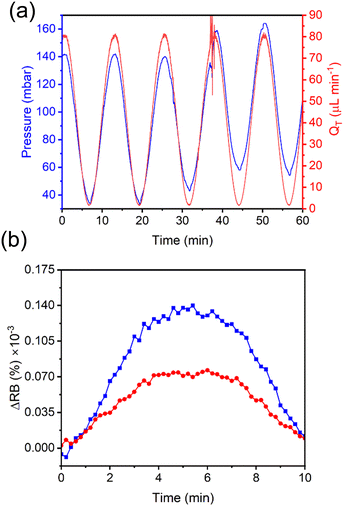
In addition to shear stresses, it is known that applied pressure changes can modify the birefringence of certain elastomers that contain ordered regions, sometimes known as liquid crystal elastomers.⁴⁰ We tested this by raising the end of the outlet tubes relative to the membrane-containing microfluidic device. We introduced a difference in height of approximately 30 cm, corresponding to a calculated difference in backpressure of 30 mbar. This change was made during flow cycling, resulting in on-the-fly adjustments to the pumping conditions required to maintain the pre-set oscillations in the total flow rate between Q_T = 0 and Q_T = 80 μL min⁻¹. These trends are evident from Fig. 5a. Upon introducing the sinusoidal flow rate (before increasing the backpressure), the pumping pressure required to push the liquid through the system oscillated between 37 and 142 mbar. As the outlet tubing was raised by 25 cm during the 5th cycle, the pressure profile changed. This change is most evident by observing the pressure at the lowest flow rate near 30 seconds as the adjustment was being made. A slight disturbance in the flow and pressure is observed near the peak of the 6th cycle due to the vibrations induced during the movement. We compared the RB intensity changes from the 4th cycle and the 7th cycle (Fig. 5b), representing measurements at equilibrium before and after the backpressure was changed. Interestingly, the differences in pressure from the valley to the peak of the two cycles were approximately the same at 105 mbar. However, the 7th cycle flow rate showed higher absolute pressures of nearly 30 mbar, which matches our estimation above. Despite this small difference in backpressure, the peak of the RB intensity value had nearly doubled from that measured before the application of additional backpressure, indicating a strong sensitivity to pressure. Nevertheless, both curves reached nearly 0 RB intensity at 0 μL min⁻¹. The implication of this observation is discussed below.

Fig. 5 (a) Use of the pressure pump to generate sinusoidal flow in the device with same amplitude but different pressure. The cycle numbers are labelled. (b) RB changes under zero additional backpressure (red) and 30 mbar additional backpressure (blue).

Sensitivity of the chitosan membrane to flow oscillations at different frequencies

Next, we determined the analytical relationship between the flow rate for a dynamic flow system and the RB of the membrane. We applied 3 cycles of a sinusoidal flow rate, this time using longer periods to ensure that low flow rates could be achieved. We varied the cycle periods in the order of B = 1, 3, 5, 7, and 10 min to prove that the technique can be applied to a range of dynamic flow condition. The measured flow rates from the upstream commercial thermal flow meter (Fig. 6a) were compared to the RB measurements from the on-chip chitosan membrane (Fig. 6b) with an applied backpressure of 30 mbar. At these frequencies, the two measurements were exactly in phase, demonstrating that the response time of the chitosan flow meter was appropriate for the imposed conditions, as expected from the results in Fig. 4b. The amplitude of the resulting curves from the on-chip RB measurements were related to the off-chip flow rate measurements by a calibration curve (Fig. 6c), which shows a separate linear trend between total flow rates of Q_T = 0 and 65 μL min⁻¹ and between Q_T = 65 and 80 μL min⁻¹. By fitting the data in Fig. 6c to straight lines in each of these flow ranges, we obtained a calibration curve. The slopes are 2.03% × 10⁻⁶ μL⁻¹ min for the low intensity zone (Q_T = 0 to 65 μL min⁻¹) and 1.19% × 10⁻⁶ μL⁻¹ min for the high intensity zone (Q_T = 65 to 80 μL min⁻¹). Adapting the common analytical chemistry concept of sensitivity to these data, the slopes indicate the response of the sensor to the known flow rate. This indicates that the RB has a higher sensitivity in the lower flow rate range, with the cut off being independent of the frequency of the oscillating flow rate. Decreasing the backpressure resulted in a different calibration curve with a lower sensitivity, measured to be 0.82% × 10⁻⁶ μL⁻¹ min. Therefore, backpressure controls both the relative birefringence of the membrane as well as its response to shear forces. As discussed later, the relationship between backpressure and sensitivity can be exploited for improved performance. In this proof-of-principle study we maintained an addional backpressure of approximately 30 mbar.

Fig. 6 Introduction of a sinusoidal flow in the device with 5 different frequencies and the same amplitude, as determined by a commercial flowmeter (a). The membrane RB intensity was obtained simultaneously (b). A calibration curve was obtained by fitting a straight line to the chitosan RB intensity versus the commercial flowmeter measurement of the flow rate at different cycle times and using different backpressures (c). (d) Flow rate measurements of a second sinusoidal multi-frequency flow profile using the calibrated outputs from the chitosan membrane (red) compared to the output from the commercial flow meter (blue). (e) The same sinusoidal flow profile (B = 10 min) applied to the chitosan membrane flow meter at day 1 (red dashed) and day 7 (red solid). The amplitude is Q_T = 40 μL min⁻¹ and the period time is 10 min. All data were acquired with an applied backpressure of 30 mbar, except as noted in (c).

Time stability of the chitosan membrane optical properties

We demonstrated the biomembrane flow sensor by introducing a test flow in the device on a separate day, this time starting with an oscillation with a short period of 1 min and progressively prolonging the period after each cycle until it reached 10 min. Using a single calibration curve for low flow rates, the reproduction of the measured flow rates was nearly perfect in the corresponding flow rate region. However, the applied flow rates that were outside of the appropriate total flow rate range (Q_T = 65 to 80 μL min⁻¹) were overestimated (data not shown). As expected, after independently converting the measured RB values that were generated at total flow rates above Q_T = 65 μL min⁻¹, the on-chip flow rate measurements from the membrane better replicated those obtained independently off-chip (Fig. 6d). The result suggested that the flow rate calculated from light intensity measurement could match the real flow rate and shows a better match than that obtained using only one calibration curve for the peak position of each sinusoidal flow. However, because the flow rate in a real application will not be known, the use of multiple calibration curves would have to be applied by binning data based on thresholded RB values. In this case, the membrane RB calibration should include a wide range of flow rates to obtain differing responses throughout the flow range of interest. Otherwise, the first linear region can be used, and the user would need to understand that reliable results are only possible for the flow rates in a specified flow rate range.

To observe the flow sensing stability of the chitosan membrane for long-term performance, we measured the sinusoidal flow before and after one week of operation. In between measurements, the device was maintained under the same PBS buffer with a total flow rate of Q_T = 40 μL min⁻¹ on each side. The results for the first and last days (Fig. 6e) show nearly identical behaviour. Specifically, the response curves had similar shapes and intensities, and a nearly zero baseline shift. This suggested that the chitosan membrane maintained its sensing ability for several days and that it could serve as an effective flow meter without re-calibration for at least one week.

The successful demonstration of long-term performance was established under ideal conditions. In other words, in addition to ensuring constant backpressure, we also ensured the exclusion of other potential interfering factors such as bubbles, biological contamination and solvent quality. We refer the reader to the ESI† (Section S2), where we verify that these factors indeed caused interference and should thus be avoided. In the case of the quality of solvent, we note in passing that the changes to RB with concentration of a binary solvent appears predictable, opening the door to calibrated sensing of contamination (Section S2, Fig. S1c†). It should be noted, however, that strictly non-aqueous solutions either cause the membrane to dehydrate and loose its RB (e.g., a pure acetone solution) or to maintain its RB but losing its flow rate sensitivity (e.g., for a pure oil phase, data not shown).

Chitosan membrane as a meter for closed-loop flow control

Lastly, we verified the applicability of the chitosan membrane-based meter for feedback into a closed-loop flow system (Fig. 7a). The setup for this part used both flow meters (the commercial meter and our chitosan membrane-based meter) positioned in series. A MATLAB code was used to record images from the microscope camera and then applied automatic processing to determine membrane brightness and finally relative birefringence (RB). As a first step, this process was combined with a simple calibration routine, whereby the commercial flow unit was used to provide accurate control over the flow rate while a linear sweep was applied by the pump and images were acquired from the membrane. This code was optimized to run at maximum allowable rate, including measurement acquisition from the flowmeters at 50 Hz. The code then paired the measured RB with each flow rate to create a calibration curve. Then, a second code obtained TBackspaceRB measurements from the membrane flow meter as direct feedback for the closed-loop controller, thus replacing the expensive commercial unit that is usually operated with the pump. This was done using libraries that were graciously supplied by the pump manufacturers (Fluigent, France). The reader is referred to the flowchart in the ESI,† which provides a graphical and structured overview of the control and calibration algorithms (Section S3†). The basis of operation of the custom pump control code was based on a proportional, integral, differential (PID) controller. In this setup, we left the commercial unit in the flow path as a secondary measurement of the flow rate for comparison purposes. It should be noted that our unoptimized algorithm was designed as a proof of principle to demonstrate the potential for low-cost feedback control. In particular, the measurement frequency was low, and the signal-to-noise ratio was not optimized. Slow feedback is a significant disadvantage for PID algorithms, which generally perform better with fast measurement–control cycles.

Fig. 7 (a) Schematic of the microfluidic flow meter setup with connection set between the custom-built control software and the pressure pump to integrate the chitosan-based flow meter into a closed-loop PID controller. The commercial flow meter is only used for validation measurements, and hence not connected to the pump. (b) Flow profile generated by the pressure pump (dashed) and the resulting flow profile using the chitosan flow meter for feedback to custom control algorithm (blue) and validation measurements collected by a commercial flow meter (red). (c) Flow profile driven by a 1 min⁻¹ square wave input (black) using the chitosan flow meter for feedback to custom control algorithm (red) and validation measurements by the commercial flow meter (blue dashed). Green arrows show the duration of the overshoot at the flow rate falling edge. Black and red arrows show the difference between programmed flow profile and the response from the chitosan flow meter. (d) System response to the same square wave input (black) using the commercial flow meter for feedback to the commercial control algorithm (blue) and parallel measurements by the chitosan flow meter (red dashed). Blue and red arrows show the difference in response between the commercial and chitosan flow meters, respectively, at the rising and falling edges.

As a proof-of-principle test, we selected sampling rate of 0.5 Hz, which was slow relative to that of the commercial meter (50 Hz), but gave a longer time for the image acquisition, leading to better signal to noise. The flow was initially held at the low flow rate of Q_T = 1 μL min⁻¹, which is the holding flow rate we normally use for long durations between experiments. This was followed by commands to our custom PID algorithm to produce an arbitrary flow pulse with an amplitude of Q_T = 80 μL min⁻¹ and a duration of approximately 1 min but featuring a slightly extended fall-off time (see ESI,† Section S4 where the equation for the flow pulse is given in eqn (S1)†). After these commands were sent at approximately 26 seconds, the flow quickly increased before reaching the maximum set point approximately 10 seconds later (Fig. 7b). There appeared to be no significant delay between the onset of the pressure increases and the test flow profile. A more rigorous determination of the minimum response times should be attempted with faster oscillations, which may require optimization of the data acquisition parameters and frame rate, along with improved lighting conditions to give stronger signals which may compensate for faster frame rates. Nevertheless, the response from both the chitosan and commercial flow meters traced similar flow patterns, both resembling the test flow profile that was generated by our code. Next, we attempted to reproduce a square-wave flow pattern which placed higher demand on the system due to the abrupt changes in flow rates required between the instantaneous increase/decrease flow portions and holding flow rates. To better accommodate the sudden increases and decreases in the required flow rate, we increased the data acquisition rate to 7 Hz by switching the camera acquisition to “video mode”, which eliminated control over the shutter speed, leading to narrow data acquisition windows of only 20 ms. As a result, signal to noise ratios were negatively impacted. The data produced in Fig. 7c shows two major deviations from the programmed flow rate when using the chitosan membrane as the flow meter for feedback to the closed loop flow control system. For comparison, Fig. 7d shows results when the commercial flowmeter (operating at 50 Hz) as the feedback controller. From Fig. 7c, we observed an overshoot in flow rate at the falling edge, characterized by flow values dipping below the 30 μL min⁻¹ set-point for approximately 15 seconds. This was not observed when the commercial flow rate meter was used as the control element. A second discrepancy was the rise time, which we measured to be approximately 15 seconds slower than programmed in Fig. 7c. These were likely related to several factors including differences in acquisition rate, signal to noise, and inherent response time of the membrane. While the backpressure was the same (30 mbar) for setups using the chitosan and commercial flow meter (Fig. 7c and d respectively), and their respective control algorithms, we believe that the addition of additional backpressure may at least partially address these problems. To examine the role of the membrane response, we analysed the data in Fig. 7d, which showed a tighter correlation between measured flow profile and the programmed flow profile. Specifically, using the commercial flowmeter for feedback control, we determined that the flow profile measurements from the chitosan membrane lagged the programmed flow profile by about 5 seconds during increases to flow rate and by approximately 2 seconds during decreases to flow rate. We believe that these are the limits to sensor response time, marking fundamental limits to time resolution in flow control systems. That is, improvements to control algorithm (image acquisition rate and integration time), and physical setup (higher light intensity leading to better signal to noise and higher backpressure) can reduce measured lag of 15 seconds. Further improvements may be obtained by addressing material properties of the chitosan membrane. However, it should be noted that other flow wave forms, such as sinusoidal, which gradually approach flow rate extremities can easily be accommodated with the existing chitosan membrane as demonstrated in earlier sections of this manuscript.

Discussion

There is an undeniable and increasing need for passive flow metering systems, especially to accompany pressure-based pumping systems.⁹ The window remains open to propose new approaches, while cost and readiness levels are being evaluated for other promising approaches, such as deformable sensors and pressure difference sensors. The approach of exploiting the flow-sensitive birefringence of a chitosan membrane as a passive in-line flow sensor is promising, both from the point of view of applicability to dynamic flow systems and disposability. Beyond this proof-of-principle study, there is much room for optimization. To move this research closer to application, targeted development is proposed, which includes certain “engineering” aspects. These include the determination of (i) the lowest limit on response time, (ii) the optimal backpressure (iii) the widest range of applicable flow rates, (iv) the best measurement sensitivity achievable, (v) the effect of membrane thickness and channel dimensions, and (vi) other system components that can achieve best functionality while delivering reduced cost. These goals are interconnected and achieving them requires an approach that considers how each one affects the other as well as aspects related to the setup and the application. For example, increasing backpressure stands to improve both sensitivity and responsivity, but in pressure-driven systems, comes at the expense of limitations to flow rate. The channel dimensions are important design parameters that will affect the operation of the device due to their effect on backpressure and applied shear stress, though overall backpressure may be better set with backpressure regulators, which are available, accurate, and low-cost.

Future work should generalize the approach, possibly using simulations and a dimensionless analysis that groups flow rate, device dimensions, pressure, pH and salinity. The goal of such a study would be to reveal the mechanism of RB change in response to flow and chemical conditions. As a starting point we propose tests to correlate applied shear stress and RB response, which could help scaling the approach to different channels and membrane thicknesses. For example, we note that the flow range used in this work (between 0 and 80 μL min⁻¹) corresponds to a shear stress of 0 to 1.1 Pa in an empty channel. Under this assumption, one may also predict the effect of the membrane width on the applied shear stress based on the effective reduction in channel width (W), which we found to change the range of shear stresses from 0 to 1.2 Pa for membrane thicknesses used here. Considering that shear stress is proportional to W⁻¹, we estimate that a 120 μm-wide, which is twice as thick as we used here (60 ± 5 μm), would experience an increase to shear stress of 3.2% at the same flow rate. This is supported by the data in Fig. 2c, in which RB at the growing edge increases with membrane thickness, but further tests should be conducted on established membranes at operational conditions (e.g., neutral pH). As well, we propose other methods which include certain materials development aspects. These include membrane assembly can be explored (specifically, electro-fabricated chitosan membranes), including a new approach in microfluidics that uses a novel interfacial approach using distal electrodes.⁴¹ Following the same approach, chitosan membranes with programmable birefringent properties have been synthesized and may provide an alternative and advantageous synthesis approach for future flow meters.⁴² One may also target copolymer systems that include flexible segments which can more easily respond to shear flow.

A major potential benefit of the proposed approach is related to cost. Our sensor is made from minute amounts of readily available materials with negligible costs, and the housing materials (PDMS and glass) are well represented in other marketed products. The remaining considerations for price relate to optics: linear polarizers, microscope/camera, and light source. Addressing these points can include improving sensitivity toward changes in relative birefringence without a research-grade microscope as used here. In fact, resolution of the membrane as an image may not even be required, as long as an accurate average brightness value can be obtained. A non-imaging-based approach has the potential to alleviate costs in optical elements and sensors without degrading performance. Another major area of focus required to move this technology forward is the algorithm design and optimization.

Moving beyond flow rate measurements, the role of the membrane as a chemical or biological sensor has promise as noted in Sections S1 and S2 of the ESI.† In summary, the strong effect of pH, solvent quality, and presense of microorganisms on the measured RB may be exploited for calibrated sensing at constant flow rates. The mechanisms for such changes should be further investigated, but we note in passing that, for example, the changes in RB with pH appear to be related to membrane contraction.⁴³ However, it should be noted that according to our initial measurements, membranes in contact with strictly non-aqueous liquids appear to lose their ability to respond to flow rates, thus limiting the generality of the potential application as a flow rate sensor. This occurs for different reasons. In the case of a 100% non-aqueous polar solvent such as acetone, water diffuses out of the membrane leaving it both highly contracted and non-birefringent. The situation is different in the case of a pure non-polar liquid such as oil, where water in the membrane became trapped, maintaining membrane hydration and RB levels. However, the membrane could no longer demonstrated flow rate sensitivity. We believe this is because the oil phase slips against the hydrophilic chitosan membrane, thus preventing the application of a shear force to the membrane surface, at least not in the flow ranges we attempted (0–40 μL min⁻¹). We propose that the addition of an adsorbed surfactant at the chitosan outer layer may be an approach that can re-establish flow sensitivity.

Lastly, the potential for errors and malfunctions should be addressed. For example, the natural chitosan membranes used in this work are not suitable for use in low pH streams due to the potential for membrane disassembly. Thus, an important step forward for any application (especially pH sensing) will be to lightly cross-link the chitosan fibres such that the membrane cannot re-dissolve, but not so strongly that the elastomeric properties that contribute to the reversible changes in relative birefringence are erased. As well, we demonstrated that bubbles and microbiological contamination deteriorate the membrane's functionality. Simple bubble traps can ensure that bubbles do not flow into the chitosan flow sensor. In studies using microorganisms, such as swimming bacteria, these organisms can easily follow nutrient concentration gradients upstream to their sources via chemiotaxis,⁴⁴ which could cause contamination of an upstream flow sensor. Fortunately, this problem is easily addressed using upstream filters or other approaches such as high shear barriers to maintain a sterile environment for the sensor chamber.⁴⁵

Conclusion

In this work, we demonstrated the potential use of a birefringent chitosan membrane for optofluidic applications in microfluidic devices. We discovered that the intensity of the membrane's relative birefringence was directly influenced by the flow rate within the device. By implementing a sinusoidal flow, we successfully obtained a calibration curve that enables accurate measurements of flow rate. Several areas of optimization have been identified as avenues for further development in future prototypes, including sensitivity improvement via backpressure regulation, expanded flow rate range, and faster response time. Furthermore, we discussed potential interfering factors, such as bubbles and biological contamination, as well as new opportunities for sensing. In summary, the optical chitosan membrane offers valuable prospects for advancements in flow sensing and analysis.

Experimental

Microchannel fabrication

Microchannels were fabricated in polydimethylsiloxane (PDMS) by casting against a photoresist (SF4000, Mungolux, Germany)-based X-shape mold (60 μm height). A mixture of liquid PDMS (Sylgard184, Dow, Canada) and cross-linker at certain ratio (10 : 1) was poured on top of the mold and cured in an oven at 70 °C for 4 h. At the end of each arm of the X-channel, inlet and outlet holes were added by needle punch. To bond the PDMS device to a glass slide (VWR Microscope Slide, Canada), an air plasma (PCD-001, Harrick Plasma, USA) activation was used. Then the device was annealed at 70 °C to strengthen the bonding.

Solution preparation

A solution of 1 M sodium hydroxide (NaOH, Anachemia, Canada) was prepared by dissolving 4 g of sodium hydroxide pellets in distilled water and making up the final volume to 100 mL. Two NaOH solutions were used in this work. The first was a 10.8 pH solution which was used as a trigger solution to cause chitosan to precipitate when contacted with an acidified chitosan solution. The second was used a 13 pH solution that was used to monitor the effect of high pH on the membrane RB. A solution of 1 M hydrochloric acid (HCl, Anachemia, Canada) with a final volume of 100 mL was prepared by slowly adding 8.4 mL of concentrated hydrochloric acid (37% w/w) to distilled water in a suitable container while ensuring proper ventilation and safety precautions. The solution was carefully diluted to the final volume of 100 mL with distilled water, mixed thoroughly, and the pH was adjusted using a calibrated pH meter (AB150 pH Benchtop Meters, Fisher Scientific, Canada).

Phosphate-buffered saline (PBS) buffer was prepared by dissolving 8 g of sodium chloride (NaCl), 0.2 g of potassium chloride (KCl), 1.44 g of disodium hydrogen phosphate (Na₂HPO₄), and 0.24 g of potassium dihydrogen phosphate (KH₂PO₄) in 1 L of distilled water. All chemical reagents were purchased from Sigma-Aldrich (Canada). The pH of PBS solution was adjusted to 7.4 using 1 M HCl or 1 M NaOH solutions.

The chitosan solution was prepared by adding 0.06 g of chitosan flakes (medium molecular weight, Sigma-Aldrich Canada) and 40 μL 1 M HCl solution into 10 mL of de-ionized water and stirring for 2 h. Via dropwise addition of 1 M NaOH solution, the pH of the chitosan solution was then adjusted to 5.5. DI water was added to bring the concentration of chitosan to 0.5% w/w. Finally, the chitosan solution was filtered with a 0.2 μm syringe filter before use.

Flow tests on non-aqueous liquids included acetone (≥99.0%, VWR, Canada) and low-viscosity oil (Pure Wet Lube, Weldtite Products, UK).

Flow control

Membrane synthesis was achieved by flowing the acidic polymer solution and the basic NaOH trigger solution (pH = 10.8) using separate syringe pumps. Syringe pumps were also used for application of PBS solutions during any step that required constant flow rates, such as post-formation membrane washing and long-term storage. For dynamic flow experiments, a pressure pump (LU-FEZ-2000, Flow EZ, Fluigent, France) was used to supply sinusoidal flow rates to both sides of the X-channel. Separate flow meters (FLU-M-D, Flow unit, Fluigent, France) were placed upstream of each inlet, from which the pump obtained feedback to adjust the pressure needed to achieve flow rate setpoints. We used the commercial flow meter for comparison with the on-chip membrane RB outputs for benchmarking and to generate calibration curves.

Cross-polarization measurements and conventions

Relative birefringence was measured with an inverted microscope (IX73, Olympus, Canada) configured for transmission light measurements. Objective lens was a 4× Olympus Plan Fluorite objective with a 0.13 numerical aperture. The optical path includes the microscope light source, followed by the condenser, the first linear polarizer (93493, Artec, Japan), then the microfluidic device containing the birefringent membrane surrounded by an aqueous flow stream within an isotropic PDMS/glass microfluidic device, and finally the second linear polarizer with the exact specifications of the first, but in a perpendicular orientation to the first. The two crossed polarizers were rotated together to a certain angle at which the intensity of membrane reached a maximum value and then fixed for relative birefringence test. Next, photons were collected by the microscope optics and were focused into an image on a CCD camera photosensor array (Lumenera Infinity 3-1 U, Ottawa, Canada), which was transferred to a computer for analysis.

In this work, when using a cross-polarizer, we refer to the light intensity leaving from the membrane with the term “cross-polarized membrane light transmission”, as digitized by our 8-bit camera. Because this value depends on the source light intensity, camera resolution and acquisition parameters, as well other optical considerations (microscope properties, device transparency, etc.), the units are arbitrary. For better quantification and comparability with other work, we prefer to report RB, which we define as the ratio between the cross-polarized light transmission through the membrane and the light source intensity. The units are reported in% and are accompanied by a multiplicative factor (usually ×10⁻³). The light source intensity is obtained by removing the cross-polarizers and measuring the source light intensity transmitted through the transparent device. RB is a more universal measurement because those arbitrary contributors to the cross-polarized light intensity measurement mentioned above are ratioed out by dividing by the light source intensity, which is also affected by the same factors.

The birefringence value of the chitosan membrane was measured by using a standard polarizing microscope with monochromatic light (using a green filtered light source). In this system, two crossed polarizers, were positioned both above and below the sample. These polarizers were precisely rotated by a motor. A CCD camera was employed to capture images at various angles. Subsequently, the acquired photos were analyzed using a custom-made MATLAB program to calculate the birefringence value.

Calculations

We characterized the change in birefringence as relative birefringence (RB) according to the following equation:

RB = I_M/I₀ (1)

where I_M is the intensity of cross-polarized light transmission through the membrane and I₀ is the light source intensity.

Using the equation below, the shear stress, τ (units) applied to chitosan membrane could also be calculated using v as follows:

τ = 6ηQ/H²W (2)

where η is the viscosity (1 mPa s⁻¹), H and W are the height and width of the channel, respectively, and Q is the flow rate. Based on flow rates ranging from Q = 0 to 80 μL min⁻¹ and the dimensions of our channels, the corresponding increase in shear stress was calculated to be in the range of τ = 0 to 1.1 Pa for a channel without a membrane.

Author contributions

Nan Jia: outline generation, writing – original draft, table and figure generation, data curation, formal analysis. Charles Larouche: simulations, programming. Tigran Galstian: supervision, editing. André Bégin-Drolet: supervision, project administration, methodology, editing. Jesse Greener: conceptualization, funding acquisition, methodology, project administration, resources, supervision, visualization, writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

JG thanks the Natural Sciences and Engineering Research Council of Canada (NSERC) for funding for this work. The authors also thank Molly Gregas for technical edits. The authors also thank an anonymous reviewer for their contributions via excellent comments.

References

1. H. J. Yang and H. T. Soh, Anal. Chem., 2012, 84, 10756–10762.
2. M. Pødenphant, N. Ashley, K. Koprowska, K. U. Mir, M. Zalkovskij, B. Bilenberg and W. Bodmer, Lab Chip, 2015, 15, 4598–4606.
3. H. W. Hou, M. E. Warkiani, B. L. Khoo, Z. R. Li, R. A. Soo, D. S.-W. Tan, W.-T. Lim, J. Han, A. A. S. Bhagat and C. T. Lim, Sci. Rep., 2013, 3, 1259.
4. B. Ziaie, A. Baldi, M. Lei, Y. Gu and R. A. Siegel, Adv. Drug Delivery Rev., 2004, 56, 145–172.
5. L. Zhang and J. Sun, in Multidisciplinary Microfluidic and Nanofluidic Lab-on-a-chip, Elsevier, Amsterdam, Netherlands, 2021, ch. 16: Microfluidics for nanomaterial synthesis.
6. M. Simões, M. O. Pereira, S. Sillankorva, J. Azeredo and M. J. Vieira, Biofouling, 2007, 23, 249–258; N. Khodaparastasgarabad, J. M. Sonawane, H. Baghernavehsi, L. Gong, L. Liu and J. Greener, Lab Chip, 2023, 23, 4201–4212.
7. E. Paramonova, O. J. Kalmykowa, H. C. Van Der Mei, H. J. Busscher and P. K. Sharma, J. Dent. Res., 2009, 88, 922–926; M. A. Amirdehi, L. Gong, N. Khodaparastasgarabad, J. M. Sonawane, B. E. Logan and J. Greener, Electrochim. Acta, 2022, 405, 139771.
8. B. Purevdorj, J. W. Costerton and P. Stoodley, Appl. Environ. Microbiol., 2002, 68, 4457–4464; J. Greener, W. Y. Harvey, C. Gagné-Thivierge, S. Fakhari, S. M. Taghavi, J. Barbeau and S. J. Charette, Phys. Fluids, 2022, 34, 021902.
9. C. Cavaniol, W. Cesar, S. Descroix and J.-L. Viovy, Lab Chip, 2022, 22, 3603–3617.
10. P.-J. Zhao, R. Gan and L. Huang, Rev. Sci. Instrum., 2020, 91, 105006.
11. I. Doh, D. Sim and S. S. Kim, Sensors, 2022, 22, 3151.
12. R. Monge, J. Groenesteijn, D. Alveringh, R. J. Wiegerink, J. Lötters and L. J. Fernandez, Sens. Actuators, B, 2017, 241, 744–749.
13. J. Groenesteijn, R. G. P. P. Sanders, R. J. Wiegerink and J. C. Lotters, in 2016 IEEE 29th International Conference on Micro Electro Mechanical Systems (MEMS), IEEE, 2016, vol. 2016, pp. 193–196.
14. D. C. Leslie, C. J. Easley, E. Seker, J. M. Karlinsey, M. Utz, M. R. Begley and J. P. Landers, Nat. Phys., 2009, 5, 231–235.
15. N. Noeth, S. S. Keller and A. Boisen, Sensors, 2013, 14, 229–244.
16. R. Attia, D. C. Pregibon, P. S. Doyle, J. L. Viovy and D. Bartolo, Lab Chip, 2009, 9, 1213–1218.
17. N. Noeth, S. S. Keller and A. Boisen, J. Micromech. Microeng., 2011, 21, 015007.
18. M. Sadegh Cheri, H. Latifi, J. Sadeghi, M. Salehi Moghaddam, H. Shahraki and H. Hajghassem, Analyst, 2014, 139, 431–438.
19. V. Lien and F. Vollmer, Lab Chip, 2007, 7, 1352–1356.
20. M. S. Cheri, H. Shahraki, J. Sadeghi, M. S. Moghaddam and H. Latifi, Biomicrofluidics, 2014, 8, 054123.
21. T. Rodrigues, F. J. Galindo-Rosales and L. Campo-Deaño, Materials, 2019, 12, 8–10.
22. J. Wu, G. Zheng and L. M. Lee, Lab Chip, 2012, 12, 3566–3575.
23. W. Song and D. Psaltis, Biomicrofluidics, 2011, 5, 044110.
24. E. Rosella, N. Jia, D. Mantovani and J. Greener, J. Mater. Sci. Technol., 2021, 63, 54–61.
25. N. Jia, E. Rosella, E. Juère, R. Pouliot, F. Kleitz and J. Greener, Lab Chip, 2020, 20, 1066–1071; L. Gong, M. A. Amirdehi, J. Sonawane, N. Jia, L. T. de Oliveira and J. Greener, Lab Chip, 2022, 22, 1905–1916.
26. S. P. Miguel, A. F. Moreira and I. J. Correia, Int. J. Biol. Macromol., 2019, 127, 460–475.
27. T. Jin, T. Liu, E. Lam and A. Moores, Nanoscale Horiz., 2021, 6, 505–542.
28. T. Jin, T. Liu, S. Jiang, D. Kurdyla, B. A. Klein, V. K. Michaelis, E. Lam, J. Li and A. Moores, Green Chem., 2021, 23, 6527–6537.
29. T. Di Nardo, C. Hadad, A. Nguyen Van Nhien and A. Moores, Green Chem., 2019, 21, 3276–3285.
30. Y. Gao, Q. Ma, J. Cao, Y. Wang, X. Yang, Q. Xu, Q. Liang and Y. Sun, Int. J. Pharm., 2021, 600, 120465.
31. K. L. Ly, P. Hu, L. H. P. Pham and X. Luo, J. Mater. Chem. B, 2021, 9, 3258–3283.
32. A. G. Richardson and R. L. Pipa, Smithson. Misc. Collect., 1959, 137, 247–262.
33. C. S. Camilo, D. S. dos Santos, J. J. Rodrigues, M. L. Vega, S. P. Campana Filho, O. N. Oliveira and C. R. Mendonça, Biomacromolecules, 2003, 4, 1583–1588.
34. N. V. Pogodina, N. P. Yevlampiyeva, A. Z. Khrustalev, V. N. Marsheva, G. N. Marchenko and V. N. Tsvetkov, Polym. Sci. U.S.S.R., 1986, 28, 260–265.
35. K. Li, S. O. Correa, P. Pham, C. B. Raub and X. Luo, Biofabrication, 2017, 9, 034101.
36. M. Koike-Tani, T. Tani, S. B. Mehta, A. Verma and R. Oldenbourg, Mol. Reprod. Dev., 2015, 82, 548–562.
37. E.-K. Fleischmann, F. R. Forst, K. Köder, N. Kapernaum and R. Zentel, J. Mater. Chem. C, 2013, 1, 5885–5891.
38. R. A. M. Hikmet and R. Polesso, Adv. Mater., 2002, 14, 502–504.
39. J. Schmidtke, W. Stille, H. Finkelmann and S. T. Kim, Adv. Mater., 2002, 14, 746–749.
40. K. M. Herbert, H. E. Fowler, J. M. McCracken, K. R. Schlafmann, J. A. Koch and T. J. White, Nat. Rev. Mater., 2022, 7, 23–28.
41. P. Hu, S. A. Rooholghodos, L. H. Pham, K. L. Ly and X. Luo, Langmuir, 2020, 36, 11034–11043.
42. K. L. Ly, P. Hu, C. B. Raub and X. Luo, Membranes, 2023, 13, 294.
43. K. Lähdesmäki, O. H. S. Ollila, A. Koivuniemi, P. T. Kovanen and M. T. Hyvönen, Biochim. Biophys. Acta, 2010, 1798, 938–946.
44. I. Sampedro, R. E. Parales, T. Krell and J. E. Hill, FEMS Microbiol. Rev., 2015, 39, 17–46.
45. F. Asayesh, M. P. Zarabadi, N. Babaei Aznaveha and J. Greener, Anal. Methods, 2018, 10, 4579–4587.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3lc00985h

---