Effects of Faraday cup deterioration on Sr and Cr isotope analyses by thermal ionization mass spectrometry

Abstract

By comparing data from an extensive set of Sr and Cr isotope measurements performed on two different thermal ionization mass spectrometers (TIMS), using three sets of Faraday cups with different usage histories, we assess the effects of Faraday cup deterioration on high-precision isotope measurements by TIMS. We find that dynamic ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr measurements provide stable and reproducible results over the entire 56 months of this study, regardless of which set of Faraday cups is used. By contrast, static ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr measurements lead to deviant results, drifts over time, and in general exhibit larger scatter. For the most part, these differences can be attributed to changing Faraday cup efficiencies. For the instruments of this study we find that the center cup is most affected, consistent with this cup often receiving the highest ion beam intensities during measurements conducted in our laboratory. For Cr isotopes, we find that the correlation between mass fractionation-corrected ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr ratios observed for static measurements in several prior studies also reflects different Faraday cup efficiencies. Again, the changing efficiency of predominantly the center cup can account for the observed drift and correlation in ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr. Multi-static Cr isotope measurements reduce this drift, but still result in a residual correlation between the two ratios, suggesting this correlation in part also reflects unaccounted mass fractionation effects.

---

1. Introduction

Thermal ionization mass spectrometry (TIMS) is often the method of choice for high-precision isotope ratio measurements in geochemistry and cosmochemistry. This stems from the fact that the stability of the TIMS source allows for long-duration isotope analyses with small measurement uncertainties on individual isotope ratios. However, this in turn makes TIMS measurements susceptible to drifts in measured values that may be related to changes in instrument parameters during the course of an individual study. One such change is the deterioration of Faraday cups through the deposition of analyte atoms during measurements conducted with high ion beam intensities.¹ Primarily due to different usage histories, the deterioration of individual cups likely varies over time, and so can result in a drift of measured isotope ratios on timescales of weeks to months, introducing systematic uncertainties in the final measured isotopic compositions of samples.^2,3

Two elements that are frequently measured using TIMS are Sr and Cr. Strontium has four stable isotopes, namely ⁸⁴Sr, ⁸⁶Sr, ⁸⁷Sr, and ⁸⁸Sr with natural abundances of 0.56%, 9.86%, 7.00%, and 82.58%, respectively. Of these, ⁸⁷Sr is produced by radioactive decay of ⁸⁷Rb, making the ⁸⁷Rb–⁸⁷Sr useful for dating geological processes and as a geochemical tracer.⁴ In addition, the four Sr isotopes are produced by different stellar nucleosynthetic processes,⁵ and so measurements of ⁸⁴Sr/⁸⁶Sr are of interest to search for nucleosynthetic isotope anomalies in meteorites and meteorite components.^6–9 Like Sr, Cr also has four stable isotopes, namely ⁵⁰Cr, ⁵²Cr, ⁵³Cr, and ⁵⁴Cr with natural abundances of 4.35%, 83.79%, 9.50% and 2.36%. Of these, ⁵³Cr is produced by the decay of the short-lived, now-extinct radionuclide ⁵³Mn (half-life ∼ 3.7 Ma), making the ⁵³Mn–⁵³Cr system an important chronometer for processes occurring in the first ∼20 Ma of the solar system.^10–13 In addition, meteorites display widespread variations in ⁵⁴Cr/⁵²Cr, which are interpreted to predominantly be nucleosynthetic in origin.^14–16 Together, this makes both Sr and Cr isotope measurements versatile tools to study a wide range of processes in geochemistry and cosmochemistry.

We routinely conduct Sr and Cr isotope measurements in our laboratory since 2018, using two different TIMS instruments and three sets of Faraday cups with different usage histories. Here we report an extensive set of Sr and Cr standard measurements acquired over this long period of time, including measurements with extensively used and new Faraday cups. By systematically investigating the effect of different cup settings using different sets of cups, this provides a unique opportunity to assess the significance and overall effect of cup deterioration on high-precision isotope measurements by TIMS.

2. Materials and methods

2.1. Materials and standards

The standards used throughout this study are the certified National Institute of Standards and Technology (NIST) standard reference materials (SRM) 3112a for Cr and 987 for Sr. Both standards were prepared as ∼500 ng μl⁻¹ solutions using 6 M HCl; these solution were used for loading Sr and Cr onto the filaments. All measurements were performed using zone-refined Re filaments (99.999% Re, width 0.76 cm, purchased from H Cross Company, NJ 07074 USA), welded onto single filaments and cleaned by outgassing under vacuum (<1 × 10⁻⁵ mbar) at 4.5 A for 288 minutes using the Thermo Scientific filament degassing device.

2.2. Instrumental setup and measurement series

The isotope measurements of this study were conducted on two different instruments and using three sets of Faraday cups having different lifetimes. The first instrument is the Thermo Scientific Triton Plus at the University of Münster, for which two different sets of Faraday cups were used. The first set was used for ∼6 years for a variety of isotope measurements since installation of the instrument in 08/2015, including measurements of Ba, Nd, Sm, Cr, Sr, Dy, Er.^9,17–23 As such, the measurements conducted with this instrument setup (hereafter ‘setup #1’) provide a good example of measurements utilizing cups with an intensive pre-history. In 12/2019, a new set of Faraday cups was installed on the Triton Plus in Münster (corresponding to ‘setup #2’), and new Sr and Cr isotope measurements were conducted starting immediately after the cup installation. The second instrument used in this study is a Thermo Scientific Triton XT installed at the Max Planck Institute for Solar System Research (MPS) in 09/2022. This instrument has been used for some additional ⁸⁷Sr/⁸⁶Sr measurements, which were performed immediately after installation of the instrument (‘setup #3’). Thus, comparing measurements using setup #1 with those using setups #2 and #3 allows for the direct assessment of potential effects of using Faraday cups of different ages and usage history on high-precision isotope measurements.

We report data from three measurement campaigns, which used the three setups described above. To this end, long-term ⁸⁷Sr/⁸⁶Sr measurements of SRM 987 are reported for all three setups, while ⁸⁴Sr/⁸⁶Sr as well as ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr measurements are reported for setups #1 and #2. In addition to these long-term measurements, we also performed two single sets of experiments where the ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr ratios were measured consecutively in static mode using five different magnetic settings with masses 84 through 88 collected in the center cup (see Table 1). For each magnet setting, 4–5 static measurements were conducted. The purpose of this experiment is to systematically assess how the use of specific Faraday cups affects the final measured isotope ratios and thereby test as to whether differences in deterioration among different Faraday cups can be identified. This experiment was performed using setups #1 and #2.

Table 1 Cup settings for Sr-isotopic measurements

Line	L4	L3	L2	L1	Center	H1	H2	H3	H4
^87 Sr/ ^86 Sr measurements
1				^84Sr	^85Rb	^86Sr	^87Sr	^88Sr
2			^84Sr	^85Rb	^86Sr	^87Sr	^88Sr
3		^84Sr	^85Rb	^86Sr	^87Sr	^88Sr
^84 Sr/ ^86 Sr measurements
1					^84Sr	^85Rb	^86Sr	^87Sr	^88Sr
2			^84Sr	^85Rb	^86Sr	^87Sr	^88Sr
Cup-efficiency experiment
84-center					^84Sr	^85Rb	^86Sr	^87Sr	^88Sr
85-center				^84Sr	^85Rb	^86Sr	^87Sr	^88Sr
86-center			^84Sr	^85Rb	^86Sr	^87Sr	^88Sr
87-center		^84Sr	^85Rb	^86Sr	^87Sr	^88Sr
88-center	^84Sr	^85Rb	^86Sr	^87Sr	^88Sr

---

2.3. Strontium isotope measurements

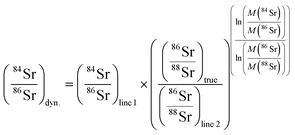
The measurements of ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr ratios were performed independently of each other and using different cup configurations (see Table 1). A gain calibration was performed before each individual measurement session (corresponding to samples loaded onto a single sample wheel). For both measurements, 1 μl of the NIST SRM 987 solution containing ∼500 ng Sr was loaded onto each filament. The sample was dried at 1 A and topped with 1 μl of Ta₂O₅ activator solution consisting of 50 mg of 99.999% pure Ta₂O₅ powder suspended in 3 ml 0.5 M H₃PO₄. After the mixture dried, the filament was heated to glow for ∼1 s and is ready for measurement. For the ⁸⁷Sr/⁸⁶Sr measurements, the filaments were stepwise heated at 370 mA min⁻¹ using the automatic heat function of the Triton until a signal of 0.2 V is reached on ⁸⁸Sr. At this point the heating rate is reduced to 250 mA min⁻¹ until a signal of 10 V on ⁸⁸Sr is reached, and the measurement is started with a signal of 10.5 V on ⁸⁸Sr. During the heating process, the lenses were focused and a peak center was performed at signals of 0.2 V and 10 V. For the measurement of ⁸⁴Sr/⁸⁶Sr, this procedure was the same, but the final signal was increased to 25–30 V on ⁸⁸Sr and an additional lens focus was performed at a signal of 15 V. For both the ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr measurements, only Faraday cups connected to feedback resistors with 10¹¹ Ω amplifiers were used, and no amplifier rotation was employed. Mass fractionation was corrected using the exponential law and ⁸⁶Sr/⁸⁸Sr = 0.1194.^24,25

The ⁸⁴Sr/⁸⁶Sr measurements consisted of two lines of data acquisition, which provide two separate static ⁸⁴Sr/⁸⁶Sr ratios for each line and a dynamic ⁸⁴Sr/⁸⁶Sr ratio (Table 1). The latter is obtained by correcting the ⁸⁴Sr/⁸⁶Sr measured in the first line for instrumental mass fractionation using ⁸⁶Sr/⁸⁸Sr measured in the second line as follows:^7,26

The ⁸⁴Sr/⁸⁶Sr and ⁸⁶Sr/⁸⁸Sr ratios measured in this manner use the same Faraday cups, and so any bias induced by different cup efficiencies cancel out.^7,26 The ⁸⁴Sr/⁸⁶Sr measurements were performed using 4 s idle time on line 1 and 10 s idle time on line 2, which ensures complete decay of the high ⁸⁸Sr beam measured in the H2 cup, which in line 2 is used to measure the ion beam on the much lower abundance isotope ⁸⁶Sr. Both lines used 4 s integration time and a peak center and lens focus was performed every five blocks. One measurement consists of 25 blocks of 20 cycles each.

The ⁸⁷Sr/⁸⁶Sr measurements used a three-line data acquisition theme following the method described in ref. 7. In this procedure, ⁸⁶Sr is collected in cups H1, C, and L1, respectively, with all other Sr isotopes collected accordingly in each line (Table 1). This procedure allows determining three static ⁸⁷Sr/⁸⁶Sr ratios for each line, as well as a multi-dynamic ⁸⁷Sr/⁸⁶Sr calculated as follows:

where the subscripts refer to magnet settings of lines 1, 2 or 3, respectively (Table 1). One measurement consists of 25 blocks of 20 cycles with 8 s integration time and 4 s idle time each. Baseline (30 s) measurement, peak center, and lens focus was done every five blocks.

For all Sr isotope measurements, possible isobaric interferences from ⁸⁷Rb on ⁸⁷Sr were monitored using the ion beam intensity on interference-free ⁸⁵Rb. Natural samples might require an Rb-interference correction, however, no ⁸⁵Rb signal was observed in any of the Sr isotope measurements of this study, reflecting the lower ionization potential of Rb, the high purity of the SRM 987 Sr standard and the low Rb blank of our procedure.

2.4. Chromium isotope measurements

The Cr isotope measurements were made in static mode following the method described in ref. 18. Approximately 1 μg Cr of NIST SRM 3112a was loaded onto outgassed Re filaments and dried at 0.7 A. The sample was covered with about 3 μl of an Al–Si-gel emitter and dried at 1.2 A for 30 s. Finally, the filament was heated to 2 A for ∼5 s, while preventing the filament from glowing to ensure complete homogenization of sample and emitter, and to maintain stickiness of this mixture on the filament.¹⁸ For the measurements, filaments were stepwise heated until reaching a signal of 10 V on ⁵²Cr using the automatic heat function of the Triton Plus using a slow heating procedure (∼30 min). Ion beams on ⁵⁰Cr, ⁵²Cr, ⁵³Cr, and ⁵⁴Cr were collected in the L3, C, H1, and H2 cups, respectively, and all cups were connected to 10¹¹ Ω feedback resistors. Measurement were typically conducted with ∼10 V on ⁵²Cr and correspond signal of 200–250 mV on ⁵⁴Cr. Isobaric interferences from ⁵⁰Ti, ⁵⁰V, and ⁵⁴Fe were monitored using ⁴⁹Ti, ⁵¹V, and ⁵⁶Fe in cups L4, L1, and H4, respectively. Each measurement consisted of 50 blocks of 30 cycles each with 4 s integration time per cycle for setup #1 and was later reduced to 25 blocks of 30 cycles for setup #2. Baseline measurements (30 s) and a lens focus were performed every three blocks.

For multi-static Cr isotope measurements, we used a 4-line routine outlined in Table 2,²⁷ where peak shapes and alignments were adjusted using the focus and dispersion lens system of the Triton Plus before each measurement session (i.e., one sample wheel), similar to multi-dynamic Sr isotope measurements. One measurement consists of 10 blocks with 20 cycles with 8 s integration time and 4 s idle time each. A peak-center and baseline (30 s) measurement was performed every two blocks and a filament and lens focus after five blocks. The final ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr ratios are calculated as averages of lines 1–4 for ⁵³Cr/⁵²Cr and lines 1–3 for ⁵⁴Cr/⁵²Cr (Table 2). This difference reflects that measurement of ⁵⁴Cr in a fourth line was not possible due to the instrument's cup setup.

Table 2 Cup settings for Cr-isotopic measurements

Line	L3	L2	L1	Center	H1	H2	H3	H4
Static Cr measurements
	^49Ti	^50Cr	^51V	^52Cr	^53Cr	^54Cr		^56Fe
Multistatic Cr measurements
1	^50Cr	^51V	^52Cr	^53Cr	^54Cr		^56Fe
2		^50Cr	^51V	^52Cr	^53Cr	^54Cr
3			^50Cr	^51V	^52Cr	^53Cr	^54Cr
4				^50Cr	^51V	^52Cr	^53Cr

---

Final mass fractionation-corrected ratios of ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr for all Cr measurements were obtained by internally normalizing to a fixed ⁵⁰Cr/⁵²Cr ratio of 0.051859 using the exponential law.^25,28 During measurements using setup #1, a total of 108 standard measurements were made over a period of 12 months, while with setup #2 65 standard measurements were made during the first three months after installation of the new Faraday cups.

3. Results and discussion

3.1. Effects of cup deterioration on Sr isotope measurements

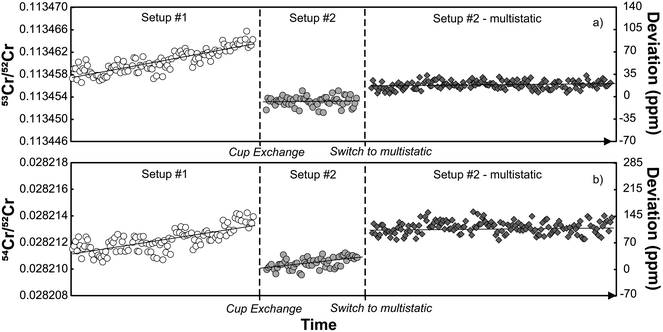
The results of static and dynamic ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr measurements using two or three instrument setups, respectively, are shown in Fig. 1. While there is significant scatter for the static ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr measurements for each setup, the dynamic ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr measurements show excellent long-term reproducibility during the 56 months course of this study (for Sr measurements) with mean values of ⁸⁴Sr/⁸⁶Sr = 0.056491 ± 0.000002 (2s.d.; n = 203) and ⁸⁷Sr/⁸⁶Sr = 0.710245 ± 0.000004 (2s.d.; n = 50). By contrast, static measurements for one particular cup configuration deviate from the dynamic ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr ratios by ∼150 and ∼100 ppm, respectively, and also show more scatter, which is predominantly caused by drift of the measured isotope ratios with time. This is particularly evident for the static ⁸⁷Sr/⁸⁶Sr measurements using setups #2 and #3 (Fig. 1). Notably, comparison of the static ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr measurements using the three different setups show no obvious difference, i.e., using new Faraday cups in setups #2 and #3 do not appear to have resulted in significant improvement over the measurements performed using setup #1, which used aged Faraday cups. Thus, it is clear that dynamic ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr measurements provide much more reproducible and long-term stable results than static measurements (e.g., ref. 29). However, from these measurements alone it remains unclear to what extent the offset and poorer reproducibility of the static measurements is related to deterioration of the Faraday cups.

Fig. 1 Mass fractionation-corrected ⁸⁴Sr/⁸⁶Sr (a) and ⁸⁷Sr/⁸⁶Sr ratios (b) for the SRM 987 Sr standard for setups #1, #2, and #3. For each setup, results for static measurements from individual lines and the results of the corresponding dynamic measurements are shown. Squares denote static results for line 1, diamonds for line 2, and triangles for line 3. Dashed lines show the external reproducibility (2s.d.) of the dynamic measurements.

To assess this effect more rigorously, we performed static ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr measurements using setups #1 and #2, and using five different magnetic settings with masses 84 through 88 collected in the center cup (see Table 1). As shown in Fig. 2, for both ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr the deviations from the dynamic values are smaller using setup #2 (new cups) compared to setup #1 (old cups), although some deviations remain. To assess whether these deviations can be linked to a specific Faraday cup, we modeled the effect of different Faraday cup efficiency factors on the measured isotope ratios. The cup efficiency can be understood as the ratio of the ion current in the high-ohmage feedback resistor connected to each cup to the ion current that is injected into the cup.¹ The cup efficiency is not to be confused with the amplifier gain factor, which is a conversion factor between the true input voltage from the cup to the output voltage and is determined before each analytical session (see above). Our calculations show that the different ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr ratios measured for the different magnetic settings using setup #1 are well reproduced by modifying the efficiency factor of only the central Faraday cup (Fig. 2). This is consistent with results of a prior study²⁹ and the observation that for measurements with either ⁸⁴Sr or ⁸⁵Rb collected in the center cup, the variations among the static and dynamic ⁸⁷Sr/⁸⁶Sr measurements are the smallest (Fig. 2). This is because for these magnetic settings, the center cup is not used for either ⁸⁶Sr, ⁸⁷Sr, or ⁸⁸Sr, which are the three isotopes used for the calculation of mass-fractionation-corrected ⁸⁷Sr/⁸⁶Sr ratios. In detail, the variable ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr ratios measured using the different magnetic settings are reproduced by arbitrarily setting the cup efficiency of the center cup to 0.9999, while keeping the cup efficiencies of all other cups at 1. This does not mean that only the center cup is deteriorated, but it shows this cup appears to be affected the most in this specific case. As discussed by ref. 1, the main cause of changes in cup efficiency is the number of ions already collected in a specific cup. This is consistent with the quite extensive usage history of about six years for this set of Faraday cups and with the fact that for most measurements conducted on this instrument, the center cup usually received the highest ion beams. For instance, the instrument has been used for extensive static Cr isotope measurements (see Section 3.2 below), where the most abundant isotope ⁵²Cr is collected in the center cup.

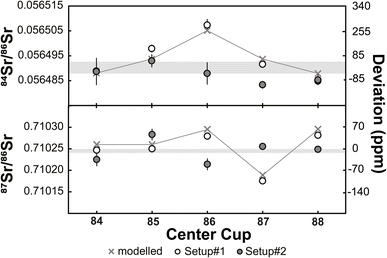Fig. 2 Mass fractionation-corrected ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr ratios for NIST SRM 987 measured with different magnet settings (Table 1) and using Faraday cups with extensive pre-usage (setup #1) and new cups (setup #2). Also shown are expected variations if the cup efficiency factor of the center cup is set to 0.9999, while the factor for all other cups is 1. These expected variations are in good agreement with the measured isotope ratios using setup #1. Horizontal grey bands show dynamic results for ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr with their respective external reproducibility (±2s.d.).

We conducted the same measurements with setup #2, i.e., using a new set of Faraday cups. The absolute ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr ratios measured deviate from those obtained using setup #1, but as noted above, also deviate from the dynamic results obtained using both setups. However, the deviations observed for setup #2 cannot be attributed to the relative difference in the efficiency of an individual cup. This is not surprising because, given that a new set of Faraday cups has been used, there is no single cup that should be systematically different from all other cups. As such, the differences among the static ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr ratios measured for different magnetic settings, and the deviations of these values from the dynamic measurements, most likely reflect small inherent variations in Faraday cup efficiencies related to differences in material and surface properties among the individual cups.

Fig. 3 compares the ⁸⁴Sr/⁸⁶Sr ratios with different magnet settings of this study to available data from previous studies. Two observations stand out. First, the variable ⁸⁴Sr/⁸⁶Sr ratios reported in prior studies show a similar pattern as our results for different magnetic settings, where the largest offsets are observed when ⁸⁶Sr is measured in the center cup. Of note, when ⁸⁵Rb or ⁸⁷Sr are collected in the center cup, the offsets are much smaller, most likely because the center cup is not used for measurement of ⁸⁴Sr, ⁸⁶Sr, or ⁸⁸Sr, i.e., the three isotopes used for calculation of mass-fractionated ⁸⁴Sr/⁸⁶Sr ratios. Thus, systematic differences for different magnet settings and larger cup deterioration for the center cup are not a feature specific to a single TIMS instrument, but also appear to be present for other TIMS instruments. Second, the dynamic ⁸⁴Sr/⁸⁶Sr measurements of all studies are in very good agreement, suggesting that differences in reported ⁸⁴Sr/⁸⁶Sr ratios predominantly are due to unaccounted variations in Faraday cup efficiencies.

Fig. 3 Comparison of ⁸⁴Sr/⁸⁶Sr ratios for NIST SRM 987 measured in this and in prior studies. Note the good agreement of the results except for instrument setups where ⁸⁶Sr is collected in the center cup. Small crosses and solid line are the modelled results from Fig. 2. For details see text.

3.2. Effect of cup deterioration on Cr isotope measurements

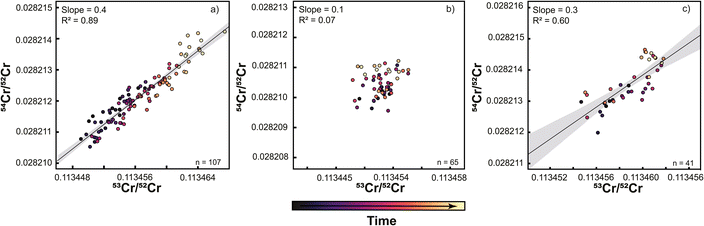
During the course of the Sr isotope measurements described above, the TIMS instrument in Münster (setups #1 and #2) was also extensively used for Cr isotope measurements. Given the evidence for deterioration of the central cup based on the Sr isotope measurements, the question arises how this deterioration affected the Cr isotope measurements. As shown in Fig. 4, both the ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr measured for the SRM 3112a standard using setup #1 drift over time to higher values, resulting in a strong positive correlation between these two ratios (Fig. 4 and 5). This correlation has also been observed in several prior studies.^16,27,30 Immediately after the cup exchange (setup #2), the measured ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr ratios drop substantially by ∼90 ppm and ∼130 ppm, respectively, to values that are even lower than the value at the beginning of the measurement series using setup #1. However, even for setup #2 a slight drift in measured ⁵⁴Cr/⁵²Cr ratios can be observed, and after about 8 months of use, a weak correlation between the measured ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr ratios emerges again (Fig. 5). As shown in Fig. 5, this drift and the resulting correlation is a temporal effect, as later measurements systematically yielded higher ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr ratios compared to the earlier measurements.

Fig. 4 Mass fractionation-corrected ⁵³Cr/⁵²Cr (a) and ⁵⁴Cr/⁵²Cr ratios (b) for the SRM 3112a Cr standard obtained by static measurements using setup #1 and setup #2, and multistatic measurements using setup #2.

Fig. 5 Mass fractionation-corrected ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr ratios of NIST SRM 3112a obtained by static measurements using setup #1 (a) and setup #2 (b and c). Note the strong correlation of ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr obtained using setup #1 (a), which disappears for the initial measurements using setup #2 (two months) (b), but reappears relatively quickly after about eight months (c). Color-coding of data points indicates the relative time of individual measurements for each setup, demonstrating that the correlation of ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr ratios reflects a temporal drift of both ratios to higher values over time.

To assess whether the correlation of ⁵³Cr/⁵²Cr versus⁵⁴Cr/⁵²Cr ratios is due to Faraday cup deterioration, we calculated the change of both ratios resulting from a different cup efficiency of the central cup. As shown above, for the Sr isotope measurements using setup #1 we found that a cup efficiency of 0.9999 for the center cup, and 1 for all other cups, can account for the observed variations in measured ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr ratios. We find that these cup efficiencies result in higher measured ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr ratios compared to the ratios obtained with an efficiency of 1 for all Faraday cups, and a positive correlation between the two ratios with a slope that is in good agreement with the slopes observed for measurements with setup #1 and the later measurements with setup #2 (Fig. 6). Thus, as for Sr isotopes, the observed offsets in measured Cr isotope ratios can be attributed to Faraday cup deterioration of mainly the center cup.

Fig. 6 Effect of changing Faraday cup efficiency on mass fractionation-corrected ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr ratios. Calculations assume that the cup efficiency of only the center cup changes and show that factors of 0.9999 and 0.99995, instead of 1, result in a positive correlation between ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr ratios similar to the correlation observed for the standard measurements.

The correlation of ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr ratios has most commonly been attributed to residual mass fractionation that has not been accounted for by the correction for instrumental mass fractionation.^16,27,30 However, our results show that at least for static measurements this correlation more likely results from changes in the Faraday cup efficiency of especially the center cup, which is used to collect the ion beam of the most abundant Cr isotope, ⁵²Cr, and is, as such, most susceptible to cup deterioration.

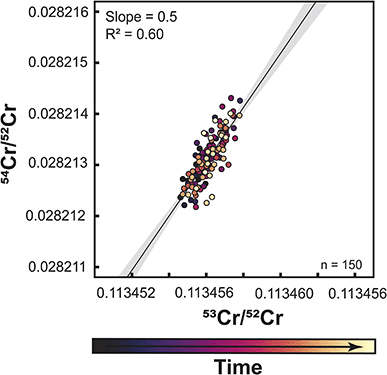
To overcome these problems inherent to static Cr isotope measurements, several studies used a multi-static setup, where Cr isotopes are measured in four or five different lines.^27,31 The same amount of sample (1 μg) was loaded onto one filament for multistatic measurements as for single static measurements, but the measurement time is four times as long as one static measurement. The idea of this approach is that the effects of different cup efficiencies should average out, as through the multi-line data acquisition all Cr isotopes are on average measured using the same set of Faraday cups. To assess if this is the case, we performed multi-static Cr isotope measurements using setup #2, which were all conducted after the static measurements conducted with this setup. We find that over a period of 9 months, both the ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr ratios no longer exhibit drift, thus allowing precise measurements of both ratios. However, when the multi-static ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr ratios are plotted against each other, a correlation with a similar slope as before is still apparent (Fig. 7). A similar observation has been made by ref. 27, using a similar setup as in this study. Importantly though, unlike for the static measurements, for the multi-static measurements the ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr ratios do not evolve over time and, as such, are unlikely to be related to the increasing aging of the Faraday cups. This is consistent with the idea that the effects of Faraday cup efficiencies should nearly cancel out in a multi-static measurement setup and suggests that the observed residual ⁵³Cr/⁵²Cr versus⁵⁴Cr/⁵²Cr correlation in part reflects unaccounted mass fractionation effects.²⁷ Nevertheless, in the dataset of this study the overall range of ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr ratios is larger for the static than for the multi-static measurements, indicating that at least for single-line static measurements, aging of the Faraday cups is the dominant factor causing the observed ⁵³Cr/⁵²Cr versus⁵⁴Cr/⁵²Cr correlation.

Fig. 7 Multistatic mass-fractionation-corrected ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr ratios measured using setup #2. As for the static measurements, there is a residual correlation between ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr, but the overall variations are smaller and the correlation does not reflect a temporal change in measured ratios, suggesting this correlation is due to residual mass fractionation effects.

4. Conclusions

This study compares the results of long-term high-precision Sr (i.e., ⁸⁴Sr/⁸⁶Sr, ⁸⁷Sr/⁸⁶Sr) and Cr (i.e., ⁵³Cr/⁵²Cr, ⁵⁴Cr/⁵²Cr) isotope measurements for the NIST SRM 987 and NIST SRM 3112a standards, respectively, acquired on two thermal ionization mass spectrometers equipped with three different sets of Faraday cups having varying usage histories of between six years and one month. This extensive data set allows assessing the influence of Faraday cup deterioration on the precision and accuracy of the isotope measurements. Our results show that for static measurements drift and scatter of mass fractionation-corrected ⁸⁴Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr as well as ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr ratios can be attributed to increasing deterioration of predominantly the center cup. For Sr isotopes, this problem can be overcome by dynamic measurements, which in this study provided stable and reproducible results over a period of 56 months for all three sets of Faraday cups used. For Cr isotopes, we find that the correlation between mass fractionated-corrected ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr ratios observed for static measurements in several prior studies can also largely be attributed to deterioration of the center cup. This residual correlation disappears when new Faraday cups are used, but appears again after only a few months of use and increases over time. Multistatic measurements minimize the long-term drift in mass fractionation-corrected ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr ratios, but a small residual correlation between ⁵³Cr/⁵²Cr and ⁵⁴Cr/⁵²Cr remains, which most likely reflects residual mass fractionation. Finally, the comparisons to literature data for both Sr and Cr isotopes reveal that the effects of Faraday cup deterioration described here are not specific to the TIMS instruments of this study, but appear to be relatively common among TIMS instruments used for high-precision isotope measurements in other laboratories.

Author contributions

Jonas M. Schneider: conceptualization, formal analysis, investigation, methodology, visualization, writing – original draft. Thorsten Kleine: conceptualization, funding acquisition, project administration, resources, supervision, writing – review & editing.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) (project ID 263649064-TRR170) and the European Research Council Advanced Grant Holy Earth (grant no. 101019380). This is TRR 170 pub. no. 215. Open Access funding provided by the Max Planck Society.

References

1. Y. Di, E. Krestianinov, S. Zink and Y. Amelin, High-precision multidynamic Sr isotope analysis using thermal ionization mass spectrometer (TIMS) with correction of fractionation drift, Chem. Geol., 2021, 582, 120411,  DOI:10.1016/j.chemgeo.2021.120411.
2. R. Fukai, T. Yokoyama and S. Kagami, Evaluation of the long-term fluctuation in isotope ratios measured by TIMS with the static, dynamic, and multistatic methods: a case study for Nd isotope measurements, Int. J. Mass Spectrom., 2017, 414, 1–7,  DOI:10.1016/j.ijms.2016.12.016.
3. L. Qin, R. W. Carlson and C. M. O. Alexander, Correlated nucleosynthetic isotopic variability in Cr, Sr, Ba, Sm, Nd and Hf in Murchison and QUE 97008, Geochim. Cosmochim. Acta, 2011, 75, 7806–7828,  DOI:10.1016/j.gca.2011.10.009.
4. G. Faure and J. L. Powell, Strontium Isotope Geology, Springer-Verlag, 1972.
5. D. A. Papanastassiou and G. J. Wasserburg, Strontium isotopic anomalies in the Allende Meteorite, Geophys. Res. Lett., 1978, 5, 595–598,  DOI:10.1029/GL005i007p00595.
6. F. Moynier, J. M. D. Day, W. Okui, T. Yokoyama, A. Bouvier, R. J. Walker and F. A. Podosek, Planetary-scale strontium isotopic heterogeneity and the age of volatile depletion of early solar system materials, Astrophys. J., 2012, 758, 45,  DOI:10.1088/0004-637X/758/1/45.
7. U. Hans, T. Kleine and B. Bourdon, Rb–Sr chronology of volatile depletion in differentiated protoplanets: BABI, ADOR and ALL revisited, Earth Planet. Sci. Lett., 2013, 374, 204–214,  DOI:10.1016/j.epsl.2013.05.029.
8. B. L. A. Charlier, F. L. H. Tissot, H. Vollstaedt, N. Dauphas, C. J. N. Wilson and R. T. Marquez, Survival of presolar p-nuclide carriers in the nebula revealed by stepwise leaching of Allende refractory inclusions, Sci. Adv., 2021, 7, eabf6222,  DOI:10.1126/sciadv.abf6222.
9. J. M. Schneider, C. Burkhardt and T. Kleine, Distribution of s-, r-, and p-process Nuclides in the Early Solar System Inferred from Sr Isotope Anomalies in Meteorites, Astrophys. J. Lett., 2023, 952, L25,  DOI:10.3847/2041-8213/ace187.
10. J.-L. Birck and C. J. Allègre, Manganese—chromium isotope systematics and the development of the early solar system, Nature, 1988, 331, 579–584,  DOI:10.1038/331579a0.
11. A. Trinquier, J.-L. Birck, C. J. Allègre, C. Göpel and D. Ulfbeck, 53Mn–53Cr systematics of the early Solar System revisited, Geochim. Cosmochim. Acta, 2008, 72, 5146–5163,  DOI:10.1016/j.gca.2008.03.023.
12. L. Qin and X. Wang, Chromium Isotope Geochemistry, Rev. Mineral. Geochem., 2017, 82, 379–414,  DOI:10.2138/rmg.2017.82.10.
13. A. Anand, J. Pape, M. Wille, K. Mezger and B. Hofmann, Early differentiation of magmatic iron meteorite parent bodies from Mn–Cr chronometry, Geochem. Perspect. Lett., 2021, 20, 6–10,  DOI:10.7185/geochemlet.2136.
14. M. Rotaru, J. L. Birck and C. J. Allègre, Clues to early solar system history from chromium isotopes in carbonaceous chondrites, Nature, 1992, 358, 465–470,  DOI:10.1038/358465a0.
15. A. Trinquier, J. Birck and C. J. Allegre, Widespread ⁵⁴ Cr Heterogeneity in the Inner Solar System, Astrophys. J., 2007, 655, 1179–1185,  DOI:10.1086/510360.
16. L. Qin, C. M. O. Alexander, R. W. Carlson, M. F. Horan and T. Yokoyama, Contributors to chromium isotope variation of meteorites, Geochim. Cosmochim. Acta, 2010, 74, 1122–1145,  DOI:10.1016/j.gca.2009.11.005.
17. J. L. Hellmann, J. M. Schneider, E. Wölfer, J. Drążkowska, C. A. Jansen, T. Hopp, C. Burkhardt and T. Kleine, Origin of Isotopic Diversity among Carbonaceous Chondrites, Astrophys. J. Lett., 2023, 946, L34,  DOI:10.3847/2041-8213/acc102.
18. J. M. Schneider, C. Burkhardt, Y. Marrocchi, G. A. Brennecka and T. Kleine, Early evolution of the solar accretion disk inferred from Cr-Ti-O isotopes in individual chondrules, Earth Planet. Sci. Lett., 2020, 551, 11658,  DOI:10.1016/j.epsl.2020.116585.
19. Q. R. Shollenberger, J. Render and G. A. Brennecka, Er, Yb, and Hf isotopic compositions of refractory inclusions: an integrated isotopic fingerprint of the solar system's earliest reservoir, Earth Planet. Sci. Lett., 2018, 495, 12–23,  DOI:10.1016/j.epsl.2018.05.007.
20. Q. R. Shollenberger, L. E. Borg, E. C. Ramon, M. A. Sharp and G. A. Brennecka, Samarium isotope compositions of uranium ore concentrates: a novel nuclear forensic signature, Talanta, 2021, 221, 121431,  DOI:10.1016/j.talanta.2020.121431.
21. G. J. Archer, G. A. Brennecka, P. Gleißner, A. Stracke, H. Becker and T. Kleine, Lack of late-accreted material as the origin of 182W excesses in the Archean mantle: evidence from the Pilbara Craton, Western Australia, Earth Planet. Sci. Lett., 2019, 528, 115841,  DOI:10.1016/j.epsl.2019.115841.
22. J. Render and G. A. Brennecka, Isotopic signatures as tools to reconstruct the primordial architecture of the solar system, Earth Planet. Sci. Lett., 2021, 555, 116705,  DOI:10.1016/j.epsl.2020.116705.
23. G. A. Brennecka and T. Kleine, A Low Abundance of 135Cs in the Early Solar System from Barium Isotopic Signatures of Volatile-depleted Meteorites, Astrophys. J. Lett., 2017, 837, L9,  DOI:10.3847/2041-8213/aa61a2.
24. J. Meija, T. B. Coplen, M. Berglund, W. A. Brand, P. D. Bièvre, M. Gröning, N. E. Holden, J. Irrgeher, R. D. Loss, T. Walczyk and T. Prohaska, Isotopic compositions of the elements 2013 (IUPAC Technical Report), Pure Appl. Chem., 2016, 88, 293–306,  DOI:10.1515/pac-2015-0503.
25. W. A. Russell, D. A. Papanastassiou and T. A. Tombrello, Ca isotope fractionation on the Earth and other solar system materials, Geochim. Cosmochim. Acta, 1978, 42, 1075–1090,  DOI:10.1016/0016-7037(78)90105-9.
26. E. Yobregat, C. Fitoussi and B. Bourdon, A new method for TIMS high precision analysis of Ba and Sr isotopes for cosmochemical studies, J. Anal. At. Spectrom., 2017, 32, 1388–1399,  10.1039/C7JA00012J.
27. A. Trinquier, J.-L. Birck and C. J. Allègre, High-precision analysis of chromium isotopes in terrestrial and meteorite samples by thermal ionization mass spectrometry, J. Anal. At. Spectrom., 2008, 23, 1565,  10.1039/b809755k.
28. W. R. Shields, T. J. Murphy, E. J. Catanzaro and E. L. Garner, Absolute isotopic abundance ratios and the atomic weight of a reference sample of chromium, J. Res. Natl. Bur. Stand., Sect. A, 1966, 70, 193,  DOI:10.6028/jres.070A.016.
29. G. Wang, Y. Wu and J. Xu, Optimization techniques for improving the precision of isotopic analysis by thermal ionization mass spectrometry, taking strontium, neodymium, lead, and osmium as examples, Spectrosc. Lett., 2016, 49, 85–90,  DOI:10.1080/00387010.2015.1084639.
30. G. W. Lugmair and A. Shukolyukov, Early solar system timescales according to 53Mn-53Cr systematics, Geochim. Cosmochim. Acta, 1998, 62, 2863–2886,  DOI:10.1016/S0016-7037(98)00189-6.
31. M. Cornet, C. Fitoussi, B. Bourdon and E. Pili, Determination of chromium isotopic composition in various geological material by thermal ionization mass spectrometry, Int. J. Mass Spectrom., 2022, 480, 116897,  DOI:10.1016/j.ijms.2022.116897.
32. T. Henshall, D. L. Cook, M. Garҫon and M. Schönbächler, High-precision strontium isotope analysis of geological samples by thermal ionisation mass spectrometry, Chem. Geol., 2018, 482, 113–120,  DOI:10.1016/j.chemgeo.2018.02.010.
33. R. Fukai and T. Yokoyama, Nucleosynthetic Sr–Nd Isotope Correlations in Chondrites: Evidence for Nebular Thermal Processing and Dust Transportation in the Early Solar System, Astrophys. J., 2019, 879, 79,  DOI:10.3847/1538-4357/ab0e0d.
34. R. Andreasen and M. Sharma, Mixing and Homogenization in the Early Solar System: Clues from Sr, Ba, Nd, and Sm Isotopes in Meteorites, Astrophys. J., 2007, 665, 874–883,  DOI:10.1086/518819.

---