Cavity-constrained LIBS combined with the gray wolf optimization algorithm for optimizing bidirectional long short-term memory (GWO-BiLSTM) networks for classification prediction of different brands of cigarettes
Junjie
Chen
 ab,
Xiaojian
Hao
*ab,
Biming
Mo
ab,
Shuaijun
Li
ab,
Xiaojian
Hao
*ab,
Biming
Mo
ab,
Shuaijun
Li
 ab,
Junjie
Ma
ab,
Xiaodong
Liang
ab,
Zheng
Wang
ab and
Heng
Zhang
c
ab,
Junjie
Ma
ab,
Xiaodong
Liang
ab,
Zheng
Wang
ab and
Heng
Zhang
c
aScience and Technology on Electronic Test and Measurement Laboratory, North University of China, Taiyuan, Shanxi, China. E-mail: haoxiaojian@nuc.edu.cn
bState Key Laboratory of Dynamic Measurement Technology, North University of China, Taiyuan, Shanxi, China
cJincheng Research Institute of Opto-mechatronics Industry, Jincheng, Shanxi, China
First published on 9th August 2024
Abstract
As a kind of plant with complex chemical composition, the different compositions of tobacco determine the quality of tobacco, which in turn determines the quality of its cigarette products, so high-precision and rapid identification of different brands of cigarettes is of great significance for combating the market of counterfeit and shoddy cigarettes and safeguarding people's life and health. Traditional cigarette detection methods are time-consuming and subjective, and the analysis results are not objective and precise enough, whereas this study proposes a combination of cavity-constrained laser-induced breakdown spectroscopy (LIBS) and gray wolf optimization algorithm optimized bidirectional long short-term memory (GWO-BiLSTM) networks for classifying and identifying cigarette samples of 10 different brands. The signal-to-noise ratio and enhancement factor of the spectral intensity signal, LIBS plasma temperature and density are compared for different sizes of cavity constraints, and an optimal spectral enhancement size of 5 mm in both cavity height and diameter is selected. Comparing four different spectral downscaling methods, namely, principal component analysis (PCA), robust principal component analysis (RPCA), linear discriminant analysis (LDA), and t-distribution-stochastic neighborhood embedding (t-SNE), the LDA downscaling model is selected to achieve effective downscaling of the LIBS spectral data. By comparing the classification performance of the three models, the long short-term memory (LSTM) network, bidirectional long short-term memory (BiLSTM) network, and GWO-BiLSTM network, the GWO-BiLSTM model can achieve a classification accuracy of up to 98.31% in the test set. The results show that the classification method for different brands of cigarettes proposed in this study can effectively solve the technical pain points of traditional tobacco detection methods and provide a technical means to prevent the circulation of counterfeit cigarettes.
1 Introduction
Tobacco is a kind of natural plant with complex chemical composition,1 and different brands of cigarettes have different quality tobacco content ratios, so high-precision rapid identification of different brands of cigarettes is of great significance for combating the market of counterfeit and shoddy cigarettes and protecting the rights and interests of consumers.2 Traditional cigarette identification mainly relies on artificial sensory evaluation methods, i.e., determination by tobacco experts using their sense of sight, smell, touch, taste, etc. However, this method is time-consuming and subjective, and the analysis results are not objective and precise enough.3 Laser-induced breakdown spectroscopy (LIBS) is an advanced spectroscopic technique for material analysis, which utilizes short pulses of laser light to irradiate on the surface of the sample for localized transient heating with high energy density and sustained collision ionization to produce an avalanche effect, which results in an exponential increase in the density of free electrons and ultimately the formation of high temperature, high pressure, and high conductivity plasma. De-excitation radiation occurs during the cooling process of the plasma, generating characteristic spectra, and researchers analyze the wavelengths and spectral intensities of the corresponding emission spectra to obtain information on the chemical composition and elemental content of the samples.4 Compared with traditional chemical analysis methods, LIBS technology has the advantages of no contact, no sample preparation, on-line detection, and low detection cost. Moreover, LIBS technology has been widely used in the fields of materials science,5 environmental testing,6 medicine,7 mineral exploration,8 archaeological identification,9 metal processing,10etc. At present, the rapid classification of material samples and product quality evaluation using LIBS technology has become a hotspot of application in the field of material detection and spectral analysis.In recent years, there have been some scholars who have conducted relevant studies on tobacco by using the LIBS technology. Silvestre et al.11 used LIBS to directly measure the elemental concentrations of Ba, Ca, K and Mn in tobacco and compared them with those determined by inductively coupled plasma emission spectrometry (ICP-OES) with a 95% confidence level. Ahmed et al.12 utilized LIBS to quantify the presence of trace elements in different brands of Pakistani tobacco by comparing the results with those measured by laser ablation time-of-flight mass spectrometry (LA-TOFMS) measurements, and the error in the determination of trace element concentration was within 2%. Gondal et al.13 used pulsed UV laser induced breakdown spectroscopy to determine the concentration of elemental fluorine in cigarettes and the limit of detection for elemental fluorine was 14 ppm using a LIBS spectrometer. All these studies show that the LIBS technique has a strong prospect for application in the quantitative analysis of internal elements in tobacco but to the best of our knowledge no research group has yet brought the technology to the forefront of quantitative analysis of internal elements in cigarettes. To our knowledge, no research group has yet combined the LIBS technique with tobacco for taxonomic identification.
There are also several research groups that have utilized LIBS techniques to classify and identify substances with the assistance of machine learning and have demonstrated strong substance identification capabilities. Stefas et al.14 utilized LIBS combined with different machine learning algorithms to classify 10 different honey samples, and the results showed that with the assistance of machine learning algorithms, the honey samples were all classified with greater than 95% accuracy. Zhang et al.15 used the LIBS technique combined with linear discriminant analysis (LDA) and a support vector machine (SVM) to classify and recognize ginkgo biloba leaves from eight different locations in Xi'an City, respectively, and the accuracy of origin recognition of ginkgo biloba leaves reached 97.50% and 96.25% for LDA and SVM, respectively, and the results show that the LIBS technique can track ginkgo biloba with the help of multivariate statistical methods for the geographic origin. Tang et al.16 used the unsupervised learning algorithm of laser-induced breakdown combined with a self-organizing map (SOM) and K-means to differentiate industrial polymers in open air, and the K-means clustering algorithm could achieve a classification accuracy of 99.2% for 20 polymers, which verified the feasibility of clustering industrial polymers using LIBS. Moros et al.17 used LIBS combined with a decision tree algorithm to classify 10 different refractory residues, and the experimental results showed that the classification accuracy was as high as 75%. Zhao et al.18 utilized LIBS combined with a convolutional neural network (CNN) to classify brands of iron ore, and the classification accuracy of 5-fold cross-validation reached 99.88%. These above studies show that the combination of LIBS technology and machine learning algorithms has a broad application prospect for classifying and recognizing product substances such as food, plants, polymers and ores.
Currently, there is still a lack of relevant research on the rapid detection of original tobacco and the real-time rapid classification of different brands of cigarettes; therefore, in order to address these issues, this paper constructs a cavity constraint-based LIBS system (CC-LIBS) and an intelligent qualitative analysis model based on the gray wolf algorithm optimization of bidirectional long short-term memory (GWO-BiLSTM) networks from the following aspects to provide a fast and reliable method for cigarette brand classification as well as tobacco authentication, providing a fast and reliable method to provide an efficient and accurate way for the current tobacco anti-counterfeiting detection technology.
• The enhancement factor, signal-to-noise ratio (SNR), plasma temperature, and plasma density of LIBS data for different aluminum cavity sizes were comprehensively compared to obtain the cigarette spectral data for the optimal cavity enhancement size.
• Efficient extraction of spectral features using linear discriminant analysis for efficient optimization of spectral data.
• An intelligent qualitative analysis model based on the gray wolf algorithm for optimizing bidirectional long- and short-term memory networks was designed independently to improve the performance of the qualitative analysis model.
2 Experimental
In this section the preparation of experimental samples for this work and the LIBS system construction are described in detail.2.1 LIBS setup
Fig. 1 illustrates the experimental setup of the LIBS system in this work. An Nd:YAG laser (CFR 200 pulsed, Quantel, France) was used with an operating wavelength of 1064 nm, a pulse repetition frequency of 10 Hz, a pulse duration of 10 ns, a laser pulse delay of 4 μs, and a pulse energy of up to 200 mJ. The laser was focused using a quartz lens with a focal length of 36 mm and a thickness of 1 inch to generate plasma on the sample surface. The plasma emission spectra were collected from the sample surface using an optical acquisition spectroscopy kit, and the spectra were transmitted to a 7-channel spectrometer (Avantes, Holland, spectral range: 190–950 nm and resolution: 0.1 nm) via an optical fiber to collect the spectra. The spectrometer was connected to a computer for storing and analyzing the spectral data. The sample was placed on a freely movable sample stage with XYZ axes, and an aluminum cavity was placed above the excited region of the sample for spectral enhancement, with a moving accuracy of less than 1 μm and a maximum travel of 5 cm, and a CCD camera was located directly above the sample, so that the sample image could be referred to when the sample was moved during the experiment.2.2 Sample preparation
A total of 10 samples of cigarettes of different brands were used in this experiment, and there were some differences in elemental species and elemental contents between cigarettes of different origins, as shown in Fig. 2, and the 10 different brands of cigarettes were from different regions. The specific information about the cigarettes is shown in Table 1, and all 10 samples came from the Tobacco Monopoly Bureau of Taiyuan City, Shanxi Province (China National Tobacco Corporation, Shanxi Province). Each sample was pulverized using a pulverizer for 30 s, and then the cigarette samples were further ground using a natural agate mortar and pestle, and the samples were stirred well with a stirring bar. Then about 0.8 g of the samples were weighed using an electronic balance, and the cigarette samples were pressed using a tablet press at a pressure of 20 MPa for 120 s. The cigarette samples were pressed into circular tablets with a diameter of 32 mm and a flat surface for LIBS analysis.| Label | Brand of cigarette | Place of origin |
|---|---|---|
| JY001 | Fu rong wang | Changde City, Hunan Province |
| JY002 | Hao mao | Baoji City, Shaanxi Province |
| JY003 | Hong ta shan | Yuxi City, Yunnan Province |
| JY004 | Huang jin ye | Zhengzhou City, Henan Province |
| JY005 | Kuan zhai | Chengdu City, Sichuan Province |
| JY006 | Tai shan | Jinan City, Shandong Province |
| JY007 | Tian zi | Chongqing City |
| JY008 | Xiao Xiong mao | Kunming City, Yunnan Province |
| JY009 | Ying chun | Changchun City, Jilin Province |
| JY010 | Zhong hua | Hengyang City, Hunan Province |
We set the experimental parameters: the laser energy was set to 200 mJ, the laser spot size was 75 μm, the repetition frequency was 2 Hz, and the acquisition delay time was 0.03 μs. In order to improve the representativeness of the cigarette samples, cigarette samples of each brand were produced from 9 batches of produced cigarettes, 10 pressed samples were produced from different batches of the same brand, and each pressed sample was sampled 9 times, respectively. In order to minimize the sample differences and to improve the reproducibility of the spectral data of the cigarette samples, 2 sets of laser pulses were first cleaned on the sample surface to remove the oxidized substances on the sample surface to ensure the uniformity of the surface of different cigarette press samples. In this study, the number of laser pulses was set to be cleaned 2 times and ablated 10 times, and the average value of each ablated point going for 10 times was taken as the spectral intensity value of the point, and a 3 × 3 square excitation region was formed using each sample press to obtain a total of 8100 spectral data.
3 Data analysis algorithms
3.1 Linear discriminant analysis (LDA)
LDA is a classical supervised learning algorithm that projects high-dimensional data into a low-dimensional space while maximizing the interclass distance and minimizing the intraclass distance, making the separation between different classes more obvious.19 Specifically, LDA determines the projection direction by calculating the intraclass scatter matrix and interclass scatter matrix and then projects the data in this direction.20 LDA achieves data dimensionality reduction while retaining the most important information, which improves the differentiation between different classes, and is more conducive to subsequent classification tasks.3.2 Bidirectional long short term memory (BiLSTM) network
LSTM is a special kind of Recurrent Neural Network (RNN), which aims to avoid the problem of long-term dependence and successfully solves the problems of long-distance information loss, gradient explosion and gradient disappearance in long sequences of the original recurrent neural network, which can retain information of high importance and delete redundant memory and has good modeling ability.21 The structure of the LSTM network is shown in Fig. 3, in which “×” denotes the inner product operation, “+” denotes the add operation, “σ” denotes the sigmoid activation function, and “tanh” denotes the hyperbolic tangent activation function.The LSTM structure includes input gates It, forgetting gates Ft and output gates Ot, as well as temporary memory states ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) t, current memory states Ct and final hidden layer states Ht. The computational eqn (1)–(6) describe the computational process in LSTM, which includes the computation of each gate and the updating formula of the state.
t, current memory states Ct and final hidden layer states Ht. The computational eqn (1)–(6) describe the computational process in LSTM, which includes the computation of each gate and the updating formula of the state.
However, the classical LSTM neural network can only learn the dependencies from the front to the back data.22 In order to make the traditional LSTM neural network better capture the long-term dependencies in the sequences, the backward LSTM neural network is introduced. BiLSTM is composed of forward LSTM and reverse LSTM, and the input information is in the two directions of frontward and reverse, respectively. Calculations are performed on the information acquired in both the front and back directions, in order to be able to process the bi-directional correlation features of the sequence data in a more complete way and to provide a more accurate representation of the features.23Fig. 4 shows the structure of BiLSTM.
| It = σ(XtWxi + Ht−1Whi + bi) | (1) |
| Ft = σ(XtWxf + Ht−1Whf + bf) | (2) |
| Ot = σ(XtWxo + Ht−1Who + bo) | (3) |
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) t = tanh(XtWxc + Ht−1Whc + bc) t = tanh(XtWxc + Ht−1Whc + bc) | (4) |
Ct = Ft × Ct−1 + It × ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) t t | (5) |
| Ht = Ot × tanh(Ct) | (6) |
In the BiLSTM neural network, the last outputs of forward and reverse are spliced as inputs to the next layer.24 The spliced output includes the combined forward and reverse information, which can provide more accurate prediction conditions for the neural network, and eqn (7) describes the splicing process of the output:
 | (7) |
3.3 Grey wolf optimization (GWO)
GWO is a group intelligence optimization algorithm, which is based on the principle of mimicking the predatory behavior of gray wolf packs, which is essentially a kind of statistical optimization. The algorithm is simple to operate, has fewer setup parameters, is highly robust, and has faster convergence speed and higher solution accuracy.25 Gray wolf packs are generally divided into 4 classes, i.e. α, β, δ, and ω (power size decreases in order). Gray wolf pack predation behavior is mainly divided into three steps: encircling prey, pursuing prey and attacking prey.26 The distance formula and position update formula between gray wolf and prey are as follows: | (8) |
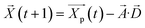 | (9) |
![[A with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0041_20d1.gif) and
and ![[C with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0043_20d1.gif) are coefficient vectors,
are coefficient vectors,  is the position vector of the prey, and
is the position vector of the prey, and ![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) represents the position vector of the gray wolf. The coefficient vector is computed as follows:
represents the position vector of the gray wolf. The coefficient vector is computed as follows: | (10) |
 | (11) |
In the above equation, ![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) is the convergence factor, which decreases linearly from 2 to 0 during the iteration process and
is the convergence factor, which decreases linearly from 2 to 0 during the iteration process and  and
and 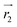 are random vectors in [0,1]. When the gray wolf identifies the prey location, it guides the ω – rank wolf pack to surround the prey under the leadership of α, β and δ. The mathematical model of the ω – rank wolf pack to surround the prey location is as follows:
are random vectors in [0,1]. When the gray wolf identifies the prey location, it guides the ω – rank wolf pack to surround the prey under the leadership of α, β and δ. The mathematical model of the ω – rank wolf pack to surround the prey location is as follows:
 | (12) |
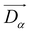 ,
,  , and
, and  denote the distance between α, β and δ and the wolf pack of rank ω, respectively.
denote the distance between α, β and δ and the wolf pack of rank ω, respectively. 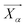 ,
,  and
and 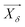 denote the current positions of α, β and δ, respectively.
denote the current positions of α, β and δ, respectively.  ,
, 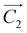 and
and  are random vectors and
are random vectors and ![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) is the position of the current rank wolf pack.
is the position of the current rank wolf pack. | (13) |
 | (14) |
Eqn (13) defines the step length and direction of the ω – rank wolves toward α, β and δ, respectively, and eqn (14) defines the final position of the ω – rank wolves. During the iterative optimization process, the value of ![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) decreases linearly from 2 to 0, corresponding to the value of
decreases linearly from 2 to 0, corresponding to the value of ![[A with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0041_20d1.gif) varying in the interval [−a,a], and
varying in the interval [−a,a], and ![[C with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0043_20d1.gif) is a random vector between [0,2], which denotes the random weight of the impact of the location of the gray wolf on the prey.
is a random vector between [0,2], which denotes the random weight of the impact of the location of the gray wolf on the prey.
The GWO algorithm is represented in Fig. 5 searching for prey in a two-dimensional space while updating the positions of α, β and δ. The final position of α, β and δ is a randomized circle defined by the positions of α, β and δ in the search space. We can observe that the final position is a random position within a circle defined by the positions of α, β and δ in the search space. In other words the α, β and δ ranked packs estimate the position of the prey while the ω ranked packs update their position randomly around the prey and finally attack the prey successfully.
4 Results and discussion
4.1 LIBS spectroscopy under cavity confinement
In order to further improve the LIBS spectral intensity of cigarette samples, cylindrical aluminum cavity constraints are used to enhance the spectral intensity in this paper. In order to select the optimal size combination for spectral enhancement, the JY010 sample is selected for spectral enhancement experiments, and 30 different combinations of aluminum cavities with heights of 1 mm, 2 mm, 3 mm, 4 mm, 5 mm, and 6 mm and diameters of 2 mm, 3 mm, 4 mm, 5 mm, and 6 mm are used for the experiments, and 100 experiments are conducted for each size of aluminum cavities to obtain a total of 3000 experimental data. The final spectral intensity value of each size is taken as the arithmetic mean of 100 experiments. In this paper, the enhancement factor and signal-to-noise ratio are used to measure the spectral signal enhancement ability of different sizes of aluminum cavities. In this study, the enhancement factor refers to the ratio of the spectral intensity under the constraint of a certain aluminum cavity to the spectral intensity without constraint, and the signal-to-noise ratio is used to describe the ratio coefficient between the intensity of the LIBS spectral signal and the intensity of the background noise,27 and we choose the O I 777.227 nm emission spectral line, which is free of self-absorption spectral lines and is not affected by the surrounding spectral lines, to calculate the enhancement factor and the signal-to-noise ratio, and the results are shown in Fig. 6 and 7. | ||
| Fig. 6 Plot of variation in the constraint enhancement factor for aluminum cavities of different sizes. | ||
In Fig. 6, we can see that with the increase in the height of the cylindrical aluminum cavity, the enhancement factor shows a tendency to increase and then decrease and reaches a maximum value at a height of 5 mm. This is because as the height of the cavity increases, the height of the plasma plume limited by the cavity also increases, which is more effective in reflecting the shock wave and compressing the plasma plume, but if the height of the cavity is too large, the cavity will block part of the light radiated by the plasma, and therefore the spectral intensity collected at a height of 6 mm is smaller than that at 5 mm. For aluminum cavities with different diameters of the same height, the enhancement factors are all maximal at a diameter of 5 mm and decrease at 6 mm. This is due to the fact that in a cavity with a diameter of 6 mm, the shock wave encounters the cavity wall reflecting back to the center for a longer period of time, and the intensity of the shock wave is weakened, which makes the spectral enhancement effect decrease, and finally we find that the enhancement factor is maximal at a height and a diameter of 5 mm, with a maximum value of 4.02.
In Fig. 7, we can see that with the increase in the cavity height, the signal-to-noise ratio also shows a trend of increasing and then decreasing, and at the same height, the signal-to-noise ratio of the aluminum cavity with a diameter of 5 mm is the maximum, and this trend is the same as that of the enhancement factor. The outgoing signal-to-noise ratio is 9.63 without cavity constraints, and reaches a maximum of 32.57 with an aluminum cavity of 5 mm in height and diameter, which is 3.38 times higher than the signal-to-noise ratio without cavity constraints.
 | ||
| Fig. 7 Plot of variation in the constrained signal-to-noise ratio for different sizes of aluminum cavities. | ||
The effect of cavity confinement of different sizes is further illustrated by calculating the plasma temperature and density. The plasma temperature is an important parameter describing the nature of the plasma, and a higher temperature indicates a higher excitation capacity.28 According to local thermodynamic equilibrium (LTE) conditions,29 the plasma temperature is calculated using the Boltzmann slope method. And eqn (15) is derived from the Saha–Boltzmann equation.
 | (15) |
 as the vertical coordinate and
as the vertical coordinate and  as the horizontal coordinate and fitting a straight line with a slope. In this paper, the plasma temperature was calculated using the spectral parameters of four Ca plasmas (612.21 nm, 616.09 nm, 643.92 nm, and 646.22 nm), and the plasma density was estimated by using the full width at half-maximum (FWHM) of the Ca 612.21 nm line, and the data were obtained from the NIST library. The plasma temperature and density variations for cavity confinement at different sizes are shown in Fig. 8 and 9, respectively. The McWhirter criterion is satisfied for cavity confinement at different sizes, which indicates that all 30 cavity confinement sizes satisfy the necessary conditions for local thermodynamic equilibrium (LTE).
as the horizontal coordinate and fitting a straight line with a slope. In this paper, the plasma temperature was calculated using the spectral parameters of four Ca plasmas (612.21 nm, 616.09 nm, 643.92 nm, and 646.22 nm), and the plasma density was estimated by using the full width at half-maximum (FWHM) of the Ca 612.21 nm line, and the data were obtained from the NIST library. The plasma temperature and density variations for cavity confinement at different sizes are shown in Fig. 8 and 9, respectively. The McWhirter criterion is satisfied for cavity confinement at different sizes, which indicates that all 30 cavity confinement sizes satisfy the necessary conditions for local thermodynamic equilibrium (LTE).
The results show that the plasma temperature and density without cavity confinement are 5928 K and 2.75 × 1016/cm3, respectively, but for the plasma temperature for different sizes of cavity confinement, there is a significant difference, and its trend is roughly the same as that of the enhancement factor and the signal-to-noise ratio, and the plasma temperature is the highest when the height is 5 mm and the diameter is 5 mm, reaching 8891 K. From Fig. 9, we can observe that the variation of plasma density for different sizes is small, and it is difficult to find an obvious rule of change, but also the plasma density at a height of 5 mm and a diameter of 5 mm achieves a maximum value of 3.8 × 1016/cm3. The reason for these changes is that the plasma produced by laser induction is expanding outward in a hemispherical shape with the laser centerline. At the same time, the initial explosion generates an outward shock wave, the propagation speed of which is much larger than the expansion speed of the plasma, and when the shock wave encounters the inner wall of the cavity confinement, reflection occurs, which leads to further excitation of the plasma, and the excitation effect of the plasma and the number of particles are further increased, so that the temperature and density of the plasma are also increased.
In order to further improve the credibility of the cavity-enhanced LIBS spectroscopic signals in this article, this study is analyzed in comparison with the work related to cavity confinement enhancement by other research groups. Guo et al.30 used a hemispherical cavity to enhance the spectral signals of three low-concentration elements of vanadium, chromium and manganese in steel samples. The results showed that the hemispherical cavity with a diameter of 5 mm had the best enhancement effect, and the enhancement factors of the spectral emission intensities of three low-concentration elements of vanadium, chromium and manganese were 4.2, 3.1 and 2.87, respectively, which were the same as the optimal cavity diameter in this study. Moreover, the maximum enhancement factor of spectral emission intensity of the elements in this study is 4.02. Su et al.31 used brass samples to investigate the optimal enhancement size of the cylindrical cavity, and the results show that the plasma emission intensity and stability are best when the cavity diameter and height are 3 mm and 1 mm, respectively, and the plasma emission intensity shows a tendency to increase and then decrease with an increase in the cavity height, which is the same as the conclusions obtained in the present study. However, since the plasma volume and expansion depend on the LIBS experimental parameters, the optimal cylindrical spectral enhancement cavity size may vary for a specific cavity limited by the LIBS application.
 | (16) |
In order to validate the effect of cavity constraints on the reproducibility of the LIBS signals, in this study, the comparative analyses of the spectral data of the 10 brands of cigarettes were performed on Mg 280.270 nm, Ca 422.673 nm, H 656.271 nm, and O 777.194 nm characteristic spectral lines before and after the addition of cavity constraints. The relative standard deviation (RSD) of the characteristic spectral lines was analyzed in this study, which was calculated as eqn (16), in which the spectral intensity value of each LIBS dataset is the average of the spectral intensity values and n is the total amount of spectral data. Specifically, the RSD corresponds to the degree of variability of the spectral data and helps assess the reliability and consistency of the measurements. The RSD of the four characteristic spectral line elements was calculated based on 810 spectral datasets for each brand of cigarette, as shown in Fig. 10. It can be seen that the RSD values of the four characteristic spectral lines decreased substantially in all brand cigarette samples; for example, the RSD value of Ca 422.673 nm for the JY003 labeled sample decreased from 16.73% to 8.09%, the RSD value of H 656.271 nm for the JY004 labeled sample decreased from 13.17% to 3.15%, the RSD value of O 777.194 nm for the JY007 labeled sample decreased from 13.17% to 3.15%, and the RSD value of O 777.194 nm for the JY007 labeled sample decreased from 13.17% to 3.15%. The RSD value of O 777.194 nm for the JY007 labeled sample was reduced from 9.93% to 2.89%, which indicates that the spectral data of the cigarette samples became more stable and reproducible after the addition of cavity constraints, implying that the detection results are more representative.
 | ||
| Fig. 10 Comparison of RSD of each characteristic spectral line of 10 brands of cigarettes before and after adding cavity constraints. | ||
4.2 Analysis of LIBS spectral data using different downscaling algorithms
By comparing the enhancement factor, signal-to-noise ratio, plasma temperature and density of LIBS spectra under the constraint of cylindrical aluminum cavities of different sizes, cylindrical aluminum cavities with a height and diameter of 5 mm were selected for experimental data collection, in which 70% of the spectral data was the training set and 30% of the spectral data was the test set. In order to prove the stability of the qualitative analysis model, in this study, the spectral data of both the training set and the test set were randomly extracted, and the results of the 5-fold cross-validation were used as the final results of the qualitative model. 810 spectral datasets were collected from each brand of cigarette samples for the optimal cavity enhancement size, of which 70% were randomly extracted for the training set and 30 percent were extracted for the test set, i.e., 567 spectral datasets for the training set and 243 spectral datasets for the test set, totaling 5670 spectral datasets for the training set and 2430 spectral datasets for the test set for 10 kinds of cigarette samples, and the data of the training and test sets for the different kinds of cigarette samples of different brands are independent of each other. The spectra of 10 different brands of cigarettes were described by the same coordinate system, as shown in Fig. 11. The 10 cigarette spectra have a high degree of similarity, but there are significant differences in spectral intensity at different local spectral wavelengths, with the most pronounced spectral differences in the blue dashed portion of the figure. Fortunately, it is these differences in spectral characteristics that allow us to try to distinguish and identify them.32In order to avoid the existence of obvious order-of-magnitude differences between the input variables, these signals were subjected to a maximum–minimum normalization process, which is calculated as shown in eqn (17), where max{xj} is the maximum value of the sample data and min{xj}is the minimum value of the sample data. Max–min normalization is a linear transformation of the original data so that the resultant values are mapped between [0,1], eliminating the effects of the variables and the range of variability, while preserving the relationship between the data to the greatest extent possible.
 | (17) |
Each laser ablation point has a total of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 248 dimensions in the wavelength range of 180–950 nm, which leads to the problem of dimensionality catastrophe in LIBS spectral data, so it is necessary to choose a suitable dimensionality reduction algorithm to reduce the complexity of the data computation and to improve the computational speed. In this paper, four classical dimensionality reduction algorithms are selected, namely PCA, RPCA, LDA, and t-SNE. Fig. 12 and 13 show the visualized 2D and 3D plots of the four dimensionality reduction algorithms, respectively, in which we can find that there is a serious overlap in the LIBS spectral data of 10 different brands of cigarettes processed by the three dimensionality reduction algorithms of PCA, RPCA, and t-SNE. For the LDA dimensionality reduction algorithm, in its visualized 2D map, two brands of cigarette samples, JY001 and JY003, can be effectively distinguished, and in the 3D map, the four cigarette samples, JY001, JY003, JY004 and JY010, are further effectively distinguished, and the other six cigarette samples are still seriously overlapped. However, by comparing with the other three dimensionality reduction algorithms, the LDA dimensionality reduction algorithm improves the differentiation between different categories of cigarette samples on the basis of realizing data dimensionality reduction, which is more conducive to the subsequent classification task. Therefore, in this paper, the 3-dimensional feature spectral data processed by the LDA dimensionality reduction algorithm are used as input for the qualitative analysis algorithm later.
248 dimensions in the wavelength range of 180–950 nm, which leads to the problem of dimensionality catastrophe in LIBS spectral data, so it is necessary to choose a suitable dimensionality reduction algorithm to reduce the complexity of the data computation and to improve the computational speed. In this paper, four classical dimensionality reduction algorithms are selected, namely PCA, RPCA, LDA, and t-SNE. Fig. 12 and 13 show the visualized 2D and 3D plots of the four dimensionality reduction algorithms, respectively, in which we can find that there is a serious overlap in the LIBS spectral data of 10 different brands of cigarettes processed by the three dimensionality reduction algorithms of PCA, RPCA, and t-SNE. For the LDA dimensionality reduction algorithm, in its visualized 2D map, two brands of cigarette samples, JY001 and JY003, can be effectively distinguished, and in the 3D map, the four cigarette samples, JY001, JY003, JY004 and JY010, are further effectively distinguished, and the other six cigarette samples are still seriously overlapped. However, by comparing with the other three dimensionality reduction algorithms, the LDA dimensionality reduction algorithm improves the differentiation between different categories of cigarette samples on the basis of realizing data dimensionality reduction, which is more conducive to the subsequent classification task. Therefore, in this paper, the 3-dimensional feature spectral data processed by the LDA dimensionality reduction algorithm are used as input for the qualitative analysis algorithm later.
 | ||
| Fig. 12 Visualization of four dimensionality reduction algorithms, PCA, LDA, t-SNE, and RPCA, in 2D graphs. | ||
4.3 Gray wolf optimization algorithm for optimizing bidirectional long short-term memory (GWO-BiLSTM) networks
After the original LIBS spectral data were downscaled by the LDA algorithm, the gray wolf optimization algorithm was used to perform the parameter global optimization search for the bidirectional long short-term temporal memory network, in which the parameters to be optimized were the number of nodes in the hidden layer, the learning rate, and the regularization parameter, and the constraints are shown in Table 2. First, 30 wolves were set up for the optimization search, and the maximum number of iterations was set to be 10, and the position of each wolf pack represents the solution of each possible BiLSTM model. The fitness value is calculated using the position of the wolf packs in the initial stage, and the distance between the gray wolves of classes α, β and δ and the wolf packs of class ω is determined according to the fitness value.33 In the process of parameter optimization, boundary processing is required for positions that are out of the constraint range to meet the optimization range of the parameters. In the process of model calculation, the positions of gray wolves of three grades α, β and δ are repeatedly updated. The fitness value is calculated until the number of iterations reaches 10 optimization stops, and the final optimal number of hidden layer nodes obtained is 12, the learning rate is 0.0193, and the regularization parameter is 0.0029. The optimal parameters obtained are inputted to the BiLSTM model to be trained for 1000 times, and finally after taking the 5-fold cross-validation the classification accuracy is 98.31%, and its confusion matrix is shown in Fig. 14, which indicates that the optimized BiLSTM model based on the gray wolf algorithm has significant classification and recognition ability for 10 different brands of cigarettes.| The grey wolf algorithm optimizes the parameters | Range of constraints |
|---|---|
| Number of hidden layer nodes | [10,30] |
| Learning rate | [0.001,0.1] |
| Regularization parameter | [0.0001,0.1] |
In order to further evaluate the classification performance of the GWO-BiLSTM model for 10 different brands of cigarettes, we analyzed the accuracy,34 recall,35 precision,36 F1 score,37 and specificity38 of the model for recognizing 10 different brands of cigarettes, where the accuracy is calculated as eqn (18), the recall using eqn (19), the precision using eqn (20), the F1 score using eqn (21), and specificity is calculated using eqn (22).
 | (18) |
 | (19) |
 | (20) |
 | (21) |
 | (22) |
In the above equation, TP is the number of samples where the real label is a positive case and the prediction result is also a positive case, FP is the number of samples where the real label is a negative case and the prediction result is a positive case, TN is the number of samples where the real label is a negative case and the prediction result is also a negative case, and FN is the number of samples where the real label is a positive case and the prediction result is a negative case. Precision is the proportion of correctly predicted positive case data to the data predicted as positive cases; the F1 score is the reconciled average of precision and recall, and the higher its value, the better the balance of the model in terms of checking accuracy and completeness; and specificity measures the model's ability to recognize negative cases.
The classification performance of the GWO-BiLSTM model for different cigarette brands is shown in Table 3, from which it can be found that the GWO-BiLSTM model achieves a 100% recognition rate for JY001, JY003, JY004, JY007, and JY010, and all of them have perfect recall, precision, F1-score, and specificity. The other five brands of cigarettes also have good recognition ability, with the lowest classification accuracy of 98.477%. The experimental results demonstrate the reliability and stability of the GWO-BiLSTM model, which has good recognition and generalization ability for 10 different brands of cigarettes.
| Accuracy | Recall | Precision | F1-score | Specificity | |
|---|---|---|---|---|---|
| JY001 | 1 | 1 | 1 | 1 | 1 |
| JY002 | 0.99877 | 1 | 0.98780 | 0.99387 | 0.99863 |
| JY003 | 1 | 1 | 1 | 1 | 1 |
| JY004 | 1 | 1 | 1 | 1 | 1 |
| JY005 | 0.99959 | 0.99589 | 1 | 0.99794 | 1 |
| JY006 | 0.99054 | 0.97119 | 0.93651 | 0.95354 | 0.99268 |
| JY007 | 1 | 1 | 1 | 1 | 1 |
| JY008 | 0.99259 | 1 | 0.93103 | 0.96429 | 0.99177 |
| JY009 | 0.98477 | 0.86420 | 0.98131 | 0.91904 | 0.99817 |
| JY010 | 1 | 1 | 1 | 1 | 1 |
4.4 Comparison with other machine learning models
In order to verify the superior performance of the GWO-BiLSTM model, we also selected two models, LSTM and BiLSTM, to compare with the GWO-BiLSTM model, using the same dataset as that used by the GWO-BiLSTM model, selected the optimal results of the 2 comparison models, and compared the corresponding convergence curves as well as the confusion matrices of the 3 models to evaluate the classification performance of the GWO-BiLSTM model for 10 different cigarette brands, as shown in Fig. 15 and 16. The comparison of the classification accuracy of the 3 models is presented in Fig. 17. | ||
| Fig. 16 From left to right, the test set confusion matrices for LSTM, BiLSTM and GWO-BiLSTM are plotted. | ||
The LSTM model constructs a 3-layer network structure, in which 128-dimensional spectral data features are selected as inputs, a hidden layer consisting of 64 neurons is also set up, and the “softmax” function is selected for the output layer to perform the classification task, and the accuracy of the test set under the network structure can reach up to 90.86% through several experimental tests.
The BiLSTM model is better at capturing bi-directional spectral information than the LSTM model, and the information provided by the past features is taken into account while extracting the future features. The network structure of the BiLSTM model is 4-layer, in which 256-dimensional spectral features are selected as the inputs, the first hidden layer contains 128 neurons, the second hidden layer contains 64 neurons, and the output layer is still selected as the “softmax” function for the classification task, and the grid search model is used to find the optimal parameters with an accuracy of 93.66%.
As can be seen from the loss convergence curve comparison graphs of the training set and test set of the three models in Fig. 15, all three models have excellent prediction ability, and in terms of model loss, the loss of the LSTM model is higher than that of the BiLSTM model and the GWO-BiLSTM model, which may be due to the fact that the LSTM model extracts the spectral feature information only in one direction, whereas the BiLSTM model is able to extract feature information in both directions, so it shows higher classification accuracy, but the GWO-BiLSTM model can show the most superior classification effect because it not only captures feature information in both directions, but also intelligently optimizes the key parameters in the BiLSTM model through the GWO algorithm. As shown in Fig. 17, the classification accuracy of the three qualitative models gradually improves, which also represents that the network model based on the underlying structure of the LSTM model is continuously optimized and iterated, and the optimal qualitative analysis model is finally obtained.
Through the selection of the optimal size of the cavity constraint, the selection of the optimal cigarette spectral downscaling algorithm, and the comparison of the classification accuracies of the three model confusion matrices and the test set, we can clearly find that the GWO-BiLSTM model shows excellent performance in recognizing different kinds of cigarettes, and the method can achieve high-precision cigarette brand recognition, providing a good identification of counterfeit and shoddy cigarette products.
5 Conclusions
In this study, a combination of cavity-constrained LIBS and GWO-BiLSTM is utilized to classify and identify 10 different brands of cigarette samples. The signal-to-noise ratio and enhancement factor of spectral intensity signals, LIBS plasma temperature and density were compared for different sizes of cavity confinement, and an optimal spectral enhancement size of 5 mm in both cavity height and diameter was selected. Comparing four different spectral downscaling methods, PCA, RPCA, LDA and t-SNE, the LDA downscaling model is selected to realize effective downscaling of LIBS spectral data. By comparing the classification performance of the three models, LSTM, BiLSTM and GWO-BiLSTM, the classification accuracy of the GWO-BiLSTM model in the test set can reach 98.31%. This study provides new ideas and technical means for the identification method of tobacco samples, which is of great scientific and applied significance to the tobacco authenticity identification industry as well as the protection of cigarette consumers' rights and interests. Through this study, we have demonstrated an efficient, rapid and accurate tobacco identification technique, which provides a technical means to effectively prevent the circulation of counterfeit and substandard cigarettes.Data availability
The data in this study cannot be provided due to legal and ethical confidentiality requirements. The LIBS data of cigarettes involve the core formula of the relevant tobacco manufacturers, so please allow us not to provide it to you.Author contributions
Junjie Chen: data curation, investigation, formal analysis, methodology, visualization, software, writing – original draft. Xiaojian Hao: conceptualization, supervision, validation, funding acquisition. Biming Mo: validation. Shuaijun Li: conceptualization, project administration. Junjie Ma: visualization. Xiaodong Liang: validation. Zheng Wang: conceptualization, validation. Heng Zhang: validation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research work was supported by the National Natural Science Foundation of China (No. 52075504), Shanxi Province Key R&D Program Projects (No. 202302150101016), the State Key Laboratory of Quantum Optics and Optical Quantum Devices (Shanxi University) Open Project (No. KF202301), the Fund for Shanxi Key Subjects Construction (1331KSC), the Open Project Program of Shanxi Key Laboratory of Advanced Semiconductor Optoelectronic Devices and Systems (2023SZKF11), the Postgraduate Scientific Research Innovation Project of Shanxi Province in 2023 (No. 2023KY584), and the fund for the Postgraduate Scientific Research Innovation Project of Shanxi Province in 2023 (No. 2023KY608).References
- L. Zhao, S. Shang, Y. Tian, Y. Gao, Z. Song, L. Peng, Z. Li and B. Wang, Front. Plant Sci., 2023, 14, 1123100, DOI:10.3389/fpls.2023.1123100.
- U. Majewska, M. Piotrowska, I. Sychowska, D. Banaś, A. Kubala-Kukuś, J. Wudarczyk-Moćko, I. Stabrawa and S. Góźdź, J. Anal. Toxicol., 2018, 42, 409–416, DOI:10.1093/jat/bky016.
- H.-M. Park and J.-H. Park, IEEE Access, 2023, 11, 142951–142963, DOI:10.1109/ACCESS.2023.3343780.
- W. Hao, X. Hao, Y. Yang, X. Liu, Y. Liu, P. Sun and R. Sun, J. Anal. At. Spectrom., 2021, 36, 2509–2518, 10.1039/d1ja00078k.
- J. Wang, X. Hao, B. Pan, X. Huang, H. Sun and P. Pei, Opt. Express, 2023, 31, 8098–8109, DOI:10.1364/OE.481822.
- X. Zhang, Y. Ge, E. Wan, Y. Liu and J. Yao, Plasma Sci. Technol., 2022, 24, 084002, DOI:10.1088/2058-6272/ac639b.
- R. Gaudiuso, E. Ewusi-Annan, W. Xia and N. Melikechi, Spectrochim. Acta, Part B, 2020, 171, 105931, DOI:10.1016/j.sab.2020.105931.
- W. Zhao, C. Li, C. Yan, H. Min, Y. An and S. Liu, Anal. Chim. Acta, 2021, 1166, 338574, DOI:10.1016/j.aca.2021.338574.
- J. Qi, T. Zhang, H. Tang and H. Li, Spectrochim. Acta, Part B, 2018, 149, 288–293, DOI:10.1016/j.sab.2018.09.006.
- J. Moros, L. M. Cabalín and J. J. Laserna, Anal. Chim. Acta, 2022, 1191, 339294, DOI:10.1016/j.aca.2021.339294.
- D. M. Silvestre, F. de Oliveira Leme, C. S. Nomura and A. N. do Nascimento, Microchem. J., 2016, 126, 545–550, DOI:10.1016/j.microc.2016.01.015.
- N. Ahmed, Z. A. Umar, R. Ahmed and M. Aslam Baig, Spectrochim. Acta, Part B, 2017, 136, 39–44, DOI:10.1016/j.sab.2017.08.006.
- M. A. Gondal, Y. B. Habibullah, L. E. Oloore and M. A. Iqbal, Appl. Opt., 2015, 54, 5560–5567, DOI:10.1364/AO.54.005560.
- D. Stefas, N. Gyftokostas and S. Couris, Spectrochim. Acta, Part B, 2020, 172, 105969, DOI:10.1016/j.sab.2020.105969.
- D. Zhang, J. Ding, Z. Feng, R. Yang, Y. Yang, S. Yu, B. Xie and J. Zhu, Spectrochim. Acta, Part B, 2021, 180, 106192, DOI:10.1016/j.sab.2021.106192.
- Y. Tang, Y. Guo, Q. Sun, S. Tang, J. Li, L. Guo and J. Duan, Optik, 2018, 165, 179–185, DOI:10.1016/j.ijleo.2018.03.121.
- J. Moros, L. M. Cabalín and J. J. Laserna, Anal. Chim. Acta, 2022, 1191, 339294, DOI:10.1016/j.aca.2021.339294.
- W. Zhao, C. Li, C. Yan, H. Min, Y. An and S. Liu, Anal. Chim. Acta, 2021, 1166, 338574, DOI:10.1016/j.aca.2021.338574.
- J. Yan, S. Li, K. Liu, R. Zhou, W. Zhang, Z. Hao, X. Li, D. Wang, Q. Li and X. Zeng, Anal. Chim. Acta, 2020, 1111, 139–146, DOI:10.1016/j.aca.2020.03.030.
- P. Yang, R. Zhou, W. Zhang, S. Tang, Z. Hao, X. Li, Y. Lu and X. Zeng, Appl. Opt., 2018, 57, 8297–8302, DOI:10.1364/AO.57.008297.
- C. Lin, X. Tuo, L. Wu, G. Zhang and X. Zeng, Batteries, 2024, 10, 71, DOI:10.3390/batteries10030071.
- P. Khalilian, F. Rezaei, N. Darkhal, P. Karimi, A. Safi, V. Palleschi, N. Melikechi and S. H. Tavassoli, Sci. Rep., 2024, 14, 5169, DOI:10.1038/s41598-024-55502-x.
- Z. Li, L. Li, J. Chen and D. Wang, Energy, 2024, 286, 129504, DOI:10.1016/j.energy.2023.129504.
- H. Lin, S. Zhang, Q. Li, Y. Li, J. Li and Y. Yang, Measurement, 2023, 207, 112384, DOI:10.1016/j.measurement.2022.112384.
- S. Mirjalili, S. M. Mirjalili and A. Lewis, Adv. Eng. Software, 2014, 69, 46–61, DOI:10.1016/j.advengsoft.2013.12.007.
- S. Gupta and K. Deep, Eng. Comput., 2019, 36, 1777–1800, DOI:10.1007/s00366-019-00795-0.
- M. Huang, S. Wu, Z. Liu, L. Xue, M. Yao, M. Liu, Z. Ai and J. Li, Appl. Phys. B: Lasers Opt., 2023, 129, 167, DOI:10.1007/s00340-023-08110-y.
- M. Cui, Y. Deguchi, Z. Wang, Y. Fujita, R. Liu, F.-J. Shiou and S. Zhao, Spectrochim. Acta, Part B, 2018, 142, 14–22, DOI:10.1016/j.sab.2018.02.002.
- W. Ke, X. Wang, M. Chen, H. Yuan, A. Yang, J. Chu, D. Liu and M. Rong, J. Anal. At. Spectrom., 2023, 38, 212–220, 10.1039/d2ja00256f.
- L. B. Guo, Z. Q. Hao, M. Shen, W. Xiong, X. N. He, Z. Q. Xie, M. Gao, X. Y. Li, X. Y. Zeng and Y. F. Lu, Opt. Express, 2013, 21, 18188–18195, DOI:10.1364/OE.21.018188.
- X. Su, W. Zhou and H. Qian, Opt. Express, 2014, 22, 28437–28442, DOI:10.1364/OE.22.028437.
- J. Wang, X. Hao, B. Pan, X. Huang, H. Sun and P. Pei, Opt. Lett., 2023, 48, 399–402, DOI:10.1364/OL.478629.
- G. Taş, C. Bal and A. Uysal, Electr. Eng., 2023, 105, 3383–3397, DOI:10.1007/s00202-023-01934-z.
- J. Chen, J. Pisonero, S. Chen, X. Wang, Q. Fan and Y. Duan, Spectrochim. Acta, Part B, 2020, 166, 105801, DOI:10.1016/j.sab.2020.105801.
- C. Wang, J. Wang, J. Wang, H. Du and J. Wang, Laser Phys., 2021, 31, 035601, DOI:10.1088/1555-6611/abdfc8.
- Q. Zeng, G. Chen, W. Li, Z. Li, J. Tong, M. Yuan, B. Wang, H. Ma, Y. Liu, L. Guo and H. Yu, Plasma Sci. Technol., 2022, 24, 084009, DOI:10.1088/2058-6272/ac72e3.
- D. J. Díaz-Romero, S. Van den Eynde, W. Sterkens, A. Eckert, I. Zaplana, T. Goedemé and J. Peeters, Spectrochim. Acta, Part B, 2022, 196, 106519, DOI:10.1016/j.sab.2022.106519.
- N. d. A. Porto, J. V. Roque, C. A. Wartha, W. Cardoso, L. A. Peternelli, M. H. P. Barbosa and R. F. Teófilo, Spectrochim. Acta, Part A, 2019, 218, 69–75, DOI:10.1016/j.saa.2019.03.114.
| This journal is © The Royal Society of Chemistry 2024 |












